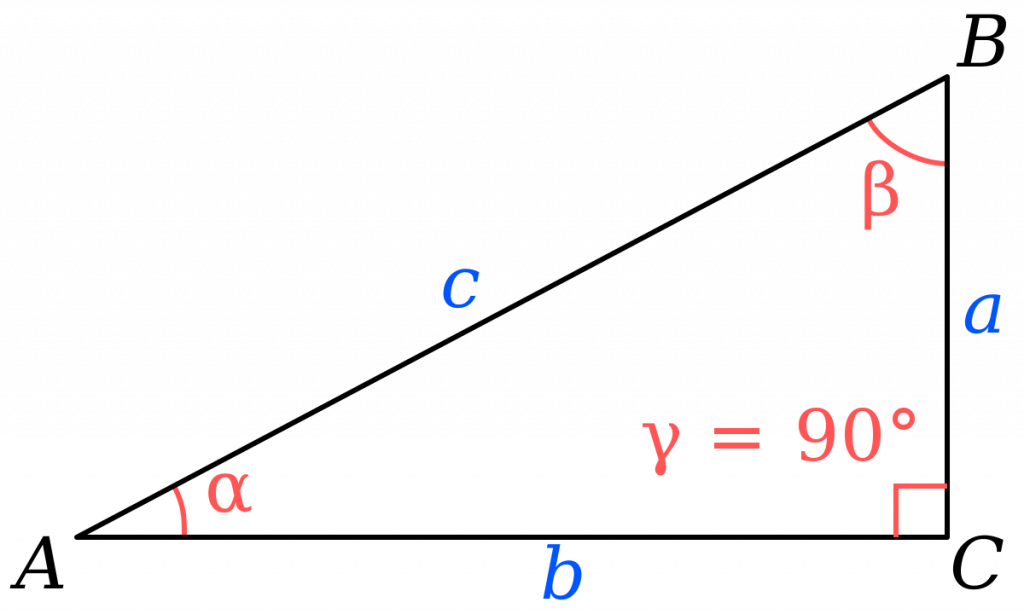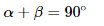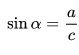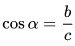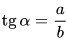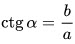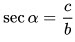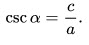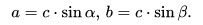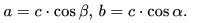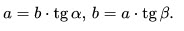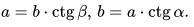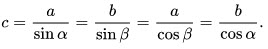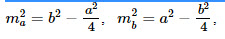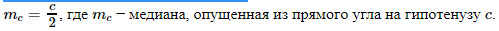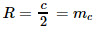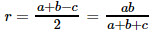Сумма острых углов прямоугольного треугольника
Чему равна сумма острых углов прямоугольного треугольника? Это свойство прямоугольного треугольника вытекает из теоремы о сумме углов треугольника.
Утверждение.
Сумма острых углов прямоугольного треугольника равна 90º.
Дано:
∆ABC,
∠C=90º.
Доказать:
∠A+∠B=90º.
Доказательство:
По теореме о сумме углов треугольника,
∠A+∠B+∠C=180º.
По условию, ∠C=90º.
Отсюда, ∠A+∠B+90º=180º.
Следовательно, ∠A+∠B=180º-90º= 90º.
Что и требовалось доказать.
Добавить комментарий
Некоторые фигуры имеют особые свойства, которые не повторяются в других. К таким особенностям относится теорема о сумме острых углов прямоугольного треугольника, и как следствие несколько свойств, касательно градусной меры и длины катета по отношению к гипотенузе. Использование такого утверждения на практике упрощает поиск решения для разных заданий.
Теорема и доказательство
Фигура, в которой один из углов равен 900, имеет название прямоугольного треугольника. Напротив этого него всего находится гипотенуза. Стороны, которые размещены вокруг 900, являются катетами. Углы вокруг гипотенузы всегда будут острыми, и это аксиома, которая не требует доказательства.
Потому сумма острых углов прямоугольного треугольника всегда равна 900. Это утверждение является следствием теоремы о сумме углов любой треугольной фигуры.
Чтобы доказать чему равна сумма прямоугольного треугольника, стоит рассмотреть фигуру, где <С =900, соответственно <А +<В =900.
Согласно утверждению о сумме всех углов фигуры <А +<В + <С= 1800.
Если <С – прямой, то на два отставные приходится тоже 900. Таким образом, теорема доказана.Доказательство теоремы об острых углах в прямоугольном треугольнике
Свойство фигуры
Из теоремы, где сумма прямоугольного треугольника равна 900, следуют некоторые свойства. Итак, если в прямоугольном треугольнике один из углов равен 450, то фигура равнобедренная. Чтобы доказать, стоит припустить верность этого свойства. Далее согласно теореме
• <С - <А =<В; • <С - 400 = 450.
А если в фигуре один из углов имеет значение 450, то треугольник равнобедренный. Учитывая свойство, что сумма углов прямоугольного треугольника равна 90 градусам, следует, что 900-450=450.
А это означает, что в фигуре <А=<B= 450, соответственно катеты будут равными и весь треугольник – равнобедренным.
Сторона прямоугольника, которая лежит напротив 300, будет равна половине гипотенузы. Это утверждение в обратном направлении – если катет вдвое раз меньше от стороны, что находится напротив 900, то он размещен напротив 300.
Чтобы доказать верность этого свойства, пусть один из углов будет 300,<С=900, а третий – будет 900-300=600. Если дорисовать треугольник в зеркальном отображении, то в результате получится равносторонний треугольник. Все углы в нем будут по 600. Перпендикуляр одновременно будет и медианой, которая делит сторону на пополам. Таким образом, катет, что размещен напротив 300,будет равным половине гипотенузы.
Пример заданий
В треугольнике, где <С=900, <А=460,найти <В. Решение простое, с учетом утверждения, получается, что <В=900 – <А=460.
Пример второй задачи. Фигура, где <С=900, а острый угол втрое меньше другого, то есть <1=3*<2. Найти градусное значение <1, <2.
Естественно <1, <2 будут меньшими за 900, следовательно, один будет большим за другого. Существует два варианта их значений:
• <1 будет меньшим в три раза за 900. Тогда <1=900/3=300, и второй <2=900-300=600. • <1 будет втрое раз меньшим за <2. Пусть <1=х, то <2=3х. Затем 3х+х=900, х=900/4=22,50 <2=22,50*3=67,50.
Итак, задание имеет 2 решения – 300,600 и 22,50, 67,50.
Еще один пример задания. Фигура, где <С=900, а катет 8 см., <1=450. Найти длину второй стороны, прилежащей в <C.
Если <1=450, то <2=450. А это означает, что фигура является равнобедренной, то есть 2 катета будут иметь одинаковую длину в 8 см.
В прямоугольном треугольнике сумма острых углов равна 900, следовательно, если один из них будет 450, то фигура равнобедренная. Также утверждение, где катет лежит напротив 300, то он в 2 раза меньший от гипотенузы будет превосходить из этой теоремы.
Сумма углов треугольника равна (180°).
Доказательство
Рассмотрим произвольный треугольник (KLM) и докажем, что
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
1. Через вершину (L) параллельно стороне (KM) проведём прямую (a).
2. При пересечении параллельных прямых (a) и (KM) секущей (KL), углы, которые обозначаются (1), будут накрест лежащими углами, а углы, обозначенные (2) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е.
∠
(1) (+)
∠
(2) (+)
∠
(3 =)
180°
, или
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна
90°
.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен
45°
.
Следствие 3. В равностороннем треугольнике каждый угол равен
60°
.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказательство
Из равенств
∠
(KML) (+)
∠
(BML=)
180°
и
∠
(K) (+)
∠
(L) (+)
∠
(KML =)
180°
получаем, что
∠
(BML =)
∠
(K) (+)
∠
(L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
У треугольника (KLM) все углы острые.
У треугольника (KMN) угол (K = 90)
°
.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.
У треугольника (KLM) один угол тупой.
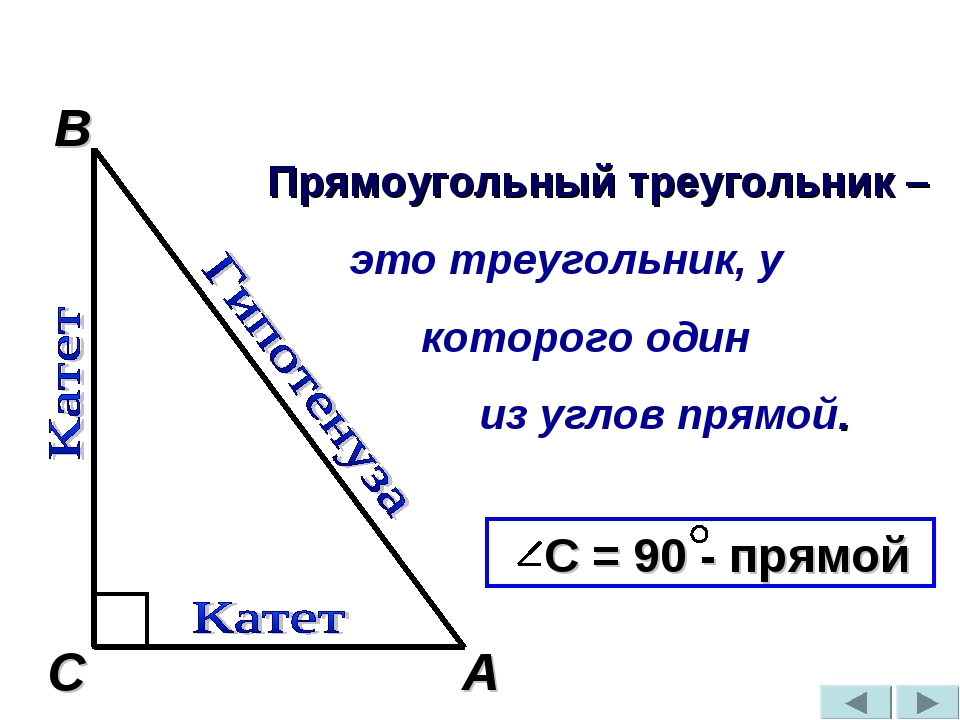
Прямоугольный треугольник – это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
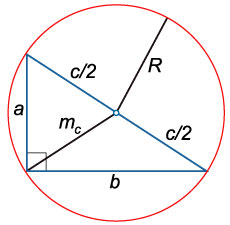
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
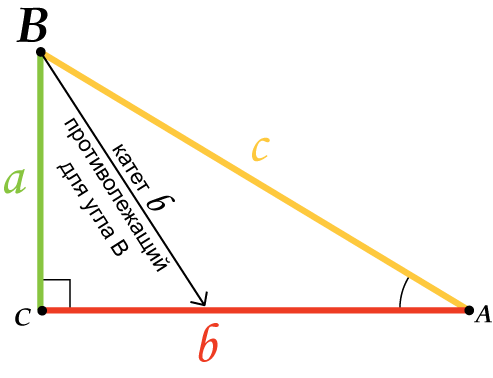
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А$: $ВС$ – противолежащий катет; $АС$ – прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = – 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$
Как найти углы прямоугольного треугольника
Онлайн калькулятор
Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Формула
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Все формулы прямоугольного треугольника – примеры расчетов
Формулы
1. Сумма острых углов прямоугольного треугольника равна 90 0 :
2. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе:
3. Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе:
4. Тангенс острого угла равен отношению противолежащего катета к прилежащему катету:
5. Котангенс острого угла равен отношению прилежащего катета к противолежащему катету:
6. Секанс острого угла равен отношению гипотенузы к прилежащему катету:
7. Косеканс острого угла равен отношению гипотенузы к противолежащему:
8. Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла:
9. Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла:
10. Катет, противолежащий углу, равен произведению второго катета на тангенс угла:
11. Катет, прилежащий углу, равен произведению второго катета на котангенс угла:
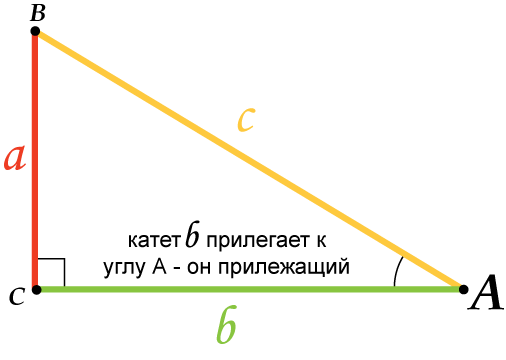
12. Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними):
13. Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
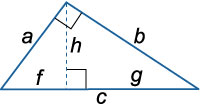
14. Медианы, проведенные к катетам прямоугольного треугольника:
15. Медиана, проведенная к гипотенузе:
16. Радиус окружности, описанной около прямоугольного треугольника:
17. Радиус окружности, вписанной в прямоугольный треугольник:
18. Площадь прямоугольного треугольника равна половине произведения катетов треугольника:
Углы прямоугольного треугольника
Калькулятор расчёта углов прямоугольного треугольника
Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).
Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.
Формула тангенса
- tg α – тангенс угла α
- a – противолежащий катет
- b – прилежащий катет
Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.
Углы треугольника
Сумма углов треугольника всегда равна 180 градусов:
Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.
Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:
Острый угол — угол, значение которого меньше 90°.
У прямоугольного треугольника один угол прямой, а два других угла – острые.
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/formuly-pryamougolnogo-treugolnika.html
http://kalk.top/sz/corners-pr-triangle
[/spoiler]