План урока:
Понятие вектора
Равенство векторов
Сложение векторов
Свойства сложения
Вычитание векторов
Умножение вектора на число
Решение задач с помощью векторов
Понятие вектора
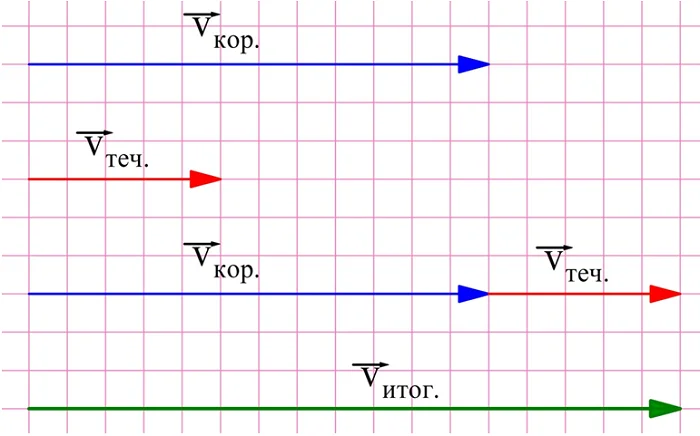
Рассмотрим простейшую задачу. Корабль, двигатель которого развивает скорость 20 км/ч, плывет по течению реки, при этом скорость течения составляет 2 км/ч. Какова скорость корабля относительно берега? Очевидно, в данном случае надо сложить скорость течения и собственную скорость корабля:
20 км/ч + 2 км/ч = 22 км/ч
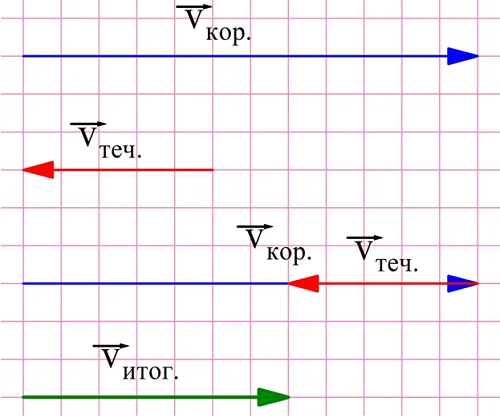
Теперь посмотрим на почти такую же задачу, которая отличается лишь тем, что корабль плывет уже против течения. Для ее решения скорости уже придется вычитать:
20 км/ч – 2 км/ч = 18 км/ч
Получается, что ответ задачи во многом зависит не только от величин скоростей, но и от их направления. Возможны и более сложные случаи, когда корабль двигается на воде перпендикулярно течению или, например, под углом в 60°. Величины, при операции с которыми необходимо учитывать их направление, называют векторными величинами, или просто векторами.
Помимо скорости к ним относят ускорение, силу, импульс, напряженность магнитного и электрического поля и многие другие величины. Те же величины, для которых нельзя указать направление, называют скалярными величинами. Это масса, температура, плотность и т. п. Для выполнения действий с векторами необходимо разработать общие правила их сложения, вычитания, умножения, которые будут справедливы независимо от физической природы векторных величин. И разработать эти правила помогает как раз геометрия.
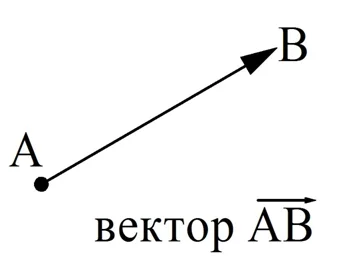
Для начала введем понятие вектора. Любой отрезок имеет два конца, которые обычно не отличают друг от друга. Однако если одну из этих точек считать началом отрезка, а другую – собственно концом, то у отрезка появится направление. В таком случае его можно считать вектором.
Часто вектора называют направленными отрезками. Обозначают их с помощью стрелок.
На этом рисунке показан вектор, начало которого находится в точке А, а конец – в точке В. При записи в формулах сначала пишут букву, означающую начало вектора, потом обозначение его конца, а над этими двумя буквами ставят стрелочку:
С практической точки зрения приходится вводить в рассмотрение особый нулевой вектор. У него начало и конец совпадают, то есть он представляет собой всего лишь одну точку:
Нулевой вектор необходим, так как нам необходимо научиться выполнять действия над векторами. Мы знаем, что в обычной алгебре используется число ноль. В векторной же алгебре аналогом нуля является как раз нулевой вектор.
Каждый вектор имеет свою длину, которая равна расстоянию между его началом и концом. То есть, если его начало находится в точке А, а конец в точке В, то длина вектора будет совпадать с длиной отрезка АВ. Обозначают длину с помощью вертикальных скобок:
Естественно, что длина нулевого вектора равна нулю.
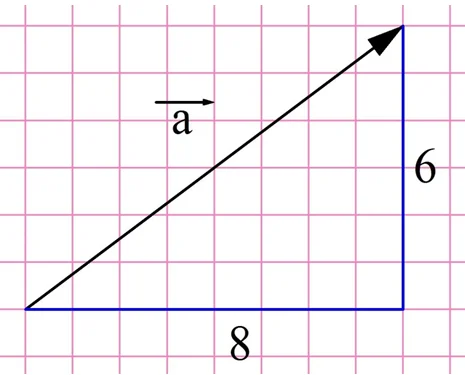
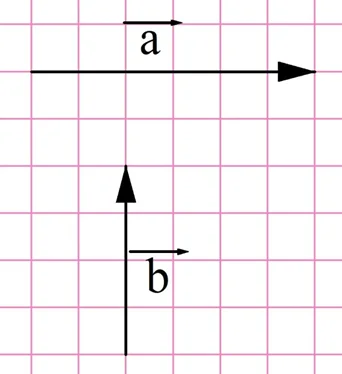
Задание. Найдите модуль вектора, изображенного на рисунке:
Решение. Легко выполнить построение, при котором вектор окажется гипотенузой в прямоугольном треугольнике
Тогда длину вектора можно найти по теореме Пифагора:
Равенство векторов
Через начало и конец векторов можно провести прямую. В связи с этим можно ввести понятие коллинеарных векторов.
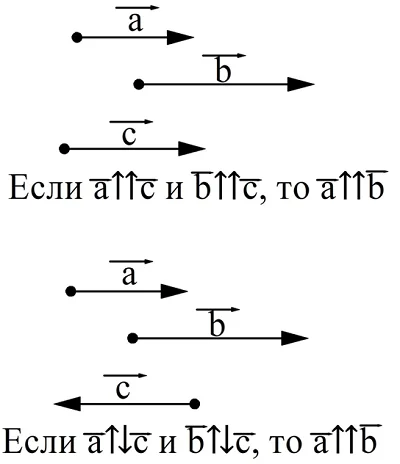
На рисунке коллинеарны вектора а и b, так как они лежат на одной прямой. Также коллинеарны с и d, так как они лежат на параллельных прямых. А вот вектора a и c неколлинеарны, так как они лежат на пересекающихся прямых.
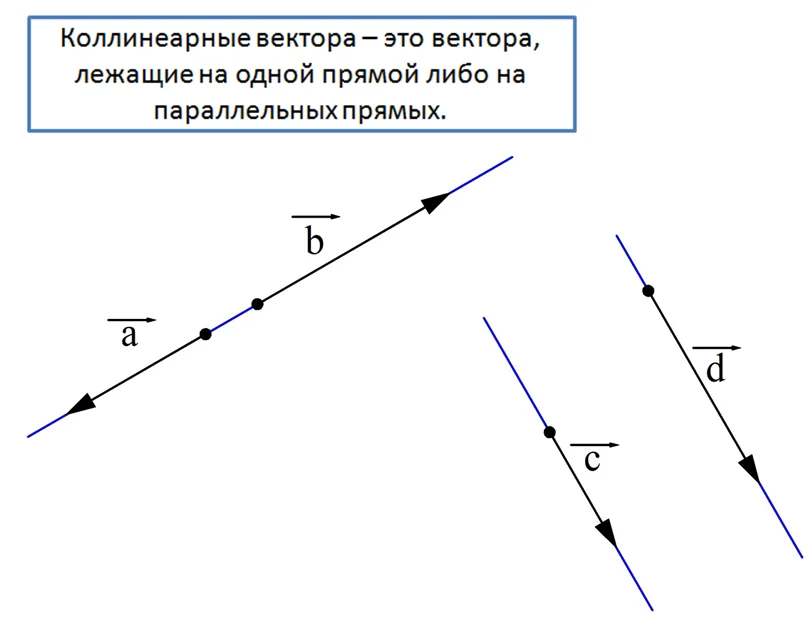
Для пары коллинеарных векторов можно определить, являются ли они сонаправленными или противоположно направленными.
Для обозначения сонаправленных векторов используется символ «⇈», а для противоположно направленных «⇅». Можно сформулировать две очевидных теоремы о коллинеарных векторах.
Проиллюстрируем эти правила с помощью рисунка:
Особняком стоит нулевой вектор. Он представляет собой точку, а потому не имеет определенного направления. Поэтому условно его считают сонаправленным с любым другим вектором.
Теперь мы можем дать определение равенству векторов.
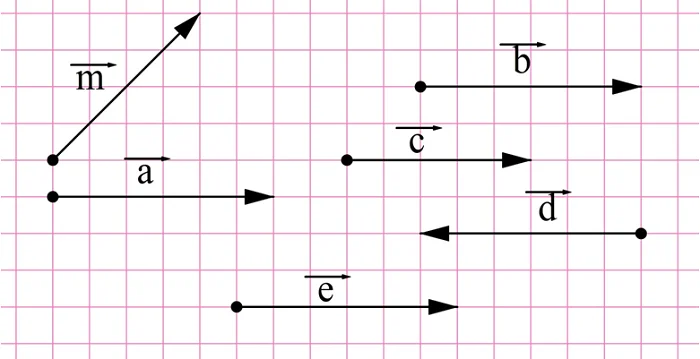
Задание. Найдите на картинке равные вектора.
Решение. Здесь равны вектора а, b и e. Они сонаправлены и имеют длину 6. Вектор с сонаправлен с ними, но его длина составляет только 5 клеток. Длина вектора d составляет 6 клеток, но он не сонаправлен с другими векторами. Наконец, вектор m также не сонаправлен с другими векторами и даже не коллинеарен им.
Ответ: a, b и e.
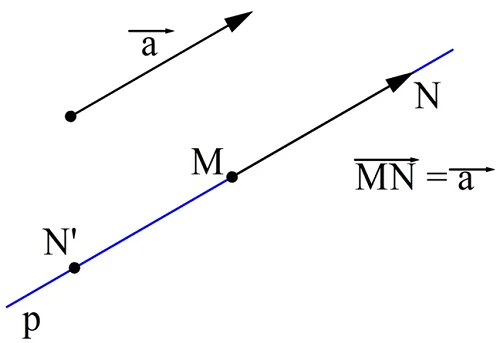
Если началом вектора является некоторая точка А, то можно сказать, что вектор отложен от точки А. Докажем важное утверждение:
Доказать его можно построением. Пусть есть вектор а и точка М. Проведем через М прямую p, параллельную вектору а. Такая прямая будет единственной. Если точка М и вектор лежат на одной прямой, то в качестве прямой p возьмем именно эту прямую. Далее от точки М можно отложить отрезки МN и МN’, длина которых будет совпадать с длиной вектора а. В результате получится два вектора,MN и MN’, один из которых будет сонаправлен с а, а другой – противоположно направленный.
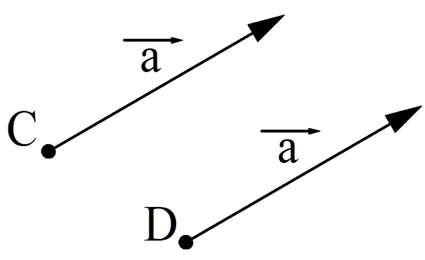
Часто равные вектора, отложенные от разных точек, обозначают одной буквой. Можно считать, что это один и тот же вектор, просто приложенный к разным точкам.
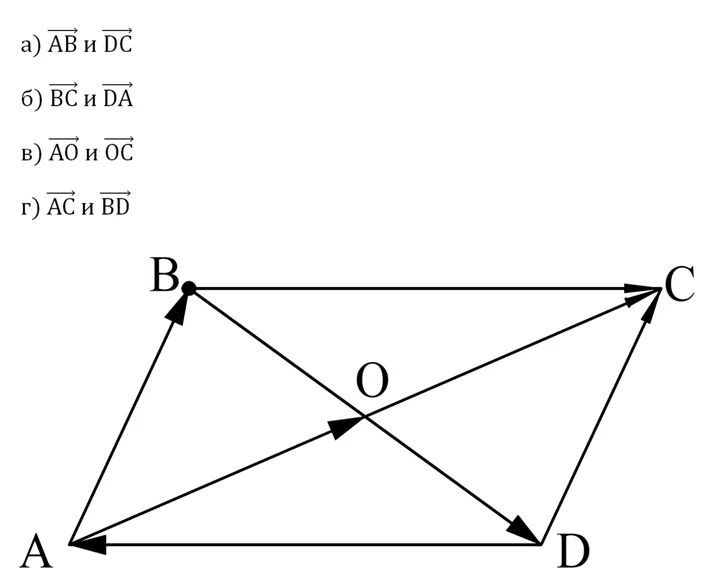
Задание. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Определите, равны ли вектора:
Решение.
а) Отрезки АВ и DC равны, ведь это противоположные стороны параллелограмма, по той же причине эти отрезки параллельны. Видно, что они сонаправлены, значит, вектора равны.
б) Отрезки ВС и DA параллельны и равны, но эти вектора противоположно направлены, поэтому вектора НЕ равны друг другу.
в) Точка пересечения диагоналей параллелограмма делит их пополам, поэтому длины отрезков АО и ОС одинаковы. Вектора АО и ОС лежат на одной прямой, то есть они коллинеарны. При этом они ещё и сонаправлены, поэтому АО и ОС – равные векторы.
г) Вектора АС и BD лежат на пересекающихся прямых, то есть они не коллинеарны. Этого уже достаточно, чтобы считать их НЕ равными друг другу.
Ответ: а) д; б) нет; в) да; г) нет.
Сложение векторов
Пусть некоторый объект сначала находился в точке А, а потом переместился в точку В. Тогда его перемещение удобно обозначить с помощью вектора АВ. Далее пусть этот объект из точки В переместился в другую точку С.
С одной точки зрения, объект совершил сразу два перемещения, из А в В и из В в С, которые можно представить векторами:
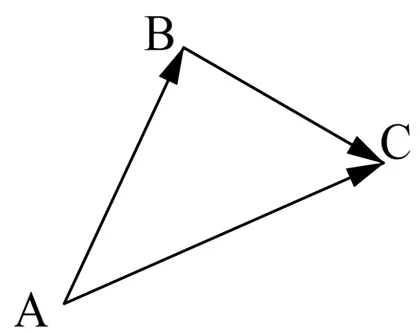
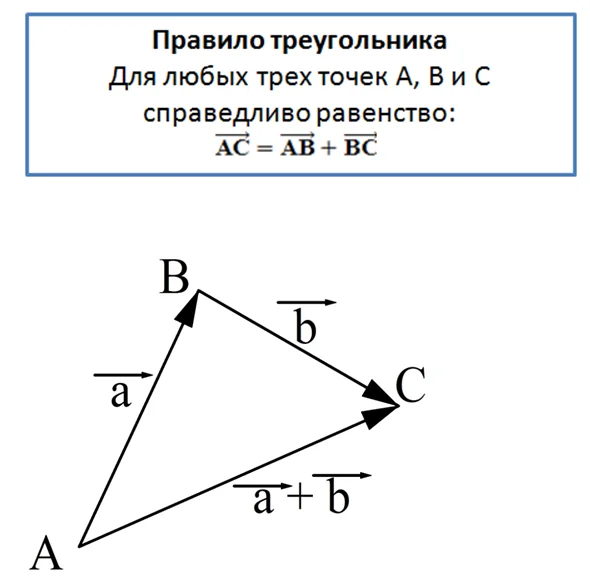
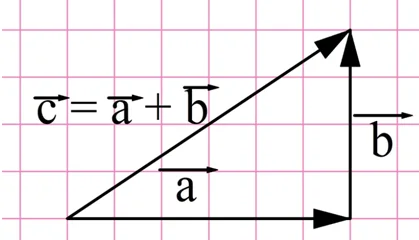
Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать вектора. Его называют правилом треугольника.
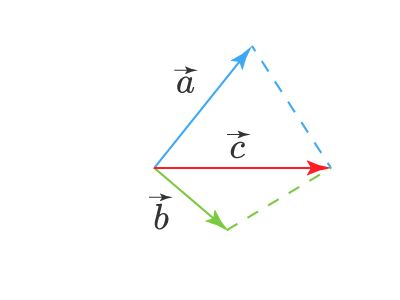
С помощью правила треугольника удобно складывать вектора, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму:
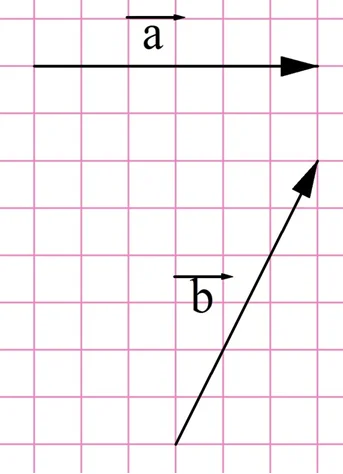
Задание. На рисунке показаны два вектора. Постройте в тетради их сумму и найдите длину получившегося вектора.
Решение. Перенесем вектор b к концу вектора а. Далее по правилу треугольника на удастся найти их сумму (обозначим этот вектор буквой с):
Теперь найдем длину получившегося вектора. Он является гипотенузой в прямоугольном треугольнике, причем длины катетов в этом треугольнике можно определить по рисунку, они составляют 4 и 6. Тогда длину гипотенузы можно найти по теореме Пифагора:
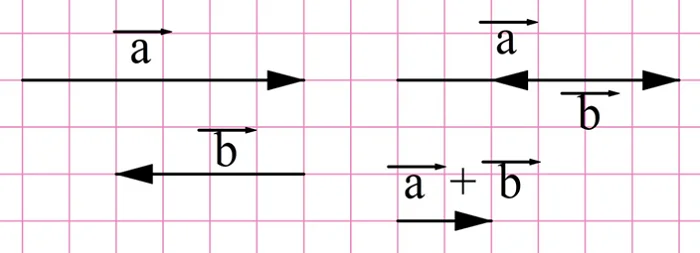
Отдельно рассмотрим случаи, когда складываются коллинеарные вектора. В этом случае получающаяся сумма окажется коллинеарной каждому слагаемому. Если вектора сонаправлены, то их длина итогового вектора окажется равной сумме длин складываемых векторов:
Если складываются противоположно направленные вектора, то длина их суммы окажется разностью длин складываемых векторов.
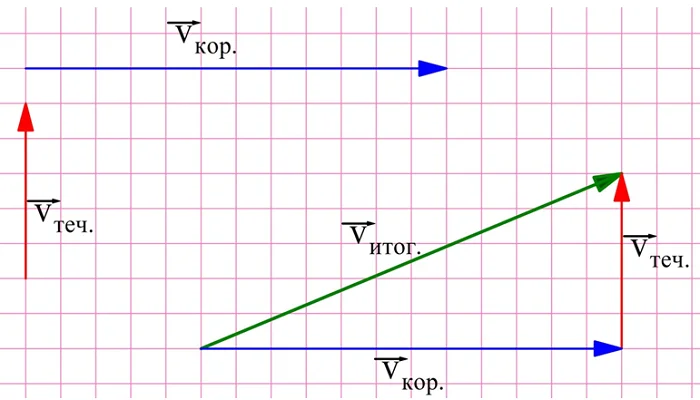
Именно по этой причине при решении простейших задач на движение корабля по реке скорость корабля и скорость течения либо складывают, либо вычитают. Дело в том, что в этих задачах складываются вектора скоростей корабля и течения. Когда судно плывет по течению, эти векторы сонаправлены, а когда плавание идет против течения, векторы оказываются противоположно направленными.
Задание. Корабль развивает в неподвижной воде скорость 12 км/ч. Он плывет по реке, скорость воды в которой составляет 5 км/ч. Найдите скорость корабля относительно берега, если:
а) судно плывет по течению;
б) судно плывет против течения;
в) судно плывет перпендикулярно течению.
Решение. Во всех случаях итоговая скорость судна является векторной суммой собственной скорости судна и течения реки:
Однако направления этих векторов различны. Найдем решение графически, с помощью построений. В первом случае вектора по условию сонаправлены:
Приложив другу к другу отрезки длиной 12 и 5, получим отрезок длиной 17. Это значит, что в первом случае скорость корабля относительно берега составит 17 км/ч.
Во втором случае вектора уже окажутся противоположно направленными:
Отрезок, соответствующий итоговой скорости, здесь уже равен 7 клеткам, значит, итоговая скорость составляет 7 км/ч.
В третьем случае вектора скоростей перпендикулярны:
При построении получился прямоугольный треугольник, вектор итоговой скорости в нем оказался в роли гипотенузы. Найти его длину можно по теореме Пифагора, ведь катеты нам известны:
Свойства сложения
Действия с векторами во многом подобны действиям с обычными числами. Напомним, что в алгебре при прибавлении к числу нуля оно не менялось:
a + 0 = a
Аналогично и при прибавлении к вектору нулевого вектора он не изменится:
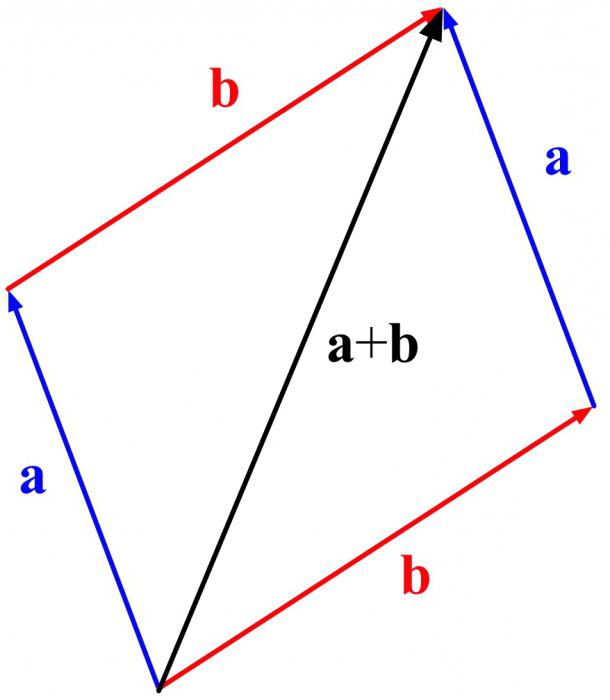
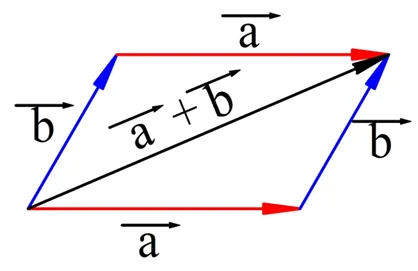
Работает ли это правило с векторами? Оказывается, что да. Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы:
Видно, что диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Они обозначены как векторы a и b, причем в данном случае к а прибавляется b. Но одновременно эта же диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Напомним, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены одним вектором. В этом случае уже к b прибавляется a. Результат при этом получается одинаковый, поэтому можно записать, что
На этом примере мы увидели, как работает ещё одно правило сложения векторов, который называется правилом параллелограмма. Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма.
Задание. Сложите с помощью правила параллелограмма вектора, изображенные на рисунке:
Решение. Надо всего лишь построить параллелограмм, как показано на рисунке. Его диагональ и окажется искомым вектором:
Ещё один закон, использующийся в алгебре, называется сочетательным законом, записывается он так:
Оказывается, что и при действиях с векторами он также работает, то есть справедливо соотношение:
Здесь оранжевый вектор – это сумма красного (а) и синего (b) вектора. Если к оранжевому вектору добавить зеленый (с), то получится фиолетовый вектор, который, таким образом, является суммой
Желтый вектор – это сумма синего и зеленого вектора. Видно, что фиолетовый вектор представляет собой сумму красного и желтого, то есть он представляет сумму
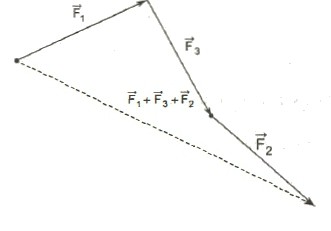
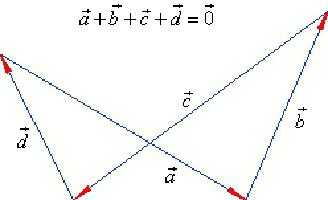
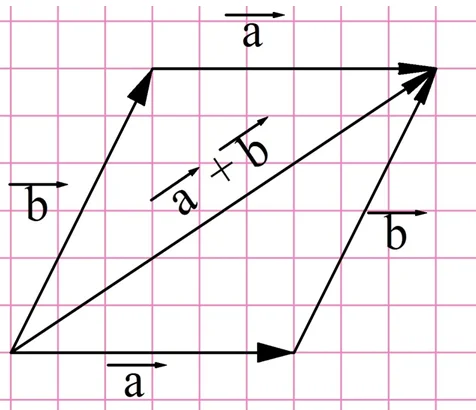
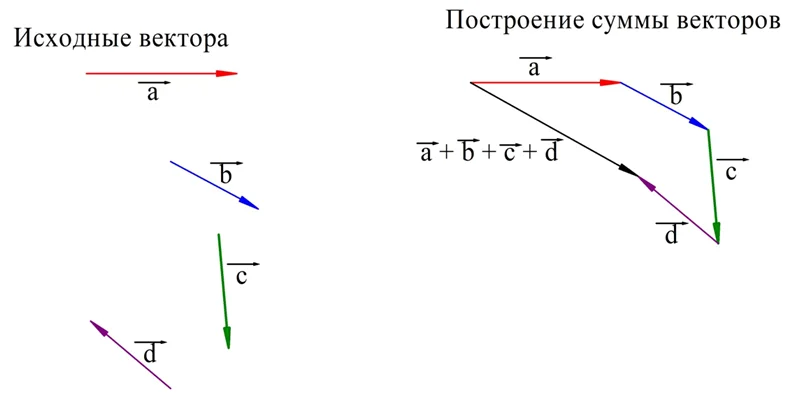
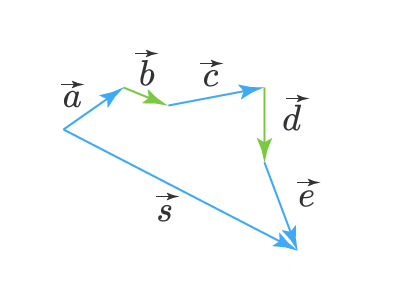
Складывать можно любое количество векторов. В этом случае надо последовательно прикладывать эти вектора друг к другу, выстраивая «цепочку» векторов. Например, сложение 4 векторов, показанных на рисунке, будет осуществляться следующим образом:
Этот способ сложения векторов именуют правилом многоугольника. Естественно, в силу переместительного закона вектора можно прикладывать друг к другу в разной последовательности, при этом результат будет получаться один и тот же.
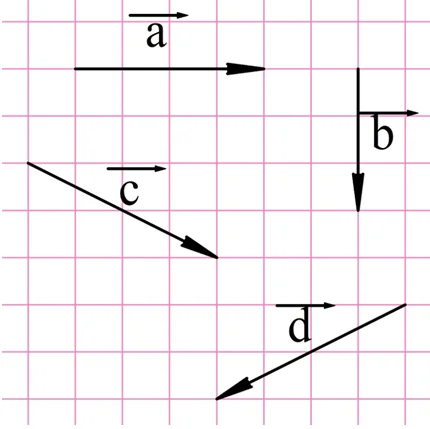
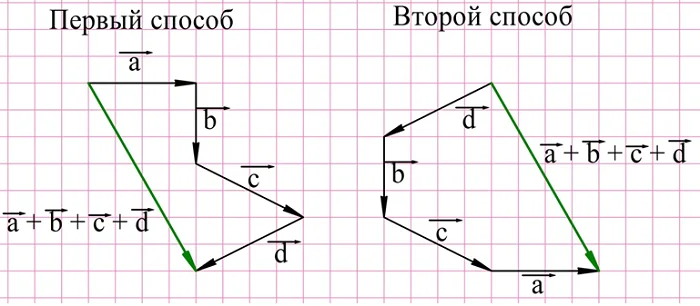
Задание. Сложите, используя правило многоугольника, вектора, изображенные на рисунке. Выполните сложение двумя разными способами:
В первом случае последовательно сложим вектора a, b, c и d. Во втором случае изменим последовательность сложения. Например, сложим их в порядке d, b, c, a:
Видно, что каждый из двух способов дал один и тот же результат, что ещё раз подтверждает справедливость переместительного закона сложения векторов.
Вычитание векторов
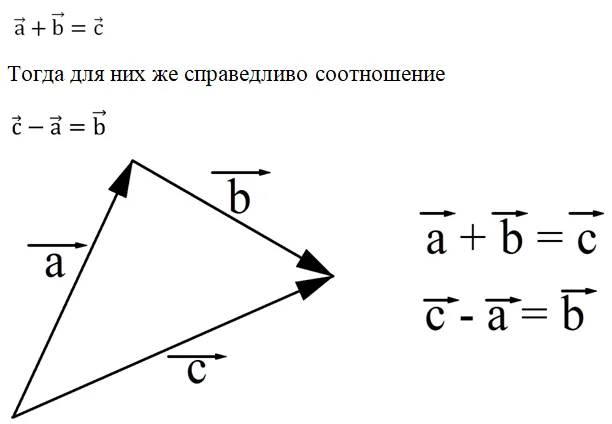
Напомним, что в алгебре операция вычитания вводится как операция обратная сложению. То есть если для трех чисел верно соотношение
a + b = c
то разностью чисел с и a как раз окажется b:
c – a = b
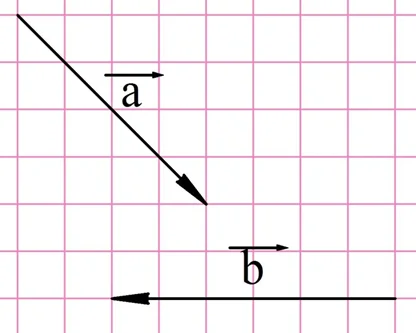
Аналогично вычитание понимается и в векторной алгебре. Пусть построены вектора а, b и c так, что
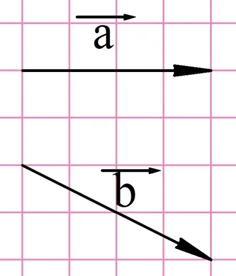
Этот пример показывает, как строить разность двух векторов. На рисунке вектора с и a отложены от одной точки, а вектор b, являющийся их разницей, проведен от конца вычитаемого вектора к концу уменьшаемого вектора.
В данном случае под уменьшаемым вектором понимается тот, который в разнице стоит перед знаком минус, а вычитаемый вектор – тот, который находится уже после этого знака. Например, в записи
Вектор а – уменьшаемый, а вектор b – вычитаемый.
Задание. Постройте в тетради разность векторов, изображенных на рисунке:
Решение. Заметим, что в условии не сказано, какой вектор из какого надо вычитать. Поэтому можно построить сразу два ответа:
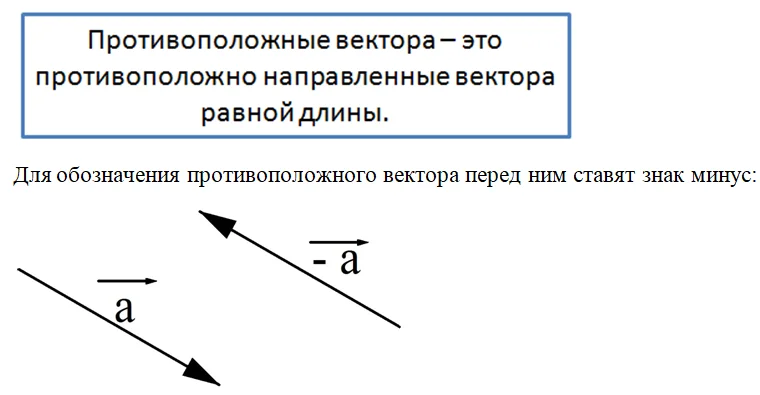
Несложно заметить, две получившиеся разности представляют собой противоположно направленные векторы одной длины. Такие векторы называются противоположными.
Очевидно, что если сложить друг с другом два противоположных вектора, то получится нулевой вектор:
Противоположные вектора играют в векторной алгебре такую же роль, как и противоположные числа. С их помощью удобно выполнять вычитание векторов. Напомним, что для обычных чисел справедливо соотношение:
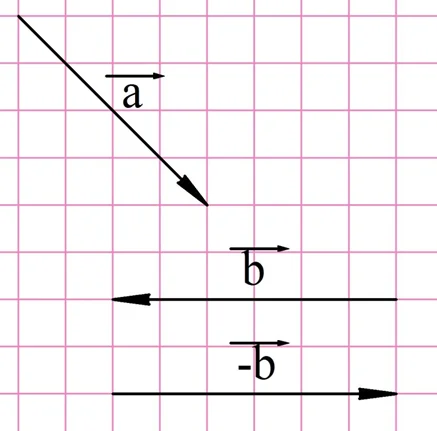
Поэтому операцию вычитания можно заменить операцией сложения, если вместо вычитаемого вектора взять вектор, противоположный ему. Рассмотрим этот способ на примере. Пусть из a надо вычесть b:
На первом шаге надо построить вектор, противоположный b:
Теперь надо просто сложить a и (– b):
В итоге нам удалось построить разность векторов а и b.
Умножение вектора на число
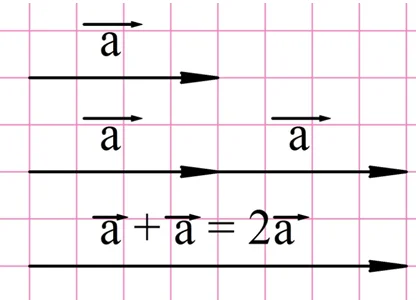
Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2:
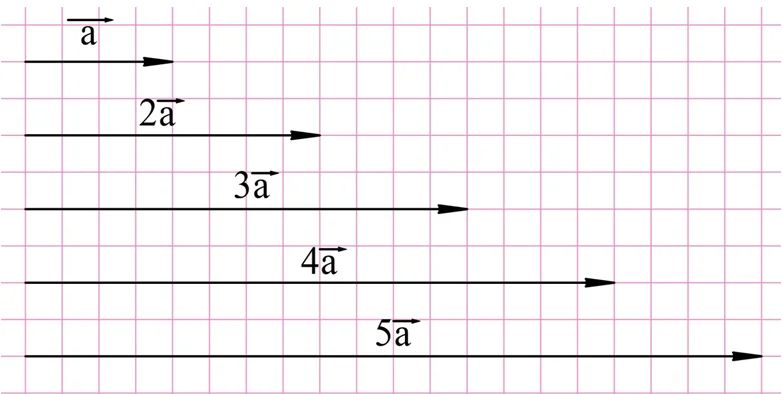
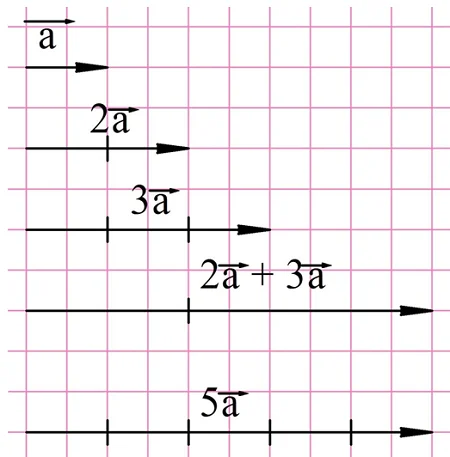
Аналогично можно построить вектора, которые больше исходного не в 2, а в 3,4 и т. д. раз:
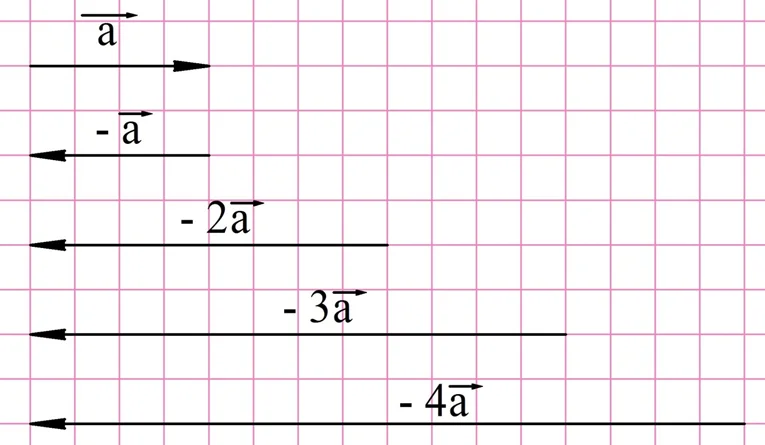
Итак, чтобы умножить вектор на положительное число k, надо построить сонаправленный с ним вектор, длина которого в k раз больше.А как умножать вектор на отрицательное число? Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор. Зная это, легко умножать вектор и на другие отрицательные числа:
Естественно, что если вектор умножается на ноль, то в результате получается нулевой вектор.
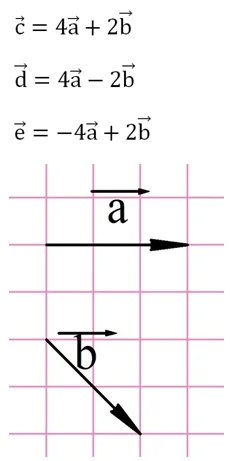
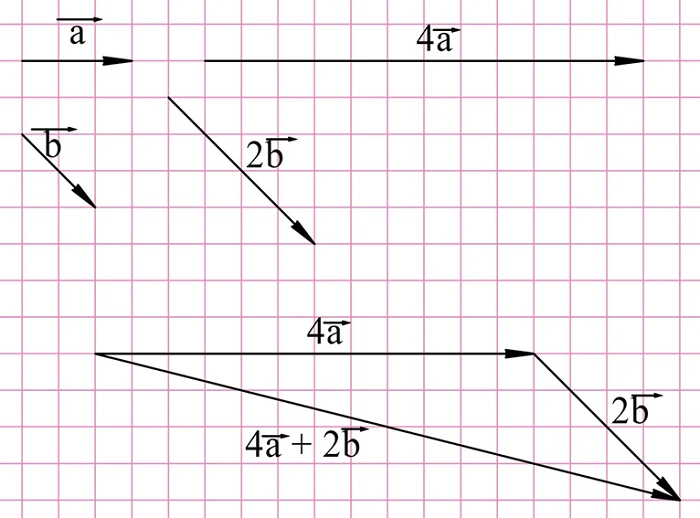
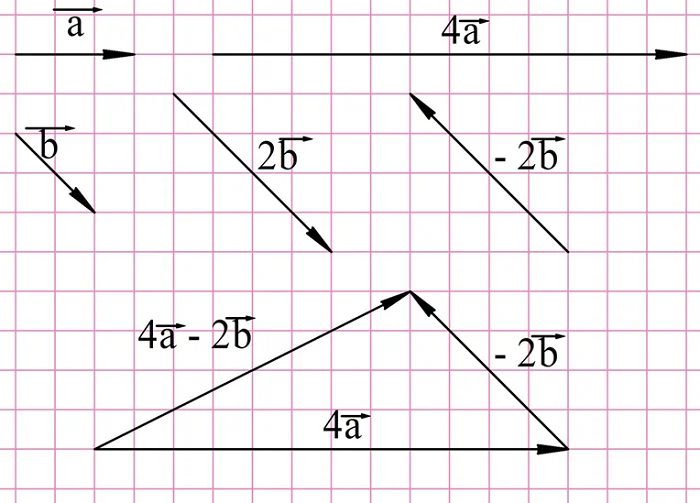
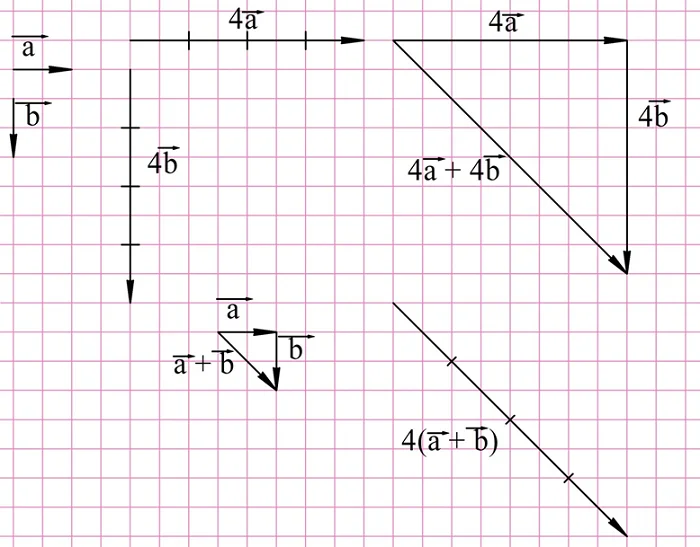
Задание. На рисунке показаны вектора а и b. Найдите вектора
Решение. Для построения снам надо сначала умножить исходные вектора на 4 и 2, а далее полученные результаты сложить:
Для нахождения вектора d надо построить вектор, противоположный вектору 2b, и уже его складывать с 4a:
Наконец, для нахождения вектора е необходимо построить противоположный вектор уже для 4а:
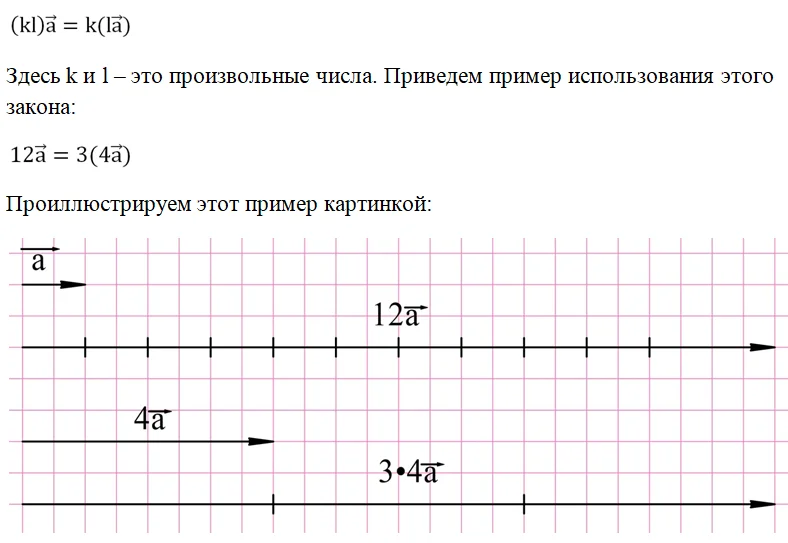
Некоторые правила обычной алгебры, касающиеся операции умножения, справедливы и для векторов. Первый такое правило – это сочетательный закон:
Видно, что мы можем либо сразу умножить вектор а на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится.
Также в отношении операции умножения векторов на число справедлив распределительный закона, которые позволяют раскрывать скобки:
Например, пусть нам надо сложить вектора 2а и 3а. Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим вектора 2а и 3а и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор а на число 5:
Есть ещё один распределительный закон, в котором в скобках находится уже сумма векторов, а не чисел:
Этот закон можно применить в случае, когда нам необходимо, например, сложить вектора 4а и 4b. Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить aи b, и уже потом эту сумму умножить на 4:
Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны вектора а, b и с, и надо найти вектор
Видно, что выражение значительно упростилось.
Решение задач с помощью векторов
Вектора активно используются в физике при решении многих задач, однако они также помогают доказывать геометрические теоремы. Рассмотрим несколько примеров, и начнем со вспомогательной задачи.
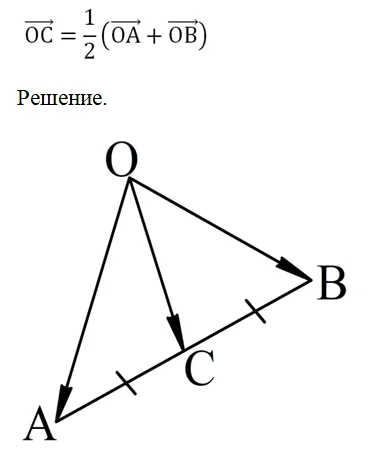
Задание. Известно, что С – это середина отрезка АВ. Докажите, что для любой точки О выполняется равенство:
Используя правило треугольника, вектор ОС можно представить в виде двух различных сумм:
Проанализируем выражение в скобках. Вектора АС и ВС коллинеарны, ведь они лежат на одной прямой АВ. При этом они противоположно направлены. Длина у них одинакова, ведь С – середина АВ. Тогда по определению АС и ВС – противоположные вектора, и их сумма равна нулю:
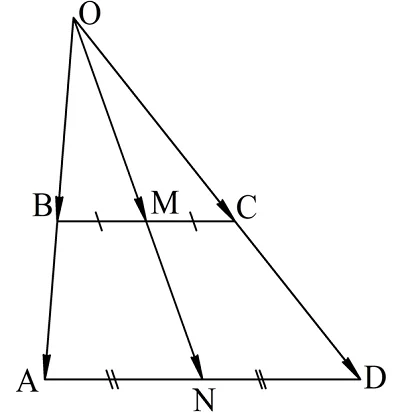
Задание. Докажите, что если в трапеции провести прямую, проходящую через середины ее оснований, то она также пройдет через точку, в которой пересекаются продолжения боковых сторон трапеции.
Решение. Построим трапецию, обозначим ее вершины и середины оснований:
Здесь ABCD – трапеция, основаниями которой являются отрезки ВС и AD. M и N – их середины. Прямые АВ и CD пересекаются в точке O. Необходимо доказать, что прямая MN также проходит через О.
Заметим, что ∆ОВС и ∆ОАD подобны. Действительно, у них есть общий ∠ВОС, а ∠ОВС и ∠ОАD одинаковы как односторонние углы при секущей АВ, поэтому треугольники подобны по 1-ому признаку. Обозначим коэффициент подобия буквой k, тогда можно записать, что
Так как отрезки ОА и АВ лежат на одной прямой, то вектора ОА и АВ коллинеарны и притом сонаправлены, поэтому в (1) отрезки можно заменить векторами:
(это соотношение мы доказали в предыдущей, вспомогательной задаче).
Аналогичную формулу можно составить и для второго основания и его середины N:
Полученное нами равенство означает, что вектора ON и ОМ коллинеарны, а значит, лежат на одной прямой (эти вектора не могут лежать на параллельных прямых, так как имеют общую точку О). Тогда получается, что О, M и N лежат на одной прямой, ч. т. д.
В статье Понятие вектора мы сказали, что векторы можно складывать друг с другом. Рассмотрим этот вопрос подробнее.
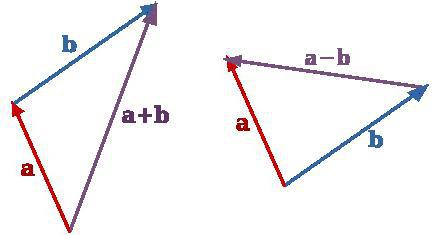
Пусть нам даны два вектора a⃗vec{a} и b⃗vec{b}. Что понимать под суммой этих двух векторов, то есть под a⃗+b⃗vec{a}+vec{b}? Во первых, сумма двух векторов это вектор. То есть, если мы складываем два вектора (две стрелки) то снова получаем вектор (стрелку). Существуют два способа (или правила) как можно складывать векторы. Они, конечно, дают один и тот же самый результат. Говорят о правиле треугольника и правиле параллелограмма. Оба эти правила графические, то есть сумма векторов находится путем геометрического построения. О сумме векторов, выраженной через координаты векторов речь пойдет в другой статье.
Правило треугольника
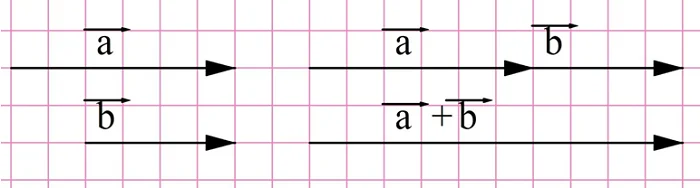
Вот нам даны два вектора a⃗vec{a} и b⃗vec{b}. Для того чтобы найти их сумму, пользуясь правилом треугольника, нужно чтобы начало одного из векторов находилось в точке конца другого вектора. То есть, чтобы точки начала одного вектора и конца другого вектора совпадали. Но что делать, если это не так? Для этого нужно параллельно перенести любой из векторов так чтобы это условие выполнялось. Например, пусть вначале векторы у нас расположены так:
Перенесем теперь вектор b⃗vec{b} параллельно самому себе так чтобы его начало совпало с концом вектора a⃗vec{a}. Получим:
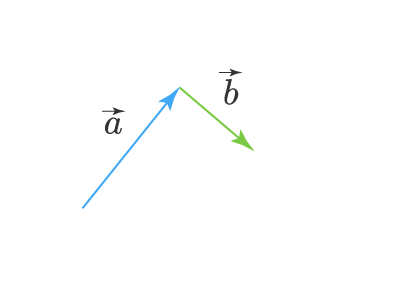
Теперь, чтобы найти сумму этих векторов, нужно провести вектор (стрелку) из начала вектора a⃗vec{a} в конец вектора b⃗vec{b}. Получим вектор c⃗=a⃗+b⃗vec{c}=vec{a}+vec{b}:
Правило параллелограмма
Решим ту же задачу вторым способом. Для этого нам нужно сделать так чтобы векторы a⃗vec{a} и b⃗vec{b} исходили из одной точки, то есть, чтобы точки начала этих векторов совпали. Получим:
Теперь построим на этих двух векторах параллелограмм. Суммой векторов a⃗vec{a} и b⃗vec{b} будет вектор, совпадающий с диагональю этого параллелограмма, и начало этого суммарного вектора c⃗vec{c} будет совпадать с началом векторов a⃗vec{a} и b⃗vec{b}:
На самом деле, по своему смыслу, оба эти правила это одно и то же правило. Просто так уж вышло, что в зависимости от построения треугольника или параллелограмма, говорят о соответствующем правиле складывания векторов.
Сумма любого числа векторов
Складывать между собой можно не только два вектора, но и любое их количество. Для этого удобно воспользоваться правилом треугольника. Пусть у нас есть векторы a⃗,b⃗,c⃗,d⃗,e⃗vec{a}, vec{b}, vec{c}, vec{d}, vec{e}. Пусть мы перенесли параллельно векторы так, что начало каждого последующего вектора берет свое начало в конце предыдущего вектора, тогда сумма этих векторов, вектор s⃗vec{s} — это вектор с началом, совпадающим с началом первого вектора (вектора a⃗vec{a}) и концом, совпадающим с концом последнего вектора (вектора e⃗vec{e}):
Тест по теме “Сумма векторов”
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
-
Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
-
Разность векторов
- Формула вычитания векторов
- Примеры задач
Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c, начало которого совпадает с началом a, а конец – с концом b. При этом конец вектора a должен совпадать с началом вектора b.
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c, совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
ci = ai + bi
Элементы вектора c равняются попарной сумме соответствующих элементов a и b.
| Для плоских задач | a + b = {ax + bx; ay + by} |
| Для трехмерных задач | a + b = {ax + bx; ay + by; az + bz} |
| Для n-мерных векторов | a + b = {a1 + b1; a2 + b2; … an + bn} |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
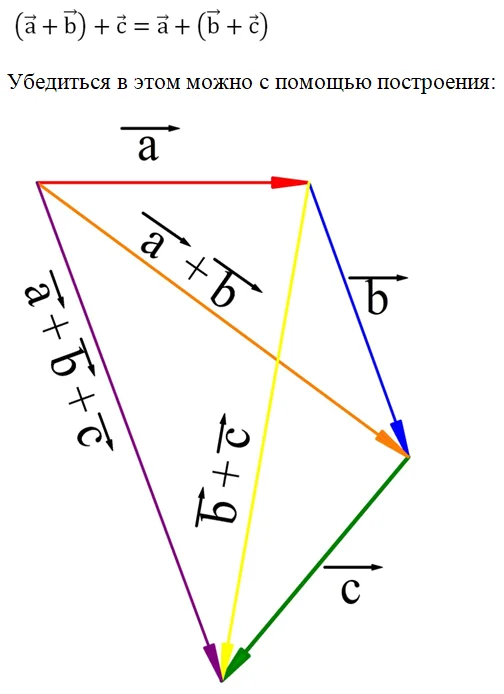
2. Ассоциативность: (a + b) + c = a + (b + c)
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (-a) = 0
Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.
Если из вектора a вычесть b, то получится c, причем должно соблюдаться условие: b + c = a
Формула вычитания векторов
ci = ai – bi
Элементы вектора c равны попарной разности соответствующих элементов a и b.
| Для плоских задач | a – b = {ax – bx; ay – by} |
| Для трехмерных задач | a – b = {ax – bx; ay – by; az – bz} |
| Для n-мерных векторов | a – b = {a1 – b1; a2 – b2; … an – bn} |
Примеры задач
Задание 1
Вычислим сумму векторов a = {3; 5} и b = {2; 7}.
Решение:
a + b = {3 + 2; 5 + 7} = {5; 12}.
Задание 2
Найдем разность векторов a = {4; 8; -2} и b = {-1; 9; 5}.
Решение:
a – b = {4 – (-1); 8 – 9; -2 – 5} = {5; -1; -7}.
Содержание
- Сложение и вычитание векторов
- Сумма векторов. Сложение векторов. Правило треугольника
- Разность векторов. Вычитание векторов
- Умножение вектора на число
- Сложение векторов — свойства, правила и примеры решения задач
- Общие сведения
- Сложение координат
- Правило параллелограмма
- Альтернативные методы
- Сумма и разность векторов
- Сумма векторов
- Формула сложения векторов
- Формула вычитания векторов
Сложение и вычитание векторов
Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec <0>)
Длина нулевого вектора равна нулю:
( left| vec <0>right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <— , — , — > right) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
Источник
Сложение векторов — свойства, правила и примеры решения задач
Отрезок, который имеет направление, называется вектором. По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.
Общие сведения
Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.
Обозначают отрезок помощью заглавных латинских букв, сверху которых ставится чёрточка. Рисуют же его с помощью прямой ограниченной линии.
Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.
Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.
Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:
- коллинеарными — отрезки лежат на одной линии или ей параллельны;
- соноправленными — замкнутые линии направление которых одинаковое;
- противоположными — вектора направлены в разные стороны;
- ортогональными — перпендикулярными друг другу;
- компланарными — лежащими на одной плоскости или ей параллельные;
- равными — ограниченными прямыми, совпадающими как по направлению, так и по величине.
Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.
Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.
Сложение координат
Существует простое правило применимое для направленных отрезков и позволяющее найти их сумму. Заключается оно в следующем: если необходимо прибавить один вектор к другому описывающийся каждый своими координатами, достаточно сложить соответствующие их орты. Например, предположим есть два вектора a и b. Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).
Это теорема доказывается просто. Пусть даны отрезки f (x 1; y 1) и g (x 2; y 2). В системе координат относительно рассматриваемых векторов получится: f = x 1 a + y 1 b; g = x 2 a + y 2 b. Тогда искомая сумма будет: f + g = x1a + y1b + x2a + y2b = a (x 1 + x 2) + b (y 1 + y 2). Что и нужно было доказать. Это правило применимо к векторам имеющим любые координаты. Например, пусть есть a (1; 2), b (-3; 1). Нужно найти их сумму. С помощью формулы сложения получится новый направленный отрезок с координатами a + b = (1 — 3; 2 + 1) = (-2; 3).
Как и при операциях с простыми числами при работе с векторными выражениями используют различные их свойства. Существует три правила сложения векторов:
Приведённые свойства соответственно называют переместительным, сочетательным, нулевым законом. Например, предположим есть два направленных отрезка a (2; 2) и b (-4; 1). Согласно первому свойству, очерёдность значения не имеет, поэтому что при прибавлении b к a, что при a к b результат будет одинаковый: a + b = (2 -4; 2 + 1) = (-2; 3), b + a = (-4 + 2; 1 +2) = (-2; 3). По аналогии можно проверить правильность утверждения и двух оставшихся свойств.
Следует отметить, что при сложении двух противоположных ограниченных прямых сумма будет равняться нуль-вектору: a + (-a) = 0. Это утверждение не требует доказательства, так как здесь используется фундаментальный закон алгебры — правило знаков.
Правило параллелограмма
По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.
Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.
Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.
Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.
Простыми словами это правило можно рассказать так: сумма двух отрезков будет равняться диагонали параллелограмма, построенного на исходных векторах. Эта теорема чаще используется не в геометрии, а физике, например, при сложении сил.
Альтернативные методы
Операцию по сложению двух векторов можно выполнить и с помощью правила треугольника. Делается это так. Выбирается любая точка на плоскости, от которой откладываются два вектора. При этом необходимо соблюдать их размерность и наклон по отношению друг к другу. Затем две конечные точки соединяют прямой. Её длина и будет искомой величиной. То есть в итоге должна получиться равнобедренная фигура.
Применение метода сложения векторов по правилу треугольника позволяет довольно легко находить сумму для трёх и более отрезков. Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.
При сложении нескольких векторов удобно выполнять следующую последовательность построений:
- от выбранной точки пространства рисуется вектор, равняющийся первому слагаемому;
- от конечной точки откладывается вектор, совпадающий со вторым слагаемым;
- приведённая последовательность потеряется необходимое число раз;
- прямой линией соединяется точка, с которой началось построение с конечной последнего вектора;
- длина полученного отрезка и будет являться результатом сложения.
Этот способ получил название метод многоугольника. Он довольно часто применяется на практике, позволяя, довольно просто выполнить нахождение суммы. Из правила треугольника, а, следовательно, и многоугольника, вытекает следствие, которое подтверждает, что если складывается отрезок с нулевым векторным выражением, то в ответе получится длина, совпадающая со значимым слагаемым.
Следует отметить, что методы используются только, если направление отрезков является сонаправленным.
Если же отрезки неколлинеарные, то от конца одного откладывается другой. Тогда искомая сумма будет равняться длине линии, первой точкой которой будет начало одной векторной прямой, а конец совпадать с точкой, завершающей другую. То есть сумма — это отрезок, начало которого совпадает с началом обеих линий, а длина равна разности их длин, при этом направление его будет совпадать с тем что больше по длине.
Источник
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
» data-lang=»default» data-override=»<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Для плоских задач | Для трехмерных задач | Для n-мерных векторов | 
Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие: Формула вычитания векторовЭлементы вектора c равны попарной разности соответствующих элементов a и b . » data-lang=»default» data-override=»<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″> Adblock
|
Сложив два вектора, в результате получим новый вектор.
Векторы могут располагаться один относительно другого:
В этом уравнении над буквами используются значки векторов. Эти значки указывают на то, что действия выполняются с помощью геометрии. То есть, учитывается направление векторов.
Важно! Любое выражение, записанное в векторном виде, учитывает направление векторов.
Если векторы направлены в противоположные стороны, то результат сложения будет сонаправлен с более длинным вектором.
Если векторы не параллельны (см. рис. ), для их сложения пользуются одним из двух правил:
Правило параллелограмма удобно применять к векторам, выходящим из одной общей точки (начала векторов совмещены).
Вычтем один вектор из второго вектора. В результате получим новый вектор.
Вектор «( -vec )» — это вектор «( vec )», развернутый в противоположную сторону.
Вычитание заменяют сложением. Складывают вектор с противоположно направленным вектором.
Складываем и вычитаем векторы, используя их координаты
Когда известны координаты двух векторов, сложение или вычитание провести достаточно легко. Для этого нужно сложить или вычесть соответствующие координаты векторов.
Для удобства обычно выписывают один вектор под другим.
Примеры сложения векторов в физике
Напоминание:
Складывать и вычитать можно только те векторы, которые имеют одинаковую размерность. То есть, длина которых измеряется в одинаковых единицах.
Рассмотрим формулу связи между начальной и конечной скоростями при равноускоренном движении
( vec = vec> + vec cdot t )
Примечания:
— Скорость всегда направлена в ту сторону, в которую тело движется (в направлении движения тела).
— Ускорение направлено в сторону действия силы (из второго закона Ньютона).
Обратите внимание: Направление силы не всегда будет совпадать с направлением, в котором тело двигалось изначально.
Силу можно направить в любую сторону. Она будет толкать или тянуть тело в ту сторону, в которую она направлена. Поэтому, конечная скорость ( vec ), начальная скорость ( vec> ) и ускорение ( vec ) могут иметь различные направления.
Векторы складывают с помощью геометрии, то есть, учитывают их направления.
Поэтому, формула ( vec = vec> + vec cdot t ) записана в векторном виде.
Векторы на ЕГЭ по математике. Действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор 
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора 
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы 



Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 



По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов 

Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



Умножение вектора на число
При умножении вектора 



Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 

Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
Правила, по которым происходит сложение векторов
Как происходит сложение векторов, не всегда понятно ученикам. Дети не представляют того, что за ними скрывается. Приходится просто запоминать правила, а не вдумываться в суть. Поэтому именно о принципах сложения и вычитания векторных величин требуется много знаний.
В результате сложения двух и более векторов всегда получается еще один. Причем он всегда обязательно будет одинаковым, независимо от приема его нахождения.
Чаще всего в школьном курсе геометрии рассматривается сложение двух векторов. Оно может быть выполнено по правилу треугольника или параллелограмма. Эти рисунки выглядят по-разному, но результат от действия один.
Как происходит сложение по правилу треугольника?
Оно применяется тогда, когда векторы неколлинеарные. То есть не лежат на одной прямой или на параллельных.
В этом случае от некоторой произвольной точки нужно отложить первый вектор. Из его конца требуется провести параллельный и равный второму. Результатом станет вектор, исходящий из начала первого и завершающийся в конце второго. Рисунок напоминает треугольник. Отсюда и название правила.
Если векторы коллинеарные, то это правило тоже можно применять. Только рисунок будет расположен вдоль одной линии.
Как выполняется сложение по правилу параллелограмма?
Опять же? применяется только для неколлинеарных векторов. Построение выполняется по другому принципу. Хотя начало такое же. Нужно отложить первый вектор. И от его начала – второй. На их основе достроить параллелограмм и провести диагональ из начала обоих векторов. Она и будет результатом. Так выполняется сложение векторов по правилу параллелограмма.
До сих пор их было два. А как быть, если их 3 или 10? Использовать следующий прием.
Как и когда применяется правило многоугольника?
Если требуется выполнить сложение векторов, число которых — больше двух, пугаться не стоит. Достаточно последовательно отложить их все и соединить начало цепочки с ее концом. Этот вектор и будет искомой суммой.
Какие свойства действительны для действий с векторами?
О нулевом векторе. Которое утверждает, что при сложении с ним получается исходный.
О противоположном векторе. То есть о таком, который имеет противоположное направление и равное по модулю значение. Их сумма будет равна нулю.
О коммутативности сложения. То, что известно еще с начальной школы. Смена мест слагаемых не приводит к изменению результата. Другими словами, неважно какой вектор откладывать сначала. Ответ все равно будет верным и единственным.
Об ассоциативности сложения. Этот закон позволяет складывать попарно любые векторы из тройки и к ним прибавлять третий. Если записать это с помощью знаков, то получится следующее:
первый + (второй + третий) = второй + (первый + третий) = третий + (первый + второй).
Что известно о разности векторов?
Отдельной операции вычитания не существует. Это связано с тем, что оно, по сути, является сложением. Только второму из них задается противоположное направление. А потом все выполняется так, как если бы рассматривалось сложение векторов. Поэтому об их разности практически не говорят.
Для того чтобы упростить работу с их вычитанием, видоизменено правило треугольника. Теперь (при вычитании) второй вектор нужно отложить из начала первого. Ответом будет тот, что соединяет конечную точку уменьшаемого с ней же вычитаемого. Хотя можно и откладывать так, как было описано ранее, просто изменив направление второго.
Как найти сумму и разность векторов в координатах?
В задаче даны координаты векторов и требуется узнать их значения для итогового. При этом построений выполнять не нужно. То есть можно воспользоваться несложными формулами, которые описывают правило сложения векторов. Они выглядят так:
а (х, у, z) + в (k, l, m) = с (х+k, y+l, z+m);
а (х, у, z) -в (k, l, m) = с (х-k, y-l, z-m).
Легко заметить, что координаты нужно просто сложить или вычесть в зависимости от конкретного задания.
Первый пример с решением
Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.
Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.
Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.
А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.
Ответ. Разность АО и ВО равна 8 см.
Второй пример и его подробное решение
Условие. У ромба АВСД диагонали равны 12 и 16 см. Точка их пересечения обозначена буквой О. Вычислите длину вектора, образованного разностью векторов АО и ВО.
Решение. Пусть обозначение вершин ромба будет таким же, как в предыдущей задаче. Аналогично решению первого примера получается, что искомая разность равна вектору АВ. А его длина неизвестна. Решение задачи свелось к тому, чтобы вычислить одну из сторон ромба.
Для этой цели потребуется рассмотреть треугольник АВО. Он прямоугольный, потому что диагонали ромба пересекаются под углом в 90 градусов. А его катеты равны половинам диагоналей. То есть 6 и 8 см. Искомая в задаче сторона совпадает с гипотенузой в этом треугольнике.
Для ее нахождения потребуется теорема Пифагора. Квадрат гипотенузы будет равен сумме чисел 6 2 и 8 2 . После возведения в квадрат получатся значения: 36 и 64. Их сумма — 100. Отсюда следует, что гипотенуза равна 10 см.
Ответ. Разность векторов АО и ВО составляет 10 см.
Третий пример с детальным решением
Условие. Вычислить разность и сумму двух векторов. Известны их координаты: у первого — 1 и 2, у второго — 4 и 8.
Решение. Для нахождения суммы потребуется сложить попарно первые и вторые координаты. Результатом будут числа 5 и 10. Ответом будет вектор с координатами (5; 10).
Для разности нужно выполнить вычитание координат. После выполнения этого действия получатся числа -3 и -6. Они и будут координатами искомого вектора.
Ответ. Сумма векторов — (5; 10), их разность — (-3; -6).
Четвертый пример
Условие. Длина вектора АВ равна 6 см, ВС — 8 см. Второй отложен от конца первого под углом в 90 градусов. Вычислить: а) разность модулей векторов ВА и ВС и модуль разности ВА и ВС; б) сумму этих же модулей и модуль суммы.
Решение: а) Длины векторов уже даны в задаче. Поэтому вычислить их разность не составит труда. 6 – 8 = -2. Несколько сложнее обстоит дело с модулем разности. Сначала нужно узнать, какой вектор будет являться результатом вычитания. Для этой цели следует отложить вектор ВА, который направлен в противоположную сторону АВ. Потом от его конца провести вектор ВС, направив его в сторону, противоположную исходному. Результатом вычитания получится вектор СА. Его модуль можно вычислить по теореме Пифагора. Несложные вычисления приводят к значению 10 см.
б) Сумма модулей векторов получается равной 14 см. Для поиска второго ответа потребуется некоторое преобразование. Вектор ВА противоположно направлен тому, который дан — АВ. Оба вектора направлены из одной точки. В этой ситуации можно использовать правило параллелограмма. Результатом сложения будет диагональ, причем не просто параллелограмма, а прямоугольника. Его диагонали равны, значит, модуль суммы такой же, как в предыдущем пункте.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vektory-na-ege-po-matematike-v-zadache-v6-dejstviya-nad-vektorami/
http://www.syl.ru/article/191003/mod_pravila-po-kotoryim-proishodit-slojenie-vektorov
[/spoiler]




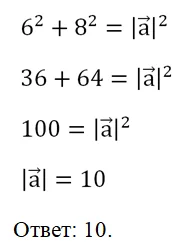




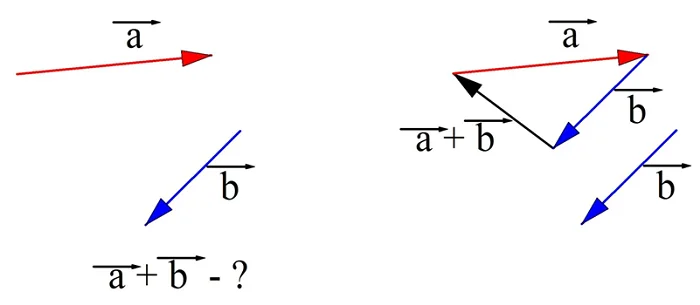
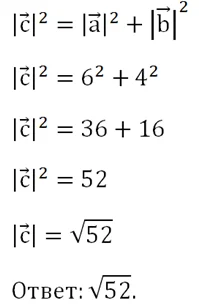


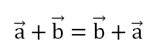
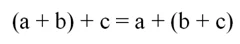


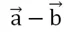
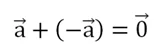
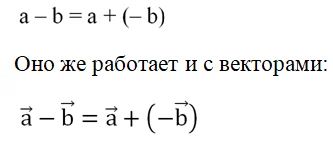
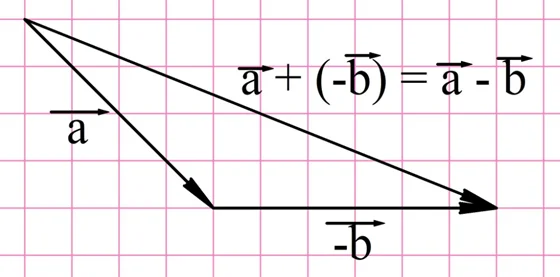
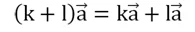
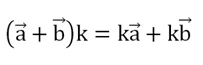



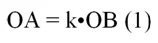

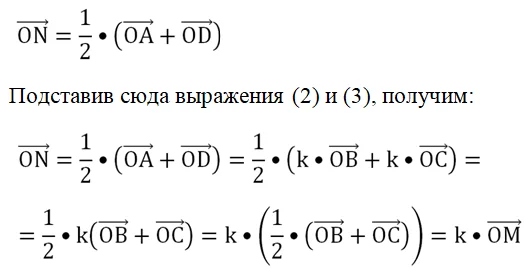



































 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»