Как найти сумму периметра трапеции

Как найти сумму периметра трапеции

Содержание:

  • Формула
  • Примеры вычисления периметра трапеции

Формула

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

В общем случае для произвольной трапеции
$ABCD$ со сторонами $AB=a$, $BC=b$, $CD=c$, $AD=d$ периметр вычисляется по формуле:

$$P_{Delta A B C D}=a+b+c+d$$

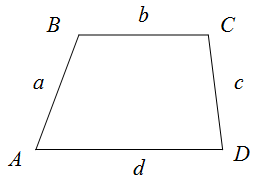
Если трапеция $ABCD$ равнобокая, то по определению её
боковые стороны равны $AB=CD=a$ и формула для
нахождения периметра примет вид:

$$P_{Delta A B C D}=2 a+b+d$$

Примеры вычисления периметра трапеции

Пример

Задание. Найти периметр трапеции
$ABCD$ со сторонами
$AB=1,5$ см,
$BC=2$ см,
$CD=1$ см,
$AD=3$ см.

Решение. Для нахождения периметра трапеции
$ABCD$ воспользуемся формулой

$$P_{Delta A B C D}=A B+B C+C D+A D$$

Подставляя в неё заданные в условии длины сторон, получим:

$P_{Delta A B C D}=1,5+2+1+3=7,5$ (см)

Ответ. $P_{Delta A B C D}=7,5$ (см)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Заданна равнобокая трапеция
$ABCD$ с основаниями
$BC=3$ см,
$AD=7$ см и высотой
$BK=2 sqrt{3}$ см. Найти периметр заданной трапеции.

Решение. Сделаем рисунок.

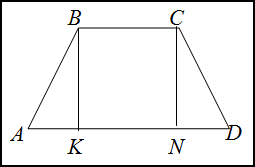
Опустим высоту $CN$. Полученный в
результате четырехугольник
$BCKN$ является прямоугольником, поэтому
$BC=KN$. Треугольники $Delta A B K quad$ и $quad Delta N C D$ – прямоугольные и равны между собой. Тогда
$AK=ND$. Найдем чему равно $AK$:

$A K=(A D-B C): 2 Rightarrow A K=(7-3): 2=2$ (см)

Из $Delta ABK$ по теореме Пифагора найдем боковую сторону
$AB$ трапеции:

$=sqrt{12+4}=sqrt{16}=4$ (см)

Тогда периметр рассматриваемой равнобокой трапеции

$P_{Delta A B C D}=2 cdot 4+3+7=18$ (см)

Ответ. $P_{Delta A B C D}=18$ (см)

Читать дальше: как найти периметр ромба.

Источник

Как найти периметр трапеции

Содержание:

  • Основные свойства трапеции
  • Способы нахождений периметра

    • По всем сторонам
    • По сторонам равнобедренной трапеции
    • Через среднюю линию
  • Примеры решения задач

Определения

​Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.

Периметр трапеции — это сумма длин всех его сторон.

Основные свойства трапеции

  • средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;

Свойство 1

 
  • биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;

Свойство 2

 
  • треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;

Свойство 3

 
  • треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;

Свойство 4

 
  • если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;

Свойство 5

 
  • точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;

Свойство 6

 
  • середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;

Свойство 7

 

Свойства равнобедренной трапеции

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

  • в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
  • диагонали равны;
  • равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
  • если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.

Способы нахождений периметра

Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.

По всем сторонам

Периметр по всем сторон

 

Формула для нахождения периметра выглядит так:

P=a+b+c+d

где a, b, c, d — стороны трапеции.

По сторонам равнобедренной трапеции

Периметр по сторон 2

 

Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:

(P=2times a+b+c)

или

(P=2times c+a+b)

Через среднюю линию

Через среднюю линию

 

Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:

(P=2times l+AB+CD)

где l — средняя линия фигуры.

Примеры решения задач

Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.

Задача 1

Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.

Решение:

Нам пригодится самая первая формула для расчета:

P=a+b+c+d.

Подставляем значения и получаем:

P=4+7+5+10=26;см.

Ответ: 26 см.

Задача 2

Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.

Решение:

Так как трапеция равнобедренная, удобнее всего будет использовать формулу:

(P=2times a+b+c)

Таким образом, получается:

(P=2times 7+5+8=27) см.

Ответ: 27 см.

Задача 3

Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.

Решение:

Считать будем по формуле

(P=2times l+a+c)

(P=2times 6+5+9=26) см.

Ответ: 26 см.

Насколько полезной была для вас статья?

Рейтинг: 3.82 (Голосов: 11)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Периметр трапеции: онлайн-калькулятор

Чтобы вычислить периметр трапеции, необходимо найти сумму всех ее сторон. Такое действие несложно выполнить самостоятельно. Но если все величины представлены в разных единицах измерения, придется перед решением произвести конвертацию. Часто именно на этом этапе происходит потеря данных.

Расчет без ошибок поможет сделать сервис с калькуляторами по материалам алгебры и геометрии. Вводите данные, которые приведены в условии, и получайте подробные расчеты и ответ. Вычисление включает перевод единиц измерения. На это не придется тратить время и сомневаться в верности действий.

Как найти периметр трапеции: онлайн калькулятор

Программа вычисляет периметр трапеции по формуле:

где a, b, c, d – стороны фигуры.

Сайт удобно использовать. Приступайте к подсчетам без регистрации и платежей в удобное для вас время. Переключайтесь между темами. Тренируйтесь столько, сколько необходимо для освоения материала. Готовое решение поможет запомнить алгоритм и применить его при самостоятельных вычислениях.

Сервис помогает:

  • Студентам. Программа позволяет быстро произвести расчеты и получить точный ответ, который можно использовать без пересчета в комплексной задаче.
  • Школьникам. Программы, сгруппированные по разделам, дают возможность потренироваться в решении задач по нужной теме, подготовиться к контрольной или поступлению в университет.
  • Родителям. Проверку домашнего задания ребенка теперь можно выполнить намного быстрее, не изучая перед этим тему из учебника и не выбирая необходимую формулу.
  • Учителям. Подготовить индивидуальные задания для самостоятельной работы на каждого ученика теперь можно автоматически. Таким же образом проверить результаты.
Источник


Загрузить PDF


Загрузить PDF

Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции. При помощи известных величин, а также геометрических и тригонометрических правил можно найти неизвестные стороны трапеции.

  1. Изображение с названием Find the Perimeter of a Trapezoid Step 1

    1

    Запишите формулу для вычисления периметра трапеции. Формула: P=T+B+L+R, где P – периметр, T – верхнее основание, B – нижнее основание, L – левая боковая сторона, R – правая боковая сторона.[1]

  2. Изображение с названием Find the Perimeter of a Trapezoid Step 2

    2

    В формулу подставьте известные длины сторон. Не используйте этот метод, если не даны значения всех четырех сторон.

    • Например, верхнее основание трапеции равно 2 см, нижнее основание равно 3 см, а каждая боковая сторона равна 1 см. В этом случае формула примет следующий вид:
      P=2+3+1+1

  3. Изображение с названием Find the Perimeter of a Trapezoid Step 3

    3

    Сложите длины сторон. Так вы найдете периметр трапеции.

    Реклама

  1. Изображение с названием Find the Perimeter of a Trapezoid Step 4

    1

    Разбейте трапецию на прямоугольник и два прямоугольных треугольника. Для этого из каждой вершины трапеции проведите высоту.

    • Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.

  2. Изображение с названием Find the Perimeter of a Trapezoid Step 5

    2

    Обозначьте каждую высоту. Так как высоты являются противоположными сторонами прямоугольника, они равны.[2]

    • Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).

  3. Изображение с названием Find the Perimeter of a Trapezoid Step 6

    3

    Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника). Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.[3]
     Не используйте этот метод, если не дано значение верхнего основания.

    • Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.

  4. Изображение с названием Find the Perimeter of a Trapezoid Step 7

    4

    Запишите теорему Пифагора для первого прямоугольного треугольника. Формула: a^{{2}}+b^{{2}}=c^{{2}}, где c – гипотенуза треугольника (сторона, противоположная прямому углу), a – высота треугольника, b – основание треугольника.[4]

  5. Изображение с названием Find the Perimeter of a Trapezoid Step 8

    5

  6. Изображение с названием Find the Perimeter of a Trapezoid Step 9

    6

    Возведите в квадрат известные значения. Затем при помощи вычитания обособьте переменную b.

  7. Изображение с названием Find the Perimeter of a Trapezoid Step 10

    7

    Извлеките квадратный корень, чтобы найти b. (Чтобы получить информацию об упрощении квадратных корней, прочитайте эту статью.) Вы найдете основание первого прямоугольного треугольника. Напишите найденное значение под основанием соответствующего треугольника.

  8. Изображение с названием Find the Perimeter of a Trapezoid Step 11

    8

    Найдите неизвестную сторону второго прямоугольного треугольника. Для этого запишите теорему Пифагора для второго треугольника и действуйте так, как описано выше. Если дана равнобедренная трапеция, у которой боковые стороны равны,[5]
    то два прямоугольных треугольника являются равными, то есть любая сторона одного треугольника равна соответствующей стороне другого.

  9. Изображение с названием Find the Perimeter of a Trapezoid Step 12

    9

    Сложите значения всех сторон трапеции. Периметр любого многоугольника равен сумме всех его сторон:P=T+B+L+R. Нижнее основание трапеции равно сумме нижней стороны прямоугольника и оснований двух треугольников. В интернете поищите информацию о том, как складывать квадратные корни, или просто воспользуйтесь калькулятором, чтобы преобразовать квадратные корни в десятичные дроби.

    Реклама

  1. Изображение с названием Find the Perimeter of a Trapezoid Step 13

    1

    Разбейте трапецию на прямоугольник и два прямоугольных треугольника. Для этого из каждой вершины трапеции проведите высоту.

    • Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.

  2. Изображение с названием Find the Perimeter of a Trapezoid Step 14

    2

    Обозначьте каждую высоту. Так как высоты являются противоположными сторонами прямоугольника, они равны.[6]

    • Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).

  3. Изображение с названием Find the Perimeter of a Trapezoid Step 15

    3

    Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника). Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.[7]

    • Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.

  4. Изображение с названием Find the Perimeter of a Trapezoid Step 16

    4

  5. Изображение с названием Find the Perimeter of a Trapezoid Step 17

    5

    В формулу синуса подставьте известные величины. Вместо противоположной стороны подставьте высоту треугольника. Вы найдете гипотенузу, то есть боковую сторону трапеции.

    • Например, если нижний угол трапеции равен 35 градусов, а высота треугольника равна 6 см, то формула запишется так:
      sin(35)={frac {6}{H}}

  6. Изображение с названием Find the Perimeter of a Trapezoid Step 18

    6

    Найдите синус угла. Это делается при помощи научного калькулятора, а именно клавиши SIN. Найденное значение подставьте в формулу.

    • При помощи калькулятора вы найдете, что синус угла в 35 градусов приблизительно равен 0,5738. Таким образом, формула примет следующий вид:
      0,5738={frac {6}{H}}

  7. Изображение с названием Find the Perimeter of a Trapezoid Step 19

    7

    Найдите переменную H. Для этого каждую сторону уравнения (формулы) умножьте на Н, а затем каждую сторону уравнения разделите на синус угла. Или просто разделите высоту треугольника на синус угла.

  8. Изображение с названием Find the Perimeter of a Trapezoid Step 20

    8

    Найдите гипотенузу второго прямоугольного треугольника. Напишите функцию (формулу) синуса угла второго прямоугольного треугольника: sin theta ={frac {B}{H}}. Так вы найдете гипотенузу второго треугольника, которая является второй боковой стороной трапеции.

  9. Изображение с названием Find the Perimeter of a Trapezoid Step 21

    9

    Запишите теорему Пифагора для первого прямоугольного треугольника. Формула: a^{{2}}+b^{{2}}=c^{{2}}, где c – гипотенуза треугольника (сторона, противоположная прямому углу), a – высота треугольника.

  10. Изображение с названием Find the Perimeter of a Trapezoid Step 22

    10

  11. Изображение с названием Find the Perimeter of a Trapezoid Step 23

    11

    Найдите b. Вы получите основание первого прямоугольного треугольника, которое является первой неизвестной частью нижнего основания трапеции.

  12. Изображение с названием Find the Perimeter of a Trapezoid Step 24

    12

  13. Изображение с названием Find the Perimeter of a Trapezoid Step 25

    13

    Сложите значения всех сторон трапеции. Периметр любого многоугольника равен сумме всех его сторон:P=T+B+L+R. Нижнее основание трапеции равно сумме нижней стороны прямоугольника и оснований двух треугольников.

    • В нашем примере:6+(8,5639+6+6)+10,4566+8,4854=45,5059
      Таким образом, приблизительный периметр трапеции равен 45,5059 см.

    Реклама

Советы

  • Для специальных прямоугольных треугольников (треугольник 30-60-90[8]
     или треугольник 90-45-45[9]
    ) существуют формулы, при помощи которых можно найти неизвестные стороны без использования функции синуса или теоремы Пифагора.
  • Чтобы найти синус угла, воспользуйтесь научным калькулятором – введите угол, а затем нажмите клавишу SIN. Или используйте тригонометрические таблицы.[10]

Реклама

Что вам понадобится

  • Калькулятор
  • Карандаш
  • Бумага

Об этой статье

Эту страницу просматривали 118 928 раз.

Была ли эта статья полезной?

Источник

В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.

  • Формула вычисления периметра

  • Примеры задач

Формула вычисления периметра

Периметр (P) трапеции равняется сумме длин всех ее сторон.

P = a + b + c + d

Периметр трапеции

  • b и d – основания трапеции;
  • a и с – ее боковые стороны.

Периметр равнобедренной трапеции

В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:

P =  2a + b + d или P = 2с + b + d

Периметр равнобедренной трапеции

Периметр прямоугольной трапеции

Для расчета периметра используется такая же формула, что и для разносторонней трапеции.

P = a + b + c + d

Периметр прямоугольной трапеции

Примеры задач

Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.

Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.

Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.

Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.

Источник

Добавить комментарий