Чему равна сумма двух перпендикулярных векторов.
На этой странице сайта, в категории Геометрия размещен ответ на вопрос
Чему равна сумма двух перпендикулярных векторов?. По уровню сложности вопрос рассчитан на учащихся
5 – 9 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.
Опубликовано 3 года назад по предмету
Геометрия
от borko
чему равна сумма двух перпендикулярных векторов
-
Ответ
Ответ дан
RoceteerrДля начала надо перенести их так, чтобы они начинались в одной точке. Сумма их векторов будет равна вектору, соединяющему их концы.
Либо гипотенузе этих двух катетов, т.к. они образуют прямоугольный треугольник. -
Сумма их векторов будет равна вектору, соединяющему их концы. Либо гипотенузе этих двух катетов, т. К. они образуют прямоугольный треугольник.
-
Сумма их векторов будет равна вектору, соединяющему их концы. Либо гипотенузе этих двух катетов, т. К. они образуют прямоугольный треугольник.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Содержание
- Пример пошагового метода параллелограмма
- Частный случай: сумма перпендикулярных векторов
- Решенные упражнения
- – Упражнение 1
- Решение
- – Упражнение 2.
- Решение
- Ссылки
В метод параллелограмма это графический метод сложения двух векторов на плоскости. Он часто используется, чтобы найти равнодействующую двух сил, приложенных к телу, или двух скоростей, как в случае пловца, который пытается пересечь реку перпендикулярно и отклоняется течением.
Чтобы построить параллелограмм, начала добавляемых векторов в масштабе должны совпадать в одной точке.

Затем параллельно каждому вектору проводят вспомогательные линии, доходящие до крайности другого, как показано на рисунке выше.
Сумма или результирующий вектор, также называемый чистой силой, является вектором Fсеть, который получается путем рисования вектора, идущего от общего начала координат F1 Y F2, до точки пересечения вспомогательных параллельных прямых. На схеме рисунка они представлены пунктирными линиями.
Метод получил свое название от фигуры, которая образована слагаемыми векторами и вспомогательными линиями, которая в точности представляет собой параллелограмм. Главная диагональ параллелограмма – это вектор суммы.
Очень важно отметить, что порядок, в котором размещаются слагаемые векторы, вообще не изменяет сумму, так как эта операция между векторами является коммутативной.
Пример пошагового метода параллелограмма
На следующем изображении показаны векторы v Y или в условных единицах. Вектор v измеряет 3,61 единицы и образует угол 56,3 ° с горизонтом, в то время как или он измеряет 6,32 единицы и угол 18.4º относительно указанной опорной линии.
Мы собираемся найти его векторную сумму, используя метод параллелограмма.

Необходимо выбрать соответствующий масштаб, например, показанный на следующем рисунке, в котором плоскость разделена сеткой. Ширина квадрата соответствует одной (1) единице.
Поскольку векторы не изменяются при преобразовании, они располагаются так, чтобы их начало совпадало с началом системы координат (левое изображение).

Теперь давайте выполним следующие шаги:
- Участок к концу вектора v сегментированная линия, параллельная вектору или.
- Повторите процедуру, но на этот раз с концом вектора. или.
- Нарисуйте главную диагональ, идущую от общего начала до точки пересечения сегментированных линий.
Результат виден на правом изображении, на котором появляется результирующий вектор. Р.
Если мы хотим узнать величину р, мы можем измерить его длину и сравнить с имеющимся у нас масштабом. Что касается его направления, то в качестве ориентиров можно использовать, например, горизонтальную или вертикальную ось.
При использовании горизонтальной оси или оси x угол, р форма с указанной осью измеряется транспортиром, и таким образом мы знаем направление р.
Кроме того, величина и направление р можно вычислить с помощью теорем косинусов и синусов, так как образовавшийся параллелограмм можно разделить на два равных треугольника, сторонами которых являются модули векторов или, v Y р. См. Рабочий пример 1.
Частный случай: сумма перпендикулярных векторов
Когда векторы перпендикулярны друг другу, образующаяся фигура представляет собой прямоугольник. Модуль полученного вектора соответствует длине диагонали, которую легко вычислить с помощью теоремы Пифагора.

Решенные упражнения
– Упражнение 1
У нас есть вектор v, который имеет размер 3,61 единицы и составляет угол 56,3 ° с горизонтом, а вектор или, размер которого составляет 6,32 единицы и составляет угол 18,4 ° (рисунок 2). Определите модуль результирующего вектора р = или + v и направление, которое указанный вектор образует с горизонтальной осью.
Решение
Метод параллелограмма применяется в соответствии с шагами, описанными выше, для получения вектора р. Как было сказано ранее, если векторы аккуратно нарисованы по шкале и с помощью линейки и транспортира, величина и направление р они измеряются прямо на чертеже.

Их также можно рассчитать напрямую, с помощью тригонометрии и свойств углов. Когда образованный треугольник не правильный, как в этом случае, применяется теорема косинусов, чтобы найти недостающую сторону.
В треугольнике справа стороны измеряют u, v и R. Чтобы применить теорему косинусов, необходимо знать угол между v Y или, который мы можем найти с помощью сетки, адекватно позиционируя углы, указанные в утверждении.
Этот угол равен α и состоит из:
α = (90-56.3º) + 90º +18.4º = 142.1º
Согласно теореме косинусов:
р2 = v2 + ты2 – 2u⋅v⋅cos α = 3,612 + 6.322 – 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 ед.
Наконец, угол между р а по горизонтальной оси θ = 18,4 º + γ. Угол γ можно найти с помощью теоремы синусов:
грех α / R = грех γ / u
Таким образом:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13.6º
θ = 18.4 º + 13.6 º = 32º
– Упражнение 2.
Пловец собирается пересечь реку, плывя перпендикулярно течению с постоянной скоростью 2,0 м / с. Пловец стартует из точки А, но заканчивается в точке В, расположенной ниже по течению, из-за отклонившего его течения.
Если скорость течения составляет 0,8 м / с, и все скорости предполагаются постоянными, найдите скорость пловца, которую видит наблюдатель, стоящий на берегу.
Решение

Наблюдатель, стоящий на берегу, увидит, как пловец отклоняется в зависимости от полученной скорости. Vр. Чтобы найти ответ, нам нужно векторно сложить скорость пловца относительно воды и скорость течения, которую мы называем V Река:
V р = V пловец + V Река
На рисунке, который не в масштабе, векторы были добавлены для получения V р. В этом случае можно применить теорему Пифагора, чтобы получить его величину:
Vр2 = 2.02 + 0.82 = 4.64
Vр = 2,15 м / с
Направление, в котором пловец отклоняется от перпендикулярного направления, легко вычислить, учитывая, что:
θ = arctg (2 / 0,8) = 68,2º
Затем пловец отклоняется на 90º – 68,2º = 27,2º от своего первоначального направления.
Ссылки
- Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
- Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
- Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
- Сирс, Земанский. 2016. Университетская физика с современной физикой. 14-го. Ред. Том 1.

Добавил:
Low
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
247
Добавлен:
07.10.2014
Размер:
30.72 Кб
Скачать
Закажи выполнение студенческой работы, избавься от головной боли и сдай на отлично
?
Временно скрыть
Больше не показывать
Какую работу нужно написать?
27.Сложение взаимно
перпендикулярных колебаний.
Траектория движения
описывается уравнением эллипса:
x²/A₁²+y²/A₂²-×cosφ=sin2φ
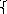
x=A1sinωt
y=A2sin(ωt+φ)
Это уравнения
траектории в параметрическом виде.
Для
получения явной зависимости между
координатами x
и y
надо из уравнений исключить параметр
t.
Из
первого уравнения: cosωt
= x/A;
sinωt
= +-√1-x²/A²;
Из второго: y
= B[cosωt
* cosα
* sinωt
* sinα]
После
подстановки:
![]() .
.
Избавимся от корня:![]() .
.
x²/A² +
y²/B² – 2xy/AB*cosα = sin²α- это
уравнение
эллипса.
Сложив два вектора, в результате получим новый вектор.
Векторы могут располагаться один относительно другого:
- параллельно,
- не параллельно.
Складываем параллельные векторы
Если векторы параллельны, складывать так:
- А) К концу первого вектора приложить начало второго вектора
- Б) из начала первого вектора к концу второго вектора провести новый вектор

Рис. 1. Складываем параллельные векторы
( vec{a} + vec{c} = vec{g} )
Примечание:
В этом уравнении над буквами используются значки векторов. Эти значки указывают на то, что действия выполняются с помощью геометрии. То есть, учитывается направление векторов.
Важно! Любое выражение, записанное в векторном виде, учитывает направление векторов.
Это можно пояснить так:
- сложив два числа 3 и 4 получим только одно решение (3 + 4 = 7).
- складывая два вектора с длинами 3 и 4, можно в результате получить вектор, длина которого лежит в диапазоне от «1» до «7».
- Если векторы, которые складываем, были направлены в противоположные стороны, получим вектор, длина которого равняется единице.
- А если векторы были сонаправленными – то длина результирующего вектора будет равна семи.
- Ну а, если векторы были препендикулярными, то конечный вектор будет иметь длину, равную пяти.
Если векторы направлены в противоположные стороны, то результат сложения будет сонаправлен с более длинным вектором.

Рис. 2. Складываем параллельные противоположно направленные векторы
( vec{a} + vec{s} = vec{w} )
Складываем не параллельные векторы
Если векторы не параллельны (см. рис. ), для их сложения пользуются одним из двух правил:
- правило треугольника;
- правило параллелограмма;

Рис. 3. Не параллельные векторы
Примечание:
Правило параллелограмма удобно применять к векторам, выходящим из одной общей точки (начала векторов совмещены).
Правило треугольника
К концу первого вектора приложить начало второго вектора

Рис. 4. Располагаем не параллельные векторы, чтобы сложить их по правилу треугольника
Из свободного начала к свободному концу провести вектор

Рис. 5. Складываем не параллельные векторы по правилу треугольника
( vec{a} + vec{b} = vec{c} )
Правило параллелограмма
Совместить начала векторов

Рис. 6. Совмещаем начала не параллельных векторов, чтобы сложить их по правилу параллелограмма
Провести пунктиры, чтобы получить параллелограмм

Рис. 7. Достраиваем пунктирами параллелограмм, чтобы сложить векторы
Из точки, в которой находятся начала провести диагональ

Рис. 8. Проводим диагональ параллелограмма, чтобы сложить векторы
( vec{a} + vec{b} = vec{c} )
Как вычитать векторы
Вычтем один вектор из второго вектора. В результате получим новый вектор.
Вектор «( -vec{b} )» — это вектор «( vec{b} )», развернутый в противоположную сторону.

Рис. 9. Вектор и противоположно направленный ему вектор
Вычитание заменяют сложением. Складывают вектор с противоположно направленным вектором.
Ведь ( vec{a}-vec{b} ) то же, что и ( vec{a}+ left(-vec{b} right)).

Рис. 10. Складываем вектор «a» и противоположно направленный вектор «-b»
( vec{a} + left(-vec{b} right) = vec{g} )
Складываем и вычитаем векторы, используя их координаты
Когда известны координаты двух векторов, сложение или вычитание провести достаточно легко. Для этого нужно сложить или вычесть соответствующие координаты векторов.
Для удобства обычно выписывают один вектор под другим.
( vec{a} = left{ a_{x} ; a_{y} ; a_{z} ;right} )
( vec{b} = left{ b_{x} ; b_{y} ; b_{z} ;right} )
Рассмотрим примеры:
1. Сложение.
( vec{a} + vec{b} = vec{c} )
( vec{c} = left{ a_{x}+ b_{x} ; a_{y}+ b_{y} ; a_{z} + b_{z} right} )
2. Вычитание.
( vec{a} — vec{b} = vec{d} )
( vec{d} = left{ a_{x}- b_{x} ; a_{y}- b_{y} ; a_{z} — b_{z} right} )
Примеры сложения векторов в физике
Напоминание:
Складывать и вычитать можно только те векторы, которые имеют одинаковую размерность. То есть, длина которых измеряется в одинаковых единицах.
Рассмотрим формулу связи между начальной и конечной скоростями при равноускоренном движении
( vec{v} = vec{v_{0}} + vec{a} cdot t )
Скорость ( vec{v} )измеряют в метрах деленых на секунду, а ускорение ( vec{a} ) – в метрах, деленых на секунду в квадрате.
Размерность векторов ( vec{v} ) и ( vec{a} ) отличается. Значит, выполнять математические действия совместно над ними нельзя.
Если преобразовать вектор ( vec{a} ) ускорения так, что он получит размерность скорости, тогда можно будет складывать его с вектором скорости.
Чтобы из размерности ускорения получить метры, деленные на секунду, нужно размерность ускорения домножить на секунду.
Поэтому, в формулу для равноускоренного движения входит ( vec{a} cdot t ) — ускорение, домноженное на время.
Теперь векторы ( vec{v_{0}} ) и ( vec{a} cdot t ) имеют одинаковую размерность и их можно складывать, или вычитать.
Примечания:
— Скорость всегда направлена в ту сторону, в которую тело движется (в направлении движения тела).
— Ускорение направлено в сторону действия силы (из второго закона Ньютона).
Обратите внимание: Направление силы не всегда будет совпадать с направлением, в котором тело двигалось изначально.
Силу можно направить в любую сторону. Она будет толкать или тянуть тело в ту сторону, в которую она направлена. Поэтому, конечная скорость ( vec{v} ), начальная скорость ( vec{v_{0}} ) и ускорение ( vec{a} ) могут иметь различные направления.
Векторы складывают с помощью геометрии, то есть, учитывают их направления.
Поэтому, формула ( vec{v} = vec{v_{0}} + vec{a} cdot t ) записана в векторном виде.
