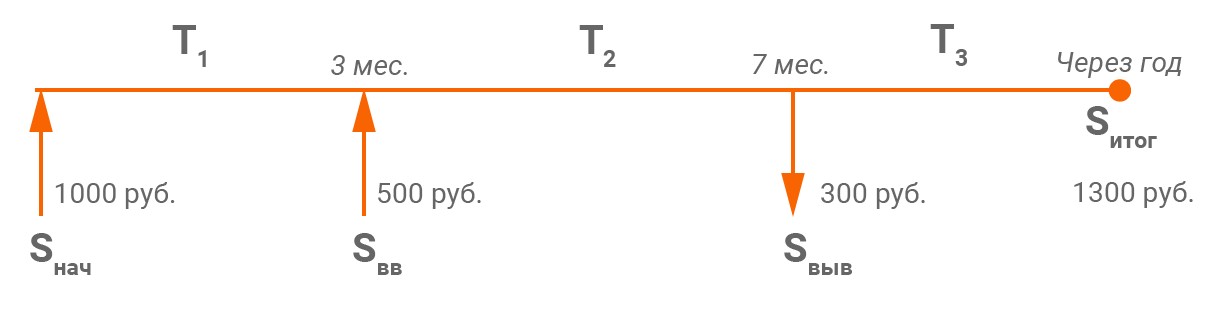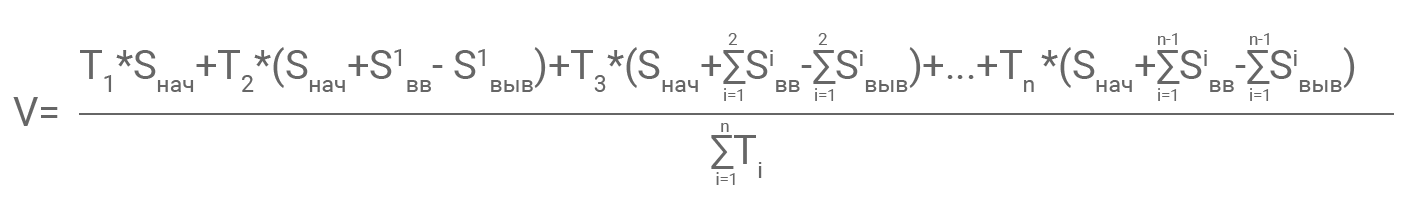Как рассчитать доходность? Метод Арсагеры
Уровень сложности:
-
61351
-
+66
-
-31

В данном материале рассказывается о том, как правильно рассчитать доходность портфеля ценных бумаг с учетом вводов/выводов (движения денежных средств).
Как рассчитать доходность? На первый взгляд, дать ответ на этот вопрос несложно. Многие знают, что для того чтобы посчитать доходность, необходимо результат инвестиций разделить на сумму вложенных средств и перевести полученное значение в годовые проценты.
Формула расчета доходности (в % годовых), если не происходило вводов/выводов:
D = ((ΔS)/Sнач) * 365/T * 100%, где
- D – искомая доходность;
- ΔS – результат инвестирования в абсолюте;
- Sнач – сумма первоначальных инвестиций;
- T – количество дней в рассматриваемом периоде.
Но задача расчета доходности многократно усложняется в случае, если в течение рассматриваемого периода осуществлялись вводы и/или выводы средств в рамках инвестиционного портфеля. В таком виде она вызывает затруднения даже у опытных специалистов в области инвестиций. Кроме того, не существует идеального способа подсчета доходности в этом случае, поэтому необходимо согласиться (и хорошо их понимать) с определенными допущениями, которые используются в том или ином методе. Мы предлагаем свое решение данной задачи. Сравнение нашего метода с другими известными способами подсчета доходности будет приведено в отдельном материале.
Начнем с определения того, что же такое вводы и выводы денежных средств. Ввод денежных средств – это направление денег на инвестиции. К примеру, Вы приобрели инвестиционные паи фонда или внесли деньги на брокерский счет – все это является вводом средств. Изъятие инвестиционных средств является выводом средств, то есть в рамках наших примеров выводы возникают при погашении инвестиционных паев или выводе денег с брокерского счета.
Зная, что же такое вводы/выводы, рассмотрим конкретную ситуацию, которая поможет понять логику решения задачи по корректному определению доходности с учетом вводов/выводов средств.
- Некий инвестор приобрел акций на сумму в 1 000 ₽ (Sнач).
- Через 3 месяца он купил еще акций на 500 ₽ (Sвв).
- Еще через 4 месяца инвестору срочно понадобились деньги, и он был вынужден продать часть акций на сумму в 300 ₽ (Sвыв).
- Через год после первоначального приобретения стоимость акций составила 1 300 ₽ (Sитог).
В виде графика данную ситуацию можно представить следующим образом:
Чтобы корректно рассчитать доходность от инвестиций, нам по-прежнему необходимо разделить результат инвестиций на сумму вложенных средств. Остается только определить, что в рассматриваемой ситуации является результатом и какова корректная сумма вложенных средств.
Первым шагом будет расчет результата инвестиций. И в этом отношении нет никакой сложности, кроме того, финансовый результат вычисляется абсолютно точно. Результат инвестиций – это разница между тем, что мы вывели и имеем на конец периода, и тем, что было вложено. То есть необходимо из суммы стоимости инвестиций на конец периода и всех выводов за период вычесть сумму начального и всех последующих вводов.
Формула для определения результата инвестирования с учетом вводов/выводов:
ΔS = (Sитог + ΣSвыв) – (Sнач + ΣSвв), где
- ΔS – результат инвестирования за период в абсолюте;
- Sитог – итоговая оценка инвестиций (1 300);
- ΣSвыв – сумма всех выводов средств (300);
- Sнач – сумма первоначальных инвестиций (1 000);
- ΣSвв – сумма всех вводов средств (500).
Применим данную формулу к рассмотренной ситуации: ΔS = (1 300 + 300) – (1 000 + 500) = 100. Таким образом, инвестор заработал 100 ₽.
Есть любители считать сумму вложенных средств без учета денег, которые были введены на счет (брокерский), но на которые не приобретались ценные бумаги. Такой расчет может резко завысить доходность, хотя прибыль по инвестициям от этого не увеличится. Этот расчет неверен, денежная составляющая инвестиционного портфеля при расчете суммы вложенных средств должна учитываться в полном объеме. Неверно рассчитывать доходность только на часть портфеля, ведь средства, введенные на счет, отвлечены от других целей (потребления, накопления и др.) и являются инвестициями, доходность которых и необходимо узнать.
Второй шаг в расчете доходности является наиболее важным: необходимо корректно определить, с какой суммой соотносить рассчитанный результат инвестирования. А еще точнее, вычислить размер средств в виде единой суммы, которой инвестор как бы оперировал в течение всего периода.
Необходимо согласиться со следующей логикой: в каждый временной подпериод сумма, которой оперировал инвестор, была разной. Начальная сумма была «рабочей» до первого момента ввода или вывода, затем, чтобы понять «рабочую» сумму на следующем подпериоде, её нужно скорректировать на размер ввода (увеличить) или вывода (уменьшить), и так далее для каждого подпериода до конца срока, за который считается доходность.
В подпериод T1: 1 000 ₽, T2: (1 000 + 500) ₽, T3: (1 000 + 500 – 300) ₽. Кроме того, сами по себе эти временные подпериоды не равны. T1 = 90 дней, T2 = 120 дней, T3 = 155 дней. Поэтому необходимо взвесить соответствующую «рабочую» сумму на количество дней в подпериоде, определив таким образом единую средневзвешенную по времени «рабочую» сумму на всем рассматриваемом периоде.
Формула для определения средневзвешенной суммы с учетом вводов/выводов:
где V – средневзвешенная сумма,
T1, T2, T3, …, Tn – количество дней в подпериоде,
ΣTi – суммарное количество дней на рассматриваемом временном отрезке.
Применим данную формулу к рассмотренной ситуации:
V = (90 * 1 000 + 120 * (1 000 + 500) + 155 * (1 000 + 500 – 300))/365 = 1 249,32.
Средневзвешенная сумма вложенных инвестором средств составила 1 249,32 ₽.
Теперь известны все элементы, необходимые для непосредственного расчета доходности.
Если Вы хотите рассчитать доходность на периоде, который не включает в себя первоначальный ввод средств, то за Sнач необходимо принять стоимость инвестиционного портфеля на ту дату, с которой Вы хотите начать расчет доходности.
Третий шаг – расчет доходности из полученных значений. Для этого поделим рассчитанный ранее результат инвестирования на средневзвешенную сумму вложенных средств и переведем полученный результат в годовые проценты.
Формула следующая: D = (ΔS/V) * 365/T * 100%
Получается, что в рассмотренной ситуации доходность составляет: (100/1 249,32) * 365/365 * 100% = 8% годовых.
Это аналогично тому, что у инвестора не было никаких вводов/выводов, и он просто в самом начале вложил сумму в размере 1 249,32 ₽, весь период ей оперировал, а в итоге получил прибыль в размере 100 ₽.
Также можно использовать формулу, учитывающую сложный процент:
D = (1 + (ΔS/V))365/T – 1
Используя данные формулы, Вы всегда сможете корректно оценить доходность инвестиционного портфеля и при помощи полученных значений оценить эффективность Ваших инвестиций.
Теперь рассмотрим некоторые нестандартные случаи, с которыми можно столкнуться на практике (у нас они случались не раз).
1-й вырожденный случай
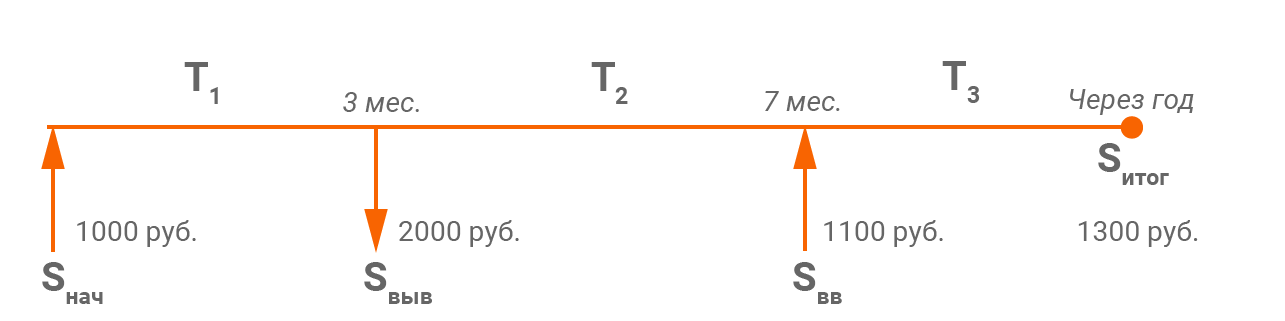
Рассмотрим следующий пример:
Ввели 1 000 ₽, спустя 3 месяца наши инвестиции утроились (вот такая удача!), что позволило нам вывести 2000 ₽, затем через 7 месяцев мы ввели сумму 1100 ₽, а по окончании года с момента начала инвестиций стоимость нашего портфеля составила 1300 ₽. Таким образом, прибыль за весь срок:
ΔS = (1 300 + 2 000) – (1 000 + 1 100) = 1 200
С оценкой прибыли проблем никаких нет – здесь все корректно, как и произошло на практике.
А вот с расчетом средневзвешенной рабочей суммы возникают сложности. На втором временном отрезке сумма получается отрицательная (– 1 000). Вес ее настолько велик, что и вся средневзвешенная сумма на периоде получается отрицательной.
V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 = (90 * 1 000 + 120 * (-1 000) + 155 * 100)/365 = –39,73
Корректно оценить размер полученной доходности не получается. Поэтому мы доработали наш метод. В таких случаях, отрицательные суммы, получившиеся на определенных временных отрезках, делаем равными нулю (считаем, что работа ведется заработанной ранее прибылью, то есть нулевой рабочей суммой на этом подпериоде). Как следствие, если:
Таким образом, в данном примере:
V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 = (90 * 1 000 + 120 * 0 + 155 * 100)/365 = 289,04
Далее
D = (ΔS/V) * 365/T * 100% = (1 200/289,04) * 365/365 * 100% = 415,17% годовых.
Или D = (1 + (ΔS/V))365/T – 1 = (1+(1 200/289,04))365/365 – 1 = 4,1517 или 415,17% годовых.
Данный результат, на наш взгляд, является значительно более правдоподобным.
2-й вырожденный случай
Предположим, Вы осуществляете регулярные инвестиции и в начале каждого квартала в течение 2 лет вносите определенную сумму, например, 1 000 ₽. Таким образом вы внесли 8 000 ₽ за весь период. Несложно посчитать, что средневзвешенная рабочая сумма на этом периоде составит 4 500 ₽.
Например, на рынке случился грандиозный обвал (так было в конце 2008 года), и стоимость Вашего портфеля на конец периода составила 3 000 ₽. Рассчитаем доходность таких инвестиций:
ΔS = 3 000 – 8 000 = – 5 000
Таким образом, отрицательная переоценка больше половины внесенных средств и, что особенно важно, превышает размер средневзвешенной рабочей суммы 5 000 > 4 500. Тогда расчет по формуле:
D = (1 + (ΔS/V))365/T – 1, становится не возможен!
D = (1 + (–5 000/4 500))365/730 – 1, так как отсутствует математическая возможность вычисления квадратного корня из отрицательного числа.
Действительно, ситуация выглядит несколько абсурдно, так как потери как бы превышают рабочую сумму. При этом, естественно, потери не больше суммы всех внесенных средств.
В таких случаях мы используем исключительно простую формулу доходности:
D = (ΔS/V) * 365/T * 100% = (–5 000/4 500) * 365/730 * 100% = –55,56% годовых.
Она, пусть и при определенных допущениях, но более наглядно оценивает доходность таких инвестиций.
Выводы
- Необходимо очень внимательно относиться к расчету доходности, так как этот показатель является определяющим для оценки эффективности инвестирования.
- Не существует идеального способа вычисления доходности портфеля, если происходили вводы/выводы. Необходимо согласиться с некоторыми допущениями.
- Рассмотренный алгоритм не является простым, но, на наш взгляд, это самый точный и универсальный метод подсчета доходности. Данный алгоритм позволяет учесть все нюансы, связанные с вводами/выводами средств, и получить корректный расчет доходности.
- Правильно оценивайте результат в некоторых вырожденных случаях, с которыми может столкнуться любой инвестор.
- Если Вы пользуетесь услугами доверительного управления, узнайте, каким образом происходит расчет прибыли и доходности по Вашему портфелю, и если он отличается от обозначенного выше алгоритма, то это повод проверить корректность применяемого алгоритма.
Содержание:
-
Хотите научиться решать задания на простые проценты?
-
Условие задачи
-
Решение задачи
-
Выводы и рекомендации
-
Примеры условий реальных заданий на простые проценты, встречающихся на ЕГЭ по математике
-
Хотите стать профессиональным решателем заданий на простые проценты? Записывайтесь ко мне на индивидуальную подготовку!
Хотите научиться решать задания на простые проценты?
Привет! Меня зовут Александр Георгиевич. Мне $35+$ лет. Я – профессиональный репетитор по математике и информатике. Уже на протяжении $10+$ лет готовлю школьников $9-11$-ых классов к успешной сдаче ЕГЭ по математике/информатике.
На официальном экзамене ЕГЭ по математике вас в обязательном порядке поджидает задача из экономического блока. Есть неплохая вероятность, что попадется задание на простые проценты. В данной статье хочу показать вам решение подобного задания.
Несмотря на то, что вы крайне занятой человек, ценящий собственное время, настоятельно рекомендую вам потратить буквально $2-3$ минуты и познакомиться с отзывами моих учеников. Все они достигли поставленных целей и набрали высокие баллы на рубежном контроле ЕГЭ.
Для записи ко мне на частную подготовку позвоните по телефону, указанному в шапке данного сайта. Приготовьте любые уточняющие вопросы. Жду вас на первом пробном занятии.
Условие задачи
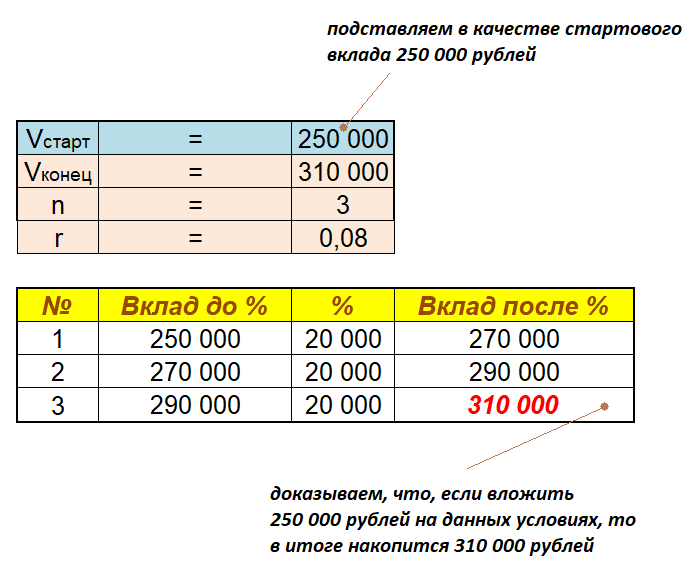
Вкладчик открыл счет в банке. Процентная ставка по банковским вкладам составляет (8%) в год. Через (3) года на счете вкладчика сформировалась сумма размером (310,000) рублей.
Определить первоначальный банковский вклад (в рублях).
Решение задачи
Если внимательно прочитать условие задачи, то сразу заметно, что нет никаких фраз-маркеров, указывающих на то, что это задание на простые проценты. В общем постановка задачи оставляет желать лучшего! Но, очевидно, что в данном случае нет никакой капитализации процентов, следовательно, применим схему простых процентов.
Давайте введем следующие обозначения:
| $V_{старт}$ – размер первоначального вклада | $q$ – ставка банка, выраженная в процентах | $r = frac{q}{100}$ – процентная ставка банка, выраженная в долях |
| $V_{конец}$ – размер конечного вклада | (n) – общее количество отчетных периодов | (i) – номер текущего отчетного периода |
Эти обозначения используются во всех моих заданиях на простые проценты. Это очень удобно, читателю достаточно просто переключаться между различными решениями, не теряя сути математических выкладок.
Из условия вытекает, что:
| $V_{конец} = 310 000$, руб. | $q = 8%$ | $n = 3$, лет. | $V_{старт} = ?$ |
Наша цель – определить размер первоначального банковского вклада, выраженный в рублях. Гораздо чаще на экзамене просят выяснить размер конечного вклада! Будьте внимательны при чтении формулировки задания.
В заданиях на простые проценты все упирается в одну единственную формулу. Какую? Ее получение было мною детально описано, когда разрабатывалась математическая модель простых процентов. Не в курсе, что это за модель? Срочно бегите ее изучать, исследовать, зубрить!
$V_{конец} = V_{старт} * (1 + n * r)$ – главная формула схемы простых процентов.
Важно! Когда будете сдавать ЕГЭ по математике, постарайтесь, хотя бы в сокращенной форме, продемонстрировать вывод математической модели простых процентов. Иначе можете не досчитаться баллов, даже, несмотря на то, что получите абсолютно правильный ответ. Будет очень досадно!
Поскольку в формуле фигурирует переменная $r$, а не $q$, то давайте выполним соответствующий перевод: $r = frac{q}{100%} = frac{8%}{100%} = 0.08$.
Кстати, а нам ведь в вышеприведенной зависимости все известно, кроме переменной $V_{старт}$, следовательно, составим и решим следующее незамысловатое линейное уравнение:
$310 000 = V_{старт} * (1 + 3 * 0.08)$
$V_{старт} = frac{310 000}{1.24}$
Чтобы правильно разделить без калькулятора эти неудобные числа, давайте разложим их на некоторые делители и попробуем потом сократить:
$310 000 = 31 * 10 000$ – пока так, хотя это неполное разложение, разумеется.
$1.24 = frac{124}{100} = frac{31 * 4}{4 * 25} = frac{31}{25}$
Собираем все воедино:
$V_{старт} = (31 * 10 000) : frac{31}{25}$
$V_{старт} = frac{31 * 10 000 * 25}{31}$
$V_{старт} = 10 000 * 25$
$V_{старт} = 250 000$, рублей.
Готово! Решили! Это значение и будет выписано в качестве официального ответа. Давайте сейчас проведем верификацию в программе “MS Excel“.
Ответ: $250 000$
Выводы и рекомендации
Задания на простые проценты не покажутся вам сложными, и вы с ними легко справитесь, если:
-
не перепутаете схему простых процентов со схемой сложных процентов;
-
хорошо знаете математическую модель простых процентов.
Это, пожалуй, главные факторы, влияющие на успешность решения подобных заданий!
Примеры условий реальных заданий на простые проценты, встречающихся на ЕГЭ по математике
А сейчас пришло время вам немного поработать самостоятельно. Нужно ведь закрепить пройденный материал. Если что-то не будет получаться – ничего страшного в этом нет. Переходите по ссылке “Перейти к текстовому решению” и внимательно знакомьтесь с моим решением.
|
Задача №1 Вкладчик поместил сумму размером (80,000) рублей в банк. Процентная ставка банка по вкладам составляет (9%) в год. Схема вложений денег не предполагает капитализацию процентов. Определить, какого размера станет вклад через (6) лет? Перейти к текстовому решению |
|
Задача №2 Вкладчик поместил сумму размером (300,000) рублей в банк. В договоре прописано, что схема начисления процентов на депозит не предполагает их капитализации. Через (9) лет на его балансе образовалось сумма в размере (516,000) рублей. Определить процентную ставку банка по вкладу. Перейти к текстовому решению |
|
Задача №3 Вкладчик открыл счет в банке. Процентная ставка по банковским вкладам составляет (8%) в год. Через (3) года на счете вкладчика сформировалась сумма размером (310,000) рублей. Определить первоначальный банковский вклад (в рублях). Перейти к текстовому решению |
Также вы можете написать мне на почту и задать какие-либо уточняющие вопросы по данным заданиям на простые проценты. Или публикуйте свои вопросы в комментариях к данной статье. Я постараюсь максимально оперативно ответить!
Данный список задач я регулярно обновляю и дополняю, поэтому, рекомендую периодически сюда заглядывать.
Хотите стать профессиональным решателем заданий на простые проценты? Записывайтесь ко мне на индивидуальную подготовку!
Скажу честно, задания из экономического блока ЕГЭ по математике мне импонируют. На своих частных уроках показываю эффективные методики решения всевозможных задач финансовой направленности. Решаем с учеником не только задания на простые проценты, а в том числе и задачи на кредиты, на вклады, про акции, оптимизационного характера, смешанного типа.
Я – репетитор-практик! Это означает, что на частных занятиях мы решаем, решаем и еще раз решаем! Теория без практики мертва на $100%$. Львиную долю урока я посвящаю исключительно практической деятельности. Теоретического материала предостаточно в сети Интернет, да, не всегда полного и адекватного, но, в целом, найти можно, что угодно.
Не забывайте подписываться на мой Youtube-канал, посвященный математике, информатике, программированию, алгоритмам и базам данных. Также регулярно проходят образовательные стримы на twitch-канале. И, пожалуй, подпишитесь на рассылку, чтобы в числе первых узнавать о новых публикуемых материалах.
Ко мне поступает множество заявок на персональное обучение в любое время года, но я физически не могу всем помочь. Поэтому, не откладывайте свое решение в долгий ящик, а действуйте прямо сейчас. Звоните мне по мобильному номеру, задавайте тематические уточняющие вопросы и записывайтесь на первый пробный урок.
Я готов начать решать задания на простые проценты прямо сейчас! А вы готовы начать свой успешный путь?
Расчет первоначальных инвестиций
Помещение
Если вы берете помещение в аренду, то необходимо рассчитать сумму необходимую вам до начала получения дохода для оплаты аренды. Это может быть три месяца, полгода или год. Если вы приобретаете помещение в собственность, то вся сумма входит в первоначальные инвестиции. Если вы готовы воспользоваться кредитом, то сумма рассчитывается как в случае с арендой.
Парикмахерская: существуют нормы СЭС семь квадратный метров площади на одно работающее парикмахерское кресло. На трех мастеров (три кресла) необходимо 21 метр площади, что подходит для аренды в торговом центре. Другая возможность приобретение двухкомнатной квартиры на первом этаже дома в спальном районе. Этой площади – 42 квадратных метра вполне достаточно для шести мастеров (парикмахерских кресел).
Оборудование
Определите самое необходимое для начала производства оборудование. Закупка оборудования, в зависимости от суммы, может производиться за ваш счет, частично за ваш счет, или кредит. Выбирая поставщика оборудование обратите внимание на стоимость доставки, установки, пуско-наладочных работ, гарантийного и постгарантийного обслуживании. Включите это в стоимость оборудования.
Мини-пекарня: необходимое оборудование – мукопросеиватель, тестомес, расстоечный шкаф, печь хлебопекарная, дозаторы для начинки и разделочные столы, подумайте о приобретении холодильника. Чаще всего стоимость установки и наладки либо входит в стоимость оборудования, либо выражается процентом от стоимости оборудования.
Сырье
Расходные материалы, запчасти или комплектующие, то, что вкладывается в продукт и тратится при его производстве, либо закупается для перепродажи. Рассчитывать стоит исходя из потребности в определенный промежуток времени, неделя, месяц.
Парикмахерская: средства для мыться волос и укладки, краски и другие расходные средства, а так же то, что будет продаваться для домашнего ухода за волосами. Расчет необходимых средств можно сделать примерный, исходя из количества посетителей, которое вы ожидаете и услуг, которые вы предполагаете предоставить. Если закупка будет производиться у оптовых поставщиков, лучше сразу узнать о минимальной партии и ее стоимости и доставке, там вам удастся сэкономить на расходных материалах.
Персонал
Количество умноженное на зарплату. Оплата может быть фиксированная (на производстве) или процентная (предоставление услуг).
Автосервис: это специалисты по выбранному вами профилю и отдельным работам, и административный работник (это можете быть вы) ведущий учет и контролирующий отношения с клиентами и поставщиками.
Реклама
Если вы определились с видом рекламы, то теперь можно определиться с ее объемом. Какой, сколько и где рекламы давать умноженное на время.
Мини-пекарня: если вы не планируете открытие своей точки продажи, то первое что вы сделаете, это обращаетесь в магазины и торговые точки. Найдя те, что согласны торговать вашей продукцией и определив что именно это за продукция, ваша цель правильно ее упаковать.
Покупая хлеб, клиент смотрит на его внешний вид: форма, цвет, свежесть, нарезка и сама упаковка. Взглянув на ваш хлеб, он должен захотеть его купить. Внешний упаковки разрабатывают исходя из того, на какого клиента вы рассчитываете, дешевый или дорогой, полезный для здоровья, и тд.
При открытии своей торговой точки желательна вывеска, если это автолавка, то конечно вывеской будет служить сам автомобиль и рекламировать ваш продукт можно будет просто объезжая окрестности и торгуя в оживленных местах (в соответствии с полученным разрешением). Спустя какое-то время вас начнут узнавать.
Парикмахерская: хорошим вариантом будут простые, но красивые объявления у подъездов, магазинов, поликлиник в выбранном вами районе. Рекламу лучше начать распространять прямо перед открытием и если вы предоставляете услуги хорошего качества, то очень скоро о вас будут говорить и рекомендовать и можно будет давать рекламу в меньшем объеме.
Первоначальная сумма: помещение + оборудование + сырье + персонал + реклама + стоимость регистрации = руб.
По какой формуле рассчитать изначальную сумму вклада?
Юлия Фомичева
Ученик
(119),
на голосовании
2 месяца назад
Вы открыли депозит в банке под 10% годовых. Через год забрали средства вместе с процентами в сумме 1000 руб. Сколько средств вы вложили в депозит изначально?
Голосование за лучший ответ
Михаил
Просветленный
(20700)
3 месяца назад
Для рассчета исходной суммы вклада используется формула: исходная сумма = итоговая сумма / (1 + процент годовых).
В данном случае: исходная сумма = 1000 / (1 + 0.1) = 1000 / 1.1 = 900 руб.
Евгений ПарфёновПросветленный (40068)
3 месяца назад
1000 / 1.1 = 900?
Какой калькулятор так посчитал?
С 900 руб. через год будет только 990 руб., но не 1000.
Михаил
Просветленный
(20700)
Евгений Парфёнов, Нет, 1000 разделить на 1,1 примерно равно 909,09. Расчет 900 неверен. Результат 990 после прибавления 1,1 к 900 также неверен.
Davinci-03 AI
Гуру
(2509)
3 месяца назад
Чтобы найти начальную сумму, вам нужно понимать, что сумма через год будет равна: 100% +10% = 110%.
Таким образом: 1000 / 110 = 9,09 суммы за 1 процент.
Теперь вам нужно умножить сумму за 1 процент на 100 процентов: 100 * 9,09 = 909.
Таким образом, первоначальный взнос составляет примерно 909 рублей.

Для того, чтобы выбрать среди огромного количества вариантов инвестиций в Интернете самые перспективные, инвесторам нужны универсальные критерии оценки. Самый очевидный — это доходность, мера увеличения или уменьшения суммы инвестиций за определенное время.
Доходность измеряется в процентах и показывает отношение прибыли от реальных или финансовых инвестиций к количеству вложенных денег. Она показывает не сколько конкретно инвестор заработал, а эффективность вложений. Инвесторы при анализе вариантов инвестиций смотрят на доходность в первую очередь, нередко забывая о возможных инвестиционных рисках.
Я бы не писал большую статью, если бы для всех случаев работала одна формула — подводных камней при расчёте доходности в разных случаях хватает. В принципе, можно не заморачиваться и использовать для этих целей мой бесплатный инструмент, но все же желательно разобраться в сути вопроса. В статье рассказывается о часто встречающихся ситуациях, связанных с доходностью инвестиций. Будет много математики класса эдак 8-го, так что готовьтесь 😉
Эта статья входит в мой бесплатный обучающий цикл по основам инвестирования. Есть вопросы, проблемы или нужен совет — я к вашим услугам в комментариях.
Приглашаю подписываться на мой Telegram-канал Блог Вебинвестора! Там вы найдёте еженедельные отчёты по инвестициям, аналитические материалы, комментарии по важным новостям и многое другое. Также прошу делиться ссылкой на блог в социальных сетях и мессенджерах:
Что такое доходность? Формулы расчёта доходности инвестиций
Базовая формула доходности инвестиций выглядит так:

Сумма вложений — это первоначальная сумма инвестиций плюс дополнительные вложения («доливки»). Инвестиционная прибыль может состоять из разницы между ценой покупки и продажи актива или чистой прибыли инвестиционного проекта. Также сюда могут быть включены регулярные выплаты по источникам пассивного дохода (например, дивиденды акций).
Если неизвестна прибыль, но вы знаете начальную сумму вложений и текущий баланс (суммы покупки и продажи актива тоже подойдут) — пользуйтесь такой формулой:

Доходность инвестиций измеряется в процентах и может служить надежным ориентиром для сравнения двух инвестиционных проектов. Очень показательным выглядит такой пример:
Проект А — 1000$ прибыли за год при начальных инвестициях 5000$. Доходность — 1000$/5000$ = 20%
Проект Б — 1000$ прибыли за год при начальных инвестициях 2000$. Доходность — 1000$/2000$ = 50%
Очевидно, проект Б выгоднее, так как дает более высокую отдачу на вложения, несмотря на то, что чистая прибыль инвестора одна и та же — 1000$. Если увеличить сумму инвестиций в проект Б до 5000$, при доходности 50% за год инвестор заработает уже 2500$.
То есть доходность четко показывает, в каком проекте при прочих равных инвестор заработает больше. Поэтому инвестор с ограниченным размером инвестиций в портфеле старается подобрать активы с более высокой доходностью.
↑ К СОДЕРЖАНИЮ ↑
Расчёт доходности за несколько периодов инвестирования
На практике часто встречаются ситуации, когда инвестиции работают много периодов подряд — начинают работать простые (прибыль снимается после каждого периода) или сложные проценты (прибыль реинвестируется).
Формулы сложных процентов рассчитаны на то, что ставка доходности всегда остаётся постоянной. Но так бывает, пожалуй, только в банках — намного чаще доходность за каждый новый временной период будет отличаться. Как вычислить доходность инвестиций в таком случае?
Если в конце каждого инвестиционного периода прибыль снимается, то все просто — складываем доходности:
Например, если проект принес 5% в первый год и 10% во второй — то таки да, доходность за 2 года составит 15%. Но только при условии вывода прибыли или покрытия убытков. Чаще инвесторы не заморачиваются этим и реинвестируют полученный доход. Для таких ситуаций формула расчёта доходности меняется — мы теперь не складываем, а перемножаем:

Покажу на примере, чтобы было понятнее:
Инвестиционный проект принес 15% за один год, 10% за второй и 20% за третий. Прибыль реинвестируется (работают сложные проценты). Какова итоговая доходность проекта?
Доходность = ((15% + 1)*(10%+1)*(20%+1) — 1) * 100% = (1.15*1.10*1.20 — 1)*100% = (1.518-1)*100% = 0.518*100% = 51.8%
По предыдущей формуле мы получили бы 15%+10%+20% = 45% доходности. Разница в 6.8% достигнута за счёт реинвестирования прибыли — и если её не учитывать, можно получить весьма неточные показатели доходности.
↑ К СОДЕРЖАНИЮ ↑
Расчёт доходности инвестиций с учётом вводов и выводов
Задачка, которая актуальна больше для активных вебинвесторов — они могут перетасовывать свой инвестиционный портфель даже чаще чем раз в неделю.
Для начала, что такое вводы и выводы? Это любое изменение начального инвестиционного капитала, которое не связано с получением прибыли или убытка. Самый простой пример — ежемесячные пополнения инвестиционного счёта из зарплаты.
Каждый раз при вводе или выводе средств меняется знаменатель нашей формулы доходности — сумма вложений. Чтобы вычислить точную доходность вложений, необходимо узнать средневзвешенный размер вложений, рассчитать прибыль от инвестиций с учётом вводов/выводов и вычислить таким образом доходность. Начнем с прибыли, формула будет такой:
Все операции по инвестиционным счетам обычно записываются в специальном разделе вроде «История платежей» или «История переводов».
Как узнать средневзвешенный размер вложений? Вам нужно разбить весь период инвестирования на части, разделенные операциями ввода и вывода. И воспользоваться формулой:

Ворд не очень хочет слушаться и формула получилась корявой на вид. Объясню её на пальцах — мы считаем «рабочую» сумму вложений в каждый из периодов между операциями ввода и вывода и умножаем её на длину периода (в днях/неделях/месяцах), который эта сумма проработала. После всё складываем и делим на полную длину периода, который вас интересует.
Давайте теперь на примере посмотрим как это работает:
Инвестор вложил 1000$ в инвестиционный инструмент. Через 4 месяца инвестор решил добавить еще 300$. Еще через 6 месяцев инвестору понадобились деньги, он снял 200$. В конце года инвестиционный счёт достиг размера 1500$. Какова доходность инвестиционного инструмента?
Шаг 1 — рассчитываем полученную инвестиционную прибыль:
Прибыль = (1500$ + 200$) — (1000$ + 300$) = 400$
Шаг 2 — считаем средневзвешенный размер вложений:
Сумма вложений = (4*1000$ + 6*(1000$+300$) + 2*(1000$+300$-200$))/12 = (4000$+7800$+2200$)/12 = 1166.67$
Шаг 3 — считаем доходность:
Доходность = (400$/1166.67$) * 100% = 0.3429 * 100% = 34.29%
И никак не 50%, если бы мы проигнорировали вводы и выводы — (1500$-1000$)/1000$ * 100% = 50%.
↑ К СОДЕРЖАНИЮ ↑
Расчёт средней доходности инвестиций
Поскольку доходность многих инвестиционных инструментов постоянно меняется, удобно использовать некоторый усредненный показатель. Средняя доходность позволяет привести колебания доходности к одному небольшому числу, которое удобно использовать для дальнейшего анализа и сравнения с другими вариантами инвестиций.
Есть два способа рассчитать среднюю доходность. Первый — по формуле сложных процентов, где у нас есть сумма первоначальных инвестиций, полученная за это время прибыль, а также мы знаем количество периодов инвестирования:

Начальная сумма инвестиций — 5000$. Доходность за 12 месяцев составила 30% (сразу в уме переводим 5000$*30% = 1500$). Какова средняя месячная доходность проекта?
Подставляем в формулу:
Средняя доходность = (((6500/5000)^1/12) — 1) * 100% = ((1.3^1/12) — 1) * 100% = (1.0221 — 1) * 100% = 0.0221 * 100% = 2.21%
Второй способ ближе к реальности — есть доходности за несколько одинаковых периодов, надо посчитать среднюю. Формула:

Проект в первый квартал принес 10% доходности, во второй 20%, в третий -5%, в четвертый 15%. Узнать среднюю доходность за квартал.
Подставляем:
Средняя доходность = (((10%+1)*(20%+1)*(-5%+1)*(15%+1))^(1/4) — 1) * 100% = ((1.1*1.2*0.95*1.15)^(1/4) — 1) * 100% = (1.0958 — 1) * 100% = 0.0958 * 100% = 9.58%
Один из частных случаев вычисления средней доходности — определение процентов годовых, с которыми мы сталкиваемся на каждом шагу в виде рекламы банковских депозитов. Зная доходность инвестиций за определенный период, мы можем рассчитать годовую доходность по такой формуле:

Инвестор вложил 20000$ и за 5 месяцев (округлим до 150 дней) заработал 2700$ прибыли. Сколько это в процентах годовых? Подставляем:
Доходность = (2700$/20000$ * 365/150) * 100% = (0.135 * 2.4333) * 100% = 0.3285 * 100% = 32.85% годовых
↑ К СОДЕРЖАНИЮ ↑
Взаимосвязь доходности и риска инвестиций
Чем больше доходность — тем лучше, вроде бы очевидно. Это правило хорошо работало бы среди безрисковых активов, но таких просто не существует. Всегда есть вероятность потерять часть или всю сумму инвестиций — такова их природа.
Более высокая доходность намного чаще достигается за счет дополнительного увеличения рисков, чем за счёт более высокого качества самого инструмента. Я обнаружил сильную взаимосвязь между показателем риска СКО (среднеквадратическое отклонение) и доходностью за год:

Ось X — доходность за год, ось Y — СКО. Линия тренда показывает, что чем выше годовая доходность, тем выше риски ПАММ-счёта в виде показателя СКО.
Такая взаимосвязь простыми словами — это корреляция, причем достаточно сильная. В исследовании 3000 ПАММ-счетов я рассчитывал корреляцию показателя СКО и доходности и получил значение 0.44, что на такой большой выборке означает крепкую зависимость. Другими словами, взаимосвязь доходности и рисков подтверждается математически.
Задача инвестора — найти собственный баланс между доходностью и риском, точнее определить свою склонность к рискованным вложениям. Для веб-инвестиций минимальная допустимая доходность — на уровне банковской, умноженная на два (большой банк сам по себе надежнее форекс-брокера). Дальше уже зависит от инвестора — сконцентрироваться на минимизации рисков и получать x2-x3 от банковской доходности или пытаться взять на себя дополнительные риски чтобы заработать больше.
Все приведенные выше формулы позволяют рассчитать конечную доходность инвестиций — мы вложили, прошло время, деньги получили. Если говорить о таких инвестиционных инструментах, как ПАММ-счета, торговые роботы, копирование сделок — этого мало, существуют торговые риски и множество других подводных камней, которые могут привести к ненужным потерям.
Инвестор должен знать, что будет происходить с его деньгами в процессе, по этой причине эти инструменты всегда сопровождаются графиками доходности.
↑ К СОДЕРЖАНИЮ ↑
Графики доходности
График доходности — незаменимый инструмент для анализа вариантов инвестирования. Он позволяет посмотреть не просто на общий результат вложений, но и оценить происходящее в промежутке между событиями «вложение денег» и «вывод прибыли».
Существует несколько видов графиков доходности. Чаще всего встречается накопительный график доходности — он показывает, насколько вырос бы в % первоначальный депозит, на основе доходностей за несколько временных промежутков или по результатам отдельных сделок.
Примерно вот так выглядит накопительный график доходности:

График чистой доходности инвестора ПАММ-счёта Solandr
По нему можно понять несколько важных вещей — например, равномерно ли растёт прибыль (чем более гладкий график, тем лучше), насколько большие просадки (то есть незафиксированные потери в процессе инвестирования) могут ожидать инвестора и т.д.
Очень подробно об анализе графиков доходности я писал в статье о том, как выбрать ПАММ-счёт для инвестирования.
Также часто используются графики доходности по неделям или месяцам:

График чистой доходности инвестора ПАММ-счёта Stability Dual Turbo по месяцам
Столбцы говорят сами за себя — март был удачным, а вот за последние три месяца прибыли вообще не было. Если смотреть только на этот график и не брать в расчёт более старые счета Stability, то можно сделать такой вывод — торговая система дала сбой и перестала приносить прибыль. Грамотной стратегией в таком случае будет вывести деньги и ждать пока ситуация вернется в нормальное состояние.
Вообще, графики доходности и ПАММ-счета — это отдельная интересная история.
↑ К СОДЕРЖАНИЮ ↑
Особенности расчёта доходности инвестиций в ПАММ-счета
Начнем с самого очевидного — графики доходности ПАММ-счетов у всех брокеров не соответствуют реальной доходности инвестора! То что мы видим — доходность именно ПАММ-счёта, то есть всей суммы инвестиций, включая и деньги управляющего, и комиссию за управление.
Когда мы видим такие цифры:

600% за полтора года, рука сразу же тянется к кнопке «Инвестировать», золотая жила же! Однако если мы учтем 29% комиссии управляющего, то реальная доходность окажется такой:

В 2 раза меньше! Я не спорю, 300% за полтора года тоже смотрятся отлично, но это далеко не 600%.
Ну а если углубиться в суть, то доходность ПАММ-счёта считается так:
- Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
- Положительный результат уменьшается на процент комиссии управляющего, кроме случаев в п.4 и 5.
- Отрицательный результат всегда остается как есть.
- Если положительный результат получен после убытка, он не уменьшается из-за комиссии, пока общая доходность не обновит максимум.
- Если после положительного результата превышен максимум общей доходности — комиссия снимается только с той части, которая превысила максимум.
В итоге получаем весьма замороченную формулу, которая необходима для высокой точности расчётов. Что делать, если вам нужно посчитать чистую доходность инвестора ПАММ-счёта? Предлагаю использовать такой алгоритм:
- Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
- Положительный результат уменьшается на процент комиссии управляющего.
- Отрицательный результат уменьшается на процент комиссии управляющего.
Все что нужно — умножить официальные цифры доходности ПАММ-счёта на единицу минус комиссия управляющего. Причем не итоговый результат, а данные с графика ПАММ-счёта (в Альпари их можно скачать в удобном виде) и посчитать по формуле доходности за несколько периодов.
Для наглядности посмотрите на один и тот же график доходности, посчитанный тремя способами:

Разница с учётом и без учёта комиссии управляющего — почти в 2 раза! По упрощенному алгоритму мы получили результат 92%, по точному — 89%. Разница не существенная, но для тысяч процентов она станет вполне заметной:

Реальная доходность инвестора ниже в 6 раз, а разница между точным и упрощенным алгоритмом 70% — на больших цифрах всё заметнее.
Кстати, вы хотите знать, откуда вообще берется эта разница? Кроме того, что упрощенный способ подсчета доходности уменьшает размер просадок, есть еще одна фишка — регулярные выплаты вознаграждения управляющего уменьшают вашу долю в ПАММ-счёте.
Вы все поймете, взглянув на эту картинку:
Зелеными кружками показаны моменты выплаты вознаграждения управляющего, красными — уменьшение ваших паёв в ПАММ-счёте. Что такое пай? Это ваша доля в ПАММ-счёте, ваш кусочек общего пирога прибыли.
Для понимания подойдет такое сравнение — паи это определенное количество акций ПАММ-счёта. По этим акциям вы получаете дивиденды — процент от прибыли компании. Количество акций уменьшается — снижаются дивиденды, соответственно и доходность вложений.
Почему же паи уменьшаются? Дело в том, что изначально вы получаете прибыль на всю сумму своих инвестиций — как и должны. Наступает момент выплаты комиссии управляющего — и она берется из вашей суммы, вашего «кусочка пирога». Кусочек стал меньше со всеми вытекающими.
То, что я вам показал — это не плохо, это как есть. Так работают ПАММ-счета, а вкладывать деньги или нет — выбор всегда за вами.
↑ К СОДЕРЖАНИЮ ↑
Друзья, я понимаю что статья довольно сложная, поэтому если есть какие-либо вопросы — задавайте их в комментариях, я постараюсь ответить. Ну и пожелание напоследок: инвестируйте в действительно доходные проекты!