Материал урока.
Мы уже знакомились с
призмами. Сегодня мы повторим основные понятия, которые связаны с ними.
Давайте вспомним, какой
многогранник мы назвали призмой.
Рассмотрим два равных
многоугольника A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях. Причем расположены
эти многоугольники так, чтобы равные стороны этих многоугольников, т.е. A1A2 и B1B2, A2A3 и B2B3 … AnA1 и BnB1, были параллельными.
Теперь проведем отрезки A1B1, A2B2,
A3B3…AnBn. В итоге,
получим n четырехугольников A1B1B2A2,
A2B2B3A3…AnBnB1A1.
Указанные
четырехугольники являются параллелограммами. Рассмотрим например,
четырехугольник A1B1B2A2. Его противоположные стороны A1A2 и B1B2 равны и параллельны по построению. Следовательно, и
стороны A1B1 и A2B2 тоже равны и параллельны. Напомню, что
четырёхугольник, у которого противоположные стороны попарно параллельны,
называется параллелограммом. Значит, рассматриваемый нами
четырехугольник A1B1B2A2 – параллелограмм.
Построенный многогранник
A1A2…AnB1B2…Bn, называется n-угольной призмой.
Равные n-угольники
называются основаниями призмы. Параллелограммы – боковыми гранями
призмы. А стороны боковых граней, не являющиеся сторонами оснований призмы,
называются боковыми ребрами призмы.
На рисунке, A1A2…AnB1B2…Bn – n-угольная призма. А1A2…An и B1B2…Bn – основания призмы, параллелограммы A1A2B2B1,…, AnA1B1Bn– боковые грани. А стороны A1B1,…, AnBn –
боковые ребра призмы. Все они равны и параллельны друг другу, как стороны
параллелограммов.
Отрезок, соединяющий две
вершины призмы, не принадлежащие одной грани, например, B1A3, называется диагональю призмы.
Призма в зависимости от
того какой многоугольник лежит в основании имеет свое название. Если в
основании лежит треугольник, то призма называется треугольной. Если
четырехугольник – то четырехугольной призмой. А если n-угольник, то n-угольной
призмой.
Теперь узнаем, что
называют высотой призмы. Выберем произвольную точку А одного из оснований и
проведем через нее прямую, перпендикулярную к плоскости другого основания и
пересекающую ее в точке B. Отрезок, AB называется высотой призмы.
В зависимости от того
перпендикулярны ли ребра основанию, призмы можно подразделить на прямые и
наклонные.
Если все боковые ребра
призмы перпендикулярны к плоскостям ее оснований, то призма называется прямой.
Если же боковые ребра не перпендикулярны основанию, то призма называется наклонной.
На рисунке изображены примеры прямой и наклонной призм.
Обратите внимание, у
прямой призмы боковые грани являются прямоугольниками, а у наклонной призмы –
параллелограммы.
Прямая призма,
основаниями которой являются правильные многоугольники, называется правильной.
Объединение боковых
граней называется боковой поверхностью призмы, а объединение всех граней
называется полной поверхностью призмы. Тогда площадью боковой
поверхности призмы называется сумма площадей ее боковых граней.
А площадью полной
поверхности призмы называется сумма площадей всех ее граней.
Это все нам известно с
курса геометрии базовой школы.
Сегодня мы выведем
новую формулу для вычисления площади боковой поверхности прямой призмы.
Сформулируем и докажем теорему.
Площадь боковой поверхности прямой призмы равна произведению периметра
основания на высоту призмы.
Доказательство.
Выше мы уже вспоминали,
что все боковые грани прямой призмы – прямоугольники. Основания этих
прямоугольников – стороны основания призмы. А высоты этих прямоугольников равны
высоте призмы. Мы знаем, что площадь боковой поверхности призмы равна сумме
площадей каждой из боковых граней, то есть в случае прямой призмы это будет
сумма произведений сторон основания на высоту призмы.
Вынесем множитель р за
скобки, тогда в скобках получим сумму сторон основания призмы, другими словами
– в скобках мы получим периметр основания.
Тогда можно записать,
что площадь боковой поверхности прямой призмы равна произведению высоты на
периметр основания.
Решим несколько задач.
Задача. Основанием прямой призмы является равнобедренная
трапеция с основаниями, которые равны и
.
Высота призмы равна .
Найти площадь боковой поверхности, если боковое ребро равно .
Решение.
Поскольку призма
прямая, то воспользуемся только что доказанной формулой.
Ответ. 400 см2.
Решим еще одну задачу.
Задача. В правильной треугольной призме сторона основания
равна , а
высота призмы равна .
Вычислить площадь боковой и полной поверхности призмы.
Решение.
Поскольку по условию
призма правильная, значит, она прямая. Применим только что доказанную формулу.
Запишем формулу для вычисления площади полной
поверхности призмы.
Ответ. 450 см2,
см2
Решим еще одну задачу.
Задача. Доказать, что площадь боковой поверхности наклонной
призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство.
В качестве примера, мы
возьмем треугольную призму, для других призм это утверждение доказывается
аналогично.
Перпендикулярным сечением
называется пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
Для построения
перпендикулярного сечения выберем, например, на ребре BB1 произвольно точку К. В плоскости грани AA1B1B через точку К проведем прямую KL перпендикулярную к ребру BB1. Эта прямая будет
перпендикулярна к ребру AA1,
поскольку ребра AA1 и BB1 параллельны.
Теперь через точку К в
плоскости грани BB1C1C
проведем прямую КМ перпендикулярную ребру BB1. Тогда из того, что BB1 перпендикулярно пересекающимся прямым KL и
КМ плоскости KLM следует, что BB1 перпендикулярно плоскости KLM.
То есть построенное
сечение KLM перпендикулярно боковому ребру. А значит, это и есть
перпендикулярное сечение призмы.
Тогда надо доказать,
что площадь боковой поверхности призмы равна произведению периметру
треугольника KLM и бокового ребра BB1.
Любая боковая грань
призмы – это параллелограмм. Рассмотрим грань ABB1A1. КL – это высота параллелограмма ABB1A1. Поэтому для нахождения площади этой грани можно
применить формулу:
В качестве основания мы
берем сторону BB1, так как
высота проводилась к этой стороне.
Аналогично можно
записать:
Запишем формулу для
вычисления площади боковой поверхности. Заменим площадь каждой грани полученной
формулой.
Решим еще одну задачу.
Задача. Боковое ребро наклонной четырехугольной призмы равно . Перпендикулярным сечением является ромб со стороной
. Найти площадь боковой поверхности.
Решение.
Воспользуемся только
что доказанным утверждением.
Решим еще одну задачу.
Задача. Основанием прямой призмы является равнобедренная
трапеция с основаниями ,
и высотой
.
Найти двугранные углы при боковых ребрах призмы.
Решение.
Для определения
двугранных углов, нам необходимо найти соответствующие линейные углы.
Ответ. 45°, 135°.
Подведем итоги
урока.
Сегодня на уроке мы
вспомнили, какая фигура называется призмой, основные элементы призмы. Виды
призм. Вывели формулы для вычисления площади боковой поверхности прямой и
наклонных призм. Решили несколько конкретных задач.
ПРИЗМА
10а класс
ПРИЗМА
01.02.2022 вторник
02.02.2022 среда
03.02.2022 четверг
Практикум по решению задач.
Ниже на странице есть видео с разборами некоторых задач из ЕГЭ по теме :”Призма”.
Посмотрите видео и решите задания на сайте решу.егэ базовый(!) уровень.
Фото решения вариантов с чертежами прислать(или показать в классе) для получения оценки больше,чем 3)
почта lud-mir@yandex.ru 08.02.2022 вторник решение задач срок до 10.02.22
09.02.2022 среда решение задач срок до 11.02.22
10 .02.2022 четверг решение задач срок до 12.02.22
1. Посмотреть урок на сайте РЭШ
2. Сделать конспект урока по видео и выписать в тетрадь
(высылать не надо! проверю в классе)
3.Выполнить задания на сайте учи.ру
4.*(на доп.оценку!) разобрать и переписать в тетрадь задания из ЕГЭ(профиль) из видео . Показать тетрадь в школе!!!! фото не надо!
5. Решить задания на сайте решу.егэ вопросы можно задать в соцсетях или в watsapp
во время уроков по расписанию включаю безлимитное решение заданий на учи.ру, там тоже есть чат для общения
Перечень вопросов, рассматриваемых в теме:
-
Понятие призмы и виды призм;
-
Элементы призмы: вершины, ребра, грани;
-
Понятие площади боковой поверхности и площади полной поверхности призмы, формулы для вычисления;
-
Призма как модель реальных объектов;
-
Пространственная теорема Пифагора.
Глоссарий по теме
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
Определение призмы. Элементы призмы.
Рассмотрим два равных многоугольника А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2…АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
Рисунок 1 – Призма
Заметим, что каждый из n четырехугольников (A1A2B1B2, …AnA1B1Bn) является параллелограммом. Убедимся в этом на примере четырехугольника A1A2B1B2. A1A2 и B1B2 параллельны по свойству параллельных плоскостей, пересеченных третьей плоскостью. А1В1 и А2В2 по условию. Таким образом, в четырехугольнике A1A2B1B2 противоположные стороны попарно параллельны, значит этот четырехугольник — параллелограмм по определению.
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
На рисунке 1 основаниями призмы являются многоугольники А1А2…Аn и В1В2…Вn. Боковые грани – параллелограммы A1A2B1B2, …, AnA1B1Bn, а боковые ребра – отрезки А1В1, А2В2, …, АnВn.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
Призму с основаниями А1А2…Аn и В1В2…Вn обозначают А1А2…АnВ1В2…Вn и называют n-угольной призмой.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).
Рисунок 2 – Наклонная призма
Виды призм
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
На рисунке 3 приведены примеры прямых призм
Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Доказательство
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.
Рисунок 4 – Прямоугольный параллелепипед
Доказательство
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С2=АА12+АС2 (1).
Выразим теперь АС. По условию в основании лежит прямоугольник, значит ΔАВС – прямоугольный. По тереме Пифагора получаем: АС2=ВС2+АВ2.
Подставив результат в (1), получим: А1С2=АА12+ВС2+АВ2.
Так как в основании прямоугольник, то ВС=АD.
Таким образом, А1С2=АА12+АD2+АВ2.
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Задание 1.
Найдите для каждой картинки пару
6)
Решение
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Задание 2
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
2) отрезок
3) точка
4) четырехугольник
Решение:
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Ответ: 2,3,4
Призма
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие призмы
Определение 1
Геометрическая фигура, образованная двумя равными $n-$угольниками, лежащими в параллельных плоскостях, вершины которых соединены между собой так, что соответствующая вершина первого $n-$угольника соединена с соответствующей вершиной второго $n-$уголника, называется призмой (рис. 1).
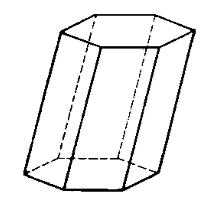
Рисунок 1. Призма
Параллельные $n-$уголники называются основаниями призмы, параллелограммы их соединяющие — боковыми гранями, стороны параллелограммов — сторонами призмы, а вершины $n-$угольников — вершинами призмы.
Виды призм
В зависимости от количества углов в основании призмы ее можно назвать треугольной, четырехугольной и так далее (рис. 2).
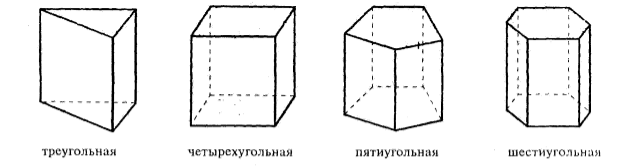
Рисунок 2.
Отметим, что параллелепипед является частным случаем четырехугольной призмы.
Определение 2
Призма, у которой все двугранные углы равны ${90}^0$ называется прямой (рис. 3). В противном же случае она является наклонной.
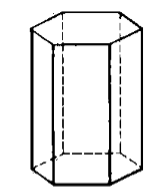
Рисунок 3. Прямая призма
Определение 3
Прямая призма, в основании которой лежат правильные $n-$уголники называется правильной (рис. 4).
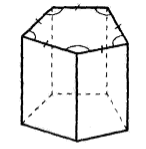
Рисунок 4.
Площадь призмы
Полная площадь призмы определяется следующим образом
где $S_{бок}$ – сумма площадей всех ее боковых граней, а $S_{осн}$ – площадь основания данной призмы.
Рассмотрим и докажем следующую теорему.
«Призма» 👇
Доказательство.
Рассмотрим прямую $n-$угнольную призму, длины оснований которой равны $a_1, a_2,dots ,a_n$ соответственно. Как мы знаем, высота прямой призмы равняется боковой стороне данной призмы. Обозначим её через $h$. Тогда, так как боковые грани являются прямоугольниками, площади боковых граней равняются, соответственно
Так как площадь боковой поверхности — сумма площадей всех боковых граней, то
Теорема доказана.
Объем призмы
Теорема 2
Объем прямой призмы с прямым треугольником при основании определяется как произведение площади его основания на высоту.
Доказательство.
Рассмотрим прямую призму $ABDA_1B_1D_1$ c прямоугольным треугольником при основании. Дополним его до прямоугольного параллелепипеда (рис. 5)
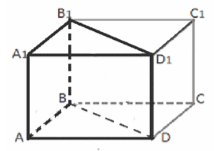
Рисунок 5.
Следовательно,
Теорема доказана.
Теорема 3
Объем прямой призмы определяется как произведение площади его основания на высоту.
Доказательство.
-
Рассмотрим прямую треугольную призму $ABDA_1B_1D_1$. Разделим ее на две призмы с прямыми треугольниками при основании с объемами $V_1 и V_2$ ($BC$ и $B_1C_1$ — высоты оснований) (рис. 6).
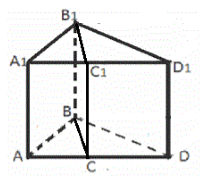
Рисунок 6.
По теореме 2, получим
[V_{пр}=V_1+ V_2=S_{ABC}h+S_{DBC}h={h(S}_{ABC}+S_{DBC})=S_{осн}h]
-
Любую призму мы всегда может разделять на несколько прямоугольных призм, следовательно эта формула верна для произвольно размерной прямой призмы.
Теорема доказана.
Пример задачи
Пример 1
Найти объем прямой призмы с равнобедренным треугольником при основании и высотой $h=3$, если боковая сторона треугольника равна $4$, а угол между ними равен ${30}^0$.
Решение.
Так как боковая сторона основания равна $3$, а угол между ними равен ${30}^0$. То
[S_{осн}=frac{1}{2}cdot 4cdot 4cdot sin{30}^0=8cdot frac{1}{2}=4]
По теореме 3, получим
[V=4cdot 3=12]
Ответ: $12.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 19.04.2023
