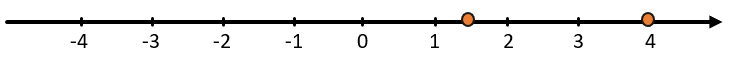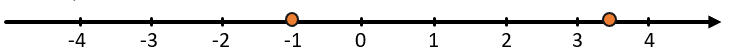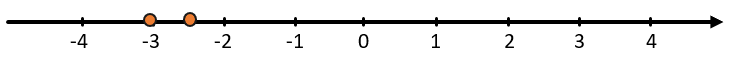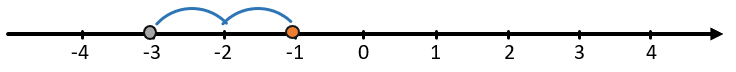Как найти сумму рациональных чисел правило

Действия с рациональными числами

• Сложение
• Вычитание
• Умножение
• Деление

Сложение

При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.

Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.

При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.

Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:

Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.

Сумма двух противоположных чисел равна нулю.

Вычитание

Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.

Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

Умножение

При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.

Ниже представлена схема (правило знаков при умножении):

+	·	+	=	+
+	·	–	=	–
–	·	+	=	–
–	·	–	=	+

Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.

При умножении любого числа на  -1  получится число, противоположное данному.

Деление

При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.

При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):

+	:	+	=	+
+	:	–	=	–
–	:	+	=	–
–	:	–	=	+

Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.

При делении любого числа на  -1  получится число, противоположное данному.

В данной публикации мы рассмотрим, что такое рациональные числа, как их сравнивать между собой, а также какие арифметические действия с ними можно выполнить (сложение, вычитание, умножение, деление и возведение в степень). Теоретические материал сопроводим практическими примерами для лучшего понимания.

Определение рационального числа

Рациональным называется число, которой можно представить в виде обыкновенной (простой) дроби. Множество рациональных чисел имеет специальное обозначение – Q.

Правила сравнения рациональных чисел:

1. Любое положительное рациональное число больше нуля. Обозначается “больше” специальным знаком “>“.
   Например: 5>0, 12>0, 144>0, 2098>0 и т.д.
2. Любое отрицательное рациональное число меньше нуля. Обозначается “меньше” символом “<“.
   Например: -3<0, -22<0, -164<0, -3042<0 и т.д.
3. Из двух положительных рациональных чисел больше то, у которого больше абсолютная величина.
   Например: 10>4, 132>26, 1216<1516 и т.д.
4. Из двух отрицательных рациональных чисел большим является то, у которого меньше абсолютная величина.
   Например: -3>-20, -14>-202, -54<-10 и т.д.

Арифметические действия с рациональными числами

Сложение

1. Чтобы найти сумму рациональных чисел с одинаковыми знаками, просто складываем их модули, затем перед получившимся результатом ставим их знак.

Например:

• 5 + 2 = + (5 + 2) = +7 = 7
• 13 + 8 + 4 = + (13 + 8 + 4) = +25 = 25
• -9 + (-11) = – (9 + 11) = -20
• -14 + (-53) + (-3) = – (14 + 53 + 3) = -70

Примечание: Если перед числом не стоит знак, то подразумевается “+“, т.е. оно является положительным. Также в полученном результате “плюс” можно опускать.

2. Для того, чтобы найти сумму рациональных чисел с разными знаками, мы к числу с большим модулем прибавляем те, у которых знак совпадает с ним, и отнимаем числа с противоположными знаками (величины берем абсолютные). Затем перед результатом ставим знак числа, из которого мы всё вычитали.

Например:

• -6 + 4 = – (6 – 4) = -2
• 15 + (-11) = + (15 – 11) = +4 = 4
• -21 + 15 + 2 + (-4) = – (21 + 4 – 15 – 2) = -8
• 17 + (-6) + 10 + (-2) = + (17 + 10 – 6 – 2) = 19

Вычитание

Для нахождения разности двух рациональных чисел к уменьшаемому прибавляем противоположное вычитаемому число.

Например:

• 9 – 4 = 9 + (-4) = 5
• 3 – 7 = 3 + (-7) = – (7 – 3) = -4

Если вычитаемых несколько, то сначала складываем все положительные числа, затем – все отрицательные (в т.ч. уменьшаемое). Таким образом мы получим два рациональных числа, разность которых находим по алгоритму выше.

Например:

• 12 – 5 – 3 = 12 – (5 + 3) = 4
• 22 – 16 – 9 = 22 – (16 + 9) = 22 – 25 = – (25 – 22) = -3

Умножение

Для нахождения произведения двух рациональных чисел просто перемножаем их модули, затем перед получившимся результатом ставим:

• знак “+“, если у обоих сомножителей один и тот же знак;
• знак “–“, если сомножители имеют разные знаки.

Например:

• 3 · 7 = 21
• -15 · 4 = -60

Когда сомножителей больше двух, то:

1. Если все числа положительные – то результат будет со знаком “плюс”.
2. Если есть как положительные, так и отрицательные числа, то считаем количество последних:
   • четное количество –  результат с “плюсом”;
   • нечетное количество – результат с “минусом”.

Например:

• 5 · (-4) · 3 · (-8) = 480
• 15 · (-1) · (-3) · (-10) · 12 = -5400

Деление

Как и в случае с умножением, выполняем действие с модулями чисел, затем ставим соответствующий знак с учетом правил, описанных в пункте выше.

Например:

• 12 : 4 = 3
• 48 : (-6) = -8
• 50 : (-2) : (-5) = 5
• 128 : (-4) : (-8) : (-1) = -4

Возведение в степень

Возведение рационального числа a в степень n – это то же самое, что и умножить это число само на себя n-ое количество раз. Пишется как a ⁿ.

При этом:

• Любая степень положительного числа в результате дает положительное число.
• Четная степень отрицательного числа положительна, нечетная – отрицательна.

Например:

• 2⁶ = 2 · 2 · 2 · 2 · 2 · 2 = 64
• -3⁴ = (-3) · (-3) · (-3) · (-3) = 81
• -6³ = (-6) · (-6) · (-6) = -216

Содержание:

• Определение рационального числа
• Операции над рациональными числами

Рациональные числа появились как форма записи чисел, более “мелких”, нежели
натуральных.

Определение рационального числа

Если $m$ – нацело делится на $n$ или $n=1$, то рациональное число $frac{m}{n}$  также будет
целым числом; если при этом
$m$ будет натуральным, то в таком случае дробь $frac{m}{n}$  будет еще и натуральным числом. Поэтому для этих чисел имеет место такая цепочка вложений:
$N subset Z subset Q$ .

Операции над рациональными числами

На множестве рациональных можно ввести четыре арифметические операции:
сложение,
вычитание,
умножение и
деление; которые вычисляются по следующим правилам.

Правило вычисления суммы двух рациональных чисел:

$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$

Правило вычисления разности двух рациональных чисел:

$$frac{m}{n}-frac{p}{q}=frac{m cdot q-n cdot p}{n cdot q}$$

Правило вычисления произведения двух рациональных чисел:

$$frac{m}{n} cdot frac{p}{q}=frac{m cdot p}{n cdot q}$$

Правило вычисления частного двух рациональных чисел:

$$frac{m}{n} : frac{p}{q}=frac{m cdot q}{n cdot p}$$

Читать дальше: что такое сумма чисел.

Рациональные числа и действия с ними

Рациональные числа – это числа, представленные в виде отношения (frac{m}{n}), где m – целое число, а n – натуральное.

Они могут быть как положительными, так и отрицательными.

Целые и дробные числа вместе образуют множество рациональных.

1. Любое целое число является рациональным, потому что его можно записать в виде (frac{m}{1}).

Например:

(–4 = frac{- 4}{1})

(2 = frac{2}{1})

(0 = frac{0}{1})

1. Сумма, разность и произведение двух рациональных чисел – тоже рациональное число. Частное двух рациональных чисел тоже будет рациональным, если знаменатель не равен 0.

2. Любое рациональное число можно записать в виде десятичной или периодической дроби.

Периодическая дробь – это десятичная дробь, в записи которой бесконечное количество раз повторяется цифра или несколько цифр.

Например:

(frac{1}{3} = 0,33333333..)

Повторяющиеся цифры периодической дроби записывают в скобках, например:

(frac{1}{3} = 0,(3))

(frac{5}{11} = 0,45454545 = 0,(45))

СВОЙСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение:

1. Переместительное свойство:

(a + b = b + a)

1. Сочетательное свойство:

(a + (b + c) = (a + b) + c = (a + c) + b = a + b + c)

1. Прибавление нуля не меняет рациональное число, а сумма противоположных чисел равна нулю:

(a + 0 = a)

(a + ( – a) = 0)

Умножение:

1. Переместительное свойство:

(ab = ba)

1. Сочетательное свойство:

(a(bc) = (ab)c = (ac)b = abc)

1. Умножение на единицу не меняет рациональное число, а произведение обратных чисел равно единице:

(a bullet 1 = a)

(a bullet frac{1}{a} = 1)

1. Если один из множителей равен нулю, то и всё произведение равно 0:

(a bullet 0 = 0)

(0 bullet b = 0)

(0 bullet 0 = 0)

1. Распределительное свойство:

((a + b)c = ac + сb)

ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ

Так как рациональные числа включают в себя блок целых чисел и блок дробных чисел, действия, пройденные в рамках работы с целыми числами, сохраняются и для рациональных чисел. Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.

СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Рациональные числа можно представить на координатной прямой, где справа от нуля находятся положительные числа, а слева от нуля – обратные им, отрицательные:

Числа на такой числовой прямой возрастают слева на право, поэтому глядя на прямую можно сказать, какое числе больше.

Например:

1. Сравним числа 1,5 и 4:

Мы знаем, что 4 больше, чем 1,5 и еще раз убедились в этом с помощью числовой прямой.

(4 > 1,5)

1. Сравним числа 3,5 и -1:

Если положительные числа справа от нуля, а отрицательные слева, тогда любое положительное числа будет правее отрицательного, а значит будет больше.

(3,5 > – 1)

1. Сравним числа -2,5 и -3:

Конечно, 3 больше 2,5, но, когда мы смотрим на отрицательные числа, получается, что -2,5 правее -3, а значит больше.

(- 2,5 > – 3)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение рациональных чисел так же можно представить на числовой прямой. Знак «+» означает, что мы двигаемся в положительном направлении (вправо), знак «–» означает, что мы двигаемся в отрицательном направлении (влево).

Например:

1. Найдем сумму положительных чисел 1 + 2,5. Значит от координаты 1 пройдем 2 полных отрезка и ещё половину отрезка в положительном направлении:

Видим, что (1 + 2,5 = 3,5).

Сумма положительных чисел – положительное число.

1. Найдем сумму отрицательных чисел -1 + (-2). От координаты -1 пройдем 2 отрезка в отрицательном направлении. При сложении можно опустить знак «+» без изменения знаков слагаемых.

Получилось, что (- 1 + ( – 2) = – 3.)

Сумма отрицательных чисел – отрицательное число.

1. Найдем разность положительных чисел 4 – 1,5. Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:

Получилось, что (4 –1,5 = 2,5.)

Сумма положительного и отрицательного числа – положительное число, если из большего вычитают меньшее.

1. Найдем сумму 2 + (-4). От координаты 2пройдем 4 отрезка в отрицательном направлении:

Получим, что (2–4 = – 2.)

Сумма положительного и отрицательного числа – отрицательное число, если из меньшего вычитают большее.

1. Найдем разность 1 – (-3). Если нужно пройти в отрицательном направлении дважды, то направление движения станет положительным, то есть 1 – (-3) = 1 + 3:

Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.

1. Найдем сумму двух противоположных чисел 3 + (-3). От координаты 3 пройдем 3 отрезка в отрицательном направлении:

Видим, что (3 + ( – 3) = 0.)

Сумма двух противоположных чисел (mathbf{= 0.})

УМНОЖНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

1. Рациональные числа умножаются и делятся не смотря на знак.

2. Если перемножались или делились числа с одинаковыми знаками, то в результате получается положительное число. Если перемножались числа с разными знаками, то в результате получается отрицательное число.

Например:

(3 bullet 4 = 12)

(- 6 bullet ( – frac{1}{2}) = 3)

(7:( – 2) = – 3,5)

(- 12:frac{1}{3} = – 12 bullet 3 = – 36)