В начальной школе ребенок впервые знакомится с математикой, и его первыми примерами являются такие простые действия, как складывание или вычитание. Но иногда ребенку сложно объяснить даже такие, казалось бы, несложные и привычные взрослым примеры. Как же научиться находить сумму и разность чисел?
Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, – это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел
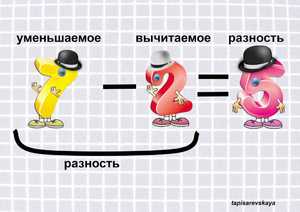
Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом “от перестановки слагаемых разность не меняется”, так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы “вычитаем”, то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
В общем виде вычитание можно записать так: a – b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Содержание
- Сумма и разность чисел
- Что такое сумма, и как ее найти
- Как найти разность чисел
- Как найти разность чисел в математике
- Арифметические действия с числами
- Разность в математике
- Видео: Математика 6 Делимость суммы и разности чисел
- Как найти разницу величин
- Математические действия с разностью чисел
- Видео: Математика 2 класс. Разность двухзначных чисел
- Простые примеры
- Более сложные примеры
- Математика для блондинок
- Свойства сложения и вычитания
- Свойства сложения
- Свойства вычитания
- Примеры использования свойств сложения и вычитания
Сумма и разность чисел
Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел
Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Источник
Как найти разность чисел в математике
Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
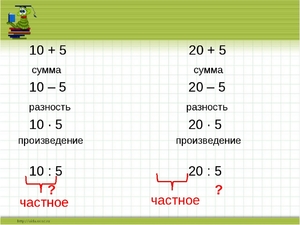
Каждый результат этих действий также имеет своё название:
- сумма — результат, получившийся при сложении чисел;
- разность — результат, получившийся при вычитании чисел;
- произведение — результат умножения чисел;
- частное — результат деления.
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить;
- разность — отнять;
- произведение — умножить;
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
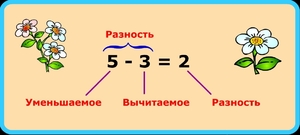
Разность чисел означает, насколько одно из них больше другого.- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
Видео: Математика 6 Делимость суммы и разности чисел
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Видео: Математика 2 класс. Разность двухзначных чисел
Простые примеры
- Пример 1. Найти разницу двух величин.
20 — уменьшаемое значение,
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
- Пример 2. Найти уменьшаемое.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
- Пример 3. Найти вычитаемое значение.
17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.
Даны целые значения: 56, 12, 4.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
7 — уменьшаемая величина;
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Источник
Свойства сложения и вычитания
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое,
- 5 — второе слагаемое,
- 7 — это сумма.
При этом саму запись (2 + 5) можно тоже назвать суммой.
Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
- Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
a + b = b + a - Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c) - Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
При этом саму запись (9 — 4) тоже можно назвать разностью.
- Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
a — 0 = a
Если из числа вычесть само число, то получится нуль.
a — a = 0 - Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
a — (b + c) = a — b — c - Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) — c = (a — c) + b (если a > c или а = с)
(a + b) — c = (b — c) + a (если b > c или b = с)
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:
Пример 1
Вычислить сумму слагаемых с использованием разных свойств:
а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15
б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22
в) 30 + 0 + 13 = 30 + 13 = 43
Пример 2
Применить разные свойства при вычислении разности:
а) 25 — 0 — 2 = 25 — 2 = 23
б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13
Пример 3
Найти значение выражения удобным способом:
а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32
б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16
Источник
Найти сумму разности .
Произведения и частное чисел .
24и3.
83 1 .
48и2.
На этой странице находится вопрос Найти сумму разности ?. Здесь же – ответы на него,
и похожие вопросы в категории Математика, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 1 – 4 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.
Содержание:
Действие вычитание и компоненты вычитания
Связь вычитания и сложения
Свойства разности
Как вычесть сумму из числа и число из суммы
Изменение разности при изменении вычитаемого и/или уменьшаемого
Правила вычитания разности
Вычитание однозначного числа
Вычитание в столбик многозначных чисел
Проверка действий сложение и вычитание
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.
Например, в кошельке было 1850 рублей. В магазине было потрачено 780 рублей. Чтобы узнать, сколько осталось денег, можно вытащить кошелек и пересчитать их. Но можно поступить по-другому: из той суммы, которая была в кошельке, отнять ту сумму, что была потрачена в магазине. Разница этих чисел, то есть, на сколько единиц изначальная сумма денег больше той суммы, которую потратили, и будет остатком денег.
Разность (или остаток) – это такое число, которое получится, если от одного числа отнять другое, то есть, от всех единиц одного числа отнять все единицы, которые содержатся в другом числе.
Уменьшаемое – это то число, от которого мы отнимаем единицы другого числа.
Вычитаемое – это число, которое мы вычитаем из другого числа. То есть, то число, на количество единиц которого мы уменьшаем другое число.
Вычитание – это арифметическое действие, которое выполняется для получения разности двух или нескольких чисел.
то есть, совершить действие вычитания – это найти такое число, которое получится, если от данного числа отнять определенное количество единиц другого числа.
Компоненты вычитания:
Про действие вычитание также говорят, что нужно из одного числа вычесть другое, или одно число уменьшить на другое.
Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.
Поэтому, уменьшаемое натуральное число всегда больше или равное вычитаемому. Другими словами, мы всегда вычитаем из большего меньшее или из равного равное.
Связь вычитания и сложения
Действие вычитание непосредственно связано с действием сложение.
Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.
А когда мы ищем разность, мы из одного числа (уменьшаемое) отнимаем некоторое количество единиц (вычитаемое), которые входят в его состав, и получаем другое количество единиц. То есть, получаем число (разность), которое также составляло уменьшаемое, пока от него не отняли вычитаемое. Поэтому разность и имеет второе название – остаток – то, что осталось от числа, после вычитания его части.
Из этого мы можем сделать вывод, что, если сложить обратно обе части одного числа (разность и вычитаемое), то мы получим уменьшаемое.
Поэтому, вычитание и сложение – это взаимно обратные действия. Если нам известна сумма двух слагаемых, мы можем превратить ее в разность двух чисел, и наоборот, разность можно перевести в сумму.
Уменьшаемое – это сумма вычитаемого и разности. То есть, разность и вычитаемое – это слагаемые.
Когда мы складываем числа, слагаемые нам известны, и нужно вычислить их сумму. А когда мы вычитаем, нам даются сумма (уменьшаемое) и одно из слагаемых (вычитаемое) этой суммы, а второе слагаемое (разность) нам нужно вычислить.
Рассмотрим это на примере. Мы нашли разность 8-5=3. Это означает, что мы разложили одно данное нам число 8 на два: 5 (данное нам уменьшаемое) и 3 (найденная нами разность). Но мы знаем, что состав числа – это слагаемые, которые в сумме дают нам это самое число. Поэтому, найденную нами разность чисел мы можем превратить в сумму чисел, сложив остаток с вычитаемым: 3+5=8.
Свойства разности натуральных чисел
Свойства разности натуральных чисел состоят из:
- Правила вычитания суммы из числа и числа из суммы;
- Зависимость разности от изменения уменьшаемого или вычитаемого.
- Правило вычитания разности из числа;
Рассмотрим каждый пункт подробнее.
Правила вычитания суммы из числа и числа из суммы
Как вычесть сумму из числа
Чтобы найти разность числа и суммы чисел нужно из данного числа вычесть последовательно каждое слагаемое суммы.
То есть, сначала мы находим разность между данным числом и первым слагаемым, потом от этой полученной разности отнимаем второе слагаемое, третье, и так далее до последнего слагаемого суммы.
Действительно, так как сумма – это объединение всех слагаемых, то очевидно, что, отнимая последовательно каждое слагаемое, каждое ее составляющее число, мы в конце концов отнимем всю сумму.
Рассмотрим это на примере из урока сложение чисел.
325+(12+64+5) = 325+81 = 406
Я запишу это в виде разности:
406-(12+64+5) = 325
и покажу, что результат будет равен первому слагаемому:
406—12 = 394;
394-64 = 330;
330-5 = 325.
Как видите, все верно.
Как вычесть число из суммы
Чтобы найти разность суммы чисел и некоторого числа, нужно отнять это число от какого-нибудь подходящего слагаемого этой суммы.
То есть, мы сначала находим разность одного из слагаемых и данного числа, а потом складываем получившийся результат последовательно с остальными слагаемыми.
Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.
Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:
325+81 = (191+65+150)
Превращаю выражение в разность:
(191+65+150)-81 = 325
и покажу, что результат также будет равен первому слагаемому:
191-81 = 110;
110+65 = 175;
175+150 = 325
или
150-81 = 69;
69+191 = 260;
260+65 = 325.
Я недаром написал в правиле, что нужно отнимать от подходящего слагаемого суммы, потому что, если оно будет меньше вычитаемого, то оно нам не подходит. Так, в нашем примере 65<81.
Отсюда следует, что это правило применимо не к любой сумме натуральных чисел, а только к той, в которой хотя бы одно из слагаемых больше, чем вычитаемое.
Как меняется разность при изменении вычитаемого или уменьшаемого
Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.
Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.
Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.
Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.
Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.
Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.
Правила вычитания разности
Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:
1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;
2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.
Это свойство выводится из предыдущих, рассмотренных нами.
Рассмотрим на примере 22-(17—3).
Для начала вычислим обычным способом: сперва узнаем разность в скобках (это будет 17-3=14), а потом вычтем 14 из 22. Получится 22-14=8.
22-(17—3) = 8
Теперь вернемся к исходному примеру и отнимем от 22 не разность 17-3, то есть, не 17 без 3 единиц, а все число 17.
22—17 = 5
Но мы ведь отняли больше, чем нужно было, поэтому нам нужно вернуть лишне взятые 3 единицы обратно, а именно, прибавить их к полученному результату.
5+3 = 8
Попробуем решить другим путем: увеличим и уменьшаемое (данное число), и вычитаемое (разность в скобках) на одно и то же число 3. Получим:
22+3-(17+3-3)
Так как 22+3=25, а 3-3=0, то в итоге получается:
25-17+0 = 8
Как видите, оба способа показали верный результат.
Вычитание однозначного числа
Вы сможете без каких-либо трудностей совершать вычитание любых чисел, если сперва хорошо натренируете себя вычитать однозначные числа в уме из однозначных и двухзначных.
А поскольку вычитание – это действие обратное сложению, тогда необходимо просто выучить на память все суммы однозначных чисел. Пользуясь ими, мы легко сможем получить необходимые вам разности.
Например, нам нужно найти разность чисел 17 и 8. Для этого нам необходимо вспомнить, какое число при сложении с числом 8 дает сумму 17? Это число 9, потому что 8+9=17. Значит, если от 17 отнять 8, мы получим: 17-8=9.
Хорошо натренировавшись в нахождении разности чисел из суммы однозначных чисел, можно переходить к более сложным случаям вычитания. Подробно эти приемы рассмотрены в разделе рубрики «Устный счет».
Вычитание в столбик многозначных чисел
Так же, как и сложение, разность многозначных чисел удобно находить, используя вычитание в столбик.
Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.
Давайте найдем разность чисел 52063-4825.
Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел, т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. минус. У нас получилась такая запись:
Вычитание в столбик выполняется подобным способом, как и при сложении, только теперь мы отнимаем единицы от единиц, десятки от десятков и так далее.
От 3 единиц в уменьшаемом мы не можем отнять 5 единиц вычитаемого, поскольку 3<5. Поэтому, мы раскладываем соседние 6 десятков на 5 десятков и 1 десяток. Этот десяток содержит 10 единиц, которые мы складываем с 3 имеющимися в уменьшаемом единицами. Теперь у нас есть 13 единиц, и мы можем отнять от них 5, получим 8 единиц. Записываем их под чертой в разряде простых единиц, а над цифрой разряда десятков в уменьшаемом ставим одну точку, чтобы не забыть, что 1 десяток единиц мы оттуда уже забрали.
Переходим к десяткам. У уменьшаемого в разряде десятков мы уже забрали 1 десяток, о чем нам напоминает поставленная точка. Поэтому, мы отнимаем 2 десятка вычитаемого не от 6, а от 5 десятков, потому что 6-1=5.
5>2, значит, действие вычитания возможно: 5-2=3. Пишем цифру 3 под чертой в разряде десятков, и переходим к сотням.
Сотен в уменьшаемом у нас нет, поэтому мы смотрим, сколько в числе содержится тысяч? Их тоже 0. Смотрим следующий разряд. Здесь у нас 5 десятков тысяч. Из них мы берем 1 десяток тысяч (ставим точку над цифрой 5 в уменьшаемом), что составляет 10 тысяч единиц. Из них (из взятых в десятках тысячах) мы занимаем 1 тысячу для того, чтобы закончить вычитание в разряде сотен (ставим точку над цифрой 0 в разряде тысяч уменьшаемого).
1 тысяча единиц – это 10 сотен. Кроме этих занятых, больше в уменьшаемом сотен нет. В вычитаемом 8 сотен, поэтому находим разность сотен уменьшаемого и вычитаемого: 10-8=2. Пишем результат под чертой в разряде сотен.
В разряде тысяч уменьшаемого у нас осталось 9 тысяч единиц (потому что 1 тысячу мы отдали для разряда сотен в качестве 10 сотен). Отнимаем от нее 4 тысячи вычитаемого, получаем: 9-4=5, которые записываем под чертой в разряде тысяч.
Десятков тысяч в уменьшаемом осталось 5-1=4 (помните, мы для разряда сотен занимали?), в вычитаемом их нет совсем, то есть, 0. Поэтому мы просто сносим цифру 4 в результат под черту в разряд десятков тысяч.
После нахождения разности чисел способом вычитания в столбик записываем ответ в строчном примере:
50063-4825 = 45238.
Как проверить действия сложение и вычитание?
После того, как вы закончили арифметическое действие, нужно проверить правильность ответа, то есть, удостовериться, что вычисление было сделано без ошибок.
Проверить сложение можно двумя способами: обратным сложением и вычитанием.
Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.
Например, в уроке сложение чисел мы находили сумму: 5728+803 = 6531. Проверим правильность результата способом обратного сложения:
Как видите, сложив слагаемые в другом порядке, мы получили тот же самый результат, а значит, вычисление было правильным.
Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.
Проверим эту же сумму вычитанием: отнимем от результата 6531 слагаемое 5728.
И этот способ проверки показал правильность нашего решения.
Проверить вычитание также возможно и сложением, и другим вычитанием.
Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.
Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238:
Проверка вычитания вычитанием также основывается на взаимосвязи вычитания и сложения, а также на переместительном законе сложения. Так как уменьшаемое – это сумма двух слагаемых: вычитаемого и остатка, и сумма не зависит от порядка сложения слагаемых, то очевидно, что мы можем отнять от уменьшаемого остаток. Если результат этого действия будет равен вычитаемому, значит наша первая разность вычислена верно.
Проверка той же самой разницы вычитанием:
Компоненты
арифметических действий и их взаимосвязь.
1.
Компоненты
при сложении:
1 слагаемое, 2 слагаемое, сумма.
2.
Компоненты
при вычитании:
уменьшаемое, вычитаемое, разность.
3.
Компоненты
при умножении:
1 множитель, 2 множитель, произведение.
4.
Компоненты
при делении:
делимое, делитель , частное.
5.
Назвать
результаты всех действий:
при сложении – сумма
при вычитании – разность
при умножении – произведение
при делении – частное
6.
Как найти
неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, нужно
из суммы вычесть известное слагаемое.
Х+4=12 или 4+х=12
Х=12-4 х=12-4
Х=8 х=8____
8+4=12 4+8=12
12=12 12=12
7.
Как найти
неизвестное уменьшаемое?
Чтобы найти неизвестное уменьшаемое, надо
к разности прибавить вычитаемое.
Х-7=3
Х=3+7
Х=10
10-7=3
3=3
8.
Как найти
неизвестное вычитаемое?
Чтобы найти неизвестное вычитаемое, надо
из уменьшаемого вычесть разность.
8-х =5
х=8-5
х=3
8-3=5
5=5
9. Как
найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо
произведение разделить на известный множитель.
х·3=6 4·х=8
х=6:3 х=8:4
х=2 х=2
2·3=6 4·2=8
6=6 8=8
10. Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо
частное умножить на делитель.
х:5=3
х=3·5
х=15
15:5=3
3=3
11.
Как найти
неизвестный делитель?
Чтобы найти неизвестный делитель, надо
делимое разделить на частное.
6:х=2
х =6:2
х=3
6:3=2
2=2
Геометрический материал.
Квадрат – это прямоугольник, у которого
все стороны равны.
13.
Что такое
прямоугольник?
Прямоугольник – это четырёхугольник, у
которого все углы прямые. Противоположные стороны прямоугольника равны.
14.
Что такое
треугольник?
Треугольник – многоугольник, у которого
три угла и три стороны.
15. Что такое четырёхугольник?
Четырёхугольник – геометрическая фигура,
у которой четыре угла и четыре стороны.
Периметр ( Ρ) – это сумма длин сторон
какой-нибудь геометрической фигуры.
Площадь (S) – это внутренняя часть
какой-нибудь геометрической фигуры
(прямоугольника, квадрата и т.д)
17.
Как найти
периметр квадрата?
У квадрата 4 стороны, равные между
собой. Чтобы найти периметр (Р) квадрата, нужно длину одной стороны (а) умножить на 4.
Р□ =
a · 4
18.
Как найти
периметр прямоугольника?
Чтобы найти периметр
прямоугольника, нужно сложить все 4 стороны прямоугольника
Или
сложить длину и ширину
прямоугольника и умножить на 2.
Ρ=a+b+a+b
или
Ρ=(a+b)·2
19.
Как найти
периметр треугольника?
Чтобы найти периметр
треугольника, нужно сложить все 3 стороны.
20.
Как найти
сторону квадрата, если известен периметр?
У квадрата 4 стороны, равные между
собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.
a=Ρ:4
21.
Как найти сторону прямоугольника, если известен
периметр и другая сторона?
Чтобы найти сторону
прямоугольника, нужно
Ρ разделить на 2
и вычесть
другую сторону.
a=Ρ:2 – b
b=Ρ:2 – a
22. В каких единицах измеряется периметр?
Периметр
измеряется в мм, см, дм, метрах.
23.
Как найти площадь квадрата?
Площадь квадрата равна произведению двух
его сторон.
S□ = a · a
24. Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, надо
длину прямоугольника умножить на его ширину.
S = a · b
25. Как найти сторону прямоугольника,
если известна площадь и другая его сторона?
Чтобы найти одну из сторон
прямоугольника, нужно площадь прямоугольника разделить на известную сторону.
a=S : b
b= S : a
26. В каких
единицах измеряется площадь?
Площадь измеряется в квадратных единицах: мм², см², дм², м².
27. Назвать единицы длины.
Единицы длины
– мм,
см,
дм, м, км.
28. Рассказать таблицу мер длины.
1см
= 10мм
1дм
= 10см
1дм
= 100мм
1м
= 10 дм
1м
= 100 см
1км = 1000м
29. Сколько
квадратных сантиметров
в
1квадратном метре?
1м²
= 10 000см²
30. Сколько
квадратных дециметров
в
1 квадратном метре?
1м²
= 100дм²
31. Рассказать таблицу мер площади.
1м²
= 100дм² = 10 000см²
1дм²
= 100см² = 10 000мм²
1см²
= 100мм²
Масса.
32. Назвать единицы массы.
Масса измеряется в граммах, килограммах,
центнерах, тоннах.
33. Рассказать таблицу мер массы.
1кг
= 1000г
1ц
= 100кг
1т
= 10ц
1т
= 1000кг
Время.
34. Назвать
единицы измерения времени.
Время
измеряется секундами, минутами, часами, сутками, неделями, месяцами,
годами, веками.
35. Рассказать таблицу мер времени.
1мин
= 60сек.
1час
= 60мин
1час
= 3600сек.
1сут.
= 24часа
1год
= 12мес. =
365сут. или 366сут.
1век
= 100лет
Взаимосвязь скорости, времени и расстояния.
36. Как
найти скорость?
Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.
v = S : t
37. Как найти время?
Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость
( v ).
t = S : v
38. Как найти расстояние?
Чтобы найти расстояние ( S ), нужно скорость ( v ) умножить на время ( t ).
S = v · t
Взаимосвязь цены, количества, стоимости.
39. Что такое цена?
Цена – стоимость одного предмета,
единицы товара.
40. Как найти стоимость?
Чтобы найти стоимость, нужно цену
умножить на количество.
Ст = Ц · К
41. Как найти цену?
Чтобы найти цену, нужно стоимость
разделить на количество.
Ц
= Ст : К
42. Как найти
количество?
Чтобы найти количество, нужно стоимость
разделить на цену.
К = Ст : Ц
43. Задачи на дроби.
Дробь – ⅔
2
– числитель
3
– знаменатель
44. Как найти дробь числа?
Чтобы найти дробь числа, нужно число
разделить на знаменатель, а потом умножить на числитель.
45. Как найти число по дроби?
Чтобы
найти число по дроби, нужно число разделить на числитель и умножить на
знаменатель.
Взаимосвязь
работы, времени и производительности.
46. Что такое производительность?
Как найти производительность?
Производительностью
( v )
называют работу, выполненную за единицу времени.
Чтобы
найти производительность ( v ), надо всю
выполненную работу разделить на время.
v = A : t
47. Как найти выполненную работу?
Выполненная работа равна
производительности, умноженной на время работы.
A = v · t
48. Как найти время работы?
Чтобы узнать время работы, надо работу
разделить на производительность.
t = A : v
49. Как
найти среднее арифметическое?
Чтобы найти среднее арифметическое надо
сумму разделить на число слагаемых.
