Последовательность u0, u1, u2,…
называютрекуррентной, если указана
зависимость общего члена последовательности
от предыдущих и заданы значения
необходимого числа начальных членов
последовательности. Саму зависимость
иногда называютрекуррентностью.
Рекуррентная последовательность
u0, u1, u2,…
называетсялинейной, если ее члены
связаны соотношением вида
un+r = a1un+r–1 + a2un+r–2 +…+ arun , (1)
где ai,i = 1, 2,…, r,
– константы, не зависящие отn.
Соотношение (1) называетсялинейным
рекуррентным уравнением порядка r.
Последовательность сумм
s0 = u0, s1 = u0 + u1, …, sn = u0 + u1 +…+ un,
…
рекуррентной последовательности,
удовлетворяющей соотношению (1), является
рекуррентной и удовлетворяет следующему
линейному рекуррентному соотношению
порядка r + 1:
sn+r+1 =
= (1 + a1)sn+r +(a2 – a1)sn+r–1+…+( ar –ar–1)sn+1 – arsn. (2)
Уравнение
zr – a1zr–1 – a2zr–2 –…– ar = 0
называется характеристическим
уравнением рекуррентной последовательности,
удовлетворяющей соотношению (1), а
многочлен в левой части характеристического
уравнения – еехарактеристическим
многочленом. Пусть1,2, …,s– корни
характеристического многочлена
(возможно, комплексные) с кратностямиp1, p2, …, ps.
Тогда члены последовательности имеют
следующий вид:
![]() ,
,
где Pi(n) – многочлен,
степень которого не превышаетpi – 1.
Примеры
1.Найти общий вид членов последовательности
3, 8, 22, 62, …,
удовлетворяющей соотношению
un+2 = 5un+1 –6un.
Решение. Составим
характеристическое уравнение:
z2 – 5z + 6 = 0.
Оно имеет два решения: z1 = 2;z2 = 3.
Значит, общий член заданной последовательности
можно представить в виде
un = a2n + b3n.
Чтобы найти значения коэффициентов aиb, воспользуемся
начальными членами последовательности:
u0 = 3,u0 = a20 + b30;
u1 = 8,u1 = a21 + b31.
Получаем следующую систему линейных
уравнений:
a + b = 3;
2a + 3b = 8.
Решая ее, находим a = 1,b = 2.
Следовательно,
un = 2n + 23n,n = 0,
1, 2, … .
2.Найти общий вид членов последовательности
2, 6, 8, 4, –8, –24, –32, –16, 32, …,
удовлетворяющей соотношению
un+2 = 2un+1 –2un.
Решение. Составим
характеристическое уравнение:
z2 – 2z + 2 = 0.
Его решениями являются комплексные
числа z1 = 1 – iиz2 = 1 + i.
Общий член заданной последовательности
имеет вид
un = a(1 – i)n + b(1 + i)n.
Для вычисления коэффициентов aиbполучаем следующую
систему линейных уравнений:
a + b = 2;
a(1 – i) + b(1 + i) = 6.
Решая ее, находим
a = 1 + 2i,
b = 1 – 2i.
Следовательно,
un = (1 + 2i)
(1 – i)n + (1 – 2i)(1 + i)n,
n = 0,
1, 2, … .
Замечание.Представим числа 1 – iи 1 + iв тригонометрической форме:
1 – i = ![]() ,
,
1 +i = ![]() .
.
Тогда
(1 – i)n = ![]() ,
,
(1 + i)n = ![]() .
.
С учетом этого
un = ![]() .
.
Последняя формула объясняет, в частности,
периодичность знаков членов
последовательности.
3.Найти общий вид членов последовательности
–1, 3, 27, 135, …,
удовлетворяющей соотношению
un+2 = 6un+1 – 9un.
Решение.
Характеристическое уравнение
z2 – 6z + 9 = 0
имеет один корень z = 3 кратности 2. Общий член заданной
последовательности можно представить
в виде
un = (an +b)3n.
Для вычисления коэффициентов aиbполучаем следующую
систему линейных уравнений:
b = –1; (a + b)3 = 3.
Находим a = 2,
b = –1.
Следовательно,
un = (2n – 1)
3n,n = 0,
1, 2, … .
4.Найти формулу для вычисления суммы
первыхnчленов
рекуррентной последовательности
1, 1, 3, 5, 11, … ,
удовлетворяющей соотношению
un+2 = un+1 + 2un.
Решение.
Найдем рекуррентное соотношение,
которому удовлетворяет последовательность
сумм
sn = 1 +1 +3 +…+ un.
Имеем:
sn+3 = sn+2 + un+3;
sn+2 = sn+1 + un+2;
sn+1 = sn + un+1.
Выразим un+3,un+2,un+1и воспользуемся рекуррентным соотношением:
sn+3 – sn+2 = sn+2 – sn+1 + 2(sn+1 – sn).
После упрощений получаем рекуррентное
соотношение для сумм:
sn+3 = 2sn+2 + sn+1 – 2sn.
Запишем характеристическое уравнение:
z3 – 2z2 –z + 2 = 0
Находим его решения:
z1 = –1;z2 = 1;z3 = 2.
Ищем snв виде
sn = = a(–1)n + b + c2n.
Так как
s0 = 1, s1 = 1 + 1 =2,
s2 = 1 + 1 +3 = 5,
то
a + b + c = 1;
–a + b + 2c = 2;
a + b + 4c = 5.
Отсюда a = 1/6,b = –1/2,c = 4/3.
Таким образом,
sn = ![]() .
.
5.Найти рекуррентное соотношение
связывающее члены последовательности
кубов натуральных чисел:
u0 = 0, u1 = 1, u2 = 8,…, un = n3,
… .
Решение. Члены
последовательности кубов удовлетворяют
следующим соотношениям:
un+1 = un + 3n2 + 3n + 1;
un+2 = un+1 + 3n2 + 9n + 7;
un+3 = un+2 + 3n2 + 15n + 19;
un+4 = un+3 + 3n2 + 21n + 37.
Вычитая из второго уравнения первое,
из третьего – второе, из
четвертого – третье, находим:
un+2 – un+1 = un+1 – un + 6n + 6;
un+3 – un+2 = un+2 – un+1 + 6n + 12;
un+4 – un+3 = un+3 – un+2 + 6n + 18.
Теперь, вычитаем первое из полученных
уравнений из второго, а второе – из
третьего:
(un+3 – un+2 ) – (un+2 – un+1) = (un+2 – un+1) – (un+1 – un) + 6 ;
(un+4 – un+3 ) – (un+3 – un+2) = (un+3 – un+2) – (un+2 – un+1) + 6 .
Теперь, вычитаем первое уравнение из
второго и получаем рекуррентное
соотношение:
un+4 = 4un+3 – 6un+2 + 4un+1 – un .
6.Найти формулу для вычисления суммы
квадратов натуральных чисел 12+ 22+ …n2.
Решение. Сначала
найдем рекуррентное соотношение,
связывающее члены последовательности
квадратов
u0 = 0, u1 = 1, u2 = 4,…, un = n2,
… .
Действуем так же, как в предыдущем
примере:
un+1 = un + 2n + 1;
un+2 = un+1 + 2n + 3;
un+3 = un+2 + 2n + 5;
un+2 – un+1 = un+1 – un + 2;
un+3 – un+2 = un+2 – un+1 + 2.
Наконец,
un+3 = 3un+2 – 3un+1 + un .
Теперь найдем рекуррентное соотношение,
которым связаны члены последовательности
сумм
sn = u0 + u1 +…+ un.
Получаем:
sn+4 = 4sn+3 – 6sn+2 + 4sn+1 – sn.
Характеристический многочлен
z4 – 4z3 + 6z2 – 4z + 1 = (z – 1)4
имеет один корень z = 1
кратности 4. Значит,snпредставимо в виде
sn = (an3 + bn2 + cn + d)1n,
то есть snявляется кубическим многочленом поn.
Чтобы найти коэффициенты, воспользуемся
начальными суммами последовательности
квадратов:
d = s0 = 0;
a + b + c + d = s1 = 1;
8a + 4b + 2c + d = s2 = 5;
27a + 9b + 3c + d = s3 = 14.
Решая эту линейную систему уравнений,
находим: a = 1/3;b = 1/2;c = 1/6;d = 0.
Таким образом,
12+ 22+ …n2 = ![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Числовые последовательности
Термин «последовательность» используют, когда говорят о расположении учеников в шеренге, очередности дней недели, расположении команд в турнирной таблице и т. п. В этом параграфе мы выясним, что такое числовая последовательность, в частности, что такое арифметическая и геометрическая прогрессии, каковы их свойства, научимся использовать свойства упомянутых прогрессий при решении прикладных задач.
- 1; 1; 2; 3; 5; 8;… — последовательность
- 2; 5; 8; 11; 14;… — арифметическая прогрессия (каждое число, начиная со второго, на 3 больше предыдущего)
- 2; 6; 18:54; 162:. . — геометрическая прогрессия (каждое число, начиная со второго, в три раза больше предыдущего)
Рассмотрим несколько примеров.
Пример:
Один подсолнух за лето «выпивает» в среднем 250 л воды. Сколько воды «выпьют» за лето 1 ,2 ,3 ,4 ,5 подсолнухов?

Решение:
Во второй строке получили несколько чисел, записанных в определенном порядке, говорят, получим последовательность чисел: 250; 500; 750: 1000; 1250, в которой на первом месте стоит число 250, на втором — 500, на пятом — 1250. В этом примере каждому натуральному числу от 1 до 5 включительно соответствует одного число из указанной последовательности. Итак, имеем функцию, областью определения которой является множество чисел 1.2.3.4.5.
Пример:
3аписать в порядке возрастания натуральные числа запись которых оканчивается цифрой 2.
Решение:
Получим последовательность чисел 2; 12; 22; 32; 42; …. в которой на первом месте стоит число 2, на втором — 12. на третьем — 22 и т. д.

В этом примере каждому натуральному числу 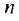 соответствует одно число из указанной последовательности. Так, натуральному числу 6 соответствует число 52 этой последовательности, числу 7 — число 62 и т. д. Следовательно, имеем функцию, областью определения которой является множество всех натуральных чисел.
соответствует одно число из указанной последовательности. Так, натуральному числу 6 соответствует число 52 этой последовательности, числу 7 — число 62 и т. д. Следовательно, имеем функцию, областью определения которой является множество всех натуральных чисел.
Определение:
Последовательностью называют функцию, заданную на множестве всех или первых 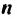 натуральных чисел.
натуральных чисел.
Числа образующие последовательность. называют членами последовательности. Если последовательность имеет конечное число членов, тогда ее называют конечной последовательностью (пример 1). Если последовательность имеет бесконечное число членов, то ее называют бесконечной последовательностью (пример 2), а в записи это показывают многоточием после последнего записанною члена последовательности.
Приведем еще примеры последовательностей:
- 4; 8; 12; 16;… — последовательность натуральных чисел, кратных 4;
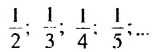 — последовательность правильных дробей с числителем 1;
— последовательность правильных дробей с числителем 1;- -1: -2 ; -3 ; -4 ;… — последовательность отрицательных целых чисел;
- 0.1; 1.1; 2.1: 3,1 — последовательность, состоящая из четырех членов;
- 7 :7 ; 7 :7 :… — последовательность, все члены которой равны 7.
- Четвертая последовательность конечная, остальные — бесконечные.
В общем случае члены последовательности, как правило, обозначают маленькими буквами с индексами внизу. Каждый индекс указывает порядковый номер члена последовательности. Например, первый член последовательности обозначают 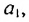 читают «а первое», второй —
читают «а первое», второй — 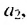 читают «а второе», член последовательности с номером
читают «а второе», член последовательности с номером 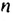 обозначают
обозначают 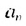 , и читают «а энное». Саму последовательность обозначают
, и читают «а энное». Саму последовательность обозначают 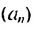 и записывают:
и записывают: 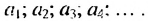 Член
Член 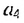 называют следующим за
называют следующим за 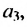 а член
а член 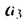 — предыдущим члену
— предыдущим члену 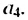 Например, рассмотрим последовательность
Например, рассмотрим последовательность 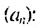 1: 3; 5;… — последовательность нечетных натуральных чисел. В ней
1: 3; 5;… — последовательность нечетных натуральных чисел. В ней 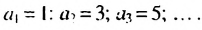 Член последовательности
Член последовательности 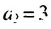 является предыдущим члену
является предыдущим члену 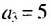 и последующим за членом
и последующим за членом 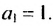
Способы задании последовательностей
Чтобы задать последовательность, нужно указать способ, при помощи которого можно найти любой ее член. Существуют различные способы задания последовательностей.
1. Последовательность можно задать описанием способа определения ее членов. Например, пусть задана последовательность, членами которой являются делители числа 15, записанные в порядке возрастания. Эту последовательность, описанную словами, можно записать так; 1 ; 3; 5: 15.
2. Конечную последовательность можно задать, перечислив ее члены. Например, 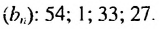
3. Последовательность можно задать таблицей, в которой напротив каждого члена последовательности указывают его порядковый номер. Например.

4. Последовательность можно задать формулой, по которой можно найти любой член последовательности, зная его номер. Например, последовательность натуральных чисел, кратных 3, можно задать формулой 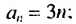 последовательность чисел, обратных натуральным, — формулой
последовательность чисел, обратных натуральным, — формулой 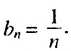 Такие формулы называют еще формулами
Такие формулы называют еще формулами  члена последовательности. Пусть последовательность
члена последовательности. Пусть последовательность 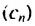 задана формулой
задана формулой 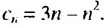 Подставляя вместо
Подставляя вместо 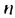 натуральные числа 1,2 ,3 …., получим:
натуральные числа 1,2 ,3 …., получим: 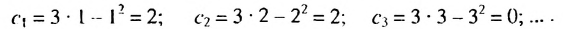
Поэтому 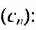 2; 2; 0 ;….
2; 2; 0 ;….
5. Последовательность можно задать так: сначала указать первый или несколько первых членов последовательности, а потом — условие, по которому можно определить любой член последовательности, зная предыдущие. Такой способ задания последовательности называют рекуррентным. Например, найдем несколько членов последовательности 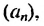 первый член которой равен -1 , второй — -3 , а каждый последующий, начиная с третьего, равен произведению двух предыдущих. Получим:
первый член которой равен -1 , второй — -3 , а каждый последующий, начиная с третьего, равен произведению двух предыдущих. Получим: 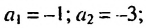
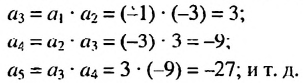
Условия, определяющие эту последовательность, можно записать так: 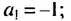
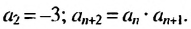 Формулу, при помощи которой любой член последовательности можно найти через предыдущие, называют рекуррентной формулой.
Формулу, при помощи которой любой член последовательности можно найти через предыдущие, называют рекуррентной формулой.
Рассмотренные выше последовательности являются числовыми последовательностями, так как их элементами являются числа. Существуют и другие последовательности. Например, последовательность передач на канале телевидения, последовательность футбольных команд в турнирной таблице и т. п.
В дальнейшем будем рассматривать только числовые последовательности.
Пример:
Записать шесть первых членов последовательности натуральных чисел, которые при делении на 3 дают остаток 2.
Решение:
Первым натуральным числом, которое при делении па 3 дает остаток 2, является число 2. Следующим является число 5 — оно на 3 больше 2, дальше 8 — на 3 больше 5 и т. д. Поэтому получим: 2; 5; 8; I I ; 14; 17.
Ответ. 2 ;5 ;8 ; 11; 14; 17
Пример:
Записать формулу 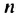 -го члена последовательности
-го члена последовательности 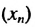 натуральных чисел, которые больше 8 и при делении на 9 дают остаток 7.
натуральных чисел, которые больше 8 и при делении на 9 дают остаток 7.
Решение:
Первым натуральным числом, которое больше 8 и при делении на 9 дает остаток 7, является число 16. Его можно записать так: 16 = 9 •1 + 7 . Вторым будет число 25, которое можно записать гак: 25 = 9 • 2 + 7, третьим — 34 = 9 • 3 + 7 и т. д. Тогда формула 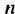 -го члена искомой последовательности
-го члена искомой последовательности 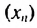 будет иметь вид:
будет иметь вид: 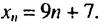 Ответ.
Ответ. 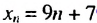
Пример:
Последовательность задана формулой 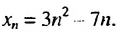 Является ли членом этой последовательности число 6?
Является ли членом этой последовательности число 6?
Решение:
Число 6 будет членом этой последовательности, если найдется такой номер 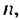 что
что 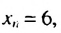 то есть
то есть 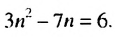 Получаем уравнение:
Получаем уравнение: 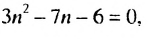 откуда
откуда 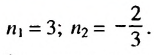 Число
Число 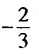 не является натуральным, а поэтому не может быть номером члена последовательности. Следовательно, число 6 является третьим членом заданной последовательности.
не является натуральным, а поэтому не может быть номером члена последовательности. Следовательно, число 6 является третьим членом заданной последовательности.
Ответ. Да.
Пример:
Записать три первых члена последовательности  если
если 
Решение:
При  = 1 по формуле
= 1 по формуле 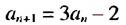 получим:
получим: 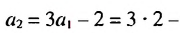
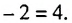 При
При 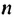 = 2 получим:
= 2 получим: 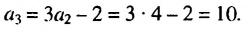 Ответ. 2; 4; 10.
Ответ. 2; 4; 10.
Арифметическая прогрессия и ее свойства
Среди числовых последовательностей важную роль играют последовательности, которые называют арифметической и геометрической прогрессиями.
Пример:
Группа туристов поднималась на гору в течение 4 ч. За первый час туристы прошли 2,5 км, а та каждый следующий — на 0,5 км меньше, чем за предыдущий. Какой путь проходили туристы за каждый час движения?
Решение:
За первый час туристы прошли 2.5 км. за второй — 2,5 – 0,5 = 2 (км), за третий — 2 – 0,5 = 1,5 (км), за четвертый — 1 км. Получили конечную последовательность чисел: 2,5; 2; 1,5; 1, в которой каждый последующий член, начиная со второю, равен предыдущему, сложенному с одним и тем же числом -0.5.
Пример:
3аписать последовательность натуральных чисел, которые при делении на 3 дают остаток 1.
Решение:
Получим: 1;4 ;7 ; 10; 13; 16; 19; 22 ;…. В этой последовательности любой член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом 3. Каждая из рассмотренных последовательностей является примером арифметической прогрессии.
Определение:
Арифметической прогрессией называют последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Это число называют разностью арифметической прогрессии и обозначают буквой d (d — начальная буква латинского слова differentia — разность). Итак, если имеется арифметическая прогрессия 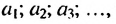 то
то 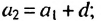
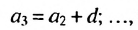 то есть для любого натурального
то есть для любого натурального 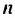 выполняется равенство
выполняется равенство
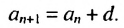
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна одному и тому же числу — разности d, то есть 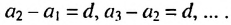 Итак,
Итак, 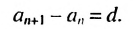
Верно и наоборот: если в некоторой числовой последовательности разность между любым ее членом, начиная со второго, и предыдущим членом равна одному и тому же числу, то такая последовательность является арифметической прогрессией.
Арифметические прогрессии могут быть конечными (пример 1) и бесконечными (пример 2).
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность. Тогда каждый последующий член можно вычислить по предыдущему по рекуррентной формуле 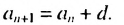 В таблице приведены примеры арифметических прогрессий для некоторых значений
В таблице приведены примеры арифметических прогрессий для некоторых значений 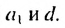

Рассмотрим свойства арифметической прогрессии.
1. В арифметической прогрессии 1; 3; 5: 7; 9 ;… каждый член, начиная со второго, является средним арифметическим двух соседних с ним членов:
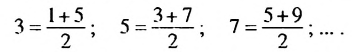
Покажем, что такое свойство имеет любая арифметическая прогрессия. Пусть имеется арифметическая прогрессия 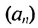 с разностью d. Тогда для натуральных значений
с разностью d. Тогда для натуральных значений 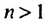 выполняются равенства:
выполняются равенства: 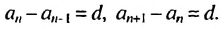 Отсюда:
Отсюда: 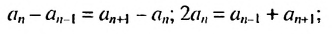
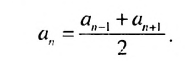
Свойство 1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов. С этим свойством арифметической прогрессии и связано ее название.
2. Рассмотрим конечную арифметическую прогрессию 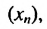 имеющую 7 членов: 3; 5; 7; 9; 11; 13; 15. Найдем сумму крайних членов прогрессии и суммы членов, равноотстоящих от крайних:
имеющую 7 членов: 3; 5; 7; 9; 11; 13; 15. Найдем сумму крайних членов прогрессии и суммы членов, равноотстоящих от крайних:
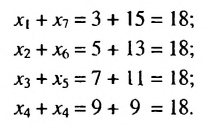
Сумма любых двух членов арифметической прогрессии, равноотстоящих от ее крайних членов, равна сумме крайних членов.
Используем эти соображения для произвольной конечной арифметической прогрессии 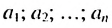 с разностью
с разностью 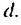 Пусть
Пусть 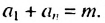 Тогда:
Тогда:
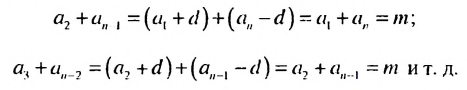
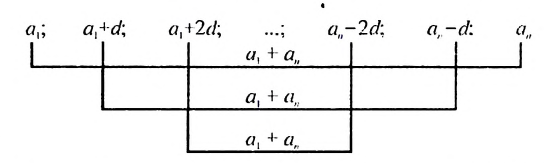
Свойство 2. Сумма любых двух членов конечной арифметической прогрессии, равноотстоящих от ее крайних членов, равна сумме крайних членов этой прогрессии.
Пример:
Найти разность и третий член арифметической прогрессии 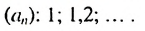
Решение:
В этой прогрессии 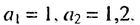 Поэтому:
Поэтому:
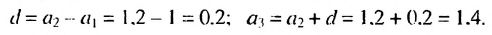 Ответ. 0.2; 1,4.
Ответ. 0.2; 1,4.
Пример:
Является ли последовательность чисел 3: 0: -3 : -6 ; -9 арифметической прогрессией?
Решение:
Обозначим члены заданной последовательности:
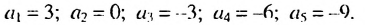 Найдем разность последующего и предыдущего членов последовательности:
Найдем разность последующего и предыдущего членов последовательности:
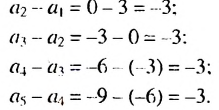
Так как полученные разности равны одному и тому же числу – 3, то эта последовательность является арифметической прогрессией.
Пример:
Между числами 7 и 15 вставить такое число, чтобы все три числа образовали арифметическую прогрессию.
Решение:
Пусть 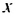 — искомое число, тогда последовательность 7; х; 15 — арифметическая прогрессия. Второй член арифметической прогрессии является средним арифметическим первого и третьего членов:
— искомое число, тогда последовательность 7; х; 15 — арифметическая прогрессия. Второй член арифметической прогрессии является средним арифметическим первого и третьего членов: 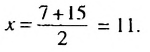 Ответ. 11 .
Ответ. 11 .
Формула n-го члена арифметической прогрессии
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность, а последующие члены можно найти по формуле 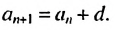
Например, найдем несколько первых членов арифметической прогрессии, в которой 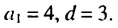 Получим:
Получим:
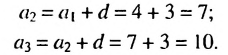
Далее можно найти 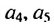 и т. д.
и т. д.
Чтобы найти член этой прогрессии с большим порядковым номером, например, 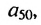 нужно выполнить много вычислений. Поэтому вычисление членов арифметической прогрессии но формуле
нужно выполнить много вычислений. Поэтому вычисление членов арифметической прогрессии но формуле 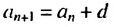 часто является неудобным. Найдем более краткий путь вычисления n-го члена арифметической прогрессии
часто является неудобным. Найдем более краткий путь вычисления n-го члена арифметической прогрессии 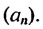
По определению арифметической прогрессии получим:
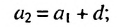
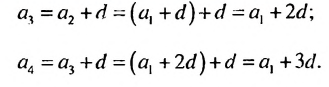
Замечаем, что в этих формулах коэффициент при d на 1 меньше порядкового номера искомого члена прогрессии. Так, 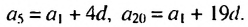 Итак, можем записать:
Итак, можем записать:
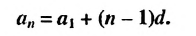
Полученную формулу называют формулой 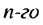 члена арифметической прогрессии.
члена арифметической прогрессии.
Пример:
Найти девятый член арифметической прогрессии 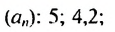
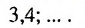
Решение:
Имеем: 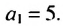 Найдем разность прогрессии:
Найдем разность прогрессии: 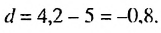 Тогда
Тогда 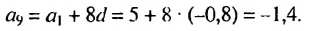 Ответ. -1,4.
Ответ. -1,4.
Пример:
Найти первый член арифметической прогрессии  в которой
в которой 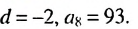
Решение:
Используя формулу 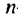 -го члена арифметической прогрессии при
-го члена арифметической прогрессии при 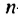 = 8, получим:
= 8, получим: 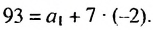 Отсюда
Отсюда 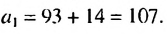 Ответ. 107.
Ответ. 107.
Пример:
Является ли число 181 членом арифметической прогрессии, в которой 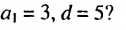
Решение:
Число 181 будет членом прогрессии, если существует такое натуральное число 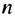 — порядковый номер члена прогрессии, что
— порядковый номер члена прогрессии, что 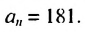 Так как
Так как 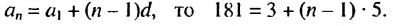 Решим полученное уравнение:
Решим полученное уравнение: 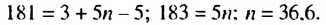 Число 36.6 не является натуральным, поэтому число 181 не является членом данной арифметической прогрессии. Ответ. Нет.
Число 36.6 не является натуральным, поэтому число 181 не является членом данной арифметической прогрессии. Ответ. Нет.
Пример:
Найти первый член и разность арифметической прогрессии 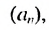 если сумма второго и пятого ее членов равна 20, а разность девятого и третьего членов равна 18.
если сумма второго и пятого ее членов равна 20, а разность девятого и третьего членов равна 18.
Решение:
По условию имеем: 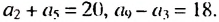 Записав члены
Записав члены 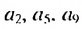 и
и 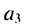 по формуле
по формуле 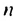 -го члена арифметической прогрессии, получим систему уравнений:
-го члена арифметической прогрессии, получим систему уравнений:
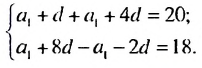 Откуда
Откуда 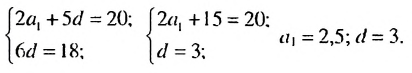
Ответ. 2.5;3 .
Формула суммы первых п членов арифметической прогрессии
Пример:
Найти сумму натуральных чисел от 1 до 100 включительно.
Решение:
Запишем суму 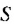 данных чисел двумя способами: в порядке возрастания и в порядке убывания слагаемых и почленно сложим полученные равенства:
данных чисел двумя способами: в порядке возрастания и в порядке убывания слагаемых и почленно сложим полученные равенства:
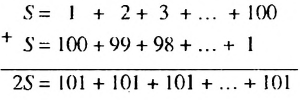
Суммы пар чисел, расположенных друг под другом в правых частях этих равенств, равны одному и тому же числу 101; таких нар 100. Поэтому
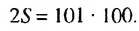
Отсюда 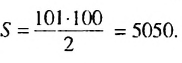
Итак, сумма всех натуральных чисел от 1 до 100 включительно равна 5050. Отметим, что последовательность натуральных чисел I; 2; …; 99: 100 является арифметической прогрессией 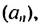 в которой
в которой 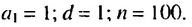 Используем рассмотренный способ для вывода формулы суммы
Используем рассмотренный способ для вывода формулы суммы 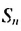 первых
первых 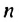 членов любой арифметической прогрессии
членов любой арифметической прогрессии 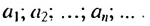 Запишем:
Запишем:
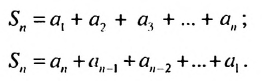
Сложим почленно эта равенства, получим:
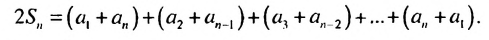
По свойству 2 арифметической прогрессии сумма каждых двух членов, взятых в скобки, равна 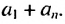 Таких сум есть
Таких сум есть 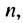 поэтому:
поэтому:
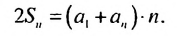
Отсюда 
Если в этой формуле вместо 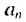 подставить выражение
подставить выражение 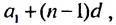 то получим:
то получим:
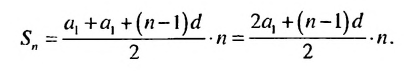
Итак,
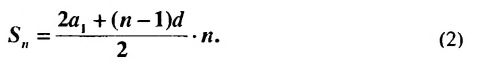
Формулы (1) и (2) называют формулами суммы первых  членов арифметической прогрессии.
членов арифметической прогрессии.
Пример:
Найти сумму первых девяти членов арифметической прогрессии 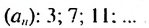
Решение:
1-й способ. Имеем: 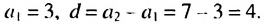 Найдем
Найдем 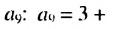
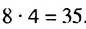 По формуле (1) находим:
По формуле (1) находим:
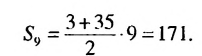
2-й способ. Зная, что 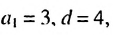 по формуле (2) находим:
по формуле (2) находим:
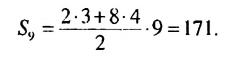
Ответ. 171.
Пример:
Найти сумму нечетных натуральных чисел, не превышающих 71.
Решение:
Нечетные натуральные числа образуют арифметическую прогрессию 1; 3: 5;……. в которой 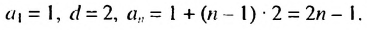 Найдем, какой порядковый номер имеет член 71 этой прогрессии:
Найдем, какой порядковый номер имеет член 71 этой прогрессии: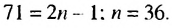 Следовательно, нужно искать сумму первых тридцати шести членов прогрессии. Имеем:
Следовательно, нужно искать сумму первых тридцати шести членов прогрессии. Имеем:
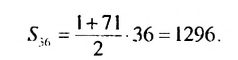
Ответ. 1296.
Пример:
Найти сумму натуральных чисел не больше 105, которые при делении на 9 дают остаток 1.
Решение:
Натуральные числа, которые при делении на 9 дают остаток 1, образуют арифметическую прогрессию 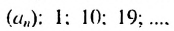 в которой
в которой 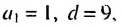
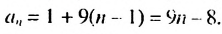 Найдем, сколько членов этой прогрессии не превышают 105. Для этого решим неравенство
Найдем, сколько членов этой прогрессии не превышают 105. Для этого решим неравенство 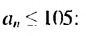
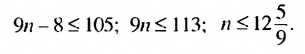
Следовательно, нужно искать сумму первых двенадцати членов прогрессии. Имеем: 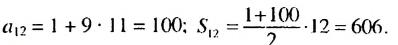 Ответ. 606.
Ответ. 606.
Пример:
Найти первый член арифметической прогрессии 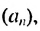 если сумма второго и двенадцатого ее членов равна 20.4, а сумма первых одиннадцати— 121.
если сумма второго и двенадцатого ее членов равна 20.4, а сумма первых одиннадцати— 121.
Решение:
По условию имеем: 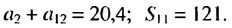 Используя формулы
Используя формулы 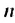 -по члена и суммы первых
-по члена и суммы первых 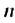 членов арифметической прогрессии, получим систему уравнений
членов арифметической прогрессии, получим систему уравнений 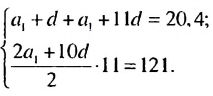 Отсюда:
Отсюда:
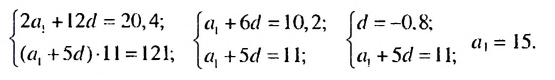
Ответ. 15.
Пример:
Сколько нужно взять первых членов арифметическом прогрессии 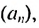 в которой
в которой 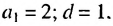 чтобы их сумма равнялась 90?
чтобы их сумма равнялась 90?
Решение:
Используя формулу суммы первых 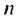 членов арифметической прогрессии
членов арифметической прогрессии 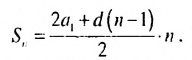 получим:
получим: 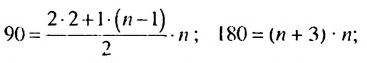
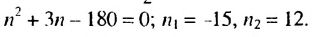 Корень
Корень 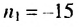 не удовлетворяет условию задачи. Следовательно,
не удовлетворяет условию задачи. Следовательно, 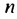 = 12. Ответ. 12.
= 12. Ответ. 12.
Геометрическая прогрессия и ее свойства
В благоприятных условиях некоторые бактерии размножаются так, что их количество удваивайся каждые 30 минут. Поэтому, если первоначально была одна бактерия, то их будет:
- через 0,5 ч 2
- через I ч 4
- через 1,5 ч 8
- через 2 ч 16
- …………………..
Во втором столбце получили последовательность чисел: 2: 4; 8; 16; каждый член которой, начиная со второго, равен предыдущему, умноженному на число 2. Такая последовательность является примером геометрической прогрессии.
Определение:
Геометрической прогрессией называют последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
Это число называют знаменателем геометрической прогрессии и обозначают буквой q (начальная буква французского слова qwoti — частное). Итак, если имеем геометрическую прогрессию 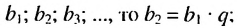
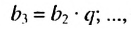 то сеть для любого натурального
то сеть для любого натурального 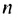 выполняется равенство
выполняется равенство 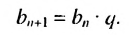
Из определения геометрической прогрессии следует, что частное от деления любого ее члена, начиная со второго, на предыдущий член равно одному и тому же числу – знаменателю то есть: 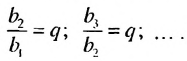 Итак,
Итак, 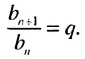 Верно и наоборот: если в некоторой последовательности частное от деления любого ее члена, начиная со второго, на предыдущий член равно одному и тому же числу, то такая последовательность является геометрической прогрессией. Геометрические прогрессии, как и арифметические, мотут быть конечными и бесконечными.
Верно и наоборот: если в некоторой последовательности частное от деления любого ее члена, начиная со второго, на предыдущий член равно одному и тому же числу, то такая последовательность является геометрической прогрессией. Геометрические прогрессии, как и арифметические, мотут быть конечными и бесконечными.
Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель. Тогда каждый последующий член по предыдущему можно вычислить по рекуррентной формуле 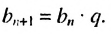
В таблице прицелены примеры геометрических прогрессий для некоторых значений 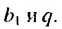

Рассмотрим свойства геометрической прогрессии.
1. В геометрической прогрессии 1; 3: 9, 27; 81;… квадрат каждого члена, начиная со второго, равен произведению двух соседних с ним членов:
Покажем, что такое свойство имеет любая геометрическая прогрессия. Пусть имеется геометрическая прогрессия 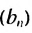 со знаменателем q. Тогда при
со знаменателем q. Тогда при 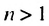 выполняются равенства:
выполняются равенства: 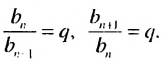 Отсюда
Отсюда 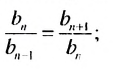
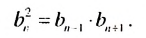
Свойство 1
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних с ним членов.
Если все члены геометрической прогрсссии являются положительными числами, то из равенства 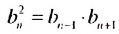 следует, что
следует, что 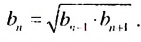 Следовательно, каждый член такой прогрессии, начиная со второго, является средним геометрическим .двух соседних с ним членов. С этим свойством геометрической профессии и связано ее название.
Следовательно, каждый член такой прогрессии, начиная со второго, является средним геометрическим .двух соседних с ним членов. С этим свойством геометрической профессии и связано ее название.
2. Рассмотрим конечную геометрическую прогрессию 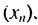 содержащую шесть членов: -1:2; 4; 8; -16:32. Найдем произведение крайних членов этой прогрессии и произведение членов, равноотстоящих от крайних:
содержащую шесть членов: -1:2; 4; 8; -16:32. Найдем произведение крайних членов этой прогрессии и произведение членов, равноотстоящих от крайних:
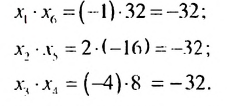
Видим, что произведения членов профессии, равноотстоящих от ее крайних членов, одинаковы и равны произведению крайних членов.
Используем эти соображения для произвольной конечной геометрической прогрессии 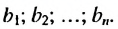 Пусть
Пусть 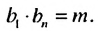 Тогда:
Тогда:
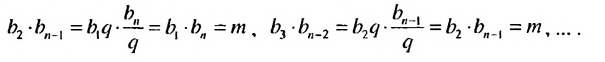
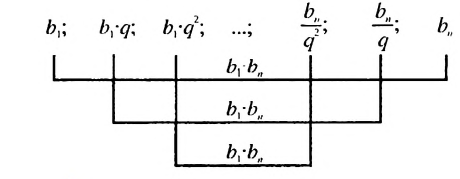
Свойство 2
Произведение любых двух членов конечной геометрической прогрессии, равноотстоящих от ее крайних членов, равно произведению крайних членов.
Пример:
Найти знаменатель и третий член геометрической npoгpеcсии 
Решение:
В этой прогрессии 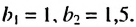 Поэтому:
Поэтому:
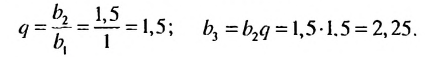
Ответ. 1,5; 2,25.
Пример:
Доказать, что последовательность 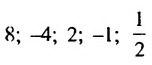 является геометрической профессией.
является геометрической профессией.
Решение:
Обозначим члены последовательности: 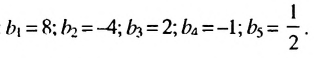 Найдем частные от деления последующего члена последовательности на предыдущий:
Найдем частные от деления последующего члена последовательности на предыдущий:
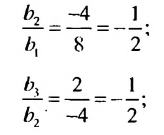
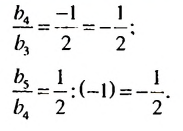
Так как полученные частные равны одному и тому же числу 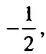 то данная последовательность является геометрической прогрессией со знаменателем
то данная последовательность является геометрической прогрессией со знаменателем 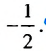
Пример:
Найти второй член геометрической прогрессии: 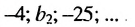
Решение:
Согласно свойству 1 геометрической прогрессии 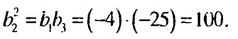 Отсюда
Отсюда 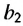 – 10 или
– 10 или 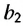 = -10. Ответ 10 или-10.
= -10. Ответ 10 или-10.
Формула n-го члена геометрической прогрессии
Чтобы задать геометричсскую прогрессию 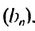 достаточно указать ее первый член и знаменатель, а следующие члены можно найти по формуле
достаточно указать ее первый член и знаменатель, а следующие члены можно найти по формуле 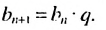 Например, запишем несколько первых членов геометрической прогрессии, в которой
Например, запишем несколько первых членов геометрической прогрессии, в которой 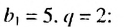
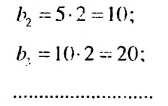
Далее можно найти 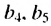 и т. д. Чтобы найти член этой прогрессии с большим порядковых! номером, например,
и т. д. Чтобы найти член этой прогрессии с большим порядковых! номером, например, 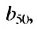 нужно выполнить мною вычислений. Поэтому вычисление членов геометрической прогрессии по формуле
нужно выполнить мною вычислений. Поэтому вычисление членов геометрической прогрессии по формуле 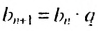 часто является неудобным. Найдем более краткий путь вычисления
часто является неудобным. Найдем более краткий путь вычисления 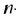 -го члена геометрической прогрессии
-го члена геометрической прогрессии 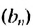 со знаменателем q. По определению геометрической прогрессии имеем:
со знаменателем q. По определению геометрической прогрессии имеем:
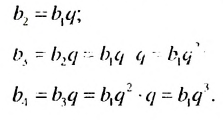
Замечаем, что в этих формулах показатель степени числа q на единицу меньше порядкового номера искомого члена прогрессии. Так, 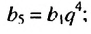
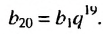 Итак, можем записать:
Итак, можем записать:
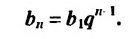 Полученную формулу называют формулой
Полученную формулу называют формулой 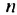 -го члена геометрической прогрессии.
-го члена геометрической прогрессии.
Пример:
Найти шестой член геометрической прогрессии 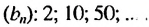
Решение:
Имеем: 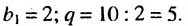 Тогда
Тогда 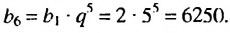 Ответ. 6250.
Ответ. 6250.
Пример:
Найти первый член геометрической прогрессии 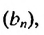 если
если 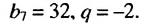
Решение:
Используя формулу 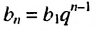 при
при 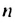 = 7, получим:
= 7, получим:
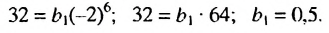 Ответ. 0,5
Ответ. 0,5
Пример:
Найти знаменатель геометрической прогрессии 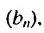 в которой
в которой 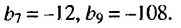
Решение:
Используя формулу 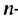 -го члена геометрической прогрессии, получим:
-го члена геометрической прогрессии, получим: 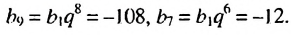 Отсюда:
Отсюда:
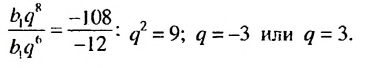
Ответ. -3 или 3.
Формула суммы первых n членов геометрической прогрессии
Пусть  — геометрическая прогрессия, знаменатель которой равен
— геометрическая прогрессия, знаменатель которой равен 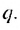 Обозначим через
Обозначим через 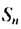 сумму первых
сумму первых 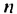 членов этой профессии. то есть
членов этой профессии. то есть
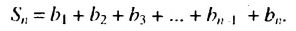 (1)
(1)
Умножив обе части этого равенства на q получим:
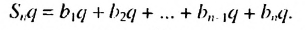
Пo определению геометрической прогрессии: 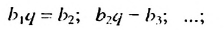
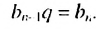 Тогда:
Тогда:
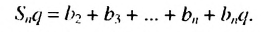 (2)
(2)
Вычтем почленно из равенства (1) равенство (2), получим:
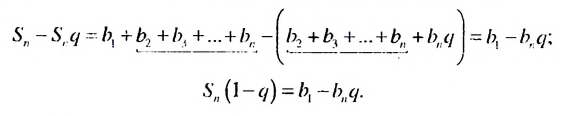
Если 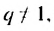 , то
, то
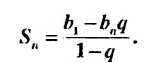 (3)
(3)
Учитывая, что 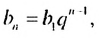 получим
получим 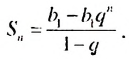 Итак,
Итак,
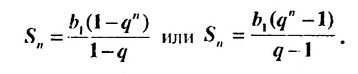 (4)
(4)
Формулы (3) и (4) называют формулами суммы первых  членов геометрической прогрессии. При
членов геометрической прогрессии. При  каждый член геометрической прогрессии равен
каждый член геометрической прогрессии равен 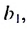 поэтому
поэтому 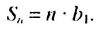
Пример:
Найти сумму восьми первых членов геометрической прогрессии 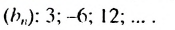
Решение:
Имеем : 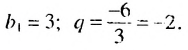 Тогда но формуле
Тогда но формуле 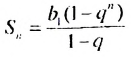 находим:
находим: 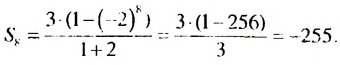
Ответ. -255.
Пример:
Найти первый член геометрической прогрессии 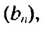 если четвертый ее член в три раза больше третьего, а сумма первых пяти членов равна -12,1.
если четвертый ее член в три раза больше третьего, а сумма первых пяти членов равна -12,1.
Решение:
Так как 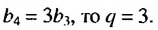 По условию
По условию 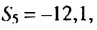 поэтому:
поэтому:
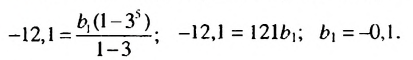
Ответ. -0,1.
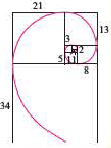
Сумма бесконечной геометрической прогрессии, в которой [q] меньше 1
Сумма бесконечной геометрической прогрессии, в которой 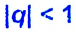
Пусть стороны прямоугольника  равны I см и 4 см (рис. 74). Его площадь равна
равны I см и 4 см (рис. 74). Его площадь равна 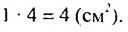
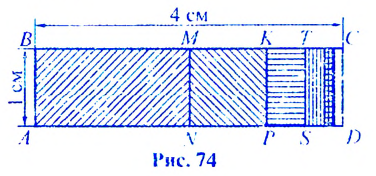
Найдем площадь этою прямоугольника иначе. Отрезком MN. соединяющим середины противоположных сторон ВС и  прямоугольника, разделим его пополам. Площади образованных прямоугольников
прямоугольника, разделим его пополам. Площади образованных прямоугольников  и
и 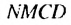 равны по
равны по 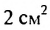 каждая. Образованный справа прямоугольник снова разделим пополам, соединив середины
каждая. Образованный справа прямоугольник снова разделим пополам, соединив середины 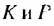 противоположных сторон. Площади образованных прямоугольников NMKP и PKCD равны по 1 см2 каждая. Аналогично образованный прямоугольник
противоположных сторон. Площади образованных прямоугольников NMKP и PKCD равны по 1 см2 каждая. Аналогично образованный прямоугольник 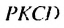 снова разделим пополам отрезком
снова разделим пополам отрезком 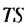 на два прямоугольника с площадями по
на два прямоугольника с площадями по 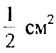 и т.д.
и т.д.
Найдем сумму площадей прямоугольников 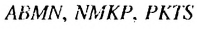 и т.д. Числовое значение суммы площадей этих прямоугольников равно суме чисел
и т.д. Числовое значение суммы площадей этих прямоугольников равно суме чисел  Последовательность
Последовательность 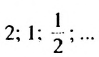 является бесконечной геометрической профессией, первый член которой равен 2, а знаменатель —
является бесконечной геометрической профессией, первый член которой равен 2, а знаменатель — 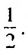 Найдем сумму первых
Найдем сумму первых 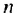 членов этой прогрессии:
членов этой прогрессии:
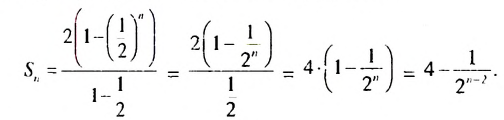
Если число 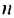 слагаемых суммы
слагаемых суммы 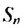 неограниченно увеличивается, то значение дроби
неограниченно увеличивается, то значение дроби 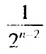 приближается к нулю, а разность
приближается к нулю, а разность 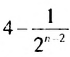 приближается к числу 4, говорят: стремится к числу 4. Число 4 называют суммой бесконечной геометрической прогрессии
приближается к числу 4, говорят: стремится к числу 4. Число 4 называют суммой бесконечной геометрической прогрессии 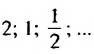 и записывают
и записывают 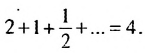
Итак, сумма площадей прямоугольников ABMN, NMKP, PKTS и т. д. равна 4 см2, то есть равна площади прямоугольника ABCD. Обобщим рассмотренный пример. Пусть 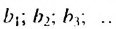 . — любая бесконечная геометрическая прогрессия, в которой
. — любая бесконечная геометрическая прогрессия, в которой 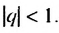 Сумму первых
Сумму первых 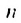 членов этой прогрессии вычисляют по формуле
членов этой прогрессии вычисляют по формуле 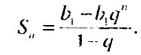 Преобразуем выражение в правой части последнего равенства:
Преобразуем выражение в правой части последнего равенства: 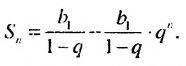 Так как
Так как 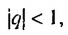 то при неограниченном увеличении
то при неограниченном увеличении 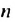 множитель
множитель 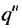 стремится к нулю, а значит, к нулю стремится и произведение
стремится к нулю, а значит, к нулю стремится и произведение 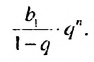 Тогда сумма
Тогда сумма 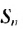 , стремится к числу
, стремится к числу 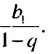 Число
Число 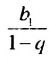 называют суммой бесконечной геометрической прогрессии со знаменателем
называют суммой бесконечной геометрической прогрессии со знаменателем 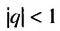 и записывают:
и записывают: 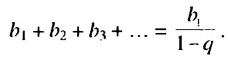 Обозначим эту сумму через S. Тогда
Обозначим эту сумму через S. Тогда
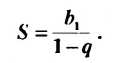
Полученную формулу называют формулой суммы бесконечной геометрической прогрессии, в которой 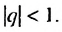
Пример:
Найти сумму бесконечной геометрической прогрессии 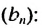 6: – 2 ; ..
6: – 2 ; ..
Решение:
По условию 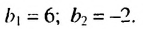 Тогда
Тогда 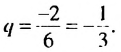 Имеем геометрическую прогрессию, в которой
Имеем геометрическую прогрессию, в которой 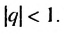 По формуле
По формуле 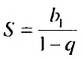 находим:
находим:
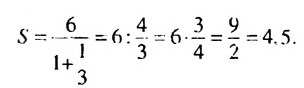
Ответ. 4,5.
Решение задач, связанных с арифметической и геометрической прогрессиями
Вычисление сумм
Изучая арифметическую и геометрическую прогрессии, мы вычисляли суммы первых 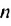 их членов. Известно также, как найти сумму бесконечной геометрической прогрессии со знаменателем
их членов. Известно также, как найти сумму бесконечной геометрической прогрессии со знаменателем 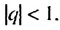 Однако существуют задачи, решая которые приходится искать суммы чисел, не образующих ни арифметическую, ни геометрическую прогрессии. Такие суммы иногда можно найти, преобразовав определенным образом их слагаемые.
Однако существуют задачи, решая которые приходится искать суммы чисел, не образующих ни арифметическую, ни геометрическую прогрессии. Такие суммы иногда можно найти, преобразовав определенным образом их слагаемые.
Пример 1. Найти сумму 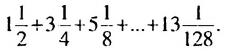
Решение:
Обозначим эту сумму через 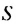 и запишем ее так:
и запишем ее так:
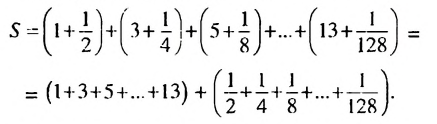
В первых скобках записана сумма членов арифметической прогрессии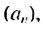 в которой
в которой 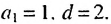 Найдем, каким но счету членом этой прогрессии является число 13:
Найдем, каким но счету членом этой прогрессии является число 13:
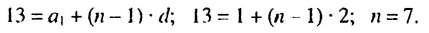
Итак, в первых скобках записана сумма первых семи членов арифметической прогрессии. Во вторых скобках записана сумма первых семи членов геометрической прогрессии 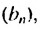 в которой
в которой 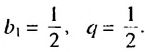 Используя формулы суммы первых
Используя формулы суммы первых 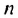 членов арифметической и геометрической прогрессий, находим:
членов арифметической и геометрической прогрессий, находим:
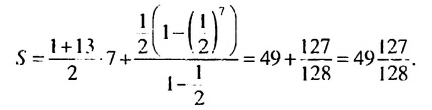
Ответ: 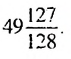
Обращение бесконечных периодических десятичных дробей в обыкновенную дробь
Рассмотрим пример.
Пример:
Записать число 0,(7) в виде обыкновенной дроби.
Решение:
Бесконечную десятичную дробь 0,(7) = 0,777… запишем в виде такой суммы: 0,(7) = 0.7 + 0,07 + 0,007 + …. Слагаемые 0,7; 0,07; 0.007;… — члены бесконечной геометрической прогрессии с первым членом 0,7 и знаменателем 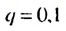
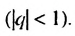 Сумма этой прогрессии:
Сумма этой прогрессии: 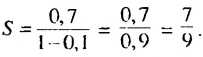 Поэтому
Поэтому 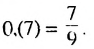
Ответ: 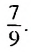
Решение уравнении
Рассмотрим пример.
Пример:
Решить уравнение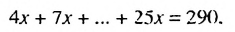 в котором коэффициенты 4 ,7 . …, 25 образуют арифметическую прогрессию.
в котором коэффициенты 4 ,7 . …, 25 образуют арифметическую прогрессию.
Решение:
Запишем уравнение так:
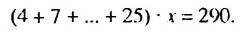
В скобках записана сумма первых членов арифметической прогрессии. в которой 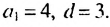 Найдем количество членов. Пусть число 25 является ее
Найдем количество членов. Пусть число 25 является ее 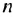 -м членом. По формуле
-м членом. По формуле 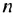 -го члена 25 = 4 + (
-го члена 25 = 4 + (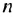 -1 )-3, откуда получим:
-1 )-3, откуда получим:
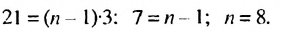
Итак, в скобках записана сумма первых 8 членов арифметической прогрессии. Тогда получим:
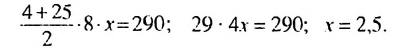
Ответ. 2,5.
Пример:
Записать число 3.1(23) в виде обыкновенной дроби.
Решение:
Число 3.1(23) = 3,12323… запишем в виде такой суммы:
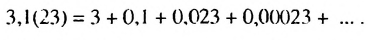 Слагаемые 0,023; 0,00023; … — члены бесконечной геометрической прогрессии с первым членом 0,023 и знаменателем
Слагаемые 0,023; 0,00023; … — члены бесконечной геометрической прогрессии с первым членом 0,023 и знаменателем 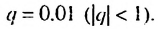 Сумма этой прогрессии равна:
Сумма этой прогрессии равна: 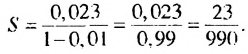 Поэтому
Поэтому
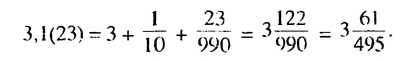
Ответ: 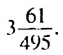
Пример:
Решить уравнение:
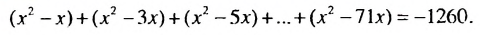
Решение:
Запишем уравнение в виде:
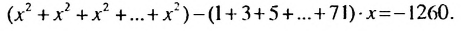 Во вторых скобках записана сумма первых
Во вторых скобках записана сумма первых 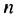 членов арифметической прогрессии. в которой
членов арифметической прогрессии. в которой 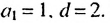 Найдем
Найдем 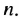 Пусть число 71 является ее
Пусть число 71 является ее 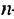 -м членом. По формуле -го члена
-м членом. По формуле -го члена 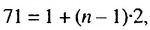 откуда
откуда 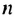 = 36. Учитывая, что в первых скобках записана сумма тридцати шести слагаемых, каждый из которых равен
= 36. Учитывая, что в первых скобках записана сумма тридцати шести слагаемых, каждый из которых равен 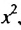 получим:
получим:
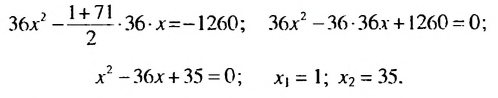
Ответ. 1; 35.
Пример:
Найти сумму 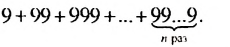
Решение:
Обозначим данную сумму через S. Записав слагаемые в виде 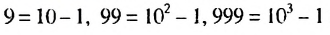 и т. д., получим:
и т. д., получим:
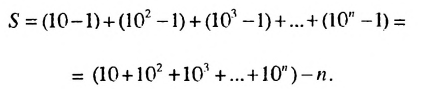
В скобках записана сумма первых 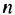 членов геометрической прогрессии
членов геометрической прогрессии 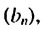 в которой
в которой 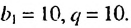 Поэтому:
Поэтому:
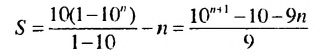
Ответ. 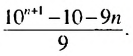
ИНТЕРЕСНО ЗНАТЬ
Слово «прогрессия» происходит от латинского слона «prcigrcssio» и значит «движение вперед» (как и слово «прогресс»). Впервые этот термин встречается в работах римского ученого Боэция (V -V I в.). Прогрессии как частные виды числовых последовательностей встречаются в папирусах II тысячелетия до н. э. Первые задачи на прогрессии, дошедшие до нас, связаны с хозяйственной деятельностью, а именно — с распределением продуктов, разделом наследства и т. п. Древнейшей задачей на прогрессии считают задачу из египетского папируса Ахмеса Райнда о распределении 100 мер хлеба между пятью людьми так, чтобы второй получил на столько больше первого, на сколько третий получил больше второго и т. д. В этой задаче речь идет об арифметической прогрессии, сумма первых пяти членов которой равна 100. В одной из задач этого папируса представлена формула первого члена арифметической прогрессии, которую в современной символике записывают так:
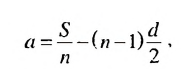
где а — первый член, 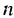 — число членов, S — сума первых
— число членов, S — сума первых 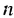 членов, d — разность прогрессии. Убедитесь, что эта формула верна. С вычислением суммы членов арифметической прогрессии связана такая интересная история. У известною немецкого математика Карла Гаусса (1777-1875) еще в школе обнаружились блестящие математические способности. Как-то учитель предложил ученикам найти сумму первых ста натуральных чисел. Едва он успел прочитать условие задачи, как маленький Гаусс поднял руку: «Готово». Весь класс был поражен скоростью, с которой он провел подсчет. Как считал Гаусс? Издавна большой популярностью пользуется задача-легенда, которая относится к началу нашей эры. Индийский царь Шерам позвал к себе изобретателя игры в шахматы, своего подданного Сету, чтобы наградить его за изобретение. Когда изобретателю предложили самому выбрать награду, он попросил за первую клетку шахматной доски дать ему 1 зерно пшеницы, за вторую — 2 зерна, за третью — 4 и т.д . Оказалось, что царь не смог выполнить просьбу Сеты. За последнюю, 64-ю, клетку шахматной доски пришлось бы отдать
членов, d — разность прогрессии. Убедитесь, что эта формула верна. С вычислением суммы членов арифметической прогрессии связана такая интересная история. У известною немецкого математика Карла Гаусса (1777-1875) еще в школе обнаружились блестящие математические способности. Как-то учитель предложил ученикам найти сумму первых ста натуральных чисел. Едва он успел прочитать условие задачи, как маленький Гаусс поднял руку: «Готово». Весь класс был поражен скоростью, с которой он провел подсчет. Как считал Гаусс? Издавна большой популярностью пользуется задача-легенда, которая относится к началу нашей эры. Индийский царь Шерам позвал к себе изобретателя игры в шахматы, своего подданного Сету, чтобы наградить его за изобретение. Когда изобретателю предложили самому выбрать награду, он попросил за первую клетку шахматной доски дать ему 1 зерно пшеницы, за вторую — 2 зерна, за третью — 4 и т.д . Оказалось, что царь не смог выполнить просьбу Сеты. За последнюю, 64-ю, клетку шахматной доски пришлось бы отдать 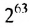 зерен пшеницы, а за все клетки количество зерен, равное сумме членов геометрической прогрессии:
зерен пшеницы, а за все клетки количество зерен, равное сумме членов геометрической прогрессии: 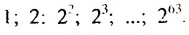 Эта сумма равна
Эта сумма равна 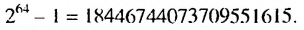 Такое количество зерен пшеницы можно собрать с плошали, приблизительно в 2000 раз больше площади всей поверхности Земли.
Такое количество зерен пшеницы можно собрать с плошали, приблизительно в 2000 раз больше площади всей поверхности Земли.
———–
Числовые последовательности
♦ Множество чисел в котором каждое число имеет свой номер 
 называется числовом последовательностью. То есть, числовая последовательность это функция определенная во множестве натуральных чисел. Например
называется числовом последовательностью. То есть, числовая последовательность это функция определенная во множестве натуральных чисел. Например 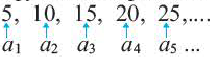
♦ Числа, образующие последовательность, называются соответственно первым, вторым, третьим, четвертым и т.д. членами последовательности. Члены последовательности, обычно обозначаются буквами, индекс буквы показывает порядковый номер члена. Например, первый член 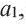 второй член
второй член 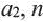 -ый член
-ый член 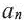 и т.д. Сама последовательность обозначается:
и т.д. Сама последовательность обозначается: 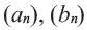 и т.д.
и т.д.
♦ Последовательности бывают конечные и бесконечные. Например, множество двузначных чисел может быть примером конечной последовательности. А последовательность натуральных чисел – бесконечна.
♦ Обычно последовательность задают с помощью формулы определящей функцию 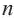 -ro члена последовательности от номера
-ro члена последовательности от номера 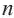 . Такую формулу называют формулой
. Такую формулу называют формулой 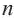 -го члена последовательности.
-го члена последовательности.
Например: 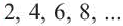 – последовательность четных чисел.Любой член этой последовательности можно найти по формуле
– последовательность четных чисел.Любой член этой последовательности можно найти по формуле 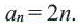 10-ый член последовательности:
10-ый член последовательности: 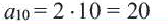
Наблюдается взаимосвязь многих природных явлений с последовательностью Фибоначчи.
Фибоначчи родился в итальянском городе Пиза: Его произведение “Книга вычислений” (Liber Abaci) оказала огромное влияние на распространение математических знаний в Европе, служила учебником – справочником европейских ученых. Особенно неоценима его роль в быстром распространении в Европе индийско-арабской десятичной системы. В то время в Европе при записи и вычислениях пользовались Римскими цифрами. В этом произведении Фибоначчи также уделил большое внимание задаче о размножении кроликов, которая дает последовательность чисел 1,1, 2, 3, 5, 8, 13, 21,… Для членов этого ряда (при 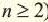 ) верно
) верно 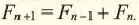 Продолжите ряд Фибоначчи для последующих трех шагов.
Продолжите ряд Фибоначчи для последующих трех шагов.

Рекуррентный и экспилитический способы задания последовательности
Формула, выражающая любой член последовательности, начиная с некоторого, через один или несколько предыдущих членов называется рекуррентной формулой, (от латинского слова recirro – возвращаться). Например, в последовательности 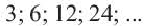 при
при 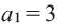 , то
, то 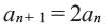 – рекуррентная формула и по этой формуле можно продолжить последовательность. Во многих случаях последовательность задается формулой, выражающей
– рекуррентная формула и по этой формуле можно продолжить последовательность. Во многих случаях последовательность задается формулой, выражающей 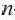 -ый член номером этого члена. Способ задания последовательности формулой
-ый член номером этого члена. Способ задания последовательности формулой 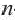 -го члена называется экспилитическим способом.
-го члена называется экспилитическим способом.
Например, 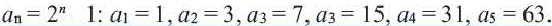
Арифметическая прогрессия, рекуррентное правило
Определение. Числовая последовательность, в которой каждый член, начиная со второго равен предыдущему, сложенному с одним и тем же для данной последовательности числом называется арифметической прогрессией. То есть арифметическая прогрессия – это такая последовательность, в которой 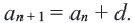 Здесь
Здесь 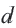 – постоянная для данной последовательности число. Число
– постоянная для данной последовательности число. Число 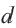 называют разностью арифметической прогрессии. Из определения следует, что равенство
называют разностью арифметической прогрессии. Из определения следует, что равенство 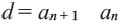 справедливо для любого натурального числа
справедливо для любого натурального числа 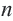 . В частных случаях,
. В частных случаях, 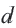
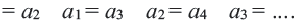 Арифметическая прогрессия с
Арифметическая прогрессия с 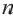 -ым членом
-ым членом 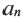 символически обозначается
символически обозначается 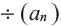 . Для того чтобы задать арифметическую прогрессию, достаточно показать его первый член и разность. Арифметическая прогрессия задается с рекуррентным соотношением
. Для того чтобы задать арифметическую прогрессию, достаточно показать его первый член и разность. Арифметическая прогрессия задается с рекуррентным соотношением 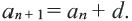
Пример 1. Определите, какие из последовательностей являются арифметической прогрессией.
а) 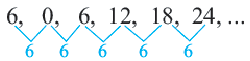 последовательность – арифметическая прогрессия, потому что разность между двумя соседними членами остается постоянной
последовательность – арифметическая прогрессия, потому что разность между двумя соседними членами остается постоянной
b) 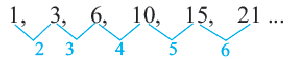 последовательность не является арифметической прогрессией, потому что разность между двумя соседними членами меняется
последовательность не является арифметической прогрессией, потому что разность между двумя соседними членами меняется
Разность арифметической прогрессии может быть положительным, отрицательным числом или нулем. При 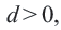 начиная со второго каждый член будет больше предыдущего (возрастающая последовательность), а при
начиная со второго каждый член будет больше предыдущего (возрастающая последовательность), а при 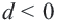 – меньше предыдущего (убывающая последовательность)
– меньше предыдущего (убывающая последовательность)
Пример 2. а) При 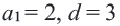 соответствующая арифметическая прогрессия будет : 2; 5; 8; 11; 14; 17; … Рекуррентная формула этой прогрессии будет:
соответствующая арифметическая прогрессия будет : 2; 5; 8; 11; 14; 17; … Рекуррентная формула этой прогрессии будет: 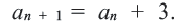
b) При условии 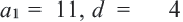 арифметическая прогрессия будет: 11; 7; 3; 1; 5; … Рекуррентная формула этой прогрессии будет:
арифметическая прогрессия будет: 11; 7; 3; 1; 5; … Рекуррентная формула этой прогрессии будет: 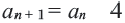
При 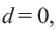 все члены будучи равными одному числу (1-му члену) образуют стационарную последовательность. Например, 5; 5; 5; …
все члены будучи равными одному числу (1-му члену) образуют стационарную последовательность. Например, 5; 5; 5; …
Формула n-го члена арифметической прогрессии
Каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же для данной последовательности числом. Согласно этому правилу: 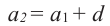
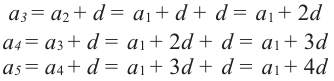
По этому правилу можно записать: 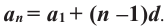
Формула 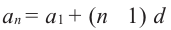 является формулой
является формулой 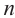 -го члена арифметической прогрессии.
-го члена арифметической прогрессии.
Пример 1. В арифметической прогрессии 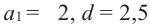 найдем
найдем 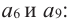
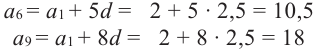
Отметим, что 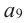 можно было бы вычислить и нижеуказанным способом:
можно было бы вычислить и нижеуказанным способом: 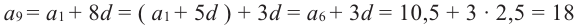
Вообще, 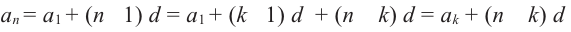 , то есть верно равенство,
, то есть верно равенство, 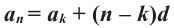
Отсюда, получаем формулу для разности прогресии: 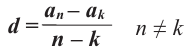
Пример 2. В арифметической прогрессии 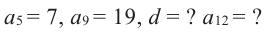
Решение: 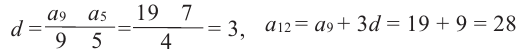
Замечание. Переписав формулу 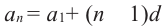 в виде
в виде 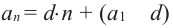 можно сделать вывод: любая прогрессия задается формулой
можно сделать вывод: любая прогрессия задается формулой 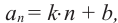 здесь
здесь 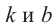 любые числа.
любые числа.
Арифметическая прогрессия и среднее арифметическое
Свойство. Любой член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов.
Действительно, из 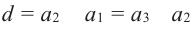 получается
получается 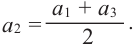
Так как в общем случае, 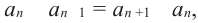 то верно равенство:
то верно равенство:
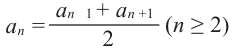
Это свойство можно обобщить таким образом. Каждый член арифметической прогрессии (начиная со второго) равен среднему арифметическому равноудаленных от него членов: 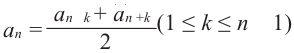
Это свойство поясняет причину названия арифметической прогрессии. Верно и обратное. Если любой член последовательности, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.
В конечной арифметической прогрессии сумма членов, расположенных на одинаковом расстоянии от концов, равна сумме крайних членов.
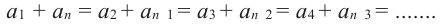
В общем, если 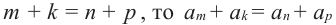
Сумма n-первых членов арифметической прогрессии
Обозначим через 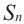 сумму
сумму 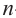 -первых членов любой арифметической прогрессии.
-первых членов любой арифметической прогрессии.
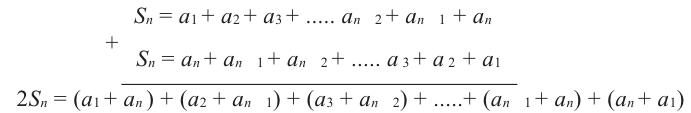
Попарные суммы 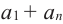 и т.д равны между собой, гак как в конечной арифметической прогрессии сумма членов, расположенных на одинаковом расстоянии от концов, равна сумме крайних членов. Всего таких пар
и т.д равны между собой, гак как в конечной арифметической прогрессии сумма членов, расположенных на одинаковом расстоянии от концов, равна сумме крайних членов. Всего таких пар 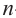 , поэтому
, поэтому 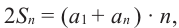 а отсюда получим:
а отсюда получим: 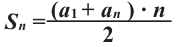
Сумма 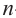 -первых членов конечной арифметической прогрессии равна произведению полусуммы крайних членов на число членов этой прогрессии. Так как:
-первых членов конечной арифметической прогрессии равна произведению полусуммы крайних членов на число членов этой прогрессии. Так как: 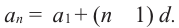 Тогда формулу суммы членов арифметической прогрессии можно написать в виде:
Тогда формулу суммы членов арифметической прогрессии можно написать в виде:
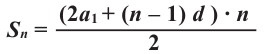
Пример 1. Найдите сумму 12-ти первых членов арифметической прогрессии заданной формулой 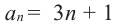 .
.
Решение: 
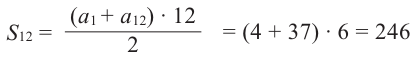
Пример 2. Найдите сумму 10-ти первых членов арифметической прогрессии 3; 5; 13;… .
Решение. 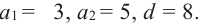
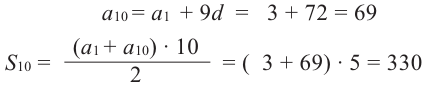
Пример 3. В зале заседаний 30 рядов. В первом ряду 24 места, а в каждом следующем ряду на одно место больше, чем в предыдущем. Сколько всего мест в зале?
Решение: 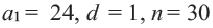
В последнем ряду: 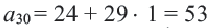 места. Всего в 30-ти рядах:
места. Всего в 30-ти рядах: 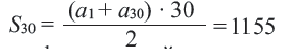
Пример 4. Сколько членов арифметической прогрессии 5; 7; 9… нужно сложить, чтобы получить 320 ?
Решение: 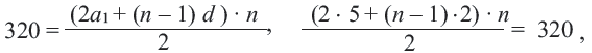
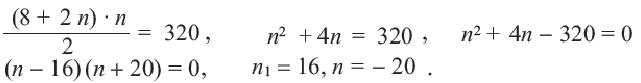
Так как количество членов не может быть отрицательным, то сумма 16-ти первых членов этой прогрессии равна 320. Перепишем сумму первых  членов арифметической прогрессии в следующем виде:
членов арифметической прогрессии в следующем виде: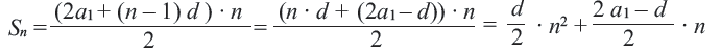 , обозначая
, обозначая 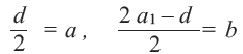 получаем, что сумму
получаем, что сумму 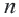 -первых членов любой арифметической прогрессии можно также записать в виде:
-первых членов любой арифметической прогрессии можно также записать в виде: 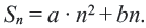 Можно считать арифметическую прогрессию заданной, если известна
Можно считать арифметическую прогрессию заданной, если известна 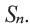
Пример 5. Найдем первый член и разность арифметической прогрессии, сумма 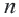 -первых членов которой задана формулой
-первых членов которой задана формулой 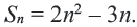
Решение: 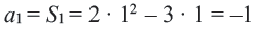
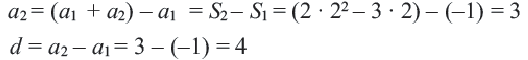
Внимание! При решении некоторых задач для определения 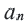 пользуются формулой
пользуются формулой 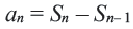 .
.
Члены геометрической прогрессии, рекуррентное правило
Определение. Геометрической прогрессией называется числовая последовательность, члены которой отличны от нуля, а каждый член, начиная со второго, равен предыдущего члену, умноженному на одно и то же, не равное нулю, число. То есть если для любого натурального числа 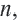 будет выполнено условие:
будет выполнено условие: 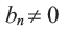 и
и 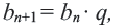 то последовательность
то последовательность 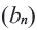 будет геометрической прогрессией. Число
будет геометрической прогрессией. Число 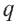 называется знаменателем геометрической прогрессии. Геометрическая прогрессия символически обозначается
называется знаменателем геометрической прогрессии. Геометрическая прогрессия символически обозначается 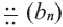 . Формула
. Формула 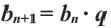 является представлением геометрической прогрессии по рекуррентному правилу. Из определения следует, что для любого натурального числа
является представлением геометрической прогрессии по рекуррентному правилу. Из определения следует, что для любого натурального числа 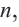 справедливо равенство:
справедливо равенство: 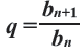 . В частности,
. В частности, 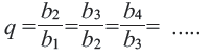
Пример 1. а) Если 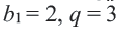 , то получится геометрическая прогрессия 2, 6, 18, 54, 162,…; b) Если
, то получится геометрическая прогрессия 2, 6, 18, 54, 162,…; b) Если 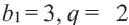 , то получится геометрическая прогрессия 3, 6, 12, 24,48,… . При
, то получится геометрическая прогрессия 3, 6, 12, 24,48,… . При 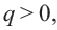 члены геометрической прогрессии имеют одинаковый знак. При
члены геометрической прогрессии имеют одинаковый знак. При 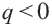 знаки членов прогрессии чередуются. При
знаки членов прогрессии чередуются. При 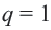 получается стационарная последовательность.
получается стационарная последовательность.
Пример 2. Какая из данных числовых последовательностей геометрическая прогрессия?
а) 4, 12, 22, 34, 48; b) 625, 125, 25, 5, 1.
Отношение каждого члена геометрической прогрессии на предыдущий всегда остается постоянной. Проверим это условие для обеих прогрессий.
а)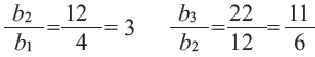 Условие не выполняется, последовательность не является геометрической прогрессией.
Условие не выполняется, последовательность не является геометрической прогрессией.
b)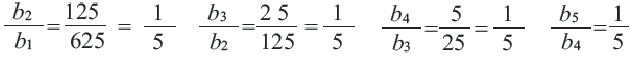 Условие выполняется, это последовательность – геометрическая прогрессия.
Условие выполняется, это последовательность – геометрическая прогрессия.
Формула n-го члена геометрической прогрессии
Вообще, чтобы в геометрической прогрессии найти 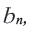 нужно перемножить
нужно перемножить 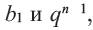 то есть
то есть 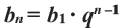
Это выражение называется формулой 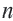 -го члена геометрической прогрессии. Для того чтобы задать геометрическую прогрессию, достаточно знать его первый член и знаменатель.
-го члена геометрической прогрессии. Для того чтобы задать геометрическую прогрессию, достаточно знать его первый член и знаменатель.
Пример 1. Если в геометрической прогрессии 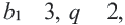 найдем
найдем 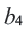 и
и 
Указание. Можно было бы вычислить следующем способом 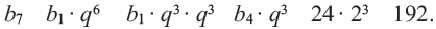
Вообще, справедливо равенство, 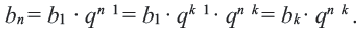
Пример 2. Найдем 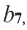 если в геометрической прогрессии
если в геометрической прогрессии 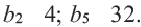
Решение: 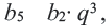 отсюда
отсюда 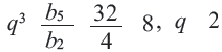 и
и 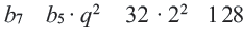
Заключение: Если известны какие-либо два члена, то можно задать геометрическую прогрессию, 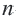 -ый член геометрической прогрессии можно найти другим путем. По определению:
-ый член геометрической прогрессии можно найти другим путем. По определению:
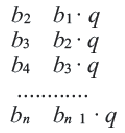
Если перемножить почленно эти  равенства, получим:
равенства, получим:
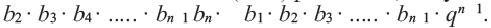
Сократив одинаковые члены в левой и правой частях, получим формулу 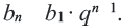
Заключение: Записав 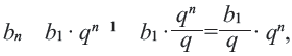 и обозначив
и обозначив 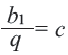 становится ясным, что любую геометрическую прогрессию можно задать формулой
становится ясным, что любую геометрическую прогрессию можно задать формулой 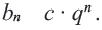 (Здесь
(Здесь 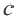 -какое-либо число отличное от нуля,
-какое-либо число отличное от нуля, 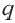 – знаменатель прогрессии).
– знаменатель прогрессии).
Члены геометрической прогрессии и среднее геометрическое
В геометрической профессии с положительными членами, начиная со второго, каждый член равен среднему геометрическому соседних с ним членов. Это свойство поясняет причину названия геометрической прогрессии. Например, в последовательности, 2, 6, 18, 54, 162,… число 18 является средним геометрическим 6 и 54. Среднее геометрическое-можно ясно увидеть, записывая отношения, выражающие знаменатель профессии. Из определения геометрической прогрессии получатся равенства:
 .
.
Взяв попарно эти равенства, получим: 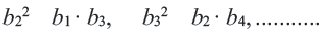 ,
, 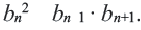 Это свойство можно задать в более общем виде. В геометрической прогрессии, начиная со второго, квадрат любого члена равен произведению равноудаленных членов последовательности, то есть
Это свойство можно задать в более общем виде. В геометрической прогрессии, начиная со второго, квадрат любого члена равен произведению равноудаленных членов последовательности, то есть 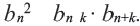 Для геометрической прогрессии с положительными членами это свойство можно записать в виде:
Для геометрической прогрессии с положительными членами это свойство можно записать в виде:

Еще одно свойство членов геометрической профессии: Если 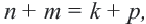 то верно равенство
то верно равенство 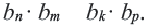
Сумма n-первых членов геометрической прогрессии
Обозначим через 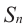 сумму
сумму 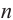 -первых членов геометрической прогрессии:
-первых членов геометрической прогрессии:
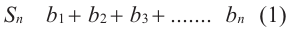
При 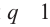 , все члены равны
, все члены равны 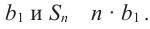 Рассмотрим случай когда
Рассмотрим случай когда 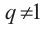 .
.
Умножим обе части (1 )-го равенства на 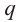 :
:
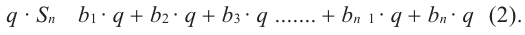
Отнимем от (2)-го равенства (1)-е. Получим: 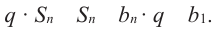
Отсюда S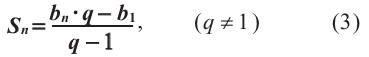
(3)-я формула называется формулой 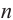 -первых членов геометрической прогрессии. Так как
-первых членов геометрической прогрессии. Так как 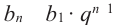 , то для
, то для 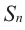 можно записать:
можно записать:
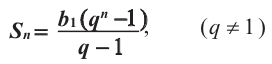
Пример. В геометрической прогрессии 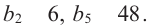 Найдите сумму первых шести членов.
Найдите сумму первых шести членов.
Решение. 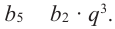 Отсюда
Отсюда 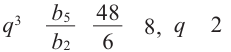
Из формулы 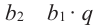 выразим
выразим 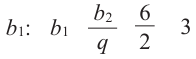
Тогда 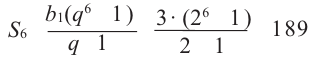
Сумма бесконечной геометрической прогрессии при 
Если число членов геометрической прогрессии бесконечно, то ее называют бесконечной геометрической профессией. Преобразуем формулу суммы 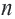 – первых членов геометрической прогрессии следующим образом.
– первых членов геометрической прогрессии следующим образом.
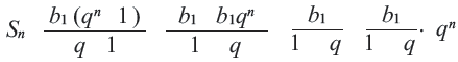
Если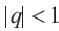 , то с бесконечным ростом
, то с бесконечным ростом 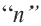 множитель
множитель 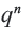 , а значит и
, а значит и 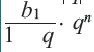 приближаются к нулю. Поэтому с ростом
приближаются к нулю. Поэтому с ростом 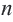 до бесконечности сумма
до бесконечности сумма 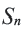 приближается к числу
приближается к числу 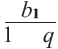 . Число
. Число 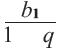 при
при 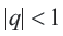 называется суммой бесконечной геометрической прогрессии.
называется суммой бесконечной геометрической прогрессии.
Если обозначить эту сумму через 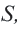 то получим:
то получим: 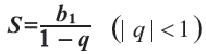 .
.
Пример. Примените формулу суммы бесконечной геометрической профессии в преобразовании периодической дроби 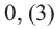 в обыкновенную.
в обыкновенную.

Так как 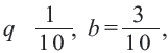 то по формуле суммы бесконечной геометрической прогрессии
то по формуле суммы бесконечной геометрической прогрессии 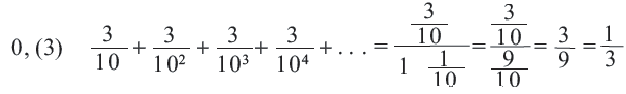
Геометрические преобразования. Движение
Параллельный перенос
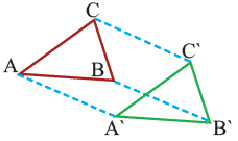
При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и тоже расстояние и фигура переходит в фигуру конгруэнтную себе. Треугольник  изображенный на рисунке получен параллельным переносом из треугольника
изображенный на рисунке получен параллельным переносом из треугольника  . Здесь
. Здесь 
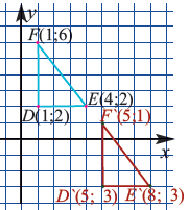
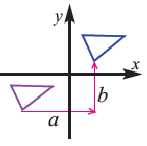
В координатной плоскости каждая точка данного треугольника  перемещена на 4 единицы направо, и на 5 единиц вниз.
перемещена на 4 единицы направо, и на 5 единиц вниз.
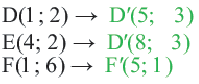
Применяя формулу расстояния между двумя точками, получим: 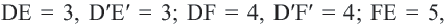
 По признаку конгруэнтности
По признаку конгруэнтности 
При параллельном переносе фигуры произвольная точка 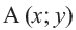 переходит в точку
переходит в точку 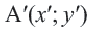 и между координатами этих точек справедливо равенство:
и между координатами этих точек справедливо равенство: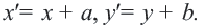
На координатной плоскости при параллельном переносе перемещение по осям координат направо и наверх выражаегся положительными, налево и вниз отрицательными единицами. Это определяется числами 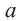 и
и 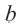 . При параллельном переносе расстояние между двумя точками не меняется.
. При параллельном переносе расстояние между двумя точками не меняется.
Действительно, при параллельном переносе произвольные точки 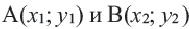 переходят в точки
переходят в точки 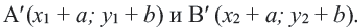
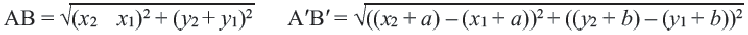 Отсюда
Отсюда 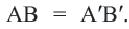 Значит, при параллельном переносе сохраняется расстояние.
Значит, при параллельном переносе сохраняется расстояние.
Координаты середины отрезка 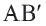
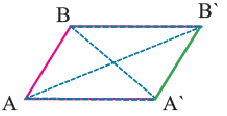
Координаты середины отрезка 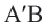 будут такими же (проверьте сами).
будут такими же (проверьте сами).
Значит, диагонали четырехугольника 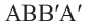 пересекаются и точкой пересечения делятся пополам. То есть, этот четырехугольник параллелограмм. А у параллелограмма противоположные стороны параллельны. При параллельном переносе прямая переходит в параллельную прямую (или в саму себя). Если при переходе одной фигуры в другую расстояния между точками сохраняются, то такое преобразование называется движением. Параллельный перенос это движение.
пересекаются и точкой пересечения делятся пополам. То есть, этот четырехугольник параллелограмм. А у параллелограмма противоположные стороны параллельны. При параллельном переносе прямая переходит в параллельную прямую (или в саму себя). Если при переходе одной фигуры в другую расстояния между точками сохраняются, то такое преобразование называется движением. Параллельный перенос это движение.
- Заказать решение задач по высшей математике
Параллельный перенос и векторы
Каждый параллельный перенос определяет один вектор. То есть при параллельном переносе перемещение всех точек фигуры выполняется по одному вектору. Выражение параллельного переноса вектором упрощает запись. Компоненты вектора 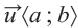 показывают изменения координат точек относительно осей
показывают изменения координат точек относительно осей  и
и 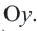
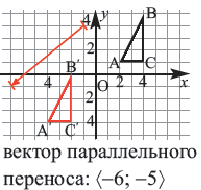
На картине изображен параллельный перенос  на вектор
на вектор 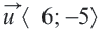 . Воспользуясь компонентами вектора, можно определить перемещение фигуры. Все точки треугольника
. Воспользуясь компонентами вектора, можно определить перемещение фигуры. Все точки треугольника 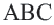 перемещаясь на длину вектора
перемещаясь на длину вектора 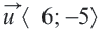 переходят в точки треугольника
переходят в точки треугольника 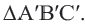
Длина вектора 
Движение и конгруэнтные фигуры
Пусть каждой точке фигуры  противопоставлена определенная точка плоскости. Множество таких точек образует фигуру
противопоставлена определенная точка плоскости. Множество таких точек образует фигуру  . В этом случае говорят, что фигура
. В этом случае говорят, что фигура  получена преобразованием фигуры
получена преобразованием фигуры  . Плоскость так же является геометрической фигурой. При преобразовании плоскости произвольная точка переходит в точку этой же плоскости и причем каждая точка преобразуется в определенную точку. Если при преобразовании одной фигуры в другую расстояние между точками сохраняется, то все геометрические свойства фигуры сохраняются и фигура преобразуется в конгруэнтную фигуру. Такие преобразования называются движением. Результат последовательных движений также является движением.
. Плоскость так же является геометрической фигурой. При преобразовании плоскости произвольная точка переходит в точку этой же плоскости и причем каждая точка преобразуется в определенную точку. Если при преобразовании одной фигуры в другую расстояние между точками сохраняется, то все геометрические свойства фигуры сохраняются и фигура преобразуется в конгруэнтную фигуру. Такие преобразования называются движением. Результат последовательных движений также является движением.
Теорема. При движении отрезок преобразуется в отрезок.
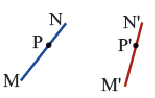
Доказательство. Пусть при движении концы отрезка  переходят соответственно в точки
переходят соответственно в точки  и
и  . Докажем, что отрезок
. Докажем, что отрезок 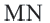 переходит в отрезок
переходит в отрезок 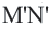 . На отрезке
. На отрезке 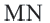 берем произвольную точку
берем произвольную точку 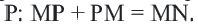 Пусть точка
Пусть точка 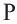 преобразуется в точку
преобразуется в точку 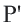 . Так как при движении расстояния между точками сохраняются
. Так как при движении расстояния между точками сохраняются 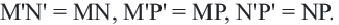 Отсюда
Отсюда 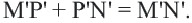 А это значит, что точка
А это значит, что точка 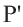 находится на отрезке
находится на отрезке 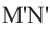 , то есть точка
, то есть точка 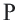 отрезка
отрезка 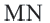 переходит в точку отрезка
переходит в точку отрезка 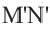 , и наоборот в точку
, и наоборот в точку 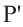 переходит точка
переходит точка 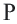 отрезка
отрезка 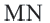 , удовлетворяющее условию
, удовлетворяющее условию 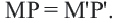 Теорема доказана.
Теорема доказана.
Следствие. При движении каждая сторона треугольника переходит в конгруэнтный отрезок, и поэтому по признаку 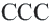 треугольник преобразуется в конгруэнтный треугольник. При движении прямая переходит в прямую, отрезок в отрезок и угол между полупрямыми сохраняется. При таких преобразованиях как параллельный перенос, центральная симметрия, осевая симметрия, поворот, фигура переходит в конгруэнтную фигуру. Исследуем это при помощи оси симметрии (отражения).
треугольник преобразуется в конгруэнтный треугольник. При движении прямая переходит в прямую, отрезок в отрезок и угол между полупрямыми сохраняется. При таких преобразованиях как параллельный перенос, центральная симметрия, осевая симметрия, поворот, фигура переходит в конгруэнтную фигуру. Исследуем это при помощи оси симметрии (отражения).
Теорема. Осевая симметрия (отражение) есть движение.
На рисунке изображено отражение отрезка 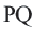 относительно прямой
относительно прямой 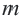 . По расположению отрезка
. По расположению отрезка  и прямой
и прямой  возможны 4 различных случая.
возможны 4 различных случая.
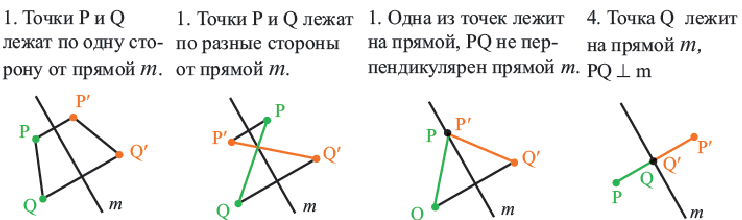
Докажем теорему для первого случая:
Текстовое доказательство
В этом случае точки  и
и  лежат по одну сторону от прямой
лежат по одну сторону от прямой  .
.
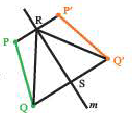
Из определения отражения следует, что, так как отрезок  – серединный перпендикулярный отрезков
– серединный перпендикулярный отрезков  , то
, то  и
и 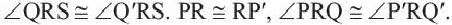 Тогда по признаку
Тогда по признаку 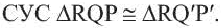 Так как у конгруэнтных треугольников соответственные стороны конгруэнтны, то
Так как у конгруэнтных треугольников соответственные стороны конгруэнтны, то 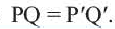 Теорема доказана.
Теорема доказана.
——
Числовые последовательности
В этой лекции вы:
Пример №356
Запишем в порядке возрастания четные натуральные числа: 2; 4; 6; 8; 10; … .
Получим последовательность четных натуральных чисел. На первом месте в ней число 2, на втором – число 4, на пятом – 10. Если и далее записывать четные натуральные числа, то, например, на десятом месте окажется число 20, на сотом – число 200. Вообще, для любого натурального числа 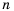 можно указать натуральное четное число, стоящее на
можно указать натуральное четное число, стоящее на 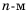 месте. Этим числом будет
месте. Этим числом будет 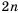 .
.
Числа, образующие последовательность, называют соответственно первым, вторым, третьим, четвертым и т. д. членами последовательности. Члены последовательности принято обозначать буквами с индексами, указывающими порядковый номер члена последовательности. Например: 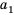 ,
, 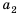 ,
, 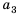 ,
, 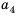 , … (читают: «
, … (читают: «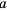 первое,
первое, 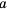 второе,
второе, 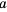 третье,
третье, 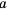 четвертое» и т. д.). В нашем примере
четвертое» и т. д.). В нашем примере 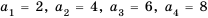 , … . Член последовательности с номером
, … . Член последовательности с номером 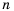 называют
называют 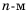 членом последовательности и обозначают
членом последовательности и обозначают 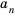 . Саму последовательность принято обозначать
. Саму последовательность принято обозначать 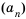 .
.
Рассмотрим два соседних члена последовательности с номерами 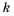 и
и 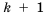 , а именно
, а именно 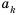 и
и 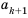 . Член
. Член 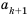 называют следующим за
называют следующим за 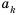 , а член
, а член 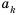 – предыдущим к
– предыдущим к 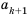 .
.
Поскольку в последовательности четных натуральных чисел на 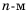 месте стоит число
месте стоит число 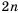 , то можем записать, что
, то можем записать, что 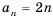 . Таким образом, имеем формулу
. Таким образом, имеем формулу 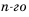 члена последовательности четных натуральных чисел.
члена последовательности четных натуральных чисел.
Эта последовательность содержит бесконечное число членов. Такую последовательность называют бесконечной. В записи бесконечной последовательности после перечисления нескольких ее первых членов ставят многоточие. Если же последовательность содержит конечное число членов, то ее называют конечной.
Пример №357
Последовательность двузначных натуральных чисел 10; 11; 12; …; 98; 99 является конечной. Она содержит 90 членов и может быть задана формулой 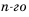 члена:
члена: 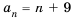 .
.
Зная формулу 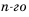 члена последовательности, можем найти любой ее член.
члена последовательности, можем найти любой ее член.
Пример №358
Последовательность задана формулой 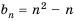 . Найдем несколько ее членов:
. Найдем несколько ее членов: 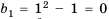 – первый член,
– первый член, 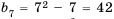 – седьмой,
– седьмой, 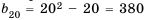 – двадцатый,
– двадцатый, 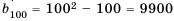 – сотый.
– сотый.
Формула 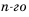 члена является достаточно удобным, но не единственным способом задания последовательности.
члена является достаточно удобным, но не единственным способом задания последовательности.
Пример №359
Конечную последовательность можно задать перечислением ее членов. Например, 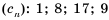 .
.
Пример №360
Последовательность можно задать описанием ее членов. Например, последовательность натуральных делителей числа 18, записанных в порядке возрастания, выглядит так: 1; 2; 3; 6; 9; 18.
Пример №361
Конечную последовательность можно задать и в виде таблицы. Например:

Последовательность можно задавать, указав первый или несколько первых членов последовательности, а затем – формулу, позволяющую найти остальные члены последовательности через предыдущие. Такую формулу называют рекуррентной, а способ задания последовательности – рекуррентным.
Пример №362
Пусть первый член последовательности 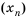 равен 2, а каждый следующий равен квадрату предыдущего, то есть
равен 2, а каждый следующий равен квадрату предыдущего, то есть 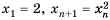 . Тогда по известному первому члену можно найти второй:
. Тогда по известному первому члену можно найти второй: 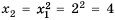 , по известному второму можно найти третий:
, по известному второму можно найти третий: 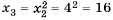 и так далее.
и так далее.
Получим последовательность: 2; 4; 16; 256; 65 536; … .
Пример №363
Найдем третий, четвертый и пятый члены последовательности 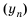 , заданной рекуррентно:
, заданной рекуррентно: 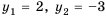 ,
, 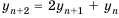 .
.
Получим:
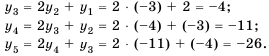
Последовательности, рассмотренные выше, являются числовыми последовательностями, так как состоят из чисел. Иногда рассматривают последовательности, членами которых являются выражения, функции и т. п. В дальнейшем будем рассматривать только числовые последовательности.
 Математики уже очень давно занимаются изучением числовых последовательностей. Понятие числовой последовательности возникло и развилось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:
Математики уже очень давно занимаются изучением числовых последовательностей. Понятие числовой последовательности возникло и развилось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:
- 1, 2, 3, 4, 5,… – последовательность натуральных чисел;
- 2, 4, 6, 8, 10,… – последовательность четных чисел;
- 1, 3, 5, 7, 9,… – последовательность нечетных чисел;
- 1,4,9,16,25,… – последовательность квадратов натуральных чисел;
- 2, 3, 5, 7, 11,… – последовательность простых чисел;
 – последовательность чисел, обратных натуральным.
– последовательность чисел, обратных натуральным.
Для всех этих последовательностей, кроме пятой, можно записать формулу  члена. Для последовательности простых чисел формула
члена. Для последовательности простых чисел формула  члена не была известна древним математикам… Нет ее и поныне!
члена не была известна древним математикам… Нет ее и поныне!
Одной из наиболее известных является числовая последовательность, которую называют последовательностью Фибоначчи в честь итальянца Л. Пизанского (Фибоначчи) (ок. 1170 – ок. 1250). Он первым рассмотрел последовательность чисел, два первых члена которой – единицы и каждый член которой, начиная с третьего, равен сумме двух предыдущих:
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144 ….
Лишь несколько веков спустя была найдена формула  члена последовательности Фибоначчи:
члена последовательности Фибоначчи:
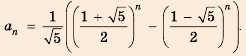
Арифметическая прогрессия, ее свойства. формула n-го члена арифметической прогрессии
Рассмотрим числовую последовательность, первый член которой равен 4, а каждый следующий, начиная со второго, равен предыдущему, сложенному с числом 3:
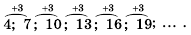
Такую последовательность называют арифметической прогрессией.
Последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, называют арифметической прогрессией.
Это число называют разностью арифметической прогрессии и обозначают буквой 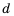 (от начальной буквы латинского слова differentia – разность). Значит, если
(от начальной буквы латинского слова differentia – разность). Значит, если 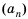 – арифметическая прогрессия, то имеют место равенства:
– арифметическая прогрессия, то имеют место равенства:
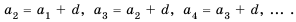
Таким образом, для любого натурального 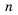 получим равенство:
получим равенство: 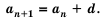
Тогда: 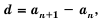 то есть
то есть
разность арифметической прогрессии можно найти, если от любого члена прогрессии, начиная со второго, отнять предыдущий.
Пусть первый член арифметической прогрессии равен 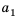 , а ее разность равна
, а ее разность равна 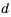 . Тогда:
. Тогда:
Заметим, что в каждой из полученных формул коэффициент у разности  на 1 меньше порядкового номера члена прогрессии, для которого записана эта формула. Действительно, чтобы найти
на 1 меньше порядкового номера члена прогрессии, для которого записана эта формула. Действительно, чтобы найти  , имея
, имея 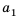 и
и 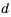 , нужно
, нужно  раз прибавить к
раз прибавить к 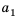 число
число 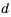 , то есть к
, то есть к 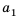 прибавить
прибавить 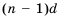 . Таким образом:
. Таким образом:
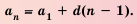 Получили формулу
Получили формулу 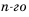 члена арифметической прогрессии.
члена арифметической прогрессии.
Рассмотрим несколько примеров применения этой формулы.
Пример №364
Последовательность 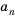 – арифметическая прогрессия,
– арифметическая прогрессия,  . Найти двадцатый член этой последовательности .
. Найти двадцатый член этой последовательности .
Решение:
Ответ. 25,2.
Пример №365
Принадлежит ли арифметической прогрессии 7; 10; 13; … число: 1) 82; 2) 102?
Решение:
В данной прогрессии  ,
, 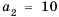 , тогда
, тогда 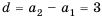 . Запишем формулу
. Запишем формулу  члена этой прогрессии:
члена этой прогрессии: 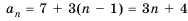 , то есть
, то есть 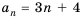 .
.
1) Допустим, число 82 является членом прогрессии  . Тогда существует такое натуральное число
. Тогда существует такое натуральное число  , что
, что 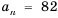 , то есть
, то есть 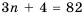 . Имеем уравнение:
. Имеем уравнение: 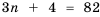 , откуда получим, что
, откуда получим, что 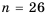 .
.
Следовательно, число 82 является двадцать шестым членом арифметической прогрессии, то есть 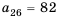 .
.
2) Рассуждая аналогично, имеем: 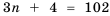 , откуда
, откуда 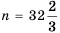 .
.
Полученное число 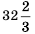 не является натуральным, а значит, арифметическая прогрессия числа 102 не содержит.
не является натуральным, а значит, арифметическая прогрессия числа 102 не содержит.
Ответ. 1) Да; 2) нет.
Пример №366
Кубики сложены рядами так, что в верхнем ряду 4 кубика, а в каждом следующем ниже ряду – на одно и то же количество кубиков больше, чем в предыдущем. Известно, что в шестом ряду 14 кубиков. Сколько кубиков в третьем ряду?
Решение:
Так как в каждом следующем ряду на одно и то же количество кубиков больше, чем в предыдущем, то числа, равные количеству кубиков в рядах, образуют арифметическую прогрессию, в которой 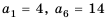 , следовательно, нам нужно найти
, следовательно, нам нужно найти 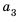 .
.
Для начала найдем разность 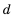 этой прогрессии. Из формулы
этой прогрессии. Из формулы  члена
члена 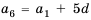 получим уравнение:
получим уравнение: 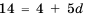 , откуда
, откуда 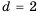 .
.
Теперь, зная значение  , найдем
, найдем  :
:
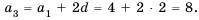
Следовательно, в третьем ряду 8 кубиков.
Заметим, что найти  можно было и без использования уравнения, например выразив
можно было и без использования уравнения, например выразив  из формулы 6-го члена прогрессии. Действительно, поскольку
из формулы 6-го члена прогрессии. Действительно, поскольку 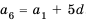 , то
, то
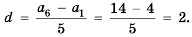
Ответ. 8 кубиков.
Докажем несколько важных свойств арифметической прогрессии.
1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов, то есть
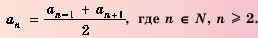
Доказательство: Используем формулу 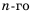 члена арифметической прогрессии, тогда:
члена арифметической прогрессии, тогда:
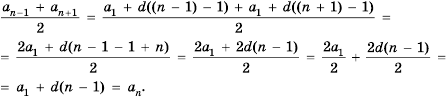
По одной из версий именно с этим свойством арифметической прогрессии связано ее название.
2. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух равноудаленных от него членов, то есть
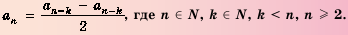
Свойство доказывается аналогично предыдущему свойству.
3. Если 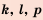 и
и  — натуральные числа и
— натуральные числа и  , то
, то  .
.
Доказательство: Используем формулу 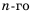 члена, тогда:
члена, тогда: 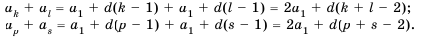
Но 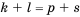 , поэтому
, поэтому 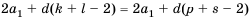 , то есть
, то есть 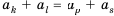 .
.
4. Любую арифметическую прогрессию можно задать формулой 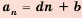 , где
, где 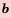 и
и 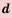 — некоторые числа.
— некоторые числа.
Доказательство: По формуле 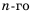 члена имеем:
члена имеем:
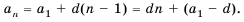
Обозначив 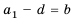 , получим:
, получим: 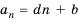 .
.
5. Последовательность 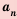 , заданная формулой вида
, заданная формулой вида 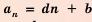 , где
, где 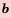 и
и 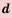 — некоторые числа, является арифметической прогрессией.
— некоторые числа, является арифметической прогрессией.
Доказательство: Рассмотрим разность 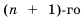 и
и 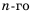 членов этой последовательности:
членов этой последовательности: Получим, что для любого
Получим, что для любого 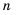 имеет место равенство
имеет место равенство 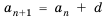 . Следовательно, последовательность (
. Следовательно, последовательность (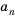 ) является арифметической прогрессией, разность которой равна
) является арифметической прогрессией, разность которой равна 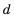 .
.
 Первые представления об арифметической прогрессии появились еще до нашей эры. В древнеегипетском папирусе Ахмеса (II тыс. до н. э.) есть такая задача: «Тебе сказано: раздели 10 мер ячменя между 10 людьми, разность же между каждым человеком и его соседом равна
Первые представления об арифметической прогрессии появились еще до нашей эры. В древнеегипетском папирусе Ахмеса (II тыс. до н. э.) есть такая задача: «Тебе сказано: раздели 10 мер ячменя между 10 людьми, разность же между каждым человеком и его соседом равна  меры». Решение задачи сводится к нахождению десяти членов арифметической прогрессии:
меры». Решение задачи сводится к нахождению десяти членов арифметической прогрессии: 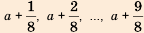 , сумма которых равна 10.
, сумма которых равна 10.
Задачи на арифметические прогрессии есть и в древнекитайском трактате «Математика в девяти книгах».
Первые из дошедших до нас задач на прогрессии связаны с запросами хозяйственной жизни и общественной практики, как, например, распределение продуктов, деление наследства и т. п.
У древних греков теория арифметических прогрессий была связана с так называемой непрерывной арифметической пропорцией:

Здесь числа 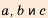 образуют арифметическую прогрессию с разностью
образуют арифметическую прогрессию с разностью 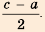 Таким образом, прогрессии рассматривались как бы продолжениями пропорций, вот почему эпитет арифметическая был перенесен с пропорций на прогрессии. Это еще одна из версий, почему эта прогрессия получила именно такое название.
Таким образом, прогрессии рассматривались как бы продолжениями пропорций, вот почему эпитет арифметическая был перенесен с пропорций на прогрессии. Это еще одна из версий, почему эта прогрессия получила именно такое название.
Сумма n первых членов арифметической прогрессии
Рассмотрим  первых членов арифметической прогрессии
первых членов арифметической прогрессии 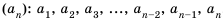 . Обозначим через
. Обозначим через 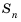 их сумму:
их сумму:
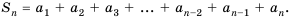
Найдем формулу для вычисления этой суммы. Запишем эту сумму дважды, разместив в первом случае слагаемые в порядке возрастания их номеров, а во втором – в порядке убывания:
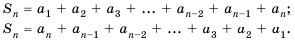
Теперь сложим эти равенства почленно и получим: 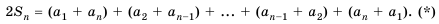
Но по свойству 3 из предыдущего параграфа: 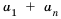
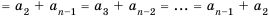 , то есть каждая сумма в скобках равенства
, то есть каждая сумма в скобках равенства 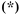 равна
равна 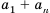 , так как
, так как 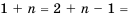
 . Тогда правая часть равенства
. Тогда правая часть равенства 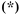 состоит из
состоит из 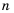 слагаемых, каждое из которых равно
слагаемых, каждое из которых равно 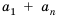 . Следовательно,
. Следовательно, 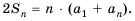
Разделив обе части этого равенства на 2, получим формулу суммы  первых членов арифметической прогрессии:
первых членов арифметической прогрессии:

Если в формуле  по формуле
по формуле  члена заменить
члена заменить 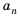 выражением
выражением 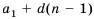 , получим:
, получим:
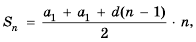
или
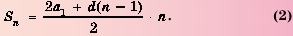
Получили еще одну формулу для вычисления суммы п первых членов арифметической прогрессии, которой удобно пользоваться, если известны первый член и разность прогрессии.
Применим формулы 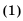 и
и 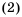 для решения примеров.
для решения примеров.
Пример №367
Найти сумму тридцати первых членов арифметической прогрессии 4; 7; 10; … .
Решение:
1-й способ. Так как 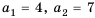 , то
, то 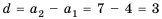 и
и 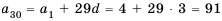 .
.
Тогда по формуле 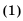 :
: 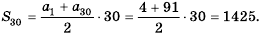
2-й способ. Так как 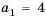 , и легко найти, что
, и легко найти, что 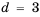 , используем формулу
, используем формулу 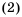 :
: 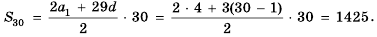
Ответ. 1425.
Пример №368
Найти сумму восемнадцати первых членов последовательности 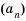 заданной формулой
заданной формулой 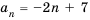 .
.
Решение:
Поскольку последовательность задана формулой 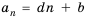 , где
, где  , то она является арифметической прогрессией (по свойству 5 из предыдущего параграфа).
, то она является арифметической прогрессией (по свойству 5 из предыдущего параграфа).
Имеем: 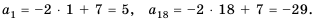
Найдем 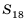 :
: 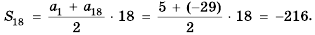
Ответ. -216.
Пример №369
Найти сумму всех натуральных чисел, кратных числу 7 и не превышающих 999.
Решение:
Натуральные числа, кратные числу 7, образуют арифметическую прогрессию: 7; 14; 21; 28; …, которую можно задать формулой 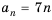 .
.
Найдем, сколько членов этой прогрессии не превышают числа 999. Для этого решим неравенство 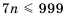 и получим,
и получим,
что 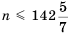 .
.
Следовательно, 142 члена прогрессии не превышают 999. Найдем их сумму, то есть 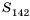
Имеем: 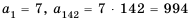 . Тогда:
. Тогда: 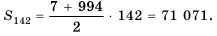
Ответ. 71 071.
Пример №370
Из двух точек, расстояние между которыми 100 м, одновременно навстречу друг другу начинают двигаться два объекта. Первый движется равномерно со скоростью 9 м/с, а второй за первую секунду проходит 7 м, а за каждую следующую на 2 м больше, чем за предыдущую. Через сколько секунд они встретятся?
Решение:
Пусть объекты встретятся через 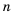 секунд. Первый за это время преодолеет
секунд. Первый за это время преодолеет 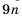 м. Расстояния, которые преодолеет второй объект за первую, вторую, третью и следующие секунды, образуют арифметическую прогрессию, у которой
м. Расстояния, которые преодолеет второй объект за первую, вторую, третью и следующие секунды, образуют арифметическую прогрессию, у которой 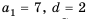 . Тогда за
. Тогда за 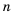 секунд второй объект преодолеет расстояние Sn> которое можно вычислить по формуле:
секунд второй объект преодолеет расстояние Sn> которое можно вычислить по формуле:
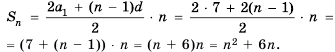
По условию 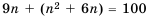 , тогда
, тогда 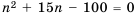 , откуда
, откуда 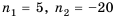 . Второй корень не удовлетворяет задаче. Следовательно,
. Второй корень не удовлетворяет задаче. Следовательно, 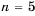 , то есть встреча произойдет через 5 с.
, то есть встреча произойдет через 5 с.
Ответ. 5 с.
 Уже в V в. до н. э. греки знали несколько прогрессий и их суммы, в частности:
Уже в V в. до н. э. греки знали несколько прогрессий и их суммы, в частности:
1) 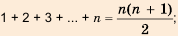
2) 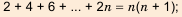
3) 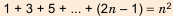 и другие.
и другие.
С вычислением суммы арифметической прогрессии связана интересная история, произошедшая с выдающимся немецким математиком Карлом Гауссом (1777-1855), который, еще учась в школе, проявил чрезвычайные математические способности. Однажды учитель предложил ученикам найти сумму ста первых натуральных чисел. Юный Гаусс мгновенно получил результат. Он заметил, что значения сумм 1 + 100, 2 + 99, 3 + 98, … одинаковы, а количество таких сумм равно 50:
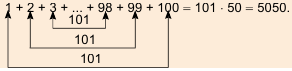
Геометрическая прогрессия, ее свойства. формула n-го члена геометрической прогрессии
Рассмотрим числовую последовательность, первый член которой равен 3, а каждый следующий, начиная со второго, равен предыдущему, умноженному на число 2:
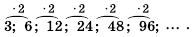
Такую последовательность называют геометрической прогрессией.
Геометрической прогрессией называют последовательность отличных от нуля чисел, каждое из которых, начиная со второго, равно предыдущему, умноженному на одно и то же число.
Это число называют знаменателем геометрической прогрессии и обозначают буквой 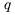 (от первой буквы французского слова quotient – частное). Поэтому если
(от первой буквы французского слова quotient – частное). Поэтому если 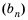 – геометрическая прогрессия, то верны следующие равенства:
– геометрическая прогрессия, то верны следующие равенства:
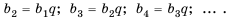
Следовательно, для любого натурального 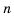 получим:
получим:
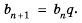
Тогда 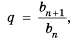 то есть
то есть
знаменатель геометрической прогрессии можно найти, ли любой член прогрессии, начиная со второго, разделить на предыдущий.
Заметим, что поскольку члены геометрической прогрессии отличны от нуля, то и знаменатель 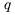 не может быть равным нулю, то есть
не может быть равным нулю, то есть 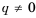 .
.
Если 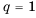 , то геометрическая прогрессия будет состоять из одинаковых чисел. Например, если
, то геометрическая прогрессия будет состоять из одинаковых чисел. Например, если 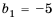 и
и 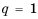 , то получим геометрическую прогрессию:
, то получим геометрическую прогрессию:
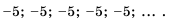
Заметим, что полученную последовательность можно также считать и арифметической прогрессией, первый член которой равен -5, а разность равна нулю.
Пусть первый член геометрической прогрессии равен  , а знаменатель равен
, а знаменатель равен 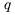 . Тогда
. Тогда
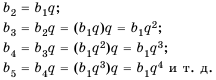
Заметим, что в каждой из полученных формул показатель степени числа 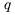 на 1 меньше порядкового номера члена прогрессии, для которого записана эта формула. Действительно, чтобы найти
на 1 меньше порядкового номера члена прогрессии, для которого записана эта формула. Действительно, чтобы найти 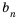 , имея
, имея 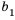 и
и 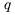 , нужно
, нужно  раз умножить
раз умножить  на
на 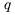 , то есть
, то есть  умножить на
умножить на 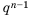 . Имеем:
. Имеем:
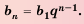
Получили формулу 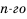 члена геометрической прогрессии.
члена геометрической прогрессии.
Рассмотрим несколько примеров применения этой формулы.
Пример №371
Последовательность 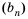 – геометрическая прогрессия,
– геометрическая прогрессия, 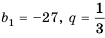 . Найти
. Найти 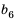 .
.
Решение:
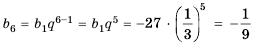 .
.
Ответ. 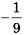 .
.
Пример №372
Найти знаменатель 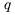 геометрической прогрессии
геометрической прогрессии 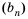 , если
, если 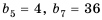 .
.
Решение:
1-й способ. 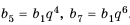 . Тогда
. Тогда 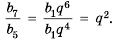
При этом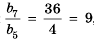 , то есть
, то есть 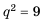 , откуда
, откуда 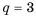 или
или 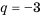 .
.
2-й способ. 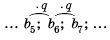 .
.
Так как 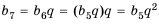 , то
, то 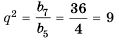 , откуда
, откуда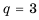 или
или 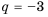 .
.
Ответ. 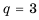 или
или 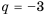 .
.
Пример №373
Дан равносторонний треугольник со стороной 8 см. Середины его сторон являются вершинами второго треугольника, а середины сторон второго являются вершинами третьего и т. д. (рис. 75). Найти площадь пятого треугольника, построенного по тому же принципу.
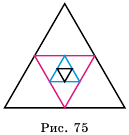
Решение:
Пусть  – площади первого, второго, третьего и т. д. треугольников. Найдем
– площади первого, второго, третьего и т. д. треугольников. Найдем  :
:
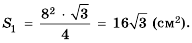
Поскольку стороны каждого следующего треугольника являются средними линиями предыдущего, то длина стороны каждого следующего треугольника будет вдвое меньше длины стороны предыдущего. Тогда сторона второго треугольника равна 4 см, а его площадь 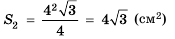 . Сторона третьего треугольника равна 2 см, тогда
. Сторона третьего треугольника равна 2 см, тогда 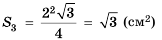 . Очевидно, что
. Очевидно, что  в 4 раза меньше, чем
в 4 раза меньше, чем  , a
, a 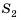 в 4 раза меньше, чем
в 4 раза меньше, чем 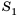 , то есть приходим к выводу, что площадь каждого следующего треугольника в 4 раза меньше площади предыдущего, и поэтому найденные числовые значения площадей
, то есть приходим к выводу, что площадь каждого следующего треугольника в 4 раза меньше площади предыдущего, и поэтому найденные числовые значения площадей 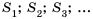 являются последовательными членами геометрической прогрессии со знаменателем
являются последовательными членами геометрической прогрессии со знаменателем 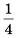 , первый член которой равен
, первый член которой равен 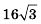 . Тогда числовое значение площади пятого треугольника является соответственно пятым членом этой прогрессии. Значит,
. Тогда числовое значение площади пятого треугольника является соответственно пятым членом этой прогрессии. Значит,
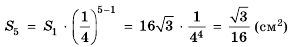
Ответ. 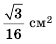
Докажем некоторые важные свойства геометрической прогрессии.
1. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних с ним членов, то есть
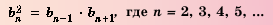
Доказательство. Воспользуемся формулой 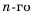 члена геометрической прогрессии. Тогда:
члена геометрической прогрессии. Тогда:
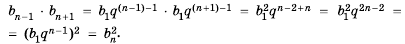
Если все члены геометрической прогрессии являются положительными числами, то 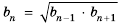 , то есть каждый член геометрической прогрессии, начиная со второго, является средним геометрическим двух соседних с ним членов.
, то есть каждый член геометрической прогрессии, начиная со второго, является средним геометрическим двух соседних с ним членов.
По одной из версий именно с этим свойством геометрической прогрессии и связано ее название.
2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух равноудаленных от него членов, то есть
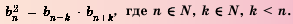
Свойство доказывается аналогично предыдущему свойству.
3. Если 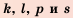 — натуральные числа и
— натуральные числа и  , то
, то 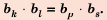 .
.
Доказательство: Воспользуемся формулой 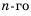 члена геометрической прогрессии:
члена геометрической прогрессии:
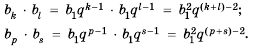
Нo 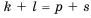 , поэтому
, поэтому 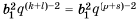 . Следовательно,
. Следовательно, 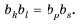
 В уже неоднократно здесь упоминавшемся папирусе Ахмеса содержится следующая задача, в которой необходимо найти сумму
В уже неоднократно здесь упоминавшемся папирусе Ахмеса содержится следующая задача, в которой необходимо найти сумму  членов геометрической прогрессии: «У семи человек по семи кошек, каждая кошка съедает по 1 мышей, каждая мышь съедает по 7 колосьев, из каждого колоса может вырасти по 7 мер ячменя. Как велики числа этого ряда и их сумма?».
членов геометрической прогрессии: «У семи человек по семи кошек, каждая кошка съедает по 1 мышей, каждая мышь съедает по 7 колосьев, из каждого колоса может вырасти по 7 мер ячменя. Как велики числа этого ряда и их сумма?».
В своей работе «Псаммит» Архимед впервые сопоставил арифметическую и геометрическую прогрессии:

и указал на связь между ними, например: 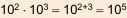 , то есть для умножения двух членов геометрической прогрессии достаточно сложить соответствующие члены арифметической прогрессии и взять полученную сумму в качестве показателя 10.
, то есть для умножения двух членов геометрической прогрессии достаточно сложить соответствующие члены арифметической прогрессии и взять полученную сумму в качестве показателя 10.
У древних греков теория геометрических прогрессий была связана с так называемой непрерывной геометрической пропорцией:
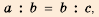 в которой числа
в которой числа  образуют геометрическую прогрессию со знаменателем
образуют геометрическую прогрессию со знаменателем 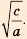 Этой связью и объясняется одна из версий названия прогрессии – геометрическая.
Этой связью и объясняется одна из версий названия прогрессии – геометрическая.
Формула сложных процентов
Бухгалтерам и работникам банков часто приходится решать задачи на проценты. Рассмотрим задачу о начислении процентного дохода. С экономической точки зрения процентный доход можно считать вознаграждением, которое платит лицо или учреждение (заемщик) за пользование в течение определенного времени определенной суммой средств, полученных от другого лица или учреждения (кредитора). Размер этого вознаграждения зависит от суммы средств и срока пользования ими.
Пример №374
Вкладчик открыл в банке депозит в размере 10 ООО грн под 11 % годовых (то есть банк обязан выплатить процентный доход в размере 11 % в год от начальной суммы вклада). Какой процентный доход получит вкладчик через год?
Решение:
11 % = 0,11, поэтому вкладчик получит 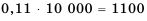 (грн) процентного дохода.
(грн) процентного дохода.
Ответ. 1100 грн.
Если вкладчик решил держать средства в банке более года, не добавляя новых средств и не забирая вложенных, то определить сумму средств на счету вкладчика через несколько лет можно с помощью формулы сложных процентов.
Пусть вкладчик положил в банк  грн под
грн под  % годовых,
% годовых,  еще называют начальным капиталом. Через год банк начислит вкладчику
еще называют начальным капиталом. Через год банк начислит вкладчику 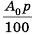 грн процентного дохода. Поэтому на счету вкладчика через год будет
грн процентного дохода. Поэтому на счету вкладчика через год будет 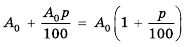 грн – наращенный капитал. Обозначим
грн – наращенный капитал. Обозначим 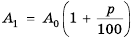 . За второй год вкладчику будет начислено
. За второй год вкладчику будет начислено 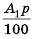 грн процентного дохода (ведь теперь банк начисляет
грн процентного дохода (ведь теперь банк начисляет 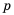 % годовых от числа
% годовых от числа 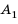 ), и его вклад будет равен:
), и его вклад будет равен:
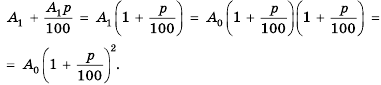
Рассуждая аналогично и применяя формулу  члена геометрической прогрессии
члена геометрической прогрессии 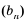 , где
, где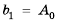 и
и 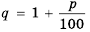 придем к выводу, что через
придем к выводу, что через  лет наращенный капитал будет равен:
лет наращенный капитал будет равен:
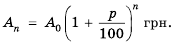
Таким образом,
начальный капитал  , вложенный в банк под
, вложенный в банк под  % годовых, через
% годовых, через  лет станет наращенным капиталом
лет станет наращенным капиталом  , размер которого определяется но формуле:
, размер которого определяется но формуле:
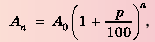
которую называют формулой сложных процентов.
Пример №375
Вкладчик открыл в банке депозит на 5000 грн под 12 % годовых. Сколько средств будет на счету вкладчика через 3 года? Какой процентный доход получит вкладчик через 3 года?
Решение:
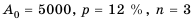 . Тогда:
. Тогда:
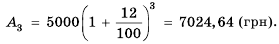
Процентный доход можно найти как разность 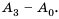
Таким образом, 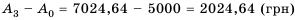 .
.
Ответ. 7024,64 грн, 2024,64 грн.
По формуле сложных процентов можно решать и другие задачи, не связанные с наращиванием капитала.
Пример №376
Население города составляет 30 000 жителей. Каждый год количество населения уменьшается на 0,2 %. Сколько жителей будет в этом городе через 10 лет?
Решение:
Так как население города ежегодно уменьшается на один и тот же процент, и это процент от количества населения каждого предыдущего года, а не от начального количества жителей, то можно воспользоваться формулой сложных процентов.
Имеем, 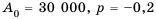 (так как население уменьшается, то
(так как население уменьшается, то 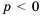 ),
), 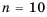 . Тогда:
. Тогда:
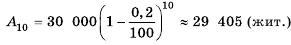 .
.
Ответ. 29 405 жителей.
Сумма n первых членов геометрической прогрессии
Рассмотрим  первых членов геометрической прогрессии
первых членов геометрической прогрессии 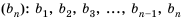 .
.
Обозначим через 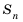 их сумму:
их сумму:
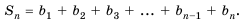
Найдем формулу для вычисления этой суммы. Имеем (учитывая формулу 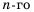 члена геометрической прогрессии):
члена геометрической прогрессии):
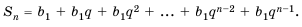
Умножим обе части этого равенства на 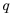 :
:
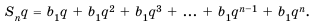
Вычтем почленно из этого равенства предыдущее:
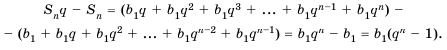
Таким образом, 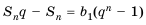 и
и 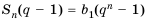 .
.
Если 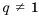 , получаем формулу суммы
, получаем формулу суммы  первых членов геометрической прогрессии:
первых членов геометрической прогрессии:

Если  , то все члены прогрессии равны первому члену и тогда
, то все члены прогрессии равны первому члену и тогда 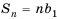 .
.
Заметим, что полученную формулу 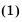 можно записать и так:
можно записать и так:
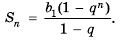
Так как 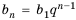 , то формулу
, то формулу 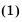 можно записать и по-другому. Действительно,
можно записать и по-другому. Действительно,
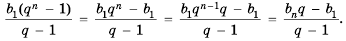
Таким образом,

Получили еще одну формулу для вычисления суммы  первых членов геометрической прогрессии, которой удобно пользоваться, если известны первый и
первых членов геометрической прогрессии, которой удобно пользоваться, если известны первый и  члены прогрессии и ее знаменатель. Применим эти формулы для решения упражнений.
члены прогрессии и ее знаменатель. Применим эти формулы для решения упражнений.
Пример №377
Найти сумму первых семи членов геометрической прогрессии 2; -6; 18; … .
Решение:
1-й способ. По условию:
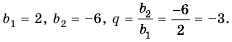
Тогда по формуле 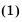 :
:
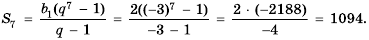
2-й способ. Известно, что 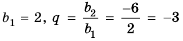 , тогда
, тогда
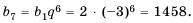
По формуле  :
:
Ответ. 1094.
Пример №378
Найти сумму первых шести членов геометрической прогрессии  , если
, если 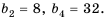
Решение:
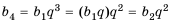 , тогда
, тогда 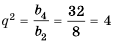 , следовательно,
, следовательно, 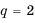 или
или 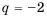 .
.
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи:
1) если 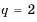 , то
, то 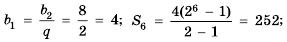
2) если 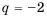 , то
, то 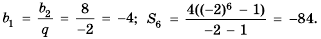
Ответ. 252 или -84.
Пример №379
Сократить дробь
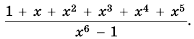
Решение:
Слагаемые в числителе дроби являются последовательными членами геометрической прогрессии 1,  ,
,  ,
, 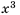 ,
, 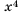 ,
,  , первый член которой равен 1, а знаменатель равен
, первый член которой равен 1, а знаменатель равен 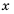 . Из условия следует, что
. Из условия следует, что 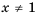 .
.
Найдем сумму всех шести членов этой прогрессии по формуле 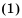 и сократим данную в условии дробь:
и сократим данную в условии дробь:
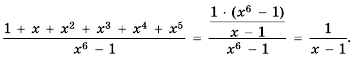
Ответ.  .
.
 Древняя индийская задача-легенда гласит- что изобретатель шахматной игры Сета в награду за свою остроумную выдумку попросил у индийского царя Шерама столько зерен пшеницы, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – два, на третью – четыре, на четвертую – восемь и т. д., пока не заполнятся все клетки.
Древняя индийская задача-легенда гласит- что изобретатель шахматной игры Сета в награду за свою остроумную выдумку попросил у индийского царя Шерама столько зерен пшеницы, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – два, на третью – четыре, на четвертую – восемь и т. д., пока не заполнятся все клетки.
Царь удивился, что изобретатель пожелал столь мало, и приказал придворным математикам подсчитать необходимое количество зерен. Каково же было изумление царя, когда он узнал, что не сможет выдать обещанную награду, так как необходимое число зерен равно 
Чтобы получить столько зерен, потребовалось бы собрать урожай с площади, в 2000 раз превышающей всю поверхность Земли. А для хранения такого урожая понадобился бы амбар, который при высоте 4 м и ширине 10 м тянулся бы на 300 000 000 км, то есть вдвое дальше, чем от Земли до Солнца.
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
- Рациональные выражения
- Квадратные корни
- Квадратные уравнения
- Неравенства
Линейной рекуррентной последовательностью (линейной рекуррентой) называется всякая числовая последовательность 
для всех
с заданными начальными членами 


Линейные рекуррентные последовательности иногда называют также возвратными последовательностями.
Теория линейных рекуррентных последовательностей является точным аналогом теории линейных дифференциальных уравнений с постоянными коэффициентами.
Примеры[править | править код]
Частными случаями линейных рекуррентных последовательностей являются последовательности:
Формула общего члена[править | править код]
Для линейных рекуррентных последовательностей существует формула, выражающая общий член последовательности через корни её характеристического многочлена
А именно, общий член выражается в виде линейной комбинации 
где 


Для чисел Фибоначчи такой формулой является формула Бине.
Пример[править | править код]
Для нахождения формулы общего члена последовательности 



.
Если уравнение имеет два различных корня 



удовлетворяет рекурентному соотношению; остаётся найти числа 

и
.
Если же дискриминант характеристического уравнения равен нулю и значит уравнение имеет единственный корень 


удовлетворяет рекурентному соотношению; остаётся найти числа 

и
.
В частности, для последовательности, определяемой следующим линейным рекуррентным уравнением второго порядка
;
,
.
корнями характеристического уравнения 


.
Окончательно:
Приложения[править | править код]
Линейные рекуррентные последовательности над кольцами вычетов традиционно используются для генерации псевдослучайных чисел.
История[править | править код]
Основы теории линейных рекуррентных последовательностей были даны в двадцатых годах восемнадцатого века Абрахамом де Муавром и Даниилом Бернулли.
Леонард Эйлер изложил её в тринадцатой главе своего «Введения в анализ бесконечно-малых» (1748).[1]
Позднее Пафнутий Львович Чебышёв и ещё позже Андрей Андреевич Марков изложили эту теорию в своих курсах исчисления конечных разностей.[2][3]
См. также[править | править код]
- Разностное уравнение
- Теорема Скулема
Примечания[править | править код]
- ↑ Л. Эйлер, Введение в анализ бесконечно-малых, т. I, M. — Л., 1936, стр. 197–218
- ↑ П. Л.Чебышев, Теория вероятностей, лекции 1879–1880 гг., М. — Л., 1936, стр. 139–147
- ↑ А. А. Марков, Исчисление конечных разностей, 2-е изд., Одесса, 1910, стр. 209–239
Литература[править | править код]
- А. И. Маркушевич. Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
- М. М. Глухов, В. П. Елизаров, А. А. Нечаев. Глава XXV. Линейные рекуррентные последовательности // Алгебра. — Учебник. В 2-x томах. — М.: Гелиос АРВ, 2003. — Т. 2. — ISBN 8-85438-072-2.
- А. Егоров. Числа Пизо // Квант. — 2005. — № 5. — С. 8—13.
- Чебраков Ю. В. Глава 2.7. Рекуррентные уравнения // Теория магических матриц. Выпуск ТММ-1. — СПб., 2010.
Линейной рекуррентной последовательностью (возвратной последовательностью, линейной рекуррентой) называется всякая числовая последовательность , задаваемая линейным рекуррентным соотношением:
для всех
с заданными начальными членами , где
— фиксированное натуральное число, называемое порядком последовательности,
— заданные числовые коэффициенты,
.
Примеры известных линейных рекуррентных последовательностей можно посмотреть под калькулятором.
![]()
Линейная рекуррентная последовательность
Размер последовательности для расчета
Начальные члены
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Точность вычисления
Знаков после запятой: 2
Примеры линейных рекуррентных последовательностей
Начнем с того, что такие известные понятия, как арифметическая прогрессия и геометрическая прогрессия, можно описать как линейные рекуррентные последовательности.
Арифметическую прогрессию с первым членом a₁ и разностью прогрессии d можно представить как линейное рекуррентное соотношение второго порядка следующего вида:
с x₁ = a₁ и x₂ = a₁+d соответственно. Вот так это выглядит для a₁ = 1 и d = 2.
Геометрическую прогрессию с первым членом a₁ и знаменателем прогрессии q можно представить как линейное рекуррентное соотношение первого порядка вида:
c x₁ = a₁. Вот как это выглядит для геометрической прогрессии со знаменателем 2.
Одной из самых известных линейных рекуррентных последовательностей являются числа Фибоначчи – это последовательность, в которой первые два числа равны 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Соотношение двух последовательных чисел Фибоначчи дает, между прочим, приближение золотого сечения.
Числа Фибоначчи относятся к последовательностям Люка – семейству пар линейных рекуррентных последовательностей второго порядка, впервые рассмотренных Эдуардом Люка. К ним же относятся и числа Люка – последовательность, в которой, как и в числах Фибоначчи, каждое последующее число равно сумме двух предыдущих чисел, но с первыми членами 2 и 1 соответственно. Числа Люка могут использоваться для проверки на простоту.
Еще две примечательные последовательности Люка это числа Пелля, с формулой
и начальными членами 0 и 1, и числа Пелля-Люка или сопутствующие числа Пелля, с той же формулой и начальными членами 2 и 2. Примечательны эти числа тем, что с их помощью можно построить бесконечную последовательность подходящих дробей для квадратного корня из двух:
Здесь в числителе половина числа Пелля-Люка (2, 6, 14, 34, …), а в знаменателе – число Пелля (1, 2, 5, 12, …), начиная со второго числа в последовательности (n=1). Помимо этого соотношение двух последовательных чисел Пелля дает приближение так называемого серебрянного сечения.
И наконец числа трибоначчи, параметры калькулятора по умолчанию, это последовательность целых чисел, где каждое последующее число является суммой трех предыдущих, с начальными членами 0, 0, и 1. Название образовано по аналогии с “Фибоначчи” с заменой на приставку “три”, от латинского tri.
Числовая последовательность
- Формулы числовых последовательностей
- Задание последовательностей описанием
- Рекуррентные формулы числовых последовательностей
- Свойства числовых последовательностей
- Примеры
п.1. Формулы числовых последовательностей
Запишем несколько первых чётных чисел и пронумеруем их:
2n
2
4
6
8
10
12
14
16
18
Этот ряд бесконечен, но, глядя на таблицу, его легко задать формулой: begin{gather*} mathrm{y_n = 2n, n in mathbb{N}} end{gather*}
Теперь, пользуясь формулой, для любого порядкового номера n мы сможем найти соответствующее чётное число.
Функцию натурального аргумента (mathrm{y_n=f(n), ninmathbb{N}}) называют числовой последовательностью.
Значения y1, y2, …, yn,… называют членами последовательности.
В символе yn число n называют индексом последовательности.
Для обозначения членов последовательности и их индексов можно использовать разные буквы: x1, x2, …, xm,…; a1, a2, …, ak,…; A1, A2, …, As,… и т.д.
Числовую последовательность как частный случай функции можно задавать аналитически (формулой), описанием (словесно), рекуррентно, графически и т.д.
Первые три способа используются чаще других.
Например:
Найти 1й, 3й и 4й члены последовательности, заданной формулой (mathrm{y_n=frac{n-1}{n+1}}) $$ mathrm{ y_1=frac{1-1}{1+1}=0, y_3=frac{3-1}{3+1}=frac12, y_4=frac{4-1}{4+1}=frac35 } $$
п.2. Задание последовательностей описанием
Последовательность, заданную формулой yn=2n, можно задать описанием как «последовательность чётных чисел».
Последовательность, заданную формулой (mathrm{y_n=frac{n-1}{n+1}}), можно задать описанием как «последовательность дробей, числитель которых на 1 меньше индекса, а знаменатель на 1 больше индекса последовательности».
Кроме того, существуют такие последовательности, которые можно задать только описанием.
Например:
1. Последовательность простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
2. Последовательность десятичных приближений числа (mathrm{sqrt{3}}) по недостатку:
1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,7302050; 1,73020508,…
п.3. Рекуррентные формулы числовых последовательностей
Важнейшим классом числовых последовательностей, которые широко используются в алгоритмах вычислительной математики, являются рекуррентные отношения (от латинского слова recurrere – возвращаться).
Рекуррентной формулой называют правило, по которому можно найти n-й член последовательности, если известны значения её предыдущих членов.
Например:
Найти y5, если y1 = 1, yn = 2yn-1 + 1
Проводим последовательные вычисления:
y2 = 2y1 + 1 = 3, y3 = 2y2 + 1 = 7, y4 = 2y3 + 1 = 15, y5 = 2y4 + 1 = 31
Интересно, что, если присмотреться, эту последовательность можно также задать аналитически: yn = 2n – 1.
п.4. Свойства числовых последовательностей
Числовую последовательность называют возрастающей, если каждый её член, начиная со второго, больше предыдущего:
y1 < y2 < y3 < … < yn < …
Например:
Последовательность квадратов натуральных чисел yn = n2 возрастающая:
1 < 4 < 9 < … < n2 < …
Числовую последовательность называют убывающей, если каждый её член, начиная со второго, меньше предыдущего:
y1 > y2 > y3 > … > yn > …
Например:
Последовательность дробей с индексом в знаменателе (mathrm{y_n=frac1n}) – убывающая: $$ 1gtfrac12gtfrac13gt…gtfrac1ngt… $$
Числовую последовательность называют ограниченной сверху, если существует такое число M, что для любого члена последовательности выполняется неравенство
yn ≤ M
Например:
Последовательность отрицательных дробей с индексом в знаменателе (mathrm{y_n=-frac1n}) ограничена сверху числом M = 0: $$ -1lt 0, -frac12lt 0, -frac13lt 0,.., -frac1nlt 0, … $$
Числовую последовательность называют ограниченной снизу, если существует такое число M, что для любого члена последовательности выполняется неравенство
yn ≥ M
Например:
Последовательность дробей с индексом в знаменателе (mathrm{y_n=frac1n}) ограничена снизу числом M = 0: $$ -1gt 0, frac12gt 0, frac13gt 0,.., frac1ngt 0, … $$
Числовую последовательность называют ограниченной, если она ограничена сверху и снизу, т.е. существуют такие числа M и K, что для любого члена последовательности выполняется неравенство
M ≤ yn ≤ K или M ≥ yn ≥ K
Например:
Последовательность дробей с индексом в знаменателе (mathrm{y_n=frac1n}) ограничена: $$ 1gt frac12gt frac13gt … gt frac1ngt … gt 0 $$ Верхней границей является M = 1, нижней границей K = 0.
Числовую последовательность называют стационарной, если для любого члена последовательности выполняется равенство
yn = C
где C – некоторое число.
Например:
Последовательность (mathrm{y_1=1, y_n=y^2_{n-1} – 4y_{n-1}+4}) стационарна, т.к. begin{gather*} mathrm{ y_2=1-4+4=1, y_3=1-4+4=1,…}\ mathrm{ y_n=1, forall nin mathbb{N}} end{gather*}
п.5. Примеры
Пример 1. Найдите первые 4 члена последовательности, заданной формулой
a) (mathrm{y_n=frac{n^2+1}{2n-1}})
yn
$$ mathrm{ frac{1^2+1}{2-1}=2 } $$
$$ mathrm{ frac{2^2+1}{4-1}=frac53=1frac23 } $$
$$ mathrm{ frac{3^2+1}{6-1}=2 } $$
$$ mathrm{ frac{4^2+1}{8-1}=frac{17}{7}=2frac37 } $$
б) (mathrm{y_n=frac{2^n}{n^2}})
yn
$$ mathrm{ frac{2^1}{1^2}=2 } $$
$$ mathrm{ frac{2^2}{2^2}=1 } $$
$$ mathrm{ frac{2^3}{3^2}=frac89 } $$
$$ mathrm{ frac{2^4}{4^2}=1 } $$
Пример 2. Найдите первые 4 члена последовательности, заданной рекуррентной формулой
a) y1 = 3, yn = 3yn – 1
yn
3
3 · 3 – 1 = 8
3 · 8 – 1 = 23
3 · 23 – 1 = 68
б) y1 = 1, y2 = 2, yn = 2yn-1 + yn-2
yn
1
2
2 · 2 + 1 = 5
2 · 5 + 2 = 12
Пример 3*. Укажите какую-либо формулу для n-го члена числовой последовательности
а) 3, 5, 7, 9, …
Это – последовательность нечётных чисел, для которой:
yn = 2n + 1
б) 5, -5, 5, -5,…
Это – знакопеременная последовательность, для которой модуль всегда равен 5, а знак меняется. Изменение знака можно записать как степень (–1). Учитывая, что нечётные члены последовательности положительные, а чётные – отрицательные, получаем:
yn = (–1)n+1 · 5
в) (mathrm{frac{1}{1cdot 2}, frac{1}{2cdot 3}, frac{1}{3cdot 4},…})
Это – последовательность дробей, у которых в знаменателе произведение текущего индекса n на следующий индекс (n + 1):
(mathrm{y_n=frac{1}{n(n+1)}})
г) 2, 5, 10, 17, 26, 37, …
Заметим, что
5 – 2 = 3, 10 – 5 = 5, 17 – 10 = 7, 26 – 17 = 9, …
Каждый последующий член отличается от предыдущего на возрастающее нечётное число. Можем записать рекуррентную формулу:
y1 = 2, yn = yn-1 + (2n –1)
Пример 4*. Пифагор изучал последовательность «треугольных» чисел, которые можно задать следующими геометрическими фигурами:
 и т.д.
и т.д.
Задайте эту последовательность 1) рекуррентной формулой; 2) аналитической формулой.
1) Запишем последовательность в явном виде, как это следует из чертежа: $$ mathrm{ y_1=1, y_2=underbrace{1}_{y_1}+2=3, y_3=underbrace{1+2}_{y_2}+3=6, y_4=underbrace{1+2+3}_{y_3}+4=10 } $$ Отсюда получаем следующую рекуррентную формулу: y1 = 1, yn = yn-1 + n
2) Для произвольного члена последовательности:
yn = 1 + 2 + 3 + … + (n – 2) + (n – 1) + n
Найдём эту сумму. Для этого запишем выражение наоборот:
yn = n + (n – 1) + (n – 2) + … + 3 + 2 + 1
И найдём сумму: begin{gather*} mathrm{ y_n+y_n=2y_n=(1+2+3+…+(n-2)+(n-1)+n)+ }\ mathrm{ +(n+(n-1)+(n-2)+…+3+2+1)= }\ mathrm{ =(1+n)+underbrace{(2+n-1)}_{=n+1}+ underbrace{3+n-2}_{=n+1}+…+underbrace{n-2+3}_{=n+1}+underbrace{n-1+2}_{=n+1}+(n+1)= }\ mathrm{ =n(n+1) } end{gather*} Получаем: (mathrm{2y_n=n(n+1)Rightarrow y_n=frac{n(n+1)}{2}}) – искомая аналитическая формула.
Ответ: 1) y1 = 1, yn = yn-1 + 2; 2) (mathrm{y_n=frac{n(n+1)}{2}})






