Как найти сумму ряда геометрической прогрессии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2022 года; проверки требуют 37 правок.

У этого термина существуют и другие значения, см. Прогрессия.

Геометри́ческая прогре́ссия — последовательность чисел , , , (члены прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего члена умножением его на фиксированное число (знаменатель прогрессии). При этом ^[1].

Геометрическая прогрессия называется бесконечно убывающей^[2], если знаменатель прогрессии по абсолютной величине меньше единицы.

Произведением первых членов геометрической прогрессии называется произведение от до , то есть выражение вида
Обозначение: .

Описание[править | править код]

Любой член геометрической прогрессии может быть вычислен по формуле

Если и , прогрессия является возрастающей последовательностью, если , — убывающей последовательностью, а при  — знакочередующейся^[3], при  — стационарной (постоянной).

Своё название прогрессия получила по своему характеристическому свойству:

то есть модуль любого члена геометрической прогрессии, кроме первого, равен среднему геометрическому (среднему пропорциональному) двух рядом с ним стоящих членов^[4].

Примеры[править | править код]

• Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата^[5]:8—9.
• Геометрической является последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
• 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — геометрическая прогрессия со знаменателем 2 из тринадцати членов.
• 50; 25; 12,5; 6,25; 3,125; … — бесконечно убывающая геометрическая прогрессия со знаменателем 1/2.
• 4; 6; 9 — геометрическая прогрессия из трёх элементов со знаменателем 3/2.
• , , ,  — стационарная геометрическая прогрессия со знаменателем 1 (и стационарная арифметическая прогрессия с разностью 0).
• 3; −6; 12; −24; 48; … — знакочередующаяся геометрическая прогрессия со знаменателем −2.
• 1; −1; 1; −1; 1; … — знакочередующаяся геометрическая прогрессия со знаменателем −1.

Свойства[править | править код]

Свойства знаменателя геометрической прогрессии[править | править код]

Знаменатель геометрической прогрессии можно найти по формулам:

• 

• 

Свойства членов геометрической прогрессии[править | править код]

• Рекуррентное соотношение для геометрической прогрессии:

• Формула общего (-го) члена:

• Обобщённая формула общего члена:

• Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Пусть — соответственно -й, -й, -й члены геометрической прогрессии, где . Тогда для всякой такой тройки выполняется комплементарное свойство геометрической прогрессии, называемое тождеством геометрической прогрессии:

• Произведение членов геометрической прогрессии начиная с k-го члена, и заканчивая n-м членом, можно рассчитать по формуле

  

• Сумма всех членов убывающей прогрессии:

, то при , и

при .

Свойства суммы геометрической прогрессии[править | править код]

• 
• 

где — сумма обратных величин, т. е. .

Свойства произведения геометрической прогрессии[править | править код]

См. также[править | править код]

• Арифметическая прогрессия
• Арифметико-геометрическая прогрессия
• Числа Фибоначчи
• Показательная функция
• Сумма ряда

Примечания[править | править код]

Решение.

Достаточно очевидно, что (0,(8)=0,8+0,08+0,008+…)  Слагаемые в правой части равенства образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен (0,8), знаменатель равен (0,1). Найдём сумму по  формуле:

Осталось выполнить нужные действия с десятичными дробями:

Таким образом, бесконечная периодическая десятичная дробь (0,(8)) обращается в обыкновенную дробь (8/9).

Ответ: (0,(8)=8/9).

Нахождение суммы числового ряда. Третья часть.

В первой и второй частях этой темы мы решили шесть примеров на нахождение суммы числового ряда. Здесь рассмотрим решение стандартных примеров, основная идея которых состоит в использовании формулы суммы первых $n$ членов геометрической прогрессии. Также в конце страницы рассмотрим один пример (Демидович, №2552), который несколько выбивается из стандартной схемы.

Напомню, что если первый член геометрической прогрессии равен $b_1$, а знаменатель её равен $q$, то сумма первых $n$ членов геометрической прогрессии такова:

$$
begin{equation}
S_n=frac{b_1(1-q^n)}{1-q}
end{equation}
$$

Что такое геометрическая прогрессия? показатьскрыть

Формулу (1) можно записать и в ином виде. Так как для геометрической прогрессии $b_n=b_1cdot q^{n-1}$, то $S_n=sumlimits_{k=1}^{n} b_k=sumlimits_{k=1}^{n}left(b_1cdot q^{k-1} right)$. Формулу (1) запишем так:

$$
begin{equation}
sumlimits_{k=1}^{n}left(b_1cdot q^{k-1} right)=frac{b_1(1-q^n)}{1-q}
end{equation}
$$

Пример №7

Найти сумму ряда $sumlimits_{n=1}^{infty}frac{2^{n}}{3^{n+2}}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{2^{n}}{3^{n+2}}$. Составим n-ю частичную сумму этого ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{2}{27}+frac{4}{81}+frac{8}{243}+frac{16}{729}+ldots+frac{2^n}{3^{n+2}}.
$$

Обратимся к числам $frac{2}{27}$, $frac{4}{81}$, $frac{8}{243}$, $frac{16}{729}$ и т.д. Каждое последующее число получается из предыдущего умножением на $frac{2}{3}$. Например, $frac{4}{81}=frac{2}{27}cdotfrac{2}{3}$, $frac{8}{243}=frac{4}{81}cdotfrac{2}{3}$, $frac{16}{729}=frac{8}{243}cdotfrac{2}{3}$ и так далее. Мы имеем геометрическую прогрессию с первым членом $b_1=frac{2}{27}$ и знаменателем $q=frac{2}{3}$. А сумма $S_n$ есть сумма первых $n$ членов этой прогрессии, которую найдём по формуле (1):

$$
S_n=frac{frac{2}{27}left(1-left(frac{2}{3}right)^nright)}{1-frac{2}{3}}=frac{2left(1-left(frac{2}{3}right)^nright)}{27-18}=frac{2left(1-left(frac{2}{3}right)^nright)}{9}.
$$

Честно говоря, мне кажется удобным не расписывать частичную сумму, а работать с сокращённой формой записи. Вот так:

$$
S_n=sumlimits_{k=1}^{n}frac{2^k}{3^{k+2}}.
$$

Так как $2^k=2^{k-1+1}=2^{k-1}cdot 2^1=2cdot 2^{k-1}$ и $3^{k+2}=3^{k-1+3}=3^{k-1}cdot 3^3=27cdot 3^{k-1}$, то:

$$
frac{2^k}{3^{k+2}}=frac{2cdot 2^{k-1}}{27cdot 3^{k-1}}=frac{2}{27}cdot frac{2^{k-1}}{3^{k-1}}=frac{2}{27}cdotleft(frac{2}{3}right)^{k-1}.
$$

Зачем мы сделали эти преобразования? Для того, чтобы подогнать нашу частичную сумму под вид левой части формулы (2):

$$
S_n=sumlimits_{k=1}^{n}left(frac{2}{27}cdotleft(frac{2}{3}right)^{k-1}right)=frac{frac{2}{27}left(1-left(frac{2}{3}right)^nright)}{1-frac{2}{3}}=frac{2left(1-left(frac{2}{3}right)^nright)}{27-18}=frac{2left(1-left(frac{2}{3}right)^nright)}{9}.
$$

Итак, $S_n=frac{2left(1-left(frac{2}{3}right)^nright)}{9}$. Теперь найдём предел $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}frac{2left(1-left(frac{2}{3}right)^nright)}{9}=frac{2left(1-0right)}{9}=frac{2}{9}.
$$

Ответ: $S=frac{2}{9}$.

Пример №8

Найти сумму ряда $sumlimits_{n=1}^{infty}frac{7cdot 2^{n+3}-4cdot (-1)^{n} 3^{n-1}}{5^{n+1}}$.

Решение

Составим n-ю частичную сумму этого ряда. Поработаем с сокращённой формой записи, так как она более компактна:

$$
S_n=sumlimits_{k=1}^{n}frac{7cdot 2^{k+3}-4cdot (-1)^{k}3^{k-1}}{5^{k+1}}.
$$

Перегруппировываем слагаемые:

$$
S_n=sumlimits_{k=1}^{n}frac{7cdot 2^{k+3}}{5^{k+1}}-sumlimits_{k=1}^{n}frac{4cdot (-1)^{k} 3^{k-1}}{5^{k+1}}=
sumlimits_{k=1}^{n}frac{7cdot 2^4cdot 2^{k-1}}{5^2cdot 5^{k-1}}-sumlimits_{k=1}^{n}frac{4cdot(-1)^{k-1}cdot(-1)cdot 3^{k-1}}{5^2cdot 5^{k-1}}=\=
sumlimits_{k=1}^{n}left(frac{112}{25}cdot left(frac{2}{5} right)^{k-1} right)+sumlimits_{k=1}^{n}left(frac{4}{25}cdotleft(-frac{3}{5}right)^{k-1} right).
$$

А теперь к обеим суммам применяем формулу (2):

$$
S_n=sumlimits_{k=1}^{n}left(frac{112}{25}cdot left(frac{2}{5} right)^{k-1} right)+sumlimits_{k=1}^{n}left(frac{4}{25}cdotleft(-frac{3}{5}right)^{k-1} right)=frac{frac{112}{25}cdotleft(1-left(frac{2}{5} right)^nright)}{1-frac{2}{5}}+frac{frac{4}{25}cdotleft(1-left(-frac{3}{5} right)^nright)}{1-left(-frac{3}{5}right)}=\
=frac{112left(1-left(frac{2}{5} right)^nright)}{15}+frac{1-left(-frac{3}{5} right)^n}{10}.
$$

Теперь найдём предел $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{112left(1-left(frac{2}{5} right)^nright)}{15}+frac{1-left(-frac{3}{5} right)^n}{10} right)=frac{112left(1-0right)}{15}+frac{1-0}{10}=frac{227}{30}.
$$

Ответ: $S=frac{227}{30}$.

Пример №9

Найти сумму ряда $sumlimits_{n=1}^{infty}left(sqrt{n+2}-2sqrt{n+1}+sqrt{n}right)$.

Решение

Составим n-ю частичную сумму этого ряда. Поработаем с сокращённой формой записи, так как она более компактна:

$$
S_n=sumlimits_{k=1}^{n}left(sqrt{k+2}-2sqrt{k+1}+sqrt{k}right).
$$

Перегруппировываем слагаемые и упрощаем сумму:

$$
S_n
=sumlimits_{k=1}^{n}left(sqrt{k+2}-2sqrt{k+1}+sqrt{k}right)
=sumlimits_{k=1}^{n}sqrt{k+2}-2sumlimits_{k=1}^{n}sqrt{k+1}+sumlimits_{k=1}^{n}sqrt{k}=\

=sumlimits_{k=3}^{n+2}sqrt{k}-2sumlimits_{k=2}^{n+1}sqrt{k}+sumlimits_{k=1}^{n}sqrt{k}=\

=sumlimits_{k=1}^{n+2}sqrt{k}-1-sqrt{2}-2cdotleft(sumlimits_{k=1}^{n+2}sqrt{k}-1-sqrt{n+2}right)+sumlimits_{k=1}^{n+2}sqrt{k}-sqrt{n+1}-sqrt{n+2}=\

=1-sqrt{2}+sqrt{n+2}-sqrt{n+1}.
$$

Теперь найдём предел $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(1-sqrt{2}+sqrt{n+2}-sqrt{n+1}right)=1-sqrt{2}+lim_{ntoinfty}left(sqrt{n+2}-sqrt{n+1}right)=\

=1-sqrt{2}+lim_{ntoinfty}frac{left(sqrt{n+2}-sqrt{n+1}right)cdotleft(sqrt{n+2}+sqrt{n+1}right)}{sqrt{n+2}+sqrt{n+1}}=1-sqrt{2}+lim_{ntoinfty}frac{n+2-(n+1)}{sqrt{n+2}+sqrt{n+1}}=\
=1-sqrt{2}+lim_{ntoinfty}frac{1}{sqrt{n+2}+sqrt{n+1}}=1-sqrt{2}+0=1-sqrt{2}.
$$

Ответ: $S=1-sqrt{2}$.

Пример №10

Найти сумму ряда $sumlimits_{n=1}^{infty}frac{n}{2^n}$.

Решение

Для таких рядов можно применить метод сдвига и последующего переиндексирования. Составим n-ю частичную сумму этого ряда. Поработаем с сокращённой формой записи, так как она более компактна:

$$
S_n=sumlimits_{k=1}^{n}frac{k}{2^k}
=frac{1}{2}+sumlimits_{k=2}^{n}frac{k}{2^k}
$$

Поменяем индексы суммирования в сокращенной записи $sumlimits_{k=2}^{n}frac{k}{2^k}$, сдвинув их на единицу:

$$
frac{1}{2}+sumlimits_{k=2}^{n}frac{k}{2^k}
=frac{1}{2}+sumlimits_{k=1}^{n-1}frac{k+1}{2^{k+1}}
=frac{1}{2}+frac{1}{2}cdotsumlimits_{k=1}^{n-1}left(frac{k}{2^k}+frac{1}{2^k}right)
=frac{1}{2}+frac{1}{2}cdotleft(sumlimits_{k=1}^{n-1}frac{k}{2^k}+sumlimits_{k=1}^{n-1}frac{1}{2^k}right)=\

=frac{1}{2}+frac{1}{2}cdotleft(sumlimits_{k=1}^{n-1}frac{k}{2^k}+frac{n}{2^n}-frac{n}{2^n}+sumlimits_{k=1}^{n-1}left(frac{1}{2}right)^kright)
=frac{1}{2}+frac{1}{2}cdotleft(sumlimits_{k=1}^{n}frac{k}{2^k}-frac{n}{2^n}+sumlimits_{k=1}^{n-1}left(frac{1}{2}right)^kright)=\

=frac{1}{2}+frac{1}{2}sumlimits_{k=1}^{n}frac{k}{2^k}+sumlimits_{k=1}^{n-1}left(frac{1}{2}right)^{k+1}-frac{n}{2^{n+1}}
=frac{1}{2}+frac{1}{2}S_n+frac{frac{1}{4}cdotleft(1-left(frac{1}{2}right)^{n-1}right)}{1-frac{1}{2}}-frac{n}{2^{n+1}}=\

=1-frac{1}{2^n}-frac{n}{2^{n+1}}+frac{1}{2}S_n.
$$

Таким образом, мы приходим к следующему равенству:

$$
S_n=1-frac{1}{2^n}-frac{n}{2^{n+1}}+frac{1}{2}S_n
$$

Из полученного равенства имеем:

$$
S_n=2-frac{1}{2^{n-1}}-frac{n}{2^n}
$$

Переходя к пределу, получим:

$$
lim_{ntoinfty}S_n
=lim_{ntoinfty}left(2-frac{1}{2^{n-1}}-frac{n}{2^n}right)
=2-0-0
=2.
$$

Ответ: $S=2$.

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} – frac{1}{2} frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$

$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$

$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$

$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$

$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$

Выносим дробь одну вторую $ frac{1}{2} $ за скобки:

$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$

$$ + … frac{1}{2n-1} – frac{1}{2n+1} + frac{1}{2n+1} – frac{1}{2n+3} bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$

$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$

Числовые
ряды
– рассмотрим числовую последовательность:
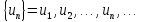u_n
–
числа.

Составим
суммы:
;

;

…………………..

;

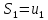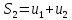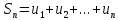Выражение:

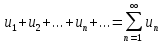
– называется числовым рядом

(1)

Числа

–
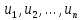
называются
членами ряда. Если они положительны, то
ряд называется знакоположительным.

–
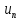называется n-ый
член ряда или общий член ряда.

–
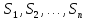частичные суммы.

Числовой
ряд (1) называется сходящимся,
если последовательность частичных сумм
сходится к некоторому числу S,
которое называется суммой ряда, т.е. ряд
сходится если существует предел:
.
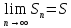Если предел не существует или равен
бесконечности, то ряд называетсярасходящимся.
Ряд может быть задан перечислением
нескольких членов или в виде формулы
общего члена ряда.

Ряд
геометрической прогрессии
– Исследуем на сходимость ряд:
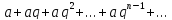Этот ряд называетсярядом
(2)

геометрической
прогрессии.
Сумму первых n-членов
ряда геометрической прогрессии находим
по формуле:
,

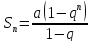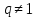
Найдем

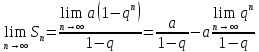
Рассмотрим
следующие случаи:

1),
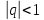тогда
,
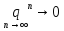поэтому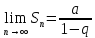
–
ряд сходится;

2),
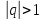тогда
,
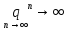и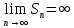
–
ряд расходится;

3),
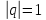тогда ряд (2) имеет вид:
,
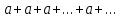его сумма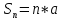,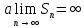– ряд расходится;

Вывод:
ряд геометрической прогрессии (2)
сходится, пр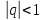и
и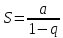его и расходится, при.

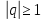25.Свойства числовых рядов. Необходимые условия сходимости ряда.

Простейшие
свойства числовых рядов:

1.Суммой
двух рядов
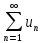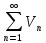иназывается ряд;

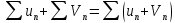2.Произведением
ряда на действительное число α
называется ряд:
;

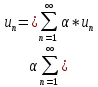3.Сходимость
ряда не нарушается, если произвольно
изменить (переставить, добавить или
отбросить) конечное число членов. Сумма
может измениться;

4.Сходящийся
ряд можно почленно умножать на любой
множитель α,
и если сумма ряда равна
,
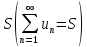то сумма;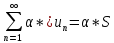

5.Сходящиеся
ряды можно почленно складывать и
вычитать:
;
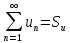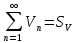,то
;

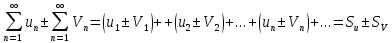Необходимое
условие сходимости ряда:

Теорема:
Если
ряд
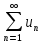сходится, то его общий член,
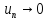т.е.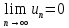

(1)

Доказательство:
Если ряд
,
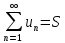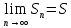.Запишем:

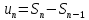
и
найдем его предел

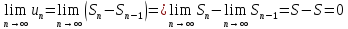
ч.т.д.

Если
условие (1) не выполняется, то ряд
расходится. Условие (1) не является
достаточным условием сходимости ряда,
т.е. из выполнения равенства
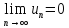не обязательно вытекает сходимость
ряда.

26.Достаточные признаки сходимости: признак Даламбера, радикальный признак Коши.

Необходимый
признак сходимости не дает, вообще
говоря, о том сходится ряд или нет.
Сходимость и расходимость ряда можно
установить с помощью достаточных
признаков.

Признак
Даламбера
– пусть дан ряд
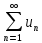знакоположительный и существует предел
отношения последнего члена ряда к
предыдущему, т.е.:,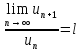
тогда, если.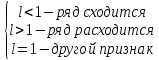

Радикальный
признак Коши
– дан знакоположительный ряд
,
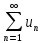если существует предел,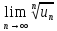
тогда если.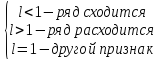

27.Достаточный признак сходимости: интегральный признак Коши. Сходимость обобщённого гармонического ряда.

Необходимый
признак сходимости не дает, вообще
говоря, о том сходится ряд или нет.
Сходимость и расходимость ряда можно
установить с помощью достаточных
признаков.

Интегральный
признак Коши
– дан знакоположительный ряд
,
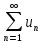пусть его члены могут быть представлены
как числовые значения некоторой функцииf(x),
которая убывает на промежутке [1;+∞),
т.е.:
;

;

…………..

;

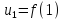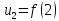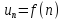тогда:
1.Если
несобственный интеграл:
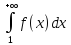сходится, то и ряд сходится;

2.Если
несобственный интеграл:
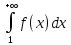расходится, то и ряд расходится;

Замечание
(о сходимости несобственного интеграла):
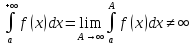интеграл сходится, еслиlim
= ∞,
или не существует, интеграл расходится.

Обобщенный
гармонический ряд:

,
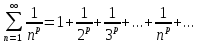где p>0
– действительное число

(1)

Ряд
(1) называется рядом Дирихле. Исследуем
ряд на сходимость по интегральному
признаку. Рассмотрим функцию
,
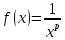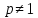это
функция убывает на интервале
(1;
).

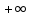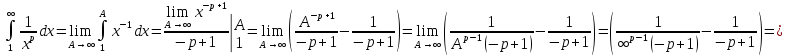
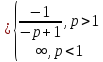
Вывод:
ряд Дирихле

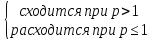
при

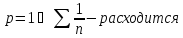
Этот
ряд удобно использовать в признаках
сравнения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #