Длброго времени суток, посмотрите, пожалуйста, верно ли я решил задачу:
Найти сумму ряда:
[math]sumlimits_{0}^{ infty} (-1)^k frac{(k+1)^2}{k!}[/math]
Ну что ясно, этот ряд сходится, т.к.по признаку Лейбница, т.к. [math]lim_{k to infty} frac{(k+1)^2}{k!} = 0[/math]
Ряд сходится абсолютно, т.к.
[math]lim_{k to infty}frac{(k+2)^2 k!}{(k+1)! (k+1)^2} =frac{(k+2)^2}{(k+1)^3} = 0[/math]
Дальше, расскроем скобки
[math]sumlimits_{0}^{ infty} (-1)^k frac{(k+1)^2}{k!} = sumlimits_{0}^{ infty} (-1)^k frac{(k^2 + 2k +1)}{k!}[/math]
Можно разделить данный ряд на 3 ряда
[math]sumlimits_{0}^{infty}(-1)^k frac{k^2}{k!}[/math]
[math]sumlimits_{0}^{infty} (-1)^k frac{2k}{k!}[/math]
[math]sumlimits_{0}^{infty} (-1)^k frac{1}{k!}[/math]
Начнем с последнего ряда. Найдем его сумму:
[math]S_3 = sumlimits_{0}^{infty} frac{(-1)^k}{k!} =e^{-1}[/math]
Теперь втрой ряд
[math]S_2 = sumlimits_{0}^{infty} (-1)^k frac{2k}{k!} = 2(0+sumlimits_{1}^{infty} (-1)^k frac{k}{k!})=2sumlimits_{1}^{infty} (-1)^k frac{1}{(k-1)!})=-2sumlimits_{0}^{infty}frac{(-1)^{k}}{k!} = -2e^{-1}[/math]
И первый ряд:
[math]S_1 =
sumlimits_{0}^{infty}(-1)^k frac{k^2}{k!} =
0 + sumlimits_{1}^{infty}(-1)^k frac{k^2}{k!} =
sumlimits_{1}^{infty}(-1)^k frac{k}{(k-1)!} =
sumlimits_{1}^{infty}(-1)^k frac{(k-1) + 1}{(k-1)!}=
sumlimits_{1}^{infty}(-1)^k frac{k-1}{(k-1)!} + sumlimits_{1}^{infty}(-1)^k frac{1}{(k-1)!} = S_4 + S_5[/math]
[math]S_4 =sumlimits_{1}^{infty}(-1)^k frac{k-1}{(k-1)!} = 0 +sumlimits_{2}^{infty}(-1)^k frac{1}{(k-2)!} =
sumlimits_{0}^{infty} frac{(-1)^k}{(k)!} = e^{-1}[/math]
[math]S_5 =sumlimits_{1}^{infty}(-1)^k frac{1}{(k-1)!} = -sumlimits_{0}^{infty} frac{(-1)^k}{(k-1)!} = e^{-1}[/math]
И так, сумма нашего ряда выходит:
[math]S = S_1+S_2+S_3 = S_1+S_2+S_4+S_5 = e^{-1}[/math]
|
|
Сумма ряда с факториалами
|
|
24/01/16 |
|
|
|
|
 |
24.01.2016, 13:20 
|
Otta |
Re: Сумма ряда с факториалами
|
||
09/05/13 |
Добавить и вычесть единицу, например. И вспоминать, чему равна сумма “главного” 🙂 ряда с факториалом в знаменателе.
|
||
|
|
|||
|
|
iifat |
Re: Сумма ряда с факториалами
|
||
16/02/13 |
|||
|
|
|||
|
|
InfiniteBum |
Re: Сумма ряда с факториалами
|
|
24/01/16 |
И вспоминать, чему равна сумма “главного” 🙂 ряда с факториалом в знаменателе. Подразумевается равенство
|
|
|
|
|
|
Otta |
Re: Сумма ряда с факториалами
|
||
09/05/13 |
|||
|
|
|||
|
Модераторы: Модераторы Математики, Супермодераторы
- Формулы и уравнения рядов
- Числовые ряды
- Функциональные ряды
- Тригонометрические ряды. Ряд Фурье
Примеры решения рядов здесь.
Числовые ряды
Факториал и двойные факториалы:
— формула Стирлинга.
Геометрическая прогрессия:
|q|<1.
Основные определения и теоремы о рядах:
{un} — заданная бесконечная числовая последовательность,
— числовой ряд,
un — члены ряда,
– частичные суммы ряда.
Сумма ряда:
сходится, S — сумма ряда.
или 
ряд сходится и суммы нет.
Отбрасывание конечного числа членов ряда не влияет на его сходимость (но влияет на сумму).
Свойства сходящихся рядов:
- Теоремы сравнения рядов с положительными членами:
≤
Если сходится, то сходится;
если расходится, то расходится.- vn ≠ 0, 0 < k < ∞.
Либо и, и сходятся,
либо и, и расходятся.
≥ 0, 
≥ 0.
≤ 
сходится, то 
vn ≠ 0, 0 < k < ∞.- Достаточные признаки сходимости числовых рядов с положительными членами (un > 0)
- Признак Даламбера
Если существует, то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0. - Признак Коши
Если существует, то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0. - Интегральный признак сходимости
1) un > 0; 2) un ≥ un+1; 3) f(x) — непрерывная невозрастающая функция, f(n) = un.
Либо и, и сходятся,
либо и, и расходятся.
, то 
, то 
сходятся,- Примеры числовых рядов
- : сходится, если a > 1; расходится, если a ≤ 1.
- : сходится, если a < 1; расходится, если a ≥ 1.
- : сходится.
- : сходятся, |q| < 1; расходятся, |q| ≥ 1.
- : сходится;
- : сходится, если a > 1; расходится, если a ≤ 1.
- : сходится условно.
- : сходится абсолютно.
- : сходится абсолютно.
: сходится, если a > 1; расходится, если a ≤ 1.
: сходится, если a < 1; расходится, если a ≥ 1.
: сходится.
: сходятся, |q| < 1; расходятся, |q| ≥ 1.
: сходится; 
: сходится, если a > 1; расходится, если a ≤ 1.
: сходится условно.
: сходится абсолютно.
: сходится абсолютно.Функциональные ряды
Функциональный ряд – сумма вида 
При 
из функционального ряда получается числовой ряд 
Если для 
числовой ряд сходится, то точка 
называется точкой сходимости функционального ряда. Если в каждой точке 
числовые ряды сходятся, то функциональный ряд называется сходящимся в области 
. Совокупность всех точек сходимости образует область сходимости функционального ряда.
– частичные суммы ряда. Функциональный ряд сходится к функции f(x), если 
Равномерная сходимость
Функциональный ряд, сходящийся для всех 
из области сходимости, называется равномерно сходящимся в этой области, если ∀ε > 0 существует не зависящий от x номер N(ε), такой, что при n > N(ε) выполняется неравенство Rn(x) < ε для всех x из области сходимости, где 
— остаток ряда.
Геометрический смысл равномерной сходимости:
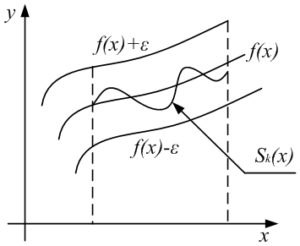
если окружить график функции y = f(x) «ε-полоской», определяемой соотношением f(x)−ε > y > f(x)+ε, то графики всех частичных сумм Sk(x), начиная с достаточно большого k, ∀x ∈ [a, b] целиком лежат в этой «ε-полоске», окружающей график предельной функции y = f(x).
— называется мажорируемым в области , если существует такой сходящийся числовой ряд 
un > 0, что для ∀x ∈ D fn(x) ≤ un, n = 1, 2, …. Ряд называется мажорантой ряда 
Признак Вейерштрасса (признак равномерной сходимости функционального ряда): функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.
Степенные ряды:
— степенной ряд по степеням 
При 
– степенной ряд по степеням x.
Область сходимости степенного ряда:
Радиус сходимости, интервал сходимости R, x ∈ (-R, R):
или 
При |x| < R ряд сходится, при |x| > R – расходится;
в точках x = ±R – дополнительное исследование.
На интервале сходимости ряд 
сходится абсолютно;
на любом отрезке из интервала сходимости он сходится равномерно.
- Свойства степенных рядов
- Степенной ряд сходится равномерно на [−R′, R′]
∀R′ < R, его можно почленно дифференцировать и интегрировать в интервале сходимости. -
- Ряды, полученные почленным дифференцированием и интегрированием, имеют тот же интервал сходимости.
- Разложение элементарных функций в степенные ряды
- , x ∈ (−∞; ∞).
- ,
x ∈ (−∞; ∞). - , x ∈ (−∞; ∞).
- , x ∈ (−∞; ∞).
- , x ∈ (−∞; ∞).
, x ∈ (−1; 1].
, x ∈ [−1; 1).- ,
x ∈ (−1; 1). - , x ∈ [−1; 1].
- , x ∈ [−1; 1].
- , x ∈ (−1; 1).
- , x ∈ (−1; 1).
- , x ∈ (−1; 1).
- , x ∈ (−1; 1).
- , x ∈ (−1; 1].
, x ∈ (−∞; ∞).
,
, x ∈ (−∞; ∞).
, x ∈ (−∞; ∞).
, x ∈ (−∞; ∞).
, x ∈ (−1; 1].
, x ∈ [−1; 1).
,
, x ∈ [−1; 1].
, x ∈ [−1; 1].
, x ∈ (−1; 1).
, x ∈ (−1; 1).
, x ∈ (−1; 1).
, x ∈ (−1; 1).
, x ∈ (−1; 1].Тригонометрические ряды
Ряд Фурье для функции с произвольным периодом Т=2l, f(x+2l) = f(x):
где 
- Разложение в ряд Фурье непериодических функций, заданных на отрезке x ∈ [0; l] или на отрезке x ∈ [-l; l]
- f1(x)=f(-x), x ∈ [-l; 0] (четное продолжение)
где x ∈ [0; l] n = 0, 1, 2,… - f1(x) = —f(−x), x ∈ [-l; 0]
(нечетное продолжение)
где x ∈ [0; l] n = 1, 2,… - На всю действительную ось ϕ(x) продолжается периодически с периодом 2l, ϕ(x) = ϕ(x + 2l). Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ±l выполняется условие: где то есть,
– левый предел f(x) в точке x = l,
– правый предел f(x) в точке x = l.
Произвольная функция f(x) задана на отрезке [0; l]; на отрезок [-l; 0] она может быть продолжена произвольным образом:
![{varphi}(x)=delim{[}{matrix{2}{1}{{f(x),~x{in}delim{[}{0;~l}{]}~} {{f_1}(x),~x{in}delim{[}{-l;~0}{]}~}}}{},~{f_1}(x)](http://matematika.electrichelp.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_966.5_1bbb3b10b711e3e999aa61f8ae6f878b.png "{varphi}(x)=delim{[}{matrix{2}{1}{{f(x),~x{in}delim{[}{0;~l}{]}~} {{f_1}(x),~x{in}delim{[}{-l;~0}{]}~}}}{},~{f_1}(x)")
– некоторая кусочно-монотонная функция.Наиболее часто встречающиеся продолжения:
x ∈ [0; l] n = 0, 1, 2,…
x ∈ [0; l] n = 1, 2,…
где 
то есть, 
– левый предел f(x) в точке x = l,
– правый предел f(x) в точке x = l.$begingroup$
How would you find the sum of the following series.
$frac{k^3+6k^2+11k+5}{(k+3)!}$ as k goes from 1 to infinity
asked Jan 16, 2017 at 3:56
$endgroup$
1
$begingroup$
Hint you can see that it can be weitten as $$frac {(k+1)(k+2)(k+3)}{(k+3)!}-frac{1 }{(k+3)!} $$ now thats equal to $frac {1}{k!}-frac {1}{(k+3)!} $ also note that $sum _0 ^infty frac {1}{n!}=e $ thus you can now find the answer
answered Jan 16, 2017 at 5:26
Archis WelankarArchis Welankar
15.7k7 gold badges31 silver badges61 bronze badges
$endgroup$
$begingroup$
In a general way, for the series $$sum_{n=1}^{+infty}frac{P(n)}{(n+a)!}text{ with }ain mathbb{N} text{ and }Ptext{ polynomial of degree }k,$$ we can express the numerator $$begin{aligned}&P(n)=A_kunderbrace{(n+a)(n+a-1)ldots}_{ktext{ factors}}+A_{k-1}underbrace{(n+a)(n+a-1)ldots}_{k-1text{ factors}}\&+cdots+A_2underbrace{(n+a)(n+a-1)}_{2text{ factors}}+A_1underbrace{(n+a)}_{1text{ factor}}+A_0,end{aligned}$$ symplify, decompose in sum of series and use $e=sum_{m=0}^{+infty}frac{1}{m!}.$
answered Jan 16, 2017 at 5:46
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Перейти к содержанию
Сумма ряда с факториалом
Просмотров 1.8к. Обновлено 15 октября 2021
Вычислить сумму ряда
5 s = ∑ (-1) * i * (x / i!) i=1 Значение x вводится с клавиатуры.
В данном случае надо найти сумму ряда произведений:
s = (-1) * 1 * (x / 1!) + (-1) * 2 * (x / 2!) + (-1) * 3 * (3 / i!) + (-1) * 4 * (x / 4!) + (-1) * 5 * (x / 5!)
Так как i меняется от 1 до 5, то каждый элемент ряда можно находить в цикле, после этого добавлять к сумме.
Поскольку элемент ряда содержит факториал, то его придется вычислять отдельно для каждого значения i. Это вычисление можно вынести в отдельную функцию.
Таким образом, алгоритм решения задачи сводится к следующему:
- Ввести значение x.
- Присвоить s 0.
- В цикле для i от 1 до 5
- получать факториал i,
- вычислять значение выражения (-1) * i * (x / i!),
- суммировать полученное значение со значением s.
- Вывести значение s на экран.
Факториал также вычисляется в цикле. Сначала в переменную записывается 1, затем значение этой переменной в цикле умножается на числа от 2 до i. (В программе ниже — до n, т.к. i используется как счетчик.)
Pascal
var
s: real;
x: integer;
i: byte;
j: longint;function factorial(n: byte): longint;
var i: byte;
begin
factorial := 1;
for i:=2 to n do
factorial := factorial * i;
end;begin
readln(x);
s := 0;
for i:=1 to 5 do begin
j := factorial(i);
s := s + ((-1) * i) * (x / j);
end;
writeln(s:5:3);
end.
-3
8.125
Язык Си
#include < stdio.h>
int factorial(short n);main() {
float s, x;
short i;
int j;
scanf("%f", &x);
s = 0;
for (i=1; i <= 5; i++) {
j = factorial(i);
s += (-1 * i) * (x / j);
}
printf("%.3fn", s);
}int factorial(short n) {
short i;
int f;
f = 1;
for (i=2; i<=n; i++)
f *= i;
return f;
}
10
-27.083
Python
def factorial(n):
f = 1
for i in range(2,n+1):
f *= i
return fx = int(input())
s = 0
for i in range(1,6):
j = factorial(i)
s += (-1 * i) * (x / j)
print("%.3f" % s)
2
-5.417
КуМир
алг
нач
вещ s, x
цел i, j
ввод x
s := 0
нц для i от 1 до 5
j := факториал(i)
s := s + ((-1) * i) * (x / j)
кц
вывод s:5:3
коналг цел факториал(цел a)
нач
цел i
знач := 1
нц для i от 2 до a
знач := знач * i
кц
кон
-0.5
1.354
Basic-256
input x
s = 0
for i=1 to 5
gosub factorial
s = s + (-1 * i) * (x / j)
next i
decimal 3
print s
endfactorial:
j = 1
for n=1 to i
j = j * n
next n
return
-2
5.417
