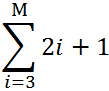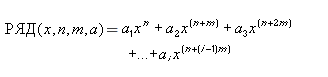Как найти сумму ряда в информатике

Как найти сумму числового и функционального ряда

Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.

Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.

Сумма числового ряда

Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:

Здесь показана начальная последовательность чисел ряда и правило суммирования:

• ∑ – математический знак суммы;
• a_i – общий аргумент;
• _i – переменная, правило для изменения каждого последующего аргумента;
• ∞ – знак бесконечности, «предел», до которого проводится суммирование.

Запись 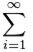обозначает: суммируются натуральные числа от 1 до «плюс бесконечности». Так как _i = 1, то подсчет суммы начинается с единицы. Если бы здесь стояло другое число (например, 2, 3), то суммировать мы начинали бы с него (с 2, 3).

В соответствии с переменной _i ряд можно записать развернуто:

= а₁ + а₂ + а₃ + а₄ + а₅ + … (до «плюс бесконечности).

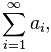
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:

S₁ = а₁

S₂ = а₁ + а₂

S₃ = а₁ + а₂ + а₃

S₄ = а₁ + а₂ + а₃ + а₄

Сумма числового ряда – это предел частичных сумм S_n. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».

Сначала найдем сумму числового ряда:

М = 10.

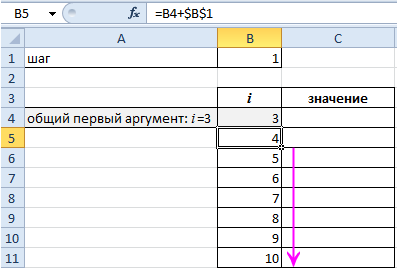
Теперь построим в Excel таблицу значений членов ряда:

Общий первый аргумент берем из формулы: i=3.

Все следующие значения _i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.

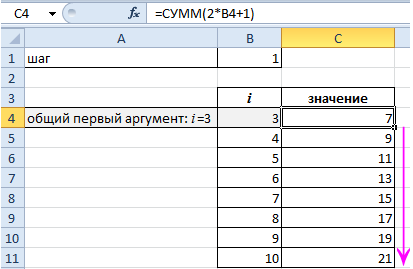
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.

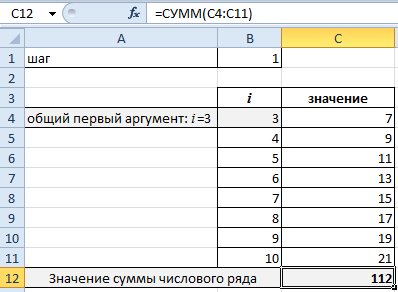
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).



Функция РЯД.СУММ в Excel

Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:

Аргументы функции:

• х – значение переменной;
• n – степень для первого аргумента;
• m – шаг, на который увеличивается степень для каждого последующего члена;
• а – коэффициенты при соответствующих степенях х.

Важные условия для работоспособности функции:

• все аргументы обязательные (то есть все должны быть заполнены);
• все аргументы – ЧИСЛОвые значения;
• вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
• количество «коэффициентов» = числу аргументов.

Вычисление суммы ряда в Excel

Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.

Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.

Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:

S₁ = a (1 + x).

На конец второго и последующих периодов – вид выражений следующий:

S₂ = a (1 + x)²;
S₃ = a (1 + x)² и т.д.

Чтобы найти общую сумму:

S_n = a (1 + x) + a (1 + x)² + a (1 + x)³ + … + a (1 + x)ⁿ

Частичные суммы в Excel можно найти с помощью функции БС().

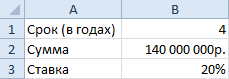
Исходные параметры для учебной задачи:

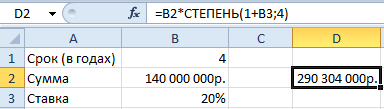
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)

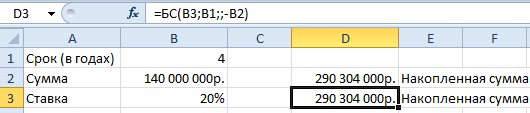
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)

Результаты одинаковые, как и должно быть.

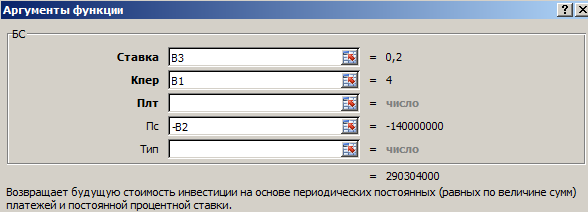
Как заполнить аргументы функции БС():

1. «Ставка» – процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
2. «Кпер» – число периодов для выплат процентов. В нашем примере – 4 года.
3. «Плт» – периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
4. «Пс» – «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».

Таким образом, функция БС помогла найти нам сумму функционального ряда.

В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.

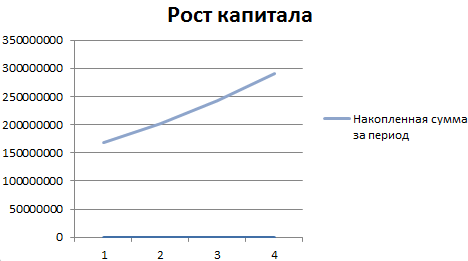
Построение графика функций суммы числового ряда

Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:

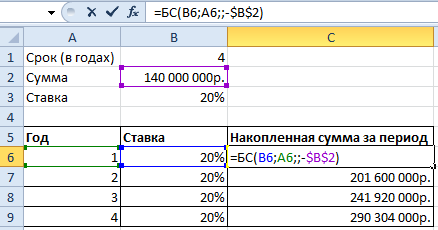
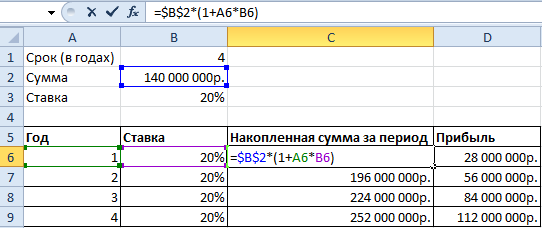
Дальше нам нужна функция для начисления сложных процентов – БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:

В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.

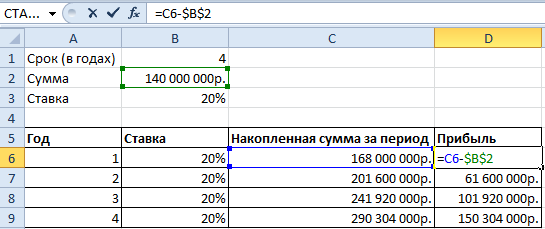
Сделаем еще один столбец, в котором отразим прибыль:

Как мы считали – в строке формул.

На основании полученных данных построим график функций.

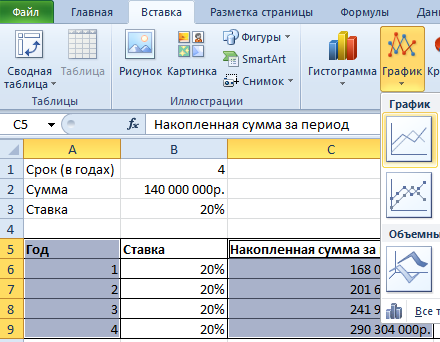
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» – инструмент «Диаграммы». Выбираем первый график:

Сделаем задачу еще более “прикладной”. В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.

Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)

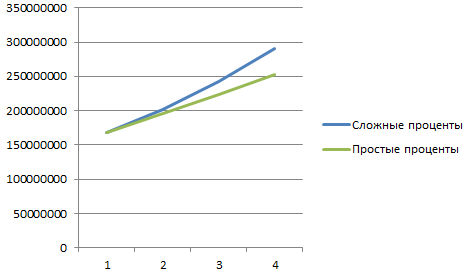
Добавим полученные значения в график «Рост капитала».

Какие именно выводы сделает инвестор – очевидно.

Математическая формула частичной суммы функционального ряда (с простыми процентами): S_n = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.

Вычисление суммы бесконечного ряда (циклы с неизвестным числом повторений)

Для
выполнения данной лабораторной работы
используют оператор цикла do
loop
{while
|until|}.

Оператор
цикла
DO
LOOP [{WHILE |
UNTIL}].
Этот
оператор называется циклом с постусловием,
т. к. проверка условия осуществляется
после каждого выполнения тела цикла,

DO

<операторы>

LOOP
[{WHILE
| UNTIL}
условие]

Цикл выполняется
до тех пор, пока условие не станет
истинным. Например, проверка на то,
чтобы задать длину последовательности,
осуществляется следующим образом:

DO

PRINT
“ВВЕДИТЕ ДЛИНУ ПОСЛЕДОВАТЕЛЬНОСТИ
N = “

INPUT
N%

LOOP
UNTIL N% >0

Цикл
выполняется до тех пор, пока пользователь
не введет положительное число.

При использовании UNTIL
цикл выполняется до тех пор, пока не
выполнится условие, а при использовании
WHILE
цикл выполняется только при выполнении
условия и заканчивается, если условие
нарушается.

Операторы
цикла
DO WHILE/UNTIL LOOP и
WHILE WEND.

Эти
циклы называются циклами с предусловием,
т. к.
проверка
проводится до начала очередной операции:

DО
[{WHILE
UNTIL}условие]

<тело
цикла>

LOOP

или

WHILE
<условие>

<тело
цикла>

WEND

Цикл WHILE
выполняется, пока условие истинно. Как
только условие нарушается, выполнение
цикла завершается. Если используется
UNTIL,
то выполнение происходит до тех пор,
пока условие не станет истинным.

Например, та же проверка вводимой длины
последовательности может быть задана
как

INPUT
N%

WHILE
N%
<=0

PRINT
“ВВЕДИТЕ ДЛИНУ ПОСЛЕДОВАТЕЛЬНОСТИ
N =“

INPUT
N%

WEND

Обратите внимание, что до первого входа
цикл переменной N%
уже должно быть присвоено какое-либо
значение!

Типичным
примером итерационного цикла служат
задачи вычисления с заданной точностью.

Итерационные
циклы широко используются в численных
методах решениях алгоритмических и
трансцендентных уравнений, при вычислении
интегралов, определении суммы бесконечного
ряда и т.д. Во всех этих задачах
вычисления прекращаются при достижении
некоторой точности (результатов).

Рассмотрим пример
вычисления суммы бесконечного ряда
чисел.

Структурный
подход предполагает использование
простейших структур, перечисленных и
списанных выше, для построения блок –
схемы алгоритмов любой сложной задачи.
Рассмотрим это на примере.

В
отчете по работе должно быть:

1. Математическая
   постановка задачи

2. Блок-схема
   алгоритма

3. Программа
   на QBASIC

4. Результаты
   выполнения задачи

Пример.
Вычислить
значение sin
x по формуле

SinX
=

Общая
формула члена ряда
гдеn
– номер члена ряда n

Вычисления
продолжать до тех пор пока
>E,
это условие
и есть условие выхода из цикла, где Е –
точность вычислений.

При достаточно
большом n возведение в степень занимает
значительное машинное время . Поэтому
каждый член ряда следует получать в
соответствии с рекуррентным соотношением

R = Rx

Где n = 3,5,7……..; R
начальное = х. Тогда рекуррентное
соотношение для получения суммы ряда
будет S = S+R (-1), где S начальное= Х. Блок
– схема алгоритма вычисления суммы
ряда представлены на рисунке 27.

Вычисления ведутся
до тех пор , пока величина члена ряда R
не станет меньше , либо равной некоторой
малой величине Е. Значение R с каждым
циклом уменьшается. После выполнения
цикла первый раз имеем

R =

S =

После
выполнения цикла второй раз

R =

S =

И
т.д.

Блок-схема

Программа
на Qbasic
имеет вид:

input
x,e

s=x

r=x

n=3

do
while r>e

r=r*x^2/((n-1)*n)*(-1)

s=s+r

n=n+2

loop

print
s

end

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Попробуем на практике разобрать работу циклов, про которые рассказано в одном из наших уроков. Выполним предложенное задание, использовав несколько разных методик и видов циклов.

Задача

Программа выводит сумму первых членов натурального ряда чисел до введённого n-числа включительно.

Решение задачи с помощью цикла while

Произведём расчёт, используя цикл с предусловием while.

n=int(input(Введите последнее число из ряда натуральных чисел=))

i=1

s=0

while i<=n:

	s=i+s

	i=i+1

print (Сумма чисел от 1 до, n, =, s)

1. Сперва задаем в переменную n самое большое натуральное число (в пределах разумного).
2. Обнулим на входе сумму s.
3. Цикл будет выполняться до тех пор, пока внутренняя переменная не достигнет значения n.

Результат выполнения программы

Решение задачи с помощью цикла for

Быстрее происходит расчёт при помощи цикла for.

n=int(input(Введите последнее число=))

s=0

for i in range(1,n+1):

	s=i+s

print (Сумма чисел от 1 до, n, =, s)

Посмотрите, в цикле записано максимальное число не n, а n+1. Это связано с тем, что цикл должен выполняться на один шаг больше, чтобы последнее значение промежуточной суммы было учтено.

Результат выполнения программы

Решение задачи с помощью списка

Ту же самую задачку можно решить, используя список. По сути, это ничего не меняет, но, как видите, код при этом занимает всего две строки:

n=int(input(Введите последнее число=))

print (Сумма чисел от 1 до, n, =, sum([i for i in range(1,n+1)]))

Результат выполнения программы

Задача на последовательность Функция перевода целого двоичного числа в десятичное

Задача — Сумма элементов ряда чисел
— программирование на Pascal, Си, Кумир, Basic-256, Python

Найти сумму n элементов следующего ряда чисел:
1 -0.5 0.25 -0.125 …
Количество элементов (n) вводится с клавиатуры.

В данном случае ряд чисел состоит из элементов, где каждый следующий меньше предыдущего в два раза по модулю и имеет обратный знак. Значит, чтобы получить следующий элемент, надо предыдущий разделить на -2.

Какой-либо переменной надо присвоить значение первого элемента ряда (в данном случае это 1). Далее в цикле добавлять ее значение к переменной, в которой накапливается сумма, после чего присваивать ей значение следующего элемента ряда, разделив текущее значение на -2. Цикл должен выполняться n раз.

Следует отметить, что чем больше n, тем меньше меняется сумма от прибавления каждого следующего элемента, т.к. на каждой итерации цикла значение элемента уменьшается в два раза (по модулю), т.е. прибавляется все меньшая и меньшая величина. Попробуйте выполнить программу, введя в качестве значения n сначала 3, затем 10 и 20. Вы увидите, что разница между первым и вторым случаем значительна, а между вторым и третьим — нет.

Pascal

var
n,i: byte;
e,s: real;
begin
readln(n);
e := 1;
s := 0;
for i:=1 to n do begin
s := s + e;
e := e / -2;
end;
writeln(s:9:7);
end. 6
0.6562500

Язык Си

#include <stdio.h>

main() {
unsigned short n,i;
float e, s;
scanf(«%d»,&n);
e = 1;
s = 0;
for (i=0;i<n;i++) {
s += e;
e /= -2;
}
printf(«%.7fn»,s);
} 10
0.6660156

Python

n = int(input())
e = 1
s = 0
for i in range(n):
s += e
e /= -2
print(s) 4
0.625

КуМир

алг сумма рядя
нач
цел n,i
вещ e,s
ввод n
e := 1
s := 0
нц для i от 1 до n
s := s + e
e := e / 2 * (-1)
кц
вывод s
кон 4
0.625

30
0.6666667

Basic-256

input n
start = 1
sum = 0
for i=1 to n
sum = sum + start
start = start / -2
next i
print sum 20
0.666666

Did you find apk for android? You can find new Free Android Games and apps.

В этой статье описаны синтаксис формулы и использование функции РЯД.СУММ в Microsoft Excel.

Описание

Многие функции могут быть аппроксимированы разложениями в степенные ряды.

Возвращает сумму степенного ряда, вычисленную по формуле:

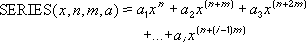
Синтаксис

РЯД.СУММ(x; n; m;коэффициенты)

Аргументы функции РЯД.СУММ описаны ниже.

• X    Обязательный. Значение переменной степенного ряда.

• n    Обязательный. Показатель степени x для первого члена степенного ряда.

• m    Обязательный. Шаг, на который увеличивается показатель степени n для каждого следующего члена степенного ряда.

• Коэффициенты    Обязательный. Набор коэффициентов при соответствующих степенях x. Количеством значений в аргументе “коэффициенты” определяется количество членов степенного ряда. Например, если в аргументе “коэффициенты” три значения, то степенной ряд содержит три слагаемых.

Замечание

Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Коэффициенты в виде чисел	Коэффициенты в виде формулы
0,785398163	=ПИ()/4
1	1
-0,5	=-1/ФАКТР(2)
0,041666667	=1/ФАКТР(4)
-0,001388889	=-1/ФАКТР(6)
Формула	Описание (результат)	Результат
=РЯД.СУММ(A3;0,2;A4:A7)	Аппроксимация косинуса ПИ/4 радиан или 45 градусов (0,707103)	0,707103