Как найти сумму с учетом инфляции

В рассмотренных выше методах наращения
все денежные величины измерялись по
номиналу, то есть не принималось во
внимание снижение реальной покупательной
способности денег за период, охватываемый
финансовой операцией. Однако в современных
условиях необходимо учитывать инфляцию,
так как без ее учета конечные результаты
представляют собой весьма условную
величину.

Инфляцию необходимо учитывать по
крайней мере в двух случаях: а) при
расчете наращенных сумм; б) при определении
реальной ставки процента (реальной
доходности) финансовой операции.

Внешними признаками инфляции являются,
прежде всего, рост цен и, как следствие,
снижение покупательной способности
денег.

Сначала определим понятия: индекс
цен

и покупательная способность денег


на примерах.

Пусть сегодня 1 кг некоторого товара
стоит 10 руб., а через год –

12,5 руб.
Тогда индекс цен на этот товар (за год)
составит

то есть цена выросла на 25%. Следовательно,
на 10 руб. по новой цене можно приобрести

кг товара, и покупательная способность
денег составит

То есть

(17)

Иначе говоря, индекс покупательной
способности денег есть величина, обратная
индексу цен. Отсюда следует, что величина

характеризует реальную покупательную
способность наращенной суммы.

Пусть темп прироста инфляции (темп
роста цен) равен

.
Тогда годовой индекс цен составит
величину

,
а за

лет индекс цен будет равен

Таким образом, наращенная за

лет сумма с учетом инфляции составит:

(18)

Отношение

является
множителем наращения, учитывающим
среднегодовые темпы инфляции.

№ 28. Пусть первоначальная сумма,
положенная в банк, равна 1 млн. руб. под
20% годовых. Найдем наращенную за два
года сумму, если среднегодовой темп
инфляции составил: а) 10%; б) 20%; в) 25%.

Решение. Найдем сначала (для
сравнения) наращенную сумму без учета
инфляции:

млн. руб.

а)

1
млн. 190 тыс. 82,4 руб.;

б)

млн. руб.;

в)

921
тыс. 600 руб.

Видно, что если

,
то покупательная способность наращенной
суммы равна покупательной способности
начальной суммы

,
то есть вкладчик, в некоторой степени,
нейтрализует инфляционный фактор. Если
же

то

то есть наращенная сумма не компенсирует
снижение покупательной способности
капитала. В этом случае банковскую
ставку называют отрицательной. И
только в случае, когда

, наблюдается реальный рост покупательной
способности вложенного в банк капитала.
Такую банковскую ставку называют
положительной.

Для уменьшения воздействия инфляции
и компенсации потерь от снижения
покупательной способности денег
используют различные методы. Один из
них – индексация процентной ставки, то
есть процентная ставка корректируется
в соответствии с темпом инфляции. Такую
ставку (скорректированную с учетом
уровня инфляции), называют брутто-ставкой.

Если речь идет о полной компенсации
инфляции при начислении простых
процентов, то брутто-ставку

находим из равенства:

то есть

(19)

А при начислении сложных процентов:

то есть

(20)

Если же применяется индекс инфляции
за весь срок кредита, а не за один год,
то вместо

используется

,
где

– срок действия кредитного соглашения.

№ 29. Рассчитать брутто-ставку по
условиям № 28.

Решение.

а)

или 32%.

Действительно,

млн. руб.;

б)

или 44%.

Действительно,

млн. руб.;

в)

или 50%.

Действительно,

млн. руб.

Другой метод компенсации инфляции
состоит в индексации первоначальной
суммы платежа

.
В этом случае эта сумма периодически
индексируется с помощью заранее
оговоренного коэффициента, например:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Наращенная сумма с учетом инфляции

Краткая теория

---

Под инфляцией понимается снижение реальной покупательной
способности денег за период финансовой операции. Инфляцию необходимо учитывать
по крайней мере в двух случаях: 1) при вычислении наращенной суммы денег; 2)
при расчете реальной доходности финансовой операции.

Введем обозначения:

 – наращенная
сумма денег;

 – индекс цен (множитель роста цен);

 – наращенная сумма с учетом обесценивания;

 – темп инфляции, относительный прирост цен за
период в %.

Темп инфляции может меняться от периода к
периоду, тогда индекс цен за несколько таких периодов равен произведению
индексов цен:

Если в каждом периоде один и тот же темп
инфляции

,
то за

 периодов индекс цен равен:

Реально наращенная сумма денег с учетом
инфляции:

При этом формулы наращения можно выбирать
разные в зависимости от вида применяемых процентов: простых, сложных,
непрерывных.

Инфляционные влияние всегда оценивается

по сложным процентам,
так как обесцениваются уже обесцененные деньги в
предыдущем периоде.

Если применяются

простые проценты,
то
инфляция увеличивается по формуле:

Очевидно, что увеличение наращенной суммы происходит, если
выполняется неравенство

Если

наращение происходит по сложным процентам, то применяется формула:

Пример решения задачи

---

Задача

C 10 августа по 10 ноября на сумму 213 тыс.руб. начисляются простые проценты по ставке 18%
годовых. Ежемесячный темп инфляции 1,20; 1,15 и 1,40% соответственно.
Рассчитайте наращенную сумму с учетом инфляции.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Вычислим индекс цен за три
месяца:

Решим задачу, используя

германский способ начисления процентов.

С 10 августа по 10 ноября –
3 месяца (90 дней).  

Наращенная сумма с учетом
инфляции:

Ответ:

Когда я был маленький, то мечтал, что у меня будет много денег, которые я положу на вклад в банке. Банк будет начислять мне проценты, и я буду жить припеваючи долго и счастливо. Я даже рассчитывал сколько денег мне требовалось на долгую и счастливую жизнь. Сначала это была очень огромная сумма ( Скрудж Макдак немного повлиял на мои детские мечты), по мере взросления она постепенно уменьшалась, приближаясь к более реальным значениям.

В конце концов я остановился на “хотя бы получать в виде процентов по вкладу сумму, эквивалентную средней заработной плате в стране“. Ставки по вкладам тогда были высокие (двузначные) и мои расчеты показывали, что накопить нужную сумму в принципе вполне реально. У меня всегда возникал вопрос: “Почему люди так не делают. Это же так просто. Копи деньги, размещай их на вкладе – и будет тебе счастье”. Про фондовый рынок я тогда еще не знал.

Загадка про (не) накапливаемый миллион!

Мои детские и юношеские мечты были разрушены новыми знаниями, которые я получал в период взросления. Я узнал что такое инфляция, номинальная и реальная доходность. И как оказалось, вклад в банке хоть и может приносить хорошую доходность в номинальном выражении, но его реальная доходность (за вычетом инфляции) находится практически на нуле. И чтобы можно было достойно жить на проценты, нужно было иметь в разы, в десятки-сотни раз больше денег, чем я предполагал изначально.

Расчет реальной доходности с учетом инфляции

Аналогично было и с инвестициями. Когда я смотрел статистику доходности фондовых рынков (индексов), особенно РФ – голова шла кругом от возможностей по заработку. Но если считать реальную доходность с учетом инфляции, данные были намного скромнее.

Именно реальная доходность показывает истинную картину: сколько денег ты заработал. Те, кто считают свои результаты по номинальным значениям, сами себя обманывают (“А в попугаях я длиннее всего”).

А как считать это самую реальную доходность с учетом инфляции? 

Большинство из нас делает это так: из номинальной доходности вычитают инфляцию и получают реальную доходность.

Реальная доходность = Номинальная доходность – Инфляция.

Уже неплохо, но формула немного неверная. Ее можно использовать, когда инфляции в стране не очень высокая. Будет погрешность в результатах, но небольшая. Если нужна точность, однозначно нужно использовать правильную формулу.

---

Приведу простой пример, как мы теряем правильный результат при неправильных расчетах реальной доходности.

У нас есть 100 рублей. Мы открываем вклад в банке на 3 года под 20% годовых. Инфляция за это время составляет – 10% в год.

Какова реальная доходность вклада? По вышеприведенной формуле – это 10% годовых (20% – 10%).

Как проверить, что мы ошиблись (или не ошиблись) в расчетах?

Считаем на пальцах:

1. За три года вклад в 100 рублей размещенный под 20% годовых – подрастет до 172,8 рублей (100 * (1+0,20)^3). Рост в 1,728 раз.
2. За эти же три года цены на товары (в следствии 10% инфляции) увеличатся в 1,331 раза [(1+0,1)^3].
3. Делим одно на другое и получаем 1,728 / 1,331 = 1,2982. То есть, наш вклад в реальном выражении подрос примерно на 29,82%.
4. Рост на 29,82% за три года – это соответствует 9% среднегодовой доходности [((1,2982^(1/3)-1)*100].

Мы только что потеряли (или нашли) целый процент доходности.

Как правильно получить реальную доходность за вычетом инфляции? 

Формула:

Реальная доходность = (Номинальная доходность – Инфляция) / (1 + Инфляция)

Проверяем формулу на нашем примере про вклад и инфляцию:

Реальная доходность = (0,2 – 0,1) / (1 + 0,1) = 0,1 / 1,1 = 0,09 или 9% годовых. Все сходится. Формула работает.

Статья в тему: Цифры, числа и проценты — как правильно считать прибыль и годовую доходность | Несколько простых способов с интересными примерами

Как потерять несколько десятков процентов реальной доходности

Теоретически можно быстро в уме высчитывать реальную доходность обычным вычитанием, при условии, что инфляция в стране небольшая. Результат будет выходить с определенной погрешностью, на которую можно закрывать глаза. Но если инфляции высокая, с помощью такого способа подсчета можно легко потерять (или добавить лишних) несколько процентов доходности (процентных пункта, если быть точнее). А в некоторых случаях, даже несколько десятков процентов!

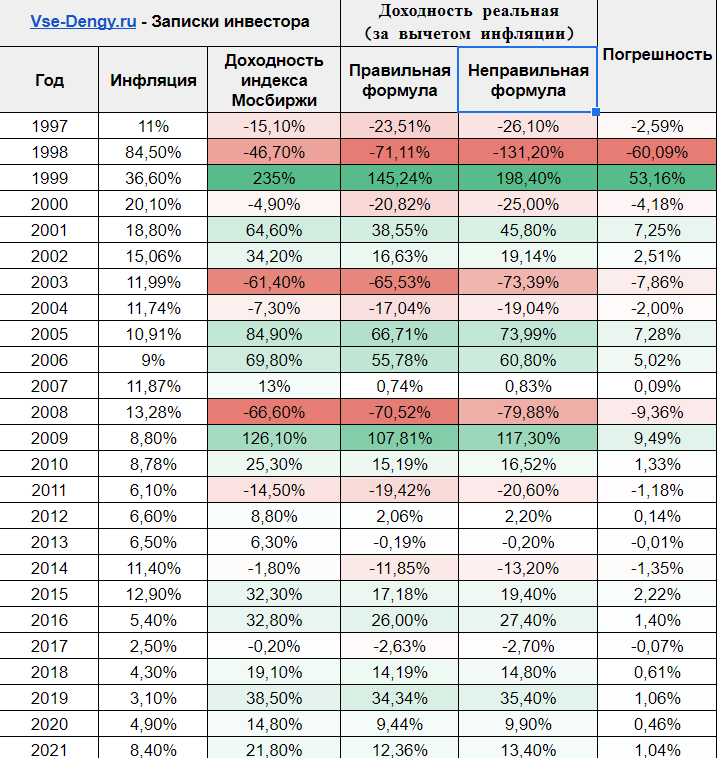
Как пример, приведу статистику доходности индекса Московской биржи (блог все таки про инвестиции) по годам, инфляцию и реальную доходность посчитанную двумя способами: вторым и неправильным. Для наглядности в крайнем правом столбце я отобразил разницу (погрешность) между двумя способами расчета реальной доходности. Вы можете посмотреть, как изменяется погрешность, в зависимости от размера доходности индекса и инфляции в стране. Обратите внимание на 1998 – 1999 года.

Удачных инвестиций!

Наверно все знают, что реальная доходность — это доходность за вычетом инфляции. Все дорожает — продукты, товары, услуги. По данным Росстата за последние 15 лет цены выросли в 5 раз. Это означает, что покупательная способность денег, просто лежавших все это время в тумбочке уменьшилась в 5 раз, раньше могли купить 5 яблок, теперь 1.

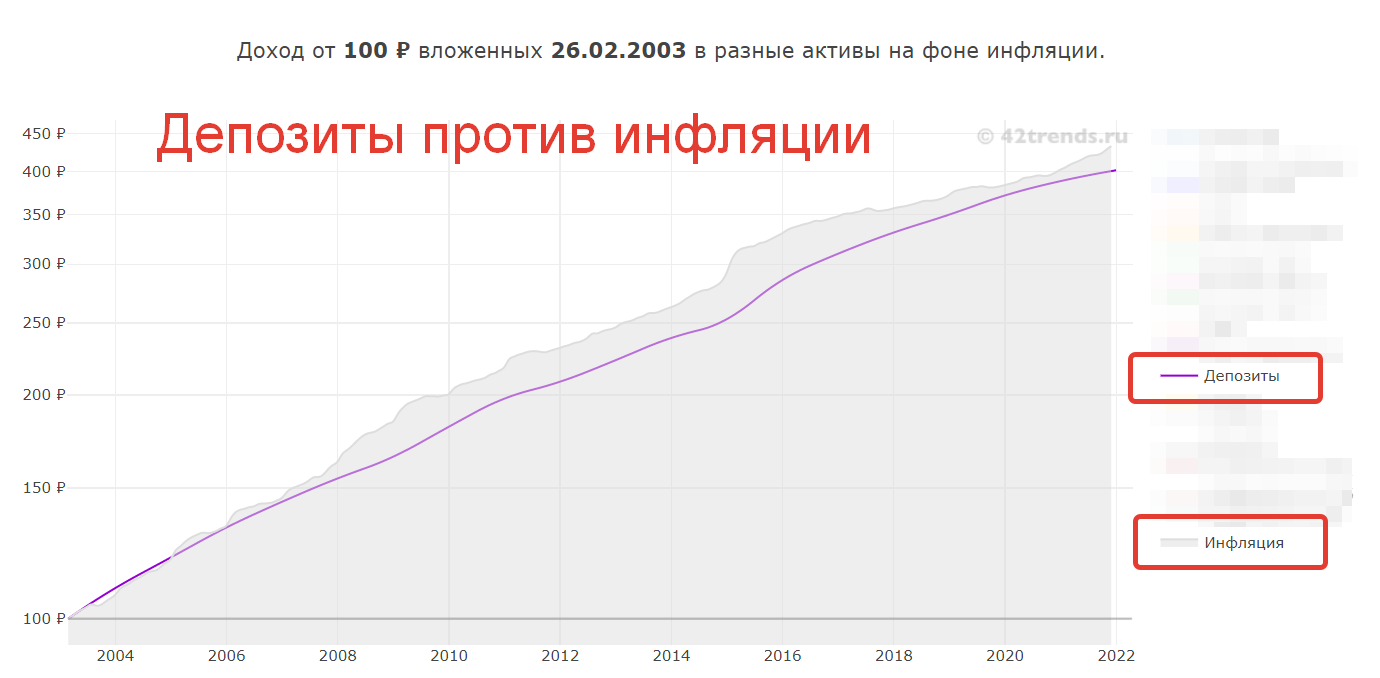
Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.

Большинство инвесторов считают реальную доходность по простой формуле:

Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.

За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:

Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция

Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.

Еще одна формула, которая дает тот же результат, выглядит так:

Поделиться в соцсетях

Подписаться на Telegram