Как найти сумму сходящегося числового ряда

35

Вычисление
суммы сходящегося числового ряда.

Прежде чем приступить к решению задач
дадим основные определения.

Определение 1.Пусть—
последовательность действительных
чисел. Выражение вида:

называется числовым рядом.

Сумму
первых
слагаемых называют
-ой
частичной суммойряда и обозначают:

К примеру,

Частичные суммы ряда
образуют бесконечную числовую
последовательность.

Выражение само по себе определенного смысла не
имеет, потому что действие сложения
производится над конечным числом
слагаемых. Этот смысл выражению предстоит
приписать нам самим.

Введем понятие суммы ряда.

Определение 2.Суммойчислового
ряданазывается предел последовательности
частичных сумм ряда,
если этот предел существует и конечен:

.

Числовой ряд при этом называется
сходящимся.

В противном случае, т.е. если
равен бесконечности или не существует,
то

ряд называется расходящимся.

Определение 3.Пусть дан ряд.

Ряд
,
полученный из исходного отбрасываниемпервых членов называется
-м
остатком ряда.

Можно доказать, что если
,
то ряд сходится (существует конечная
сумма)
и наоборот: остатоксходящегося
ряда стремится к нулю с увеличением
номера.

Основной целью теории числовых
рядов является установление факта
сходимости или расходимости тех или
иных рядов и вычисление суммы сходящихся
рядов. При этом найти точное значение
суммы ряда удается далеко не всегда. В
этом случае используются методы
приближенного вычисления суммы
ряда.
Существует довольно много
приемов, позволяющих устанавливать
сходимость или расходимость рядов.
Такие приемы называются признаками
сходимости. К рассмотрению некоторых
из них мы и приступаем.

Теорема (необходимый признак
сходимости числового ряда).

Если ряд
сходится,
то его общий член стремиться к нулю,
т.е.

.

Из необходимого признака следует,
что если
-ый
член ряда не стремиться к нулю, то ряд
расходиться. Именно это утверждение
удобно использовать для решения задач.

Отметим, что необходимый признак
не является достаточным, т.е. если
,
то о сходимости ряда ничего сказать
нельзя: он может быть как сходящимся,
так и расходящимся.

Задача №1.Исследовать ряд на
сходимость.

Решение.

.

Используя необходимый признак сходимости,
делаем вывод о том, что ряд расходиться,
поскольку
-ый
член ряда не стремиться к нулю.

Ответ: ряд
расходится.

.

Задача №2.Исследовать ряд на
сходимость.

Решение.Общий член ряда

,

.

Следовательно, ряд расходиться по
необходимому признаку. Здесь для
вычислений использовали первый
замечательный предел:
.

Ответ: ряд расходится.

Задача №3.Исследовать ряд на
сходимость.

Решение.

,

не существует. Ряд расходится по
необходимому признаку.

Ответ: ряд расходится.

Приведем пример ряда, для которого
необходимый признак не дает ответа о
его сходимости:

Задача №4. Исследовать ряд на
сходимость.

Решение.

.

Необходимый признак для данного ряда
выполняется, поэтому он может быть или
сходящимся, или расходящимся. Докажем,
что этот ряд на самом деле расходится.
Оценим частичную сумму ряда
снизу:

.

Таким образом,

и.

Тогда по определению суммы ряда имеем:

.

Ответ: ряд расходится.

Задача №5.Исследовать ряд на
сходимость.

Решение.Воспользуемся необходимым
признаком и найдем предел-го
члена ряда:

,

.

Ответ: ряд расходится.

В предыдущих задачах нашей целью
было установить сам факт существования
суммы ряда. Рассмотрим задачи, в которых
удается вычислить точное значение суммы
ряда.

Пусть дан числовой ряд
,
составленный из членов геометрической
прогрессии. Здесь—
первый член прогрессии,—
знаменатель прогрессии. Если знаменатель
прогрессии удовлетворяет условию,
то прогрессия называется бесконечно
убывающей, а ряд, составленный из членов
такой прогрессии, сходится, причем
сумма ряда равна:

.

Задача №6.Найти сумму ряда.

Решение.

Этот ряд составлен из членов бесконечно
убывающей геометрической прогрессии,
.

Сумма ряда равна:

.

Ответ:
.

Задача №7. Найти сумму ряда.

Решение.

.

Здесь первый член геометрической
прогрессии
,
знаменатель.
Тогда.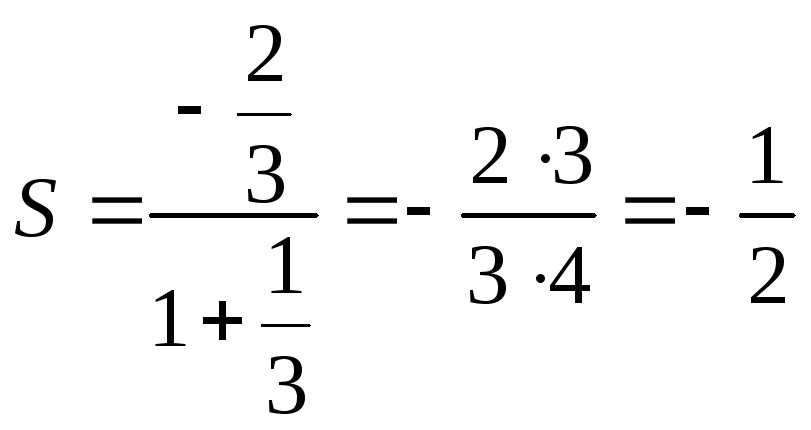

Ответ:
.

Задача №8.Найти сумму ряда.

Решение.

. Для этого ряда
.

Находим сумму:

.

Ответ:
.

Задача №9. Найти сумму ряда.

Решение.Для того чтобы найти сумму
этого ряда, представим общий член ряда
в виде суммы дробей:

.

Найдем неизвестные коэффициенты
следующим образом:

,

отсюда

.

При
из
последнего равенства получаем.

При
.

Таким образом

.

Найдем
-ую
частичную сумму ряда:

.

После сокращения противоположных
слагаемых получим

,

откуда

.

Ответ:
.

Соседние файлы в папке Ряды

• #
• #
• #

Содержание:

Числовые ряды:

При решении ряда математических задач, в том числе и в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых решается в теории рядов.

Основные понятия. Сходимость ряда

Определение. Числовым рядом называется бесконечная последовательность чисел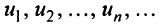

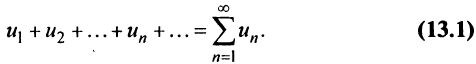
Числа 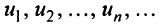называются членами ряда, а член 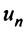— общим или 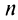-м членом ряда.

Ряд (13.1) считается заданным, если известен его общий член 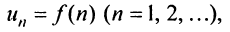т.е. задана функция 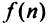натурального аргумента. Например, ряд с общим членом 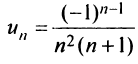имеет вид

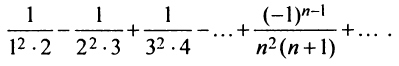
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение.

Пример:

Найти в простейшей форме общий член ряда:

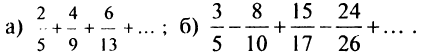
Решение:

Нетрудно убедиться, что для ряда а) общий член 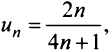а для ряда б)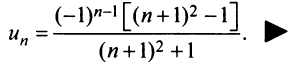

Рассмотрим суммы конечного числа членов ряда:

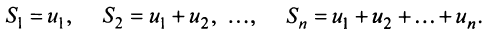
Сумма п первых членов ряда 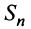называется 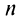-й частичной суммой ряда.

Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

Число 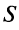называется суммой ряда. В этом смысле можно записать

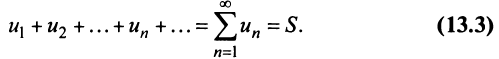
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Пример:

Исследовать сходимость геометрического ряда, т.е. ряда, составленного из членов геометрической профессии

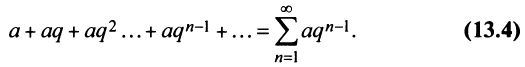
Решение:

Необходимо установить, при каких значениях знаменателя профессии 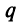ряд (13.4) сходится и при каких — расходится.

Из школьного курса алгебры известно, что сумма 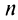первых членов геометрической профессии, т.е. 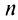-я частичная сумма ряда при 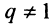равна

Возможно несколько случаев:

1) если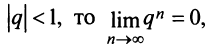

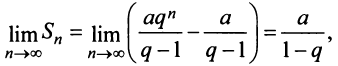т.е. ряд сходится и его сумма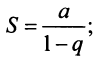

2) если 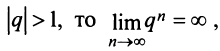следовательно, 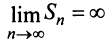и ряд расходится;

3) если 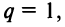то ряд (13.4) примет вид 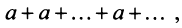его 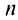-я частичная сумма 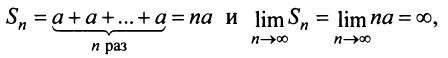т.е. ряд расходится;

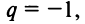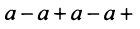
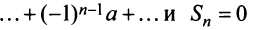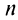4) если то ряд (13.4) примет вид при четном 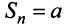и — при 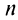нечетном, следовательно, 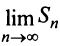не существует, и ряд расходится.

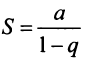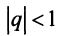Таким образом, геометрический ряд сходится к сумме при и расходится при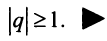

Пример:

Найти сумму ряда

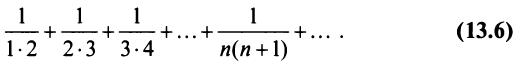
Решение:

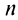-я частичная сумма ряда

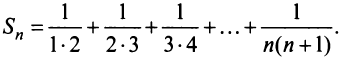Учитывая, что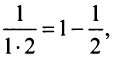

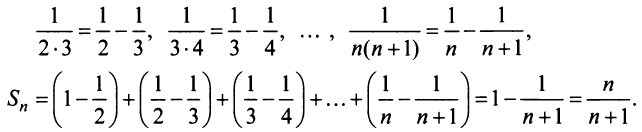Отсюда 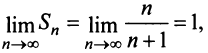т.е. сумма ряда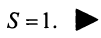

Свойства сходящихся рядов. 1. Если ряд сходится и имеет сумму 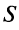, то и ряд 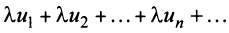(полученный умножением данного ряда на число 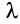) также сходится и имеет сумму .

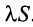2. Если ряды 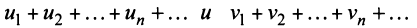сходятся и их суммы соответственно равны 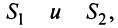то и ряд 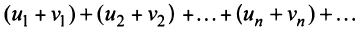(представляющий сумму данных рядов) также сходится, и его сумма равна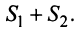

Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.

3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

Пусть в сходящемся ряде (13.1) отброшены 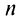членов (в принципе можно отбрасывать члены с любыми номерами, лишь бы их было конечное число). Покажем, что полученный ряд

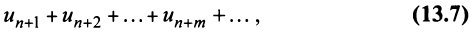
имеющий частичную сумму 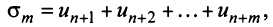также сходится.

Очевидно, что 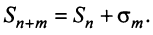Отсюда следует, что при фиксированном 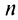конечный предел 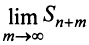существует тогда и только тогда, когда существует конечный предел 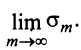. А это и означает, что ряд (13.7) сходится. ■

Ряд (13.7), полученный из данного отбрасыванием его первых 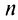членов, называется 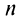-м остатком ряда.

Если сумму 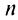-го остатка ряда обозначить через 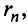т.е.

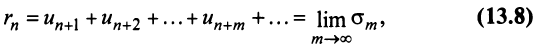
то сумму ряда (13.1) можно представить в виде

В результате мы подошли к свойству 4.

4. Для того чтобы ряд (13.1) сходился, необходимо и достаточно, чтобы при 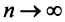остаток ряда стремился к нулю, т.е. чтобы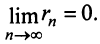

Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций (см. § 6.3).

Установить сходимость (расходимость) ряда путем определения 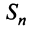и вычисления 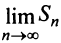(как это сделано в примерах 13.2, 13.3) возможно далеко не всегда из-за принципиальных трудностей при нахождении 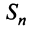(суммировании 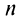членов ряда). Проще это можно сделать на основании признаков сходимости, к изучению которых мы переходим.

Необходимый признак сходимости. Гармонический ряд

Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 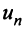при 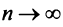равен нулю, т.е.

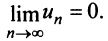
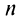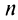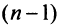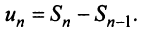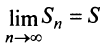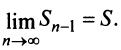Выразим -й член ряда через сумму его и членов, т.е. Так как ряд сходится, то и Поэтому

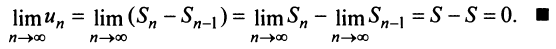
Пример №1

Проверить выполнение необходимого признака для ряда (13.6).

Решение:

Выше было доказано, что ряд (13.6) сходится, и действительно 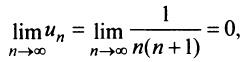т.е. необходимый признак сходимости выполняется. ►

Следствие. Если предел общего члена ряда (13.1) при 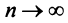не равен нулю, т.е. 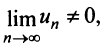то ряд расходится.

Предположим противное, т.е. ряд (13.1) сходится. Но в этом случае из приведенной выше теоремы следует 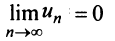, что противоречит условию, заданному в следствии, т.е. ряд (13.1) расходится. ■

Пример №2

Исследовать сходимость ряда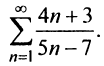

Решение:

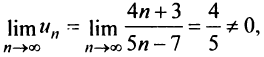т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится. ►

Замечание. Следует подчеркнуть, что рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если 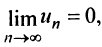то из этого еще не следует, что ряд сходится.

В качестве примера рассмотрим ряд

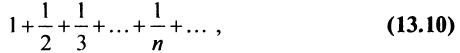
называемый гармоническим.

Необходимый признак сходимости выполнен: 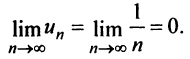Докажем, что, несмотря на это, гармонический ряд расходится.

Вначале получим вспомогательное неравенство. С этой целью запишем сумму первых 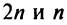членов ряда:

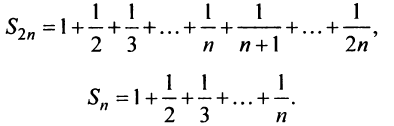
Найдем разность

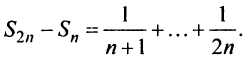
Заменяя в сумме каждое слагаемое наименьшим, равным 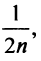придем к вспомогательному неравенству

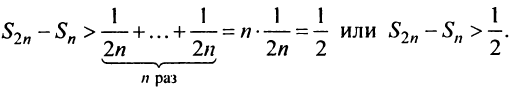
Предположим противное, т.е. что гармонический ряд сходится, тогда 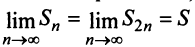и, переходя к пределу в неравенстве (см. § 6.5), получим, что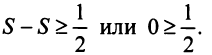

Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится. ■

В следующих двух параграфах рассмотрим достаточные признаки сходимости.

Ряды с положительными членами

Теорема (признак сравнения). Пусть даны два ряда с положительными членами: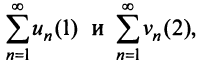 причем члены первого ряда не превосходят членов второго, т.е. при любом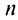

Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.

а) Пусть частичные суммы рядов 1 и 2 соответственно равны 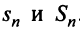. По условию ряд 2 сходится, следовательно, существует 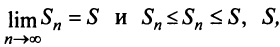так как члены ряда 2 положительны. Рассмотрим последовательность частичных сумм 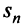ряда 1. Эта последовательность является: возрастающей (так как с ростом 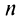увеличивается сумма 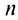положительных слагаемых) и ограниченной (так как 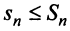в силу условия (13.11), т.е. ).

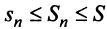Следовательно, на основании признака существования предела (см. § 6.5) последовательность 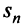имеет предел, т.е. ряд 1 сходится.

б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходится и ряд 1, что противоречит предположению; т.е. ряд 2 расходится. ■

Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие (13.11) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами 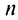. Достаточно, чтобы оно выполнялось, начиная с некоторого номера 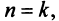или чтобы имело место неравенство 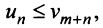где 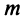— некоторое целое число.

Пример №3

Исследовать сходимость ряда

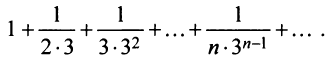
Решение:

Сравним данный ряд со сходящимся геометрическим рядом 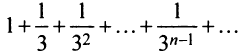(его знаменатель ).

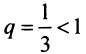Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 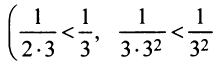и вообще 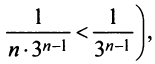то на основании признака сравнения ряд сходится. ►

Пример №4

Исследовать сходимость ряда

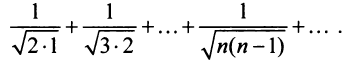
Решение:

Сравним данный ряд с гармоническим 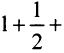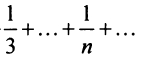, мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на расходимость ряда). Так как 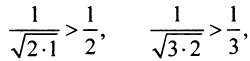и вообще 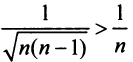(ибо 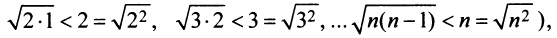т.е. члены данного ряда больше членов расходящегося гармонического ряда, то на основании признака сравнения ряд расходится. ►

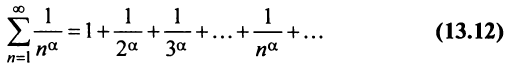
сходится при 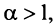расходится при 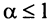здесь же отметим, что при 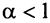расходимость ряда (13.12) следует из признака сравнения, так как в этом случае члены ряда 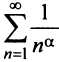больше соответствующих членов гармонического ряда 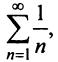а в частном случае при 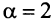сходимость ряда (13.12) может быть доказана сравнением этого ряда со сходящимся (13.6)).

Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (13.11), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п.). В ряде случаев более простым оказывается предельный признак сравнения.

Теорема (предельный признак сравнения)

Теорема (предельный признак сравнения). Если 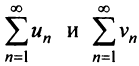— ряды с положительными членами и существует конечный предел отношения их общих членов 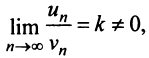то ряды одновременно сходятся либо расходятся.

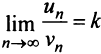Так как , то по определению предела числовой последовательности (см. § 6.1) для любого 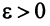существует такой номер 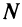, что для всех 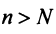выполняется неравенство

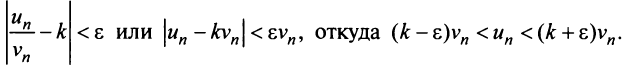
Если ряд 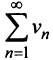сходится, то сходится ряд 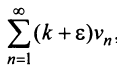и в силу признака сравнения будет сходиться ряд 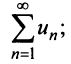аналогично, если сходится ряд 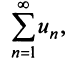сходится ряд 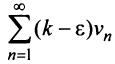и сходится 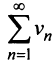. Таким образом, из сходимости одного ряда следует сходимость другого. Утверждение теоремы о расходимости рядов доказывается аналогично. 

Пример №5

Исследовать сходимость ряда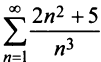

Решение:

Сравним данный ряд с расходящимся гармоническим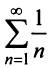 (выбор такого ряда для сравнения может подсказать то, что при больших 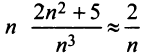). Так как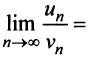 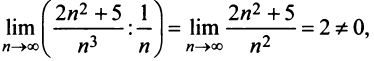то данный ряд, так же как и гармонический, расходится. ►

Весьма удобным на практике является признак Даламбера.

Теорема (признак Даламбера)

Теорема (признак Даламбера). Пусть для ряда 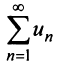с положительными членами существует предел отношения 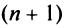-го члена к 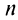-му члену 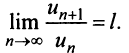Тогда, если 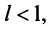то ряд сходится; если 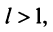то ряд расходится; если 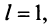то вопрос о сходимости ряда остается нерешенным.

 Из определения предела последовательности следует, что для любого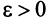 существует такой номер 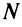, что для всех 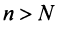выполняется неравенство 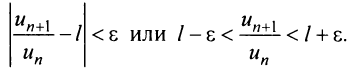1) Пусть 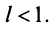Выберем 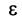настолько малым, что число

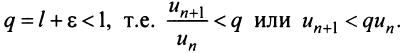
Последнее неравенство будет выполняться для всех 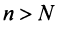, т.е. для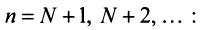

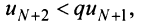
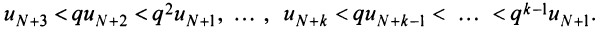
Получили, что члены ряда 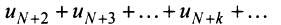меньше соответствующих членов геометрического ряда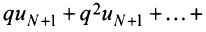 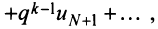сходящегося при 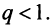Следовательно, на основании признака сравнения этот ряд сходится, а значит, сходится и рассматриваемый ряд 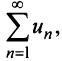отличающийся от полученного на первые 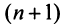членов.

2) Пусть 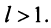Возьмем 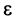настолько малым, что 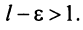Тогда из условия 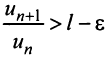следует, что 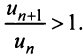Это означает, что члены ряда возрастают, начиная с номера 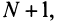поэтому предел общего члена ряда не равен нулю, т.е. не выполнен необходимый признак сходимости, и ряд расходится. ■

Пример №6

Исследовать сходимость рядов:

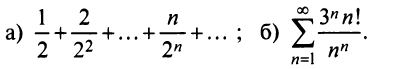
Решение:

а) Так как 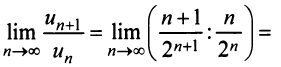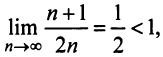то по признаку Даламбера ряд сходится.

б) Так как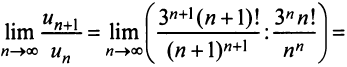

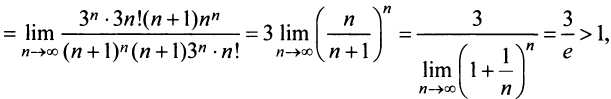то по признаку Даламбера ряд расходится. ►

Замечание 1. Если 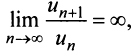то ряд расходится.

Замечание 2. Если 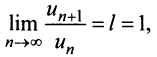то, как отмечалось выше, признак Даламбера ответа о сходимости ряда не дает, и рекомендуется перейти к другим признакам сходимости.

Теорема (интегральный признак сходимости)

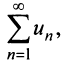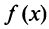Теорема (интегральный признак сходимости). Пусть дан ряд члены которого положительны и не возрастают, т.е.а функция , определенная при 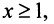непрерывная и невозрастающая и

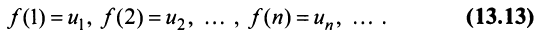
Тогда для сходимости ряда 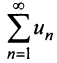необходимо и достаточно, чтобы сходился несобственный интеграл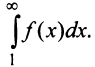

Рассмотрим ряд

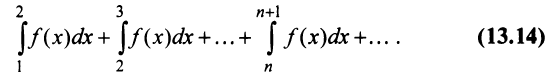
Его 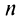-й частичной суммой будет

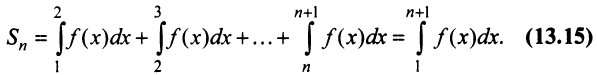
Сходимость ряда (13.14) означает существование предела последовательности его частичных сумм (13.15), т.е. сходимость несобственного интеграла 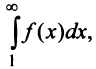поскольку 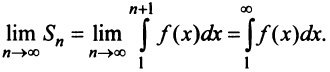В силу монотонности функции 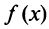на любом отрезке 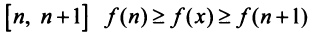или, учитывая (13.13),

Интегрируя (13.16) на отрезке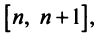 получим

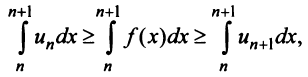
откуда

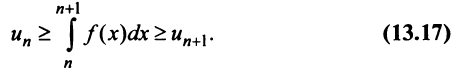
Если ряд 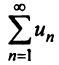сходится, то по признаку сравнения рядов в силу первого неравенства (13.17) должен сходиться ряд (13.14), а значит, и несобственный интеграл 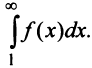Обратно, если сходится J/(jc)c&, т.е. ряд (13.14), то согласно тому же признаку сравнения на основании второго неравенства (13.17) будет сходиться ряд 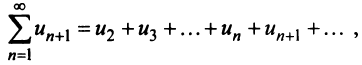а следовательно, и данный ряд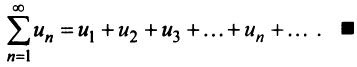

Пример №7

Исследовать сходимость обобщенного гармонического ряда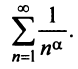

Решение:

Пусть 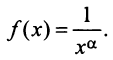Функция 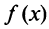при 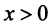(а значит, и при 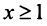) положительная и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла 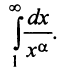Имеем 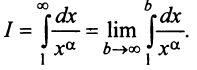Если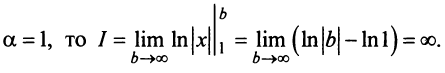

Если 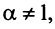то

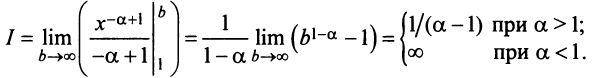Итак, данный ряд сходится при 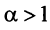и расходится при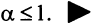

Ряды с членами произвольного знака

Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны

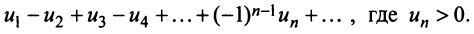
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 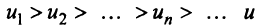и предел его общего члена при 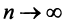равен нулю, т.е.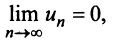то ряд сходится, а его сумма не превосходит первого члена: .

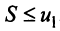 Рассмотрим последовательность частичных сумм четного числа членов при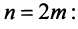

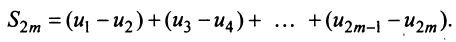
Эта последовательность возрастающая (так как с ростом 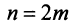увеличивается число положительных слагаемых в скобках) и ограниченная (это видно из того, что 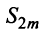можно представить в виде

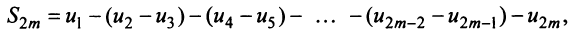
откуда следует, что 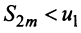). На основании признака существования предела (см. § 6.5) последовательность 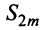имеет предел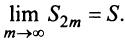

Попутно заметим, что, переходя к пределу в неравенстве 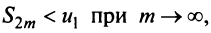получим, что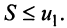

Теперь рассмотрим последовательность частичных сумм нечетного числа членов при 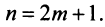Очевидно, что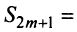 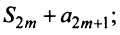поэтому, учитывая необходимый признак сходимости ряда,

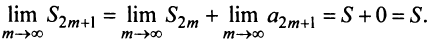
Итак, при любом 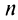(четном или нечетном) 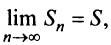т.е. ряд сходится. Рис. 13.1 иллюстрирует сходимость 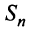к числу 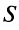слева при четном 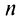и справа при нечетном . ■

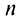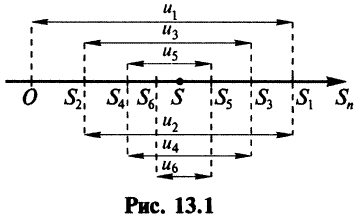
Из рис. 13.1 вытекает еще одна оценка для суммы 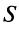сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница: при любом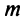

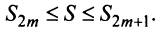
Пример №8

Исследовать сходимость ряда

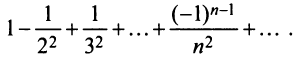
Решение:

Так как члены знакочередующегося ряда убывают по абсолютной величине 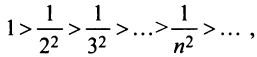и предел общего члена 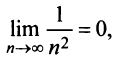то по признаку Лейбница ряд сходится. ►

Замечание. В теореме Лейбница существенно не только условие 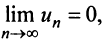но и условие 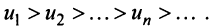Так, например, для ряда ,

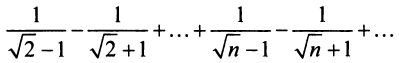второе условие нарушено и, хотя 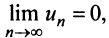ряд расходится. Это видно, если данный ряд представить (после попарного сложения его членов) в виде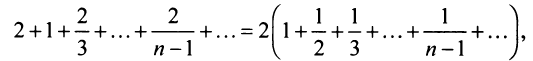

т.е. «удвоенного» гармонического ряда.

Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

По формуле (13.9) сумму сходящегося ряда можно представить как сумму 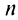членов ряда и суммы 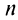-гo остатка ряда, т.е. 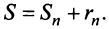Полагая приближенно 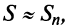мы допускаем погрешность, равную 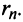Так как при четном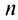 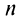-й остаток знакочередующегося ряда 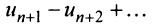представляет ряд, удовлетворяющий условиям теоремы Лейбница, то его сумма 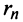не превосходит первого члена 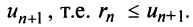Так как при нечетном 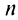для 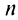-го остатка ряда 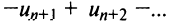его сумма 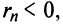то, очевидно, что при любом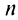

Пример №9

Какое число членов ряда 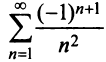надо взять, чтобы вычислить его сумму с точностью до 0,001?

Решение:

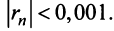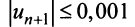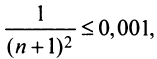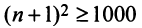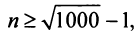По условию Учитывая следствие теоремы Лейбница (13.18), запишем более сильное неравенство или откуда и или 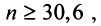т.е. необходимо взять не менее 31 члена ряда. ►

Знакопеременные ряды. Пусть знакопеременный ряд (13.1), в котором любой его член 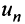может быть как положительным, так и отрицательным.

Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда (13.1)

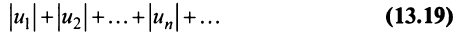
сходится, то сходится и данный ряд.

 Обозначим 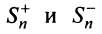суммы абсолютных величин членов данного ряда (13.1), входящих в него со знаком «плюс» и «минус».

Тогда частичная сумма данного ряда 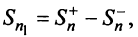а ряда, составленного из абсолютных величин его членов, 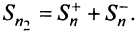По условию ряд (13.19) сходится, следовательно, существует конечный предел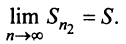

Последовательности 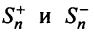являются возрастающими (так как с увеличением 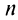увеличиваются 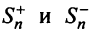) и ограниченными

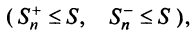значит, существуют пределы 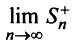и 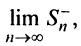и соответственно предел частичной суммы данного ряда

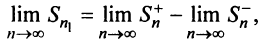т.е. ряд (13.1) сходится. ■

Следует отметить, что обратное утверждение неверно. Ряд (13.19) может расходиться, а ряд (13.1) сходиться. Например, ряд 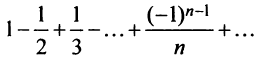сходится по признаку Лейбница, а ряд из абсолютных величин его членов 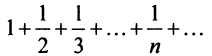(гармонический ряд) расходится.

Поэтому введем следующие определения.

Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Таким образом, рассмотренный выше ряд 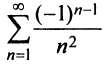— абсолютно сходящийся, а ряд 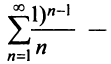условно сходящимся.

Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.

Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.

Условно сходящиеся ряды такими свойствами не обладают.

Возьмем, например, ряд 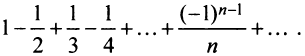Переставим члены местами и сгруппируем их следующим образом:

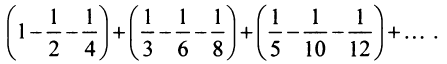
Перепишем ряд в виде:

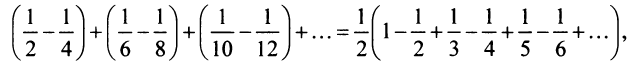
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.

Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.

Пример №10

Найти сумму ряда 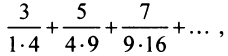доказав его сходимость.

Решение:

Очевидно, что общий член ряда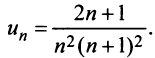

Представим сумму 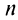членов ряда в виде 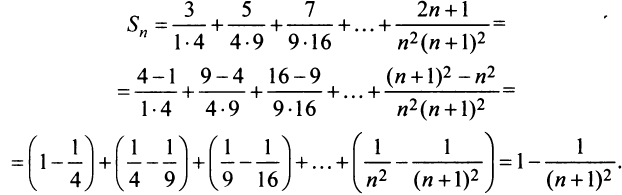Так как при 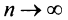последовательность 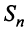имеет конечный предел, то ряд сходится, и его сумма

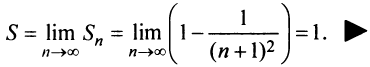
Пример №11

Исследовать сходимость ряда:

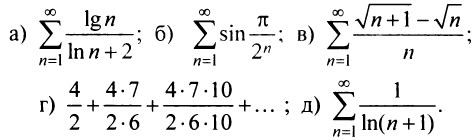
Решение:

а) Проверим выполнение необходимого признака сходимости, найдя предел общего члена:

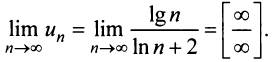
Для вычисления предела отношения двух бесконечно больших функций натурального аргумента правило Лопиталя непосредственно применять нельзя, ибо для таких функций не определено понятие производной. Поэтому применяя теорему о «погружении» дискретного аргумента 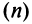в непрерывный 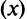, получим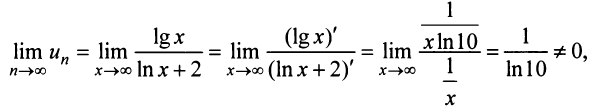

следовательно, ряд расходится.

б) Очевидно, что задан ряд с положительными членами, так как 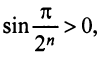ибо аргумент синуса 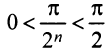при любом 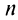. Так как члены данного ряда меньше членов сходящегося геометрического ряда со знаменателем

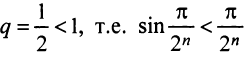(ибо при 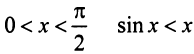), то данный ряд сходится.

в) Представим общий член ряда в виде

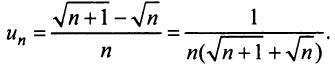Применим предельный признак сравнения, сравнив данный ряд со сходящимся «эталонным» рядом (13.12) при 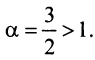Так как предел отношения общих членов двух рядов

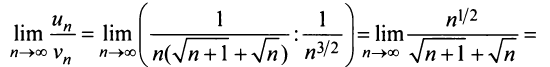
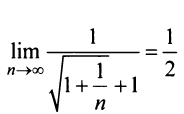
есть конечное число, не равное нулю, то данный ряд, так же как и «эталонный», сходится.

г) Применим признак Даламбера, заметив, что общий член ряда 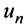имеет вид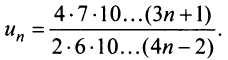

Тогда 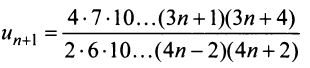и 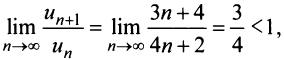т.е. данный ряд сходится.

д) Применим признак Даламбера:

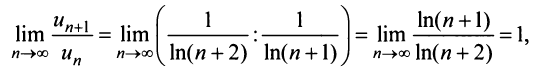
т.е. вопрос о сходимости ряда остается открытым. Проверим выполнение необходимого признака (с этого можно было начать исследование): 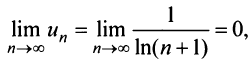т.е. необходимый признак выполнен, но вопрос о сходимости ряда по-прежнему не решен.

Применим признак сравнения в более простой предельной форме. Сравним данный ряд, например, с гармоническим.

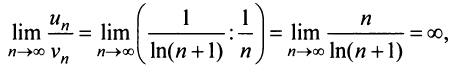т.е. ответа о сходимости ряда нет. Аналогичная картина ( 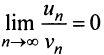или 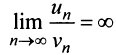) наблюдается и при использовании других «эталонных» рядов (см. § 13.3). Применим, наконец, признак сравнения в обычной форме. Сравним данный ряд с тем же гармоническим рядом, у которого отброшен первый член:

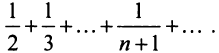Так как члены рассматриваемого ряда больше членов расходящегося гармонического ряда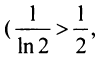 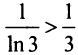и вообще

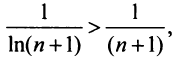что вытекает из очевидного неравенства 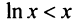), то данный ряд расходится. ►

Пример №12

Исследовать сходимость ряда:

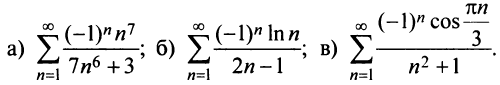
Решение:

а) Предел общего члена ряда 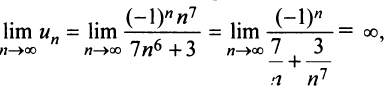так как знаменатель дроби стремится к нулю, а числитель колеблется, принимая значения 1 (при четном 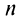) и —1 (при нечетном 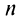). Следовательно, необходимый признак сходимости не выполнен, и ряд расходится.

б) Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине —

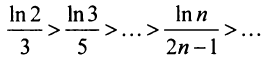
и предел общего члена 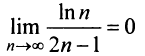(это можно установить, например, с помощью правила Лопиталя), то по признаку Лейбница ряд сходится. Ряд 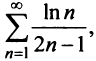составленный из абсолютных величин членов данного ряда, расходится, так как его члены больше членов расходящегося гармонического ряда, умноженного на 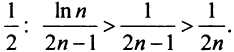Следовательно, данный ряд условно сходящийся.

в) Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося ряда (13.12) при 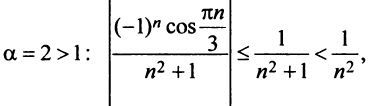следовательно, данный ряд сходится и притом абсолютно. ►

Определение ряда и его сходимость

Пусть

бесконечная последовательность чисел.

Определение 27.1.1. Выражение

называется числовым рядом, а элементы последовательности 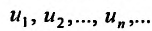членами ряда.

Поскольку выражение (27.1.2) рассматривается как единое целое, то для задания ряда необходимо задать каждый его член 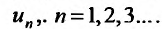Обычно член ряда задается как некоторая функция от своего номера. Аналитическое выражение этой функции называют общим членом ряда. Например, общим членом ряда геометрической прогрессии 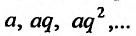является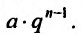

Припишем теперь определенный смысл выражению (27.1.2), т.е. введем определение.

Определение 27.1.2. Сумма n первых членов ряда (27.1.2) 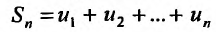называется n-ой частичной суммой этого ряда.

Ясно, что первая, вторая, третья и т.д. частичные суммы ряда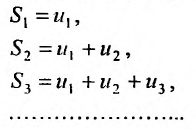

составляют бесконечную последовательность: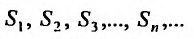

Определение 27.1.3. Ряд (27.1.2) называется сходящимся, если последовательность 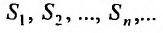его частичных сумм имеет конечный предел: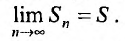

Значение S этого предела называется суммой ряда (27.1.2). Ряд (27.1.2) называется расходящимся, если последовательность его частичных сумм предела не имеет (например, если члены последовательности возрастают по модулю неограниченно).

Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов.

В принципе можно доказывать сходимость или расходимость каждого ряда, а также вычислять сумму сходящегося ряда, опираясь непосредственно на определения сходимости и суммы. Для этого в каждом случае составляется аналитическое выражение для n- ой частичной суммы ряда и находится предел этого выражения при возрастании n.

Пример:

Для ряда 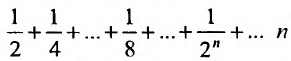-я частичная сумма 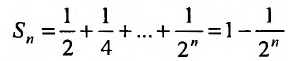, и предел ее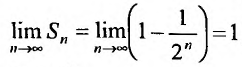, поэтому этот ряд сходится и его сумма равна 1.

Пример:

Последовательность вида

называется геометрической прогрессией, где а – первый член, а

q – её знаменатель; выражение 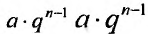называется общим членом геометрической прогрессии.

Числовой ряд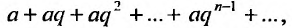 члены которого являются членами геометрической прогрессии, называется геометрическим рядом со знаменателем q .

Если в прогрессии (27.1.3) имеется только конечное число членов, то прогрессия называется конечной; в противном случае, если за каждым членом прогрессии следует ещё хотя бы один член, то прогрессия называется бесконечной.

В случае конечной прогрессии 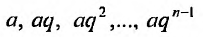можно говорить о сумме всех её членов 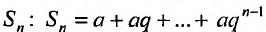, которую можно назвать n- ой частичной суммой геометрического ряда.

Известно, что при 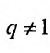, эта сумма равна 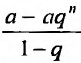. Из определения 27.1.3 следует, что суммой геометрического ряда

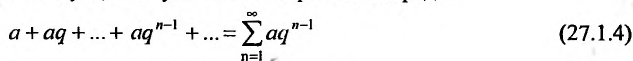
называется предел её частичных сумм 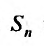при неограниченном возрастании n:

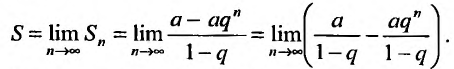
Так как а и q от n не зависят, то последнюю формулу представим в виде:

Если 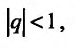то предел 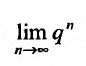равен нулю, и мы получаем

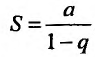, т.е. при 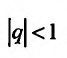прогрессия (27.1.5) сходится. Следователь-

но, сходится и ряд (27.1.4). Если же 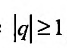, то предел справа в равенстве (27.1.5) не существует и, следовательно, ряд (27.1.4) расходится.

Итак, мы привели примеры, в которых исследование сходимости рядов проводили, применяя определение 27.1.3., т.е. вычисляли частичные суммы и находили предел их последовательностей. Ясно, что в общем случае, составление аналитического выражения для n- ой частичной суммы трудный вопрос. Кроме того, при исследовании рядов нередко значения сумм не представляют интереса, т.к. нужно определить только сходится ряд или нет. Поэтому представляют интерес методы анализа рядов, когда не требуется вычислять суммы рядов. Далее перейдем к изложению таких методов.

Свойства сходящихся рядов

Пусть дан ряд

Определение 27.2.1. Ряд 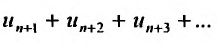называется n-м остатком ряда (27.2.1.)

Очевидно, m- я частичная суммаn -го остатка ряда равна разности 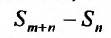частичных сумм самого ряда. Кроме того, 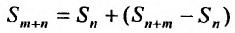, откуда, переходя к пределу по m при 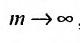, получим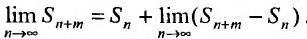

Предел слева есть сумма исходного ряда, а предел справа-сумма 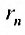его n – го остатка: 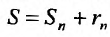. Ясно, что из существования предела в левой части равенства следует существование другого предела в правой части и наоборот. Поэтому если сходится один из остатков ряда, то сходится и сам ряд. Точно так же из сходимости ряда следует сходимость каждого его остатка. Кроме того, справедлива следующая теорема.

Теорема 27.2.1. Если ряд (27.2.1) сходится, то сумма его n-го остатка с ростом n стремится к нулю.

Доказательство. Выше показано, что 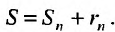. Так как это равенство справедливо для любого n, то мы можем перейти в нем по n к пределу: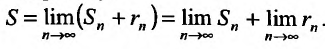

Но для сходящегося ряда 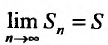, поэтому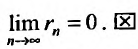

Рассмотрим теперь свойства сходящихся рядов, которые позволяют действовать с ними, как с конечными суммами.

Теорема 27.2.2. Если ряд

имеет сумму S, то ряд

полученный из предыдущего умножением всех членов на одно и тоже число a, имеет сумму aS.

Доказательство. Обозначим последовательность частичных сумм ряда (27.2.2) 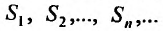Тогда последовательность частичных сумм ряда (27.2.3) очевидно будет иметь вид: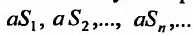. И поэтому 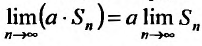. Так как ряд

(27.2.2) сходится, то 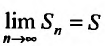существует и, следовательно, существует предел 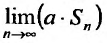ив силу этого же равенства он равен aS.

Теорема 27.2.3. Если ряды

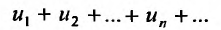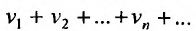и сходятся, а их суммы соответственно равны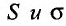, то и ряд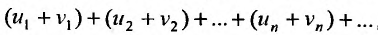называемый суммой данных рядов, также сходится и его сумма равна сумме сумм данных рядов 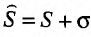, другими словами, сходящиеся ряды можно почленно складывать.

Доказательство. Пусть 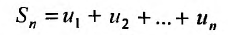и

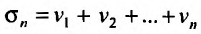. Тогда n -ая частичная сумм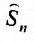а ряда

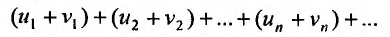будет равна 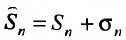и так как 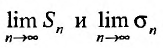существуют, то

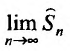существует и равен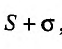, т.е.

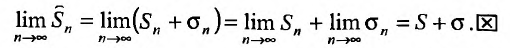
Следствие. Разность двух сходящихся рядов-ряд сходящийся.

Теорема 27.2.4. Свойства сходимости или расходимости ря-,ki не нарушается, если в ряде исключить или приписать к нему любое конечное число членов.

Доказательство. Пусть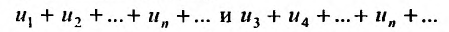 два ряда, причём второй получается из первого исключением первых двух членов. Тогда, если 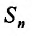– n-я частичная сумма первого ряда, а 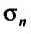– n-я частичная сумма второго ряда, то, очевидно, что

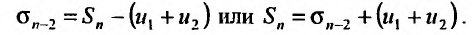
Из этого равенства следует, что, если 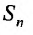имеет предел, то 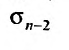также имеет предел. Ясно, что эти пределы будут различны, а, именно 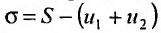Если же 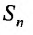не имеет предела, то 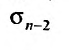также не имеет предела.

Теорема 27.2.5. (Необходимое условие сходимости ряда). Если ряд 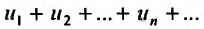сходится, то его общий член стремится к нулю, т.е.

Доказательство. Пусть ряд 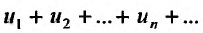сходится и его сумма равна S. Из определения n -ой частичной суммы следует, что общий член ряда можно представить в виде разности и-ой частичной суммы и (n-1)-ой частичной суммы: 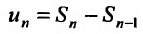. Переходя к пределу в этом равенстве, получим утверждение теоремы:

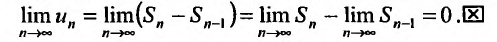
Отметим, что условие (27.2.4) не является достаточным, т.е. общий член может стремиться к нулю, но ряд все же может быть расходящимся. Но если общий член ряда не стремится к нулю, то ряд будет расходящийся.

• Заказать решение задач по высшей математике

Пример №13

Исследуем на сходимость гармонический ряд

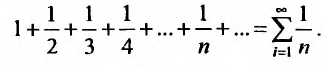
Решение:

Вначале находим предел общего члена: 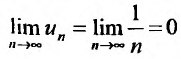. Нетрудно, однако, показать, что сумма n первых членов гармонического ряда беспредельно возрастает. Для этого сгруппируем слагаемые, начиная со второго, в группы из 1, 2, 4, 8,… членов: 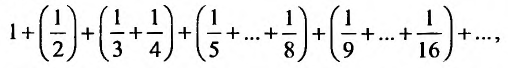так что в k – ой группе будет 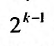членов. Fx л и в каждой групп заменим все члены последним, то получим ряд:

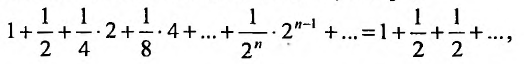сумма n первых членов которого, равна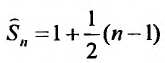, очевидно, стремится к :

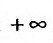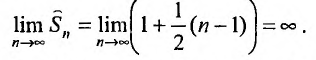Но сумма n первых членов заданного гармонического ряда больше суммы n первых членов преобразованного ряда, т.е. 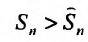. Тогда 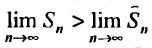, что означает, что 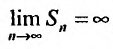следовательно, гармонический ряд расходится.

Пример №14

Найти формулу для общего члена ряда

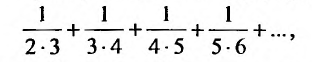
считая, что каждый его последующий член определяется по тому же закону, по которому образованы записанные члены, и найти ею сумму.

Решение:

Каждый член данного ряда представляет собой дробь, числитель которой равен 1, а знаменатель равен произведению двух последовательных натуральных чисел 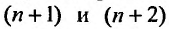. Следовательно, искомая формула общего члена ряда имеет вид:

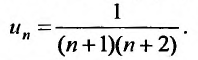
Для вычисления суммы ряда составим n -ую частичную сумму:

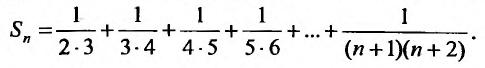
Представим выражение для общего члена в виде разности:

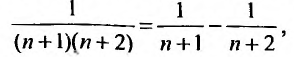
тогда

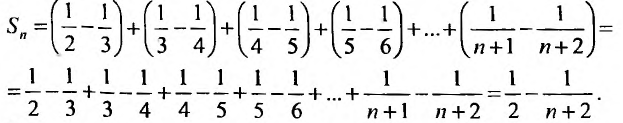
Переходя к пределу, получаем сумму ряда:

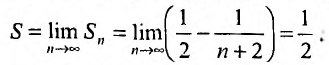
Пример №15

Исследовать сходимость ряда

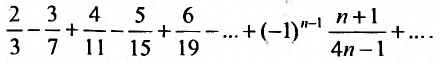
Решение:

Общий член ряда определяется формулой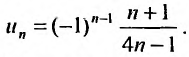

Вычислим предел модуля общего члена: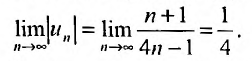

Так как предел общего члена не стремится к нулю, то ряд расходится.

Признаки сходимости числовых знакоположительных рядов

Рассмотрим числовые ряды с положительными членами. Существует много приёмов, называемых признаками сходимости, позволяющих установить сходимость или расходимость числовых рядов Так мы познакомились с методом исследования сходимости ряда на основании выяснения имеет ли предел последовательность частичных сумм. Стремление к нулю члена ряда по мерс роста его номера также является признаком сходимости, хотя только необходимым. Ниже мы приведём ряд достаточных признаков сходимости.

Признаки сравнения

Теорема 27.3.1. (I признак сравнения). Пусть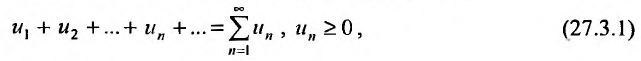

и

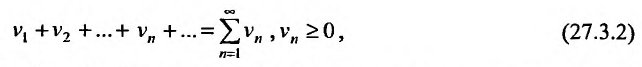
два ряда, причём члены первого ряда, начиная с некоторого номера k , не превосходят соответствующих членов второго

Тогда из сходимости ряда (27.3.2) следует сходимость ряда (27.3.1), а из расходимости ряда (27.3.1) следует расходимость ряда (27.3.2).

Доказательство. Так как исключение конечного числа членов ряда не влияет на его сходимость (теорема 27.2.4.), то достаточно доказать теорему для случая когда неравенства (27.3.3) выполняются для k = 1.

Пусть 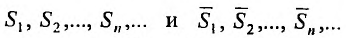последовательности частичных сумм рядов (27.3.1) и (27.3.2) соответственно. Это возрастающие последовательности, так как члены рядов неотрицательные числа. В силу неравенств (27.3.3), имеем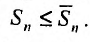

Пусть ряд (27.3.2) сходится. Тогда сходится соответствующая последовательность частичных сумм ряда (27.3.2), т.е.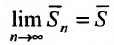

Поскольку выполняются неравенства (27.3.3), то члены последовательности частичных сумм ряда (27.3.1) удовлетворяют неравенству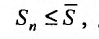 для всех т. Следовательно, последовательность 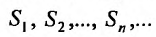возрастает и ограничена: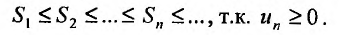

Поэтому, в силу признака Больцано-Всйсрштраса, последовательность частичных сумм ряда (27.3.1) сходится. По определению 27.1.3, сходится и ряд (27.3.1).

Пусть теперь ряд (27.3.1) расходится. Это значит, что его частичные суммы неограниченно возрастают. Но тогда, в силу неравенств (27.3.3), неограниченно возрастают и частичные суммы ряда (27.3.2), что означает, что этот ряд расходится. 

Пример №16

Пусть дан ряд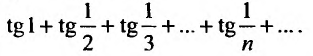

Исследуем его сходимость.

Решение:

Необходимый признак выполняется, т.е.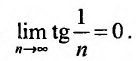

Для исследования сходимости заданного ряда применим 1 признак

сравнения (теорему 27.3.1). Сравним заданный ряд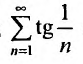с гармоничсским рядом 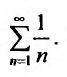. Так как выполняются неравенства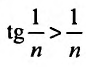то ряд 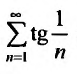расходится, потому что расходится гармонический ряд.

Пример №17

Исследовать сходимость ряда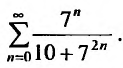

Решение:

Очевидно, что предел общего члена при возрастании т стремится к нулю.

Сравним данный ряд, общий член которого 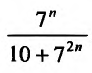с гармоническим рядом 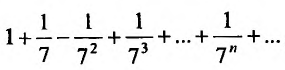который сходится, так как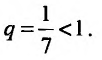

Поскольку 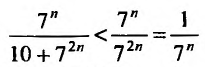для 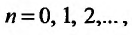т.е. выполняются неравенства (27.3.3), то на основании первого признака сравнения заключаем, что исследуемый ряд также сходится.

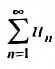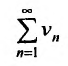Теорема 27.3.2. (II признак сравнения). Если для рядов и отношение общих членов 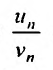стремится к некоторому положительному и конечному пределу:

то ряды 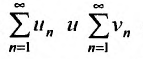сходятся или расходятся одновременно.

Доказательство. Предельное соотношение (27.3.4), в силу определения 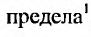означает, что, начиная с некоторою номера N ,

выполняется неравенство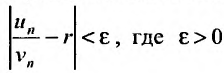. Это неравенство равносильно неравенству:

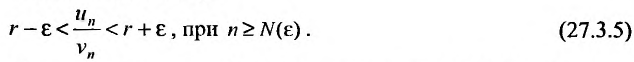
Обозначив 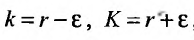, неравенство (27.3.5) запишется в виде:

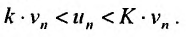
Предположим, что ряд 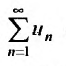сходится. Поскольку выполняется неравенство 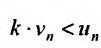то, из первого признака сравнения, следует сходимость ряда 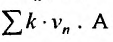в силу теоремы 27.2.2, и ряда 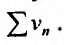. Если же ряд 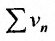расходится, то расходится и ряд 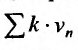по теореме 27.2.2. Тогда, поскольку выполняется неравенство 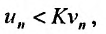, расходится и ряд 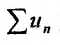в силу I признака сравнения. Аналогично рассуждая можно показать, что из сходимости ряда 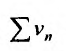следует сходимость ряда 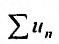по I признаку сравнения с использованием теоремы 27.2.2. 13

Последовательность 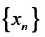называется сходящейся, если существует такое вещественное число а , что для любого положительного числа 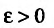найдется номер 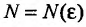такой, что для всех 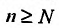выполняется неравенство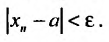

Пример №18

Исследовать сходимость ряда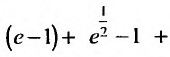

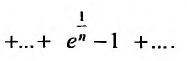
Решение:

Очевидно, что 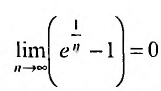. Поэтому, воспользуемся признаком сравнения, сравнив заданный ряд с гармоническим. Найдем предел отношения общих членов исследуемого ряда и гармонического:

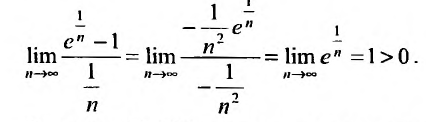
Теорема 27.3.2 выполняется, поэтому из расходимости гармонического ряда 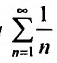следует расходимость исследуемого ряда.

Признаки Д’Аламбсра и Коши

Иногда вместо признаков сравнения оказываются полезными некоторые специальные признаки сходимости ряда. Отметим среди них признаки Д’Аламбсра и Коши, непосредственно получающиеся из признаков сравнения, если в качестве ряда сравнения взять соответствующим образом выбранную геометрическую прогрессию.

Теорема 27.3.3. (признак Д’Аламбера). Если для ряда

с положительными членами существует такой номер 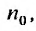, начиная с которого, т.е. при 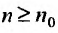, отношение последующего члена к предыдущему удовлетворяет неравенству: 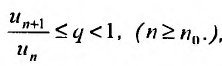, то ряд (27.3.6) сходится. Если же существует номер 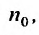, начиная с которого, т.е. при 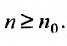отношение последующего члена к предыдущему больше единицы: 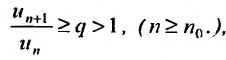то ряд (27.3.6) расходится.

Доказательство. Пусть 0 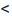q 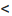1 и пусть существует такой номер 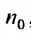, что при 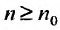. выполняется неравенство: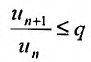Перепишем это неравенство в виде: 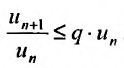. Тогда, начиная с номера 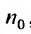буду последовательно выполнятся неравенства:

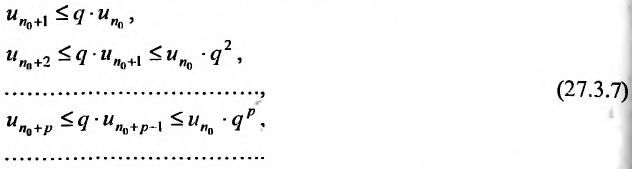
Ряд 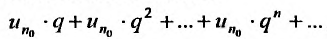, являясь суммой член геометрической прогрессии со знаменателем 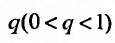, сходите Из неравенств (27.3.7) следует, что по I признаку сравнения, сходится и ряд 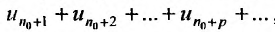значит и весь ряд (27.3.6

т.к. на сходимость ряда не влияет исключение конечного числа е^ членов.

Если же существует такое 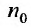, что выполняется неравенств 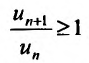для всех 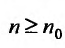, то, переписав его в виде 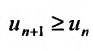, можно для всех 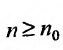, последовательно записать следующие неравенство

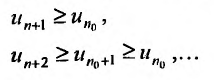
Так как по предположению 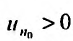, то n-ный член ряда будучи ограниченным снизу положительной постоянной не стремится к нулю. Следовательно, не выполняется необходимое условие сходимости ряда, и поэтому ряд (27.3.6) расходится.

Следствие 1. Пусть существует предел отношения последующего члена ряда (27.3.6) к предыдущему равный r :

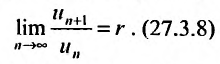
Тогда, если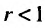 то ряд (27.3.6) сходится: если же 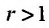то ряд (21.3.6) расходится.

Доказательство. Воспользовавшись определением предела, для фиксированного 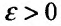, можно утверждать, что начиная с некоторого номера 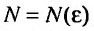, для всех 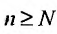, все отношения 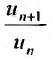будут отличатся от значения предела r на число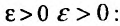

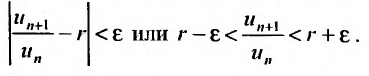
Рассмотрим правую часть двойного неравенства: 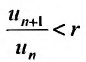. Тогда сославшись на доказанную теорему 27.3.3, в случае если r 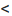1, получаем сходимость ряда. Рассматривая левую часть неравенства

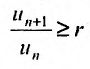, получаем расходимость ряда приr > 1. Следствие доказано.

Пример №19

Рассмотрим ряд 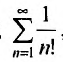, сходимость которого исследуем, используя признак Даламбера, т.е. следствие 1.

Решение:

Выпишем вначале значения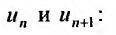

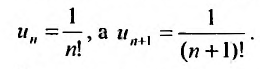
Затем вычислим предел отношения последующего члена ряда к предыдущему:

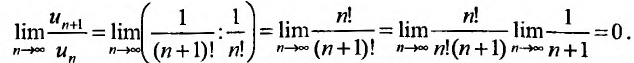
Так как этот предел меньше 1, то, в силу следствия 1, данный ряд сходится.

Заметим, что при исследовании сходимости ряда обычно (как правило, но не всегда) применяют следствие 1 из теоремы 27.3.3.

Теорема 27.3.4. (признак Kouiu). Если для ряда

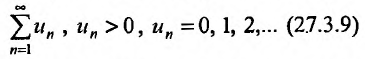
с положительными членами, начиная с некоторого номера 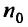. выполняется неравенство 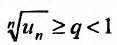для всех 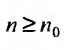, то ряд (27.3.6) сходится. Если же существует такой номер 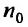, начиная с которого выполняется неравенство 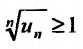для всех 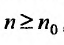, то данный ряд расходится.

Доказательство. Пусть существует такой номер 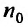, что при всех 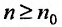выполняется неравенство 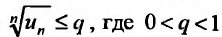Тогда, возводя обе части неравенства в степень n, получим 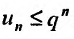. Так как сходится геометрический ряд 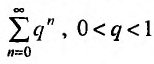, то на основании признака сравнения, получаем, что ряд 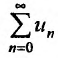сходится. Если же существует номер 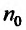, такой что 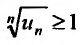для всех 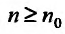, то ясно, что 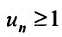, и значит 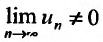(не выполняется необходимый признак сходимости), поэтому ряд 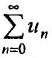расходится.

Следствие 2. Пусть существует предел корня n -ой степени из n-го члена ряда (27.3.9):

Тогда, если 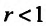, то ряд (27.3.9) сходится, если же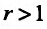, то ряд (27.3.9) расходится.

Доказательство. Из определения предела следует, что для фиксированного 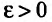существует номер 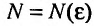, начиная с которого выполняется неравенство 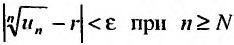Это неравенство равносильно неравенству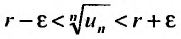. Из правой части неравенства следует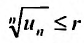, поскольку 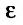сколь угодно малое число. Тогда из теоремы 27.3.4, получаем сходимость ряда (27.3.9). Рассматривая левую часть неравенства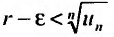, получим 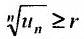и если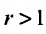, то из теоремы 27.3.4 следует расходимость ряда (27.3.9). Следствие доказано.

Пример №20

Рассмотрим ряд 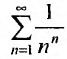, сходимость которого исследуем по признаку Коши, т.е. применим следствие 2.

Решение:

Выпишем значение n-го члена ряда 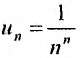н вычислим предел корня n -ой степени: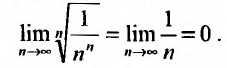

Так как этот предел меньше 1, то, согласно следствию 2, ряд сходится.

Замечание. Если пределы (27.3.8) и (27.3.10) равны 1, то для исследования сходимости ряда (27.3.9) нужно применять другие признаки, с которыми можно ознакомиться в [3].

Интегральный признак сходимости

Рассмотрим признак, достоинство которого состоит в исключительно высокой его чувствительности. Этим признаком проводится исследование сходимости там, где сформулированные признаки Д’Аламбсра и Коши «не работают».

Каждый член числового ряда 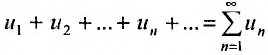можно рассматривать как значение функции f от его номера:

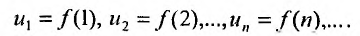
Эта функция определена пока только для целых положительных значений аргумента. Поэтому, доопределив значение функции f для всех нецелых значений аргумента, больших единицы, мы сможем, говорить о функции f(x), принимающей значения для любого 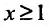и при х = n, равные членам числового ряда. Теорема 27.3.5. Пусть дан ряд

члены которого положительны и не возрастают 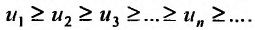Если функция f, определённая для всех 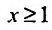, неотрицательна и монотонно убывает, то ряд (27.3.11) сходится или расходится тогда и только тогда, когда сходится или

расходится интеграл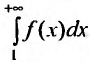

Доказательство. Пусть члены ряда (27.3.11) удовлетворяют условиям теоремы. Изобразим их графически, откладывая по оси Ох независимую переменную, а по оси Оу – соответствующие значения .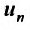

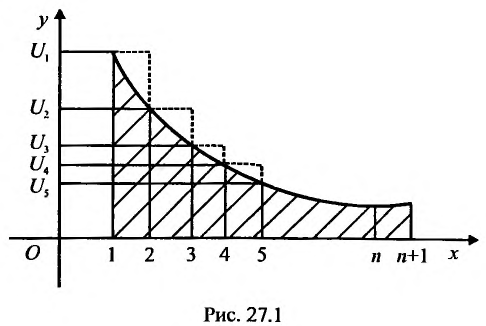
При таком графическом изображении сумма n первых членов ряда 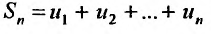представляет сумму площадей описанных прямоугольников, которая заключает внутри себя площадь, ограниченной кривой 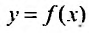, осью Ох и прямыми 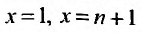и поэтому будет выполняться неравенство:

С другой стороны, криволинейная трапеция содержит сумму площадей вписанных прямоугольников, которая равна 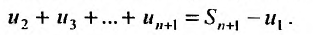Поэтому, выполняется неравенство:

Из (27.3.12) и (27.3.13) следует неравенство:

Предположим, что несобственный интеграл 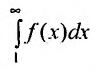сходится. Это означает, что 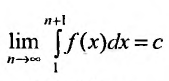является конечным числом. Тогда из неравенства (27.3.14) следует, что последовательность частичных сумм 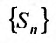возрастающая и ограничена при всех n. Тогда в силу теоремы: “возрастающая последовательность, ограниченная сверху, сходится”, числовой ряд (27.3.11) сходится. Если же несобствснный интеграл 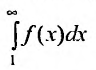расходится, т.е. 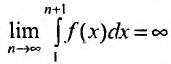, то из неравенства (27.3.12) следует, что последовательность частичных сумм 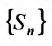не ограничена. Тогда в силу определения 27.1.3 ряд будет расходящимся.

Пример №21

Исследовать сходимость ряда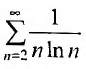

Решение:

Применим интегральный признак. Рассмотрим функцию 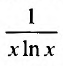которая положительна и убывает при х> 2, и исследуем сходимость несобственного интеграла:

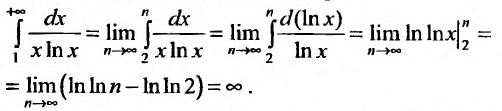
Так как несобственный интеграл расходится, то расходится и ряд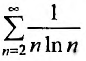 в силу инте1рального признака Коши.

Замечание. Исследовать сходимость данного ряда при помощи следствий 1 и 2 не представляется возможным, так как соответствующие пределы равны 1.

Пример №22

Исследовать сходимость ряда Дирихле

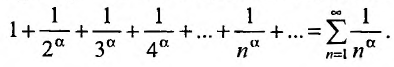
Решение:

Если 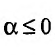, то общий член ряда 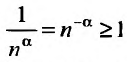не стремится к нулю. На основании следствия из необходимого признака сходимости, следует расходимость ряда Дирихле при .

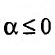Пусть а > 0, тогда необходимый признак, очевидно, выполняется. Применим интегральный признак Коши. Введем функцию

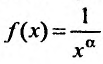, которая положительная и не возрастает при 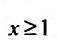и исследуем сходимость несобственного интеграла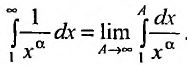

Вычислим определенный интеграл, записанный под знаком предела:

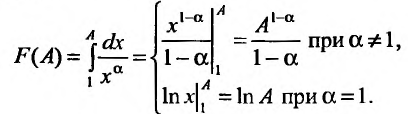
Если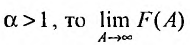 существует и равен 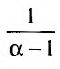а при 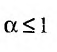указанный предел не существует.

Таким образом, при a>1 несобственный интеграл 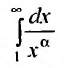сходится, следовательно, сходится и ряд Дирихле, а при 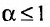несобственный интеграл расходится, следовательно, расходится и ряд Дирихле.

Ряд, называемый также бесконечная сумма — одно из центральных понятий математического анализа. В простейшем случае ряд записывается как бесконечная сумма чисел^[1]:

Краткая запись: (иногда нумерацию слагаемых начинают не с 1, а с 0)

Здесь  — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.

Чтобы присвоить числовому ряду значение суммы, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:

Если последовательность частичных сумм имеет предел (конечный или бесконечный), то говорят, что сумма ряда равна При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится^[1].

Для выяснения ключевого в анализе вопроса, сходится или нет заданный ряд, предложены многочисленные признаки сходимости.

Числовые ряды и их обобщения (см. ниже о нечисловых рядах) используются повсеместно в математическом анализе для вычислений, для анализа поведения разнообразных функций, при решении алгебраических или дифференциальных уравнений. Разложение функции в ряд можно рассматривать как обобщение задания вектора координатами, эта операция позволяет свести исследование сложной функции к анализу элементарных функций и облегчает численные расчёты^[2]. Ряды — незаменимый инструмент исследования не только в математике, но и в физике, астрономии, информатике, статистике, экономике и других науках.

Числовые ряды[править | править код]

Примеры[править | править код]

Простейшим примером сходящегося ряда является сумма членов бесконечной геометрической прогрессии^[3] со знаменателем :

Частичная сумма Предел этого выражения это и есть сумма бесконечной геометрической прогрессии^[1]. Например, при получается ряд, сумма которого равна 2:

Десятичную дробь с бесконечной дробной частью можно рассматривать как сумму ряда^[3]; например, число есть сумма следующего ряда:

Более сложным примером является ряд обратных квадратов, сумму которого лучшие математики Европы не могли найти более 100 лет^[4]:

Ряд расходится, сумма его бесконечна. Расходится и гармонический ряд: «Ряд Гранди» расходится, его частичные суммы колеблются от 1 до 0, поэтому предела частичных сумм не существует, суммы у этого ряда нет^[5].

Классификация[править | править код]

Положительный ряд^[6] — вещественный ряд, все члены которого неотрицательны. У положительных рядов сумма всегда существует, но может быть бесконечна^[7].

Знакочередующийся ряд — вещественный ряд, в котором знаки членов чередуются: плюс, минус, плюс, минус и т. д. Для таких рядов существует простой признак сходимости Лейбница. Знакочередующийся вариант приведенного выше гармонического ряда, в отличие от последнего, сходится^[8]:

Абсолютная и условная сходимость[править | править код]

Говорят, что вещественный или комплексный ряд сходится абсолютно, если сходится ряд из модулей (абсолютных величин) его членов^[8]:

Абсолютно сходящийся ряд сходится и в обычном смысле этого понятия. При этом всякий такой ряд обладает важным свойством переместительности: при любой перестановке членов абсолютно сходящегося ряда получается сходящийся ряд с той же суммой^[9]. В частности, у положительных сходящихся рядов можно как угодно переставлять члены ряда, на сходимость и на сумму это не влияет^[10].

Если числовой ряд сходится, но не абсолютно, он называется условно сходящимся. Пример:

Сам ряд сходится, но ряд его абсолютных величин (гармонический ряд) расходится^[8].

Свойства условно сходящихся рядов^[8].

• Если ряд сходится условно, то как ряд из его положительных членов, так и ряд из его отрицательных членов расходятся.
  • Следствие (критерий абсолютной сходимости): ряд из вещественных чисел сходится абсолютно тогда и только тогда, когда сходятся как ряд из положительных его членов, так и ряд из отрицательных членов.
• (теорема Римана): Перестановкой членов условно-сходящегося ряда можно получить ряд с любой заданной вещественной суммой.

Операции над рядами[править | править код]

Пусть заданы сходящиеся ряды и . Тогда:

Если оба ряда сходятся к и соответственно, то их сумма и разность также сходятся. Сумма сходящегося и расходящегося рядов всегда расходится^[11]:

,

Если оба ряда сходятся абсолютно, то сумма и разность этих рядов также сходятся абсолютно^[12].

• Их произведением Коши^[en] называется ряд , где:

Если хотя бы один из исходных рядов сходится абсолютно, то произведение рядов сходится^[13].

Необходимый признак сходимости числового ряда[править | править код]

Ряд может сходиться лишь в том случае, когда член (общий член ряда) с возрастанием его номера стремится к нулю^[14]:

Это необходимый признак сходимости ряда, но он не является достаточным — у гармонического ряда, например, общий член с ростом номера неограниченно уменьшается, тем не менее ряд расходится. Если же общий член ряда не стремится к нулю, то ряд заведомо расходится^[14].

Сходящиеся ряды[править | править код]

Свойство 1. Если ряд

(1.1)

сходится и его сумма равна , то ряд

(1.2)

где  — произвольное число, также сходится и его сумма равна . Если же ряд (1.1) расходится и , то ряд (1.2) расходится.

Свойство 2 (ассоциативный закон). В сходящемся ряде можно произвольно объединять соседние члены в группы без нарушения их порядка^[15].

Этим свойством можно воспользоваться для доказательства расходимости ряда: если после указанной группировки получается расходящийся ряд, то и исходный ряд также расходится.

Нерешённые проблемы[править | править код]

До сих пор неизвестно, сходится ли «ряд Флинт Хиллз» (Flint Hills Series)^[16]:

Если удастся доказать, что этот ряд сходится, то как следствие получится важный факт: мера иррациональности числа меньше, чем 2,5.

Известно, что сумма ряда обратных квадратов и суммы других рядов с обратными чётными степенями выражаются через степени числа но мало что известно про сумму обратных кубов («константу Апери»):

.

Никто пока не сумел связать это значение с классическими константами или элементарными функциями^[17].

Ряды с нечисловыми членами[править | править код]

Понятие бесконечного ряда и его суммы можно ввести не только для чисел, но и для других математических объектов, для которых определены сложение и понятие близости, позволяющее определить предел. Например, в анализе широко используются ряды из функций: степенные ряды, ряды Фурье, ряды Лорана. Членами ряда могут быть также векторы, матрицы и др.

Общее определение[править | править код]

Ряд (или бесконечная сумма) в математике — последовательность элементов (членов данного ряда) некоторого топологического векторного пространства, рассматриваемая вместе с множеством частичных сумм членов ряда (частичные суммы определяются так же, как и в числовых рядах). Если для последовательности частичных сумм определён предел: то значение называется суммой данного ряда, а сам ряд называется сходящимся (в противном случае — расходящимся)^[18].

Ряды всегда можно почленно складывать или вычитать, причём сумма и разность сходящихся рядов также сходятся. Если члены рядов берутся из кольца или поля, то ряды сами образуют кольцо относительно сложения и произведения Коши^[en].

Функциональные ряды[править | править код]

Определение и свойства[править | править код]

Ряд называется функциональным, если все его члены — функции, определённые на некотором множестве:

краткая запись:

Частичные суммы в этом случае также являются функциями, заданными на том же множестве. Ряд называется сходящимся на множестве , если при любом фиксированном сходится числовой ряд^[2]:

Множество называется областью сходимости ряда. Сумма ряда, очевидно, также является функцией на

Пример — разложение в ряд рациональной дроби:

Этот ряд сходится в интервале .

Среди основных типов функциональных рядов:

• степенные ряды (в частности, ряды Тейлора);
• тригонометрические ряды; в частности, ряды Фурье;
• ряды Лорана.

Кроме определённой выше «поточечной» сходимости, в разных пространствах могут быть использованы и другие нормы близости, от которых зависит существование предела частичных сумм. Например, можно определить «чебышёвскую норму»^[19].

Равномерная сходимость[править | править код]

Вообще говоря, свойства суммы могут отличаться от свойств членов ряда — например, сумма ряда непрерывных функций может не быть непрерывной^[20].

Говорят, что сходящийся на множестве функциональный ряд равномерно сходится (на этом множестве)^[21], если последовательность частичных сумм ряда равномерно сходится на .

Существуют несколько признаков, позволяющих убедиться в равномерной сходимости ряда^[21]:

• Признак Вейерштрасса
• Признак Абеля
• Признак Дирихле

Важность понятия равномерной сходимости ряда показывают следующие теоремы (все функции считаются вещественными).

сходятся на , причём ряд производных сходится равномерно, то сумма ряда имеет производную, и дифференцировать ряд можно почленно^[23]:

Условие равномерной сходимости гарантирует, что ряд справа сходится.

Пример неравномерно сходящегося степенного ряда — геометрическая прогрессия В промежутке она сходится к функции но не равномерно (о чём свидетельствует бесконечный скачок суммы при приближении к 1)^[25].

Ряды матриц[править | править код]

В кольце числовых квадратных матриц фиксированного порядка назовём -окрестностью матрицы множество матриц, все компоненты которых отличаются от соответствующих компонент меньше, чем на Опираясь на такую топологию, предел последовательности матриц определяется покомпонентно^[26], то есть матрица является пределом последовательности матриц , если каждая её компонента является пределом соответствующей последовательности

Теперь можно определить по общим правилам ряды из числовых матриц, понятие сходимости ряда (в том числе абсолютной сходимости) и суммы сходящегося ряда. Другими словами, ряд матриц порядка сходится, если сходятся рядов его компонент, и суммой будет матрица, содержащая соответствующие пределы этих рядов^[26].

Степенной ряд для матриц имеет вид^[26]:

где  — заданные числовые коэффициенты,  — единичная матрица,  — матрица неизвестных. Этот ряд равносилен системе из числовых рядов. Для оценки его сходимости составим обычный степенной ряд из комплексных чисел:

Пусть радиус сходимости этого ряда равен Тогда верны следующие теоремы^[26]:

Пример степенного ряда из матриц см. в статье Экспонента матрицы. С помощью рядов можно определить стандартные функции для квадратных матриц (например, синус).

Вариации и обобщения[править | править код]

Обобщением понятия ряда является понятие двойного ряда, члены которого нумеруются не одним, а двумя индексами^[27].

Обобщением понятия суммы ряда является понятие суммирующей функции ряда, выбор которой делает понятие суммы расходящегося (в классическом смысле) ряда приемлемым. Предложено множество вариантов такого обобщения: сходимость по Пуассону — Абелю, Борелю, Чезаро, Эйлеру, Ламберту и другие^[28].

История[править | править код]

Античный период[править | править код]

Античные математики, в соответствии с пифагорейской идеологией, отвергали все актуально бесконечные понятия, в том числе и бесконечные ряды. Тем не менее некоторые ограниченные применения понятия ряда имели место. Например, Архимед для вычисления площади сегмента параболы фактически нашёл сумму бесконечной геометрической прогрессии^[29]:

Ван дер Варден пишет об этом: «Архимед не говорит о сумме бесконечно убывающей геометрической прогрессии, ему ещё не известно выражение „сумма бесконечного ряда“, однако он прекрасно владеет сущностью этого понятия». В нескольких решённых Архимедом задачах на вычисление площади или объёма он использует, в современной терминологии, верхние и нижние интегральные суммы с неограниченно возрастающим числом членов. Из-за отсутствия понятия предела для обоснования результата использовался громоздкий метод исчерпывания^[29].

Керальская школа[править | править код]

Математики Индии, не связанные пифагорейскими ограничениями, существенно продвинули теорию рядов и успешно её применяли. Наибольшего успеха в XV—XVI веках добилась Керальская школа астрономии и математики (южная Индия). Для астрономических вычислений керальцы смогли впервые в истории найти разложение тригонометрических и иных функций в бесконечные ряды:

Общей теории таких разложения у них, впрочем, не было, для получения этих формул было проведено спрямление дуги окружности^[30][31]. В Европе аналогичный ряд для арктангенса впервые опубликовал Джеймс Грегори в 1671 году, а ряды для синуса и косинуса — Исаак Ньютон в 1666 году.

Из ряда для арктангенса керальцы получили хорошее приближение для числа :

В Европе достижения керальской школы долгое время оставались неизвестными и были переоткрыты независимо.

XVII век[править | править код]

До примерно XVII века бесконечные ряды в трудах европейских математиков появлялись редко. Заслуживает упоминания труд английского математика XIV века Ричарда Суайнсхеда, который просуммировал ряд^[32]:

В XVII веке бесконечные ряды уже вызывают общий интерес и начинают использоваться при решении многих практических задач — приближённые вычисления, интерполирование, теория логарифмов и др.

В 1647 году Грегуар де Сен-Венсан обнаружил связь логарифма и площади под гиперболой (см. рисунок). В 1650 году, исходя из геометрических соображений, итальянский математик Пьетро Менголи опубликовал в трактате «Новые арифметические квадратуры» разложение в бесконечный ряд^[33]:

Менголи исследовал также другие ряды и доказал, что гармонический ряд расходится; Менголи также показал, что ряд обратных квадратов сходится, хотя не смог найти его сумму^[33].

В 1668 году немецкий математик Николас Меркатор (Кауфман), проживавший тогда в Лондоне, в трактате «Logarithmotechnia» впервые рассмотрел разложение в ряд не числа, а функции, тем самым положив начало теории степенных рядов^[33]:

Как универсальный инструмент исследования функций и численных расчётов бесконечные ряды использовали Исаак Ньютон и Готфрид Вильгельм Лейбниц, создатели математического анализа. Ещё в середине XVII века Ньютон и Грегори открыли биномиальное разложение для любого, не только целого показателя степени (впервые опубликован в «Алгебре» Валлиса, 1685 год):

Ряд сходится при С помощью этой формулы Ньютон сумел впервые выполнить вычисление дуги эллипса в виде ряда (в современной терминологии, он вычислил эллиптический интеграл)^[34]. Ньютон также показал, как с помощью рядов решать уравнения, включая дифференциальные уравнения первого порядка, и исследовать интегралы, не выражающиеся через элементарные функции^[35].

К концу XVII века стали известны разложения в ряды всех элементарных функций. Лейбниц и Грегори открыли (1674) первое в Европе разложение числа (ряд Лейбница):

На рубеже веков (1689—1704) ученик Лейбница Якоб Бернулли опубликовал первую монографию в пяти томах под заголовком «Арифметические предложения о бесконечных рядах и их конечных суммах» (Propositiones arithmeticae de seriebus infinitis carumque summa finita). Он показал применение рядов для решения самых разнообразных задач.

XVIII—XIX века[править | править код]

В 1715 году Брук Тейлор опубликовал фундаментальный ряд Тейлора (давно известный, впрочем, Грегори и Ньютону).

Огромный вклад в теорию рядов внёс Леонард Эйлер. Он первым сумел найти сумму ряда обратных квадратов, разработал методы улучшения сходимости рядов, начал исследование тригонометрических рядов, предложил понятие обобщённой суммы ряда, пригодное для расходящихся рядов. Само понятие «аналитической функции» было связано с возможностью её представления в виде степенного ряда.

В XIX веке Коши и Вейерштрасс построили строгие основания анализа и, в частности, строгую теорию рядов. Было введено важное понятие равномерной сходимости, сформулированы разнообразные признаки сходимости.

Бурное развитие получили теория тригонометрических рядов. Ещё Даниил Бернулли высказал убеждение, что любую (непрерывную) функцию на заданном промежутке можно представить тригонометрическим рядом^[36]. Дискуссии на эту тему продолжались до 1807 года, когда Фурье опубликовал теорию представления произвольных кусочно-аналитических функций тригонометрическими рядами (окончательный вариант содержится в его «Аналитической теории тепла», 1822)^[37]. Для разложения функции в ряд Фурье привёл интегральные формулы расчёта коэффициентов^[37]. Изложение Фурье не было строгим в современном понимании, но уже содержало исследование сходимости большинства полученных им рядов.

Одновременно широкое развитие и применение в XIX веке получили ряды в комплексном анализе, в том числе ряды Лорана. Началось применение рядов в естественных науках — в небесной механике (для решения задачи трёх тел), в оптике, теории теплопроводности, ближе к концу века — в теории электромагнетизма.

В XX веке понятие ряда было распространено на широкий класс математических объектов, не обязательно числовых.

Примечания[править | править код]

Литература[править | править код]

• Виленкин Н. Я., Цукерман В. В., Доброхотова М. А., Сафонов А. Н. Ряды. — М.: Просвещение, 1982. — 160 с.
• Воробьев Н. Н. Теория рядов. — 4-е изд. — М.: Наука, 1979. — 408 с.
• Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — 872 с.
• Зорич В. А.. Глава III. Предел. § 1. Предел последовательности // Математический анализ, часть I. — М.: Наука, 1981. — С. 104—114. — 544 с.
• История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
• Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
• Письменный Д. Т. Часть 2 // Конспект лекций по высшей математике. — 6-е изд. — М.: Айрис-пресс, 2008.
• Ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 1063—1070.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — 6-е изд.. — М.: Наука, 1966. — Т. 2. — 680 с.

Ссылки[править | править код]

• Савельева Р. Ю. Высшая математика. Теория рядов.

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} – frac{1}{2} frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$

$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$

$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$

$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$

$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$

Выносим дробь одну вторую $ frac{1}{2} $ за скобки:

$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$

$$ + … frac{1}{2n-1} – frac{1}{2n+1} + frac{1}{2n+1} – frac{1}{2n+3} bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$

$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$