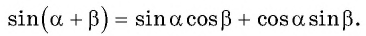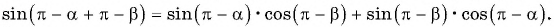Как найти сумму синусов острых углов – Сайт, где вы сможете решить свои вопросы

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Развёрнутый, прямой, острый и тупой углы

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается $a$ .

Угол A обозначается соответствующей греческой буквой $alpha$ .

Гипотенуза и катеты

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет $a$ , лежащий напротив угла $alpha$ , называется противолежащим (по отношению к углу $alpha$ ). Другой катет $b$ , который лежит на одной из сторон угла $alpha$ , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.$

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A $=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.$

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.$

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A $=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.$

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A $=genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.$

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin $displaystyle alpha = frac{a}{c}$	sin ${}^2 alpha +$ cos $displaystyle {}^2 alpha =1$	$alpha + beta = 90 ^{circ}$
cos $displaystyle alpha = frac{b}{c}$	1+tg $displaystyle {}^2 alpha =frac{1}{cos ^2 alpha}$	cos $alpha$ = sin $beta$
tg $displaystyle alpha = frac{a}{b}$	1+ctg $displaystyle {}^2 alpha =frac{1}{sin ^2 alpha}$	sin $alpha$ = cos $beta$
ctg $displaystyle alpha = frac{b}{a}$		tg $alpha$ = ctg $beta$

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна $180^{circ}$ . Значит, сумма двух острых углов прямоугольного треугольника равнa $90^{circ}$ .
С одной стороны, $sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ как отношение противолежащего катета к гипотенузе. С другой стороны, $cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ , поскольку для угла $beta$ катет а будет прилежащим. Получаем, что $cos beta =sin alpha$ . Иными словами, $cos left( 90^{circ}-A right) = sin A$ .
Возьмем теорему Пифагора: $a^2+b^2=c^2$ . Поделим обе части на $c^2,$ получаем $displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 ,$ то есть $sin ^2 A+cos^2 A=1.$
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на $cos^2 A$ , получим: $1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }.$ Это значит, что если нам дан тангенс острого угла $alpha$ , то мы сразу можем найти его косинус. Аналогично, $1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.$

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна $180^{circ}$ .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: $a^2+b^2=c^2$ .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от $0^{circ}$ до $90^{circ}$ .

$varphi$	0	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}$
sin $varphi$	0	$displaystyle frac{1}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{sqrt{3}}{2}$	$1$
cos $varphi$	$1$	$displaystyle frac{sqrt{3}}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{1}{2}$	0
tg $varphi$	0	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	$1$	$sqrt{3}$	−
ctg $varphi$	−	$sqrt{3}$	$1$	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и $A_1B_1C_1$ — два прямоугольных треугольника с прямыми углами С и $C_1$ и равными острыми углами А и $A_1.$

Треугольники АВС и $A_1B_1C_1$ подобны по первому признаку подобия треугольников, поэтому $displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .$

Из этих равенств следует, что $displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} ,$ т. е. sin А = sin $A_1.$

Аналогично, $displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1},$ т. е. cos А = cos $A_1,$ и $displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1},$ т. е. tg A = tg $A_1.$

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен $90^{circ}$ , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку $A+B = 90^{circ}$ , sin A = cos B = 0,1.

Задача 2. В треугольнике $ABC$ угол $C$ равен $90^{circ}$ , $AB=5$ , $sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}$ .

Найдите $AC$ .

Решение:

$sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.$

Отсюда

$BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.$

Найдем AC по теореме Пифагора.

$AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.$

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен $90^circ ,$ AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против $angle C.$ Значит, sin A $displaystyle = frac{BC}{AB}= frac{5}{13}.$

Катет, прилежащий к $angle A$ – это катет АС, следовательно, cos⁡ А $displaystyle = frac{AC}{AB}=frac{AC}{13}.$

Длину катета АС найдем по теореме Пифагора: $AC^2+BC^2=AB^2.$

Тогда $AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.$

cos⁡ А $displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;$

tg A $displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.$

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен $90^circ ,$ AC = 2, sin A= $displaystyle frac{sqrt{17}}{17} .$

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A $displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17},$ $displaystyle frac{a}{c} = frac{sqrt{17}}{17} ,$ $displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.$

По теореме Пифагора $a^2+b^2=c^2,$ получим

$a^2+2^2=(sqrt{17} a)^2;$

$a^2+4=17a^2;$

$16a^2=4,$ $displaystyle a= frac{1}{2}=0,5;$

$BC = 0,5.$

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен $90^circ ,$ $AC = 4,$ tg A = $displaystyle frac{33}{4sqrt{33}} .$ Найдите AB.

Решение:

AC = b = 4, tg A $displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},$

$displaystyle frac{a}{4}=frac{33}{4sqrt{33}},$ $displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},$

$AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.$

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен $90^ circ,$ CH – высота, AB = 13, tg A = $displaystyle frac{1}{5} .$ Найдите AH.

Решение:

AВ = с = 13, tg A = $displaystyle frac{a}{b}=frac{1}{5} ,$ тогда b = 5a.

По теореме Пифагора $triangle$ ABC: $a^2+b^2=c^2,$

$a^2+(5a)^2=13^2,$

$26 a^2=169,$

$displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}},$ тогда $displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.$

$triangle AHC approx triangle ACB$ (по двум углам), следовательно $displaystyle frac{AH}{AC}=frac{AC}{AB} ,$ откуда

$displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.$

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен $90^circ,$

CH – высота, BC = 3, sin A = $displaystyle frac{1}{6} .$

Найдите AH.

Решение:

Так как sin A = $displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6},$ тогда $displaystyle frac{3}{c} = frac{1}{6} ,$ c = АВ = 18.

sin A = $displaystyle frac{a}{c}$ = cos⁡ B = $displaystyle frac{1}{6} .$

Рассмотрим $triangle$ BHC:

${cos B= }displaystyle frac{BH}{BC}$ = $displaystyle frac{1}{6} ,$ получим $displaystyle frac{BH}{3}=displaystyle frac{1}{6},$

тогда BH = $displaystyle frac{3}{6}=displaystyle frac{1}{2}$ = 0,5,

AH = AB – BH = 18 – 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BC = 3, cos A = $displaystyle frac{sqrt{35}}{6}.$

Найдите АH.

Решение:

Так как для $triangle$ АВС: $cos$ A = $displaystyle frac{AC}{AB}=$ sin В = $displaystyle frac{sqrt{35}}{6},$

а для $triangle$ ВНС: sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{sqrt{35}}{6}$ , откуда СН = $displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},$

По теореме Пифагора найдем ВН:

$BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=$

$=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.$

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для $triangle$ АВС получим:

${CH}^2=AH cdot BH,$ тогда $AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.$

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = ${cos B}.$

Рассмотрим $triangle$ BHC : ${cos B= }displaystyle frac{BH}{BC}.$

ВС найдем по теореме Пифагора:

ВС= $sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,$

тогда ${cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28,$ а значит и sin A = ${cos B }$ = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = $;$ cos A = $displaystyle frac{b}{c}$ = $displaystyle frac{AC}{AB}$ = ${sin B },$

тогда tg A = $displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB,$ который найдем из $triangle$ BHC:

$ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.$

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, tg A = $displaystyle frac{2}{3}.$ Найдите АН.

Решение:

По определению tg A= $displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.$

Для $triangle$ BHC: $ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3}$ , значит $displaystyle frac{12}{CH}=displaystyle frac{2}{3},$ СН = $displaystyle frac{12 cdot 3}{2}=18.$

Для $triangle$ АHC: tg A= $displaystyle frac{CH}{AH}=displaystyle frac{2}{3},$ то $displaystyle frac{18}{AH}=displaystyle frac{2}{3},$ AH = $displaystyle frac{18 cdot 3}{2}=27.$

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, sin A = $displaystyle frac{2}{3}.$ Найдите АВ.

Решение:

Так как cos В = $displaystyle frac{BC}{AB}$ = sin A = $displaystyle frac{2}{3}.$

Из $triangle$ СВН имеем cos В = $displaystyle frac{HB}{BC}$ = $displaystyle frac{2}{3},$ тогда ВС = $displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.$

В $triangle$ АВС имеем sinA = $displaystyle frac{BC}{AB}$ = $displaystyle frac{2}{3},$ тогда AВ = $displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.$

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 ${}^circ,$ из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из $triangle$ ВСН:

$HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=$

$sqrt{8 cdot 32}= sqrt{8 cdot 2 cdot 16}=16.$

sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{12}{20}=displaystyle frac{3}{5}.$

Для $triangle$ АВС: cos A = $displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5},$ получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = $displaystyle frac{AC}{AB}=displaystyle frac{3}{5},$ то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора ${AC}^2+{BC}^2= {AB}^2,$ получим ${(3x)}^2+{(20)}^2= {(5x)}^2$
${25x}^2-{9x}^2= {20}^2 ,$

${16x}^2= {20}^2,$

$x^2= {left(displaystyle frac{20}{4}right)}^2,$
х = 5 ( так как х $textgreater$ 0). Значит, $AC=15, AB=25.$

2-й способ. $\$

$triangle HBC approx triangle CBA$ (по двум углам), значит $displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB}$ или $displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,$

k = $displaystyle frac{16}{20}=displaystyle frac{4}{5} ,$ тогда $displaystyle frac{12}{AC}=displaystyle frac{4}{5},$ АС = $displaystyle frac{12 cdot 5}{4}=15$ ; $displaystyle frac{20}{AB}=displaystyle frac{4}{5},$ АВ = $displaystyle frac{20 cdot 5}{4}=25.$

3-й способ.

${CH}^2=AH cdot HB$ (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда ${12}^2=AH cdot 16,$ АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)}$ = $sqrt{5cdot 45}=sqrt{5cdot 5cdot 9}=15.$

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного $triangle$ ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = $sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}$ = $sqrt{900}=30;$

cos C = $displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.$

Для $triangle$ АВС: sin А = $displaystyle frac{BC}{AC}$ = cos C = $displaystyle frac{3}{5}.$

Для $triangle$ АНВ: sin А = $displaystyle frac{BH}{AB}$ = $displaystyle frac{3}{5},$ то $displaystyle frac{24}{AB}$ = $displaystyle frac{3}{5},$ АВ = $displaystyle frac{24 cdot 5}{3}=40.$

Из основного тригонометрического тождества найдем

cos A = $sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.$

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = $displaystyle frac{7}{25}.$

Найдите площадь треугольника.

Решение:

В прямоугольном $triangle$ АСЕ sin А = $displaystyle frac{CE}{AC},$

значит $CE=AC cdot sinA=50 cdot$ $displaystyle frac{7}{25}$ = 14.

Второй катет найдем, используя теорему Пифагора: $AE= sqrt{{AC}^2-{CE}^2};$

$AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.$

Площадь прямоугольного треугольника равна S = $displaystyle frac{1}{2}ab,$

поэтому $S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.$

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin $angle ACK.$ Результат округлите до сотых.

Решение:

$triangle CAK approx triangle BAC ( angle$ A-общий, $angle AKC=angle ACB=90{}^circ$ ),

значит $angle ACK=angle ABC,$ sin $angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.$

Найдем АС по теореме Пифагора из $triangle$ САВ:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=$

$=sqrt{(13-12)(13+12)}=sqrt{25}= 5.$

Тогда sin $angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.$

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = $displaystyle frac{12}{13}.$ Найдите высоту СН.

Решение:

Так как АС = ВС, то $triangle$ АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = $displaystyle frac{1}{2}AB=36.$

Поскольку $triangle$ АСН — прямоугольный,

cos A = $displaystyle frac{AH}{AC}=$ $displaystyle frac{12}{13},$ то есть $displaystyle frac{36}{AC}=$ $displaystyle frac{12}{13}$ $Rightarrow$ АС = $displaystyle frac{36 cdot 13}{12}=39.$

По теореме Пифагора ${AH}^2+{CH}^2={AC}^2,$ тогда

$CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=$

$=sqrt{(39-36)(39+36)}=sqrt{3cdot 3cdot 25}=15.$

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 ${}^circ,$ sin A = $displaystyle frac{11}{14},$ AC = 10 $sqrt{3}.$ Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = $displaystyle frac{BC}{AB}=$ $displaystyle frac{11}{14},$ то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора $AC^2+{BC}^2={AB}^2;$

${(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;$

${(14x)}^2-{(11x)}^2 = 3 cdot 100;$

(14х- 11х)(14х + 11х) = 3 $cdot$ 100;

$3cdot 25 x^2 = 3 cdot 100.$

$x^2=4,$ учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 $cdot$ 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством ${sin}^2A+{cos}^2A=1;$

cos A = $sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.$

По определению cos A = $displaystyle frac{AC}{AB},$ значит $displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.$

Так как АС=10 $sqrt{3},$ то $displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14},$ откуда АВ = $displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}}$ = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 $sqrt{3}$ и 4.

Решение:

Пусть $angle$ ВАО = $alpha .$

Диагонали ромба делят его углы пополам, значит, $angle DAO=angle BAO$ = $alpha .$

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = $displaystyle frac{1}{2} AC=2sqrt{3},$ а катет ВО = $displaystyle frac{1}{2}BD =2.$

Поэтому tg $alpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}},$ откуда $alpha =30{}^circ .$

$angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .$

Ответ: ${60}^circ,$ ${120}^circ,$ ${60}^circ,$ ${120}^circ .$

Часто в задачах встречаются треугольники с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ или с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ . Основные соотношения для них запоминайте наизусть!

Прямоугольные треугольники с углами 30, 60, 90 и 45, 45, 90 градусов

Для треугольника с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ катет, лежащий напротив угла в $30^{circ}$ , равен половине гипотенузы.

Треугольник с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ — равнобедренный. В нем гипотенуза в $sqrt{2}$ раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 ${}^circ,$ угол А равен 30 ${}^circ,$ АВ = 2 $sqrt{3} .$

Найдите высоту CH.

Решение:

Рассмотрим $triangle$ АВС:

По свойству катета, лежащего против угла ${30}^circ,$ имеем ВС = $displaystyle frac{1}{2}$ АВ = $sqrt{3}.$

В $triangle$ BHC: $angle BHC=90{}^circ ,; angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно, ВН = $displaystyle frac{1}{2}$ BC = $displaystyle frac{sqrt{3}}{2}.$

По теореме Пифагора найдем НС:

$HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=$

$=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.$

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, АВ = 2, $angle A=30{}^circ .$ Найдите АH.

Решение:

Из $triangle$ АВС найдем ВС = $displaystyle frac{1}{2}$ АВ = 1 (по свойству катета, лежащего против угла 30 ${}^circ$ ),

$angle A=30{}^circ ,$ то $angle B=60{}^circ .$

Из $triangle$ ВСН: $angle BHC=90{}^circ , angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно,

ВН = $displaystyle frac{1}{2}$ ВС = $displaystyle frac{1}{2}.$

АН = АВ — НВ = 2 – $displaystyle frac{1}{2}$ = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α+β2 и α-β2. Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

sinα+sinβ=2sinα+β2cosα-β2sinα-sinβ=2sinα-β2cosα+β2

Формулы суммы и разности для косинусов

cosα+cosβ=2cosα+β2cosα-β2cosα-cosβ=-2sinα+β2cosα-β2, cosα-cosβ=2sinα+β2·β-α2

Данные формулы справедливы для любых углов α и β. Углы α+β2 и α-β2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.

Определения формул сумм и разности синусов и косинусов

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.

Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.

Вывод формул суммы и разности синусов и косинусов

Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже

sin(α+β)=sinα·cosβ+cosα·sinβsin(α-β)=sinα·cosβ-cosα·sinβcos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβ

Также представим сами углы в виде суммы полусумм и полуразностей.

α=α+β2+α-β2=α2+β2+α2-β2β=α+β2-α-β2=α2+β2-α2+β2

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sinα+sinβ заменим α и β на выражения для этих углов, приведенные выше. Получим

sinα+sinβ=sinα+β2+α-β2+sinα+β2-α-β2

Теперь к первому выражению применяем формулу сложения, а ко второму – формулу синуса разностей углов (см. формулы выше)

sinα+β2+α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2sinα+β2-α-β2=sinα+β2cosα-β2-cosα+β2sinα-β2sinα+β2+α-β2+sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2Раскроем скобки, приведем подобные слагаемые и получим искомую формулу

sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα+β2cosα-β2

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

sinα-sinβ=sinα+β2+α-β2-sinα+β2-α-β2sinα+β2+α-β2-sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2-sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα-β2cosα+β2

Вывод формулы суммы косинусов

cosα+cosβ=cosα+β2+α-β2+cosα+β2-α-β2cosα+β2+α-β2+cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2+cosα+β2cosα-β2+sinα+β2sinα-β2==2cosα+β2cosα-β2

Вывод формулы разности косинусов

cosα-cosβ=cosα+β2+α-β2-cosα+β2-α-β2cosα+β2+α-β2-cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2-cosα+β2cosα-β2+sinα+β2sinα-β2==-2sinα+β2sinα-β2

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α=π2, β=π6. Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α=π2, β=π6sinπ2+sinπ6=1+12=32sinπ2+sinπ6=2sinπ2+π62cosπ2-π62=2sinπ3cosπ6=2·32·32=32

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α=165°, β=75°. Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α=165°, β=75°sinα-sinβ=sin165°-sin75°sin165-sin75=2·sin165°-75°2cos165°+75°2==2·sin45°·cos120°=2·22·-12=22

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Содержание:

Известные значения синуса, косинуса, тангенса углов можно использовать для вычисления значений синуса, косинуса, тангенса других углов.

Угол 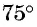Синус, косинус, тангенс суммы и разности с примерами решения

Выведем формулу 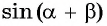Синус, косинус, тангенс суммы и разности с примерами решения — синуса суммы двух углов. Рассмотрим случай, когда 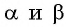— острые углы в треугольнике 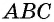(рис. 115).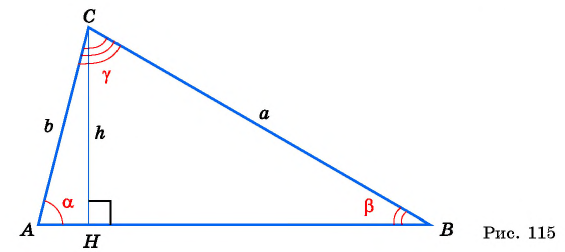

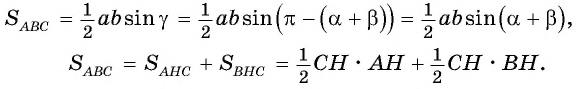
Выразим площадь треугольника Синус, косинус, тангенс суммы и разности с примерами решения дважды:

Синус, косинус, тангенс суммы и разности с примерами решения

Треугольник 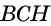Синус, косинус, тангенс суммы и разности с примерами решения — прямоугольный, тогда 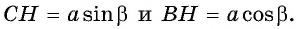Из прямоугольного треугольника 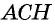имеем: 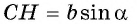и Тогда

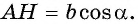Синус, косинус, тангенс суммы и разности с примерами решения

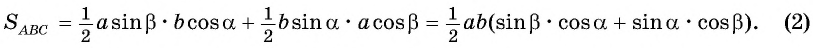
Приравняем правые части равенств (1) и (2):

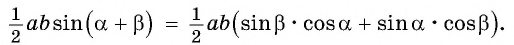
Синус, косинус, тангенс суммы и разности с примерами решения

Разделим обе части равенства на 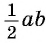Синус, косинус, тангенс суммы и разности с примерами решения и получим формулу синуса суммы двух углов:

Если углы 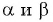Синус, косинус, тангенс суммы и разности с примерами решения не являются острыми, то можно воспользоваться свойством периодичности синуса и формулами приведения.

Например, если 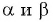Синус, косинус, тангенс суммы и разности с примерами решения являются углами второй четверти, то 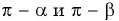— острые углы.

Применим к ним выведенную для острых углов формулу синуса суммы:

Воспользуемся формулами приведения в левой части равенства (3) и получим: 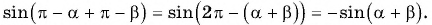Синус, косинус, тангенс суммы и разности с примерами решения

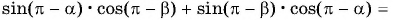
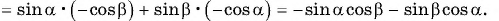
Применим формулы приведения к правой части равенства (3): Синус, косинус, тангенс суммы и разности с примерами решения

Таким образом,

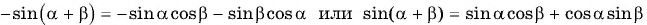Синус, косинус, тангенс суммы и разности с примерами решения — формула синуса суммы двух углов.

Остальные случаи принадлежности углов различным четвертям рассматриваются аналогично предыдущему.

Синус суммы

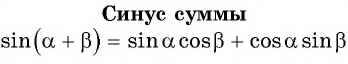
Синус, косинус, тангенс суммы и разности с примерами решения

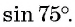
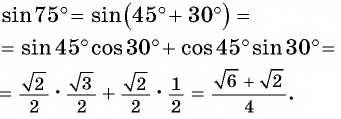
Воспользуемся полученной формулой Синус, косинус, тангенс суммы и разности с примерами решения

Синус, косинус, тангенс суммы и разности с примерами решения

Выведем формулу синуса разности двух углов.

Для этого Синус, косинус, тангенс суммы и разности с примерами решения представим в виде 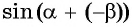и применим формулу синуса суммы двух углов:

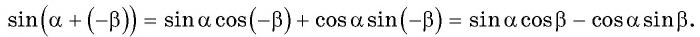
Синус, косинус, тангенс суммы и разности с примерами решения

Получили формулу синуса разности двух углов:

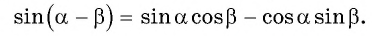
Синус, косинус, тангенс суммы и разности с примерами решения

Синус разности

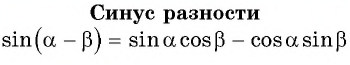
Синус, косинус, тангенс суммы и разности с примерами решения

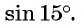
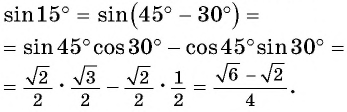
Вычислим, например, Синус, косинус, тангенс суммы и разности с примерами решения

Синус, косинус, тангенс суммы и разности с примерами решения

Для вывода формулы косинуса суммы двух углов воспользуемся формулами приведения и получим: 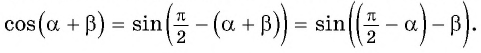Синус, косинус, тангенс суммы и разности с примерами решения

Тогда по формуле синуса разности двух углов имеем:

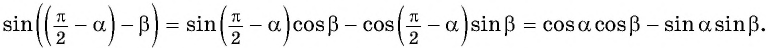
Синус, косинус, тангенс суммы и разности с примерами решения

Получили формулу косинуса суммы двух углов:

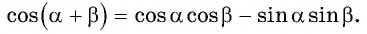
Синус, косинус, тангенс суммы и разности с примерами решения

Косинус суммы

Синус, косинус, тангенс суммы и разности с примерами решения

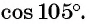
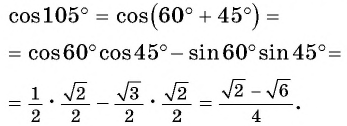
Применим полученную формулу и вычислим, например, Синус, косинус, тангенс суммы и разности с примерами решения

Синус, косинус, тангенс суммы и разности с примерами решения

Представив разность Синус, косинус, тангенс суммы и разности с примерами решения в виде суммы 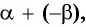можно получить формулу косинуса разности двух углов: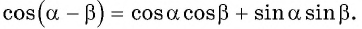

Косинус разности

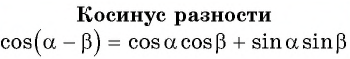Синус, косинус, тангенс суммы и разности с примерами решения Найдем, например,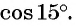

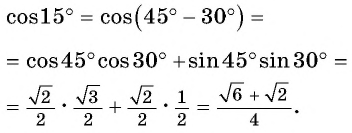
Синус, косинус, тангенс суммы и разности с примерами решения

Пример №1

Вычислите:

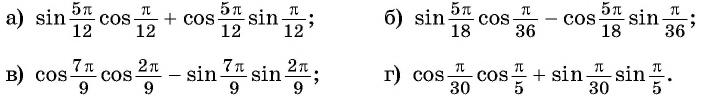
Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

Применим полученные формулы «справа налево»: 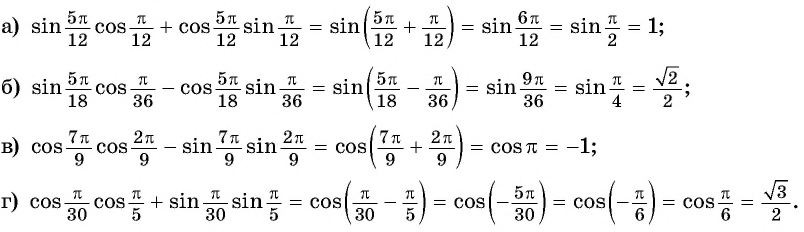Синус, косинус, тангенс суммы и разности с примерами решения Выведем формулы тангенса суммы и тангенса разности двух углов.

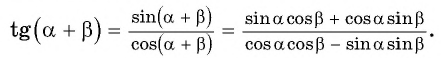Синус, косинус, тангенс суммы и разности с примерами решения Разделим числитель и знаменатель дроби на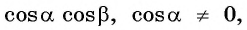 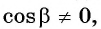тогда:

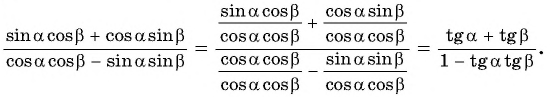
Синус, косинус, тангенс суммы и разности с примерами решения

Таким образом, получили формулу тангенса суммы двух углов:

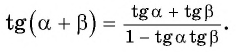
Синус, косинус, тангенс суммы и разности с примерами решения

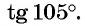
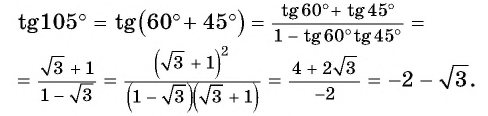
Воспользуемся формулой тангенса суммы и вычислим, например, Синус, косинус, тангенс суммы и разности с примерами решения

Синус, косинус, тангенс суммы и разности с примерами решения

Тангенс суммы

Синус, косинус, тангенс суммы и разности с примерами решения Представив разность в виде суммы можно получить формулу тангенса разности двух углов:

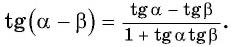Синус, косинус, тангенс суммы и разности с примерами решения Найдем, например,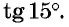

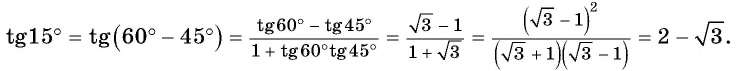
Тангенс разности

Синус, косинус, тангенс суммы и разности с примерами решения

Пример №2

Вычислите:

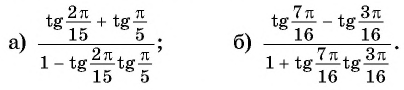
Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

Применим формулы тангенса суммы и тангенса разности «справа налево»:

Синус, косинус, тангенс суммы и разности с примерами решения

Полученные формулы синуса суммы, синуса разности, косинуса суммы, косинуса разности, тангенса суммы, тангенса разности двух углов называют формулами сложения.

Примеры заданий и их решения

Пример №3

С помощью формул сложения преобразуйте выражение:

Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

а) По формуле синуса разности получим:

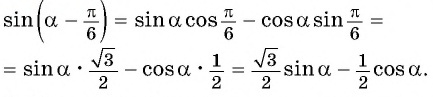
Синус, косинус, тангенс суммы и разности с примерами решения

б) Применим формулу тангенса суммы:

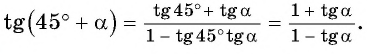
Синус, косинус, тангенс суммы и разности с примерами решения

Пример №4

Найдите значение выражения:

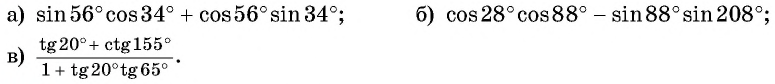
Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

а) По формуле синуса суммы получим:

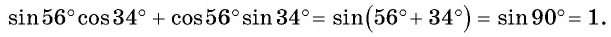
Синус, косинус, тангенс суммы и разности с примерами решения

б) По формулам приведения получим, что 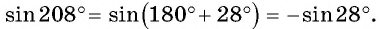Синус, косинус, тангенс суммы и разности с примерами решения

Тогда 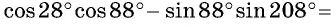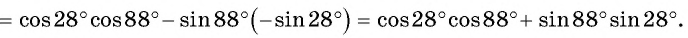Синус, косинус, тангенс суммы и разности с примерами решения Воспользуемся формулой косинуса разности и получим:

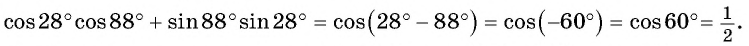
Синус, косинус, тангенс суммы и разности с примерами решения

в) По формулам приведения 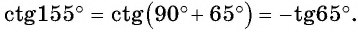Синус, косинус, тангенс суммы и разности с примерами решения

Тогда 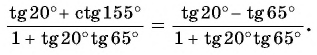Синус, косинус, тангенс суммы и разности с примерами решения

По формуле тангенса разности:

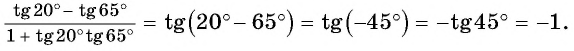
Синус, косинус, тангенс суммы и разности с примерами решения

Пример №5

Вычислите:

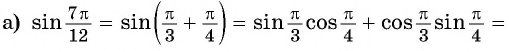
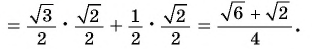
Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

Синус, косинус, тангенс суммы и разности с примерами решения

б) По формулам приведения: 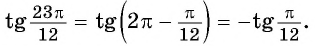Синус, косинус, тангенс суммы и разности с примерами решения

По формуле тангенса разности получим:

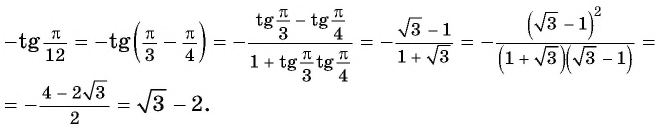
Синус, косинус, тангенс суммы и разности с примерами решения

Таким образом, 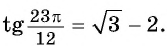Синус, косинус, тангенс суммы и разности с примерами решения

Заказать решение задач по высшей математике

Пример №6

Упростите выражение:

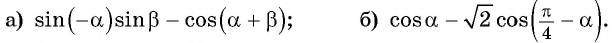
Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

а) Воспользуемся нечетностью синуса и формулой косинуса разности:

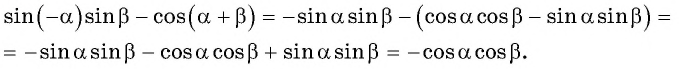
Синус, косинус, тангенс суммы и разности с примерами решения

б) Применим формулу косинуса разности и получим: 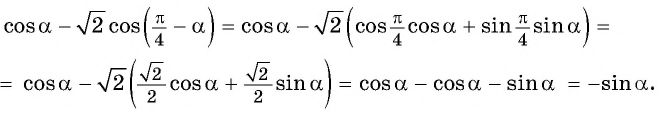Синус, косинус, тангенс суммы и разности с примерами решения

Пример №7

Решите уравнение 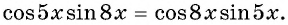Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

Запишем уравнение в виде 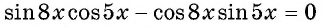Синус, косинус, тангенс суммы и разности с примерами решения и по формуле синуса разности получим: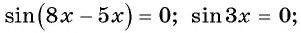

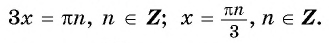
Ответ: 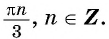Синус, косинус, тангенс суммы и разности с примерами решения

Пример №8

Вычислите 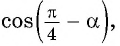Синус, косинус, тангенс суммы и разности с примерами решения если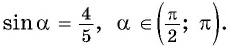

Решение:

Применим формулу косинуса разности:

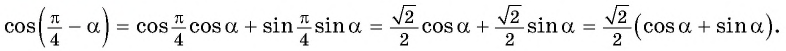
Синус, косинус, тангенс суммы и разности с примерами решения

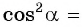
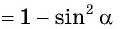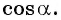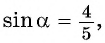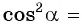
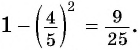Из основного тригонометрического тождества выразим Синус, косинус, тангенс суммы и разности с примерами решения и найдем Так как то Значит, 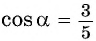или 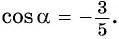Поскольку 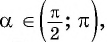т. е. 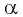угол второй четверти, то 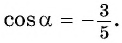Тогда

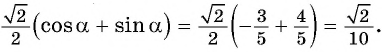
Синус, косинус, тангенс суммы и разности с примерами решения

Пример №9

Докажите тождество 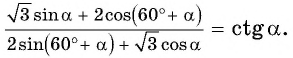Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

Воспользуемся формулами сложения и получим:

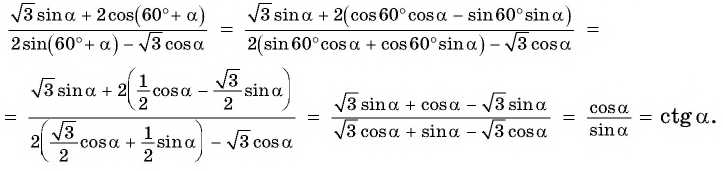
Синус, косинус, тангенс суммы и разности с примерами решения

Пример №10

Найдите значение выражения:

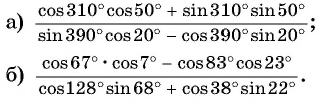
Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

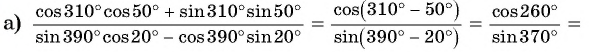
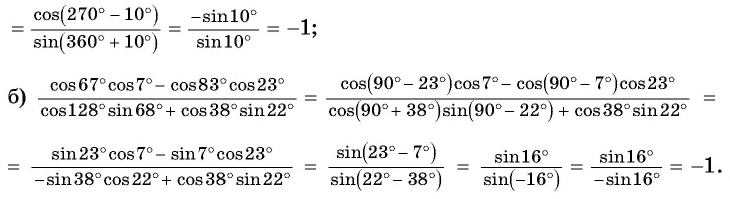Синус, косинус, тангенс суммы и разности с примерами решения 9.

Пример №11

Найдите множество значений функции

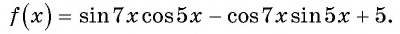
Синус, косинус, тангенс суммы и разности с примерами решения

Решение:

Применим формулу синуса разности и запишем функцию в виде 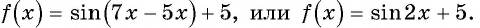Синус, косинус, тангенс суммы и разности с примерами решения

Так как 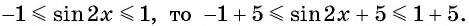Синус, косинус, тангенс суммы и разности с примерами решения Таким образом, имеем: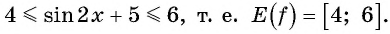

Формулы двойного аргумента
Формулы преобразования суммы и разности синусов (косинусов) в произведение
Корень n-й степени из числа и его свойства
Свойства и график функции y=ⁿ√x (n>1, n∈N)
Арксинус, арккосинус, арктангенс и арккотангенс числа
Тригонометрические уравнения
Тригонометрические неравенства
Формулы приведения

Источник

Сумма и разность синусов и косинусов: вывод формул, примеры

Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α – β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

sin α + sin β = 2 sin α + β 2 cos α – β 2 sin α – sin β = 2 sin α – β 2 cos α + β 2

cos α + cos β = 2 cos α + β 2 cos α – β 2 cos α – cos β = – 2 sin α + β 2 cos α – β 2 , cos α – cos β = 2 sin α + β 2 · β – α 2

Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α – β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.

Определения формул сумм и разности синусов и косинусов

Вывод формул суммы и разности синусов и косинусов

sin ( α + β ) = sin α · cos β + cos α · sin β sin ( α – β ) = sin α · cos β – cos α · sin β cos ( α + β ) = cos α · cos β – sin α · sin β cos ( α – β ) = cos α · cos β + sin α · sin β

Также представим сами углы в виде суммы полусумм и полуразностей.

α = α + β 2 + α – β 2 = α 2 + β 2 + α 2 – β 2 β = α + β 2 – α – β 2 = α 2 + β 2 – α 2 + β 2

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим

sin α + sin β = sin α + β 2 + α – β 2 + sin α + β 2 – α – β 2

sin α + β 2 + α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 sin α + β 2 + α – β 2 + sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 + sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу

sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 + sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 = = 2 sin α + β 2 cos α – β 2

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

sin α – sin β = sin α + β 2 + α – β 2 – sin α + β 2 – α – β 2 sin α + β 2 + α – β 2 – sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 – sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 = = 2 sin α – β 2 cos α + β 2

Вывод формулы суммы косинусов

Вывод формулы разности косинусов

cos α – cos β = cos α + β 2 + α – β 2 – cos α + β 2 – α – β 2 cos α + β 2 + α – β 2 – cos α + β 2 – α – β 2 = cos α + β 2 cos α – β 2 – sin α + β 2 sin α – β 2 – cos α + β 2 cos α – β 2 + sin α + β 2 sin α – β 2 = = – 2 sin α + β 2 sin α – β 2

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 – π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α = 165 ° , β = 75 ° sin α – sin β = sin 165 ° – sin 75 ° sin 165 – sin 75 = 2 · sin 165 ° – 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · – 1 2 = 2 2

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° – α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° – α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° – α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

sin120° = sin(180° – 60°) = sin60° = 3/√2;
sin150° = sin(180° – 30°) = sin30° = 1/2;
sin135° = sin(180° – 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° – α)

Так как sin(180° – α) = sinα, то sinγ = sin(180° – α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° – 45° – 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Сумма и разность синусов и косинусов

Время чтения: 16 минут

Тригонометрия – это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.

Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.

Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.

В математике применяются основные определения, связанные с тригонометрией. А именно:

синус – соотношение стороны противолежащего катета к стороне гипотенузы, (sin);
косинус – это прилежащая сторона катет к гипотенузе, обозначается как (cos);

Стоит выделить главные тригонометрические тождества, существующие в математике:

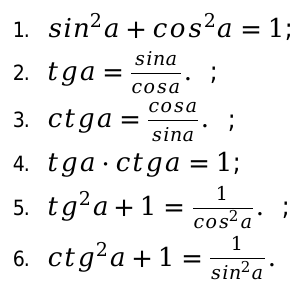
Применим основные формулы тригонометрии, решая задачи.

Пример:

Известно: ;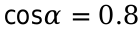

Необходимо определить: косинус, тангенс, котангенс, соответствующего угла a.

Для определения значения косинуса в квадрате, возводим число 0,8 в квадрат и вычисляем синус. Полученное значение подставляем в формулу и можем определить тангенс угла 0,8. Таким же методом, вычисляем котангенс

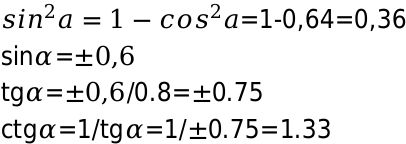
Решение довольно простое и особых сложней не вызывает.

Основные формулы для приведения заданных значений:

Формулы помогают, преобразовать основные тождества и перейти к вычислению углов в пределах 90 градусов. Это очень удобно, не только в алгебре, но и во всей математике.

Существует два основных способа, использования формул приведения:

Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.

Используя основные определения математики, а именно тригонометрии. Можно определить нужные нам данные.

Значения функций тригонометрии на для основных угловых значений.

синуса (sin):

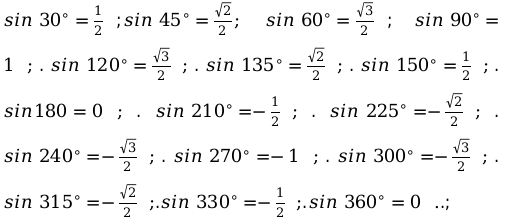
косинуса (cos):

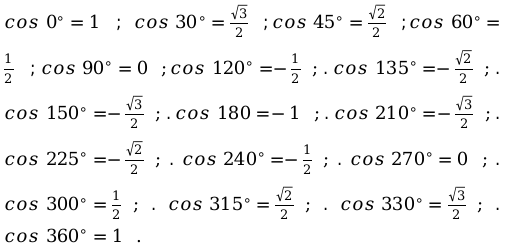
Преобразовав формулы сложения, мы получим тригонометрические уравнения угла.

Формулы кратности значения угла:

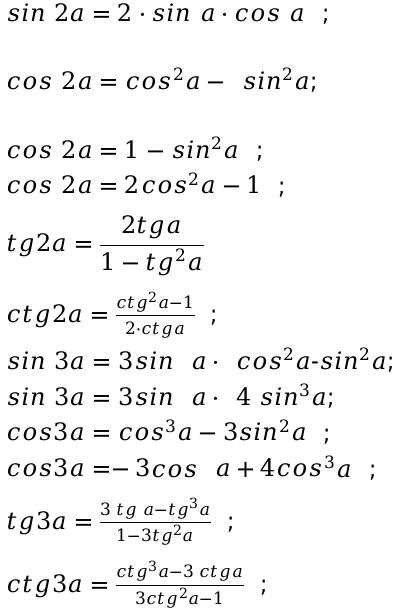
Формулы угла, определяющие половину значения (половинного угла):

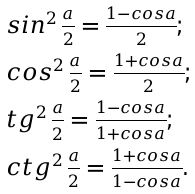
Более подробно в данном материале мы рассмотрим все уравнения суммы и разности, связанные именно с функцией косинус и синус.

Основные формулы для определения суммы и разности cos и sin

Перейдем к рассмотрению к простой форме разности и суммы функций.

Рассматриваемое уравнений можно представить, как – произведение. Преобразовать на множители косинус или синус, и тем самым упростить процесс вычисления.

Составим и запишем основные формулы для функции синус.

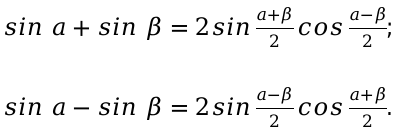
Следующим основным шагом, будет составить уравнения для косинуса. Применим все изученные свойства данной функции тригонометрии и вычислим правильный ответ.

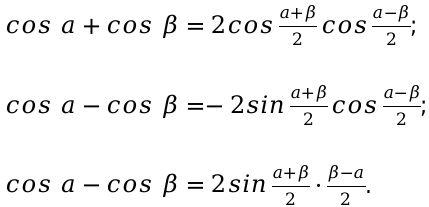
Выведем основные формулы для решения функций двух угловых значений. Для этого нужно применить составленные выше формулы сложения и вычитания. Их рассмотрение было в предыдущих материалах, посвященных тригонометрии. Поэтому лишний раз не стоит их заново переписывать. Так как рекомендовалась их обязательно заучить наизусть. Для более быстрого и правильного решения уравнений. И для последующего использования при изучении других смежных тем, где эти функции применяются.

Формулы можно представить также в виде полусуммы и полуразности угловых значений и получить следующие формулы.

Запишем уравнение для каждого угла раздельно и получим следующие формулы в виде уравнения:

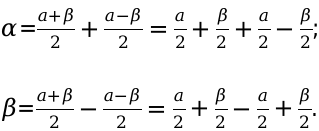
Сравним записанные формулы для угловых значений. Проанализировав их становится очевидно, что полученные суммы функций одинаковы по значению.

Выведем основную формулу для решения:

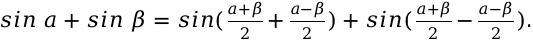
Далее первую часть выражения преобразуем, для этого применим формулу для сложения функций. Значения, которые находятся после знака равно, преобразуются при помощи формулы синуса для разности.

Подставляя в формулу значения, получаем следующее выражение:

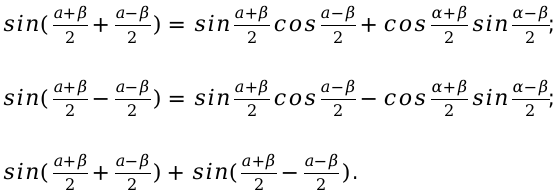
Далее необходимо раскрыть скобки и полученные значения привести в подобные слагаемые. Произведя все действия мы в конечном итоге получаем нужную нам формулу.

Запишем формулу следующего вида:

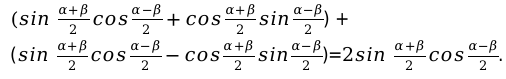
Другие, формулы преобразуются аналогичным способом

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/teorema-sinusov

http://www.napishem.ru/spravochnik/matematika/summa-i-raznost-sinusov-i-kosinusov.html

[/spoiler]

Источник

Определение

Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.

В математике применяются основные определения, связанные с тригонометрией. А именно:

синус — соотношение стороны противолежащего катета к стороне гипотенузы, (sin);
косинус — это прилежащая сторона катет к гипотенузе, обозначается как (cos);

Стоит выделить главные тригонометрические тождества, существующие в математике:

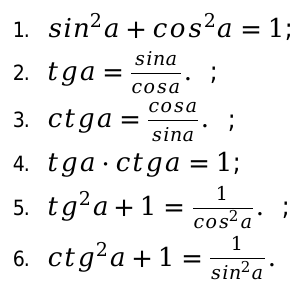
Применим основные формулы тригонометрии, решая задачи.

Пример:

Известно: [cos alpha=0.8];

Необходимо определить: косинус, тангенс, котангенс, соответствующего угла a.

Решение:

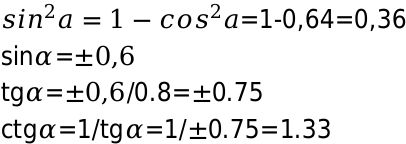
Пример решения задач 1

Решение довольно простое и особых сложней не вызывает.

Основные формулы для приведения заданных значений:

Существует два основных способа, использования формул приведения:

Если угол можно записать как [(pi / 2 pm alpha)] или [left(3^{*} pi / 2 pm alpharight)], то название функции меняется с косинуса на определение синус, тангенс, в свою очередь на котангенс, либо наоборот. Если же угол можно представить в виде [(pi pm alpha)] или [(2 * pi pm alpha)], то название функции не меняется.

Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.

Используя основные определения математики, а именно тригонометрии. Можно определить нужные нам данные.

Значения функций тригонометрии на для основных угловых значений.

синуса (sin):

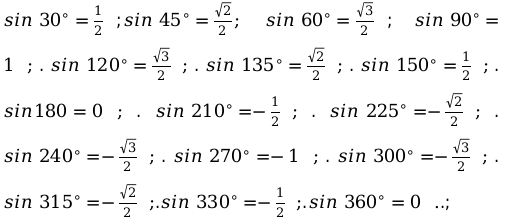
Значения функций для синуса

косинуса (cos):

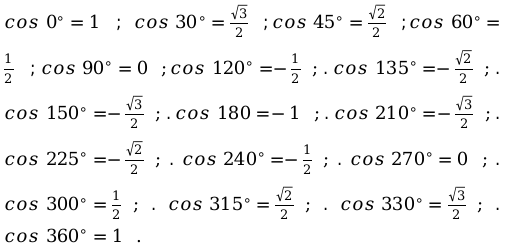
Значения функций для косинуса

Преобразовав формулы сложения, мы получим тригонометрические уравнения угла.

Формулы кратности значения угла:

Формулы кратности значения угла

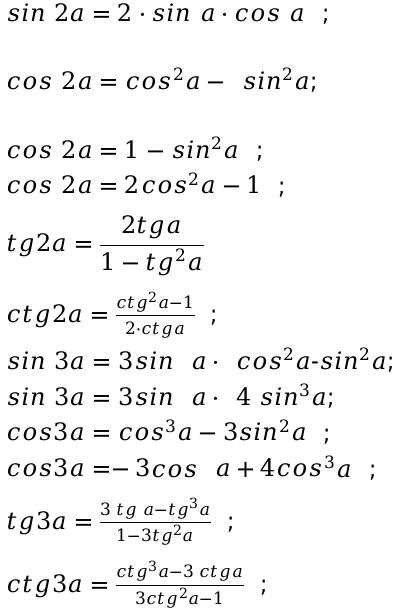
Формулы угла, определяющие половину значения (половинного угла):

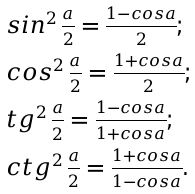
Формулы угла

Основные формулы для определения суммы и разности cos и sin

Перейдем к рассмотрению к простой форме разности и суммы функций.

Рассматриваемое уравнений можно представить, как — произведение. Преобразовать на множители косинус или синус, и тем самым упростить процесс вычисления.

Составим и запишем основные формулы для функции синус.

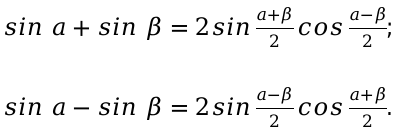
основные формулы для функции синус

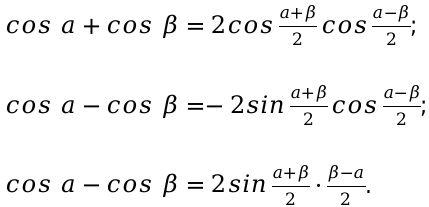
Уравнения для косинуса

Запишем уравнение для каждого угла раздельно и получим следующие формулы в виде уравнения:

[
alpha=frac{a+beta}{2}+frac{a-beta}{2}=frac{a}{2}+frac{beta}{2}+frac{a}{2}-frac{beta}{2}
]

[
beta=frac{a+beta}{2}-frac{a-beta}{2}=frac{a}{2}+frac{beta}{2}-frac{a}{2}+frac{beta}{2}
]

Выведем основную формулу для решения:

[
sin a+sin beta=sin left(frac{a+beta}{2}+frac{a-beta}{2}right)+sin left(frac{a+beta}{2}-frac{a-beta}{2}right) .
]

Подставляя в формулу значения, получаем следующее выражение:

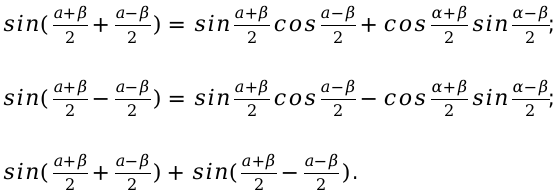
Пример решения задачи 1

Запишем формулу следующего вида:

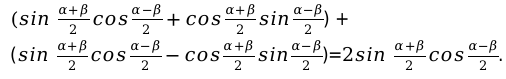
Пример решения задачи 2

Другие, формулы преобразуются аналогичным способом

Нет времени решать самому?

Наши эксперты помогут!

Итоговые формулы сложения и вычитания тригонометрических функций

Формула определения разности для синуса:

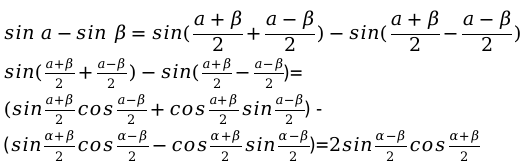
Формула определения разности для синуса

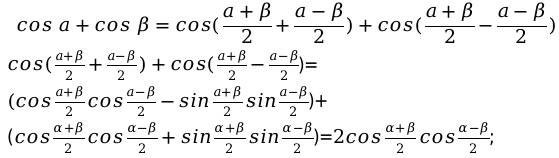
Формула для расчета суммы косинуса:

Формула для расчета суммы косинуса

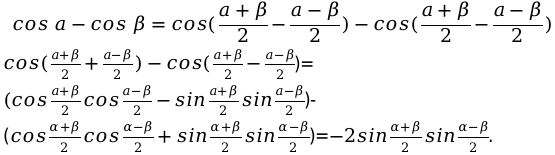
Формула для расчета суммы косинуса 1

Рассмотрим на практике применение изученного материала. Для этого решим несколько задач, подставляя числовые угловые значения

Пример №1:

По заданию нужно проверить сумму угловых значений для изученной функции подставив данные в формулу.

Заданы значения: [alpha=frac{pi}{2} ; beta=frac{pi}{6}].

Подберем нужную формулу и произведем вычисление:

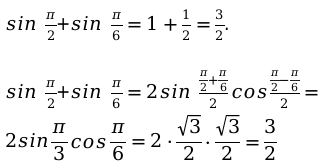
Пример решения задачи 3

Пример №2:

В этом примере рассмотрим вариант решения и применения формулы, для разности функции синуса.

Заданы следующие значения.

Углы: [alpha=165^{circ}, beta=75^{circ}]

Подставим угловые значения в формулу:

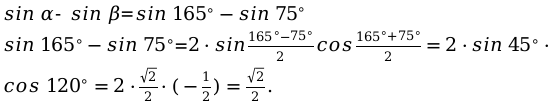
Пример решения задачи 4

Пример №3:

Нужно найти сумму тригонометрической функции.

Для этого заданы угловые значения.

Применяя основные изученные формулы, решим данную задачу.

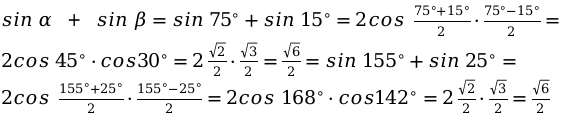
Пример решения задачи 5

Применяя вышеизложенные формулы можно перейти к произведению функций.

В целом, данная тема, считается основой в алгебре. Однако стоит вспомнить, что данные функции имеют главную роль и в других технических науках.

Они встречаются во многих теоремах, особенно это свойственно для физики.

Для всех технических наук, характерна взаимосвязь между основными законами и теоремами. Поэтому для успешного решения задач разного уровня, необходимо изучать и уметь их всех применять на практике.

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Формулы суммы и разности синусов и косинусов

Вывод формул суммы и разности синусов и косинусов

Вывод формулы суммы синусов

Вывод формулы разности синусов

Вывод формулы суммы косинусов

Вывод формулы разности косинусов

Примеры решения практических задач

Синус суммы

Синус разности

Косинус суммы

Косинус разности

Пример №1

Тангенс суммы

Тангенс разности

Пример №2

Примеры заданий и их решения

Пример №3

Пример №4

Пример №5

Пример №6

Пример №7

Пример №8

Пример №9

Пример №10

Пример №11

Сумма и разность синусов и косинусов: вывод формул, примеры

Формулы суммы и разности синусов и косинусов

Вывод формул суммы и разности синусов и косинусов

Вывод формулы суммы синусов

Вывод формулы разности синусов

Вывод формулы суммы косинусов

Вывод формулы разности косинусов

Примеры решения практических задач

Теорема синусов

Доказательство теоремы синусов

Доказательство следствия из теоремы синусов

Теорема о вписанном в окружность угле

Примеры решения задач

Запоминаем

Сумма и разность синусов и косинусов

Основные формулы для определения суммы и разности cos и sin

Основные формулы для определения суммы и разности cos и sin

Итоговые формулы сложения и вычитания тригонометрических функций

Вам также может понравиться

Как найти прямое восхождение в астрономии

Как исправить документ ворд если он только для чтения

Как найти мужика в симс

Добавить комментарий Отменить ответ