Приветствую Вас, уважаемые Читатели! В школе каждый из Вас обязательно встречался с теоремами синусов и косинусов. Вот их формулировки, если кто забыл:
Но кто из Вас слышал о теореме тангенсов, ведь она же напрашивается по аналогии! И действительно, такая формулировка существует, а сейчас покажу Вам её простой вывод! Поехали!
Использовать будет теорему синусов. Положим:
А теперь рассмотрим такое выражение:
Используем известные формулы суммы и разности синусов:
И получаем в два счета выражение, которое и называется теоремой тангенсов:
Впервые теорема была получена в XIII веке персидским математиком Насиром ад-Дином Ат-Туси.
Кроме того её называют формулой Региомонтана по имени немецкого астронома и математика Иоганна Мюллера (лат. Regiomontanus), установившего эту формулу уже в XV веке.
Тангенсы – вообще интересная шутка. Вы знаете, например, что сумма тангенсов углов треугольника равна их произведению? Я об этом обязательно расскажу!
Спасибо за внимание! Ставьте “Нравится” этой статье и подписывайтесь на канал!
Читайте также:
- Золотое сечение и банковские карты: правда или миф ?
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое .
Формулы тангенса суммы и разности углов устанавливают соотношение между тангенсом общей суммы или разности аргументов и тангенсами отдельных аргументов — слагаемых.
При всех допустимых значениях аргументов справедливы формулы:
тангенса суммы аргументов:
tg(α+β)=tgα+tgβ1−tgα⋅tgβ
; (1)
тангенса разности аргументов:
tg(α−β)=tgα−tgβ1+tgα⋅tgβ
. (2)
Оговорка о допустимых значениях аргументов означает, что все тангенсы имеют смысл, т. е. выполняются условия:
, для формулы (1),
α−β≠π2+πm,m∈ℤ
, для формулы (2).
Эти формулы очень важны и широко применяются не только в математике, но и в физике — особенно в радиотехнике.
Вывод формул естественным образом получается из определения функции тангенса и использования уже известных формул синуса и косинуса суммы и разности аргументов.
Докажем формулу тангенса суммы аргументов. Имеем:
.
Разделим каждое из слагаемых числителя и знаменателя на
cosα⋅cosβ
,
учитывая, что значение дроби от этого не изменится и что
cosα⋅cosβ≠0
из принятых выше условий
для допустимых значений аргументов, т. е.
α≠π2+πk,β≠π2+πnk,n∈ℤ
. Тогда:
tg(α+β)=sin(α+β)cos(α+β)=sinα⋅cosβ+cosα⋅sinβcosα⋅cosβ−sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ+cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ−sinα⋅sinβcosα⋅cosβ=tgα+tgβ1−tgα⋅tgβ
— что и требовалось доказать.
Аналогично доказывается формула тангенса разности аргументов:
tg(α−β)=sin(α−β)cos(α−β)=sinα⋅cosβ−cosα⋅sinβcosα⋅cosβ+sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ−cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ+sinα⋅sinβcosα⋅cosβ=tgα−tgβ1+tgα⋅tgβ.
Ниже в табличном виде представлены формулы сумм основных тригонометрических функций.
Содержание
- Прямые и производные функции: sin, cos, tg, ctg
- Обратные функции: arcsin, arccos, arctg, arcctg
Прямые и производные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).
| Действие | Формула |
| Сумма синусов |  |
| Сумма косинусов |  |
| Сумма тангенсов | tg α + tg β = sin (α + β) / cos α cos β |
| Сумма котангенсов | ctg α + ctg β = sin (α + β) / sin α sin β |
microexcel.ru
Обратные функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
| Действие | Формула |
| Сумма арксинусов |
 |
| Сумма арккосинусов |
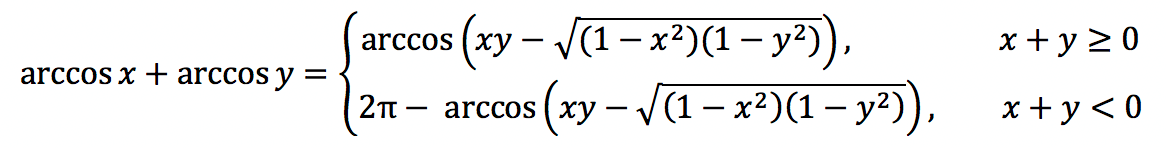 |
| Сумма арктангенсов |
 |
| Сумма арккотангенсов |
 |
microexcel.ru
Сумма тангенсов
ОПРЕДЕЛЕНИЕ
Сумма тангенсов двух углов (
alpha
) и (
beta
) равна отношению синуса суммы (
alpha+beta
) к произведению косинусов этих углов:
(
operatorname{tg} alpha+operatorname{tg} beta=frac{sin (alpha+beta)}{cos alpha cdot cos beta}
)
Примеры решения задач
ПРИМЕР 1
Проверить, что (
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)
Применим формулу суммы тангенсов
(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=frac{sin left(15^{circ}+60^{circ}right)}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}
)
Представим (
cos 15^{circ}
) в (
cos 15^{circ}=cos left(90^{circ}-75^{circ}right)=sin 75^{circ}
) и подставим в предыдущее равенство: (
frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{sin 75^{circ} cos 60^{circ}}=frac{1}{cos 60^{circ}}=2
)
т.е.
(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)
ПРИМЕР 2
Найти значение выражения (
operatorname{tg}^{3 pi}+operatorname{tg} frac{pi}{8}
)
Представим сумму разность в виде
(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=frac{sin left(frac{3 pi}{8}+frac{pi}{8}right)}{cos frac{3 pi}{8} cdot cos frac{pi}{8}}=frac{sin frac{pi}{2}}{frac{1}{2}left(cos frac{pi}{4}+cos frac{pi}{2}right)}=frac{1}{frac{1}{2}left(frac{sqrt{2}}{2}+0right)}=frac{4}{sqrt{2}}=2 sqrt{2}
)
(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=2 sqrt{2}
)
Продолжаем наш разговор про наиболее употребляемые формулы в тригонометрии. Важнейшие из них – формулы сложения.
Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.
Для начала мы приведем полный список формул сложения, потом докажем их и разберем несколько наглядных примеров.
Основные формулы сложения в тригонометрии
Выделяют восемь основных формул: синус суммы и синус разности двух углов, косинусы суммы и разности, тангенсы и котангенсы суммы и разности соответственно. Ниже приведены их стандартные формулировки и вычисления.
1.Синус суммы двух углов можно получить следующим образом:
– вычисляем произведение синуса первого угла на косинус второго;
– умножаем косинус первого угла на синус первого;
– складываем получившиеся значения.
Графическое написание формулы выглядит так: sin (α+β)=sin α·cos β+cos α·sin β
2. Синус разности вычисляется почти так же, только полученные произведения нужно не сложить, а вычесть друг из друга. Таким образом, вычисляем произведения синуса первого угла на косинус второго и косинуса первого угла на синус второго и находим их разность. Формула пишется так: sin (α-β)=sin α·cos β+sin α·sin β
3. Косинус суммы. Для него находим произведения косинуса первого угла на косинус второго и синуса первого угла на синус второго соответственно и находим их разность: cos (α+β)=cos α·cos β-sin α·sin β
4. Косинус разности: вычисляем произведения синусов и косинусов данных углов, как и ранее, и складываем их. Формула: cos (α-β)=cos α·cos β+sin α·sin β
5. Тангенс суммы. Эта формула выражается дробью, в числителе которой – сумма тангенсов искомых углов, а в знаменателе – единица, из которой вычитается произведение тангенсов искомых углов. Все понятно из ее графической записи: tg (α+β)=tg α+tg β1-tg α·tg β
6. Тангенс разности. Вычисляем значения разности и произведения тангенсов данных углов и поступаем с ними схожим образом. В знаменателе мы прибавляем к единице, а не наоборот: tg (α-β)=tg α-tg β1+tg α·tg β
7. Котангенс суммы. Для вычислений по этой формуле нам понадобятся произведение и сумма котангенсов данных углов, с которыми мы поступаем следующим образом: ctg (α+β)=-1+ctg α·ctg βctg α+ctg β
8. Котангенс разности. Формула схожа с предыдущей, но в числителе и знаменателе – минус, а не плюс ctg (α-β)=-1-ctg α·ctg βctg α-ctg β.
Вы, наверное, заметили, что эти формулы попарно схожи. При помощи знаков ±(плюс-минус) и ∓(минус-плюс) мы можем сгруппировать их для удобства записи:
sin (α±β)=sin α·cos β±cos α·sin βcos (α±β)=cos α·cos β∓sin α·sin βtg (α±β)=tg α±tg β1∓tg α·tg βctg (α±β)=-1±ctg α·ctg βctg α±ctg β
Соответственно, мы имеем одну формулу записи для суммы и разности каждого значения, просто в одном случае мы обращаем внимание на верхний знак, в другом – на нижний.
Мы можем взять любые углы α и β, и формулы сложения для косинуса и синуса подойдут для них. Если мы можем правильно определить значения тангенсов и котангенсов этих углов, то формулы сложения для тангенса и котангенса будут также для них справедливы.
Доказательства формул сложения
Как и большинство понятий в алгебре, формулы сложения могут быть доказаны. Первая формула, которую мы докажем, – формула косинуса разности. Из нее потом можно легко вывести остальные доказательства.
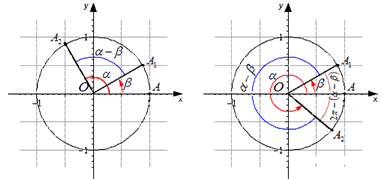
Уточним основные понятия. Нам понадобится единичная окружность. Она получится, если мы возьмем некую точку A и повернем вокруг центра (точки O) углы α и β . Тогда угол между векторами OA1→ и OA→2 будет равняться (α-β)+2π·z или 2π-(α-β)+2π·z (z – любое целое число). Получившиеся вектора образуют угол, который равен α-β или 2π-(α-β), или он может отличаться от этих значений на целое число полных оборотов. Взгляните на рисунок:
Мы воспользовались формулами приведения и получили следующие результаты:
cos ((α-β)+2π·z)=cos (α-β)cos (2π-(α-β)+2π·z)=cos (α-β)
Итог: косинус угла между векторами OA1→ и OA2→ равняется косинусу угла α-β, следовательно, cos (OA1→ OA2→) = cos (α-β).
Далее мы переходим к самому доказательству формулы косинуса разности.
Вспомним определения синуса и косинуса: синус – функция угла, равная отношению катета противолежащего угла к гипотенузе, косинус – это синус дополнительного угла. Следовательно, точки A1 и A2 имеют координаты (cos α, sin α) и (cos β, sin β).
Получим следующее:
OA1→=(cos α, sin α) и OA2→=(cos β, sin β)
Если непонятно, взгляните на координаты точек, расположенных в начале и конце векторов.
Длины векторов равны 1, т.к. у нас единичная окружность.
Разберем теперь скалярное произведение векторов OA1→ и OA2→. В координатах оно выглядит так:
(OA1→,OA2)→ = cos α·cos β+sin α·sin β
Из этого мы можем вывести равенство:
cos (α-β) = cos α·cos β+sin α·sin β
Таким образом, формула косинуса разности доказана.
Теперь мы докажем следующую формулу – косинуса суммы. Это проще, поскольку мы можем воспользоваться предыдущими расчетами. Возьмем представление α+β=α-(-β). У нас есть:
cos (α+β)=cos (α-(- β))==cos α·cos (-β)+sin α·sin (-β)==cos α·cos β+sin α·sin β
Это и есть доказательство формулы косинуса суммы. В последней строчке использовано свойство синуса и косинуса противоположных углов.
Формулу синуса суммы можно вывести из формулы косинуса разности. Возьмем для этого формулу приведения:
вида sin (α+β)=cos (π2(α+β)). Так
sin (α+β)=cos (π2(α+β))=cos ((π2-α)-β)==cos (π2-α)·cosβ+sin (π2-α)·sin β==sin α·cos β+cos α·sin β
А вот доказательство формулы синуса разности:
sin (α-β)=sin (α+(-β))=sin α·cos (-β)+cos α·sin (-β)==sin α·cos β-cos α·sin β
Обратите внимание на использование свойств синуса и косинуса противоположных углов в последнем вычислении.
Далее нам нужны доказательства формул сложения для тангенса и котангенса. Вспомним основные определения (тангенс – отношение синуса к косинусу, а котангенс –наоборот) и возьмем уже выведенные заранее формулы. У нас получилось:
tg (α+β)=sin (α+β)cos (α+β)=sin α·cos β+cos α·sin βcos α·cos β-sin α·sin β
У нас получилась сложная дробь. Далее нам нужно разделить ее числитель и знаменатель на cos α·cos β, учитывая что cos α≠0 и cos β≠0, получаем:
sin α·cos β+cos α·sin βcos α·cos βcos α·cos β-sin α·sin βcos α·cos β=sin α·cos βcos α·cos β+cos α·sin βcos α·cos βcos α·cos βcos α·cos β-sin α·sin βcos α·cos β
Теперь сокращаем дроби и получаем формулу следующего вида: sin αcos α+sin βcos β1-sin αcos α·sin βcos β=tg α+tg β1-tg α·tg β.
У нас получилось tg (α+β) = tg α+tg β1-tg α·tg β. Это и есть доказательство формулы сложения тангенса.
Следующая формула, которую мы будем доказывать – формула тангенса разности. Все наглядно показано в вычислениях:
tg (α-β)= tg (α+(-β))=tg α+tg (-β)1-tg α·tg (-β)=tg α-tg β1+tg α·tg β
Формулы для котангенса доказываются схожим образом:
ctg (α+β)=cos (α+β)sin (α+β)=cos α·cos β-sin α·sin βsin α·cos β+cos α·sin β==cos α·cos β-sin α·sin βsin α·sin βsin α·cos β+cos α·sin βsin α·sin β=cos α·cos βsin α·sin β-1sin α·cos βsin α·sin β+cos α·sin βsin α·sin β==-1+ctg α·ctg βctg α+ctg β
Далее:
ctg (α-β)=ctg (α+(-β))=-1+ctg α·ctg (-β)ctg α+ctg (-β)=-1-ctg α·ctg βctg α-ctg β
Примеры сложения с помощью тригонометрических формул
В этом пункте мы рассмотрим, как применить эти сложные на вид вычисления на практике. Их можно использовать:
– при преобразовании тригонометрических выражений;
– для вычисления точных значений синуса, косинуса, тангенса и котангенса углов, которые отличаются от основных (0, π6, π4, π3, π2);
– для доказательства других тригонометрических формул, например, формулы двойного угла.
Разберем задачи с использованием формул сложения.
Задача: Вычислите точное значение тангенса 15 градусов.
Решение
Для наглядности мы 15 градусов можно представить в виде разности 45-30. В этом случае решение задачи можно получить с помощью формулы тангенса разности. Возьмем формулу, которую мы приводили выше, и укажем в ней имеющиеся нам известные значения: tg15°=tg(45°-30°)=tg45°-tg30°1+tg45°·tg30°
Вычисляем ответ: tg45°-tg30°1+tg45°·tg30°=1-331+1·33==3-13+1=(3-1)·(3-1)(3+1)·(3-1)=(3)2-23+1(3)2-1=2-3
Ответ: tg15°=2-3
Задача: Выберем формулу сложения для проверки формулы приведения следующего вида:sin (π2+α)=cos α
Нам подойдет формула синуса суммы. Итого: sin (π2+α)=sin π2·cos α+cos π2·sin α=1·cos α+0·sin α=cos α
Ответ: sin (π2+α)=cos α – наша формула доказана.