Сумма углов треугольника

Сумма углов треугольника — это сумма
всех внутренних углов треугольника.
Так, как углы измеряются в градусах, соответственно значение
суммы углов треугольника также измеряется в градусах.
Сумма углов треугольника есть величина постоянная,
неизменяемая, она равна 180 градусам, вне зависимости
от вида рассматриваемого треугольника.
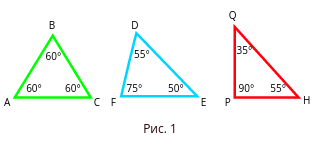
На рисунке 1 изображены равносторонний,
разносторонний и прямоугольный треугольники,
их суммы внутренних углов равны 180 градусам.
Также, существует теорема, которая доказывает
утверждение о том, что сумма углов треугольника
180 градусов, она называется теоремой
о сумме углов треугольника.
Теорема о сумме углов треугольника — это теорема в
геометрии о сумме углов произвольного треугольника на плоскости.
Сумма углов треугольника – определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.

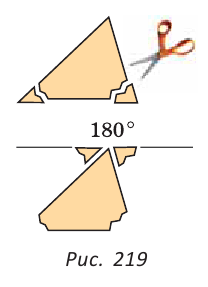
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
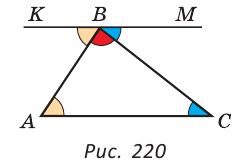
Дано:  АВС (рис. 220).
АВС (рис. 220).
Доказать:  A+
A+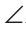 B +
B +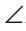 C = 180°.
C = 180°.
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 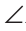 KBA =
KBA =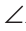 A как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей АВ, a
A как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей АВ, a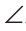 MBC =
MBC =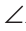 C как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей ВС. Так как углы КВА, ABC и МВС образуют развернутый угол, то
C как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей ВС. Так как углы КВА, ABC и МВС образуют развернутый угол, то
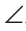 KBA +
KBA + ABC +
ABC + MBC = 180°. Отсюда
MBC = 180°. Отсюда A +
A + B +
B + C = 180°. Теорема доказана.
C = 180°. Теорема доказана.
Следствия.
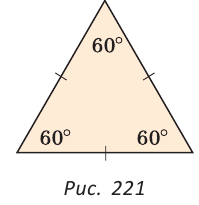
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
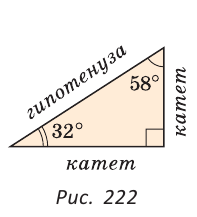
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то 1 =
1 = 2.
2.
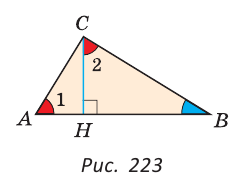
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
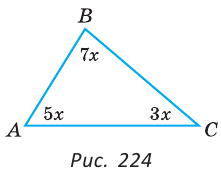
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 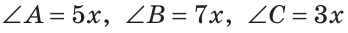 (
( 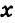 — градусная мера одной части).
— градусная мера одной части).
Так как сумма углов треугольника равна 180°, то
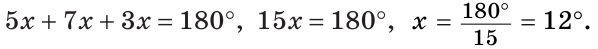
Тогда 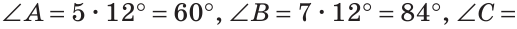
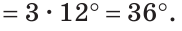
Ответ: 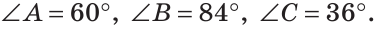
Пример:
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
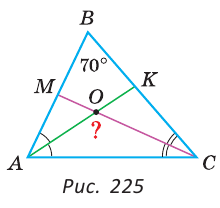
Решение:
Сумма углов А и С треугольника ABC равна 180° – 70° = 110°. Так как биссектриса делит угол пополам, то
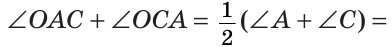
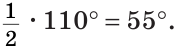
Из треугольника АОС находим: 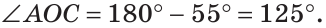
Замечание. Если 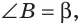 то, рассуждая аналогично, получим формулу:
то, рассуждая аналогично, получим формулу: 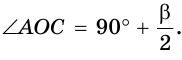 Если, например,
Если, например, 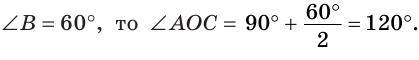
Пример:
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 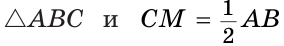 (рис. 226).
(рис. 226).
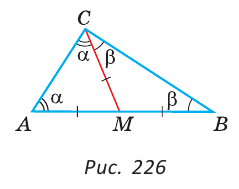
Докажем, что ACB = 90°. Обозначим
ACB = 90°. Обозначим  A =
A =  ,
, В =
В =  . Так как медиана делит сторону пополам, то AM = MB =
. Так как медиана делит сторону пополам, то AM = MB =  АВ. Тогда СМ=АМ=МВ. Так как
АВ. Тогда СМ=АМ=МВ. Так как  АМС — равнобедренный, то
АМС — равнобедренный, то A =
A = ACM =
ACM =  как углы при основании равнобедренного треугольника. Аналогично,
как углы при основании равнобедренного треугольника. Аналогично,  СМВ — равнобедренный и
СМВ — равнобедренный и  B =
B = BCM =
BCM =  . Сумма углов треугольника ABC, с одной стороны, равна 2
. Сумма углов треугольника ABC, с одной стороны, равна 2  + 2
+ 2 , с другой — равна 180°. Отсюда 2
, с другой — равна 180°. Отсюда 2  + 2
+ 2  = 180°, 2(
= 180°, 2(  +
+  ) = 180°,
) = 180°,  +
+  = 90°. Но
= 90°. Но ACB =
ACB =  +
+  , поэтому
, поэтому
 ACB = 90°.
ACB = 90°.
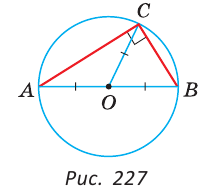
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228)  C=90°,
C=90°, A=
A= ,
, B=
B= .
.
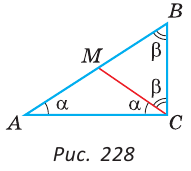
Проведем отрезок СМ так, что ACM=
ACM= , и докажем, что СМ — медиана и что СМ=
, и докажем, что СМ — медиана и что СМ= АВ. Угол В дополняет угол А до 90°, a
АВ. Угол В дополняет угол А до 90°, a BCM дополняет
BCM дополняет ACM до 90°. Поскольку
ACM до 90°. Поскольку  ACM =
ACM = A =
A =  , то
, то BCM =
BCM = . Треугольники АМС и ВМС — равнобедренные по признаку равнобедренного треугольника. Тогда AM = МС и МВ = МС. Отсюда СМ — медиана и СМ =
. Треугольники АМС и ВМС — равнобедренные по признаку равнобедренного треугольника. Тогда AM = МС и МВ = МС. Отсюда СМ — медиана и СМ =  АВ.
АВ.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
[spoiler title=”источники:”]
http://www.evkova.org/summa-uglov-treugolnika
http://mozgan.ru/Geometry/AreaTriangle
[/spoiler]
| Треугольник | |
|---|---|
 |
|
| Рёбра | 3 |
| Символ Шлефли | {3} |
Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади)[1].
Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла[2], т.е. как часть плоскости, ограниченную тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому исследование его свойств проводилось начиная с глубокой древности.
Понятие треугольника допускает различные обобщения. Можно определить это понятие в неевклидовой геометрии (например, на сфере): на таких поверхностях треугольник определяется как три точки, соединённые геодезическими линиями. В 

Иногда рассматривают вырожденный треугольник, три вершины которого лежат на одной прямой. Если не оговорено иное, треугольник в данной статье предполагается невырожденным.
Основные элементы треугольника[править | править код]

Вершины, стороны, углы[править | править код]
Традиционно вершины треугольника обозначаются заглавными буквами латинского алфавита: 







Треугольник 
Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (


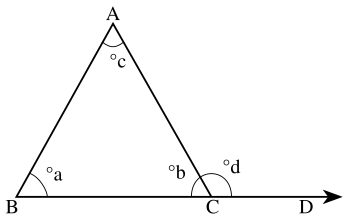
Внешним углом 



Внешним углом 





Периметром треугольника называют сумму длин трёх его сторон, а половину этой величины называют полупериметром.
Классификация треугольников[править | править код]
По виду наибольшего угла[править | править код]
Основной источник: [3]
Поскольку в евклидовой геометрии сумма углов треугольника равна 

- Если все углы треугольника острые, то треугольник называется остроугольным.
- Если один из углов треугольника прямой (равен
), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
- Если один из углов треугольника тупой (больше
), то треугольник называется тупоугольным, Остальные два угла, очевидно, острые (треугольников с двумя тупыми или прямыми углами быть не может).
По числу равных сторон (или по степени симметричности)[править | править код]
- Разносторонним называется треугольник, у которого все три стороны не равны.
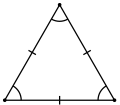
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием[4]. В равнобедренном треугольнике углы при основании равны.
- Равносторонним или правильным называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают. Равносторонний треугольник является частным случаем равнобедренного треугольника.
| Треугольник | Количество осей симметрии | Количество пар равных сторон |
|---|---|---|
| Разносторонний | Нет | Нет |
| Равнобедренный | 1 | 1 |
| Равносторонний | 3 | 3 |
Медианы, высоты, биссектрисы[править | править код]

Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы. Треугольник с вершинами в серединах медиан называется срединным треугольником. Основания медиан данного треугольника образуют так называемый дополнительный треугольник.
Длину медианы 

для других медиан аналогично.
-

Высота в треугольниках различного типа
-

Высоты пересекаются в ортоцентре
Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника. Треугольник с вершинами в основаниях высот называется ортотреугольником.
Длину высоты 

; для других высот аналогично.
Длины высот, опущенных на стороны. можно также найти по формулам:[5]:p.64
.

Биссектриса 
Биссектрисой (биссéктором) треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).
Если треугольник разносторонний (не равнобедренный), то биссектриса, проведённая из любой его вершины, лежит между медианой и высотой, проведёнными из той же вершины. Ещё одно важное свойство биссектрисы: она делит противоположную сторону на части, пропорциональные прилегающим к ней сторонам[6].
Длину биссектрисы 

, где
— полупериметр.
.
; здесь
— высота.
Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный.
Описанная и вписанная окружности[править | править код]

Треугольник АВС и его окружности: вписанная (синяя), описанная (красная) и три вневписанные (зелёные)
Описанная окружность (см. рис. справа) — окружность, проходящая через все три вершины треугольника. Описанная окружность всегда единственна, её центр совпадает с точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины сторон. В тупоугольном треугольнике этот центр лежит вне треугольника[6].
Вписанная окружность (см. рис. справа) — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром, он совпадает с точкой пересечения биссектрис треугольника.
Следующие формулы позволяют вычислить радиусы описанной 

где
— площадь треугольника,
— его полупериметр.
,
где 
Ещё два полезных соотношения:
[7]
.
Существует также формула Карно[8]:
,
где 











Расстояние от центра описанной окружности например до стороны 
;
расстояние от ортоцентра например до вершины 
.
Признаки равенства треугольников[править | править код]

Равенство по двум сторонам и углу между ними

Равенство по стороне и двум прилежащим углам

Равенство по трем сторонам
Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:[9]
,
,
(равенство по двум сторонам и углу между ними);
,
,
(равенство по стороне и двум прилежащим углам);
,
,
(равенство по трём сторонам).
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
Дополнительный признак: треугольники равны, если у них совпадают две стороны и угол, лежащий против большей из этих сторон[10].
Дополнительный признак {по двум сторонам и углу не между ними, если этот угол прямой или тупой}.
Если в треугольниках 




В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.
Признаки подобия треугольников[править | править код]
Основные свойства элементов треугольника[править | править код]
Свойства углов[править | править код]
Во всяком треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы[10].
Каждый внешний угол треугольника равен разности между 180° и соответствующим внутренним углом. Для внешнего угла также имеет место теорема о внешнем угле треугольника: внешний угол равен сумме двух других внутренних углов, с ним не смежных[10].
Неравенство треугольника[править | править код]
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон невырожденного треугольника связаны следующими неравенствами:
.
Дополнительное свойство: каждая сторона треугольника больше разности двух других сторон[10].
Теорема о сумме углов треугольника[править | править код]

Сумма внутренних углов треугольника всегда равна 180°:
.
В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше.
Теорема синусов[править | править код]
,
где 
Теорема косинусов[править | править код]
.
Является обобщением теоремы Пифагора.
- Замечание. теоремой косинусов также называют следующие две формулы, легко выводимые из основной теоремы косинусов (см. с. 51, ф. (1.11-2))[12].
.
Теорема о проекциях[править | править код]
Источник: [13].
.
Теорема тангенсов (формулы Региомонтана)[править | править код]
Теорема котангенсов[править | править код]
.
Формулы Мольвейде[править | править код]
.
Решение треугольников[править | править код]
Вычисление неизвестных сторон, углов и других характеристик треугольника, исходя из известных, исторически получило название «решения треугольников». При этом используются приведенные выше общие тригонометрические теоремы, а также признаки равенства и подобия треугольников.
Площадь треугольника[править | править код]
- Далее используются обозначения
- Площадь треугольника связана с его основными элементами следующими соотношениями.
— формула Герона
[14]
[15]
— ориентированная площадь треугольника.
— см. Аналоги формулы Герона
- Частные случаи
-
— для прямоугольного треугольника
— для равностороннего треугольника
Другие формулы[править | править код]
- Существуют другие формулы, такие, как например,[16]
для угла 
- В 1885 г. Бейкер (Baker)[17] предложил список более ста формул площади треугольника. Он, в частности, включает:
,
,
,
.
Неравенства для площади треугольника[править | править код]
Для площади справедливы неравенства:
и
,
где в обоих случаях равенство достигается тогда и только тогда, когда треугольник равносторонний (правильный).
История изучения[править | править код]
Свойства треугольника, изучаемые в школе, за редким исключением, известны с ранней античности. Зачатки тригонометрических знаний можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.[21]
Общая и достаточно полная теория геометрии треугольников (как плоских, так и сферических) появилась в Древней Греции[22]. В частности, во второй книге „Начал“ Евклида теорема 12 представляет собой словесный аналог теоремы косинусов для тупоугольных треугольников[23]. Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Свойствами элементов треугольников (углов, сторон, биссектрис и др.) после Евклида занимались Архимед, Менелай, Клавдий Птолемей, Папп Александрийский[24].
В IV веке, после упадка античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров[25]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен.
В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Их астрономические трактаты, аналогичные индийским сиддхантам, назывались „зиджи“; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории[26]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век).
Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века[27]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника[28].
Фундаментальное изложение тригонометрии (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году[29]. Его „Трактат о полном четырёхстороннике“ содержит практические способы решения типичных задач, в том числе труднейших, решённых самим ат-Туси[30]. Таким образом, к концу XIII века были открыты базовые теоремы, необходимые для практической работы с треугольниками.
В Европе развитие тригонометрической теории стало чрезвычайно важным в Новое время, в первую очередь для артиллерии, оптики и навигации при дальних морских путешествиях. В 1551 году появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10»[31]. Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций.
Изучение треугольника продолжилось в XVII веке: была доказана теорема Дезарга (1636), открыта точка Торричелли (1640) и изучены её свойства. Джованни Чева доказал свою теорему о трансверсалях (1678). Лейбниц показал, как вычислять расстояние от центра тяжести треугольника до других его замечательных точек[24]. В XVIII веке были обнаружены прямая Эйлера и окружность шести точек (1765).
В начале XIX века была открыта точка Жергонна. В 1828 году была доказана теорема Фейербаха. К концу XIX века относится творчество Эмиля Лемуана, Анри Брокара, Жозефа Нойберга. Окружность девяти точек исследовали Понселе, Брианшон и Штейнер, Были обнаружены ранее неизвестные геометрические связи и образы — например, окружность Брокара, точки Штейнера и Тарри. В 1860 году Шлёмильх доказал теорему: три прямые, соединяющие середины сторон треугольника с серединами его соответствующих высот, пересекаются в одной точке. В 1937 году советский математик С. И. Зетель показал, что эта теорема верна не только для высот, но и для любых других чевиан. Исследования перечисленных выше геометров превратили геометрию треугольника в самостоятельный раздел математики[32].
Значительный вклад в геометрию треугольника внёс в конце XIX — начале XX века Фрэнк Морли. Он доказал, что геометрическое место центров кардиоид, вписанных в треугольник, состоит из девяти прямых, которые, взятые по три, параллельны трём сторонам равностороннего треугольника. Кроме того, 27 точек, в которых пересекаются эти девять прямых, являются точками пересечения двух трисектрис треугольника, принадлежащих к одной и той же его стороне. Наибольшую известность получил частный случай этой теоремы: внутренние трисектрисы углов треугольника, прилежащих к одной и той же стороне, пересекаются попарно в трёх вершинах равностороннего треугольника. Обобщение этих работ опубликовал Анри Лебег (1940), он
ввел 
С 1830-х годов в геометрии треугольника стали широко использоваться трилинейные координаты точек. Активно развивалась теория преобразований — проективное, изогональное, изотомическое и другие. Полезной оказалась идея рассмотрения задач теории треугольников на комплексной плоскости.
[32].
Дополнительные сведения[править | править код]
Все факты, изложенные в этом разделе, относятся к евклидовой геометрии.
- Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трёх таких отрезков, проведённых из трёх разных вершин треугольника и пересекающихся в одной точке. Они удовлетворяют условиям теоремы Чевы. Чевианы, соединяющие вершину треугольника с точками противоположной стороны, отстоящими на заданное отношение
от её концов, называют недианами.
- Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника. Три средние линии треугольника разделяют его на четыре равных треугольника в 4 раза меньшей площади, чем площадь исходного треугольника.
- Серединные перпендикуляры (медиатрисы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.
- Чевианы, лежащие на прямых, симметричных медианам относительно биссектрис, называются симедианами. Они проходят через одну точку — точку Лемуана.
- Чевианы, лежащие на прямых, изотомически сопряжённых биссектрисам относительно оснований медиан, называются антибиссектрисами. Они проходят через одну точку — центр антибиссектрис.
- Кливер треугольника — это отрезок, одна вершина которого находится в середине одной из сторон треугольника, вторая вершина находится на одной из двух оставшихся сторон, при этом кливер разбивает периметр пополам.
- Некоторые точки в треугольнике — «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли. Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это — точки Аполлония. Точки
и
такие, что
и
называются точками Брокара.
Некоторые замечательные прямые треугольника[править | править код]
- В любом треугольнике центр тяжести, ортоцентр, центр описанной окружности и центр окружности Эйлера лежат на одной прямой, называемой прямой Эйлера.
- В любом треугольнике центр тяжести, центр круга, вписанного в него (инцентр), его точка Нагеля и центр круга, вписанного в дополнительный треугольник
(или Центр Шпикера), лежат на одной прямой, называемой второй прямой Эйлера (прямой Нагеля)
- Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара. На ней лежат точки Аполлония.
- Также на одной прямой лежат точки Торричелли и точка Лемуана.
- Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек описанной окружности перпендикулярны.
Трилинейные поляры треугольника[править | править код]
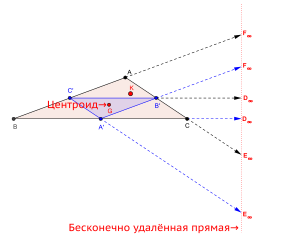
Бесконечно удалённая прямая — трилинейная поляра центроида
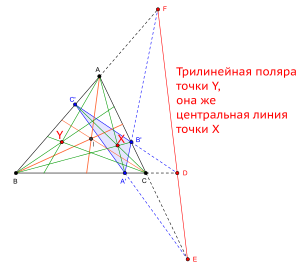
Построение трилинейной поляры точки

Ось Лемуана — трилинейная поляра точки Лемуана показана красным цветом
- Трилинейная полярой точки Лемуана служит ось Лемуана (см. рис.)

Ось внешних биссектрис или антиортовая ось (antiorthic axis) — трилинейная поляра центра вписанной окружности (инцентра) треугольника 

Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра
- Ортоцентрическая ось
(Orthic axis) — трилинейная поляра ортоцентра (см. рис.)
- Трилинейные поляры точек, лежащих на описанной конике, пересекаются в одной точке (для описанной окружности это — точка Лемуана, для описанного эллипса Штейнера — центроид).
Вписанные и описанные фигуры для треугольника[править | править код]
Преобразования[править | править код]
Ниже описаны 3 вида преобразований: 1) Изогональное сопряжение, 2) Изотомическое сопряжение, 3) Изоциркулярное преобразование.
Изогональное сопряжение[править | править код]
- Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны).
- Изогонально сопряжёнными являются многие пары замечательных точек:
- Центр описанной окружности и ортоцентр (точка пересечения высот),
- Центроид (точка пересечения медиан) и точка Лемуана (точка пересечения симедиан),
- Центр девяти точек и точка Косниты треугольника, связанная с теоремой Косниты[34];
- Две точки Брокара;
- Точки Аполлония и точки Торричелли.
- Точка Жергонна и центр отрицательной гомотетии вписанной и описанной окружности.
- Точка Нагеля и центр положительной гомотетии вписанной и описанной окружности (точка Веррьера).
- Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают.
- Фокусы вписанных эллипсов изогонально сопряжены.
- Изогональное сопряжение имеет ровно четыре неподвижные точки (то есть точки, которые сопряжены самим себе): центр вписанной окружности и центры вневписанных окружностей треугольника[35].
- Если для любой внутренней точки треугольника построить три точки, симметричные ей относительно сторон, а затем через три последние провести окружность, то ее центр изогонально сопряжен исходной точке[36].
Изогональные сопряжения линий треугольника[править | править код]
- Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники — в прямые.
- Так, изогонально сопряжены:
- гипербола Киперта и ось Брокара,
- гипербола Енжабека и прямая Эйлера,
- гипербола Фейербаха и линия центров вписанной и описанной окружностей.
- Некоторые известные кубики — например, кубика Томсона — изогонально самосопряжены в том смысле, что при изогональном сопряжении всех их точек в треугольнике снова получаются кубики.
Изотомическое сопряжение[править | править код]
Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением. Оно также переводит прямые в описанные коники.
- Изотомически сопряжены следующие точки:
- точка Жергонна и Нагеля,
- точка пересечения биссектрис (инцентр) и точка пересечения антибиссектрис,
- Точке Лемуана (точке пересечения симедиан) треугольника изотомически сопряжена его точке Брокара,
- Центроид (точка пересечения медиан) изотомически сопряжён сам себе.
При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.
Композиция изогонального (или изотомического) сопряжения и трилинейной поляры[править | править код]
Изоциркулярное преобразование[править | править код]
Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием [39]. Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция — проективное преобразование, которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.
Тригонометрические тождества только с углами[править | править код]
(первое тождество для тангенсов)
Замечание. Соотношение выше применимо только тогда, когда ни один из углов не равен 90° (в таком случае функция тангенса всегда определена).
,[40]
(второе тождество для тангенсов)
,
(первое тождество для синусов)
,[40]
(второе тождество для синусов)
,[7]
(тождество для косинусов)
(тождество для отношения радиусов)
Замечание. При делении обеих частей второго тождества для тангенсов на произведение 
,
по форме (но не по содержанию) очень похожее на первое тождество для тангенсов.
Разные соотношения[править | править код]
Метрические соотношения в треугольнике приведены для 
Где:
,
и
— стороны треугольника,
,
— отрезки, на которые биссектриса
делит сторону
,
,
,
— медианы, проведённые соответственно к сторонам
,
и
,
,
,
— высоты, опущенные соответственно на стороны
,
и
,
— радиус вписанной окружности,
— радиус описанной окружности,
— полупериметр,
— площадь,
— расстояние между центрами вписанной и описанной окружностей.
- Для любого треугольника, у которого стороны связаны неравенствами
, а площадь равна
, длины срединных перпендикуляров или медиатрис, заключённых внутри треугольника, опущенных на соответствующую сторону (отмеченную нижним индексом), равны[41]:Corollaries 5 and 6
,
и
.
Формулы площади треугольника в декартовых координатах на плоскости[править | править код]
- Обозначения
-
— координаты вершин треугольника.
Общая формула площади треугольника в декартовых координатах на плоскости[править | править код]
В частности, если вершина A находится в начале координат (0, 0), а координаты двух других вершин есть B = (xB, yB) и C = (xC, yC), то площадь может быть вычислена в виде 1⁄2 от абсолютного значения определителя
Последнюю формулу площади треугольника в английской литературе именуют формулой площади, заключенной внутри ломаной натянутого на гвозди шнурка (shoelace formula), или геодезической формулой (surveyor’s formula[42]), или формулой площади Гаусса.
Вычисление площади треугольника в пространстве с помощью векторов[править | править код]
Пусть вершины треугольника находятся в точках 


Введём вектор площади ![mathbf {S} ={frac {1}{2}}[mathbf {r} _{B}-mathbf {r} _{A},mathbf {r} _{C}-mathbf {r} _{A}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b21515fcc2caefebf9c4876eab2cfdb298b8b05)
Положим 



и аналогично
Площадь треугольника равна 
Альтернативой служит вычисление длин сторон (по теореме Пифагора) и далее по формуле Герона.
Вычисление площади треугольника через комплексные декартовы координаты его вершин[править | править код]
Если обозначить комплексные декартовы координаты (на комплексной плоскости) вершин треугольника соответственно через 





,
что эквивалентно формуле площади, заключенной внутри ломаной натянутого на гвозди шнурка (shoelace formula), или геодезической формуле (surveyor’s formula[42]), или формуле площади Гаусса.
Треугольник в неевклидовых геометриях[править | править код]
На сфере[править | править код]

Свойства треугольника со сторонами 





Сумма углов (невырожденного) треугольника строго больше 
Любые подобные треугольники равны.
Теорема синусов (здесь и далее сторону сферического треугольника принято измерять не линейной мерой, а величиной опирающегося на неё центрального угла):
,
Теоремы косинусов:
,
.
На плоскости Лобачевского[править | править код]
Для треугольника со сторонами 





Сумма углов (невырожденного) треугольника строго меньше 
Как и на сфере, любые подобные треугольники равны.
Теорема синусов
,
Теоремы косинусов
,
.
Связь суммы углов с площадью треугольника[править | править код]
Значение для суммы углов треугольника во всех трёх случаях (евклидова плоскость, сфера, плоскость Лобачевского) является следствием формулы Гаусса — Бонне
.
В случае треугольника эйлерова характеристика 





|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 января 2017) |
Треугольник в римановой геометрии[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 января 2017) |
Обозначение[править | править код]
| Символ | Юникод | Название |
|---|---|---|
| △ | U+25B3 | white up-pointing triangle |
См. также[править | править код]
- Глоссарий планиметрии
- Тригонометрические тождества
- Тригонометрия
- Энциклопедия центров треугольника
Дополнительные статьи о геометрии треугольника можно найти в категориях:
- Категория:Геометрия треугольника.
- Категория:Теоремы евклидовой геометрии
- Категория:Планиметрия
- Категория:Теоремы планиметрии
Примечания[править | править код]
- ↑ Треугольник // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5.
- ↑ 1 2 Справочник по элементарной математике, 1978, с. 218.
- ↑ Подходова Н. С. [и др.] Раздел II. Теория обучения математике. Глава 7. Математические понятия. Методика работы с ними (п. 7.5. Классификация понятий) // Методика обучения математике в 2 ч. Часть 1 : учебник для вузов / под ред. Н. С. Подходовой, В. И. Снегуровой. — М.: Издательство Юрайт, 2023. — С. 139. — 274 с. — ISBN 978-5-534-08766-6, ББК 74.202.5я73. — ISBN 978-5-534-14731-5.
- ↑ Основанием равнобедренного треугольника всегда называют сторону, не равную двум другим.
- ↑ 1 2 Altshiller-Court, Nathan, College Geometry, Dover, 2007.
- ↑ 1 2 Справочник по элементарной математике, 1978, с. 221.
- ↑ 1 2 Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. задача на с. 120—125. параграф 57, с.73.
- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 41.
- ↑ 1 2 3 4 Справочник по элементарной математике, 1978, с. 219.
- ↑ Шарыгин И. Ф. Глава 3. (п. 3.2. Признаки равенства треугольников) // Геометрия. 7—9 кл.: учеб. для общеобразоват. учреждений / И. Ф. Шарыгин, ответств.ред. Т. С. Зельдман. — М.: Дрофа, 2012. — С. 79—80. — 462 с. — 3000 экз. — ISBN 978-5-358-09918-0, ББК 22.151я72, УДК 373.167.1:514.
- ↑ Корн Г., Корн Т. Справочник по математике, 1973.
- ↑ Корн Г., Корн Т. Справочник по математике, 1973, ф. 1.11-4.
- ↑ Sa ́ndor Nagydobai Kiss, «A Distance Property of the Feuerbach Point and Its Extension», Forum Geometricorum 16, 2016, 283—290. http://forumgeom.fau.edu/FG2016volume16/FG201634.pdf Архивная копия от 24 октября 2018 на Wayback Machine
- ↑ Pathan, Alex, and Tony Collyer, “Area properties of triangles revisited, ” Mathematical Gazette 89, November 2005, 495—497.
- ↑ Mitchell, Douglas W., “The area of a quadrilateral, ” Mathematical Gazette 93, July 2009, 306—309.
- ↑ Baker, Marcus, “A collection of formulae for the area of a plane triangle, « Annals of Mathematics, part 1 in vol. 1(6), January 1885, 134—138; part 2 in vol. 2(1), September 1885, 11-18. The formulas given here are #9, #39a, #39b, #42, and #49. The reader is advised that several of the formulas in this source are not correct.
- ↑ Chakerian, G. D. „A Distorted View of Geometry.“ Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- ↑ Rosenberg, Steven; Spillane, Michael; and Wulf, Daniel B. „Heron triangles and moduli spaces“, Mathematics Teacher 101, May 2008, 656—663.
- ↑ Posamentier, Alfred S., and Lehmann, Ingmar, The Secrets of Triangles, Prometheus Books, 2012.
- ↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5.
- ↑ Глейзер Г. И., 1982, с. 77.
- ↑ Глейзер Г. И., 1982, с. 94—95.
- ↑ 1 2 Из истории геометрии треугольника, 1963, с. 129.
- ↑ Матвиевская Г. П., 2012, с. 40—44.
- ↑ Матвиевская Г. П., 2012, с. 51—55.
- ↑ Матвиевская Г. П., 2012, с. 92—96.
- ↑ Матвиевская Г. П., 2012, с. 111.
- ↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
- ↑ Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I. — С. 105.
- ↑ История математики, том I, 1970, с. 320.
- ↑ 1 2 Из истории геометрии треугольника, 1963, с. 130—132.
- ↑ Из истории геометрии треугольника, 1963, с. 132—133.
- ↑ Rigby, John (1997), Brief notes on some forgotten geometrical theorems. Mathematics and Informatics Quarterly, volume 7, pages 156—158 (as cited by Kimberling).
- ↑ В. В. Прасолов. Точки Брокара и изогональное сопряжение. — М.: МЦНПО, 2000. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-49-9.
- ↑ Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду. Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова. Москва: МЦНМО, 2009.
- ↑ Kimberling, Clark. Central Points and Central Lines in the Plane of a Triangle (англ.) // Mathematics Magazine : magazine. — 1994. — June (vol. 67, no. 3). — P. 163—187. — doi:10.2307/2690608.
- ↑ Kimberling, Clark. Triangle Centers and Central Triangles. — Winnipeg, Canada: Utilitas Mathematica Publishing, Inc., 1998. — С. 285. Архивная копия от 10 марта 2016 на Wayback Machine
- ↑ Мякишев А.Г. Элементы геометрии треугольника(Серия: «Библиотека „Математическое просвещение“») М.:МЦНМО,2002.с.14—17
- ↑ 1 2 Vardan Verdiyan & Daniel Campos Salas, «Simple trigonometric substitutions with broad results», Mathematical Reflections no 6, 2007.
- ↑ Mitchell, Douglas W. (2013), «Perpendicular Bisectors of Triangle Sides», Forum Geometricorum 13, 53-59.
- ↑ 1 2 Bart Braden. The Surveyor’s Area Formula (англ.) // The College Mathematics Journal (англ.) (рус. : magazine. — 1986. — Vol. 17, no. 4. — P. 326—337. — doi:10.2307/2686282. Архивировано 6 апреля 2015 года.
Литература[править | править код]
- Адамар Ж. Элементарная геометрия. Часть 1: Планиметрия. Изд. 4-е, М.: Учпедгиз, 1957. 608 с.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 с.
- Ефремов Дм. Новая геометрия треугольника. Одесса, 1902.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Мякишев А. Г. Элементы геометрии треугольника. — М.: МЦНМО, 2002.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 48-50. — ISBN 5-94057-170-0.
- История
- Гайдук Ю. М., Хованский А. М. Из истории геометрии треугольника // Вопросы истории физико-математических наук. — М.: Высшая школа, 1963. — С. 129—133. — 524 с.
- Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76—95. — 240 с.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
Ссылки[править | править код]
- Расчёт элементов треугольника.
- Расчёт параметров треугольника по координатам его вершин.
Сумма углов треугольника
Доказательство теоремы:
Нарисуем треугольник. Через одну из его вершин проведем прямую, параллельную противоположной стороне, и найдем на рисунке равные углы.
Угол 1 равен углу BAC, они накрест лежащие. Угол 2 равен углу ACB, они тоже накрест лежащие.
Сумма угла 1, угла ABC и угла 2 составляет развернутый угол.
A развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.

Разберем задачи ЕГЭ и ОГЭ, в которых фигурирует сумма углов треугольника.
Заметим, что они похожи друг на друга. Одна и та же задача на тему «Сумма углов треугольника» может встретиться и на ОГЭ, и на ЕГЭ по математике. И уровень сложности заданий по этой теме в ЕГЭ и ОГЭ примерно одинаковый.
Задачи ЕГЭ по теме: Сумма углов треугольника
Задача 1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Решение:
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х.
Получим уравнение:
и найдем x = 17.
Тогда .
Ответ: 51.
Обратите внимание, что это даже не геометрия, а алгебра. Мы составили уравнение и решили его.
Задача 2.
Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Решение:
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны
.
Ответ: 41.
Задача 3.
На рисунке угол 1 равен , угол 2 равен
, угол 3 равен
. Найдите угол 4. Ответ дайте в градусах.

Решение:
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.

Сначала найдем угол 5.
Он равен
Тогда
Угол 4, смежный с углом 7 равен
Ответ:
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Задача 4.
Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.
Решение:
Пусть углы треугольника равны 2x, 3x и 4x. Запишем, чему равна сумма углов этого треугольника.
Тогда
Здесь мы тоже составили уравнение и решили его. Так же, как на уроках алгебры.
Ответ: 40.
Задача 5. В треугольнике ABC проведена биссектриса AL, угол ALC равен , угол ABC равен
. Найдите угол ACB. Ответ дайте в градусах.

Решение:
ALC — внешний угол
и он равен сумме двух внутренних углов, не смежных с ним. Значит,
.
AL — биссектриса , а это значит, что
.
По теореме о сумме углов треугольника получаем:
Ответ: 125.
Задача 6. В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, B=61
D=151
Найдите величину угла A. Ответ дайте в градусах.

Решение:
Если соединить точки B и D, получим два равных треугольника. Они равны по трем сторонам. В равных треугольниках напротив равных сторон лежат равные углы.

В треугольнике ABD сумма двух углов
Тогда , по теореме о сумме углов треугольника.
Ответ: 74.
Задача 7. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен . Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:
AC и BD — диаметры окружности. Значит, — равнобедренный, в нем
— как радиусы.
как вертикальные углы, тогда по теореме о сумме углов в треугольнике:
.
Ответ: 28.
Задача 8. В треугольнике ABC AD — биссектриса, угол C равен , угол CAD равен
. Найдите угол B. Ответ дайте в градусах.

Решение:
AD — биссектриса, отсюда следует, что .
Тогда по теореме о сумме углов треугольника .
Ответ: 66.
Задача 9. В треугольнике ABC CD — медиана, угол C равен , угол B равен
. Найдите угол ACD. Ответ дайте в градусах.

Решение:
В треугольнике ABC угол C равен , угол B равен
, тогда угол A равен
.
CD — медиана. А медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Значит, .
Поэтому треугольник ADC равнобедренный и .
Ответ: 55.
Задача 10. В треугольнике ABC угол C равен , биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах

Решение:
В треугольнике ABC угол C равен , отсюда по теореме о сумме углов треугольника
.
Биссектрисы AD и BE пересекаются в точке O. Угол OAB — это половина угла CAB, угол OBA — это половина угла CBA. Теперь применим теорему о сумме углов треугольника к треугольнику AOB.
Ответ: 119.
Задача 11. В треугольнике ABC угол A равен , углы B и C — острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.

Решение:
BD – высота тогда
— прямоугольный,
CE — высота тогда
— прямоугольный и
.
Углы и
— смежные, поэтому
.
Ответ: 124.
Задача 11. В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

Решение:
Обозначим на рисунке вершины треугольника ABC, биссектрису CК и высоту CН. Биссектриса CК делит прямой угол на два угла по . Угол BCН равен разности углов BCК и КCН, то есть
.

Треугольники BCН и BAC подобны по двум углам. Значит, угол BAC равен углу BCН, то есть
Ответ: 31.
Задача 12. Острые углы прямоугольного треугольника равны и
. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Решение:
Обозначим на рисунке медиану CМ и высоту CН.

Пусть и
. Высота CН разбивает прямоугольный треугольник на два треугольника, подобных исходному. Значит, угол BCН равен углу BAC, то есть
.
у которых углы равны т. е. угол C разбился на углы
и
Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Получили два равнобедренных треугольника, BCМ и ACМ. В треугольнике ACМ углы A и C равны 6 градусов каждый.
Тогда угол МCН между высотой и медианой равен:
Ответ: 78.
Задачи ОГЭ по математике по теме: Сумма углов треугольника.
Задача 13. В треугольнике два угла равны и
. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов в треугольнике равна , поэтому
третий угол равен .
Ответ: 37.
Задача 14. Один из острых углов прямоугольного треугольника равен 34. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма острых углов прямоугольного треугольника равна . Поэтому второй острый угол равен:
.
Ответ: 56.
Задача 15.
В треугольнике ABC известно, что AB=BC, . Найдите угол BCA. Ответ дайте в градусах.

Решение:
В треугольнике ABC известно, что AB=BC. Значит, треугольник ABС равнобедренный, и углы при основании AС равны,
т.е. .
Ответ: 36.
Задача 16. В остроугольном треугольнике ABC проведена высота BH, . Найдите угол ABH. Ответ дайте в градусах.

Решение:
BH — высота , тогда
— прямоугольный, в нем
и
Используя теорему о сумме углов в треугольнике, найдем угол ABH:
Ответ: 53.
Задача 17. В треугольнике ABC угол C равен . Найдите внешний угол при вершине C. Ответ дайте в градусах.

Решение:
Внешний угол треугольника AВC при вершине C является смежным углом с углом ACB, а сумма смежных углов равна .
Значит, внешний угол треугольника ABC при вершине C равен: .
Ответ: 47.
Задача 18. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и . Найдите угол BOC. Ответ дайте в градусах.

Решение:
— равнобедренный,
.
— вписанный угол и опирается на дугу BC, а
— центральный угол и также опирается на дугу BC. Центральный угол в два раза больше вписанного опирающегося на ту же дугу,
.
Ответ: 155.
Задача 19. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ABC=123
. Найдите угол BOC. Ответ дайте в градусах.

Решение:
— равнобедренный треугольник, отсюда
.
— вписанный угол, он опирается на дугу BC, а
— центральный угол и также опирается на дугу BC. Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу, значит,
.
Ответ: 57.
Задача 20. В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен . Найдите угол ACB. Ответ дайте в градусах.

Решение:
AC и BD — диаметры, отсюда следует, что — равнобедренный,
— радиусы.
как вертикальные углы, тогда по теореме о сумме углов в треугольнике
.
Ответ: 33.
Задача 21. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен . Ответ дайте в градусах.

Решение:
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. A это означает, что AB — диаметр. Угол, опирающийся на диаметр, равен , и треугольник ABC – прямоугольный. И если
, то второй острый угол этого треугольника равен:
Ответ: 15.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Сумма углов треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023
Сумма углов треугольника равна (180°).

Доказательство
Рассмотрим произвольный треугольник (KLM) и докажем, что
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
1. Через вершину (L) параллельно стороне (KM) проведём прямую (a).
2. При пересечении параллельных прямых (a) и (KM) секущей (KL), углы, которые обозначаются (1), будут накрест лежащими углами, а углы, обозначенные (2) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е.
∠
(1) (+)
∠
(2) (+)
∠
(3 =)
180°
, или
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна
90°
.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен
45°
.
Следствие 3. В равностороннем треугольнике каждый угол равен
60°
.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Доказательство
Из равенств
∠
(KML) (+)
∠
(BML=)
180°
и
∠
(K) (+)
∠
(L) (+)
∠
(KML =)
180°
получаем, что
∠
(BML =)
∠
(K) (+)
∠
(L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.

У треугольника (KLM) все углы острые.

У треугольника (KMN) угол (K = 90)
°
.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.

У треугольника (KLM) один угол тупой.
Треугольник
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

- типы треугольников
- вершины углы и стороны треугольника
- медианы треугольника
- биссектрисы треугольника
- высоты треугольника
- окружность вписанная в треугольник
- окружность описанная вокруг треугольника
- связь между вписанной и описанной окружностями треугольника
- средняя линия треугольника
- периметр треугольника
- формулы площади треугольника
- равенство треугольников
- подобие треугольников
- прямоугольные треугольники
Типы треугольников
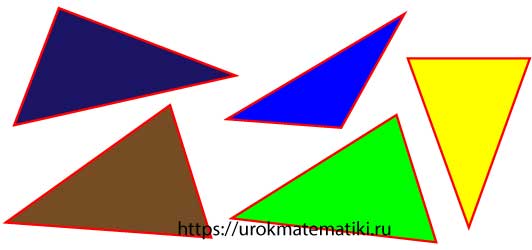
По величине углов
Остроугольный треугольник

— все углы треугольника острые.
Тупоугольный треугольник

— один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник

— один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник
— все три стороны не равны.
Равнобедренный треугольник

— две стороны равны.
Равносторонний (правильный) треугольник

— все три стороны равны.
Вершины, углы и стороны треугольника
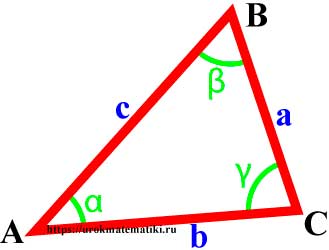
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
- если α > β, тогда a > b
- если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
asinα = bsinβ = csinγ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 – 2bc·cos α
b2 = a2 + c2 – 2ac·cos β
c2 = a2 + b2 – 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a = 232mb2+mc2-ma2b = 232ma2+mc2-mb2c = 232ma2+mb2-mc2
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.
- В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD=
BOOE=COOF=21 - Медиана треугольника делит треугольник на две равновеликие частиS∆ABD=S∆ACDS∆BEA=S∆BECS∆CBF=S∆CAF
- Треугольник делится тремя медианами на шесть равновеликих треугольниковS∆AOF=S∆AOE=S∆BOF=S∆BOD=S∆COD=S∆COE
- Из векторов, образующих медианы, можно составить треугольник
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 122b2+2c2-a2mb = 122a2+2c2-b2mc = 122a2+2b2-c2
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
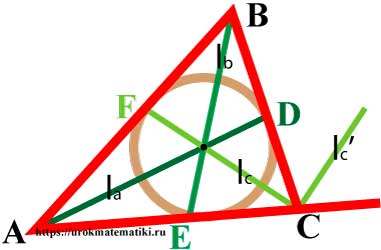
Свойства биссектрис треугольника
- Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, – центре вписанной окружности.
- Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB=
ECBC - Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°
Угол между
lc и lc’ = 90°
- Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
la = 2bcpp-ab+clb = 2acpp-ba+clc = 2abpp-ca+b
где p = a+b+c2 — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
la = 2bc cosα2b+clb = 2ac cosβ2a+clc = 2ab cosγ2a+b
Высоты треугольника
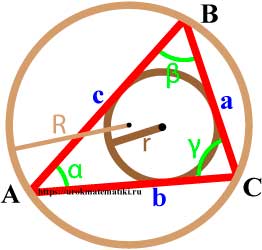
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
- Если в треугольнике две высоты равны, то треугольник — равнобедренный.
- ha:hb:hc=1a:1b:1c=
BC:AC:AB - 1ha:1hb:1hc=1r
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
ha = b sin γ = c sin βhb = c sin α = a sin γhc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь
ha = 2Sahb = 2Sbhc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности
ha = bc2Rhb = ac2Rhc = ab2R
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
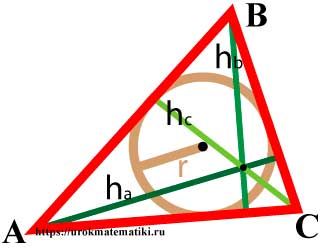
Свойства окружности вписанной в треугольник
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
r = Sp
Радиус вписанной в треугольник окружности через три стороны
r = a+b-cb+c-ac+a-b4a+b+c
Формулы высот треугольника через две стороны и радиус описанной окружности
1r=1ha+1hb+1hc
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
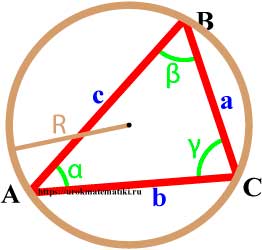
Свойства окружности описанной вокруг треугольника
- Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
- Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
R = abc4S
Радиус описанной окружности через площадь и три угла
R = S2 sinα sinβ sinγ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
R =a2 sinα+b2 sinβ+c2 sinγ
Связь между вписанной и описанной окружностями треугольника
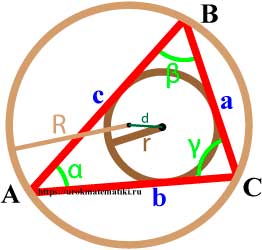
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
d2 = R2 – 2Rr
Радиус описанной окружности через площадь и три угла
rR = 4sinα2 sinβ2 sinγ2 = cosα + cosβ + cosγ
2Rr =abca+b+c
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
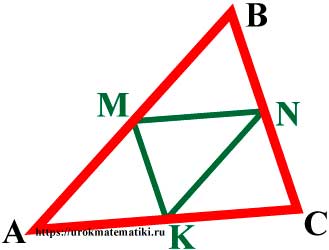
Свойства средней линии треугольника
- Любой треугольник имеет три средних линии.
- Средняя линия треугольника параллельна основанию и равна его половине.
MN= 12AC; KN= 12AB; KM= 12BCMN || AC; KN || AB; KM || BC - Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника.
S∆MBN = 14S∆ABC; S∆MAK = 14S∆ABC;
S∆NCK = 14S∆ABC - При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
∆MBN ~ ∆ABC;
∆AMK ~ ∆ABC;
∆KNC ~ ∆ABC;
∆NKM ~ ∆ABC
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
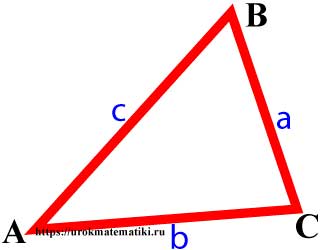
Периметр треугольника ∆ABC равен сумме длин его сторон.
P = a + b + c
Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S = 12 a · ha
,
S = 12 b · hb
,
S = 12 c · hc
,
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.
S = pp-ap-bp-c
,
где p — полупериметр треугольника: p = a + b + c2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 12 a · b · sinγ
,
S = 12 b · c · sinα
,
S = 12 a · c · sinβ
,
где a, b, c — стороны треугольника,
γ — угол между сторонами a и b,
α — угол между сторонами b и c,
β — угол между сторонами a и c.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
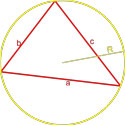
S = a · b · c4R
,
a, b, c — стороны треугольника,
R – радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S = p · r
,
где S — площадь треугольника,
r – радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c2
Равенство треугольников
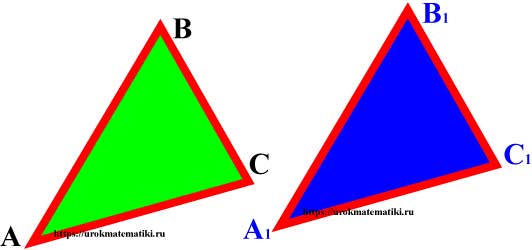
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Теорема.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Теорема.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Теорема.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
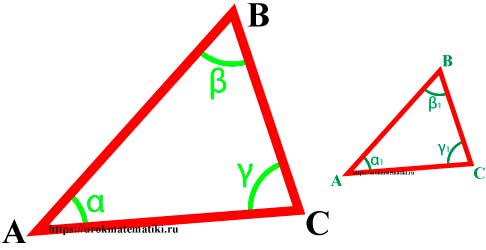
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
∆АВС~∆MNK=> α=α1
,
β=β1
,
γ=γ1
и
ABMN=BCNK=ACMK=k
где k — коэффициент подобия.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK=k2
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
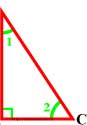
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∠ 1+∠ 2=90°.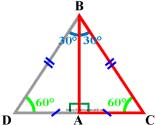
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.
Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK=k2
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике






![{displaystyle {dfrac {a-b}{a+b}}={dfrac {operatorname {tg} {dfrac {alpha -beta }{2}}}{operatorname {tg} {dfrac {alpha +beta }{2}}}}={dfrac {operatorname {tg} {dfrac {alpha -beta }{2}}}{operatorname {ctg} {dfrac {gamma }{2}}}};quad {frac {b-c}{b+c}}={frac {operatorname {tg} [{frac {1}{2}}(beta -gamma )]}{operatorname {tg} [{frac {1}{2}}(beta +gamma )]}};{frac {a-c}{a+c}}={frac {operatorname {tg} [{frac {1}{2}}(alpha -gamma )]}{operatorname {tg} [{frac {1}{2}}(alpha +gamma )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04c97f77f6f451b3556bf0038f041c4f87fa2095)






















