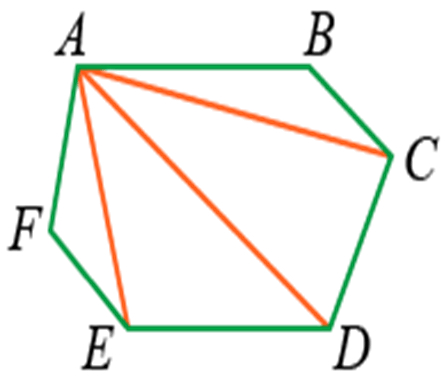
Плоская фигура, образованная замкнутым рядом прямолинейных отрезков, называется многоугольником. На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника; сумма длин сторон АВ + ВС + CD + … + FA называется периметром и обозначается р, а иногда 2р (тогда р — полупериметр).
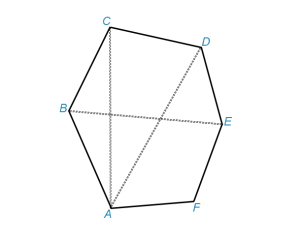 рис.1
рис.1
В элементарной геометрии рассматриваются только простые многоугольники, т. е. такие, контур которых не имеет самопересечений.
Многоугольники, контур которых имеет самопересечения, называются звездчатыми многоугольниками. На рис.2 изображен звездчатый многоугольник ABCDE.
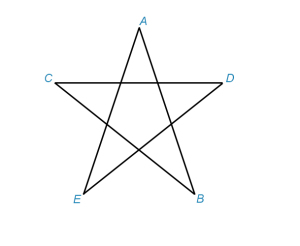 рис.2
рис.2
Если все диагонали многоугольника лежат внутри него, многоугольник называется выпуклым.
Шестиугольник на рис.1 выпуклый; пятиугольник на рис.3 невыпуклый (диагональ ЕС лежит вне многоугольника).
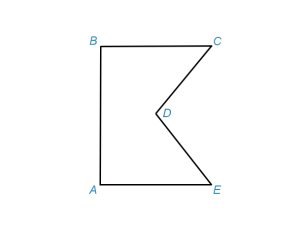 рис.3
рис.3
Сумма внутренних углов во всяком выпуклом многоугольнике равна 180° (n-2), где n — число сторон многоугольника*.
* В учебниках геометрии это свойство высказывается обычно только для выпуклых многоугольников. Но оно справедливо для всех простых многоугольников. Но оно справедливо для всех простых многоугольников. Нужно заметить, что в невыпуклом многоугольнике один или несколько внутренних углов превышают 180°. Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.
Чему равна сумма углов многоугольника?
В евклидовой геометрии сумма углов плоского n-угольника равна 180°(n–2). В частности:
- сумма углов треугольника — 180°;
- сумма углов четырехугольника — 360°;
- сумма углов пятиугольника — 540°;
- сумма углов шестиугольника — 720°;
- сумма углов семиугольника — 900°;
- сумма углов восьмиугольника — 1080°.
Доказательство данной теоремы для случая выпуклого n-угольника
В случае n=3 мы имеем дело с треугольником.
Сумма углов треугольника
всегда равна 180°. В случае n>3 нужно провести из любой вершины многоугольника диагонали ко все несмежным вершинам. Таких диагоналей будет n–3, и они разобью многоугольник на n–2 прилегающих друг к другу треугольников. Сумма углов многоугольника совпадает с суммой углов всех этих треугольников. Сумма углов в каждом треугольнике равна 180°, а число этих треугольников есть n–2. Следовательно, сумма углов n-угольника равна 180°(n–2). Теорема доказана.
Для невыпуклого n-угольника сумма углов также равна 180°(n–2). Доказательство аналогично, но использует в дополнение лемму о том, что любой многоугольник может быть разрезан диагоналями на треугольники.
Источники:
- ru.wikipedia.org — Википедия: Теорема о сумме углов многоугольника (с доказательством)
- ru.wikipedia.org — Википедия: Теорема о сумме углов треугольника (с доказательством)
- profmeter.com.ua — Теорема о сумме углов выпуклого многоугольника
Дополнительно на Геноне:
- Чему равна сумма углов треугольника?
Последнее редактирование ответа: 23.10.2011
-

Оставить отзывОставить отзыв
Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!
Если Вы хотите получить уведомление об
исправлении ответа укажите свой e-mail:Неправильный формат адреса электронной почты
 Похожие вопросы
Похожие вопросы
- Кто такой Евклид?
- Каковы свойства прямоугольника?
- Что такое прямоугольник?
- Какова биография Евклида?
- Что такое биссектриса?
- Что такое треугольник?
- Какие бывают треугольники?
- Что такое медиана?
- Каковы свойства треугольников?
- О чем говорится в тереме синусов?
В соответствии с пользовательским соглашением администрация не несет ответственности за содержание материалов, которые размещают пользователи. Для урегулирования спорных вопросов и претензий Вы можете связаться с администрацией сайта genon.ru.
Размещенные на сайте материалы могут содержать информацию, предназначенную для пользователей старше 18 лет, согласно Федерального закона №436-ФЗ от 29.12.2010 года “О защите детей от информации, причиняющей вред их здоровью и развитию”. Обращение к пользователям 18+.
В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.
Поговорим подробнее о видах многоугольников и их характеристиках.
Определение
Многоугольник — это замкнутая ломаная линия.
Многоугольник — это простое понятие: Если в замкнутой ломаной линии соседние стороны имеют общую точку и любые две стороны не являются продолжением друг друга, то фигура называется многоугольником.
При изучении темы, что такое многоугольники, применяются следующие термины:
- Вершины многоугольника.
- Стороны замкнутой ломаной.
- Углы, образованные между смежными сторонами.
- Отрезки между несмежными вершинами называются диагоналями.
- Сумма длин всех сторон фигуры является периметром.
- Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.
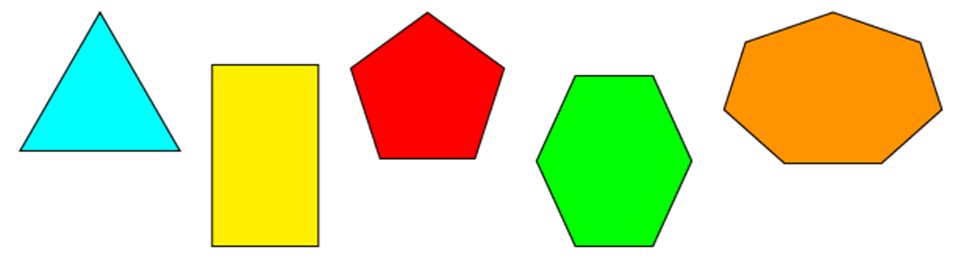
Наименования данных фигур зависят от количества сторон:
- Треугольник – это 3 стороны.
- Четырехугольник имеет 4 стороны.
- Пятиугольник – это 5 сторон и пр.
Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.
Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.
Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.
Виды многоугольников
Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.
Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.
Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.
Что такое правильные многоугольники
Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.
На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали
Периметром многоугольника называется сумма длин его сторон.
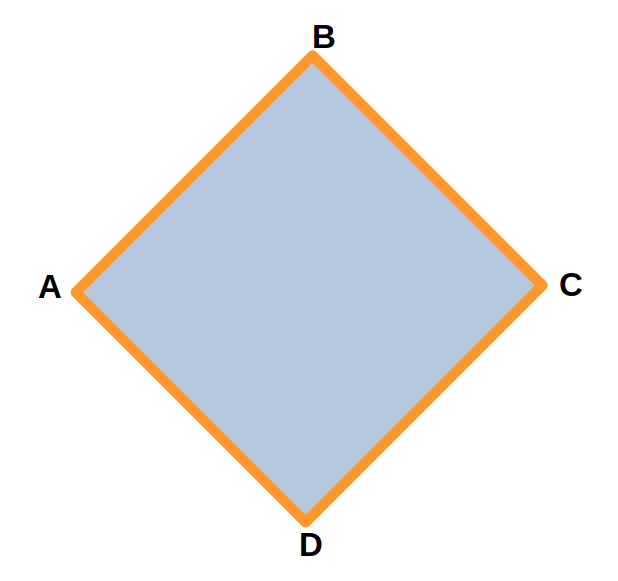
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.
Пример
Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти
периметр четырехугольника.
Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см
Ответ: периметр четырехугольника ABCD равен 12 см.
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.
Например, отрезок AD будет являться диагональю фигуры ABCDEF:
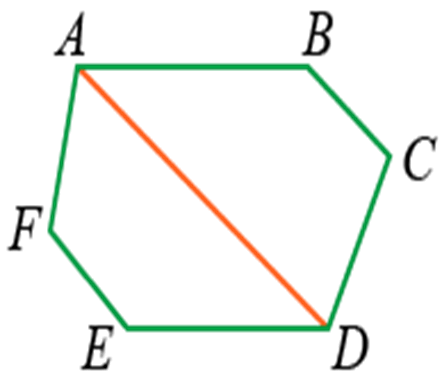
Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:
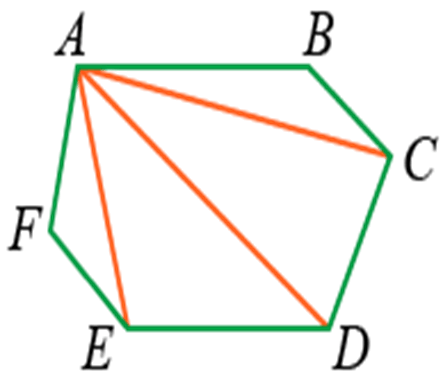
Количество треугольников будет на 2 меньше, чем число сторон:
Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.
Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.
Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.
Сумма углов выпуклого многоугольника
Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.
Внутренним называется угол между смежными сторонами.
Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.
Например, ∠LBC является внешним углом для ABCDEF.
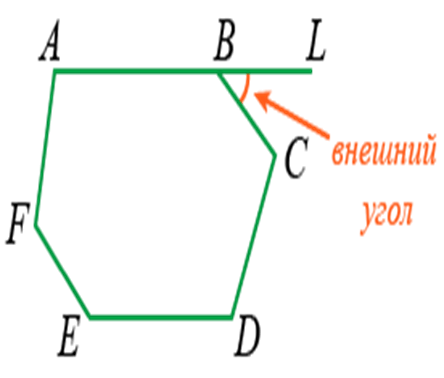
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.
Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.
Сумма внутренних углов
Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.
Обозначения выглядят следующим образом:
- сумма углов – s;
- число сторон – n;
- два прямых угла (2 · 90 = 180°) – 2d.
Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).
Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).
Пример:
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.
Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.
Нет времени решать самому?
Наши эксперты помогут!
Сумма внешних углов
Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.
Где:
- s — сумма внешних углов;
- 4d — четыре прямых угла (4 · 90 = 360°).
Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).
Например, ∠1 и ∠2:
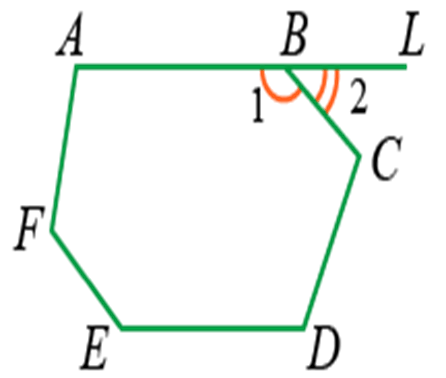
Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.
Пример
Задание: Найдите сумму углов выпуклого двенадцатиугольника.
Решение: Для выпуклого n-угольника сумма углов равна 180° (n -2).
Если имеется 12 вершин, то сумма всех углов будет рассчитываться следующим образом: 2 · 90 · (12 – 2) = 1800°.
Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.
Теорема о сумме углов многоугольника выражает сумму углов евклидова многоугольника через число его сторон.
Формулировка[править | править код]
Сумма внутренних углов плоского 

Замечания[править | править код]
- Теорема следует из существования триангуляции многоугольника без дополнительных вершин и теоремы о сумме углов треугольника.
- Существование триангуляции очень просто доказывается для выпуклых многоугольников, в случае невыпуклых многоугольников оно не вполне очевидно.
- Утверждение теоремы эквивалентно тому, что сумма ориентированных внешних углов многоугольника равна ±360°.
Вариации и обобщения[править | править код]
- Задача о триангуляции многоугольника.
- Теорема о сумме углов треугольника — важный частный случай теоремы.
- Теорема о повороте кривой — дифференциальногеометрический вариант теоремы о сумме углов многоугольника.
- Формула Гаусса — Бонне — аналогичный результат для искривлённых поверностей.
Литература[править | править код]
- § 82 в А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
Многоугольники |
|||||
|---|---|---|---|---|---|
| По числу сторон |
|
||||
| Правильные |
|
||||
| Треугольники |
|
||||
| Четырёхугольники |
|
||||
| См. также |
|
math-public:mnogougolniki
Содержание
Назад — Оглавление — Вперед
Многоугольники.
Ломаная
Определение
Ломаной линией, или короче, ломаной, называется конечная последовательность отрезков, такая, что один из концов первого отрезка служит концом второго, другой конец второго отрезка служит концом третьего и т.д. При этом соседние отрезки не лежат на одной прямой. Эти отрезки называют звеньями ломаной.
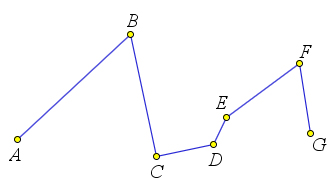
Виды ломаной
-
Ломаная называется замкнутой, если начало первого отрезка совпадает с концом последнего.
-
Ломаная может пересекать сама себя, коснуться сама себя, налегать на себя. Если таких особенностей нет, то такая ломаная называется простой.
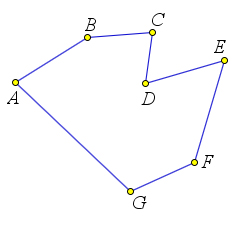
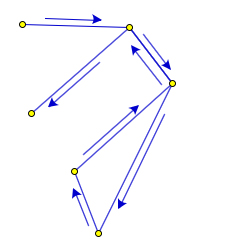
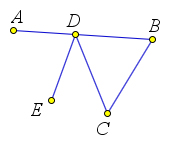
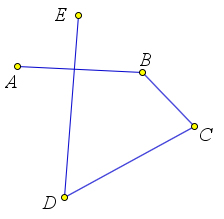
Многоугольники
Определение
Простая замкнутая ломаная вместе с частью плоскости, ограниченной ею, называется многоугольником.
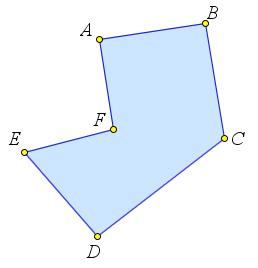
Замечание
В каждой вершине многоугольника его стороны задают некоторый угол многоугольника. Он может быть как меньше развернутого, так и больше развернутого.
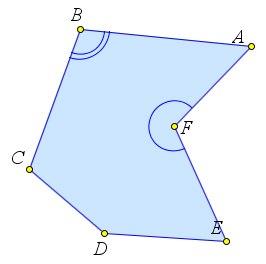
Свойство
У каждого многоугольника есть угол, меньший $180^circ$.
Доказательство
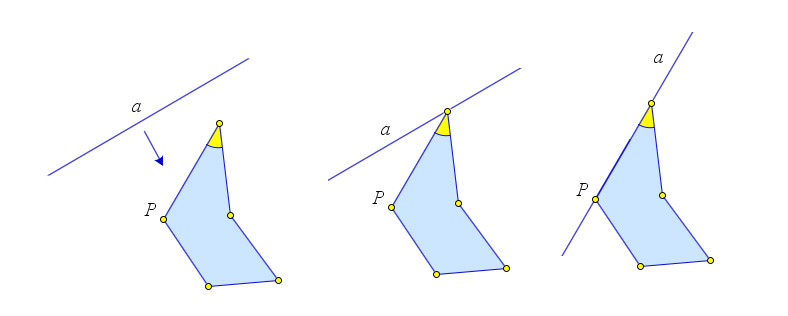
Пусть дан многоугольник $P$.
Проведем какую-нибудь прямую, не пересекающую его. Будем перемещать ее параллельно в сторону многоугольника. В некоторый момент мы впервые получим прямую $a$, имеющую с многоугольником $P$ хотя бы одну общую точку. От этой прямой многоугольник лежит по одну сторону (при этом некоторые его точки лежат на прямой $a$).
На прямой $a$ лежит хотя бы одна вершина многоугольника. В ней сходится две его стороны, расположенные по одну сторону от прямой $a$ (считая и тот случай, когда одна из них лежит на этой прямой). А значит, при этой вершине угол меньше развернутого.
Определение
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Если многоугольник не является выпуклым, его называют невыпуклым.
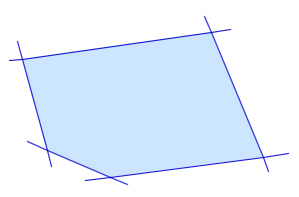
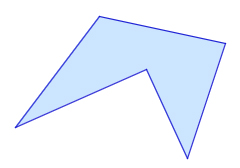
Замечание
Выпуклый многоугольник является пересечением полуплоскостей, ограниченных прямыми, которые содержат стороны многоугольника.
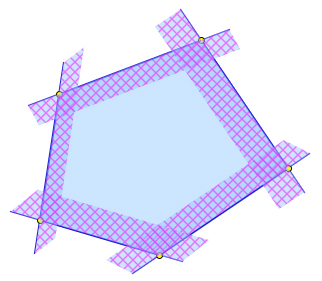
Свойства выпуклого многоугольника
-
У выпуклого многоугольника все углы меньше $180^circ$.
-
Отрезок, соединяющий любые две точки выпуклого многоугольника (в частности, любая его диагональ), содержится в этом многоугольнике.
Доказательство
Докажем первое свойство
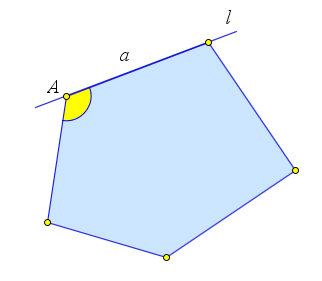
Возьмем любой угол $A$ выпуклого многоугольника $P$ и его сторону $a$, идущую из вершины $A$. Пусть $l$ – прямая, содержащая сторону $a$. Так как многоугольник $P$ выпуклый, то он лежит по одну сторону от прямой $l$. Следовательно, и его угол $A$ лежит по одну сторону от этой прямой. Значит угол $A$ меньше развернутого угла, то есть меньше $180^circ$.
Докажем второе свойство
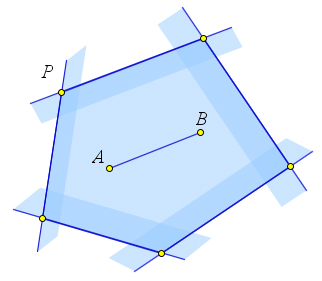
Возьмем любые две точки $A$ и $B$ выпуклого многоугольника $P$. Многоугольник $P$ является пересечением нескольких полуплоскостей. Отрезок $AB$ содержится в каждой из этих полуплоскостей. Поэтому он содержится и в многоугольнике $P$.
Определение
Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины.
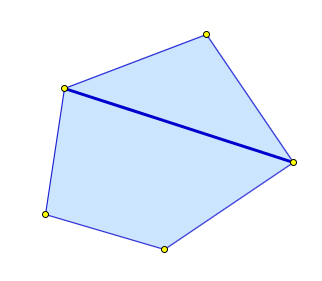
Теорема (о количестве диагоналей n-угольника)
Количество диагоналей выпуклого $n$-угольника вычисляется по формуле $dfrac{n(n-3)}{2}$.
Доказательство
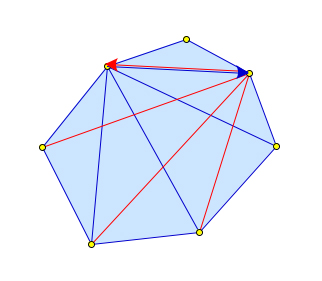
Из каждой вершины n-угольника можно провести $n-3$ диагонали (нельзя провести диагональ в соседние вершины и в саму эту вершину). Если посчитать все такие возможные отрезки, то их будет $ncdot(n-3)$, так как вершин $n$. Но каждая диагональ будет посчитана дважды. Таким образом, количество диагоналей n-угольника равно $dfrac{n(n-3)}{2}$.
Теорема (о сумме углов n-угольника)
Сумма углов выпуклого $n$-угольника равна $180^circ(n-2)$.
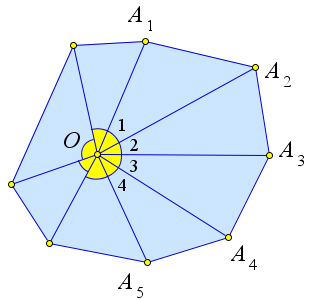
Доказательство
Рассмотрим $n$-угольник $A_1A_2A_3ldots A_n$.
Возьмём внутри этого многоугольника произвольную точку $O$.
Сумма углов всех треугольников $A_1OA_2$, $A_2OA_3$, $A_3OA_4$, $ldots$, $A_{n-1}OA_n$
равна $180^circcdot n$.
C другой стороны эта сумма складывается из суммы всех внутренних углов многоугольника и полного угла $angle O=angle 1+angle 2+angle 3+ldots=360^circ$.
Тогда сумма углов рассматриваемого $n$-угольника равна $180^circcdot n-360^circ=180^circcdot(n-2)$.
Теорема
Сумма углов невыпуклого $n$-угольника равна $180^circ(n-2)$.
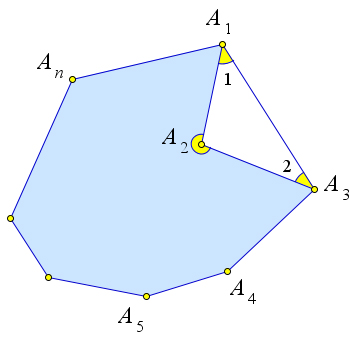
(без доказательства)
Теорема (о сумме внешних углов выпуклого n-угольника)
Сумма внешних углов выпуклого $n$-угольника равна $360^circ$.
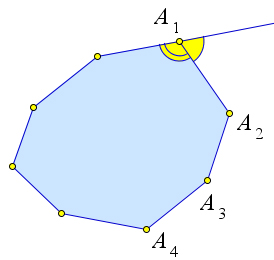
Доказательство
Внешний угол при вершине $A_1$ равен $180^circ-angle A_1$.
Сумма всех внешних углов равна:
$sumlimits_{n}(180^circ-angle A_n)=ncdot180^circ –
sumlimits_{n}A_n=ncdot180^circ – 180^circcdot(n-2)=360^circ$.
· Последнее изменение: 2022/01/14 17:49 —
mesuslina

