Сумма углов прямоугольного треугольника

4.5
Средняя оценка: 4.5
Всего получено оценок: 265.
Обновлено 9 Июля, 2021
4.5
Средняя оценка: 4.5
Всего получено оценок: 265.
Обновлено 9 Июля, 2021
Сумма углов любого треугольника – величина устойчивая. Но прямоугольный треугольник выделяется среди прочих набором специфических свойств. Сумма углов не является исключением, поэтому стоит поговорить об этом свойстве прямоугольных треугольников, чтобы не возникало вопросов в дальнейшем изучении.
Опыт работы учителем математики – более 33 лет.
Треугольник
Несмотря на свою обособленность от прочих фигур, треугольник является таким же многоугольником, как и прямоугольник, квадрат или ромб. Все отличие только в количестве углов. Существует формула, по которой определяется сумма углов любого многоугольника в зависимости от количества сторон, поговорим о ней немного позже.
Итак, треугольник это фигура, имеющая три стороны и три угла. Традиционно, одна из сторон считается основанием, а две другие стороны зовутся боковыми. Обозначение не является принципиальным, поэтому любая из сторон треугольника принимается за условное основание. Такое обозначение нужно только для облегчения понимания чертежа.
Треугольник в математике считается минимально возможно фигурой. Любая из возможных фигур может быть разбита на треугольники. Это свойство иногда используется при решении задач.
Сумма углов треугольника
Есть два варианта нахождения общей суммы углов треугольника:
- Математический анализ. За столь страшными словами кроется обычная простая формула:
180*(n-2)- где n – количество сторон многоугольника.
- Второй способ – геометрический. Именно таким образом было в первый раз выведено утверждение о том, что сумма углов треугольника равна 180 градусам. Рассмотрим его подробнее.
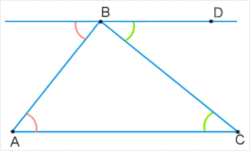
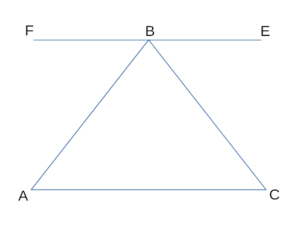
Пусть треугольник АВС – произвольный треугольник с основанием АС. Тогда построим прямую ВD, проходящую через точку В, параллельно основанию. Тогда получается две параллельные прямые: АС и ВD с двумя секущими АВ и ВС.
Рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.
Важно понимать, что наружные углы нельзя называть внешними углами треугольника, так как внешние углы получаются с помощью продолжения одной из сторон треугольника, а прямая ВD продолжением стороны треугольника не является.
Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.
Прямоугольный треугольник
Прямоугольный треугольник содержит угол в 90 градусов. Такой угол зовут прямым, отсюда и название фигуры. Чему равна сумма углов прямоугольного треугольника? Так же,как и в любом другом треугольнике – 180 градусам. Но если один из углов определен и равен 90 градусам, то можно определить сумму двух оставшихся:
180-90=90 – то есть сумма непрямых углов прямоугольного треугольника равна 90 градусам.
Но непрямые углы это нематематическое определение. Может ли в прямоугольном треугольнике еще один угол быть прямым? Если бы такой угол мог существовать, то он был бы равен 90 градусам. То есть оставшийся третий угол:
90-90=0 – и третий угол в этом случае был бы нулевым, что невозможно. Так же, как и невозможно существование тупого угла в прямоугольном треугольнике. Потому что тупой угол всегда больше 90 градусов.
Значит, можно сделать вывод о том, что в прямоугольном треугольнике сумма острых углов равна 90 градусам.
Что мы узнали?
Мы поговорили о формуле суммы углов прямоугольного треугольника. Вывели ее геометрическим способом и определили аналитический способ вывода, который вытекает из геометрического. Рассказали, почему невозможно существование тупоугольного прямоугольного треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 265.
А какая ваша оценка?
Сумма острых углов прямоугольного треугольника
Чему равна сумма острых углов прямоугольного треугольника? Это свойство прямоугольного треугольника вытекает из теоремы о сумме углов треугольника.
Утверждение.
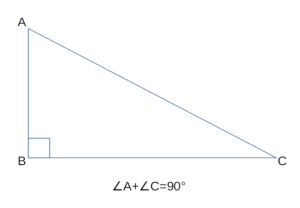
Сумма острых углов прямоугольного треугольника равна 90º.
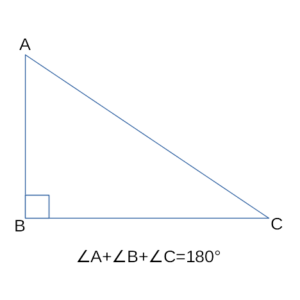
Дано:
∆ABC,
∠C=90º.
Доказать:
∠A+∠B=90º.
Доказательство:
По теореме о сумме углов треугольника,
∠A+∠B+∠C=180º.
По условию, ∠C=90º.
Отсюда, ∠A+∠B+90º=180º.
Следовательно, ∠A+∠B=180º-90º= 90º.
Что и требовалось доказать.
Добавить комментарий
Обновлено 04.08.2020
Содержание
- Теорема о сумме углов прямоугольного треугольника
- Докажем, что в любом треугольнике сумма углов 180°:
- Докажем, что в прямоугольном треугольнике сумма острых углов 90°:
- Следствия из доказанных теорем:
Теорема о сумме углов прямоугольного треугольника
Сумма углов прямоугольного треугольника равна 180°
Докажем, что в любом треугольнике сумма углов 180°:
- АBC — треугольник
- Доп. построение: через вершину B проведем прямую FE параллельно основанию AC
- ∠CBE=∠C(внутренние накрест лежащие при параллельных FEAC, и секущей BC) и A(внутренние накрест лежащие при и секущей AB)
- ∠FBE=∠FBA+∠B+∠CBE(так как развернутый) ⇒ 180°=A+B+C ч.т.д.
Сумма острых углов прямоугольного треугольника равна 90°
Докажем, что в прямоугольном треугольнике сумма острых углов 90°:
- △ABC- прямоугольный
- ∠B — прямой(так как △ABC- прямоугольный)
- ∠A+∠B+∠C=180°(сумма углов треугольника) ⇒ ∠А+∠C=180°-∠B ⇒ ∠A+∠C=90° ч.т.д
Следствия из доказанных теорем:
- Сумма острых углов прямоугольного треугольника равна 90°.
- В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
- В равностороннем треугольнике каждый угол равен 60°.
- В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Всем привет. Сегодня наша тема посвящена прямоугольным треугольникам. этой статье мы собрали все основные свойства прямоугольного треугольника которые вам понадобятся при решении ЕГЭ.
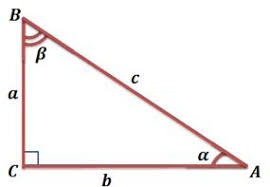
Прямоугольный треугольник – треугольник, имеющий прямой угол. Сторону противолежащую прямому углу называют гипотенузой, а стороны образующие прямой угол – катетами.
1. Катет противолежащий углу в 30˚, равен половине гипотенузы.
2. Сумма острых углов в прямоугольном треугольнике равна 90˚.
3. Высота проведенная из вершины прямого угла, разбивает прямоугольник на два подобных треугольника. И оба эти треугольника подобны исходному. ACH ∼ BCH ∼ ABC.
4. Медиана проведенная к гипотенузе в прямоугольном треугольнике равна ее половине. А так же является радиусом описанной окружности.
5. Центр описанной окружности, является серединой гипотенузы. Радиус описанной окружности равен половине гипотенузы и медиане проведенной из прямого угла. Диаметр описанной окружности равен гипотенузе.
6. Радиус вписанной окружности в прямоугольный треугольник равен сумме катетов минус гипотенузу, поделенные пополам.
Теорема Пифагора
Квадрат длины гипотенузы равен сумме квадратов длин катетов. Или квадрат гипотенузы равен сумме квадратов катетов.
Прямоугольный треугольник со сторонами 3, 4 и 5 называется египетским треугольником. Применяется для построения прямых углов на земной поверхности.
Площадь прямоугольного треугольника
- Можно найти зная два катета.
- Через гипотенузу и высоту проведенную к гипотенузе.
Понравилась статья? Если да, то подписывайся на мой канал. Если нет, то напиши почему, мне важно твое мнение!
Прямоугольный треугольник – это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А$: $ВС$ – противолежащий катет; $АС$ – прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = – 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$