Вектор-функции
Предел и непрерывность вектор-функции.
Понятие вектор-функции.
Если каждому значению (tin E), где (Esubsetmathbb), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).
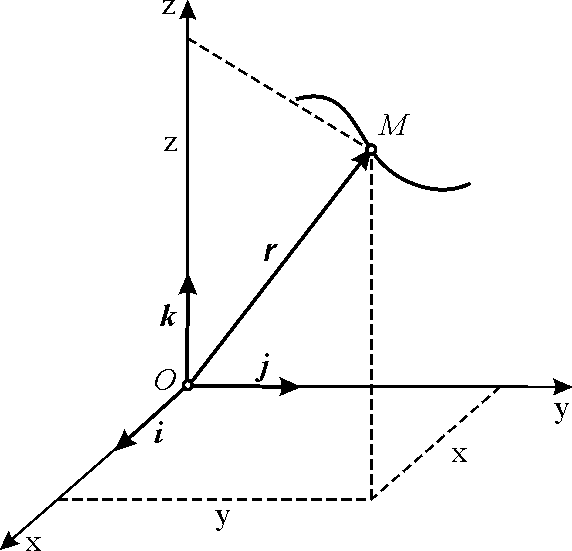
Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.
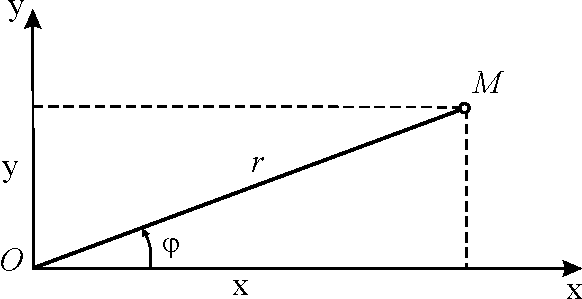
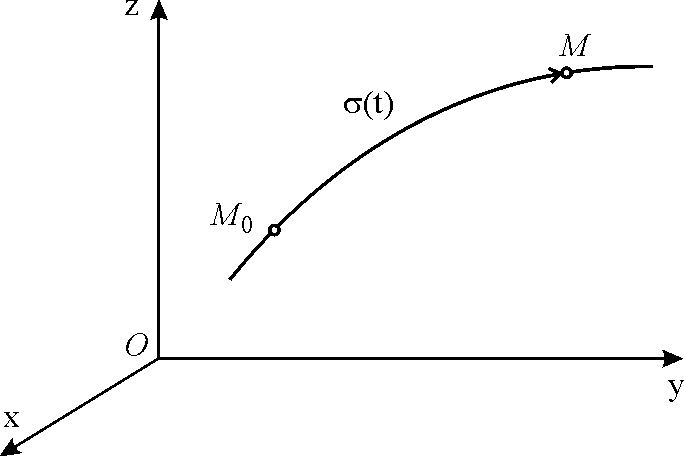
В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.
Предел вектор-функции.
Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_>r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_> |r(t)-a|=0,label
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).
Рис. 20.1
Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_<1>,a_<2>,a_<3>)), то
$$
lim_>r(t)=alabel
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label
$$
Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref, то выполняется условие eqref.
Обратно: если выполняются условия eqref, то из равенства eqref следует, что выполнено условие eqref. (bullet)
При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox <при> trightarrow t_<0>.nonumber
$$
Свойства пределов вектор-функций.
(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$
Если (r(t)rightarrow a) при (trightarrow t_<0>), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_<0>), то (f(t)r(t)rightarrow Aa) при (trightarrow t_<0>), то есть
$$
lim_f(t)r(t)=lim_>f(t)lim_r(t).label
$$
(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref. (bullet)
(circ) По условию (r_(t)=a_+alpha_), где (a_i(t)rightarrow 0) при (trightarrow t_<0> (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_<1>(t)+alpha_2(t)rightarrow 0) при (trightarrow t_<0>), откуда следует eqref. Докажем формулу eqref. В силу свойств скалярного произведения
$$
(r_<1>(t),r_2(t))-(a_1,a_2)=(alpha_<1>(t),a_<2>)+(alpha_<2>(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_<1>(t),alpha_<2>(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).
Аналогично доказывается формула eqref, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)
Непрерывность вектор-функции.
Вектор-функцию (r(t)) называют непрерывной при (t=t_<0>), если
$$
lim_>r(t)=r(t_0).label
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_<0>) в силу эквивалентности условий eqref и eqref означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_<0>).
Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_<0>). Тогда условие eqref означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label
$$
Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_<0>), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_<0>).
Производная и дифференциал вектор-функции.
Производная вектор-функции.
Если существует (displaystyle lim_<Delta trightarrow 0>frac<Delta r><Delta t>) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot(t_0)).
Таким образом,
$$
r'(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r(t_<0>)><Delta t>.label
$$
Аналогично вводится понятие второй производной
$$
r″(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r'(t_<0>)><Delta t>nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_<0>)=(x'(t_0),y'(t_0),z'(t_0))label
$$
Утверждение eqref следует из определения eqref и свойств пределов вектор-функций.
Аналогично, если существует (r″(t_<0>)), то
$$
r″(t_<0>)=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref, то есть вектор-функция (r(t)), имеющая производную в точке (t_<0>), непрерывна при (t=t_<0>).
(circ) Формулы eqref-eqref справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref. Пусть (Delta r_) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin
(r_<1>,r_<2>)’=displaystylelim_<Delta trightarrow 0>frac<(r_<1>(t+Delta t),r_<2>(t+Delta t))-(r_<1>(t),r_<2>(t))><Delta t>=\
=lim_<Delta trightarrow 0>left[left(r_<1>(t),frac<Delta r_<2>(t)><Delta t>right)+left(frac<Delta r_<1>(t)><Delta t>,r_2(t)right)+left(frac<Delta r_<1>(t)><Delta t>,Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
endnonumber
$$
так как (displaystyle frac<triangle mathrm_><triangle t>rightarrow r_‘(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)
Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).
Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.
(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^<2>)’=(C^<2>)’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$
Дифференциал вектор-функции.
Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_<0>), называют дифференцируемой при (t=t_<0>), если ее приращение (Delta r=r(t_<0>+Delta t)-r(t_<0>)) в точке (t_<0>) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
Полагая (dt=Delta t), запишем равенство eqref в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac
$$
Замена переменного.
Если функция (t=t(s)) дифференцируема при (s=s_<0>, t(s_<0>)=t_<0>), а вектор-функция (r(t)) дифференцируема в точке (t_<0>), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_<0>), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_'(t_<0>)t_‘(s_<0>),label
$$
где индекс указывает, по какому переменному производится дифференцирование.
(circ) Функция (alpha(Delta(t))) в формуле eqref не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).
Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_<0>+Delta s)-t(s_<0>)rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref на (Delta sneq 0), получим
$$
frac<Delta r><Delta s>=r'(t_0)frac<Delta t><Delta s>+alpha(Delta t)frac<Delta t><Delta s>.label
$$
Правая часть eqref имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref, и справедливо равенство eqref. Формулу eqref запишем кратко в виде равенства
$$
r_’=r_’t_’,label
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label
$$
для вектор-функции, вообще говоря, неверна.
(circ) В самом деле, пусть формула eqref верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)
Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label
$$
(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label
$$
Преобразуем левую часть неравенства eqref:
$$
begin
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
endnonumber
$$
Тогда равенство eqref примет вид
$$
|r(beta)-r(alpha)|^<2>=(r(beta)-r(alpha),r'(xi))(beta-alpha).label
$$
Если (r(beta)=r(alpha)), то неравенство eqref справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref получим
$$
|r(beta)-r(alpha)|^<2>leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref. (bullet)
Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_^frac(t_<0>)>(t-t_<0>)^+varepsilon(t-t_<0>),label
$$
где (varepsilon(t-t_0)=o((t-t_<0>)^)) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_<0>)^varepsilon_<1>(t-t_<0>)), где (varepsilon_<1>(t-t_<0>)rightarrow 0) при (trightarrow t_<0>).Эта формула справедлива в предположении, что существует (r^<(n)>(t_0)). Для доказательства формулы eqref достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).
Нахождение градиента вектор-функции
Дата публикации Oct 20, 2018
ВЧасть 1Нам поставили задачу: вычислить градиент этой функции потерь:
Чтобы найти градиент, мы должны найти производную функцию. ВЧасть 2мы научились вычислять частную производную функции по каждой переменной. Однако большинство переменных в этой функции потерь являются векторами. Возможность найти частную производную векторных переменных особенно важна, поскольку нейронная сеть работает с большими объемами данных. Векторные и матричные операции – это простой способ представления операций с таким большим количеством данных. Как именно вы можете найти градиент вектор-функции?
Градиент скалярной функции
Скажи, что у нас есть функция,f (x, y) = 3x²y, Наши частные производные:
Если мы организуем эти части в горизонтальный вектор, мы получимградиентизР (х, у), или∇ f (x, y):
6yxэто изменение вР (х, у)в отношении изменения вИкс, в то время как3x²это изменение вР (х, у)в отношении изменения вY,
Что происходит, когда у нас есть две функции? Давайте добавим еще одну функцию,g (x, y) = 2x + y⁸, Частные производные:
Таким образом, градиент g (x, y):
Представляющие функции
Когда у нас есть несколько функций с несколькими параметрами, часто полезно представлять их более простым способом. Мы можем объединить несколько параметров функций в один векторный аргумент,Иксэто выглядит следующим образом:
Следовательно,Р (х, у, г)станетF (x₁, x₂, x₃)который становитсяе (Икс).
Мы также можем объединить несколько функций в вектор, например так:
В настоящее время,у = F (X)гдеF (X)является вектором из [f₁ (Икс), f₂ (Икс), f₃ (Икс) . п (Икс)]
Для нашего предыдущего примера с двумя функциями,f (x, y) ⇒ f (Икс)а такжеg (x, y) ⇒ g (Икс).Здесь векторИкс= [x₁, x₂], гдеx₁ = х, а такжеx₂ = у, Чтобы упростить его еще больше, мы можем объединить наши функции: [f (Икс),г(Икс)] = [f₁ (Икс), f₂ (Иксзнак равноf (x) = y.
Зачастую количество функций и количество переменных будет одинаковым, поэтому для каждой переменной существует решение.
Градиент вектор-функции
Теперь, когда у нас есть две функции, как мы можем найти градиент обеих функций? Если мы организуем оба их градиента в одну матрицу, мы переместимся из векторного исчисления в матричное исчисление. Эта матрица и организация градиентов нескольких функций с несколькими переменными, известна какМатрица Якобиана,
Есть несколько способов представления якобиана. Этот макет, где мы укладываем градиенты по вертикали, известен какмакет числителя, но другие документы будут использоватьрасположение знаменателя, который просто переворачивает его по диагонали:
Градиент функции идентичности
Давайте возьмем функцию идентичности,у = ф (х) = х, гдеFi (Икс) = xiи найдите его градиент:
Так же, как мы создали наш предыдущий якобиан, мы можем найти градиенты каждой скалярной функции и сложить их вертикально, чтобы создать якобиан тождественной функции:
Поскольку это функция идентичности, f₁ (Икс) = x₁, f₂ (Икс) = х₂ и тд. Следовательно,
Частичная производная функции по переменной, которой нет в функции, равна нулю. Например, частная производная 2x² по y равна 0. Другими словами,
Поэтому все, что не на диагонали якобиана, становится равным нулю. Между тем, частная производная любой переменной по отношению к себе равна 1. Например, частная производнаяИксв отношенииИксравен 1. Следовательно, якобиан становится:
Градиент комбинаций вектор-векторных функций
Элементарные бинарные операторыявляются операциями (такими как сложениевес+Иксиливес>Икскоторый возвращает вектор единиц и нулей), который применяет оператор последовательно, начиная с первого элемента обоих векторов, чтобы получить первый элемент вывода, затем второго элемента обоих векторов, чтобы получить второй элемент вывода… и так далее.
Эта статья представляет поэлементные бинарные операции с такими обозначениями:
Здесь ◯ означает любой поэлементный оператор (например, +), а не композицию функций.
Итак, как вы находите градиент поэлементной операции двух векторов?
Поскольку у нас есть два набора функций, нам нужны два якобиана, один из которых представляет градиент относительноИкси один по отношению квес:
Большинство арифметических операций нам понадобятся простые, поэтомуе (ш)часто просто векторвес, Другими словами,Fi (Wi) = Wi, Например, операцияW + хподходит к этой категории, так как она может быть представлена каке (ж) + д (х)гдеfi (wi) + gi (xi) = wi + xi.
При этом условии каждый элемент в двух якобианах упрощается до:
На диагонали i = j, поэтому существует значение для частной производной. Вне диагонали, однако, i ≠ j, поэтому частные производные становятся равными нулю:
Мы можем представить это более кратко как:
Попробуем найти градиент функцииW + х, Мы знаем, что все вне диагонали равно 0. Значения частичных по диагонали относительновеса такжеИксявляются:
Итак, оба якобиана имеют диагональ 1. Это выглядит знакомо . это матрица тождеств!
Давайте попробуем это с умножением:ш * х, Значения частностей по диагонали относительновеса такжеИксявляются:
Следовательно, градиент по отношению квесизш * хявляетсяDiag (Икс)в то время как градиент по отношению кИксизш * хявляетсяDiag (вес).
Применяя те же шаги для вычитания и деления, мы можем суммировать все это:
Градиент векторных сумм
Одной из наиболее распространенных операций в глубоком обучении является операция суммирования. Как мы можем найти градиент функцииу = сумма (Икс)?
у = сумма (Икс)также может быть представлен как:
Следовательно, градиент может быть представлен как:
А так как частная производная функции по переменной, которой нет в функции, равна нулю, ее можно дополнительно упростить следующим образом:
Обратите внимание, что результатом является горизонтальный вектор.
Как насчет градиентау = сумма (Иксг)? Единственное отличие состоит в том, что мы умножаем каждый частный с константой, z:
Хотя это является производной по отношению кИкс, производная по скаляруZэто просто число:
Градиент комбинаций векторных функций правила цепочки
ВЧасть 2мы узнали о правилах цепей с несколькими переменными. Однако это работает только для скаляров. Давайте посмотрим, как мы можем интегрировать это в векторные вычисления!
Давайте возьмем векторную функцию,Yзнак равное(Икс)и найти градиент. Давайте определим функцию как:
И то и другоеf₁ (х)а такжеf₂ (х)являются составными функциями. Введем промежуточные переменные дляf₁ (х)а такжеf₂ (х)и переписать нашу функцию:
Теперь мы можем использовать наше правило цепочки переменных, чтобы вычислить производную вектораY, Просто вычислите производнуюf₁ (х)а такжеf₂ (х)и поместите их один над другим:
Вуаля! У нас есть наш градиент. Однако мы пришли к нашему решению со скалярными правилами, просто сгруппировав числа в вектор. Есть ли способ представить правило цепи с несколькими переменными для векторов?
Прямо сейчас наш градиент вычисляется с помощью:
Обратите внимание, что первый член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₁надИкси второй член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₂надИкс Это как умножение матриц! Поэтому мы можем представить это как:
Давайте проверим наше новое представление правила цепочки векторов:
Мы получаем тот же ответ, что и скалярный подход! Если вместо одного параметраИксу нас есть векторный параметрИкснам просто нужно немного изменить наше правило, чтобы получить полное правило цепочки векторов:
В нашем примере выше,еэто чисто функцияг; то есть,фиявляется функциейсолдатно нетGJ(каждая функцияесоответствует ровно 1 функцииг),В этом случае все вне диагонали становится равным нулю, и:
Теперь у нас есть все части, которые мы находим в градиенте нейронной сети, с которой мы начали нашу серию:
Проверять, выписыватьсяЧасть 4чтобы узнать, как вычислить его производную!
Если вы еще этого не сделали, прочитайте части 1 и 2:
ЧитатьЧасть 4для грандиозного финала!
Скачать оригинал статьиВот,
Если вам понравилась эта статья, не забудьте оставить несколько хлопков! Оставьте комментарий ниже, если у вас есть какие-либо вопросы или предложения 🙂
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| Для плоских задач | a + b = x + bx; ay + by> |
| Для трехмерных задач | a + b = x + bx; ay + by; az + bz> |
| Для n-мерных векторов | a + b = 1 + b1; a2 + b2; . an + bn> |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| Для плоских задач | a – b = x – bx; ay – by> |
| Для трехмерных задач | a – b = x – bx; ay – by; az – bz> |
| Для n-мерных векторов | a – b = 1 – b1; a2 – b2; . an – bn> |
Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
[spoiler title=”источники:”]
http://www.machinelearningmastery.ru/step-by-step-the-math-behind-neural-networks-d002440227fb/
[/spoiler]
Вектор-функция — функция, значениями которой являются векторы в векторном пространстве 
Вектор-функция одной скалярной переменной[править | править код]
Для наглядности далее ограничимся случаем трёхмерного пространства, хотя распространение на общий случай не составляет труда. Вектор-функция одной скалярной переменной 

Выбрав координатные орты 
Рассматриваемые как радиус-векторы, значения вектор-функции образуют в пространстве некоторую кривую, для которой t является параметром.
Говорят, что вектор-функция 





- Предел суммы вектор-функций равен сумме пределов слагаемых (в предположении, что они существуют).
- Предел скалярного произведения вектор-функций равен скалярному произведению пределов сомножителей.
- Предел векторного произведения вектор-функций равен векторному произведению пределов сомножителей.
Непрерывность вектор-функции определяется традиционно.
Производная вектор-функции по параметру[править | править код]
Определим производную вектор-функции 
.
Если производная в точке 

Свойства производной вектор-функции (всюду предполагается, что производные существуют):
О применении вектор-функций одной скалярной переменной в геометрии см.: дифференциальная геометрия кривых.
Вектор-функция нескольких скалярных переменных[править | править код]
Для наглядности ограничимся случаем двух переменных в трёхмерном пространстве. Значения вектор-функции 
В координатах уравнение 
Аналогично случаю одной переменной, мы можем определить производные вектор-функции, которых теперь будет две: 
![{displaystyle left[{frac {partial mathbf {r} }{partial u}},{frac {partial mathbf {r} }{partial v}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb76838ee5f3cc707f9fa4b598bef496e871478)

Координатная сетка на сфере
Кривые на этой поверхности удобно задавать в виде:
,
где t — параметр кривой. Зависимости 
— первая координатная линия.
— вторая координатная линия.
Если на поверхности нет особых точек (![{displaystyle left[{frac {partial mathbf {r} }{partial u}},{frac {partial mathbf {r} }{partial v}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb76838ee5f3cc707f9fa4b598bef496e871478)
Подробнее о геометрических приложениях вектор-функций нескольких скалярных переменных см.: Теория поверхностей.
Литература[править | править код]
- Борисенко А. И., Тарапов И. Е. Векторный анализ и начала тензорного исчисления. 3-е изд. М.: Высшая школа, 1966.
- Краснов М. Л., Кисилев А.И., Макаренко Г.И. Векторный анализ. Наука, 1978, 160 с. (2-е изд. УРСС, 2002)
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления. Архивная копия от 14 ноября 2007 на Wayback Machine 9-е изд. М.: Наука, 1965.
Вектор-функции
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Предел и непрерывность вектор-функции.
Начать изучение
-
Понятие вектор-функции.
Начать изучение
-
Предел вектор-функции.
Начать изучение
-
Свойства пределов вектор-функций.
Начать изучение
-
Непрерывность вектор-функции.
Начать изучение
-
Производная и дифференциал вектор-функции.
Начать изучение
-
Производная вектор-функции.
Начать изучение
-
Дифференциал вектор-функции.
Начать изучение
-
Замена переменного.
Начать изучение
-
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Начать изучение
Предел и непрерывность вектор-функции.
Понятие вектор-функции.
Если каждому значению (tin E), где (Esubsetmathbb{R}), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).
Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.
В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.
Предел вектор-функции.
Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_{trightarrow t_{0}}r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_{trightarrow t_{0}} |r(t)-a|=0,label{ref1}
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).
Утверждение 1.
Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_{1},a_{2},a_{3})), то
$$
lim_{trightarrow t_{0}}r(t)=alabel{ref2}
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label{ref3}
$$
Доказательство.
В самом деле, из неравенства
$$
|r(t)-a|=sqrt{(x(t)-a_1)^2+(y(t)-a_{2})^{2}+(z(t)-a_{3})^{2}}label{ref4}
$$
следует, что
$$
|x(t)-a_1| leq |r(t)-a|,quad|y(t)-a_2| leq |r(t)-a|,quad |z(t)-a_{3}| leq |r(t)-a|.nonumber
$$
Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref{ref1}, то выполняется условие eqref{ref3}.
Обратно: если выполняются условия eqref{ref3}, то из равенства eqref{ref4} следует, что выполнено условие eqref{ref1}. (bullet)
При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref{ref2} выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox{при} trightarrow t_{0}.nonumber
$$
Свойства пределов вектор-функций.
Свойство 1.
Если (displaystyle lim_{trightarrow t_{0}}=a), то (displaystyle lim_{trightarrow t_{0}}|r(t)|=|a|).
Доказательство.
(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$
Свойство 2.
Если (r(t)rightarrow a) при (trightarrow t_{0}), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_{0}), то (f(t)r(t)rightarrow Aa) при (trightarrow t_{0}), то есть
$$
lim_{trightarrow t_0}f(t)r(t)=lim_{trightarrow t_{0}}f(t)lim_{trightarrow t_0}r(t).label{ref5}
$$
Доказательство.
(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref{ref5}. (bullet)
Свойство 3.
Если (r_1(t)rightarrow a_1, r_2(t)rightarrow a_2) при (trightarrow t_{0}), то (r_1+r_2rightarrow a_1+a_2, (r_1,r_2)rightarrow (a_1,a_2), [r_{1},r_2]rightarrow [a_1,a_2]) при (trightarrow t_{0}), то есть
$$
lim_{trightarrow t_{0}}(r_1(t)+r_2(t))=lim_{trightarrow t_{0}}r_1(t)+lim_{trightarrow t_{0}}r_2(t),label{ref6}
$$
$$
lim_{trightarrow t_{0}}(r_1(t),r_2(t))=left(lim_{trightarrow t_{0}}r_1(t),lim_{trightarrow t_{0}}r_2(t)right),label{ref7}
$$
$$
lim_{trightarrow t_{0}}[r_1(t),r_2(t)]=left[lim_{trightarrow t_{0}}r_1(t),lim_{trightarrow t_{0}}r_2(t)right].label{ref8}
$$
Доказательство.
(circ) По условию (r_{i}(t)=a_{i}+alpha_{i}), где (a_i(t)rightarrow 0) при (trightarrow t_{0} (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_{1}(t)+alpha_2(t)rightarrow 0) при (trightarrow t_{0}), откуда следует eqref{ref6}. Докажем формулу eqref{ref7}. В силу свойств скалярного произведения
$$
(r_{1}(t),r_2(t))-(a_1,a_2)=(alpha_{1}(t),a_{2})+(alpha_{2}(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_{1}(t),alpha_{2}(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).
Аналогично доказывается формула eqref{ref8}, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)
Непрерывность вектор-функции.
Вектор-функцию (r(t)) называют непрерывной при (t=t_{0}), если
$$
lim_{trightarrow t_{0}}r(t)=r(t_0).label{ref9}
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_{0}) в силу эквивалентности условий eqref{ref2} и eqref{ref3} означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_{0}).
Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_{0}). Тогда условие eqref{ref9} означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label{ref10}
$$
Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_{0}), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_{0}).
Производная и дифференциал вектор-функции.
Производная вектор-функции.
Если существует (displaystyle lim_{Delta trightarrow 0}frac{Delta r}{Delta t}) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot{r}(t_0)).
Таким образом,
$$
r'(t_{0})=lim_{Delta trightarrow 0}frac{r(t_{0}+Delta t)-r(t_{0})}{Delta t}.label{ref11}
$$
Аналогично вводится понятие второй производной
$$
r″(t_{0})=lim_{Delta trightarrow 0}frac{r'(t_{0}+Delta t)-r'(t_{0})}{Delta t}nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_{0})=(x'(t_0),y'(t_0),z'(t_0))label{ref12}
$$
Утверждение eqref{ref12} следует из определения eqref{ref11} и свойств пределов вектор-функций.
Аналогично, если существует (r″(t_{0})), то
$$
r″(t_{0})=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref{ref10}, то есть вектор-функция (r(t)), имеющая производную в точке (t_{0}), непрерывна при (t=t_{0}).
Утверждение 2.
Справедливы следующие правила дифференцирования вектор-функций:
$$
(r_{1}+r_{2})’=r_{1}’+r_{2}’,label{ref13}
$$
$$
(fr)=f’r+fr’,label{ref14}
$$
$$
(r_1,r_2)’=(r_1′,r_2)+(r_1,r_2′),label{ref15}
$$
$$
[r_1,r_2]’=[r_1′,r_2]+[r_1,r_2′].label{ref16}
$$
Доказательство
(circ) Формулы eqref{ref13}-eqref{ref16} справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref{ref15}. Пусть (Delta r_{k}) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin{array}{l}
(r_{1},r_{2})’=displaystylelim_{Delta trightarrow 0}frac{(r_{1}(t+Delta t),r_{2}(t+Delta t))-(r_{1}(t),r_{2}(t))}{Delta t}=\
=lim_{Delta trightarrow 0}left[left(r_{1}(t),frac{Delta r_{2}(t)}{Delta t}right)+left(frac{Delta r_{1}(t)}{Delta t},r_2(t)right)+left(frac{Delta r_{1}(t)}{Delta t},Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
end{array}nonumber
$$
так как (displaystyle frac{triangle mathrm{r}_{i}}{triangle t}rightarrow r_{i}'(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)
Пример 1.
Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).
Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.
Решение.
(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref{ref15}) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^{2})’=(C^{2})’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$
Дифференциал вектор-функции.
Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_{0}), называют дифференцируемой при (t=t_{0}), если ее приращение (Delta r=r(t_{0}+Delta t)-r(t_{0})) в точке (t_{0}) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label{ref17}
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
В этом случае вектор (aDelta t) называют дифференциалом вектор-функции (r(t)) в точке (t_{0}) и обозначают (dr). Таким образом,
$$
dtextbf{r}=textbf{a}Delta t.nonumber
$$
Как и в случае скалярной функции, дифференцируемость вектор-функции (r(t)) в точке (t_{0}) равносильна существованию ее производной в точке (t_0), причем
$$
textbf{r}'(t_0)=textbf{a}.label{ref18}
$$
Следовательно,
$$
dr=r'(t_{0})Delta t.label{ref19}
$$
Если функция (r(t)) дифференцируема при (t=t_{0}), то, используя равенства eqref{ref17} и eqref{ref18}, получаем
$$
Delta r=r'(t_{0})Delta t+Delta t alpha(Delta t),label{ref20}
$$
где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
Полагая (dt=Delta t), запишем равенство eqref{ref19} в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac{dr}{dt}.label{ref21} (21)
$$
Замена переменного.
Утверждение 3.
Если функция (t=t(s)) дифференцируема при (s=s_{0}, t(s_{0})=t_{0}), а вектор-функция (r(t)) дифференцируема в точке (t_{0}), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_{0}), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_{t}'(t_{0})t_{s}'(s_{0}),label{ref22}
$$
где индекс указывает, по какому переменному производится дифференцирование.
Доказательство.
(circ) Функция (alpha(Delta(t))) в формуле eqref{ref20} не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).
Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_{0}+Delta s)-t(s_{0})rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref{ref20} на (Delta sneq 0), получим
$$
frac{Delta r}{Delta s}=r'(t_0)frac{Delta t}{Delta s}+alpha(Delta t)frac{Delta t}{Delta s}.label{ref23}
$$
Правая часть eqref{ref23} имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref{ref23}, и справедливо равенство eqref{ref22}. Формулу eqref{ref22} запишем кратко в виде равенства
$$
r_{s}’=r_{t}’t_{s}’,label{ref24}
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Замечание 1.
Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label{ref25}
$$
для вектор-функции, вообще говоря, неверна.
(circ) В самом деле, пусть формула eqref{ref25} верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref{ref25} (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)
Теорема Лагранжа.
(Для вектор-функций).
Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label{ref26}
$$
Доказательство.
(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label{ref27}
$$
Преобразуем левую часть неравенства eqref{ref27}:
$$
begin{array}{l}
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
end{array}nonumber
$$
Тогда равенство eqref{ref27} примет вид
$$
|r(beta)-r(alpha)|^{2}=(r(beta)-r(alpha),r'(xi))(beta-alpha).label{ref28}
$$
Если (r(beta)=r(alpha)), то неравенство eqref{ref26} справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref{ref28} получим
$$
|r(beta)-r(alpha)|^{2}leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref{ref26}. (bullet)
Замечание 2.
Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_{k=0}^{n}frac{r^{(k)}(t_{0})}{k!}(t-t_{0})^{k}+varepsilon(t-t_{0}),label{ref29}
$$
где (varepsilon(t-t_0)=o((t-t_{0})^{n})) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_{0})^{n}varepsilon_{1}(t-t_{0})), где (varepsilon_{1}(t-t_{0})rightarrow 0) при (trightarrow t_{0}).Эта формула справедлива в предположении, что существует (r^{(n)}(t_0)). Для доказательства формулы eqref{ref29} достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).
1. Если
![]()
– постоянный
вектор, то
![]()
.
2. Производная
суммы вектор-функций равна сумме
производных слагаемых
![]()
.
3. Пусть
вектор-функция
![]()
умножается на скалярную функцию
![]()
того же скалярного аргумента. Тогда
![]()
.
4. Производные
скалярного и векторного произведения
вектор-функций соответственно определяются
выражениями:
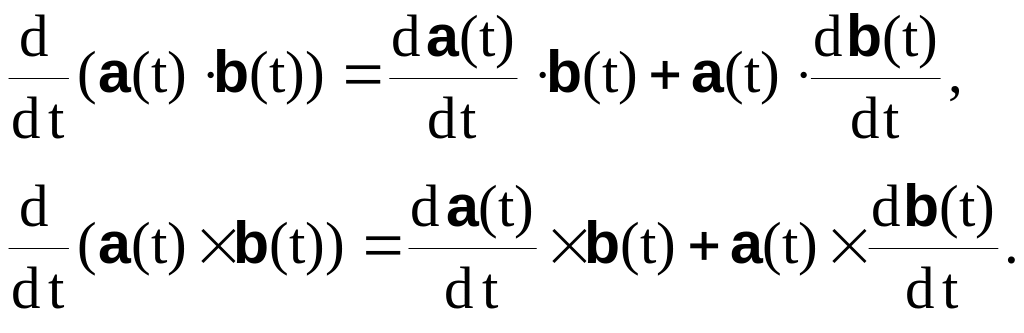
Пусть вектор-функция
![]()
задана в неподвижной прямоугольной
системе координат; тогда
![]()
,
где ![]()
– проекции
вектор-функции
на оси
![]()
(рис. 2.2). Так как векторы
![]()
постоянные, то
![]()
.
С другой стороны,
вектор
![]()
можно записать через его проекции
следующим образом:
![]()
.
Сравнивая оба
выражения, найдем проекции производной
вектора на координатные оси
![]()
, ![]()
, ![]()
.
Следовательно,
проекции производной вектора на
неподвижные оси равны производным от
соответствующих проекций вектора.
Модуль производной
определяется из равенства

.
Если модуль
вектор-функции
остается постоянным при изменении
аргумента
,
то годографом вектор-функции
будет кривая, расположенная на сфере
радиуса а. Следовательно, производная
,
направленная по касательной к годографу
вектор-функции
,
будет в этом случае перпендикулярна
вектору
.
2.5. Интегрирование вектор-функции скалярного аргумента.
Вектор-функция
![]()
называется первообразной функцией для
вектор-функции
при
![]()
,
если
дифференцируема и
![]()
, ![]()
.
Неопределенным
интегралом от вектор-функции скалярного
аргумента
![]()
называется совокупность всех первообразных
для
![]()
,
где
– какая-нибудь
из первообразных для
;
![]()
– произвольный
постоянный вектор.
Для интегралов от
вектор-функций справедливы следующие
свойства
1. ![]()
, ![]()
.
2. ![]()
.
3. Кинематика точки
3.1. Способы задания движения
Движение точки по
отношению к избранной системе отсчета
считается заданным, если известен
способ, при помощи которого можно
определить положение точки в любой
момент времени. Существуют три способа
задания движения точки: векторный,
координатный и естественный.
3.1.1. Векторный
способ. Положение точки М,
движущейся по отношению к системе
отсчета Oxyz, можно
определить, задав ее радиус-вектор
![]()
,
проведенный из начала координат О
в точку М, т.е.
![]()
(рис. 3.1).
|
При движении будет с течением времени изменяться : . (3.1)
Уравнение (3.1)
Непрерывная |
Рис. 3.1. |
данной системы
отсчета, называется траекторией
точки. Если траекторией точки
является прямая линия, движение точки
называется прямолинейным, а если
кривая – криволинейным.
При векторном
способе задания движения траектория
точки представляет собой годограф
радиуса-вектора
.
Введением
радиуса-вектора, определяющего положение
точки, мы не связываем себя с конкретной
системой координат, что позволяет широко
использовать задание радиуса-вектора
как функции времени для получения
основных кинематических характеристик
движения. Для решения же конкретных
задач обычно переходят от векторного
способа к координатному и естественному
способам задания движения.
3.1.2. Координатный
способ задания движения заключается
в представлении координат точки в виде
известных, непрерывных, дважды
дифференцируемых функций времени. Выбор
конкретной системы координат определяется
содержанием решаемой задачи.
Предпочтительнее та система координат,
использование которой наиболее
целесообразно для данной задачи.
В прямоугольной
декартовой системе координаты
точки М (рис. 3.1) задаются как
известные функции времени, т.е.
![]()
, ![]()
, ![]()
. (3.2)
Уравнения (3.2)
движения точки представляют одновременно
и уравнения траектории в параметрической
форме, где роль параметра играет время
.
Если требуется определить уравнение
траектории в координатной форме, то
нужно исключить каким-либо образом из
этих уравнений время
.
Во многих случаях
бывает предпочтительнее использовать
цилиндрические или сферические
координаты.
В цилиндрических
координатах (рис. 3.2 а) положение
точки определяется радиусом
![]()
,
углом
![]()
(азимут) и аппликатой
![]()
.
Следовательно, движение будет задано,
если
,
,
и z будут известными
функциями времени
![]()
, ![]()
, ![]()
. (3.3)
|
Рис. 3.2. |
В сферических
координатах (рис. 3.2 б) положение
точки определяется полярным радиусом
![]()
,
углом
и углом
![]()
(полюсный угол). Движение будет задано,
если
![]()
, ![]()
, ![]()
(3.4)
– известные
функции времени.
Формулы, связывающие
цилиндрические и сферические координаты
с декартовыми, соответственно будут
![]()
, ![]()
, ![]()
;
![]()
, ![]()
, ![]()
.
|
При движении и (рис. 3.3):
, |
Рис. 3.3. |
Связь этих координат
с декартовыми дается формулами
![]()
, ![]()
.
3.1.3. Естественный
способ. При естественном способе
задания движения указываются (рис. 3.4):
-
траектория точки;
-
закон движения
точки по траектории
![]()
; (3.5)
-
начало отсчета
(точка М0 на рис. 3.4); -
направление
положительного отсчета дуги по
траектории.
|
Рис. 3.4. |
Если движение |
Путь s,
проходимый точкой, всегда будет возрастать
и, следовательно, положителен, т. е.
![]()
.
Естественным
способом задания движения удобно
пользоваться, когда траектория точки
заранее известна.
Все рассмотренные
способы задания движения взаимосвязаны.
|
Рис. 3.5. |
Пусть, например,
Модуль найдется по формуле |
![]()
, (3.7)
а направление
определится направляющими косинусами
![]()
, ![]()
, ![]()
. (3.8)
|
Рис. 3.6. |
От задания
|
Интегрируя это
выражение в промежутке от
![]()
(начало движения) до какого-либо
момента времени
,
получим закон движения
![]()
.
Знак «плюс» или
«минус» перед интегралом ставится в
зависимости от выбора направления
положительного отсчета дуги; если
движение точки начинается в сторону
выбранного положительного отсчета
дуги, то следует брать знак «плюс», в
противном случае – знак «минус».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вектор-функция — функция, значениями которой являются векторы в векторном пространстве  двух, трёх или более измерений. Аргументами функции могут быть:
двух, трёх или более измерений. Аргументами функции могут быть:
Содержание
- 1 Вектор-функция одной скалярной переменной
- 1.1 Производная вектор-функции по параметру
- 2 Вектор-функция нескольких скалярных переменных
- 3 Литература
Вектор-функция одной скалярной переменной
Для наглядности далее ограничимся случаем трёхмерного пространства, хотя распространение на общий случай не составляет труда. Вектор-функция одной скалярной переменной  отображает некоторый интервал вещественных чисел
отображает некоторый интервал вещественных чисел  в множество пространственных векторов (интервал может также быть бесконечным).
в множество пространственных векторов (интервал может также быть бесконечным).
Выбрав координатные орты  , мы можем разложить вектор-функцию на три координатные функции x(t), y(t), z(t):
, мы можем разложить вектор-функцию на три координатные функции x(t), y(t), z(t):
Рассматриваемые как радиус-векторы, значения вектор-функции образуют в пространстве некоторую кривую, для которой t является параметром.
Говорят, что вектор-функция  имеет предел
имеет предел  в точке
в точке  , если
, если  (здесь и далее
(здесь и далее  обозначают модуль вектора
обозначают модуль вектора  ). Предел вектор-функции имеет обычные свойства:
). Предел вектор-функции имеет обычные свойства:
- Предел суммы вектор-функций равен сумме пределов слагаемых (в предположении, что они существуют).
- Предел скалярного произведения вектор-функций равен скалярному произведению пределов сомножителей.
- Предел векторного произведения вектор-функций равен векторному произведению пределов сомножителей.
Непрерывность вектор-функции определяется традиционно.
Производная вектор-функции по параметру
Определим производную вектор-функции  по параметру:
по параметру:
 .
.
Если производная в точке  существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут
существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут  .
.
Свойства производной вектор-функции (всюду предполагается, что производные существуют):
О применении вектор-функций одной скалярной переменной в геометрии см.: дифференциальная геометрия кривых.
Вектор-функция нескольких скалярных переменных
Для наглядности ограничимся случаем двух переменных в трёхмерном пространстве. Значения вектор-функции  (их годограф) образуют, вообще говоря, двумерную поверхность, на которой аргументы u, v можно рассматривать как внутренние координаты точек поверхности.
(их годограф) образуют, вообще говоря, двумерную поверхность, на которой аргументы u, v можно рассматривать как внутренние координаты точек поверхности.
В координатах уравнение  имеет вид:
имеет вид:
Аналогично случаю одной переменной, мы можем определить производные вектор-функции, которых теперь будет две:  . Участок поверхности будет невырожденным (то есть в нашем случае — двумерным), если на нём
. Участок поверхности будет невырожденным (то есть в нашем случае — двумерным), если на нём ![left[frac{partialmathbf{r}} {partial u}, frac{partialmathbf{r}} {partial v}right]](https://dic.academic.ru/dic.nsf/ruwiki/5d5e7657c3d287c933f8927d6d47cb5e.png) не обращается тождественно в ноль.
не обращается тождественно в ноль.

![]()
Координатная сетка на сфере
Кривые на этой поверхности удобно задавать в виде:
 ,
,
где t — параметр кривой. Зависимости  предполагаются дифференцируемыми, причём в рассматриваемой области их производные не должны одновременно обращаться в нуль. Особую роль играют координатные линии, образующие сетку координат на поверхности:
предполагаются дифференцируемыми, причём в рассматриваемой области их производные не должны одновременно обращаться в нуль. Особую роль играют координатные линии, образующие сетку координат на поверхности:
 — первая координатная линия.
— первая координатная линия. — вторая координатная линия.
— вторая координатная линия.
Если на поверхности нет особых точек (![left[frac{partialmathbf{r}} {partial u}, frac{partialmathbf{r}} {partial v}right]](https://dic.academic.ru/dic.nsf/ruwiki/5d5e7657c3d287c933f8927d6d47cb5e.png) нигде не обращается в ноль), то через каждую точку поверхности проходят точно две координатные линии.
нигде не обращается в ноль), то через каждую точку поверхности проходят точно две координатные линии.
Подробнее о геометрических приложениях вектор-функций нескольких скалярных переменных см.: Теория поверхностей.
Литература
- Борисенко А. И., Тарапов И. Е. Векторный анализ и начала тензорного исчисления. 3-е изд. М.: Высшая школа, 1966.
- Краснов М. Л., Кисилев А.И., Макаренко Г.И. Векторный анализ. Наука, 1978, 160 с. (2-е изд. УРСС, 2002)
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления. 9-е изд. М.: Наука, 1965.