Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
В механике существуют два типа величин:
- скалярные величины, задающие некоторое числовое значение – время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление – скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
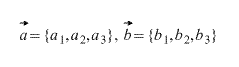
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
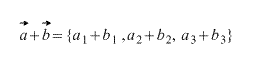
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
Правило параллелограмма. Сложение векторов по правилу параллелограмма.
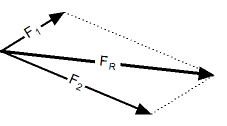 |
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
|
Правило треугольника. Сложение векторов по правилу треугольника.
 |
Сложение векторов по правилу треугольника заключается в следующем:
|
Тригонометрический способ. Сложение векторов тригонометрическим способом.
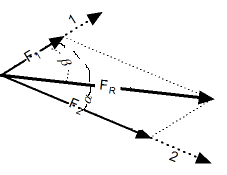 |
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
|
Пример – сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН) 2 + (8 кН) 2 – 2 (5 кН)(8 kН) cos(180 o – (80 o )) ] 1/2
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180 o – (80 o )) / (10,2 кН) ]
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| Для плоских задач | a + b = x + bx; ay + by> |
| Для трехмерных задач | a + b = x + bx; ay + by; az + bz> |
| Для n-мерных векторов | a + b = 1 + b1; a2 + b2; . an + bn> |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| Для плоских задач | a – b = x – bx; ay – by> |
| Для трехмерных задач | a – b = x – bx; ay – by; az – bz> |
| Для n-мерных векторов | a – b = 1 – b1; a2 – b2; . an – bn> |
Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
Правила, по которым происходит сложение векторов
Как происходит сложение векторов, не всегда понятно ученикам. Дети не представляют того, что за ними скрывается. Приходится просто запоминать правила, а не вдумываться в суть. Поэтому именно о принципах сложения и вычитания векторных величин требуется много знаний.
В результате сложения двух и более векторов всегда получается еще один. Причем он всегда обязательно будет одинаковым, независимо от приема его нахождения.
Чаще всего в школьном курсе геометрии рассматривается сложение двух векторов. Оно может быть выполнено по правилу треугольника или параллелограмма. Эти рисунки выглядят по-разному, но результат от действия один.
Как происходит сложение по правилу треугольника?
Оно применяется тогда, когда векторы неколлинеарные. То есть не лежат на одной прямой или на параллельных.
В этом случае от некоторой произвольной точки нужно отложить первый вектор. Из его конца требуется провести параллельный и равный второму. Результатом станет вектор, исходящий из начала первого и завершающийся в конце второго. Рисунок напоминает треугольник. Отсюда и название правила.
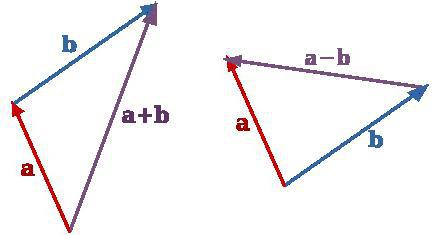
Если векторы коллинеарные, то это правило тоже можно применять. Только рисунок будет расположен вдоль одной линии.
Как выполняется сложение по правилу параллелограмма?
Опять же? применяется только для неколлинеарных векторов. Построение выполняется по другому принципу. Хотя начало такое же. Нужно отложить первый вектор. И от его начала – второй. На их основе достроить параллелограмм и провести диагональ из начала обоих векторов. Она и будет результатом. Так выполняется сложение векторов по правилу параллелограмма.
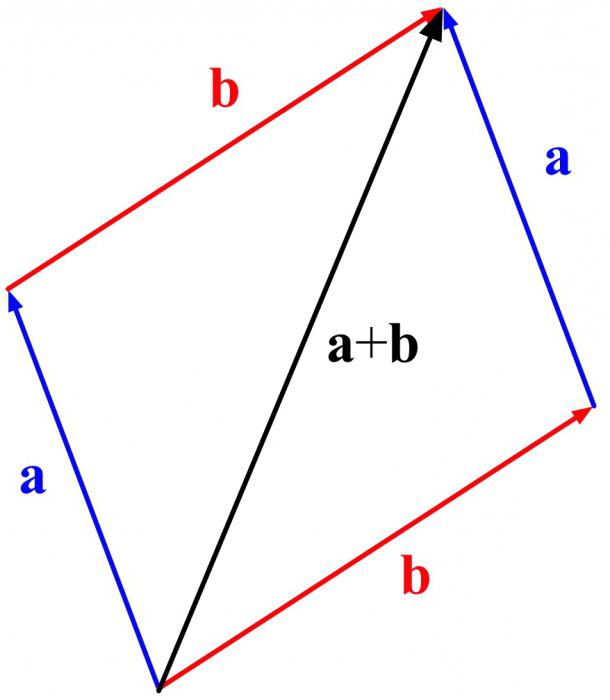
До сих пор их было два. А как быть, если их 3 или 10? Использовать следующий прием.
Как и когда применяется правило многоугольника?
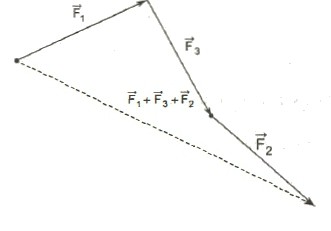
Если требуется выполнить сложение векторов, число которых — больше двух, пугаться не стоит. Достаточно последовательно отложить их все и соединить начало цепочки с ее концом. Этот вектор и будет искомой суммой.
Какие свойства действительны для действий с векторами?
О нулевом векторе. Которое утверждает, что при сложении с ним получается исходный.
О противоположном векторе. То есть о таком, который имеет противоположное направление и равное по модулю значение. Их сумма будет равна нулю.
О коммутативности сложения. То, что известно еще с начальной школы. Смена мест слагаемых не приводит к изменению результата. Другими словами, неважно какой вектор откладывать сначала. Ответ все равно будет верным и единственным.
Об ассоциативности сложения. Этот закон позволяет складывать попарно любые векторы из тройки и к ним прибавлять третий. Если записать это с помощью знаков, то получится следующее:
первый + (второй + третий) = второй + (первый + третий) = третий + (первый + второй).
Что известно о разности векторов?
Отдельной операции вычитания не существует. Это связано с тем, что оно, по сути, является сложением. Только второму из них задается противоположное направление. А потом все выполняется так, как если бы рассматривалось сложение векторов. Поэтому об их разности практически не говорят.
Для того чтобы упростить работу с их вычитанием, видоизменено правило треугольника. Теперь (при вычитании) второй вектор нужно отложить из начала первого. Ответом будет тот, что соединяет конечную точку уменьшаемого с ней же вычитаемого. Хотя можно и откладывать так, как было описано ранее, просто изменив направление второго.
Как найти сумму и разность векторов в координатах?
В задаче даны координаты векторов и требуется узнать их значения для итогового. При этом построений выполнять не нужно. То есть можно воспользоваться несложными формулами, которые описывают правило сложения векторов. Они выглядят так:
а (х, у, z) + в (k, l, m) = с (х+k, y+l, z+m);
а (х, у, z) -в (k, l, m) = с (х-k, y-l, z-m).
Легко заметить, что координаты нужно просто сложить или вычесть в зависимости от конкретного задания.
Первый пример с решением
Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.
Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.
Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.
А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.
Ответ. Разность АО и ВО равна 8 см.
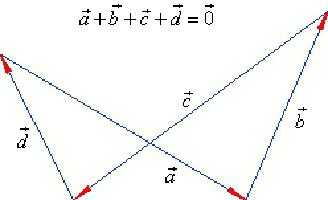
Второй пример и его подробное решение
Условие. У ромба АВСД диагонали равны 12 и 16 см. Точка их пересечения обозначена буквой О. Вычислите длину вектора, образованного разностью векторов АО и ВО.
Решение. Пусть обозначение вершин ромба будет таким же, как в предыдущей задаче. Аналогично решению первого примера получается, что искомая разность равна вектору АВ. А его длина неизвестна. Решение задачи свелось к тому, чтобы вычислить одну из сторон ромба.
Для этой цели потребуется рассмотреть треугольник АВО. Он прямоугольный, потому что диагонали ромба пересекаются под углом в 90 градусов. А его катеты равны половинам диагоналей. То есть 6 и 8 см. Искомая в задаче сторона совпадает с гипотенузой в этом треугольнике.
Для ее нахождения потребуется теорема Пифагора. Квадрат гипотенузы будет равен сумме чисел 6 2 и 8 2 . После возведения в квадрат получатся значения: 36 и 64. Их сумма — 100. Отсюда следует, что гипотенуза равна 10 см.
Ответ. Разность векторов АО и ВО составляет 10 см.
Третий пример с детальным решением
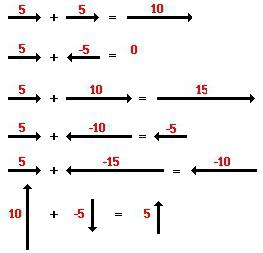
Условие. Вычислить разность и сумму двух векторов. Известны их координаты: у первого — 1 и 2, у второго — 4 и 8.
Решение. Для нахождения суммы потребуется сложить попарно первые и вторые координаты. Результатом будут числа 5 и 10. Ответом будет вектор с координатами (5; 10).
Для разности нужно выполнить вычитание координат. После выполнения этого действия получатся числа -3 и -6. Они и будут координатами искомого вектора.
Ответ. Сумма векторов — (5; 10), их разность — (-3; -6).
Четвертый пример
Условие. Длина вектора АВ равна 6 см, ВС — 8 см. Второй отложен от конца первого под углом в 90 градусов. Вычислить: а) разность модулей векторов ВА и ВС и модуль разности ВА и ВС; б) сумму этих же модулей и модуль суммы.
Решение: а) Длины векторов уже даны в задаче. Поэтому вычислить их разность не составит труда. 6 – 8 = -2. Несколько сложнее обстоит дело с модулем разности. Сначала нужно узнать, какой вектор будет являться результатом вычитания. Для этой цели следует отложить вектор ВА, который направлен в противоположную сторону АВ. Потом от его конца провести вектор ВС, направив его в сторону, противоположную исходному. Результатом вычитания получится вектор СА. Его модуль можно вычислить по теореме Пифагора. Несложные вычисления приводят к значению 10 см.
б) Сумма модулей векторов получается равной 14 см. Для поиска второго ответа потребуется некоторое преобразование. Вектор ВА противоположно направлен тому, который дан — АВ. Оба вектора направлены из одной точки. В этой ситуации можно использовать правило параллелограмма. Результатом сложения будет диагональ, причем не просто параллелограмма, а прямоугольника. Его диагонали равны, значит, модуль суммы такой же, как в предыдущем пункте.
[spoiler title=”источники:”]
http://www.syl.ru/article/191003/mod_pravila-po-kotoryim-proishodit-slojenie-vektorov
[/spoiler]
Векторы. Действия с векторами. Задание 4 (2015)
Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.
Как обычно, немного самой необходимой теории.
Вектор – это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:

Здесь точка А – начало вектора, а точка В – его конец.
У вектора есть два параметра: его длина и направление.
Длина вектора – это длина отрезка, соединяющего начало и конец вектора. Длина вектора  обозначается
обозначается 
Два вектора называются равными, если они имеют одинаковую длину и сонаправлены.
Два вектора называются сонаправленными, если они лежат на параллельных прямых и направлены в одну сторону: вектора  и
и  сонаправлены:
сонаправлены:

Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора  и
и  , а также
, а также  и
и  направлены в противоположные стороны:
направлены в противоположные стороны:

Вектора, лежащие на параллельных прямых называются коллинеарными: вектора  ,
,  и
и  – коллинеарны.
– коллинеарны.
Произведением вектора  на число
на число  называется вектор, сонаправленный вектору
называется вектор, сонаправленный вектору  , если
, если 
 , и направленный в противоположную сторону, если
, и направленный в противоположную сторону, если 
 , и длина которого равна длине вектора
, и длина которого равна длине вектора  , умноженной на
, умноженной на  :
:
 =k
=k :
:

Чтобы сложить два вектора  и
и  , нужно начало вектора
, нужно начало вектора  соединить с концом вектора
соединить с концом вектора  . Вектор суммы соединяет начало вектора
. Вектор суммы соединяет начало вектора  с концом вектора
с концом вектора  :
:

Это правило сложения векторов называется правилом треугольника.
Чтобы сложить два вектора по правилу параллелограмма, нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:

Разность двух векторов определяется через сумму: разностью векторов  и
и  называется такой вектор
называется такой вектор  , который в сумме с вектором
, который в сумме с вектором  даст вектор
даст вектор  :
:
 :
: 
Отсюда вытекает правило нахождения разности двух векторов: чтобы из вектора  вычесть вектор
вычесть вектор  , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора
, нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора  с концом вектора
с концом вектора  ( то есть конец вычитаемого с концом уменьшаемого):
( то есть конец вычитаемого с концом уменьшаемого):

Чтобы найти угол между вектором  и вектором
и вектором  , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
, нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами: 

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

Предлагаю вам решить задачи из Открытого банка заданий для подготовки к ЕГЭ по математике, а затем сверить све решение с ВИДЕОУРОКАМИ:
1. Задание 4 (№ 27709)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов  и
и  .
.

2. Задание 4 (№ 27710)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов  и
и  . (чертеж из предыдущей задачи).
. (чертеж из предыдущей задачи).
3. Задание 4 (№ 27711)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов  и
и  .
.

4. Задание 4 (№ 27712)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину разности векторов  и
и  . (чертеж из предыдущей задачи).
. (чертеж из предыдущей задачи).
5. Задание 4 (№ 27713)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  .
.

6. Задание 4 (№ 27714)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  +
+  .
.

7.Задание 4 (№ 27715)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  –
–  .(чертеж из предыдущей задачи).
.(чертеж из предыдущей задачи).
8.Задание 4 (№ 27716)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  –
–  .
.

9. Задание 4 (№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора  +
+  .
.

10. Задание 4 (№ 27718)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора  –
–  .(чертеж из предыдущей задачи).
.(чертеж из предыдущей задачи).
11.Задание 4 (№ 27719)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов  и
и  .(чертеж из предыдущей задачи).
.(чертеж из предыдущей задачи).
12. Задание 4 (№ 27720)
Стороны правильного треугольника ABC равны  Найдите длину вектора
Найдите длину вектора  +
+ .
.

13. Задание 4 (№ 27721)
Стороны правильного треугольника ABC равны 3. Найдите длину вектора  –
– .(чертеж из предыдущей задачи).
.(чертеж из предыдущей задачи).
14. Задание 4 (№ 27722)
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов  и
и  . (чертеж из предыдущей задачи).
. (чертеж из предыдущей задачи).
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр “Час ЕГЭ”, попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
-
Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
-
Разность векторов
- Формула вычитания векторов
- Примеры задач
Сумма векторов
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:
Суммой a и b является вектор c, начало которого совпадает с началом a, а конец – с концом b. При этом конец вектора a должен совпадать с началом вектора b.
Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c, совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
ci = ai + bi
Элементы вектора c равняются попарной сумме соответствующих элементов a и b.
| Для плоских задач | a + b = {ax + bx; ay + by} |
| Для трехмерных задач | a + b = {ax + bx; ay + by; az + bz} |
| Для n-мерных векторов | a + b = {a1 + b1; a2 + b2; … an + bn} |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: (a + b) + c = a + (b + c)
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (-a) = 0
Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b, то получится c, причем должно соблюдаться условие: b + c = a
Формула вычитания векторов
ci = ai – bi
Элементы вектора c равны попарной разности соответствующих элементов a и b.
| Для плоских задач | a – b = {ax – bx; ay – by} |
| Для трехмерных задач | a – b = {ax – bx; ay – by; az – bz} |
| Для n-мерных векторов | a – b = {a1 – b1; a2 – b2; … an – bn} |
Примеры задач
Задание 1
Вычислим сумму векторов a = {3; 5} и b = {2; 7}.
Решение:
a + b = {3 + 2; 5 + 7} = {5; 12}.
Задание 2
Найдем разность векторов a = {4; 8; -2} и b = {-1; 9; 5}.
Решение:
a – b = {4 – (-1); 8 – 9; -2 – 5} = {5; -1; -7}.
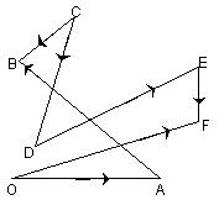
Дан ромб EFKL найдите сумму векторов : a)EF и EL ; b) KL и FK.
Вы зашли на страницу вопроса Дан ромб EFKL найдите сумму векторов : a)EF и EL ; b) KL и FK?, который относится к
категории Алгебра. По уровню сложности вопрос соответствует учебной
программе для учащихся 5 – 9 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
Содержание:
- Формула
- Примеры нахождения суммы векторов
Формула
Чтобы найти сумму векторов $bar{a}+bar{b}$, которые заданны координатами
$bar{a}=(a_x;a_y)$ и $bar{b}=(b_x;b_y)$, необходимо сложить соответствующие
координаты этих векторов,
то есть
$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y}right)$$
В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их сумма равна
$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y} ; a_{z}+b_{z}right)$$
Примеры нахождения суммы векторов
Пример
Задание. Найти сумму векторов
$bar{a}+bar{b}$,
$bar{a}=(2;0)$ и
$bar{b}=(1;3)$
Решение. Для нахождения суммы векторов, сложим их соответствующие координаты
$$bar{a}+bar{b}=(2 ; 0)+(1 ; 3)=(2+1 ; 0+3)=(3 ; 3)$$
Ответ. $bar{a}+bar{b}==(3 ; 3)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти суммы векторов
$bar{a}+bar{b}$,
$bar{a}+bar{c}$,
$bar{b}+bar{c}$ и
$bar{a}+bar{b} +bar{c}$, если
$bar{a}=(1;-1;0)$,
$bar{b}=(3;2;-1)$ и
$bar{c}=(4;2;-1)$
Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:
$$bar{a}+bar{b}=(1+3 ;-1+2 ; 0+(-2))=(4 ; 1 ;-2)$$
$$bar{a}+bar{c}=(1+4 ;-1+2 ; 0+(-1))=(5 ; 1 ;-1)$$
$$bar{b}+bar{c}=(3+4 ; 2+2 ;-2+(-1))=(7 ; 4 ;-3)$$
$$bar{a}+bar{b}+bar{c}=(1+3+4 ;-1+2+2 ; 0+(-2)+(-1))=(8 ; 3 ;-3)$$
Ответ. $bar{a}+bar{b}=(4 ; 1 ;-2)$ , $bar{a}+bar{c}=(5 ; 1 ;-1)$ , $bar{b}+bar{c}=(7 ; 4 ;-3)$ , $bar{a}+bar{b}+bar{c}=(8 ; 3 ;-3)$
Читать дальше: как найти разность векторов.
