План урока:
Понятие вектора
Равенство векторов
Сложение векторов
Свойства сложения
Вычитание векторов
Умножение вектора на число
Решение задач с помощью векторов
Понятие вектора
Рассмотрим простейшую задачу. Корабль, двигатель которого развивает скорость 20 км/ч, плывет по течению реки, при этом скорость течения составляет 2 км/ч. Какова скорость корабля относительно берега? Очевидно, в данном случае надо сложить скорость течения и собственную скорость корабля:
20 км/ч + 2 км/ч = 22 км/ч
Теперь посмотрим на почти такую же задачу, которая отличается лишь тем, что корабль плывет уже против течения. Для ее решения скорости уже придется вычитать:
20 км/ч – 2 км/ч = 18 км/ч
Получается, что ответ задачи во многом зависит не только от величин скоростей, но и от их направления. Возможны и более сложные случаи, когда корабль двигается на воде перпендикулярно течению или, например, под углом в 60°. Величины, при операции с которыми необходимо учитывать их направление, называют векторными величинами, или просто векторами.
Помимо скорости к ним относят ускорение, силу, импульс, напряженность магнитного и электрического поля и многие другие величины. Те же величины, для которых нельзя указать направление, называют скалярными величинами. Это масса, температура, плотность и т. п. Для выполнения действий с векторами необходимо разработать общие правила их сложения, вычитания, умножения, которые будут справедливы независимо от физической природы векторных величин. И разработать эти правила помогает как раз геометрия.
Для начала введем понятие вектора. Любой отрезок имеет два конца, которые обычно не отличают друг от друга. Однако если одну из этих точек считать началом отрезка, а другую – собственно концом, то у отрезка появится направление. В таком случае его можно считать вектором.

Часто вектора называют направленными отрезками. Обозначают их с помощью стрелок.
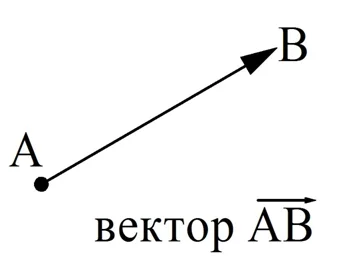
На этом рисунке показан вектор, начало которого находится в точке А, а конец – в точке В. При записи в формулах сначала пишут букву, означающую начало вектора, потом обозначение его конца, а над этими двумя буквами ставят стрелочку:

С практической точки зрения приходится вводить в рассмотрение особый нулевой вектор. У него начало и конец совпадают, то есть он представляет собой всего лишь одну точку:

Нулевой вектор необходим, так как нам необходимо научиться выполнять действия над векторами. Мы знаем, что в обычной алгебре используется число ноль. В векторной же алгебре аналогом нуля является как раз нулевой вектор.
Каждый вектор имеет свою длину, которая равна расстоянию между его началом и концом. То есть, если его начало находится в точке А, а конец в точке В, то длина вектора будет совпадать с длиной отрезка АВ. Обозначают длину с помощью вертикальных скобок:

Естественно, что длина нулевого вектора равна нулю.
Задание. Найдите модуль вектора, изображенного на рисунке:
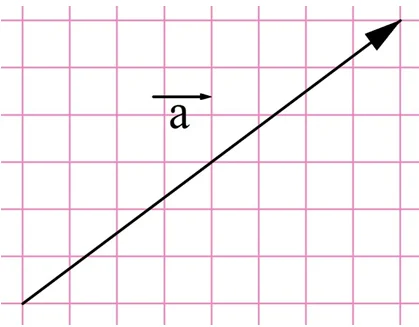
Решение. Легко выполнить построение, при котором вектор окажется гипотенузой в прямоугольном треугольнике
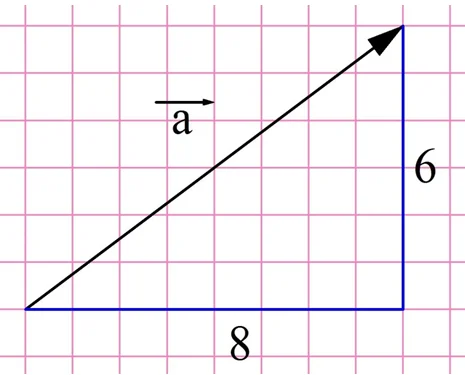
Тогда длину вектора можно найти по теореме Пифагора:
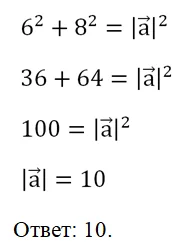
Равенство векторов
Через начало и конец векторов можно провести прямую. В связи с этим можно ввести понятие коллинеарных векторов.
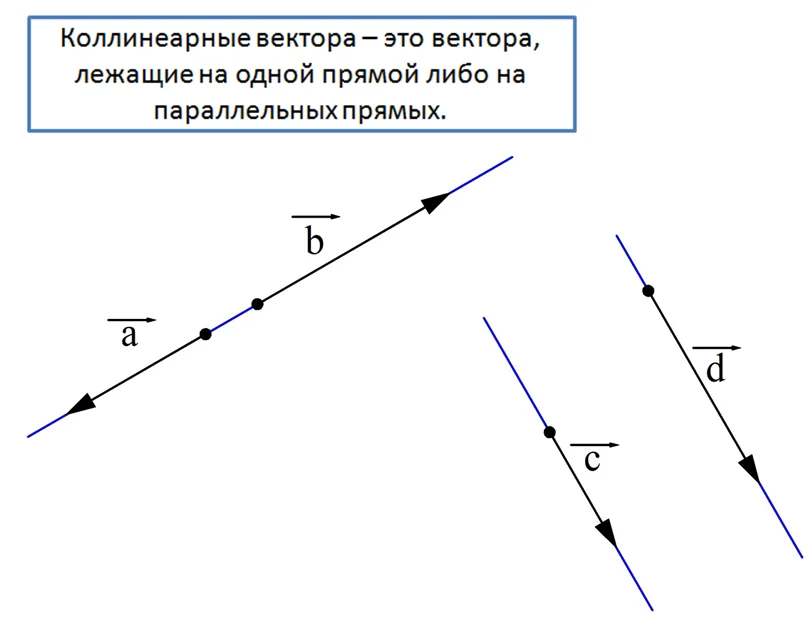
На рисунке коллинеарны вектора а и b, так как они лежат на одной прямой. Также коллинеарны с и d, так как они лежат на параллельных прямых. А вот вектора a и c неколлинеарны, так как они лежат на пересекающихся прямых.
Для пары коллинеарных векторов можно определить, являются ли они сонаправленными или противоположно направленными.
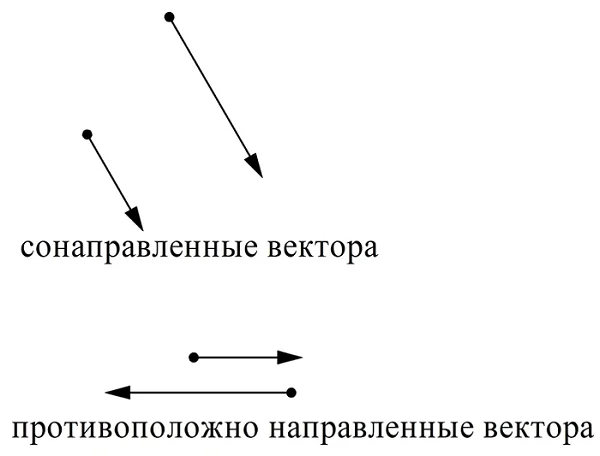
Для обозначения сонаправленных векторов используется символ «⇈», а для противоположно направленных «⇅». Можно сформулировать две очевидных теоремы о коллинеарных векторах.

Проиллюстрируем эти правила с помощью рисунка:
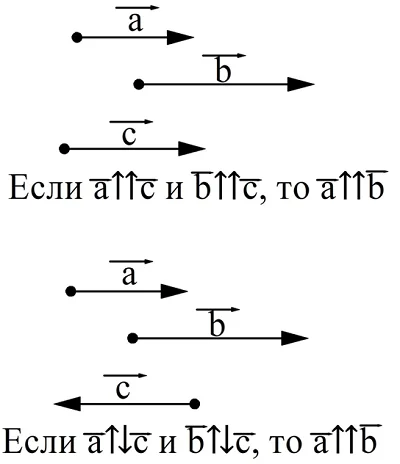
Особняком стоит нулевой вектор. Он представляет собой точку, а потому не имеет определенного направления. Поэтому условно его считают сонаправленным с любым другим вектором.
Теперь мы можем дать определение равенству векторов.

Задание. Найдите на картинке равные вектора.
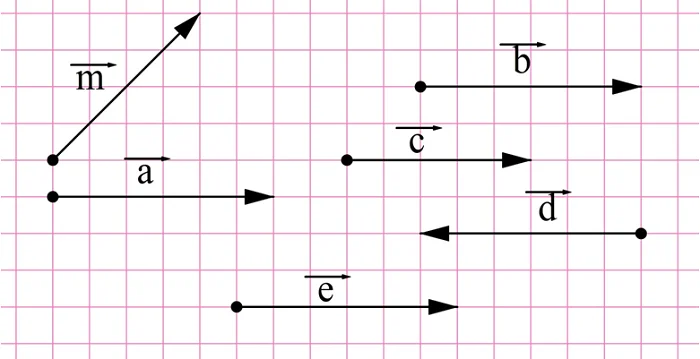
Решение. Здесь равны вектора а, b и e. Они сонаправлены и имеют длину 6. Вектор с сонаправлен с ними, но его длина составляет только 5 клеток. Длина вектора d составляет 6 клеток, но он не сонаправлен с другими векторами. Наконец, вектор m также не сонаправлен с другими векторами и даже не коллинеарен им.
Ответ: a, b и e.
Если началом вектора является некоторая точка А, то можно сказать, что вектор отложен от точки А. Докажем важное утверждение:

Доказать его можно построением. Пусть есть вектор а и точка М. Проведем через М прямую p, параллельную вектору а. Такая прямая будет единственной. Если точка М и вектор лежат на одной прямой, то в качестве прямой p возьмем именно эту прямую. Далее от точки М можно отложить отрезки МN и МN’, длина которых будет совпадать с длиной вектора а. В результате получится два вектора,MN и MN’, один из которых будет сонаправлен с а, а другой – противоположно направленный.
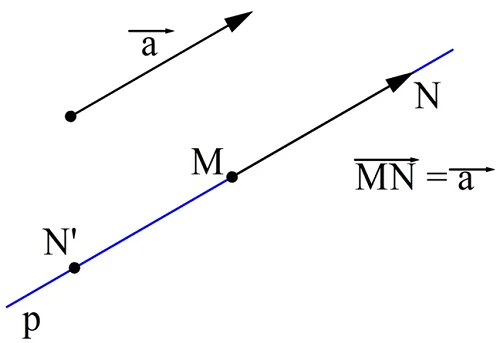
Часто равные вектора, отложенные от разных точек, обозначают одной буквой. Можно считать, что это один и тот же вектор, просто приложенный к разным точкам.
Задание. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Определите, равны ли вектора:
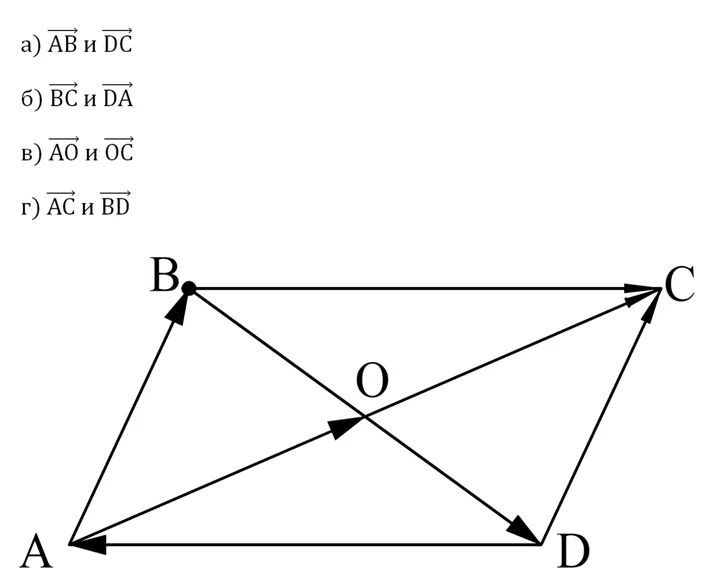
Решение.
а) Отрезки АВ и DC равны, ведь это противоположные стороны параллелограмма, по той же причине эти отрезки параллельны. Видно, что они сонаправлены, значит, вектора равны.
б) Отрезки ВС и DA параллельны и равны, но эти вектора противоположно направлены, поэтому вектора НЕ равны друг другу.
в) Точка пересечения диагоналей параллелограмма делит их пополам, поэтому длины отрезков АО и ОС одинаковы. Вектора АО и ОС лежат на одной прямой, то есть они коллинеарны. При этом они ещё и сонаправлены, поэтому АО и ОС – равные векторы.
г) Вектора АС и BD лежат на пересекающихся прямых, то есть они не коллинеарны. Этого уже достаточно, чтобы считать их НЕ равными друг другу.
Ответ: а) д; б) нет; в) да; г) нет.
Сложение векторов
Пусть некоторый объект сначала находился в точке А, а потом переместился в точку В. Тогда его перемещение удобно обозначить с помощью вектора АВ. Далее пусть этот объект из точки В переместился в другую точку С.
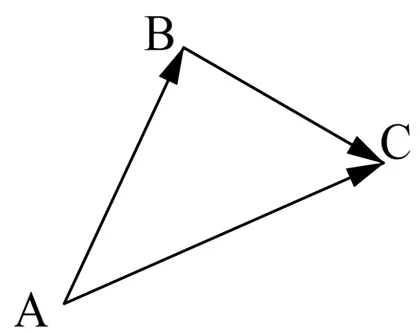
С одной точки зрения, объект совершил сразу два перемещения, из А в В и из В в С, которые можно представить векторами:

Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать вектора. Его называют правилом треугольника.
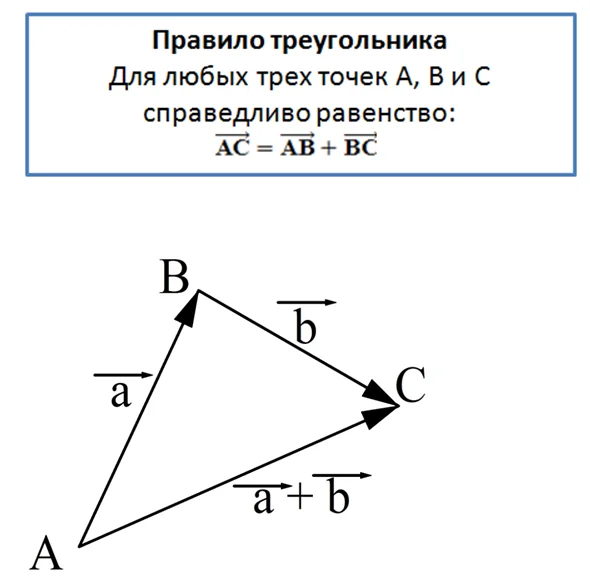
С помощью правила треугольника удобно складывать вектора, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму:
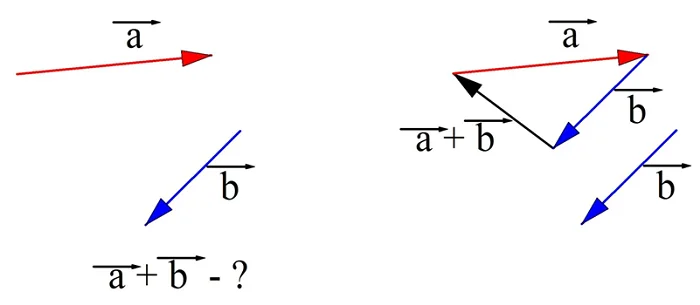
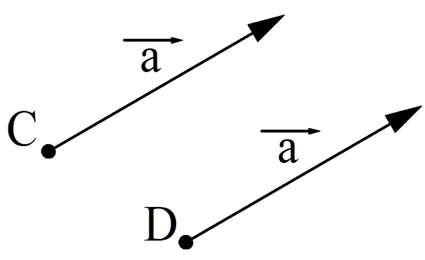
Задание. На рисунке показаны два вектора. Постройте в тетради их сумму и найдите длину получившегося вектора.
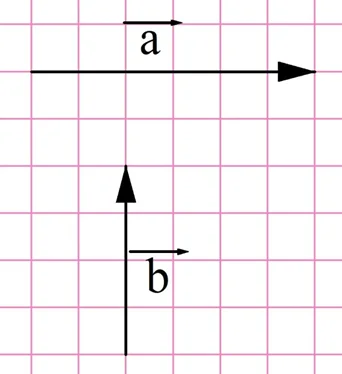
Решение. Перенесем вектор b к концу вектора а. Далее по правилу треугольника на удастся найти их сумму (обозначим этот вектор буквой с):
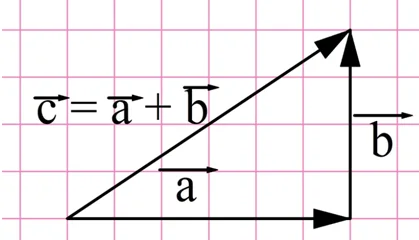
Теперь найдем длину получившегося вектора. Он является гипотенузой в прямоугольном треугольнике, причем длины катетов в этом треугольнике можно определить по рисунку, они составляют 4 и 6. Тогда длину гипотенузы можно найти по теореме Пифагора:
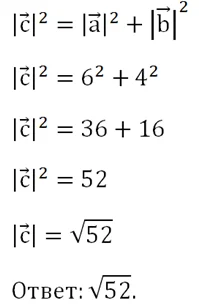
Отдельно рассмотрим случаи, когда складываются коллинеарные вектора. В этом случае получающаяся сумма окажется коллинеарной каждому слагаемому. Если вектора сонаправлены, то их длина итогового вектора окажется равной сумме длин складываемых векторов:
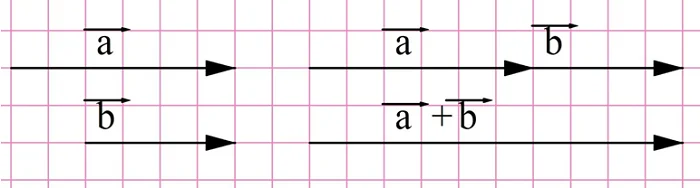
Если складываются противоположно направленные вектора, то длина их суммы окажется разностью длин складываемых векторов.
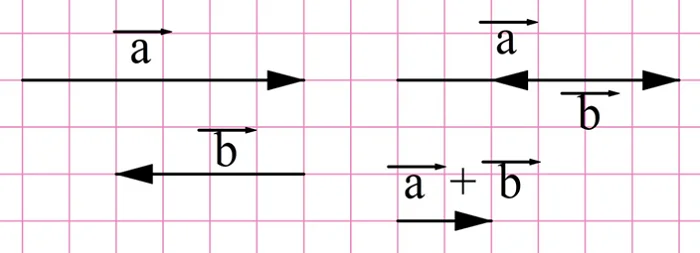
Именно по этой причине при решении простейших задач на движение корабля по реке скорость корабля и скорость течения либо складывают, либо вычитают. Дело в том, что в этих задачах складываются вектора скоростей корабля и течения. Когда судно плывет по течению, эти векторы сонаправлены, а когда плавание идет против течения, векторы оказываются противоположно направленными.
Задание. Корабль развивает в неподвижной воде скорость 12 км/ч. Он плывет по реке, скорость воды в которой составляет 5 км/ч. Найдите скорость корабля относительно берега, если:
а) судно плывет по течению;
б) судно плывет против течения;
в) судно плывет перпендикулярно течению.
Решение. Во всех случаях итоговая скорость судна является векторной суммой собственной скорости судна и течения реки:
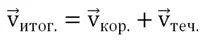
Однако направления этих векторов различны. Найдем решение графически, с помощью построений. В первом случае вектора по условию сонаправлены:
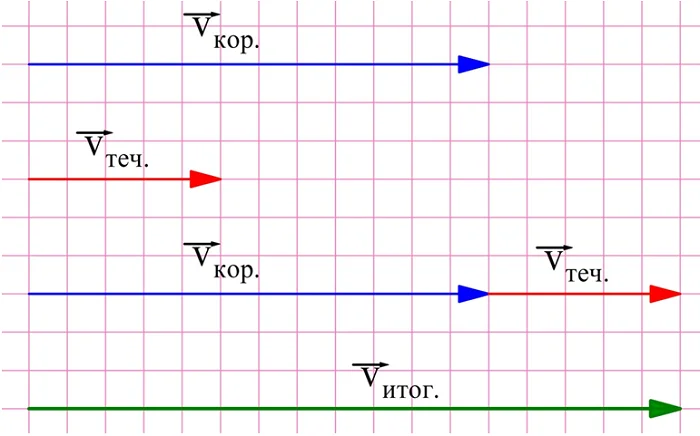
Приложив другу к другу отрезки длиной 12 и 5, получим отрезок длиной 17. Это значит, что в первом случае скорость корабля относительно берега составит 17 км/ч.
Во втором случае вектора уже окажутся противоположно направленными:
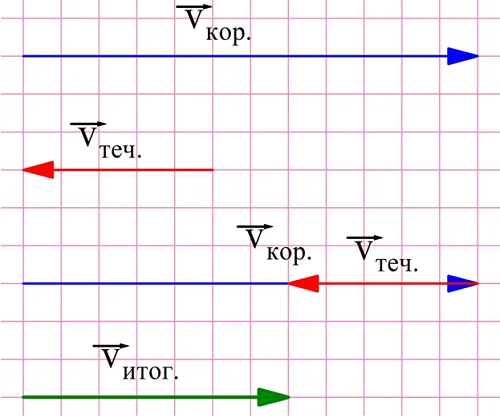
Отрезок, соответствующий итоговой скорости, здесь уже равен 7 клеткам, значит, итоговая скорость составляет 7 км/ч.
В третьем случае вектора скоростей перпендикулярны:
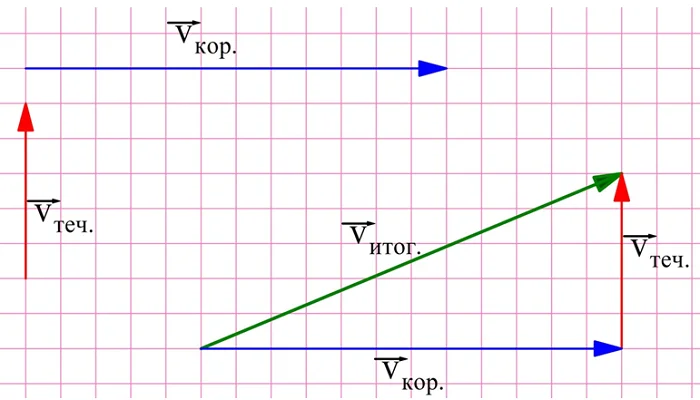
При построении получился прямоугольный треугольник, вектор итоговой скорости в нем оказался в роли гипотенузы. Найти его длину можно по теореме Пифагора, ведь катеты нам известны:

Свойства сложения
Действия с векторами во многом подобны действиям с обычными числами. Напомним, что в алгебре при прибавлении к числу нуля оно не менялось:
a + 0 = a
Аналогично и при прибавлении к вектору нулевого вектора он не изменится:

Работает ли это правило с векторами? Оказывается, что да. Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы:
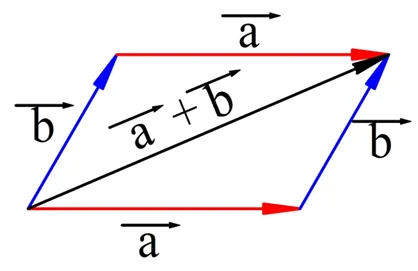
Видно, что диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Они обозначены как векторы a и b, причем в данном случае к а прибавляется b. Но одновременно эта же диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Напомним, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены одним вектором. В этом случае уже к b прибавляется a. Результат при этом получается одинаковый, поэтому можно записать, что
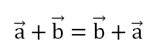
На этом примере мы увидели, как работает ещё одно правило сложения векторов, который называется правилом параллелограмма. Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма.
Задание. Сложите с помощью правила параллелограмма вектора, изображенные на рисунке:
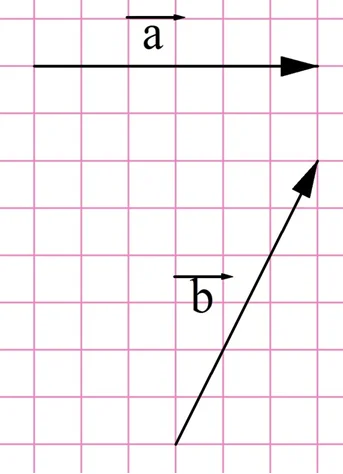
Решение. Надо всего лишь построить параллелограмм, как показано на рисунке. Его диагональ и окажется искомым вектором:
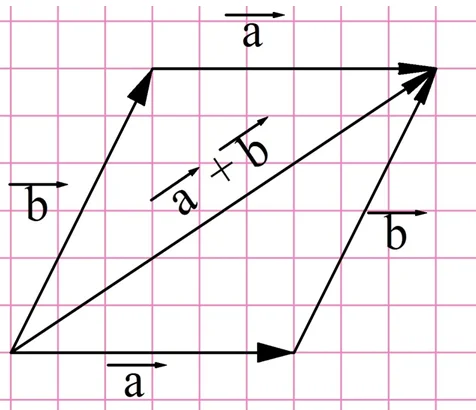
Ещё один закон, использующийся в алгебре, называется сочетательным законом, записывается он так:
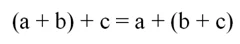
Оказывается, что и при действиях с векторами он также работает, то есть справедливо соотношение:
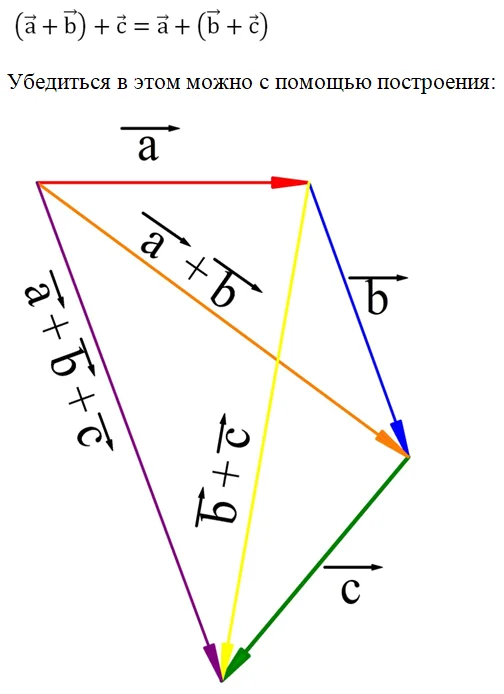
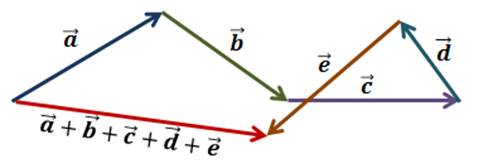
Здесь оранжевый вектор – это сумма красного (а) и синего (b) вектора. Если к оранжевому вектору добавить зеленый (с), то получится фиолетовый вектор, который, таким образом, является суммой
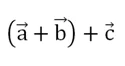
Желтый вектор – это сумма синего и зеленого вектора. Видно, что фиолетовый вектор представляет собой сумму красного и желтого, то есть он представляет сумму

Складывать можно любое количество векторов. В этом случае надо последовательно прикладывать эти вектора друг к другу, выстраивая «цепочку» векторов. Например, сложение 4 векторов, показанных на рисунке, будет осуществляться следующим образом:
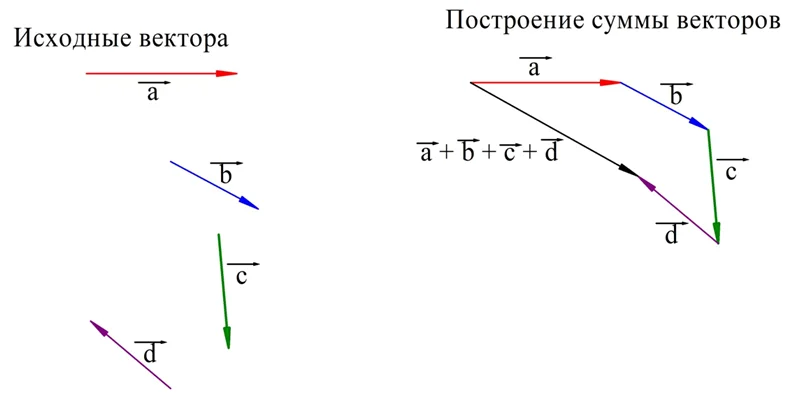
Этот способ сложения векторов именуют правилом многоугольника. Естественно, в силу переместительного закона вектора можно прикладывать друг к другу в разной последовательности, при этом результат будет получаться один и тот же.
Задание. Сложите, используя правило многоугольника, вектора, изображенные на рисунке. Выполните сложение двумя разными способами:
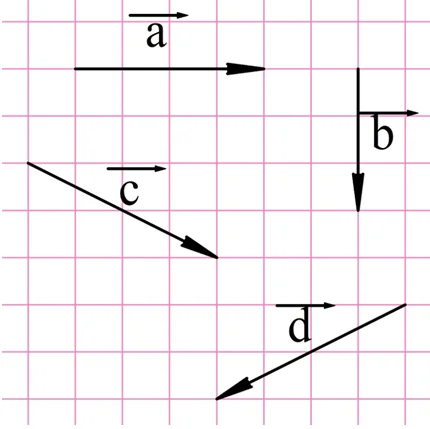
В первом случае последовательно сложим вектора a, b, c и d. Во втором случае изменим последовательность сложения. Например, сложим их в порядке d, b, c, a:
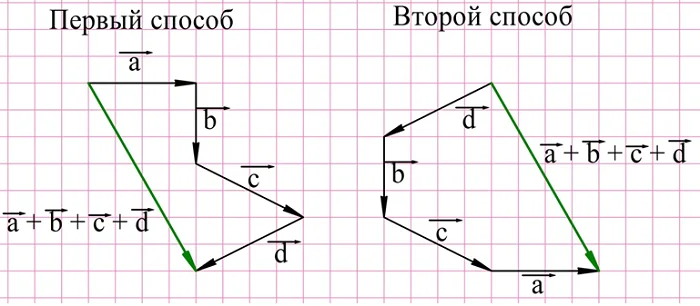
Видно, что каждый из двух способов дал один и тот же результат, что ещё раз подтверждает справедливость переместительного закона сложения векторов.
Вычитание векторов
Напомним, что в алгебре операция вычитания вводится как операция обратная сложению. То есть если для трех чисел верно соотношение
a + b = c
то разностью чисел с и a как раз окажется b:
c – a = b
Аналогично вычитание понимается и в векторной алгебре. Пусть построены вектора а, b и c так, что
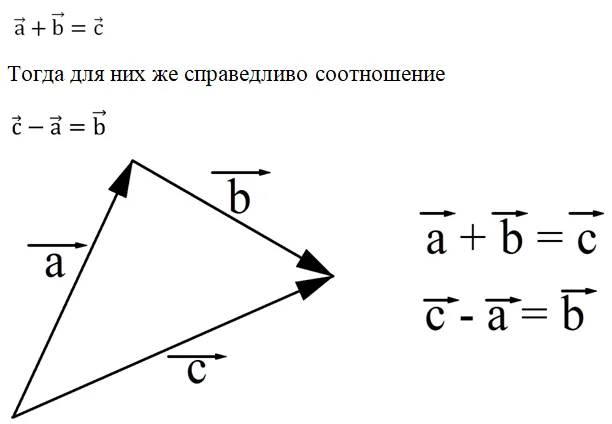
Этот пример показывает, как строить разность двух векторов. На рисунке вектора с и a отложены от одной точки, а вектор b, являющийся их разницей, проведен от конца вычитаемого вектора к концу уменьшаемого вектора.

В данном случае под уменьшаемым вектором понимается тот, который в разнице стоит перед знаком минус, а вычитаемый вектор – тот, который находится уже после этого знака. Например, в записи
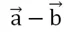
Вектор а – уменьшаемый, а вектор b – вычитаемый.
Задание. Постройте в тетради разность векторов, изображенных на рисунке:
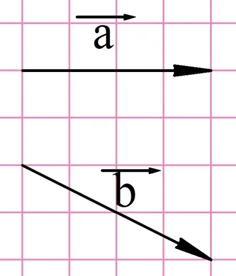
Решение. Заметим, что в условии не сказано, какой вектор из какого надо вычитать. Поэтому можно построить сразу два ответа:
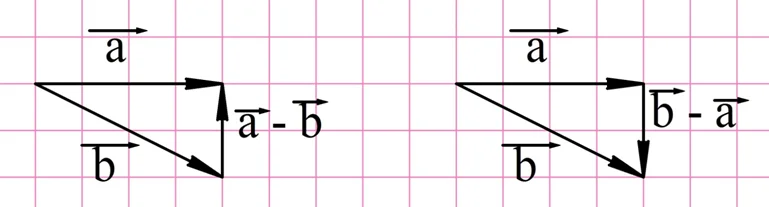
Несложно заметить, две получившиеся разности представляют собой противоположно направленные векторы одной длины. Такие векторы называются противоположными.
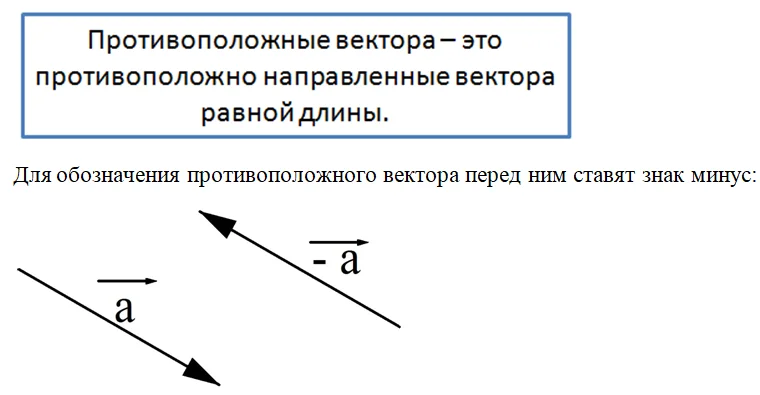
Очевидно, что если сложить друг с другом два противоположных вектора, то получится нулевой вектор:
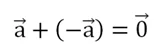
Противоположные вектора играют в векторной алгебре такую же роль, как и противоположные числа. С их помощью удобно выполнять вычитание векторов. Напомним, что для обычных чисел справедливо соотношение:
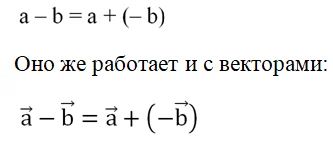
Поэтому операцию вычитания можно заменить операцией сложения, если вместо вычитаемого вектора взять вектор, противоположный ему. Рассмотрим этот способ на примере. Пусть из a надо вычесть b:
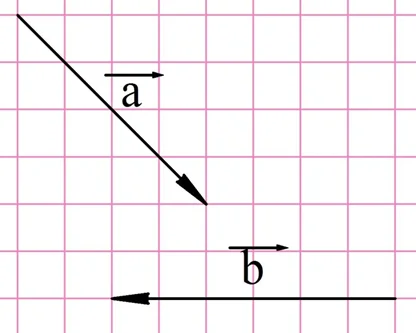
На первом шаге надо построить вектор, противоположный b:
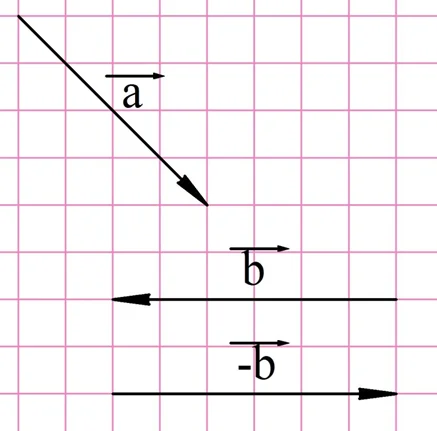
Теперь надо просто сложить a и (– b):
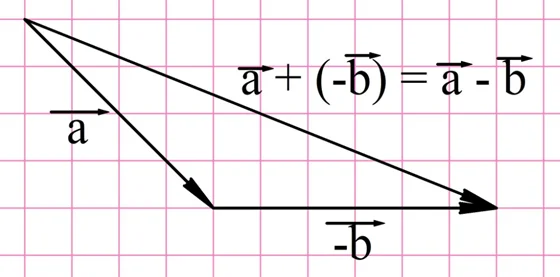
В итоге нам удалось построить разность векторов а и b.
Умножение вектора на число
Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2:
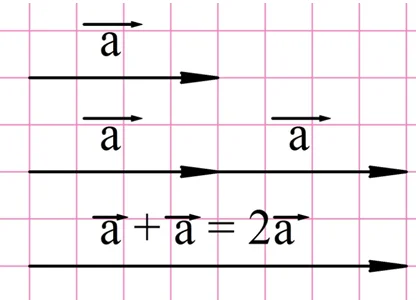
Аналогично можно построить вектора, которые больше исходного не в 2, а в 3,4 и т. д. раз:
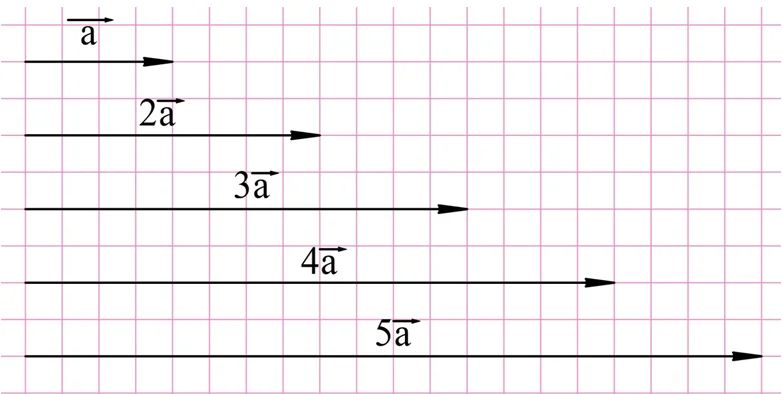
Итак, чтобы умножить вектор на положительное число k, надо построить сонаправленный с ним вектор, длина которого в k раз больше.А как умножать вектор на отрицательное число? Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор. Зная это, легко умножать вектор и на другие отрицательные числа:
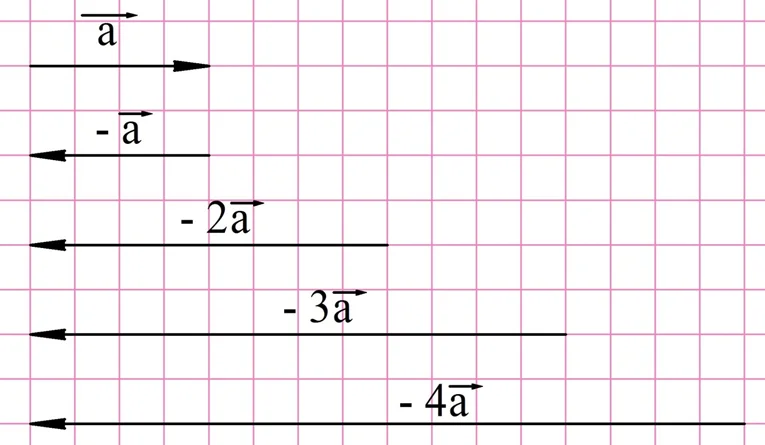
Естественно, что если вектор умножается на ноль, то в результате получается нулевой вектор.
Задание. На рисунке показаны вектора а и b. Найдите вектора
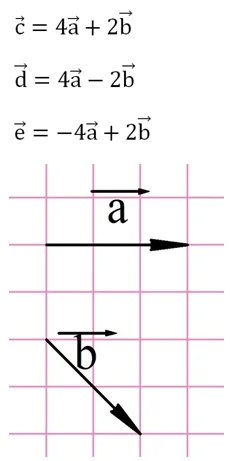
Решение. Для построения снам надо сначала умножить исходные вектора на 4 и 2, а далее полученные результаты сложить:
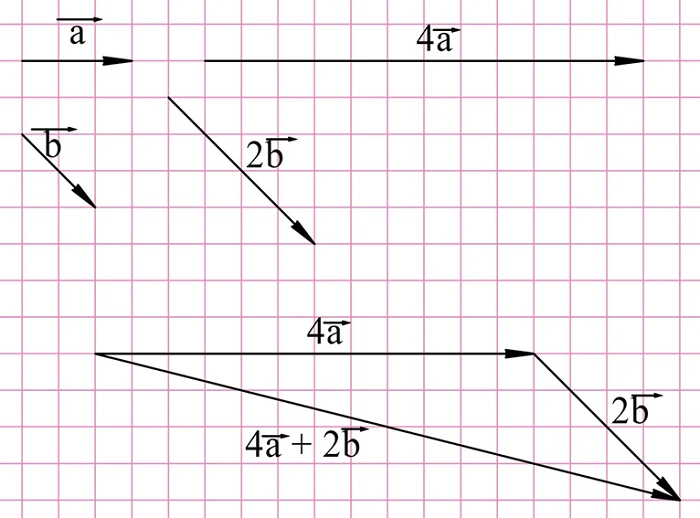
Для нахождения вектора d надо построить вектор, противоположный вектору 2b, и уже его складывать с 4a:
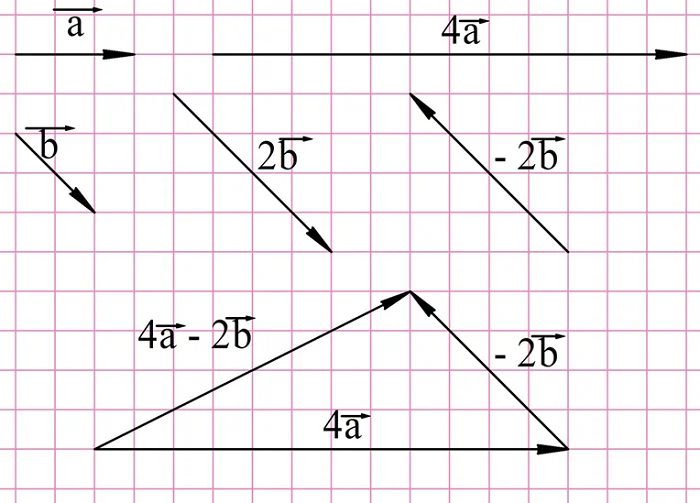
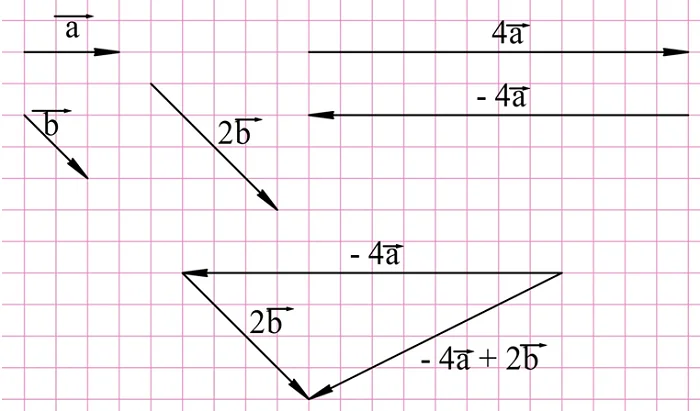
Наконец, для нахождения вектора е необходимо построить противоположный вектор уже для 4а:
Некоторые правила обычной алгебры, касающиеся операции умножения, справедливы и для векторов. Первый такое правило – это сочетательный закон:
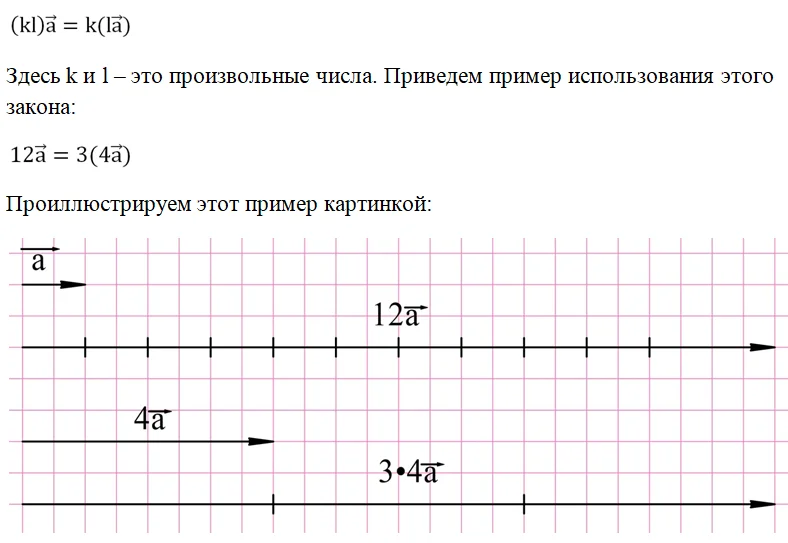
Видно, что мы можем либо сразу умножить вектор а на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится.
Также в отношении операции умножения векторов на число справедлив распределительный закона, которые позволяют раскрывать скобки:
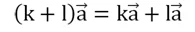
Например, пусть нам надо сложить вектора 2а и 3а. Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим вектора 2а и 3а и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор а на число 5:
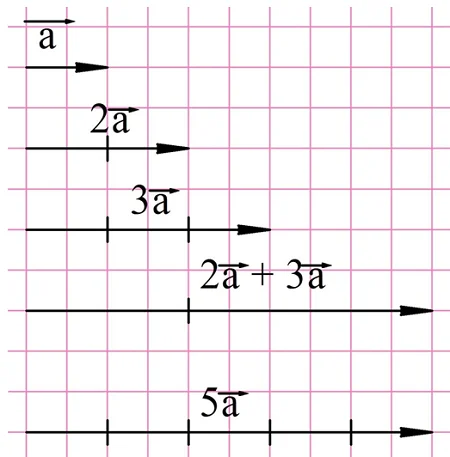
Есть ещё один распределительный закон, в котором в скобках находится уже сумма векторов, а не чисел:
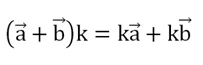
Этот закон можно применить в случае, когда нам необходимо, например, сложить вектора 4а и 4b. Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить aи b, и уже потом эту сумму умножить на 4:
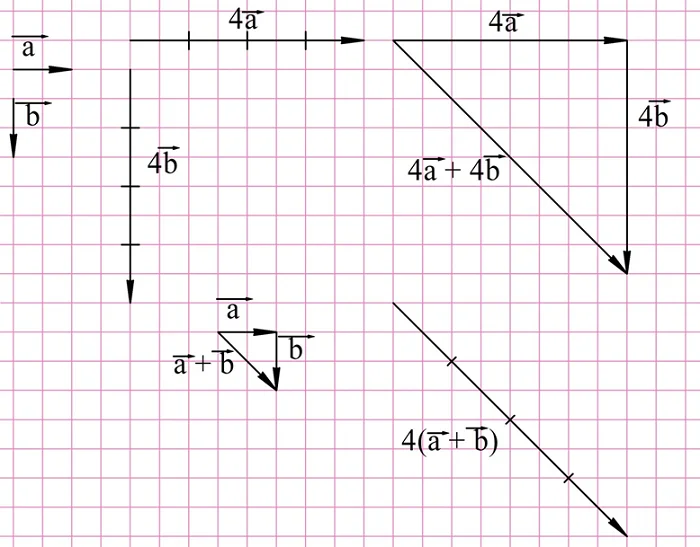
Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны вектора а, b и с, и надо найти вектор

Видно, что выражение значительно упростилось.
Решение задач с помощью векторов
Вектора активно используются в физике при решении многих задач, однако они также помогают доказывать геометрические теоремы. Рассмотрим несколько примеров, и начнем со вспомогательной задачи.
Задание. Известно, что С – это середина отрезка АВ. Докажите, что для любой точки О выполняется равенство:
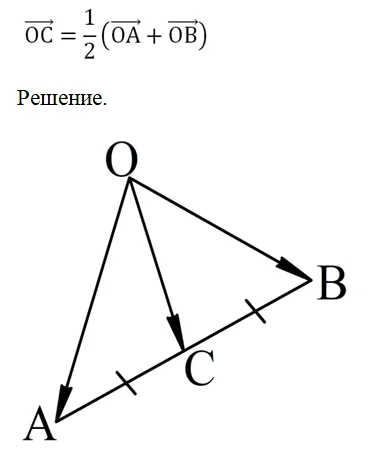
Используя правило треугольника, вектор ОС можно представить в виде двух различных сумм:

Проанализируем выражение в скобках. Вектора АС и ВС коллинеарны, ведь они лежат на одной прямой АВ. При этом они противоположно направлены. Длина у них одинакова, ведь С – середина АВ. Тогда по определению АС и ВС – противоположные вектора, и их сумма равна нулю:

Задание. Докажите, что если в трапеции провести прямую, проходящую через середины ее оснований, то она также пройдет через точку, в которой пересекаются продолжения боковых сторон трапеции.
Решение. Построим трапецию, обозначим ее вершины и середины оснований:
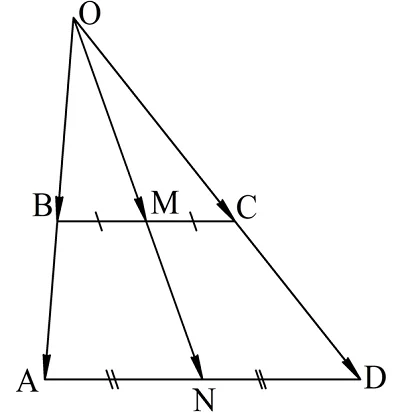
Здесь ABCD – трапеция, основаниями которой являются отрезки ВС и AD. M и N – их середины. Прямые АВ и CD пересекаются в точке O. Необходимо доказать, что прямая MN также проходит через О.
Заметим, что ∆ОВС и ∆ОАD подобны. Действительно, у них есть общий ∠ВОС, а ∠ОВС и ∠ОАD одинаковы как односторонние углы при секущей АВ, поэтому треугольники подобны по 1-ому признаку. Обозначим коэффициент подобия буквой k, тогда можно записать, что
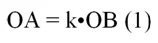
Так как отрезки ОА и АВ лежат на одной прямой, то вектора ОА и АВ коллинеарны и притом сонаправлены, поэтому в (1) отрезки можно заменить векторами:

(это соотношение мы доказали в предыдущей, вспомогательной задаче).
Аналогичную формулу можно составить и для второго основания и его середины N:
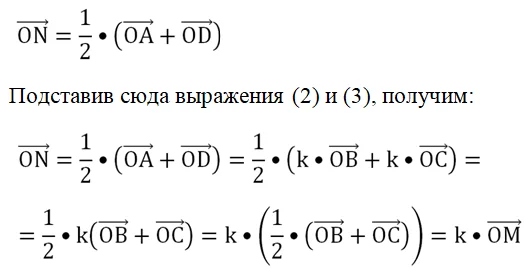
Полученное нами равенство означает, что вектора ON и ОМ коллинеарны, а значит, лежат на одной прямой (эти вектора не могут лежать на параллельных прямых, так как имеют общую точку О). Тогда получается, что О, M и N лежат на одной прямой, ч. т. д.
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| Для плоских задач | a + b = x + bx; ay + by> |
| Для трехмерных задач | a + b = x + bx; ay + by; az + bz> |
| Для n-мерных векторов | a + b = 1 + b1; a2 + b2; . an + bn> |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| Для плоских задач | a – b = x – bx; ay – by> |
| Для трехмерных задач | a – b = x – bx; ay – by; az – bz> |
| Для n-мерных векторов | a – b = 1 – b1; a2 – b2; . an – bn> |
Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
Сложение и вычитание векторов
Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec – vec = vec <0>)
Длина нулевого вектора равна нулю:
( left| vec <0>right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec – vec = left( <- , – , – > right) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
ГДЗ по геометрии 9 класс Мерзляк дидактические материалы вариант 1 – 188
Авторы: Мерзляк А.Г. , Полонский В.Б. , Рабинович Е.М. , Якир М.С. .
Издательства: Просвещение, Вентана-граф 2017-2021
Тип: Дидактические материалы, Алгоритм успеха
Подробный решебник (ГДЗ) по Геометрии за 9 (девятый) класс дидактические материалы – готовый ответ вариант 1 – 188. Авторы учебника: Мерзляк, Полонский, Рабинович, Якир. Издательство: Вентана-граф 2017-2021.
Похожие ГДЗ
ГДЗ учебник геометрия 9 класс А.Г. Мерзляк
ГДЗ Самостоятельные и контрольные работы геометрия 9 класс Мерзляк А.Г. углубленный уровень
ГДЗ учебник геометрия 9 класс Мерзляк А.Г. углубленный уровень
ГДЗ Математические диктанты, Контрольные работы (Методическое пособие) геометрия 9 класс Буцко Е.В.
ГДЗ Рабочая тетрадь геометрия 9 класс Мерзляк А.Г.
188. С помощью правила треугольника постройте сумму векторов а и Ь, изображённых на рисунке 13.
[spoiler title=”источники:”]
http://calcsbox.com/post/slozenie-i-vycitanie-vektorov.html
http://megaresheba.ru/gdz/geometriya/9-klass/didakticheskie-materiali-merzlyak/1-variant-188
[/spoiler]
Вам уже известны правила сложения двух векторов.
Cегодня мы будем учиться складывать несколько векторов.
Построим вектор суммы векторов 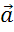 ,
, 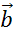 ,
, 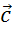 . От некоторой точки А отложим вектор
. От некоторой точки А отложим вектор
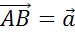 . Далее от точки B отложим вектор
. Далее от точки B отложим вектор 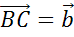 . А от точки C отложим вектор
. А от точки C отложим вектор
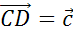 .
.
Будем последовательно складывать наши векторы, пользуясь правилом треугольника.
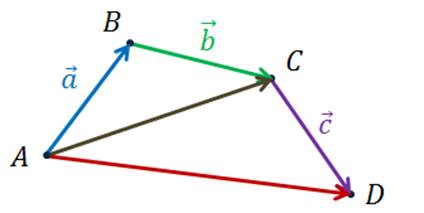
Сумма векторов 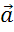 ,
, 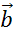 равна вектору
равна вектору 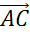 .
.
Теперь к вектору 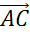 добавим вектор
добавим вектор 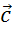 . В результате мы получаем вектор
. В результате мы получаем вектор 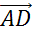 .
.
Тогда можем сказать, что сумма 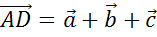 .
.
Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.
Такое правило построения суммы векторов называют правилом многоугольника.
Сформулируем его в общем виде.
Если А1, А2, …, An — произвольные точки плоскости, то сумма векторов 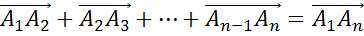
.
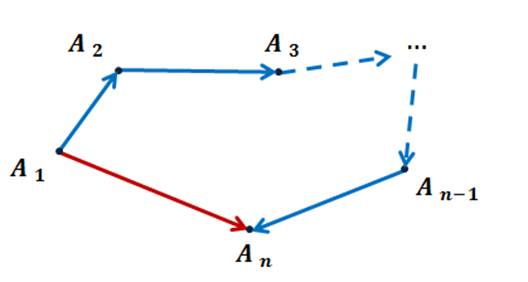
Это равенство справедливо для любых точек А1, А2, …, An. И, в частности, для случая, когда некоторые из них совпадают.
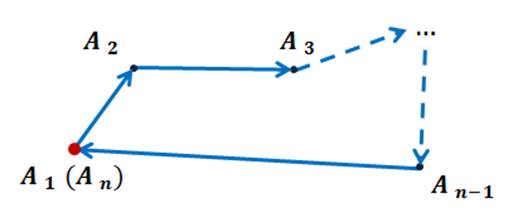
Например, если начало первого вектора совпадает с концом последнего, то сумма данных векторов равна нулевому вектору.
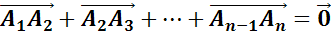
Задача. Построить вектор суммы попарно неколлинеарных векторов 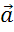 ,
, 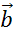 ,
, 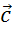 ,
, 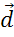 и
и 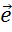 .
.
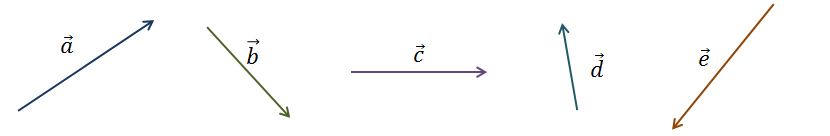
Построение
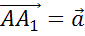
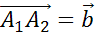
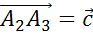
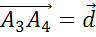
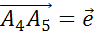
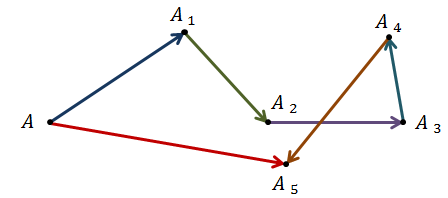
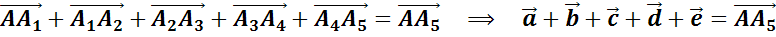 .
.
Задача. В соответствии с правилом многоугольника составить равенство,выражающее сумму нескольких векторов.
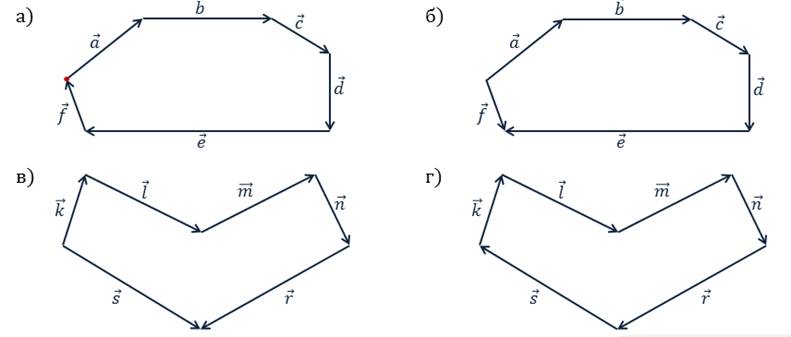
Посмотрим на первый рисунок. Мы видим, что последовательно складывают векторы 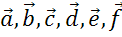 . Но, так как начало вектора
. Но, так как начало вектора 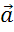 совпадает с концом вектора
совпадает с концом вектора 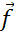 , то сумма данных векторов равна нулевому вектору
, то сумма данных векторов равна нулевому вектору 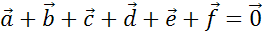 .
.
Перейдём к следующему случаю.
Видим, что сумма состоит из векторов 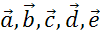 . А вот вектор
. А вот вектор 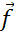 , как раз таки, и равен ей.
, как раз таки, и равен ей.
На рисунке в последовательно, друг за другом, отложены векторы 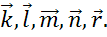 Ну, а вектор
Ну, а вектор 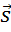 равен их сумме.
равен их сумме.
На последнем рисунке последовательно, друг за другом, отложены векторы 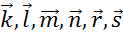 . При этом Начало вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна нулевому вектору
. При этом Начало вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна нулевому вектору 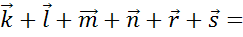
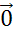 .
.
Задача. 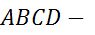 равнобокая трапеция.
равнобокая трапеция.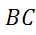 и
и 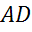 — её основания, боковая сторона равна
— её основания, боковая сторона равна 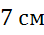 . Построить вектор
. Построить вектор 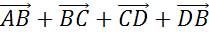 и найти его длину.
и найти его длину.
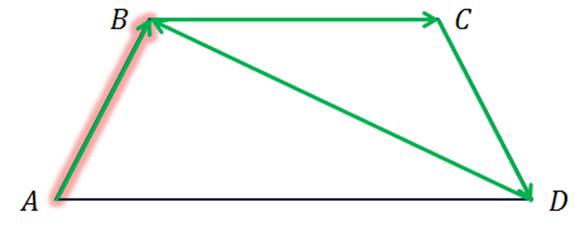
Построение
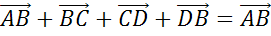
Решение.
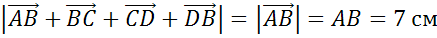
Ответ: 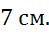
А теперь подведём итоги нашего урока.
Сегодня мы познакомились с правилом многоугольника, которое позволяет строить вектор суммы нескольких векторов.
Его суть заключается в том, что векторы-слагаемые последовательно откладывают друг от друга, суммой является вектор, начало которого совпадает с началом первого вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого.
Если эти точки совпадают, то сумма данных векторов равна нулевому вектору.
Вам уже знакомы правила сложения векторов.
Чтобы сложить неколлинеарные векторы  и
и  по правилу треугольника, нужно от некоторой точки А отложить вектор
по правилу треугольника, нужно от некоторой точки А отложить вектор 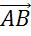 , равный вектору
, равный вектору  . Далее от точки B отложить вектор
. Далее от точки B отложить вектор 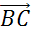 , равный вектору
, равный вектору  . Вектор
. Вектор 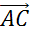 является вектором суммы двух векторов
является вектором суммы двух векторов  и
и  .
.
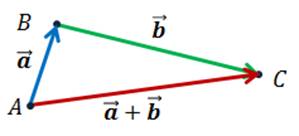
Для сложения этих же векторов можно использовать правило параллелограмма. При этом нужно отложить от произвольной точки А векторы 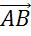 и
и 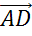 , равные векторам
, равные векторам  и
и  соответственно, и построить на них параллелограмм ABCD. Тогда вектор
соответственно, и построить на них параллелограмм ABCD. Тогда вектор 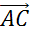 равен сумме векторов
равен сумме векторов  и
и  .
.
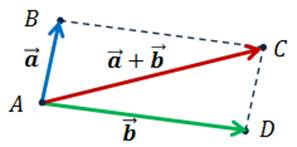
Для сложения нескольких векторов применяют правило многоугольника. При этом от некоторой точки последовательно откладывают векторы друг за другом, и вектором их суммы является вектор, проведённый от начала первого вектора к концу последнего.
Так же вам известны законы сложения векторов: переместительный и сочетательный.
На этом уроке поговорим о разности двух векторов. Её обозначают так 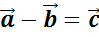 .
.
Разностью векторов 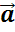 и
и 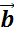 называют такой вектор
называют такой вектор 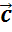 , сумма которого с вектором
, сумма которого с вектором  равна вектору
равна вектору  .
.
Чтобы получить представление о разности двух векторов, решим задачу.
Задача. По данным векторам  и
и  построить вектор
построить вектор 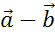 .
.
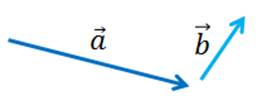
Построение
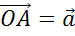
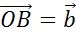
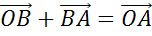
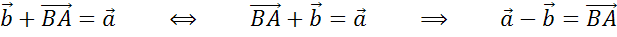 .
.
Вектор 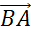 — искомый.
— искомый.
Эту задачу можно решить другим способом.
Но перед тем как его привести введём понятие вектора, противоположного данному.
Для произвольного ненулевого вектора 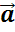 вектор
вектор 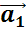 будет противоположным, если:
будет противоположным, если:
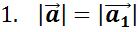
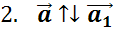
Вектор, противоположный вектору 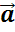 , обозначается так
, обозначается так 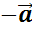 . И говорят «вектор минус a».
. И говорят «вектор минус a».
Очевидно, что сумма вектора 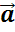 с противоположным ему равна нулевому вектору
с противоположным ему равна нулевому вектору 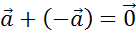 .
.
Запишем теорему о разности двух векторов.
Для любых векторов  и
и  справедливо равенство
справедливо равенство 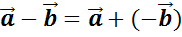 .
.
Докажем данную теорему.
Доказательство.
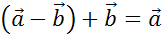
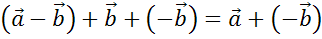
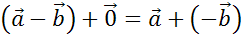
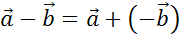
Что и требовалось доказать.
Опираясь на эту теорему, приведём ещё одно решение задачи на построение разности векторов 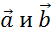 .
.
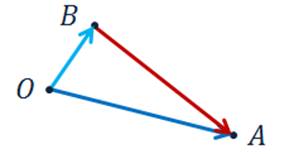
Способ
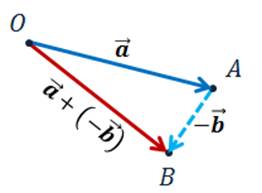
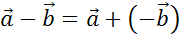
Отметим произвольную точку О и от неё отложим вектор 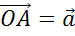 . Далее отложим от точки А вектор
. Далее отложим от точки А вектор 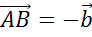 .
.
По правилу треугольника сумма 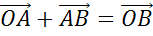 .
.
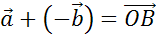
А значит, пользуясь теоремой о разности двух векторов, можем сделать вывод о том, что разность векторов 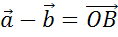 . И вектор
. И вектор 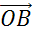 — искомый.
— искомый.
Итак, можем сделать вывод, что вектор разности двух векторов можно строить двумя способами.
Можно от некоторой точки О отложить векторы 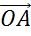 и
и 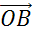 , равные векторам
, равные векторам 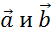 . При этом вектором их разности будет вектор
. При этом вектором их разности будет вектор 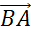 , направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
, направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
Так же, пользуясь теоремой о разности двух векторов, разность векторов 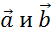 можно представить в виде суммы вектора
можно представить в виде суммы вектора 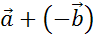 .
.
Тогда, отложив от некоторой точки О вектор 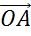 , равные вектору
, равные вектору  , а от точки А — вектор
, а от точки А — вектор 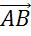 , равный вектору
, равный вектору 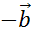 , по правилу треугольника получим вектор
, по правилу треугольника получим вектор 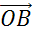 .
.
Он является вектором суммы вектора 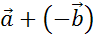 . И, соответственно, вектором разности векторов
. И, соответственно, вектором разности векторов 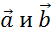 .
.
Задача. Начертить попарно неколлинеарные векторы  ,
,  и
и 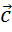 . Построить на них векторы:
. Построить на них векторы: 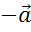 ,
, 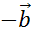 ,
, 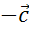 ,
, 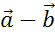 ,
, 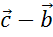 и
и 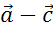 .
.
Построение.
Для начала построим векторы, противоположные данным.
Векторы являются противоположными, если их длины равны и они противоположно направлены.
Выберем точки А, B и C, от которых будем откладывать противоположные векторы.
Далее через каждую из этих точек проведём прямые параллельные векторам  ,
,  и
и 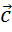 соответственно.
соответственно.
От отмеченных точек на проведённых прямых можно изобразить векторы, равные данным, и, противоположные данным. Нам нужны те, которые противоположны векторам  ,
,  и
и 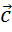 соответственно.
соответственно.
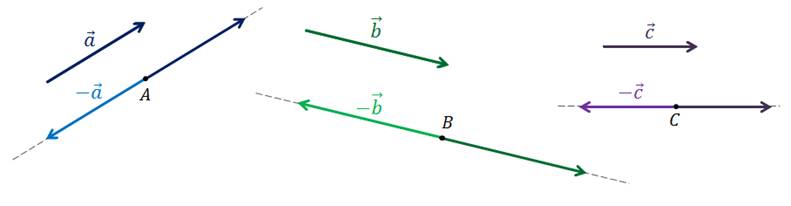
Так мы построили векторы 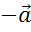 ,
, 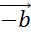 и
и 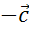 .
.
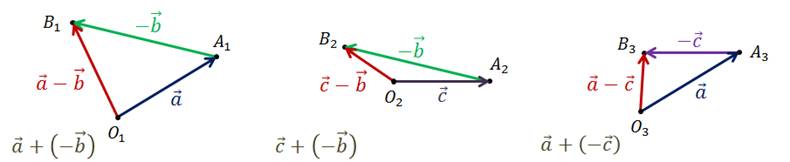
Задача. Сторона квадрата 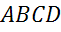 равна
равна 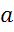 . Найти
. Найти 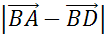 и
и 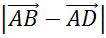 .
.
Построение.
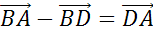
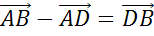
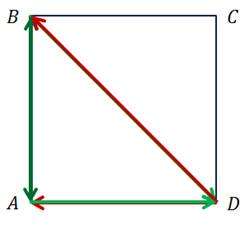
Решение.
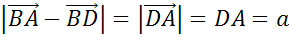
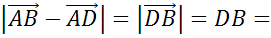
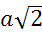
По теореме Пифагора: 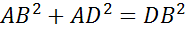
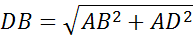
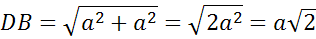
Ответ: 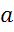 ;
; 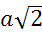 .
.
Подведём итоги нашего урока.
Сегодня вы познакомились с понятием противоположного вектора. Противоположные векторы имеют равные длины и противоположно направлены.
Мы ввели понятие разности двух векторов. Разностью векторов  ,
,  называют такой вектор
называют такой вектор 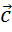 , сумма которого с вектором
, сумма которого с вектором  равна вектору
равна вектору  .
.
Для построения вектора разности мы выделили два способа.
Можно от некоторой точки О отложить векторы 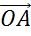 и
и 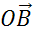 , равные векторам
, равные векторам  и
и  . При этом вектором их разности будет вектор
. При этом вектором их разности будет вектор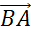 , направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
, направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
Так же, пользуясь теоремой о разности двух векторов, разность векторов  и
и  можно представить в виде суммы вектора
можно представить в виде суммы вектора  и вектора, противоположного вектору
и вектора, противоположного вектору  .
.
Тогда, отложив от некоторой точки О вектор 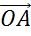 , равный вектору
, равный вектору  , а от точки А — вектор
, а от точки А — вектор 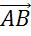 , равный вектору
, равный вектору 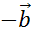 , по правилу треугольника получим вектор
, по правилу треугольника получим вектор 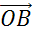 .
.
Он является вектором суммы вектора  и вектора, противоположного вектору
и вектора, противоположного вектору  . И, соответственно, вектором разности векторов
. И, соответственно, вектором разности векторов  и
и  .
.
Теперь вы владеете не только правилами сложения, а ещё и правилом вычитания векторов.
Сложив два вектора, в результате получим новый вектор.
Векторы могут располагаться один относительно другого:
- параллельно,
- не параллельно.
Складываем параллельные векторы
Если векторы параллельны, складывать так:
- А) К концу первого вектора приложить начало второго вектора
- Б) из начала первого вектора к концу второго вектора провести новый вектор

Рис. 1. Складываем параллельные векторы
( vec{a} + vec{c} = vec{g} )
Примечание:
В этом уравнении над буквами используются значки векторов. Эти значки указывают на то, что действия выполняются с помощью геометрии. То есть, учитывается направление векторов.
Важно! Любое выражение, записанное в векторном виде, учитывает направление векторов.
Это можно пояснить так:
- сложив два числа 3 и 4 получим только одно решение (3 + 4 = 7).
- складывая два вектора с длинами 3 и 4, можно в результате получить вектор, длина которого лежит в диапазоне от «1» до «7».
- Если векторы, которые складываем, были направлены в противоположные стороны, получим вектор, длина которого равняется единице.
- А если векторы были сонаправленными – то длина результирующего вектора будет равна семи.
- Ну а, если векторы были препендикулярными, то конечный вектор будет иметь длину, равную пяти.
Если векторы направлены в противоположные стороны, то результат сложения будет сонаправлен с более длинным вектором.

Рис. 2. Складываем параллельные противоположно направленные векторы
( vec{a} + vec{s} = vec{w} )
Складываем не параллельные векторы
Если векторы не параллельны (см. рис. ), для их сложения пользуются одним из двух правил:
- правило треугольника;
- правило параллелограмма;

Рис. 3. Не параллельные векторы
Примечание:
Правило параллелограмма удобно применять к векторам, выходящим из одной общей точки (начала векторов совмещены).
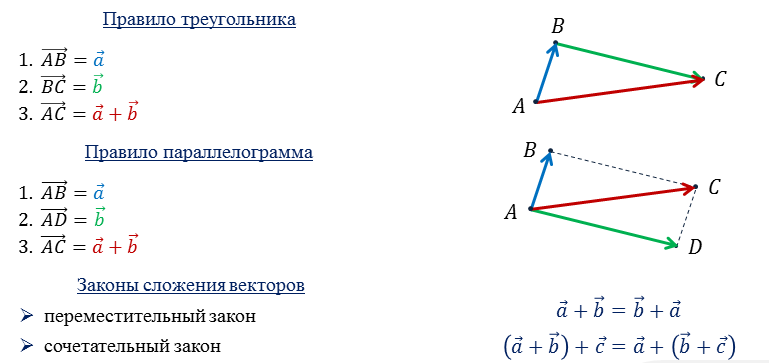
Правило треугольника
К концу первого вектора приложить начало второго вектора

Рис. 4. Располагаем не параллельные векторы, чтобы сложить их по правилу треугольника
Из свободного начала к свободному концу провести вектор

Рис. 5. Складываем не параллельные векторы по правилу треугольника
( vec{a} + vec{b} = vec{c} )
Правило параллелограмма
Совместить начала векторов

Рис. 6. Совмещаем начала не параллельных векторов, чтобы сложить их по правилу параллелограмма
Провести пунктиры, чтобы получить параллелограмм

Рис. 7. Достраиваем пунктирами параллелограмм, чтобы сложить векторы
Из точки, в которой находятся начала провести диагональ

Рис. 8. Проводим диагональ параллелограмма, чтобы сложить векторы
( vec{a} + vec{b} = vec{c} )
Как вычитать векторы
Вычтем один вектор из второго вектора. В результате получим новый вектор.
Вектор «( -vec{b} )» — это вектор «( vec{b} )», развернутый в противоположную сторону.

Рис. 9. Вектор и противоположно направленный ему вектор
Вычитание заменяют сложением. Складывают вектор с противоположно направленным вектором.
Ведь ( vec{a}-vec{b} ) то же, что и ( vec{a}+ left(-vec{b} right)).

Рис. 10. Складываем вектор «a» и противоположно направленный вектор «-b»
( vec{a} + left(-vec{b} right) = vec{g} )
Складываем и вычитаем векторы, используя их координаты
Когда известны координаты двух векторов, сложение или вычитание провести достаточно легко. Для этого нужно сложить или вычесть соответствующие координаты векторов.
Для удобства обычно выписывают один вектор под другим.
( vec{a} = left{ a_{x} ; a_{y} ; a_{z} ;right} )
( vec{b} = left{ b_{x} ; b_{y} ; b_{z} ;right} )
Рассмотрим примеры:
1. Сложение.
( vec{a} + vec{b} = vec{c} )
( vec{c} = left{ a_{x}+ b_{x} ; a_{y}+ b_{y} ; a_{z} + b_{z} right} )
2. Вычитание.
( vec{a} — vec{b} = vec{d} )
( vec{d} = left{ a_{x}- b_{x} ; a_{y}- b_{y} ; a_{z} — b_{z} right} )
Примеры сложения векторов в физике
Напоминание:
Складывать и вычитать можно только те векторы, которые имеют одинаковую размерность. То есть, длина которых измеряется в одинаковых единицах.
Рассмотрим формулу связи между начальной и конечной скоростями при равноускоренном движении
( vec{v} = vec{v_{0}} + vec{a} cdot t )
Скорость ( vec{v} )измеряют в метрах деленых на секунду, а ускорение ( vec{a} ) – в метрах, деленых на секунду в квадрате.
Размерность векторов ( vec{v} ) и ( vec{a} ) отличается. Значит, выполнять математические действия совместно над ними нельзя.
Если преобразовать вектор ( vec{a} ) ускорения так, что он получит размерность скорости, тогда можно будет складывать его с вектором скорости.
Чтобы из размерности ускорения получить метры, деленные на секунду, нужно размерность ускорения домножить на секунду.
Поэтому, в формулу для равноускоренного движения входит ( vec{a} cdot t ) — ускорение, домноженное на время.
Теперь векторы ( vec{v_{0}} ) и ( vec{a} cdot t ) имеют одинаковую размерность и их можно складывать, или вычитать.
Примечания:
— Скорость всегда направлена в ту сторону, в которую тело движется (в направлении движения тела).
— Ускорение направлено в сторону действия силы (из второго закона Ньютона).
Обратите внимание: Направление силы не всегда будет совпадать с направлением, в котором тело двигалось изначально.
Силу можно направить в любую сторону. Она будет толкать или тянуть тело в ту сторону, в которую она направлена. Поэтому, конечная скорость ( vec{v} ), начальная скорость ( vec{v_{0}} ) и ускорение ( vec{a} ) могут иметь различные направления.
Векторы складывают с помощью геометрии, то есть, учитывают их направления.
Поэтому, формула ( vec{v} = vec{v_{0}} + vec{a} cdot t ) записана в векторном виде.
Уровень А
1. Найдите построение: а) сумму (vec a + vec b), б) разность (vec a – vec b), – двух векторов, изображенных на рис. 1.
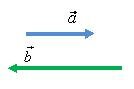
Рис. 1
Решение
Уровень В
1. Используя правила треугольника и параллелограмма, постройте векторы суммы и разности векторов (vec a) и (vec b) (рис. 1).
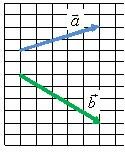
Рис. 1
Решение
2. Постройте вектор суммы трех векторов (vec a, vec b) и (vec c) (рис. 2).
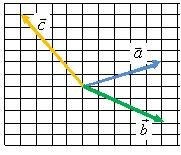
Рис. 2
Решение
