Как найти сумму векторов по координатам формула - Сайт, где вы сможете решить свои вопросы

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Сложение векторов

Формула

Чтобы складывать вектора нужно найти суммы соответствующих координат данных векторов. Например, пусть есть векторы на плоскости $ overline{a} = (x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, тогда их сумму можно найти по формуле: $$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2)$$

Если векторы заданы в пространстве тремя координатами $ overline{a} = (x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то выполнить сложение нужно по другой формуле:

$$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2; z_1+z_2) $$

При сложении первая координата первого вектора складывается с первой координатой второго вектора, вторая координата первого вектора складывается со второй координатой второго вектора и так далее в зависимости от размерности векторов. Стоит отметить, что складывать векторы можно только одинаковой размерности.

Примеры решений

Пример

Даны два вектора $ overline{a} = (1,3) $ и $ overline{b} = (2,4) $. Нужно сложить два вектора.

Решение

Итак, как складывать вектора по координатам? К первой прибавляем первую, вторую ко второй:

$$ overline{a}+overline{b} = (1+2;3+4) = (3;7) $$

В этой задаче векторы заданы в двумерном пространстве и имеют только две координаты. Если бы координат было бы три, то применять нужно вторую формулу для трехмерной задачи.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a}+overline{b} = (3;7) $$

Источник

Содержание:

Формула
Примеры нахождения суммы векторов

Формула

Чтобы найти сумму векторов $bar{a}+bar{b}$, которые заданны координатами
$bar{a}=(a_x;a_y)$ и $bar{b}=(b_x;b_y)$, необходимо сложить соответствующие
координаты этих векторов,
то есть

$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y}right)$$

В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их сумма равна

$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y} ; a_{z}+b_{z}right)$$

Примеры нахождения суммы векторов

Пример

Задание. Найти сумму векторов
$bar{a}+bar{b}$,
$bar{a}=(2;0)$ и
$bar{b}=(1;3)$

Решение. Для нахождения суммы векторов, сложим их соответствующие координаты

$$bar{a}+bar{b}=(2 ; 0)+(1 ; 3)=(2+1 ; 0+3)=(3 ; 3)$$

Ответ. $bar{a}+bar{b}==(3 ; 3)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти суммы векторов
$bar{a}+bar{b}$,
$bar{a}+bar{c}$,
$bar{b}+bar{c}$ и
$bar{a}+bar{b} +bar{c}$, если
$bar{a}=(1;-1;0)$,
$bar{b}=(3;2;-1)$ и
$bar{c}=(4;2;-1)$

Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:

$$bar{a}+bar{b}=(1+3 ;-1+2 ; 0+(-2))=(4 ; 1 ;-2)$$
$$bar{a}+bar{c}=(1+4 ;-1+2 ; 0+(-1))=(5 ; 1 ;-1)$$
$$bar{b}+bar{c}=(3+4 ; 2+2 ;-2+(-1))=(7 ; 4 ;-3)$$
$$bar{a}+bar{b}+bar{c}=(1+3+4 ;-1+2+2 ; 0+(-2)+(-1))=(8 ; 3 ;-3)$$

Ответ. $bar{a}+bar{b}=(4 ; 1 ;-2)$ , $bar{a}+bar{c}=(5 ; 1 ;-1)$ , $bar{b}+bar{c}=(7 ; 4 ;-3)$ , $bar{a}+bar{b}+bar{c}=(8 ; 3 ;-3)$

Читать дальше: как найти разность векторов.

Источник

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
Разность векторов
- Формула вычитания векторов
Примеры задач

Сумма векторов

Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c, начало которого совпадает с началом a, а конец – с концом b. При этом конец вектора a должен совпадать с началом вектора b.

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c, совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

c_i = a_i + b_i

Элементы вектора c равняются попарной сумме соответствующих элементов a и b.


Для плоских задач	a + b = {a_x + b_x; a_y + b_y}
Для трехмерных задач	a + b = {a_x + b_x; a_y + b_y; a_z + b_z}
Для n-мерных векторов	a + b = {a₁ + b₁; a₂ + b₂; … a_n + b_n}

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: (a + b) + c = a + (b + c)

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (-a) = 0

Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b, то получится c, причем должно соблюдаться условие: b + c = a

Формула вычитания векторов

c_i = a_i – b_i

Элементы вектора c равны попарной разности соответствующих элементов a и b.


Для плоских задач	a – b = {a_x – b_x; a_y – b_y}
Для трехмерных задач	a – b = {a_x – b_x; a_y – b_y; a_z – b_z}
Для n-мерных векторов	a – b = {a₁ – b₁; a₂ – b₂; … a_n – b_n}

Примеры задач

Задание 1
Вычислим сумму векторов a = {3; 5} и b = {2; 7}.

Решение:
a + b = {3 + 2; 5 + 7} = {5; 12}.

Задание 2
Найдем разность векторов a = {4; 8; -2} и b = {-1; 9; 5}.

Решение:
a – b = {4 – (-1); 8 – 9; -2 – 5} = {5; -1; -7}.

Источник

В механике существуют два типа величин:

скалярные величины, задающие некоторое числовое значение – время, температура, масса и т.д.
векторные величины, которые вместе с некоторым числовым значением задают направление – скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты – первую, из второй – вторую и т.д.):

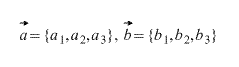
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

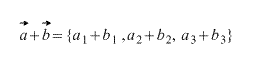
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

правило параллелограмма
правило треугольника
тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

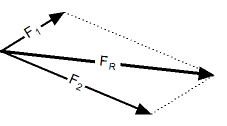Процедура сложения векторов по правилу параллелограмма заключается в следующем:

нарисовать первый вектор, учитывая его величину и направление
от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
дополнить рисунок до параллелограмма, считая, что два нарисованных вектора – это его стороны
результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем:

нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

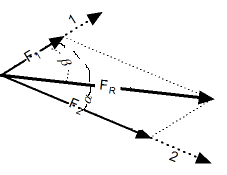Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:

F_рез. = [ F₁² + F₂² -2 F₁ F₂ cos(180^о-α) ]^1/2 (1)
- где
  - F = числовое значение вектора
  - α = угол между векторами 1 и 2

Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:

β = arcsin[ F₂*sin(180^o-α) / F_R] (2)
- где
  - α = угол между исходными векторами

Пример – сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80^o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН)² + (8 кН)² – 2 (5 кН)(8 kН) cos(180^o – (80^o)) ]^1/2

= 10,14кН

Угол между результирующей силой и первой силой равен:

β= arcsin[ (8кН) sin(180^o – (80^o)) / (10,14кН)]

= 51^o

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180^o – (80^o)) / (10,2 кН)]

= 29^o

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Распечатать: Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма.

Источник

Сложение и вычитание векторов

Навигация по странице:

Определение операции сложения векторов
Определение операции вычитания векторов
Формулы для сложения и вычитания вектора
- для плоских задач
- для пространственных задач
- для n -мерных векторов
Примеры задач на сложение и вычитание векторов
- плоские задачи
- пространственные задачи
- задачи в n -мерном пространстве

Определение.

Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:

с_i = a_i + b_i

Определение.

Вычитание векторов (разность векторов) a – b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:

с_i = a_i – b_i

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

В случае плоской задачи сумму и разность векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти, воспользовавшись следующими формулами:

a + b = {a_x + b_x; a_y + b_y}

a – b = {a_x – b_x; a_y – b_y}

Формулы сложения и вычитания векторов для пространчтвенных задач

В случае пространственной задачи сумму и разность векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти, воспользовавшись следующими формулами:

a + b = {a_x + b_x; a_y + b_y; a_z + b_z}

a – b = {a_x – b_x; a_y – b_y; a_z – b_z}

Формулы сложения и вычитания n -мерных векторов

В случае n -мерного пространства сумму и разность векторов a = {a₁ ; a₂ ; … ; a_n} и b = {b₁ ; b₂ ; … ; b_n} можно найти, воспользовавшись следующими формулами:

a + b = {a₁ + b₁; a₂ + b₂; … ; a_n + b_n}

a – b = {a₁ – b₁; a₂ – b₂; … ; a_n – b_n}

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Пример 1. Найти сумму векторов a = {1; 2} и b = {4; 8}.

Решение:

a + b = {1 + 4; 2 + 8} = {5; 10}

Пример 2. Найти разность векторов a = {1; 2} и b = {4; 8}.

Решение:

a – b = {1 – 4; 2 – 8} = {-3; -6}

Примеры пространственных задач на сложение и вычитание векторов

Пример 3. Найти сумму векторов a = {1; 2; 5} и b = {4; 8; 1}.

Решение:

a + b = {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6}

Пример 4. Найти разность векторов a = {1; 2; 5} и b = {4; 8; 1}.

Решение:

a – b = {1 – 4; 2 – 8; 5 – 1} = {-3; -6; 4}

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Пример 5. Найти сумму векторов a = {1; 2; 5; 9} и b = {4; 8; 1; -20}.

Решение:

a + b = {1 + 4; 2 + 8; 5 + 1; 9 + (-20)} = {5; 10; 6; -11}

Пример 6. Найти разность векторов a = {1; 2; 5; -1; 5} и b = {4; 8; 1; -1; 2}.

Решение:

a – b = {1 – 4; 2 – 8; 5 – 1; -1 – (-1); 5 – 2} = {-3; -6; 4; 0; 3}

Источник

Сложение векторов

Формула

Примеры решений

Формула

Примеры нахождения суммы векторов

Сумма векторов

Формула сложения векторов

Свойства сложения векторов

Разность векторов

Формула вычитания векторов

Примеры задач

Покоординатное сложение векторов.

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

Правило треугольника. Сложение векторов по правилу треугольника.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

Сложение и вычитание векторов

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

Формулы сложения и вычитания векторов для пространчтвенных задач

Формулы сложения и вычитания n -мерных векторов

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Примеры пространственных задач на сложение и вычитание векторов

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Вам также может понравиться

Как найти ширину все варианты с ответами

Как нашли планету двойника земли

Пропали аккаунты как найти

Добавить комментарий Отменить ответ