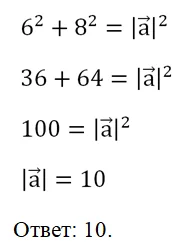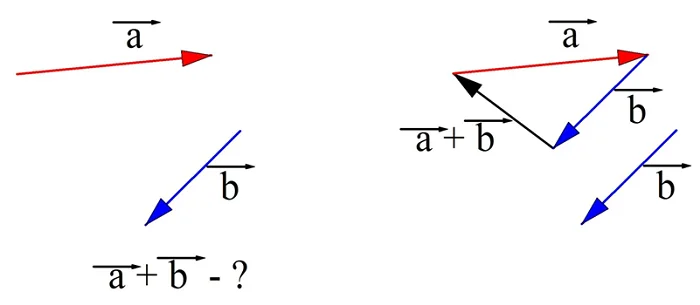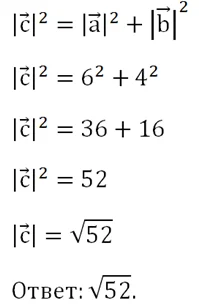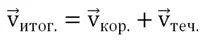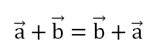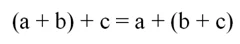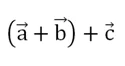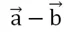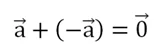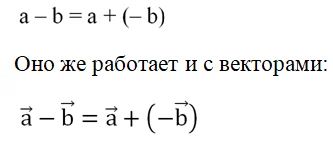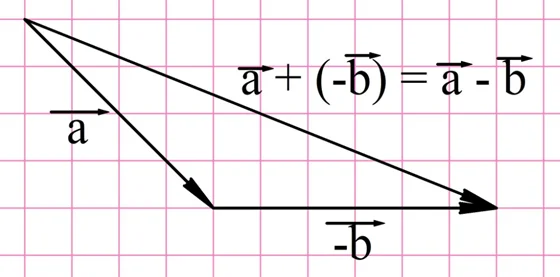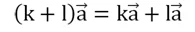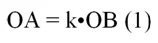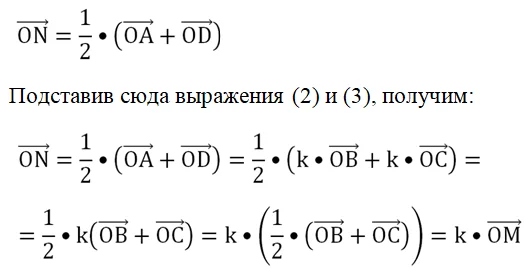Содержание:
- Формула
- Примеры нахождения суммы векторов
Формула
Чтобы найти сумму векторов $bar{a}+bar{b}$, которые заданны координатами
$bar{a}=(a_x;a_y)$ и $bar{b}=(b_x;b_y)$, необходимо сложить соответствующие
координаты этих векторов,
то есть
$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y}right)$$
В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их сумма равна
$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y} ; a_{z}+b_{z}right)$$
Примеры нахождения суммы векторов
Пример
Задание. Найти сумму векторов
$bar{a}+bar{b}$,
$bar{a}=(2;0)$ и
$bar{b}=(1;3)$
Решение. Для нахождения суммы векторов, сложим их соответствующие координаты
$$bar{a}+bar{b}=(2 ; 0)+(1 ; 3)=(2+1 ; 0+3)=(3 ; 3)$$
Ответ. $bar{a}+bar{b}==(3 ; 3)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти суммы векторов
$bar{a}+bar{b}$,
$bar{a}+bar{c}$,
$bar{b}+bar{c}$ и
$bar{a}+bar{b} +bar{c}$, если
$bar{a}=(1;-1;0)$,
$bar{b}=(3;2;-1)$ и
$bar{c}=(4;2;-1)$
Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:
$$bar{a}+bar{b}=(1+3 ;-1+2 ; 0+(-2))=(4 ; 1 ;-2)$$
$$bar{a}+bar{c}=(1+4 ;-1+2 ; 0+(-1))=(5 ; 1 ;-1)$$
$$bar{b}+bar{c}=(3+4 ; 2+2 ;-2+(-1))=(7 ; 4 ;-3)$$
$$bar{a}+bar{b}+bar{c}=(1+3+4 ;-1+2+2 ; 0+(-2)+(-1))=(8 ; 3 ;-3)$$
Ответ. $bar{a}+bar{b}=(4 ; 1 ;-2)$ , $bar{a}+bar{c}=(5 ; 1 ;-1)$ , $bar{b}+bar{c}=(7 ; 4 ;-3)$ , $bar{a}+bar{b}+bar{c}=(8 ; 3 ;-3)$
Читать дальше: как найти разность векторов.
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
-
Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
-
Разность векторов
-
Формула вычитания векторов
-
Формула вычитания векторов
- Примеры задач
Сумма векторов
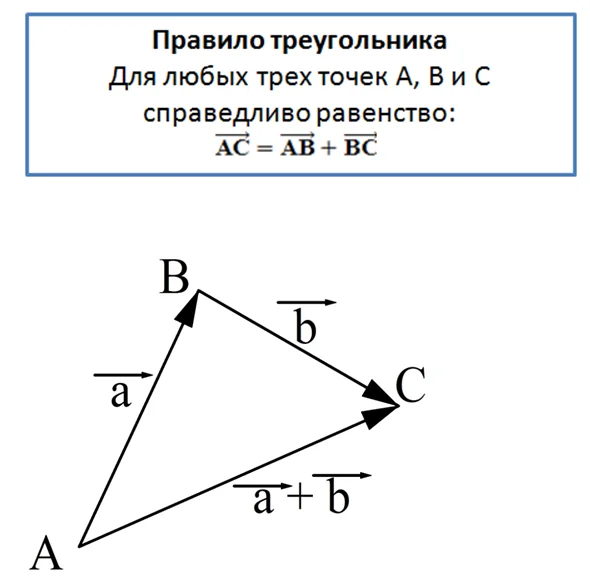
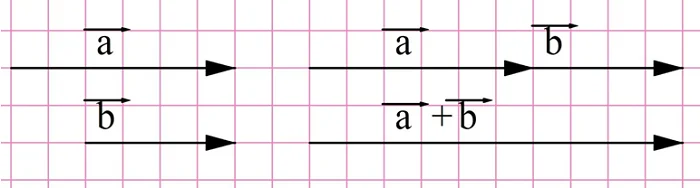
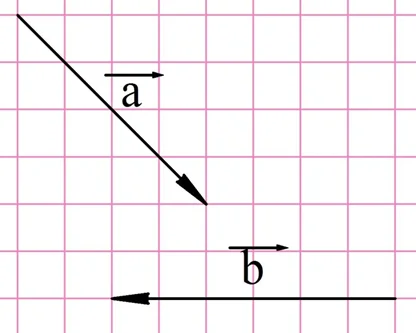
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c, начало которого совпадает с началом a, а конец – с концом b. При этом конец вектора a должен совпадать с началом вектора b.
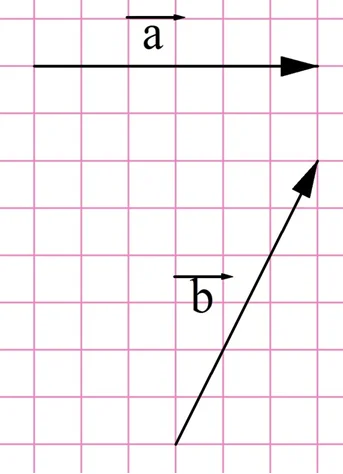
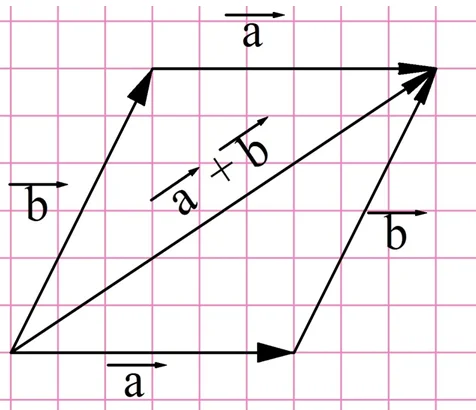
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c, совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
ci = ai + bi
Элементы вектора c равняются попарной сумме соответствующих элементов a и b.
| Для плоских задач | a + b = {ax + bx; ay + by} |
| Для трехмерных задач | a + b = {ax + bx; ay + by; az + bz} |
| Для n-мерных векторов | a + b = {a1 + b1; a2 + b2; … an + bn} |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
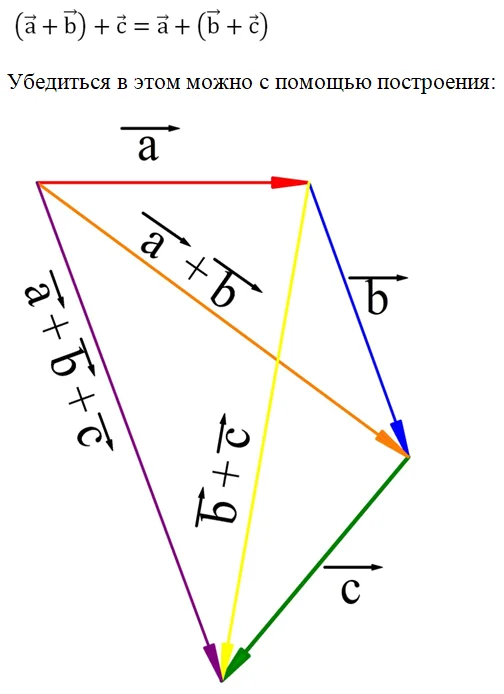
2. Ассоциативность: (a + b) + c = a + (b + c)
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (-a) = 0
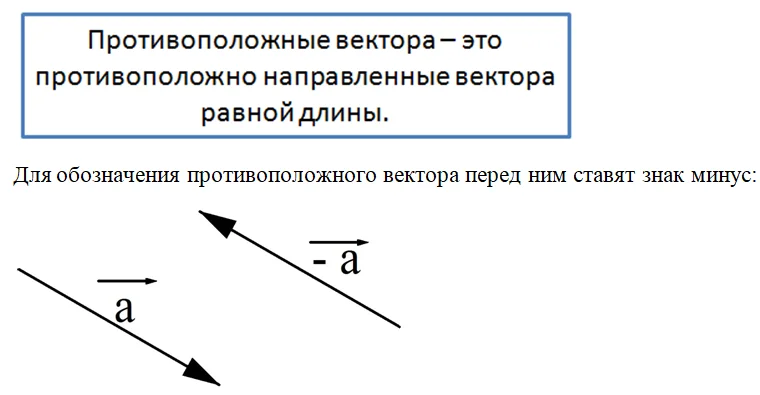
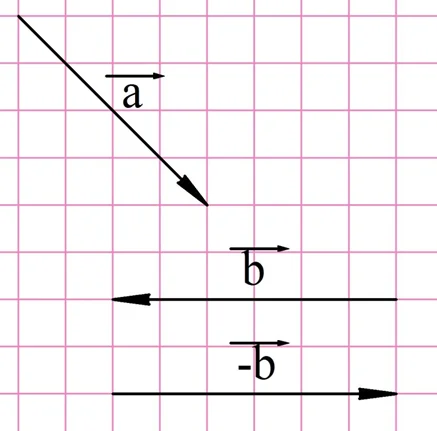
Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
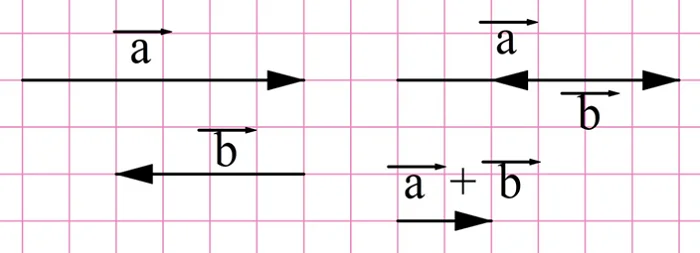
Для вычитания векторов также применяется правило треугольника.
Если из вектора a вычесть b, то получится c, причем должно соблюдаться условие: b + c = a
Формула вычитания векторов
ci = ai – bi
Элементы вектора c равны попарной разности соответствующих элементов a и b.
| Для плоских задач | a – b = {ax – bx; ay – by} |
| Для трехмерных задач | a – b = {ax – bx; ay – by; az – bz} |
| Для n-мерных векторов | a – b = {a1 – b1; a2 – b2; … an – bn} |
Примеры задач
Задание 1
Вычислим сумму векторов a = {3; 5} и b = {2; 7}.
Решение:
a + b = {3 + 2; 5 + 7} = {5; 12}.
Задание 2
Найдем разность векторов a = {4; 8; -2} и b = {-1; 9; 5}.
Решение:
a – b = {4 – (-1); 8 – 9; -2 – 5} = {5; -1; -7}.
Сложение и вычитание векторов
Навигация по странице:
- Определение операции сложения векторов
- Определение операции вычитания векторов
- Формулы для сложения и вычитания вектора
- для плоских задач
- для пространственных задач
- для n -мерных векторов
- Примеры задач на сложение и вычитание векторов
- плоские задачи
- пространственные задачи
- задачи в n -мерном пространстве
Определение.
Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
сi = ai + bi
Определение.
Вычитание векторов (разность векторов) a – b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
сi = ai – bi
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = {ax ; ay} и b = {bx ; by} можно найти, воспользовавшись следующими формулами:
a + b = {ax + bx; ay + by}
a – b = {ax – bx; ay – by}
Формулы сложения и вычитания векторов для пространчтвенных задач
В случае пространственной задачи сумму и разность векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти, воспользовавшись следующими формулами:
a + b = {ax + bx; ay + by; az + bz}
a – b = {ax – bx; ay – by; az – bz}
Формулы сложения и вычитания n -мерных векторов
В случае n -мерного пространства сумму и разность векторов a = {a1 ; a2 ; … ; an} и b = {b1 ; b2 ; … ; bn} можно найти, воспользовавшись следующими формулами:
a + b = {a1 + b1; a2 + b2; … ; an + bn}
a – b = {a1 – b1; a2 – b2; … ; an – bn}
Примеры задач на сложение и вычитание векторов
Примеры плоских задач на сложение и вычитание векторов
Пример 1. Найти сумму векторов a = {1; 2} и b = {4; 8}.
Решение:
a + b = {1 + 4; 2 + 8} = {5; 10}
Пример 2. Найти разность векторов a = {1; 2} и b = {4; 8}.
Решение:
a – b = {1 – 4; 2 – 8} = {-3; -6}
Примеры пространственных задач на сложение и вычитание векторов
Пример 3. Найти сумму векторов a = {1; 2; 5} и b = {4; 8; 1}.
Решение:
a + b = {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6}
Пример 4. Найти разность векторов a = {1; 2; 5} и b = {4; 8; 1}.
Решение:
a – b = {1 – 4; 2 – 8; 5 – 1} = {-3; -6; 4}
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Пример 5. Найти сумму векторов a = {1; 2; 5; 9} и b = {4; 8; 1; -20}.
Решение:
a + b = {1 + 4; 2 + 8; 5 + 1; 9 + (-20)} = {5; 10; 6; -11}
Пример 6. Найти разность векторов a = {1; 2; 5; -1; 5} и b = {4; 8; 1; -1; 2}.
Решение:
a – b = {1 – 4; 2 – 8; 5 – 1; -1 – (-1); 5 – 2} = {-3; -6; 4; 0; 3}
Сложение
и вычитание векторов.
Сумма
двух векторов. Законы сложения векторов. Правило параллелограмма.
Представим себе такую ситуацию.
Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в
магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой.
Сейчас мы описали принцип первого правила сложения векторов.
Правило треугольника.
Чтобы найти вектор суммы двух векторов и
, нужно:
1) совместить параллельным переносом начало вектора с концом
вектора ;
2) провести вектор из начала вектора в конец
вектора ;
3) получившийся вектор и есть вектор суммы: .

Если к вектору прибавить
нулевой вектор по правилу
треугольника, то получим вектор , т.е.
справедливо равенство: .
Утверждение. Если и
–
произвольные точки, то .
Например, .
Сложение векторов подчиняется алгебраическим законам.
ТЕОРЕМА.
Для любых векторов и
справедливы
равенства:
(переместительный
закон)
(сочетательный
закон).
Дано:
Доказать: 1)
2)
Доказательство.
Доказательство теоремы в случае, когда
векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно.
Мы рассмотрим случай, когда данные векторы неколлинеарны.
1). Отметим произвольную точку и отложим от этой точки
вектор . Воспользуемся правилом
треугольника и прибавим к нему вектор . Вектором суммы этих двух
векторов является вектор . (Рисунок слева).
Теперь от точки и отложим вектор
. По правилу треугольника
прибавим к нему вектор . Вектором суммы этих двух
векторов является вектор . (Рисунок справа).
– параллелограмм и точка
совпадает с точкой
. Значит,
, т.е.
 |
2). От точки отложим вектор
, от точки
отложим вектор
, а от точки
– вектор
. Найдём суммы векторов по
правилу треугольника.
Теорема доказана.
При доказательстве первой формулы получился параллелограмм,
причём, из точки выходят два вектора
и
, а вектор их суммы является
диагональю параллелограмма. На основе этого возникает второе правило
геометрического сложения векторов.
Правило параллелограмма.
Чтобы найти вектор суммы двух векторов и
, нужно:
1) совместить параллельным переносом начала векторов и
;
2) на этих векторах достроить параллелограмм;
3) вектором суммы является
вектор, который лежит на диагонали параллелограмма, имеющий своё начало в
начале исходных векторов.
Сумма
нескольких векторов.
Сложение нескольких векторов происходит по принципу правила
треугольника. Складываются два вектора, к вектору суммы прибавляется следующий
вектор и т.д. Приведём пример.
Сложить векторы .

и отложим от неё вектор
. Прибавим к нему вектор
по правилу треугольника.
. Теперь к вектору
прибавим вектор
.
. К вектору
прибавляем вектор
.
. Осталось к вектору
прибавить вектор
.
.
Итак, . Значит, суммой векторов
является вектор, с началом
в начале первого вектора и концом – в конце последнего. Такое сложение векторов
называется правилом многоугольника.
Правило многоугольника.
Чтобы найти вектор суммы нескольких векторов, нужно:
1) последовательно совместить параллельным переносом начало
последующего вектора с концом предыдущего;
2) вектором суммы всех векторов является вектор, с началом в
начале первого вектора и концом – в конце последнего.
Вычитание
векторов.
Определение. Разностью
двух векторов и
называется такой вектор
, что при
сложении его с вектором получается
вектор .

векторов можно производить, руководствуясь двумя понятиями: следствием из
правила треугольника сложения векторов; определением разности двух чисел. Разберём
каждое из них.
Сложим векторы и
по правилу треугольника. По
рисунку видно, что . Отсюда,
и
. Значит, разность двух
векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда
два правила:
I правило
вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно:
1) совместить параллельным переносом начала этих векторов;
2) вектором разности является вектор с началом в конце второго вектора
и концом в конце первого вектора.
II правило
вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно:
1) совместить параллельным переносом концы этих векторов;
2) вектором разности является вектор с началом в начале первого
вектора и концом в начале второго вектора.
Далее, из алгебры мы знаем, что для того, чтобы
из числа вычесть
число , нужно к числу
прибавить
число, противоположное числу , т.е.
. Такое же
правило справедливо и для векторов.
ТЕОРЕМА.
Для любых векторов справедливо
равенство:

Дано:
Доказать:
Доказательство.
1. Найдём разность векторов по
I правилу. Вектором разности является
вектор (рисунок слева). А теперь
найдём сумму векторов по правилу
треугольника, где – вектор,
противоположный вектору . Вектором
суммы является вектор (рисунок
справа). Не трудно заметить, что . Они сонаправлены и имеют
одинаковые модули.
2. А теперь докажем то же самое аналитически. По определению
разности векторов,
Что и требовалось доказать.
Из этой теоремы следует третье правило
вычитания векторов.
III правило
вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный
второму.
Используя это правило вычитания векторов,
способ сложения векторов выбирается произвольно.
1. 
является суммой векторов
и
. Определите, какой из четырёх рисунков верный.
2. Проведите векторы . Какая геометрическая фигура у вас
получилась?
3. 
является разностью векторов
и
. Определите, какой из четырёх рисунков
верный.
4. 
является суммой векторов
и
. Определите, какой из четырёх рисунков
верный.
5. 
вектор через векторы
, используя рисунок.
6. 
вектор через векторы
, используя рисунок.
7. Упростите выражения:
8. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
9. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
10. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
11. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
12. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
13. В квадрате проведены диагонали
и
. Укажите номера верных утверждений.
|
1) |
2) |
3) |
|||
|
4) |
5) |
6) |
|||
|
7) |
8) |
||||
14. – параллелограмм. Найдите сумму векторов
.
15. – прямоугольник. Диагонали
и
пересекаются в точке
. Укажите номера верных утверждений.
|
1) |
2) |
3) |
|||
|
4) |
5) |
6) |
|||
|
7) |
8) |
9) |
10) |
||
16. – параллелограмм. Выразите векторы
и
через векторы
и
.
17. – параллелограмм. Выразите векторы
и
через векторы
и
.
18. – прямоугольник. Выразите векторы
и
через векторы
и
.
19. – параллелограмм. Выразите векторы
и
через векторы
и
.
20. 
векторов , изображённых на клетчатой бумаге с
размерами клетки 1 х 1.
21. 
прямоугольника равны 20 и 21. Найдите длину суммы
векторов и
.
22. 
прямоугольника равны 7 и 24. Найдите длину разности
векторов и
.
23. 
найдите длину вектора (размеры клетки 1 х 1).
24. 
найдите длину суммы векторов и
(размеры клетки 1 х 1).
25. 
найдите длину разности векторов и
, изображённых на клетчатой бумаге с
размерами клетки 1 х 1.
План урока:
Понятие вектора
Равенство векторов
Сложение векторов
Свойства сложения
Вычитание векторов
Умножение вектора на число
Решение задач с помощью векторов
Понятие вектора
Рассмотрим простейшую задачу. Корабль, двигатель которого развивает скорость 20 км/ч, плывет по течению реки, при этом скорость течения составляет 2 км/ч. Какова скорость корабля относительно берега? Очевидно, в данном случае надо сложить скорость течения и собственную скорость корабля:
20 км/ч + 2 км/ч = 22 км/ч
Теперь посмотрим на почти такую же задачу, которая отличается лишь тем, что корабль плывет уже против течения. Для ее решения скорости уже придется вычитать:
20 км/ч – 2 км/ч = 18 км/ч
Получается, что ответ задачи во многом зависит не только от величин скоростей, но и от их направления. Возможны и более сложные случаи, когда корабль двигается на воде перпендикулярно течению или, например, под углом в 60°. Величины, при операции с которыми необходимо учитывать их направление, называют векторными величинами, или просто векторами.
Помимо скорости к ним относят ускорение, силу, импульс, напряженность магнитного и электрического поля и многие другие величины. Те же величины, для которых нельзя указать направление, называют скалярными величинами. Это масса, температура, плотность и т. п. Для выполнения действий с векторами необходимо разработать общие правила их сложения, вычитания, умножения, которые будут справедливы независимо от физической природы векторных величин. И разработать эти правила помогает как раз геометрия.
Для начала введем понятие вектора. Любой отрезок имеет два конца, которые обычно не отличают друг от друга. Однако если одну из этих точек считать началом отрезка, а другую – собственно концом, то у отрезка появится направление. В таком случае его можно считать вектором.
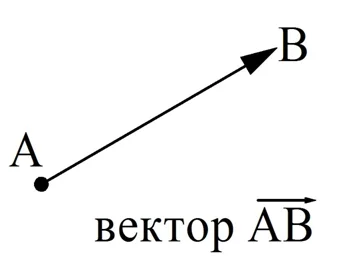
Часто вектора называют направленными отрезками. Обозначают их с помощью стрелок.
На этом рисунке показан вектор, начало которого находится в точке А, а конец – в точке В. При записи в формулах сначала пишут букву, означающую начало вектора, потом обозначение его конца, а над этими двумя буквами ставят стрелочку:
С практической точки зрения приходится вводить в рассмотрение особый нулевой вектор. У него начало и конец совпадают, то есть он представляет собой всего лишь одну точку:
Нулевой вектор необходим, так как нам необходимо научиться выполнять действия над векторами. Мы знаем, что в обычной алгебре используется число ноль. В векторной же алгебре аналогом нуля является как раз нулевой вектор.
Каждый вектор имеет свою длину, которая равна расстоянию между его началом и концом. То есть, если его начало находится в точке А, а конец в точке В, то длина вектора будет совпадать с длиной отрезка АВ. Обозначают длину с помощью вертикальных скобок:
Естественно, что длина нулевого вектора равна нулю.
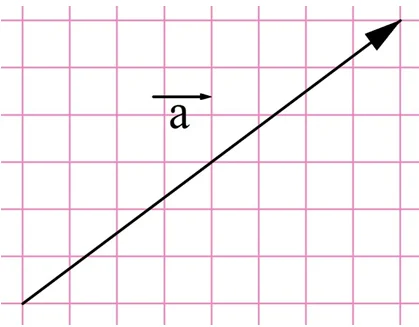
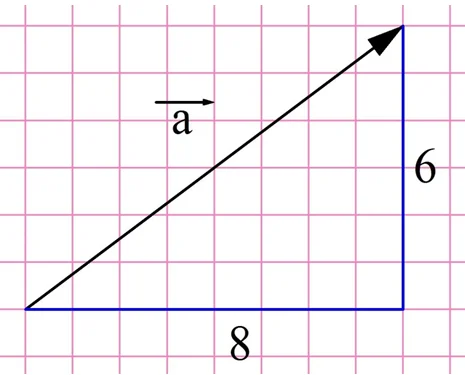
Задание. Найдите модуль вектора, изображенного на рисунке:
Решение. Легко выполнить построение, при котором вектор окажется гипотенузой в прямоугольном треугольнике
Тогда длину вектора можно найти по теореме Пифагора:
Равенство векторов
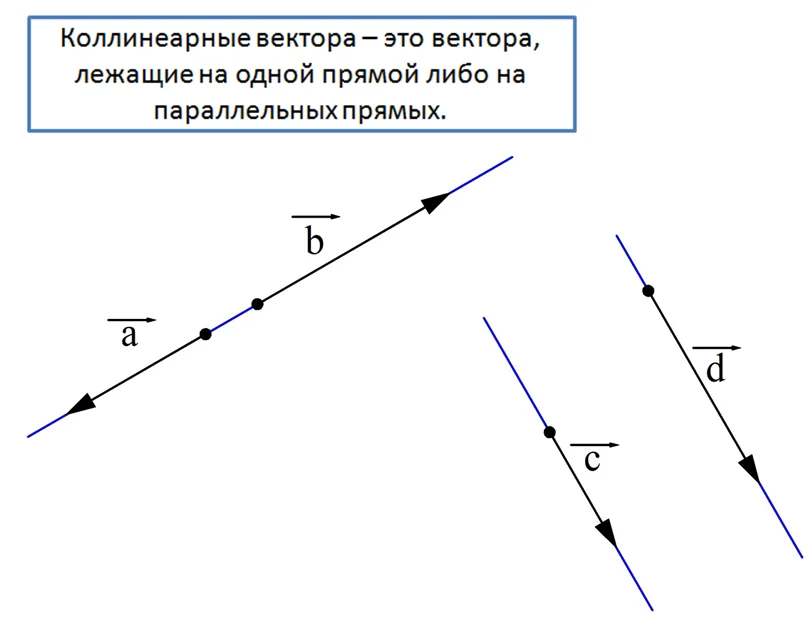
Через начало и конец векторов можно провести прямую. В связи с этим можно ввести понятие коллинеарных векторов.
На рисунке коллинеарны вектора а и b, так как они лежат на одной прямой. Также коллинеарны с и d, так как они лежат на параллельных прямых. А вот вектора a и c неколлинеарны, так как они лежат на пересекающихся прямых.
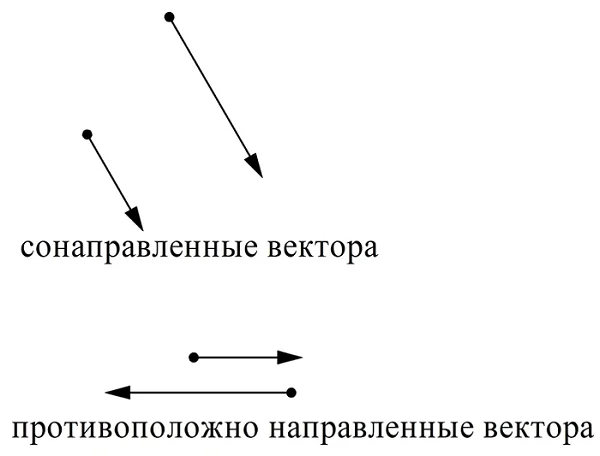
Для пары коллинеарных векторов можно определить, являются ли они сонаправленными или противоположно направленными.
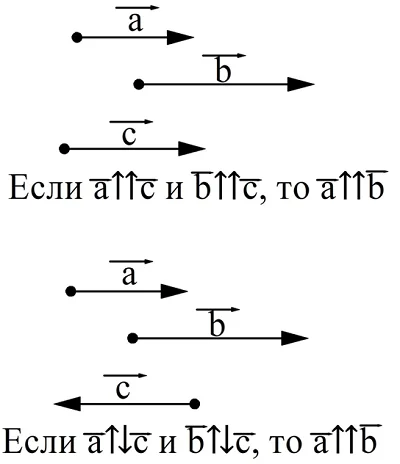
Для обозначения сонаправленных векторов используется символ «⇈», а для противоположно направленных «⇅». Можно сформулировать две очевидных теоремы о коллинеарных векторах.
Проиллюстрируем эти правила с помощью рисунка:
Особняком стоит нулевой вектор. Он представляет собой точку, а потому не имеет определенного направления. Поэтому условно его считают сонаправленным с любым другим вектором.
Теперь мы можем дать определение равенству векторов.
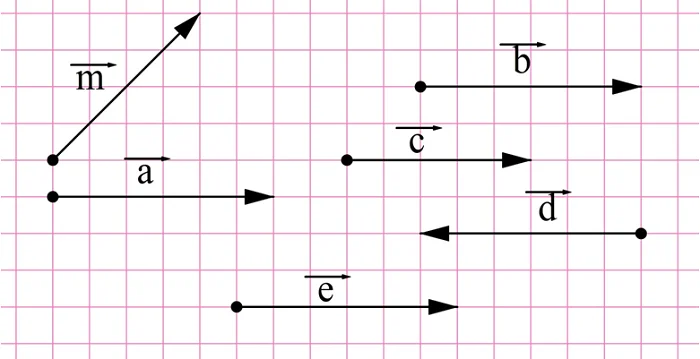
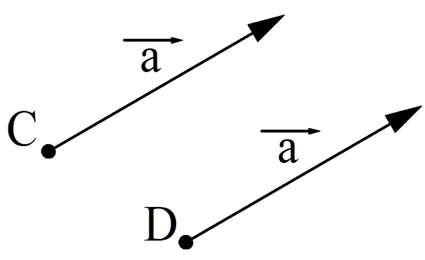
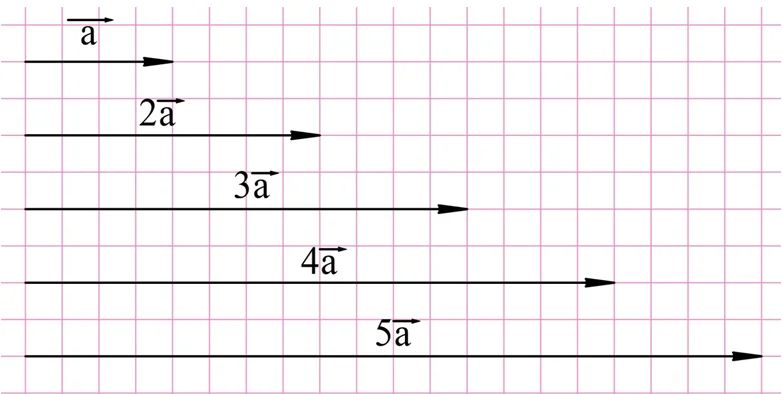
Задание. Найдите на картинке равные вектора.
Решение. Здесь равны вектора а, b и e. Они сонаправлены и имеют длину 6. Вектор с сонаправлен с ними, но его длина составляет только 5 клеток. Длина вектора d составляет 6 клеток, но он не сонаправлен с другими векторами. Наконец, вектор m также не сонаправлен с другими векторами и даже не коллинеарен им.
Ответ: a, b и e.
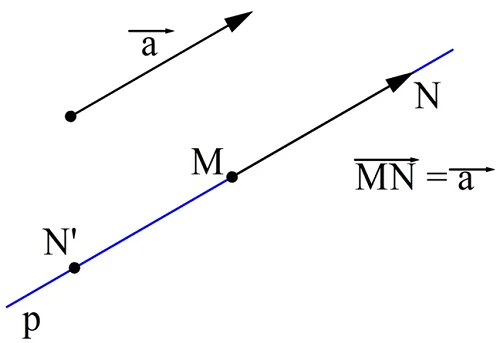
Если началом вектора является некоторая точка А, то можно сказать, что вектор отложен от точки А. Докажем важное утверждение:
Доказать его можно построением. Пусть есть вектор а и точка М. Проведем через М прямую p, параллельную вектору а. Такая прямая будет единственной. Если точка М и вектор лежат на одной прямой, то в качестве прямой p возьмем именно эту прямую. Далее от точки М можно отложить отрезки МN и МN’, длина которых будет совпадать с длиной вектора а. В результате получится два вектора,MN и MN’, один из которых будет сонаправлен с а, а другой – противоположно направленный.
Часто равные вектора, отложенные от разных точек, обозначают одной буквой. Можно считать, что это один и тот же вектор, просто приложенный к разным точкам.
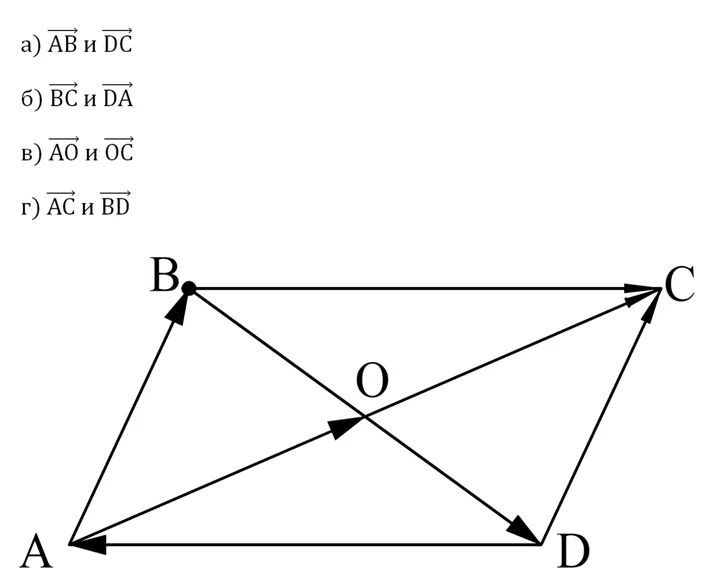
Задание. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Определите, равны ли вектора:
Решение.
а) Отрезки АВ и DC равны, ведь это противоположные стороны параллелограмма, по той же причине эти отрезки параллельны. Видно, что они сонаправлены, значит, вектора равны.
б) Отрезки ВС и DA параллельны и равны, но эти вектора противоположно направлены, поэтому вектора НЕ равны друг другу.
в) Точка пересечения диагоналей параллелограмма делит их пополам, поэтому длины отрезков АО и ОС одинаковы. Вектора АО и ОС лежат на одной прямой, то есть они коллинеарны. При этом они ещё и сонаправлены, поэтому АО и ОС – равные векторы.
г) Вектора АС и BD лежат на пересекающихся прямых, то есть они не коллинеарны. Этого уже достаточно, чтобы считать их НЕ равными друг другу.
Ответ: а) д; б) нет; в) да; г) нет.
Сложение векторов
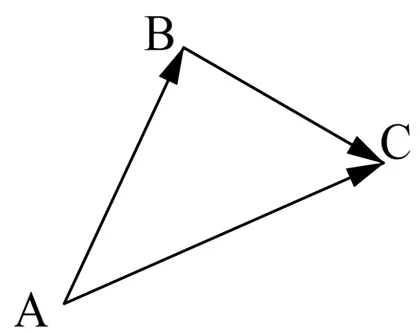
Пусть некоторый объект сначала находился в точке А, а потом переместился в точку В. Тогда его перемещение удобно обозначить с помощью вектора АВ. Далее пусть этот объект из точки В переместился в другую точку С.
С одной точки зрения, объект совершил сразу два перемещения, из А в В и из В в С, которые можно представить векторами:
Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать вектора. Его называют правилом треугольника.
С помощью правила треугольника удобно складывать вектора, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму:
Задание. На рисунке показаны два вектора. Постройте в тетради их сумму и найдите длину получившегося вектора.
Решение. Перенесем вектор b к концу вектора а. Далее по правилу треугольника на удастся найти их сумму (обозначим этот вектор буквой с):
Теперь найдем длину получившегося вектора. Он является гипотенузой в прямоугольном треугольнике, причем длины катетов в этом треугольнике можно определить по рисунку, они составляют 4 и 6. Тогда длину гипотенузы можно найти по теореме Пифагора:
Отдельно рассмотрим случаи, когда складываются коллинеарные вектора. В этом случае получающаяся сумма окажется коллинеарной каждому слагаемому. Если вектора сонаправлены, то их длина итогового вектора окажется равной сумме длин складываемых векторов:
Если складываются противоположно направленные вектора, то длина их суммы окажется разностью длин складываемых векторов.
Именно по этой причине при решении простейших задач на движение корабля по реке скорость корабля и скорость течения либо складывают, либо вычитают. Дело в том, что в этих задачах складываются вектора скоростей корабля и течения. Когда судно плывет по течению, эти векторы сонаправлены, а когда плавание идет против течения, векторы оказываются противоположно направленными.
Задание. Корабль развивает в неподвижной воде скорость 12 км/ч. Он плывет по реке, скорость воды в которой составляет 5 км/ч. Найдите скорость корабля относительно берега, если:
а) судно плывет по течению;
б) судно плывет против течения;
в) судно плывет перпендикулярно течению.
Решение. Во всех случаях итоговая скорость судна является векторной суммой собственной скорости судна и течения реки:
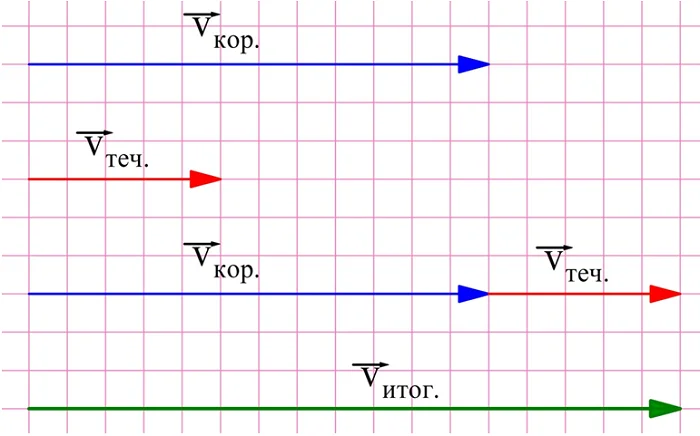
Однако направления этих векторов различны. Найдем решение графически, с помощью построений. В первом случае вектора по условию сонаправлены:
Приложив другу к другу отрезки длиной 12 и 5, получим отрезок длиной 17. Это значит, что в первом случае скорость корабля относительно берега составит 17 км/ч.
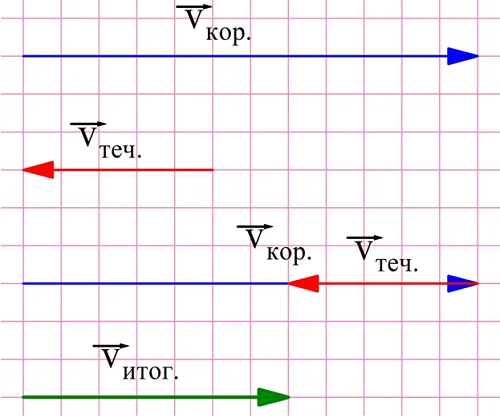
Во втором случае вектора уже окажутся противоположно направленными:
Отрезок, соответствующий итоговой скорости, здесь уже равен 7 клеткам, значит, итоговая скорость составляет 7 км/ч.
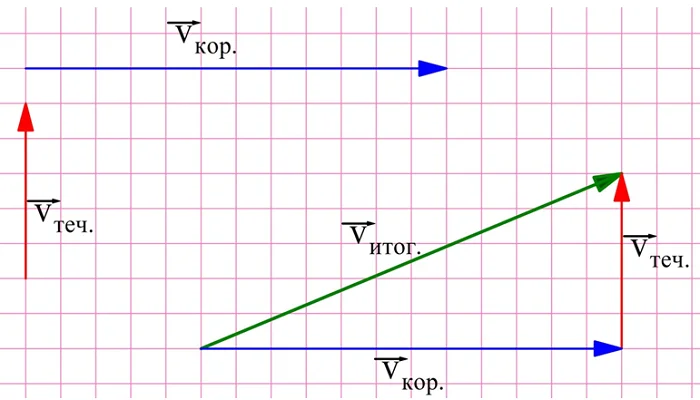
В третьем случае вектора скоростей перпендикулярны:
При построении получился прямоугольный треугольник, вектор итоговой скорости в нем оказался в роли гипотенузы. Найти его длину можно по теореме Пифагора, ведь катеты нам известны:
Свойства сложения
Действия с векторами во многом подобны действиям с обычными числами. Напомним, что в алгебре при прибавлении к числу нуля оно не менялось:
a + 0 = a
Аналогично и при прибавлении к вектору нулевого вектора он не изменится:
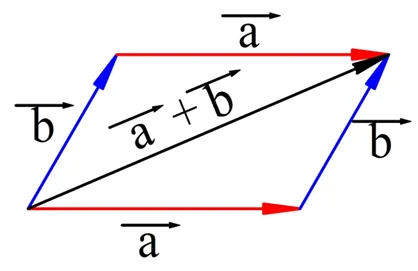
Работает ли это правило с векторами? Оказывается, что да. Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы:
Видно, что диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Они обозначены как векторы a и b, причем в данном случае к а прибавляется b. Но одновременно эта же диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Напомним, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены одним вектором. В этом случае уже к b прибавляется a. Результат при этом получается одинаковый, поэтому можно записать, что
На этом примере мы увидели, как работает ещё одно правило сложения векторов, который называется правилом параллелограмма. Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма.
Задание. Сложите с помощью правила параллелограмма вектора, изображенные на рисунке:
Решение. Надо всего лишь построить параллелограмм, как показано на рисунке. Его диагональ и окажется искомым вектором:
Ещё один закон, использующийся в алгебре, называется сочетательным законом, записывается он так:
Оказывается, что и при действиях с векторами он также работает, то есть справедливо соотношение:
Здесь оранжевый вектор – это сумма красного (а) и синего (b) вектора. Если к оранжевому вектору добавить зеленый (с), то получится фиолетовый вектор, который, таким образом, является суммой
Желтый вектор – это сумма синего и зеленого вектора. Видно, что фиолетовый вектор представляет собой сумму красного и желтого, то есть он представляет сумму
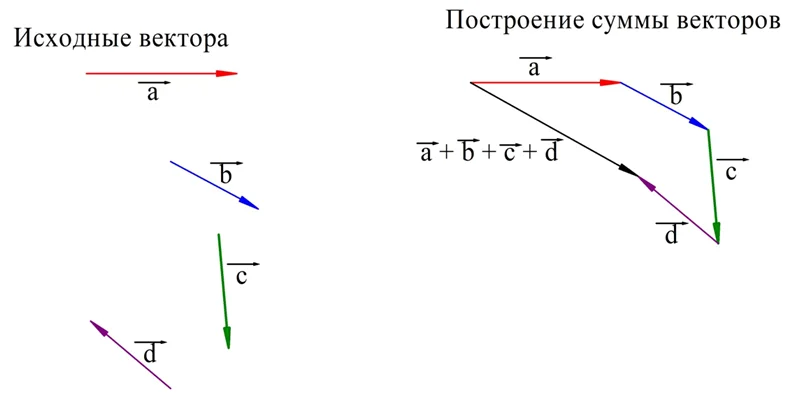
Складывать можно любое количество векторов. В этом случае надо последовательно прикладывать эти вектора друг к другу, выстраивая «цепочку» векторов. Например, сложение 4 векторов, показанных на рисунке, будет осуществляться следующим образом:
Этот способ сложения векторов именуют правилом многоугольника. Естественно, в силу переместительного закона вектора можно прикладывать друг к другу в разной последовательности, при этом результат будет получаться один и тот же.
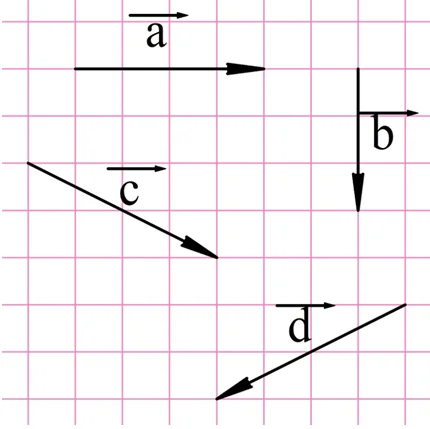
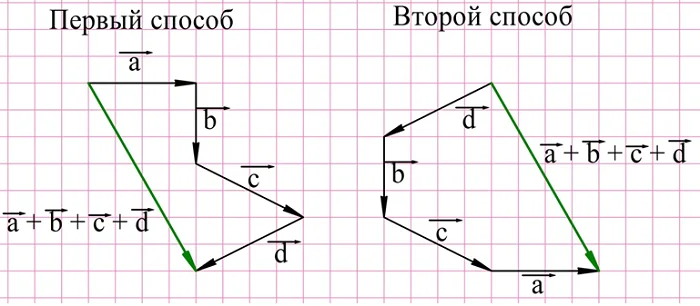
Задание. Сложите, используя правило многоугольника, вектора, изображенные на рисунке. Выполните сложение двумя разными способами:
В первом случае последовательно сложим вектора a, b, c и d. Во втором случае изменим последовательность сложения. Например, сложим их в порядке d, b, c, a:
Видно, что каждый из двух способов дал один и тот же результат, что ещё раз подтверждает справедливость переместительного закона сложения векторов.
Вычитание векторов
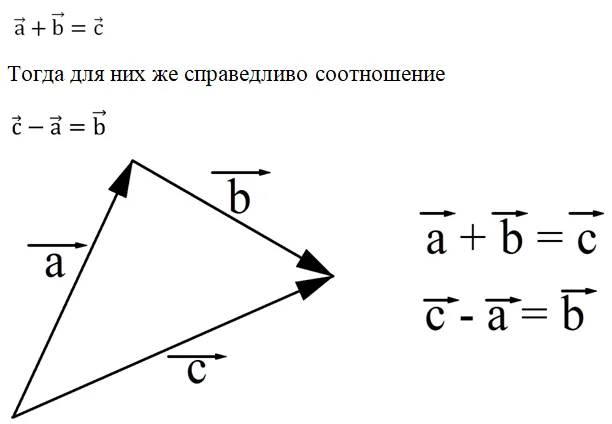
Напомним, что в алгебре операция вычитания вводится как операция обратная сложению. То есть если для трех чисел верно соотношение
a + b = c
то разностью чисел с и a как раз окажется b:
c – a = b
Аналогично вычитание понимается и в векторной алгебре. Пусть построены вектора а, b и c так, что
Этот пример показывает, как строить разность двух векторов. На рисунке вектора с и a отложены от одной точки, а вектор b, являющийся их разницей, проведен от конца вычитаемого вектора к концу уменьшаемого вектора.
В данном случае под уменьшаемым вектором понимается тот, который в разнице стоит перед знаком минус, а вычитаемый вектор – тот, который находится уже после этого знака. Например, в записи
Вектор а – уменьшаемый, а вектор b – вычитаемый.
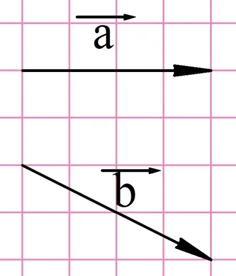
Задание. Постройте в тетради разность векторов, изображенных на рисунке:
Решение. Заметим, что в условии не сказано, какой вектор из какого надо вычитать. Поэтому можно построить сразу два ответа:
Несложно заметить, две получившиеся разности представляют собой противоположно направленные векторы одной длины. Такие векторы называются противоположными.
Очевидно, что если сложить друг с другом два противоположных вектора, то получится нулевой вектор:
Противоположные вектора играют в векторной алгебре такую же роль, как и противоположные числа. С их помощью удобно выполнять вычитание векторов. Напомним, что для обычных чисел справедливо соотношение:
Поэтому операцию вычитания можно заменить операцией сложения, если вместо вычитаемого вектора взять вектор, противоположный ему. Рассмотрим этот способ на примере. Пусть из a надо вычесть b:
На первом шаге надо построить вектор, противоположный b:
Теперь надо просто сложить a и (– b):
В итоге нам удалось построить разность векторов а и b.
Умножение вектора на число
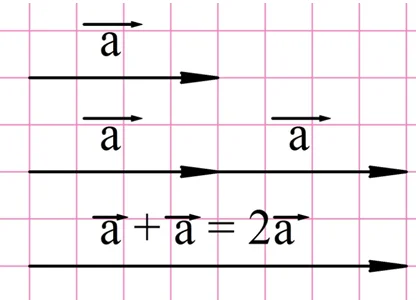
Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2:
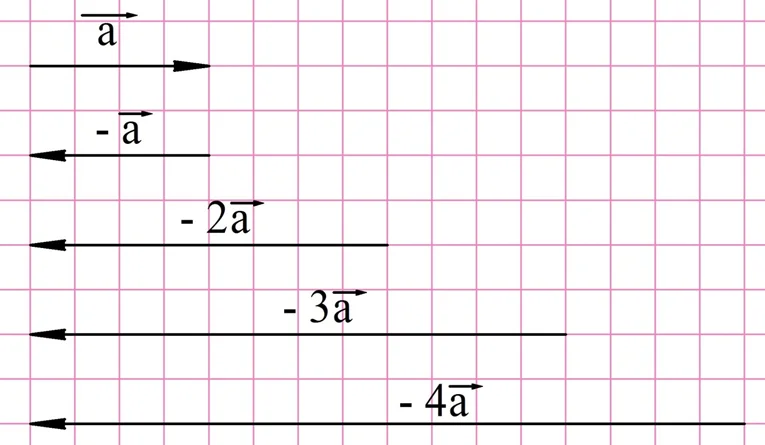
Аналогично можно построить вектора, которые больше исходного не в 2, а в 3,4 и т. д. раз:
Итак, чтобы умножить вектор на положительное число k, надо построить сонаправленный с ним вектор, длина которого в k раз больше.А как умножать вектор на отрицательное число? Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор. Зная это, легко умножать вектор и на другие отрицательные числа:
Естественно, что если вектор умножается на ноль, то в результате получается нулевой вектор.
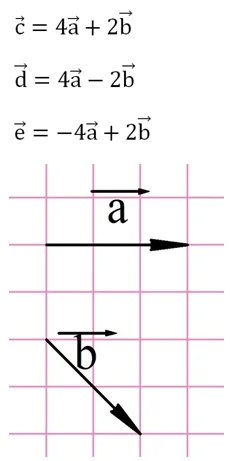
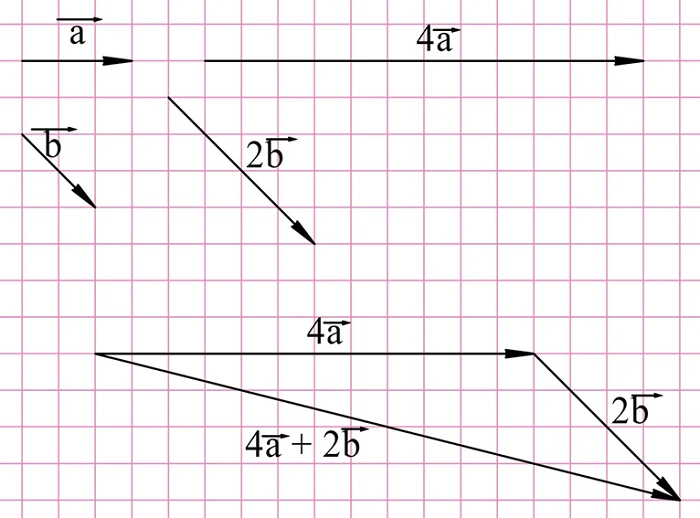
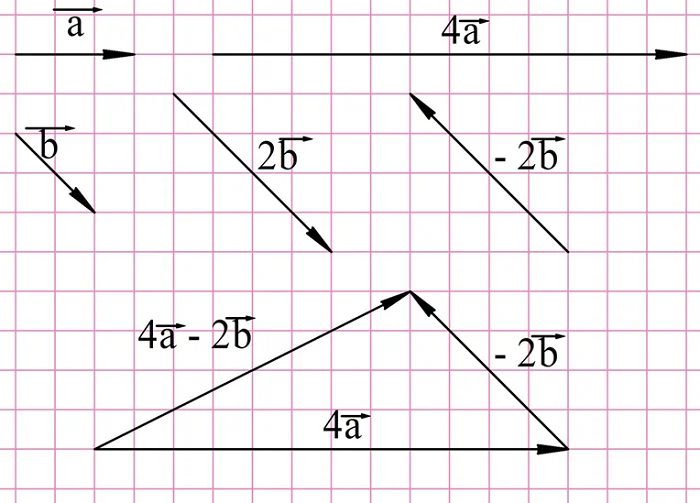
Задание. На рисунке показаны вектора а и b. Найдите вектора
Решение. Для построения снам надо сначала умножить исходные вектора на 4 и 2, а далее полученные результаты сложить:
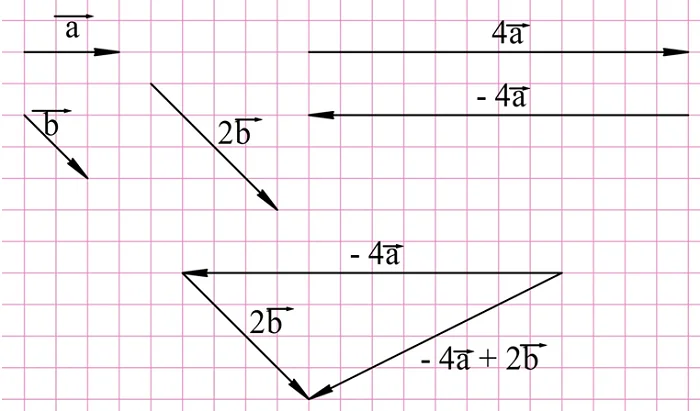
Для нахождения вектора d надо построить вектор, противоположный вектору 2b, и уже его складывать с 4a:
Наконец, для нахождения вектора е необходимо построить противоположный вектор уже для 4а:
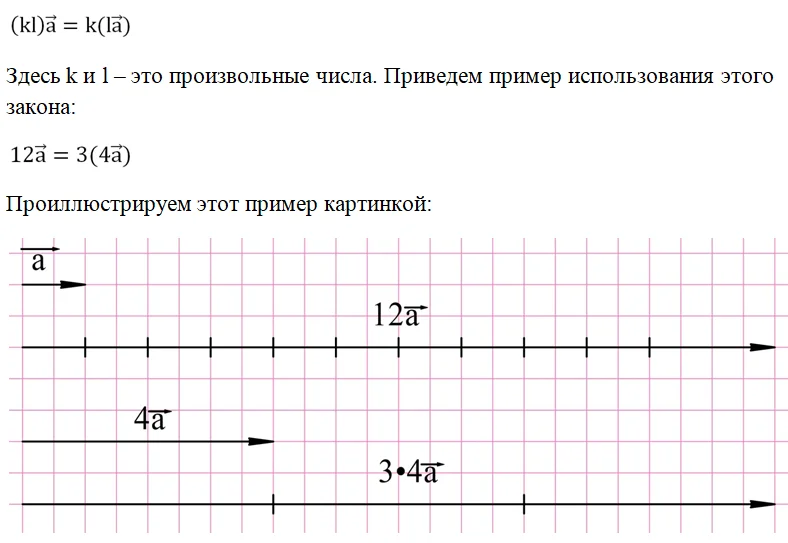
Некоторые правила обычной алгебры, касающиеся операции умножения, справедливы и для векторов. Первый такое правило – это сочетательный закон:
Видно, что мы можем либо сразу умножить вектор а на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится.
Также в отношении операции умножения векторов на число справедлив распределительный закона, которые позволяют раскрывать скобки:
Например, пусть нам надо сложить вектора 2а и 3а. Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим вектора 2а и 3а и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор а на число 5:
Есть ещё один распределительный закон, в котором в скобках находится уже сумма векторов, а не чисел:
Этот закон можно применить в случае, когда нам необходимо, например, сложить вектора 4а и 4b. Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить aи b, и уже потом эту сумму умножить на 4:
Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны вектора а, b и с, и надо найти вектор
Видно, что выражение значительно упростилось.
Решение задач с помощью векторов
Вектора активно используются в физике при решении многих задач, однако они также помогают доказывать геометрические теоремы. Рассмотрим несколько примеров, и начнем со вспомогательной задачи.
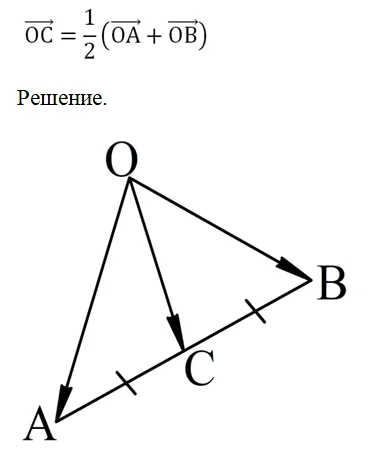
Задание. Известно, что С – это середина отрезка АВ. Докажите, что для любой точки О выполняется равенство:
Используя правило треугольника, вектор ОС можно представить в виде двух различных сумм:
Проанализируем выражение в скобках. Вектора АС и ВС коллинеарны, ведь они лежат на одной прямой АВ. При этом они противоположно направлены. Длина у них одинакова, ведь С – середина АВ. Тогда по определению АС и ВС – противоположные вектора, и их сумма равна нулю:
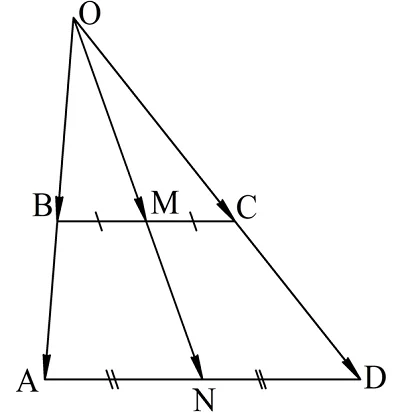
Задание. Докажите, что если в трапеции провести прямую, проходящую через середины ее оснований, то она также пройдет через точку, в которой пересекаются продолжения боковых сторон трапеции.
Решение. Построим трапецию, обозначим ее вершины и середины оснований:
Здесь ABCD – трапеция, основаниями которой являются отрезки ВС и AD. M и N – их середины. Прямые АВ и CD пересекаются в точке O. Необходимо доказать, что прямая MN также проходит через О.
Заметим, что ∆ОВС и ∆ОАD подобны. Действительно, у них есть общий ∠ВОС, а ∠ОВС и ∠ОАD одинаковы как односторонние углы при секущей АВ, поэтому треугольники подобны по 1-ому признаку. Обозначим коэффициент подобия буквой k, тогда можно записать, что
Так как отрезки ОА и АВ лежат на одной прямой, то вектора ОА и АВ коллинеарны и притом сонаправлены, поэтому в (1) отрезки можно заменить векторами:
(это соотношение мы доказали в предыдущей, вспомогательной задаче).
Аналогичную формулу можно составить и для второго основания и его середины N:
Полученное нами равенство означает, что вектора ON и ОМ коллинеарны, а значит, лежат на одной прямой (эти вектора не могут лежать на параллельных прямых, так как имеют общую точку О). Тогда получается, что О, M и N лежат на одной прямой, ч. т. д.