Содержание:
- Формула
- Примеры нахождения суммы векторов
Формула
Чтобы найти сумму векторов $bar{a}+bar{b}$, которые заданны координатами
$bar{a}=(a_x;a_y)$ и $bar{b}=(b_x;b_y)$, необходимо сложить соответствующие
координаты этих векторов,
то есть
$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y}right)$$
В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их сумма равна
$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y} ; a_{z}+b_{z}right)$$
Примеры нахождения суммы векторов
Пример
Задание. Найти сумму векторов
$bar{a}+bar{b}$,
$bar{a}=(2;0)$ и
$bar{b}=(1;3)$
Решение. Для нахождения суммы векторов, сложим их соответствующие координаты
$$bar{a}+bar{b}=(2 ; 0)+(1 ; 3)=(2+1 ; 0+3)=(3 ; 3)$$
Ответ. $bar{a}+bar{b}==(3 ; 3)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти суммы векторов
$bar{a}+bar{b}$,
$bar{a}+bar{c}$,
$bar{b}+bar{c}$ и
$bar{a}+bar{b} +bar{c}$, если
$bar{a}=(1;-1;0)$,
$bar{b}=(3;2;-1)$ и
$bar{c}=(4;2;-1)$
Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:
$$bar{a}+bar{b}=(1+3 ;-1+2 ; 0+(-2))=(4 ; 1 ;-2)$$
$$bar{a}+bar{c}=(1+4 ;-1+2 ; 0+(-1))=(5 ; 1 ;-1)$$
$$bar{b}+bar{c}=(3+4 ; 2+2 ;-2+(-1))=(7 ; 4 ;-3)$$
$$bar{a}+bar{b}+bar{c}=(1+3+4 ;-1+2+2 ; 0+(-2)+(-1))=(8 ; 3 ;-3)$$
Ответ. $bar{a}+bar{b}=(4 ; 1 ;-2)$ , $bar{a}+bar{c}=(5 ; 1 ;-1)$ , $bar{b}+bar{c}=(7 ; 4 ;-3)$ , $bar{a}+bar{b}+bar{c}=(8 ; 3 ;-3)$
Читать дальше: как найти разность векторов.
Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву и другим 200 предметам можно здесь всего за 10 минут.
Сложение векторов
Формула
Чтобы складывать вектора нужно найти суммы соответствующих координат данных векторов. Например, пусть есть векторы на плоскости $ overline{a} = (x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, тогда их сумму можно найти по формуле: $$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2)$$
Если векторы заданы в пространстве тремя координатами $ overline{a} = (x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то выполнить сложение нужно по другой формуле:
$$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2; z_1+z_2) $$
При сложении первая координата первого вектора складывается с первой координатой второго вектора, вторая координата первого вектора складывается со второй координатой второго вектора и так далее в зависимости от размерности векторов. Стоит отметить, что складывать векторы можно только одинаковой размерности.
Примеры решений
| Пример |
| Даны два вектора $ overline{a} = (1,3) $ и $ overline{b} = (2,4) $. Нужно сложить два вектора. |
| Решение |
|
Итак, как складывать вектора по координатам? К первой прибавляем первую, вторую ко второй: $$ overline{a}+overline{b} = (1+2;3+4) = (3;7) $$ В этой задаче векторы заданы в двумерном пространстве и имеют только две координаты. Если бы координат было бы три, то применять нужно вторую формулу для трехмерной задачи. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a}+overline{b} = (3;7) $$ |
Задание. Найти сумму векторов $bar+bar$, $bar=(2;0)$ и $bar=(1;3)$
Решение. Для нахождения суммы векторов, сложим их соответствующие координаты

Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!








Ищещь ответ на вопрос с которым нужна помощь?
Операции над векторами в прямоугольной системе координат
Если задана плоскость O x y с векторами a → = a x , a y и b → = ( b x , b y ) , то мы можем разложить их по координатным векторам i → и j → . Тогда это будет иметь вид a → = a x · i → + a y · j → и b → = b x · i → + b y · j → . Чтобы найти сумму a → и b → и произведение a → на λ , рассмотрим:
a → + b → = a x · i → + a y · j → + b x · i → + b y · j → = ( a x + b x ) · i → + ( a y + b y ) · j →
λ · a → = λ · ( a x · i → + a y · j → ) = ( λ · a x ) · i → + ( λ · a y ) · j →
Это равенство справедливо по свойству операций над векторами.
Разложение векторов – это a → + b → и λ · a → , представленное в частях неравенства по i → и j → координатам. Координаты векторов a → + b → и λ · a → равны соответственно ( a x + b x , a y + b y ) и ( λ · a x , λ · a y ) .
Таким же образом a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) записываются как a → + b → = a x · i → + a y · j → + a z · k → + b x · i → + b y · j → + b z · k → = ( a x + b x ) · i ⇀ + ( a y + b y ) · j → + ( a z + b z ) · k → λ · a → = λ · ( a x · i → + a y · j → + a z · k → ) = ( λ · a x ) · i → + ( λ · a y ) · j → + ( λ · a z ) · k →
а значит a → + b → = ( a x + b x , a y + b y , a z + b z ) , λ · a → = ( λ · a x , λ · a y , λ · a z )
Отсюда делаем вывод, что координаты векторов a → и b → равны сумме соответствующих координат векторов a → и b → , координаты произведения вектора a → на λ приравниваются к соответствующим координатам вектора a → , умноженным на число в заданной системе координат.
При необходимости нахождения координат суммы нескольких векторов, необходимо сложить координаты каждого вектора соответственно. Рассмотрим примеры.
Нужно выполнить сложение a → = ( 2 , 3 – 1 3 ) и b → = ( – 1 , – 1 3 ) . Чему равны координаты произведения вектора a → на 3 .
Решение
Из определения имеем, что сумма векторов равна сумме их координат соответственно, тогда a → + b → = ( 2 + ( – 1 ) , 3 – 1 3 + ( – 1 3 ) ) = ( 1 , – 1 3 ) .
Числовое значение умножается на каждую координату: 3 · a → = ( 3 · 2 , 3 · 3 – 1 3 ) = 2 3 , 3 – 3 3 .
Ответ: a → + b → = ( 1 , – 1 3 ) , 3 · a → = ( 2 3 , 3 – 3 3 )
Заданы векторы a → = ( 0 , 1 , – 2 ) , b → = ( – 1 , – 1 , 3 ) , c → = ( 4 , – 3 , 2 ) .
Каковы координаты вектора 2 · a → + 3 · ( b → – c → ) = 2 · a → + 3 · b → + ( – 3 ) · c → .
Решение
Применяя свойства векторов, получим: 2 · a → + 3 · ( b → – c → ) = 2 · a → + 3 · b → + ( – 3 ) · c → .
Подставляем значения координат и получаем: 2 · a → + 3 · b → + ( – 3 ) · c → = 2 · ( 0 , 1 , – 2 ) + 3 · ( – 1 , – 1 , 3 ) + ( – 3 ) · ( 4 , – 3 , 2 ) =
= ( 2 · 0 , 2 · 1 , 2 · ( – 2 ) ) + ( 3 · ( – 1 ) , 3 · ( – 1 ) , 3 · 3 ) + ( ( – 3 ) · 4 , ( – 3 ) · ( – 3 ) · 2 ) =
= ( 0 , 2 , – 4 ) + ( – 3 , – 3 , 9 ) + ( – 12 , 9 – 6 ) =
= ( 0 + ( – 3 ) + ( – 12 ) , 2 + ( – 3 ) + 9 , – 4 + 9 + ( – 6 ) ) = ( – 15 , 8 , – 1 )
Можно решить другим способом.
Обратим внимание на разложение a → , b → и c → :
a → = 0 · i → + 1 · j → + ( – 2 ) · k → = j → – 2 · k →
b → = ( – 1 ) · i → + ( – 1 ) · j → + 3 · k → = – i → – j → + 3 · k →
c → = 4 · i → + ( – 3 ) · j → + 2 · k → = 4 · i → – 3 · j → + 2 · k →
Исходя из свойств векторов, видим, что: 2 · a → + 3 · ( b → – c → ) = 2 · ( j → – 2 · k → ) + 3 · ( – i → – j → + 3 · k → – ( 4 · i → – 3 · j → + 2 · k → ) ) = = 2 · j → – 4 · k → + 3 · ( – 5 · i → + 2 · j → + 1 · k → ) = – 15 · i → + 8 · j → – k →
Значит, координаты вектора 2 · a → + 3 · ( b → – c → ) равны ( – 15 , 8 , – 1 ) .
Ответ: 2 · a → + 2 · ( b → – c → ) = ( – 15 , 8 , – 1 )
Сложение и вычитание векторов
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = < ax ; ay > и b = < bx ; by > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания векторов для пространчтвенных задач
В случае пространственной задачи сумму и разность векторов a = < ax ; ay ; az > и b = < bx ; by ; bz > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания n -мерных векторов
В случае n -мерного пространства сумму и разность векторов a = < a 1 ; a 2 ; . ; an > и b = < b 1 ; b 2 ; . ; bn > можно найти, воспользовавшись следующими формулами:
Примеры задач на сложение и вычитание векторов
Примеры плоских задач на сложение и вычитание векторов
Примеры пространственных задач на сложение и вычитание векторов
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/operatsii-nad-vektorami-v-prjamougolnoj-sisteme/
http://ru.onlinemschool.com/math/library/vector/add_subtract/
[/spoiler]
В механике существуют два типа величин:
- скалярные величины, задающие некоторое числовое значение – время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление – скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты – первую, из второй – вторую и т.д.):
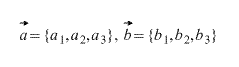
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
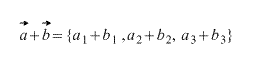
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
Правило параллелограмма. Сложение векторов по правилу параллелограмма. |
|
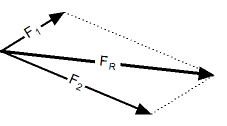 |
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
|
Правило треугольника. Сложение векторов по правилу треугольника. |
|
 |
Сложение векторов по правилу треугольника заключается в следующем:
|
Тригонометрический способ. Сложение векторов тригонометрическим способом. |
|
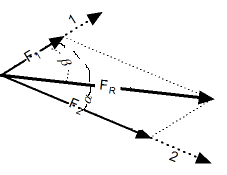 |
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
|
Пример – сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН)2 + (8 кН)2 – 2 (5 кН)(8 kН) cos(180o – (80o)) ]1/2
= 10,14кН
Угол между результирующей силой и первой силой равен:
β= arcsin[ (8кН) sin(180o – (80o)) / (10,14кН) ]
= 51o
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180o – (80o)) / (10,2 кН) ]
= 29o
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

В статье Понятие вектора мы сказали, что векторы можно складывать друг с другом. Рассмотрим этот вопрос подробнее.
Пусть нам даны два вектора a⃗vec{a} и b⃗vec{b}. Что понимать под суммой этих двух векторов, то есть под a⃗+b⃗vec{a}+vec{b}? Во первых, сумма двух векторов это вектор. То есть, если мы складываем два вектора (две стрелки) то снова получаем вектор (стрелку). Существуют два способа (или правила) как можно складывать векторы. Они, конечно, дают один и тот же самый результат. Говорят о правиле треугольника и правиле параллелограмма. Оба эти правила графические, то есть сумма векторов находится путем геометрического построения. О сумме векторов, выраженной через координаты векторов речь пойдет в другой статье.
Правило треугольника
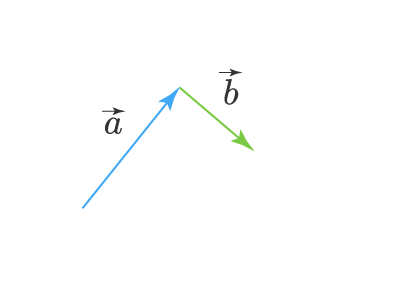
Вот нам даны два вектора a⃗vec{a} и b⃗vec{b}. Для того чтобы найти их сумму, пользуясь правилом треугольника, нужно чтобы начало одного из векторов находилось в точке конца другого вектора. То есть, чтобы точки начала одного вектора и конца другого вектора совпадали. Но что делать, если это не так? Для этого нужно параллельно перенести любой из векторов так чтобы это условие выполнялось. Например, пусть вначале векторы у нас расположены так:

Перенесем теперь вектор b⃗vec{b} параллельно самому себе так чтобы его начало совпало с концом вектора a⃗vec{a}. Получим:
Теперь, чтобы найти сумму этих векторов, нужно провести вектор (стрелку) из начала вектора a⃗vec{a} в конец вектора b⃗vec{b}. Получим вектор c⃗=a⃗+b⃗vec{c}=vec{a}+vec{b}:
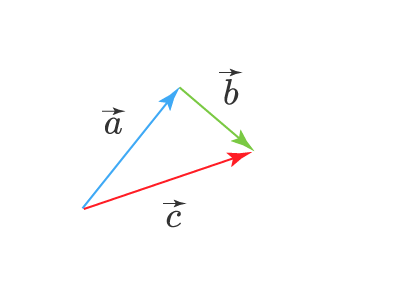
Правило параллелограмма
Решим ту же задачу вторым способом. Для этого нам нужно сделать так чтобы векторы a⃗vec{a} и b⃗vec{b} исходили из одной точки, то есть, чтобы точки начала этих векторов совпали. Получим:
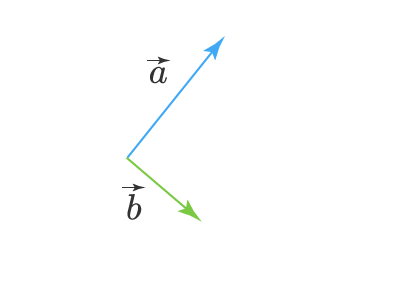
Теперь построим на этих двух векторах параллелограмм. Суммой векторов a⃗vec{a} и b⃗vec{b} будет вектор, совпадающий с диагональю этого параллелограмма, и начало этого суммарного вектора c⃗vec{c} будет совпадать с началом векторов a⃗vec{a} и b⃗vec{b}:
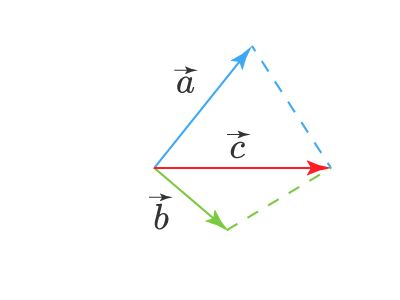
На самом деле, по своему смыслу, оба эти правила это одно и то же правило. Просто так уж вышло, что в зависимости от построения треугольника или параллелограмма, говорят о соответствующем правиле складывания векторов.
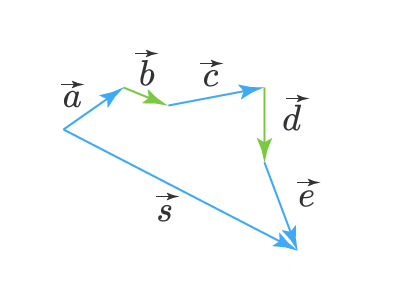
Сумма любого числа векторов
Складывать между собой можно не только два вектора, но и любое их количество. Для этого удобно воспользоваться правилом треугольника. Пусть у нас есть векторы a⃗,b⃗,c⃗,d⃗,e⃗vec{a}, vec{b}, vec{c}, vec{d}, vec{e}. Пусть мы перенесли параллельно векторы так, что начало каждого последующего вектора берет свое начало в конце предыдущего вектора, тогда сумма этих векторов, вектор s⃗vec{s} — это вектор с началом, совпадающим с началом первого вектора (вектора a⃗vec{a}) и концом, совпадающим с концом последнего вектора (вектора e⃗vec{e}):