Как найти сумму внешних углов пятиугольника – Сайт, где вы сможете решить свои вопросы

ferenerughe

Вопрос по геометрии:

Найдите сумму внутренних и сумму внешних углов взятых по одному при каждой вершине пятиугольника abcde

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Ответы и объяснения 1

reperth897

Формула для нахождения суммы внутренних углов выпуклого n – угольника: S=180*(n – 2). У пятиугольника S= 180*(5 – 2) = 180*3=540 градусов.сумма внешних углов S1=5*180-540=360.

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат – это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Найдите сумму внутренних и сумму внешних углов взятых по одному при каждой вершине пятиугольника abcde.

Вы открыли страницу вопроса Найдите сумму внутренних и сумму внешних углов взятых по одному при каждой вершине пятиугольника abcde?. Он относится к категории
Геометрия. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Геометрия,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.

Источник

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

pravilnyj-pyatiugolnik Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A₂A₁A₅=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

∠A₁O A₂=360º:5=72º.

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

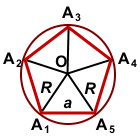
pravilnyj-pyatiugolnik-radius-opisannoj-okruzhnosti

Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

В треугольнике A₁OA₅

$[{A_1}{A_5} = a,]$

$[{A_1}O = {A_5}O = R,]$

$[angle {A_1}O{A_5} = {72^o}.]$

pravilnyj-pyatiugolnik-ploshchad Проведём из вершины высоту OF.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A₁OA₅, то есть

$[{A_1}F = frac{1}{2}{A_1}{A_5} = frac{a}{2},]$

$[angle {A_1}OF = frac{1}{2}angle {A_1}O{A_2} = {36^o}.]$

OF — радиус вписанной в A₁A₂A₃A₄A₅окружности: OF=r.

Рассмотрим прямоугольный треугольник A₁OF.

По определению синуса,

$[sin angle {A_1}OF = frac{{{A_1}F}}{{{A_1}O}},]$

откуда

$[{A_1}O = frac{{{A_1}F}}{{sin angle {A_1}OF}},]$

$[R = frac{{frac{a}{2}}}{{sin {{36}^o}}} = frac{a}{{2sin {{36}^o}}}.]$

Так как

$[sin {36^o} = sqrt {frac{{5 - sqrt 5 }}{8}} ,]$

то

$[R = frac{a}{{2sqrt {frac{{5 - sqrt 5 }}{8}} }} = frac{{asqrt 8 }}{{2sqrt {5 - sqrt 5 } }} = frac{{a cdot 2sqrt 2 }}{{2sqrt {5 - sqrt 5 } }} = ]$

$[ = frac{{asqrt 2 }}{{sqrt {5 - sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {5 - sqrt 5 } cdot sqrt {5 + sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {{5^2} - {{(sqrt 5 )}^2}} }} = ]$

$[ = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {20} }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{2sqrt 5 }} = ]$

$[ = frac{{asqrt 2 cdotsqrt {5 + sqrt 5 } cdotsqrt 5 }}{{2sqrt 5 cdotsqrt 5 }} = frac{{asqrt {50 + 10sqrt 5 } }}{{10}}.]$

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

$[R = frac{{asqrt {50 + 10sqrt 5 } }}{{10}}.]$

По определению котангенса,

$[ctgangle {A_1}OF = frac{{OF}}{{{A_1}F}},]$

$[OF = {A_1}F cdot {rm{ctg}}angle {A_1}OF = frac{a}{2} cdot {rm{ctg}}{36^o}.]$

Подставив значение котангенса 36°, получаем:

$[OF = frac{a}{2}cdotfrac{{sqrt {25 + 10sqrt 5 } }}{5}.]$

Итак, формула радиуса вписанной в правильный пятиугольник окружности

$[r = frac{{asqrt {25 + 10sqrt 5 } }}{{10}}.]$

Применив формулу

можно найти площадь правильного пятиугольника. Здесь

$[p = frac{{5a}}{2},r = frac{{asqrt {25 + 10sqrt 5 } }}{{10}},]$

следовательно, формула для нахождения площади A₁A₂A₃A₄A₅

$[S = frac{{5a}}{2}cdotfrac{{asqrt {25 + 10sqrt 5 } }}{{10}} = frac{{{a^2}sqrt {25 + 10sqrt 5 } }}{4}.]$

Все диагонали правильного пятиугольника равны.

Длина диагонали равна

$[d = frac{{a(sqrt 5 + 1)}}{2}.]$

Источник

Геометрия

найдите сумму внутренних и сумму внешних углов взятых по одному при каждой вершине пятиугольника abcde

Попроси больше объяснений

Следить

Отметить нарушение

Автор: Гость

Ответ(ы) на вопрос:

Гость:

Пожаловаться

Источник

Аватар

Геометрия, опубликовано 2018-08-22 16:33:00 by Гость

Чему равна сумма внешних углов выпуклого четырёх угольника и пятиугольника.(с решением)

Аватар

Ответ оставил Гость

Сумма внутренних углов любого (не обязательно правильного)
выпуклого n-угольника равна 180(n-2).
Каждый внутренний угол даёт в сумме с прилежащим к нему
внешним углом 180 градусов (развёрнутый угол), их сумма
при n вершинах составит 180n.
Сумму внешних углов находим вычитанием суммы внутренних
углов из суммы развёрнутых:
180n – 180(n-2) = 180*2 = 360

Вопрос

Не нашли ответа?

Если вы не нашли ответа на свой вопрос, или сомневаетесь в его правильности, то можете воспользоваться формой ниже и уточнить решение. Или воспользуйтесь формой поиска и найдите похожие ответы по предмету Геометрия.

Источник

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Есть сомнения?

Чему равна сумма внешних углов выпуклого четырёх угольника и пятиугольника.(с решением)

Вам также может понравиться

Как составить акт по авторскому надзору

Как найти клиента на оптимизацию

Как найти номера телефонов по номеру дома

Добавить комментарий Отменить ответ