Что такое внешний угол многоугольника? Сколько внешних углов у многоугольника? Чему равна сумма внешних углов многоугольника?
Определение
Внешним углом многоугольника называется угол, смежный с его внутренним.углом.
 Например, угол 1 — внешний угол при вершине A1 многоугольника
Например, угол 1 — внешний угол при вершине A1 многоугольника
![]()
так как он смежный с его внутренним углом A2A1An.

Угол 2 также является смежным углу A2A1An.
А значит, ∠2 — внешний угол при вершине A1.

∠1 = ∠2 (как вертикальные).
Таким образом, при каждой вершине многоугольника есть два равных между собой внешних угла.
У n-угольника n вершин, значит, всего внешних углов у n-угольника 2n.
Поскольку оба внешних угла при одной вершине равны, говоря о сумме внешних углов n-угольника, рассматривают внешние углы, взятые по одному при каждой вершине.
Теорема
(о сумме внешних углов выпуклого многоугольника)
Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360º.
 Дано:
Дано:
![]()
— выпуклый многоугольник,
∠1, ∠2, ∠3, …, ∠n — внешние углы при вершинах
![]()
Доказать:
![]()
Доказательство:
![]()
(как смежные).
Аналогично, сумма внешнего и внутреннего углов при каждой вершине n — угольника равна 180º.
Значит, сумма всех внутренних углов многоугольника и всех его внешних углов (взятых по одному при каждой вершине) равна 180º∙n.
Сумма всех внутренних углов выпуклого многоугольника равна 180º(n-2).
Следовательно, сумма всех внешних углов
![]()
![]()
Что и требовалось доказать.
Углы многоугольника
- Сумма внутренних углов
- Сумма внешних углов
Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
s = 2d(n – 2),
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
s = 2d(n – 2) = 180 · 4 = 720°.
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
s = 4d,
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:

Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n – 2):
s = 2dn – 2d(n – 2) = 2dn – 2dn + 4d = 4d.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Четырехугольники
- Выпуклый многоугольник
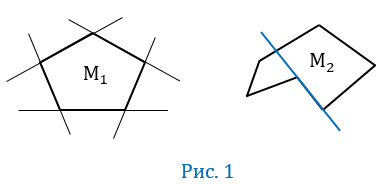
Выпуклый многоугольник – это многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. На рис.1 многоугольник М1 является выпуклым многоугольником, а многоугольник М2 – невыпуклым.
Сумма углов выпуклого многоугольника
Рассмотрим выпуклый n-угольник (рис.2,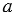 ). АnА1А2, А1А2А3, …, Аn-1АnА1 – углы этого многоугольника. Найдем их сумму.
). АnА1А2, А1А2А3, …, Аn-1АnА1 – углы этого многоугольника. Найдем их сумму.
Соединим вершину А1 диагоналями с другими вершинами (рис.2, б). В итоге получим n-2 треугольника, сумма углов которых равна сумме углов n-угольника. Сумма углов каждого треугольника равна 1800, поэтому сумма углов многоугольника А1А2…Аn равна (n-2) 1800.
1800.
Сумма углов выпуклого n-угольника равна (n – 2) 1800.
1800.
Примечание: Сумма углов невыпуклого n-угольника также равна (n – 2) 1800.
1800.
Внешний угол выпуклого многоугольника
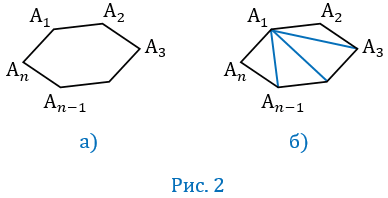
Внешний угол выпуклого многоугольника – угол, смежный с углом многоугольника. На рис.3 угол OAB внешний угол многоугольника АВСDE смежный с углом ВАЕ.
Если при каждой вершине выпуклого многоугольника А1А2…Аn взять по одному внешнему углу, то сумма этих внешних углов окажется равной
1800 – А1 + 1800 – А2 + … + 1800 – Аn = n 1800 – (A1 + A2 + … + An) = n
1800 – (A1 + A2 + … + An) = n 1800 – (n-2)
1800 – (n-2) 1800 = n
1800 = n 1800 – n
1800 – n 1800 + 2
1800 + 2 1800 = 3600.
1800 = 3600.
Сумма внешних углов выпуклого многоугольника равна 3600.
Советуем посмотреть:
Многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Трапеция
Прямоугольник
Ромб и квадрат
Осевая и центральная симметрии
Четырехугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 429,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 517,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 724,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 813,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 856,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1078,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1079,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1080,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1129,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.
Поговорим подробнее о видах многоугольников и их характеристиках.
Определение
Многоугольник — это замкнутая ломаная линия.
Многоугольник — это простое понятие: Если в замкнутой ломаной линии соседние стороны имеют общую точку и любые две стороны не являются продолжением друг друга, то фигура называется многоугольником.
При изучении темы, что такое многоугольники, применяются следующие термины:
- Вершины многоугольника.
- Стороны замкнутой ломаной.
- Углы, образованные между смежными сторонами.
- Отрезки между несмежными вершинами называются диагоналями.
- Сумма длин всех сторон фигуры является периметром.
- Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.
Наименования данных фигур зависят от количества сторон:
- Треугольник – это 3 стороны.
- Четырехугольник имеет 4 стороны.
- Пятиугольник – это 5 сторон и пр.
Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.
Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.
Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.
Виды многоугольников
Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.
Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.
Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.
Что такое правильные многоугольники
Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.
На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали
Периметром многоугольника называется сумма длин его сторон.
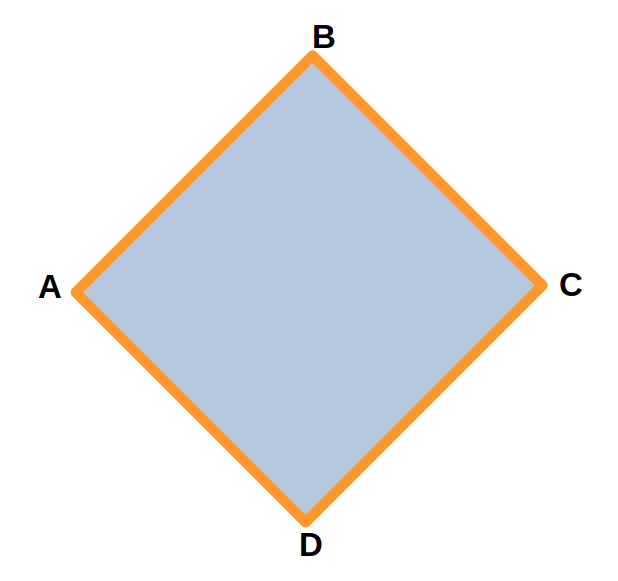
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.
Пример
Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти
периметр четырехугольника.
Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см
Ответ: периметр четырехугольника ABCD равен 12 см.
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.
Например, отрезок AD будет являться диагональю фигуры ABCDEF:
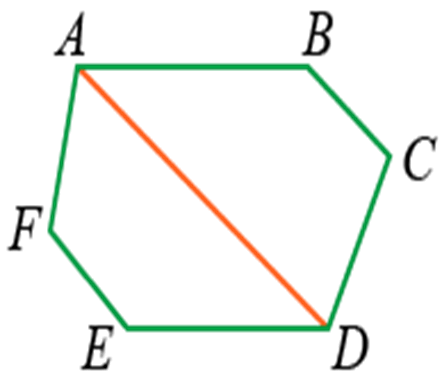
Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:
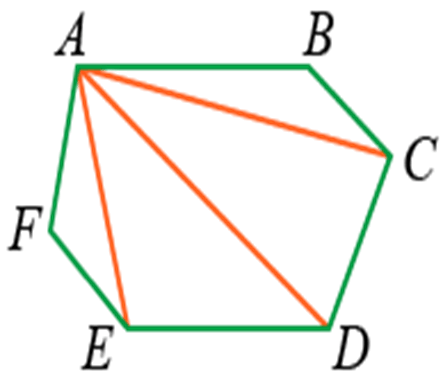
Количество треугольников будет на 2 меньше, чем число сторон:
Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.
Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.
Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.
Сумма углов выпуклого многоугольника
Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.
Внутренним называется угол между смежными сторонами.
Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.
Например, ∠LBC является внешним углом для ABCDEF.
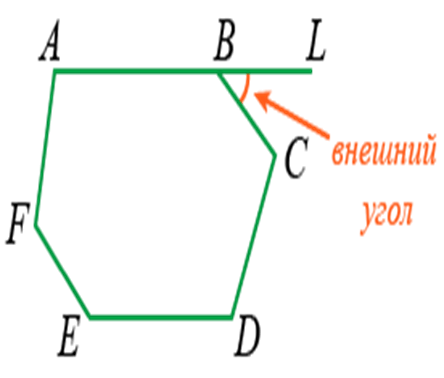
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.
Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.
Сумма внутренних углов
Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.
Обозначения выглядят следующим образом:
- сумма углов – s;
- число сторон – n;
- два прямых угла (2 · 90 = 180°) – 2d.
Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).
Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).
Пример:
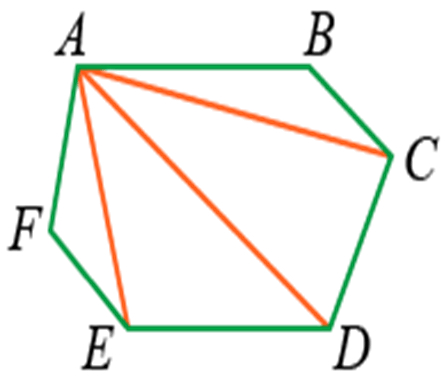
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.
Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.
Нет времени решать самому?
Наши эксперты помогут!
Сумма внешних углов
Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.
Где:
- s — сумма внешних углов;
- 4d — четыре прямых угла (4 · 90 = 360°).
Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).
Например, ∠1 и ∠2:
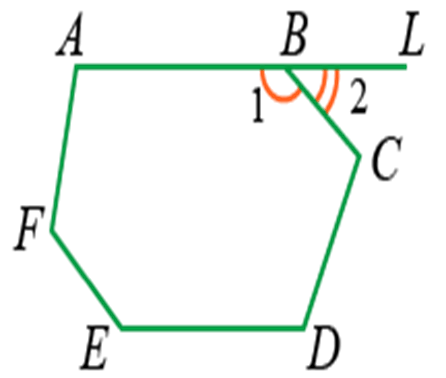
Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.
Пример
Задание: Найдите сумму углов выпуклого двенадцатиугольника.
Решение: Для выпуклого n-угольника сумма углов равна 180° (n -2).
Если имеется 12 вершин, то сумма всех углов будет рассчитываться следующим образом: 2 · 90 · (12 – 2) = 1800°.
Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.
Ученик
(112),
закрыт
10 лет назад
Serg
Высший разум
(170536)
10 лет назад
Каждый внешний угол многоугольника вместе со смежным внутренним составляет 180гр. Таких пар углов будет n, поэтому сумма всех внутренних углов и внешних (взятых по одному при каждой вершине) составляет 180n . Вычтя из нее сумму внутренних углов, получим искомую сумму внешних углов: (она не зависит от числа сторон ).
180n – 180(n-2) = 180n-180n+360гр = 360гр
Сумма внешних углов выпуклого многоугольника равна 360гр.
Федор Федор
Профи
(886)
4 года назад
Каждый внешний угол многоугольника вместе со смежным внутренним составляет 180гр. Таких пар углов будет n, поэтому сумма всех внутренних углов и внешних (взятых по одному при каждой вершине) составляет 180n . Вычтя из нее сумму внутренних углов, получим искомую сумму внешних углов: (она не зависит от числа сторон ).
180n – 180(n-2) = 180n-180n+360гр = 360гр
Сумма внешних углов выпуклого многоугольника равна 360гр.

