Как найти сумму внешних углов выпуклого многоугольника - Сайт, где вы сможете решить свои вопросы

Что такое внешний угол многоугольника? Сколько внешних углов у многоугольника? Чему равна сумма внешних углов многоугольника?

Определение

Внешним углом многоугольника называется угол, смежный с его внутренним.углом.

Например, угол 1 — внешний угол при вершине A1 многоугольника

$[{A_1}{A_2}{A_3}...{A_{n - 1}}{A_n},]$

так как он смежный с его внутренним углом A2A1An.

Угол 2 также является смежным углу A2A1An.

А значит, ∠2 — внешний угол при вершине A1.

∠1 = ∠2 (как вертикальные).

Таким образом, при каждой вершине многоугольника есть два равных между собой внешних угла.

У n-угольника n вершин, значит, всего внешних углов у n-угольника 2n.

Поскольку оба внешних угла при одной вершине равны, говоря о сумме внешних углов n-угольника, рассматривают внешние углы, взятые по одному при каждой вершине.

Теорема

(о сумме внешних углов выпуклого многоугольника)

Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360º.

Дано:

$[{A_1}{A_2}{A_3}...{A_{n - 1}}{A_n}]$

— выпуклый многоугольник,

∠1, ∠2, ∠3, …, ∠n — внешние углы при вершинах

$[{A_1},{A_2},{A_3},...,{A_n}]$

Доказать:

$[angle 1 + angle 2 + angle 3 + ... + angle n = {360^o}.]$

Доказательство:

$[angle 1 + angle {A_1} = {180^o}]$

(как смежные).

Аналогично, сумма внешнего и внутреннего углов при каждой вершине n — угольника равна 180º.

Значит, сумма всех внутренних углов многоугольника и всех его внешних углов (взятых по одному при каждой вершине) равна 180º∙n.

Сумма всех внутренних углов выпуклого многоугольника равна 180º(n-2).

Следовательно, сумма всех внешних углов

$[angle 1 + angle 2 + angle 3 + ... + angle n = {180^o} cdot n - {180^o}(n - 2) = ]$

$[ = {180^o} cdot n - {180^o} cdot n + {360^o} = {360^o}.]$

Что и требовалось доказать.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Четырехугольники
Выпуклый многоугольник

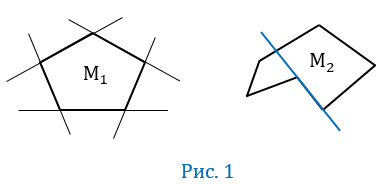
Выпуклый многоугольник – это многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. На рис.1 многоугольник М₁ является выпуклым многоугольником, а многоугольник М₂ – невыпуклым.

Сумма углов выпуклого многоугольника

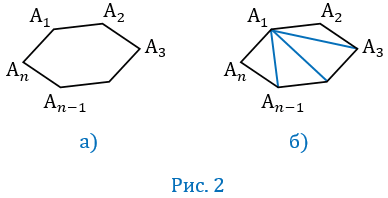
Рассмотрим выпуклый n-угольник (рис.2,). А_nА₁А₂, А₁А₂А₃, …, А_n-1А_nА₁ – углы этого многоугольника. Найдем их сумму.

Соединим вершину А₁ диагоналями с другими вершинами (рис.2, б). В итоге получим n-2 треугольника, сумма углов которых равна сумме углов n-угольника. Сумма углов каждого треугольника равна 180⁰, поэтому сумма углов многоугольника А₁А₂…А_n равна (n-2)180⁰.

Сумма углов выпуклого n-угольника равна (n – 2)180⁰.

Примечание: Сумма углов невыпуклого n-угольника также равна (n – 2)180⁰.

Внешний угол выпуклого многоугольника

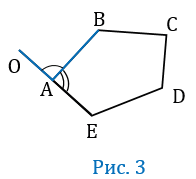
Внешний угол выпуклого многоугольника – угол, смежный с углом многоугольника. На рис.3 угол OAB внешний угол многоугольника АВСDE смежный с углом ВАЕ.

Если при каждой вершине выпуклого многоугольника А₁А₂…А_n взять по одному внешнему углу, то сумма этих внешних углов окажется равной

180⁰ – А₁ + 180⁰ – А₂ + … + 180⁰ – А_n = n180⁰ – (A₁ + A₂ + … + A_n) = n180⁰ – (n-2)180⁰ = n180⁰ – n180⁰ + 2180⁰ = 360⁰.

Сумма внешних углов выпуклого многоугольника равна 360⁰.

Советуем посмотреть:

Многоугольник

Четырехугольник

Параллелограмм

Признаки параллелограмма

Трапеция

Прямоугольник

Ромб и квадрат

Осевая и центральная симметрии

Четырехугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 363,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 365,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 378,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 15,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 731,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 813,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 818,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 856,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 860,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1078,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Углы многоугольника

Сумма внутренних углов
Сумма внешних углов

Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.

s = 2d(n – 2),

где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.

Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:

s = 2d(n – 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).

s = 4d,

где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:

Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n – 2):

s = 2dn – 2d(n – 2) = 2dn – 2dn + 4d = 4d.

Источник

Ученик

(112),
закрыт

10 лет назад

Serg

Высший разум

(170536)

10 лет назад

Каждый внешний угол многоугольника вместе со смежным внутренним составляет 180гр. Таких пар углов будет n, поэтому сумма всех внутренних углов и внешних (взятых по одному при каждой вершине) составляет 180n . Вычтя из нее сумму внутренних углов, получим искомую сумму внешних углов: (она не зависит от числа сторон ).
180n – 180(n-2) = 180n-180n+360гр = 360гр
Сумма внешних углов выпуклого многоугольника равна 360гр.

Федор Федор

Профи

(884)

4 года назад

Источник

Сумма внешних углов выпуклого многоугольника. Доказательства

Сумма внешних углов любого выпуклого n-угольника равна 360 градусов. Первое доказательство. Вот наш n-угольник, в данном случае n = 6. Вот его внешние углы, а вот внутренние углы. Сумма всех внешних и внутренних углов — это сумма n развёрнутых углов. Каждый внутренний угол плюс смежный с ним внешний угол — в сумме 180 градусов. Общая сумма внутренних и внешних равна n180 градусов. Если вычесть из этой суммы сумму внутренних углов, то получится сумма внешних. А уже доказано, что сумма внутренних углов — на 360 градусов меньше, чем n180. Значит, сумма внешних углов равна 360 градусов. ЧТД.

Второе доказательство. Чтобы путнику обойти вокруг выпуклого многоугольника — надо возле каждой вершины поворачивать на угол, равный внешнему углу при этой вершине. И при полном обходе сумма поворотов составит как раз 1 полный оборот, т.е. 360 градусов.

Источник

Сумма углов выпуклого многоугольника

Внешний угол выпуклого многоугольника

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Углы многоугольника

Сумма внутренних углов

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника. Доказательства

Вам также может понравиться

Как найти радиус орбиты астероида

Как найти площадь заштрихованной фигуры в квадрате

Задние колеса домиком киа спортейдж 3 как исправить

Добавить комментарий Отменить ответ