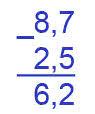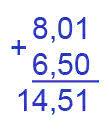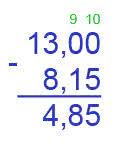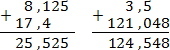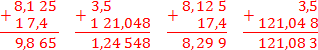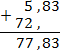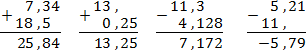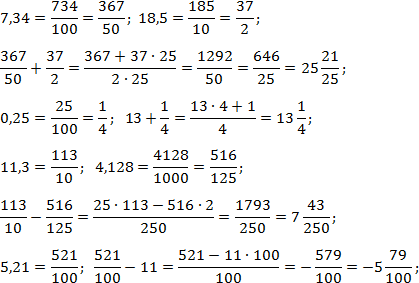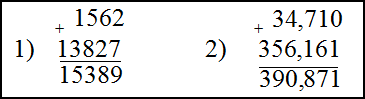Home » Уроки » Как складывать и вычитать десятичные дроби? Сложение и вычитание десятичных дробей.
Как складываются и вычитаются десятичные дроби?
Чтобы найти сумму или разность двух чисел, записанных в десятичной дроби, нужно следовать простому алгоритму:
1. Правильно записать числа столбиком. Записать числа в столбик таким образом, чтобы десятичные точки стояли друг под другом и соответствующие разряды чисел совпадали;
2. Сложить или вычесть – получить ответ.Сумма или разность полученной дроби столбиком — как обычные числа. Не забудьте записать «десятичную точку» между соответствующими разрядами;
Пример №1
Вычислите значение выражения 8,7-2,5
Решение:
8,7-2,5=6,2
Ответ:6,2
Пример №2
Вычислите значение выражения 8,01+6,5
Решение:
8,01+6,5=14,51
Ответ: 14,51
Видно, сложение десятичных дробей почти ничем не отличается от сложения обычных чисел. Самое важное — это правильно сопоставить разряды слагаемых, чтобы «десятичные точки» находились друг под другом.
Пример №3
Найдите значение выражений:
1) 15,521 + 19,3;
2) 6,5 + 924,003.
Решение:
15,521 + 19,3=34,821
6,5 + 924,003=930,503
Теперь рассмотрим неправильные решения.
Разница в решении видна сразу. Самое главное это нужно правильно записать разряды по разрядами и «десятичные точки» друг под другом.
Если нет «десятичную точку», ее ставят справа от всего числа. Например, возьмем числа 8,15 и 13. В этом случае операция сложения будет выглядеть так:
Операция вычитания:
Когда у нас встречается несколько нулей подряд при разности дробей, нужно занимать для этого нуля десяток, а всем последующим нулям, которые стоят впереди ставим девятки. Показано в примере.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Рекомендуем подписаться на новостную рассылку нашего сайта TutoMath.ru, чтобы быть в курсе всех новинок.
Напишите пожалуйста как узнать сумму десятичного числа, например : 0, 1 * 0, 2.
Если вам необходимо получить ответ на вопрос Напишите пожалуйста как узнать сумму десятичного числа, например : 0, 1 * 0, 2?, относящийся
к уровню подготовки учащихся 5 – 9 классов, вы открыли нужную страницу.
В категории Математика вы также найдете ответы на похожие вопросы по
интересующей теме, с помощью автоматического «умного» поиска. Если после
ознакомления со всеми вариантами ответа у вас остались сомнения, или
полученная информация не полностью освещает тематику, создайте свой вопрос с
помощью кнопки, которая находится вверху страницы, или обсудите вопрос с
посетителями этой страницы.
Десятичные дроби используют в самых различных сферах деятельности человека.
Они значительно упрощают вычисления и измерения.
Эта информация доступна зарегистрированным пользователям
Десятичные дроби удобны при решении профессиональных и бытовых задач.
Важным преимуществом десятичных дробей является то, что математические действия, производимые с ними, схожи по своей сути с арифметическими действиями, которые можно совершать с натуральными числами.
Десятичные дроби можно сравнивать, складывать, вычитать, умножать и делить, возводить в степень.
На данном уроке рассмотрим правила сложения и вычитания десятичных дробей.
Узнаем, как складывать и вычитать десятичные дроби столбиком.
Эта информация доступна зарегистрированным пользователям
Выясним, как на координатной прямой можно отметить десятичную дробь, не переводя ее в обыкновенную дробь.
Рассмотрим пример решения составной текстовой задачи на сложение и вычитание десятичных дробей арифметическим и алгебраическим способом.
Рассмотрим правила сложения десятичных дробей на примере.
Разберем простую арифметическую задачу.
На детский праздник купили 2,250 кг шоколадных конфет и 3,550 кг карамели.
Сколько всего конфет купили на детский праздник?
Эта информация доступна зарегистрированным пользователям
Решение:
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Чтобы найти ответ на поставленный вопрос (найти общее количество конфет), необходимо сложить шоколадные конфеты и карамель вместе.
Схематически изобразим условие задачи.
Эта информация доступна зарегистрированным пользователям
Сложим десятичные дроби 2,250 и 3,550.
Сложение десятичных дробей можно свести к сложению смешанных чисел, которые соответствуют этим дробям.
Десятичной дроби 2,250 соответствует смешанное число (mathbf{2frac{250}{1000}}).
Десятичной дроби 3,550 соответствует смешанное число (mathbf{3frac{550}{1000}}).
Нам известно, как найти сумму двух смешанных чисел.
Сложим целые части отдельно, дробные- отдельно.
(mathbf{2frac{250}{1000} + 3frac{550}{1000} = 2 + frac{250}{1000} + 3 + frac{550}{1000} = (2 + 3) + (frac{250}{1000} + frac{550}{1000}) =})
(mathbf{= 5 + frac{800}{1000} = 5frac{800}{1000}}) (кг) всего конфет купили для детского праздника.
Ответ: (mathbf{5frac{800}{1000} = 5,800}) (кг).
Такой же ответ можно получить, не обращая десятичные дроби в смешанные числа.
Выясним, как и по каким правилам складывают десятичные дроби.
Так как запись десятичных дробей основана на позиционной системе счисления, в которой значение каждого числового знака зависит от позиции (от места) в числе, десятичные дроби удобно складывать поразрядно.
В связи с этим, чтобы сложить дроби, записанные в десятичной форме, необходимо убедиться, что в числах одинаковое количество разрядов после запятой.
Сложение десятичных дробей практически не отличается от сложения натуральных чисел, удобнее всего выполнять операцию сложения в столбик, записывая соответствующие разряды друг под другом.
Чтобы сложить две десятичные дроби столбиком, необходимо соблюдать следующие правила:
Эта информация доступна зарегистрированным пользователям
- Уравнять в слагаемых количество цифр после запятой, дописав нужное количество нулей к одной из дробей.
- Записать слагаемые друг под другом так, чтобы разряды второго слагаемого располагались строго под соответствующими разрядами первого слагаемого, а запятая под запятой.
- Сложить поразрядно числа, не обращая внимание на запятую так же, как выполняется сложение столбиком натуральных чисел.
- Поставить в полученной сумме запятую под запятыми слагаемых.
Используя данный алгоритм сложения десятичных дробей, решим задачу про конфеты, рассмотренную в начале нашего урока.
Вспомним условие задачи.
2,250 кг шоколадных конфет
3,550 кг карамельных конфет
Общее количество конфет- ? кг
Решение:
Найдем общее количество конфет, купленных на праздник, сложив две десятичные дроби 2,250 и 3,550.
Количество десятичных знаков в данных дробях одинаково, поэтому сразу запишем дроби в столбик так, чтобы одноименные разряды находились друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Эта информация доступна зарегистрированным пользователям
Выполним сложение дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
Эта информация доступна зарегистрированным пользователям
Поставим десятичную запятую в полученный результат суммы под запятыми, которые стоят в слагаемых (по правилу: «запятая под запятой»).
В итоге операция сложения двух десятичных дробей выглядит так:
Эта информация доступна зарегистрированным пользователям
2,250 + 3,550 = 5,800 (кг) конфет купили для детского праздника
Ответ: 5,800 (кг).
При сложении десятичных дробей получился результат такой же, как при сложении смешанных чисел, которые этим дробям соответствуют.
Как видите, операция сложения десятичных дробей мало отличается от сложения натуральных чисел, важно только верно расположить разряды и десятичные запятые слагаемых.
Встречаются случаи, когда приходится складывать десятичные дроби, в которых различное количество десятичных знаков.
Если после запятой в одном из слагаемых десятичных знаков меньше, чем в другом, количество знаков нужно уравнять, недостающие разряды следует заменить нулем.
После этого десятичные дроби складывают.
Рассмотрим поясняющий пример.
Найдем сумму десятичных дробей 0,434 и 0,28.
В первой десятичной дроби 0,434 после запятой три десятичных знака (разряд десятых, сотых, тысячных).
Во второй десятичной дроби 0,28 после запятой два десятичных знака (разряд десятых и сотых, отсутствует разряд тысячных).
Уравняем количество десятичных знаков.
Допишем нуль справа от десятичной запятой после самой правой ненулевой цифры (в разряде тысячных).
В итоге получим десятичную дробь 0,280, равную дроби 0,28.
Столбиком запишем дроби 0,434 и 0,280 так чтобы одноименные разряды и десятичные запятые находились строго друг под другом.
Эта информация доступна зарегистрированным пользователям
Далее выполним сложение дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
Эта информация доступна зарегистрированным пользователям
При сложении сотых получается двузначное число 11, поэтому единицу запишем под чертой, а свободный десяток перенесем в старший разряд.
Поставим десятичную запятую в полученный результат суммы под запятыми, которые стоят в слагаемых (по правилу: «запятая под запятой»).
В итоге операция сложения двух десятичных дробей 0,434 и 0,280 будет выглядеть так:
Эта информация доступна зарегистрированным пользователям
Сложение десятичной дроби и натурального числа.
Иногда приходится находить сумму десятичной дроби и натурального числа.
По сути, чтобы сложить натуральное число с десятичной дробью, необходимо это натуральное число и целую часть десятичной дроби сложить, а дробную часть оставить без изменений.
При сложении десятичной дроби и натурального числа в конце натурального числа можно поставить десятичную запятую и приписать столько нулей, сколько содержится десятичных знаков в дроби.
Данные действия не изменят значение натурального числа.
Рассмотрим поясняющий пример, решим простую задачу на сложение.
С первого участка собрали 60 т зерна, а со второго на 16,8 т больше.
Сколько тонн зерна собрали со второго участка?
Эта информация доступна зарегистрированным пользователям
Решение:
Запишем кратко условие задачи.
Эта информация доступна зарегистрированным пользователям
Из условия задачи известно, что со второго участка собрали зерна больше, чем с первого, т.е. получается со второго поля убрали столько же, сколько и с первого, да еще 16,8 т.
Схематично изобразим условие задачи.
Эта информация доступна зарегистрированным пользователям
Такая задача, в которой одно число увеличивают на какое-нибудь другое число (задача на увеличение на некоторое количество единиц), решается всегда сложением.
Сложим натуральное число 60 с десятичной дробью 16,8.
Для этого прибавим к целой части десятичной дроби натуральное число, а дробную часть оставим прежней.
Целая часть десятичной дроби 16,8 равна 16, прибавим к ней 60, получим число 76, поставим запятую и припишем дробную часть заданной десятичной дроби.
16,8 + 60 = 76,8 (т) зерна собрали со второго участка.
Ответ: 76,8 (т).
Эта информация доступна зарегистрированным пользователям
Сложение десятичных дробей с обыкновенной дробью (смешанным числом).
- Сложение десятичных дробей с обыкновенной дробью (смешанным числом) можно свести к сложению обыкновенных дробей (смешанных чисел).
Для этого десятичную дробь необходимо представить в виде обыкновенной дроби.
- Сложение десятичных дробей с обыкновенной дробью (смешанным числом) можно свести к сложению десятичных дробей, представив обыкновенную дробь (смешанное число) в виде десятичной дроби.
Для примера сложим смешанное число и десятичную дробь.
Найдите сумму (mathbf{1frac{2}{10} + 0,5}).
Первый способ.
Переведем десятичную дробь в обыкновенную.
(mathbf{0,5 = frac{5}{10}})
Теперь сумму смешанного числа (mathbf{1frac{2}{10}}) и обыкновенной дроби (mathbf{frac{5}{10}}) найдем по правилу сложения смешанного числа и обыкновенной дроби.
Сложим смешанное число и правильную дробь, найдем только сумму дробной части смешанного числа и этой дроби, целую же часть смешанного числа при этом оставим без изменений.
(mathbf{1frac{2}{10} + frac{5}{10} = 1 + frac{2}{10} + frac{5}{10} = 1 + (frac{2}{10} + frac{5}{10}) = 1 + frac{7}{10} = 1frac{7}{10}})
Переведем смешанное число (mathbf{1frac{7}{10}}) в десятичную дробь.
(mathbf{1frac{7}{10} = 1,7})
Ответ: 1,7.
Второй способ.
Представим смешанное число в виде десятичной дроби.
(mathbf{1frac{2}{10} = 1,2})
Теперь сумму десятичной дроби 1,2 и десятичной дроби 0,5 найдем по правилу сложения десятичных дробей.
Сумму чисел 1,2 и 0,5 запишем столбиком, располагая соответствующие разряды друг под другом, запятая под запятой.
Эта информация доступна зарегистрированным пользователям
Ответ: 1,7.
Вычисляя сумму первым и вторым способом, получили одинаковые ответы, следовательно, рассмотренные нами способы нахождения суммы десятичной дроби и обыкновенной дроби (смешанного числа) равноправны.
Эта информация доступна зарегистрированным пользователям
Рассмотрим правила вычитания десятичных дробей.
Так как десятичная дробь- это десятичная запись обыкновенной дроби, вычитание двух десятичных дробей можно свести к разности соответствующих обыкновенных дробей.
Рассмотрим пример вычисления десятичных дробей.
Задача
Провод длинной 15,45 м разрезали на две части.
Длина первой части провода 5,20 м.
Какова длина второй части провода?
Эта информация доступна зарегистрированным пользователям
Решение:
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Две части провода вместе представляют собой целый провод.
Длина первой части провода- это известное слагаемое.
Длина второй части провода- это неизвестное слагаемое.
Схематически изобразим условие задачи.
Эта информация доступна зарегистрированным пользователям
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Найдем разность двух десятичных дробей 15,45 и 5,2.
Представим заданные десятичные дроби в виде смешанных чисел.
Десятичной дроби 15,45 соответствует смешанное число (mathbf{15frac{45}{100}}).
Десятичной дроби 5,2 соответствует смешанное число (mathbf{5frac{2}{10}}).
Приведем дроби к общему знаменателю.
Десятичная дробь 15,45 содержит два десятичных знака (разряд десятых и разряд сотых).
Десятичная дробь 5,2 содержит один десятичный знак (разряд десятых).
Чтобы уравнять количество знаков после запятой, запишем нуль в дроби 5,2 после разряда десятых.
Получим число 5,20, равное 5,2.
Десятичная дробь 5,20 соответствует смешанному числу (mathbf{5frac{20}{100}}).
После того, как мы уравняли знаменатели дробных частей смешанных чисел, можно приступать к вычитанию.
(mathbf{15frac{45}{100} – 5frac{20}{100} = (15 + frac{45}{100}) – (5 + frac{20}{100}) = (15 – 5) + (frac{45}{100} – frac{20}{100}) = 10frac{25}{100}})
Переведем смешанное число (mathbf{10frac{25}{100}}) в десятичную дробь.
(mathbf{10frac{25}{100} = 10,25}) (м) длина второй части провода
Ответ: 10,25 (м).
Такой же ответ можно получить, не переводя десятичные дроби в смешанные числа.
Так же как при сложении, десятичные дроби удобно вычитать в столбик.
Операция вычитания десятичных дробей столбиком очень похожа на вычитание натуральных чисел аналогичным способом.
Выполняя вычитание десятичных дробей столбиком, необходимо соблюдать несложные правила:
Эта информация доступна зарегистрированным пользователям
- Уравнять количество десятичных знаков в уменьшаемом и вычитаемом (если это требуется), дописав необходимое количество нулей к одной из дробей.
- Вычитаемое записать под уменьшаемым в столбик так, чтобы соответствующие их разряды находились строго друг под другом, запятая под запятой.
- Выполнить вычитание столбиком так, как вычитают натуральные числа (не обращая внимание на запятые).
- В полученной разности поставить запятую так, чтобы она находилась строго под запятыми уменьшаемого и вычитаемого.
Воспользуемся данным алгоритмом при решении задачи.
Вспомним задачу про провод, рассмотренную выше.
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Две части провода вместе представляют собой целый провод.
Длина первой части провода- это известное слагаемое.
Длина второй части провода- это неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Найдем разность двух десятичных дробей 15,45 и 5,2.
Уравняем количество знаков в уменьшаемом и вычитаемом, для этого в дробную часть десятичной дроби 5,2 в разряд сотых запишем нуль.
Получим число 5,20, равное 5,2.
Запишем уменьшаемое 15,45 и вычитаемое 5,20 столбиком так, чтобы соответствующие их разряды находились строго друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Эта информация доступна зарегистрированным пользователям
Вычтем дроби, не обращая внимание на десятичные запятые.
В полученной разности запятую поставим строго под запятыми, стоящими в уменьшаемом и вычитаемом.
Вычитание десятичных дробей столбиком будет выглядеть так:
Эта информация доступна зарегистрированным пользователям
В итоге получаем:
15,45 – 5,20 = 10,25 (м) длина второй части провода.
Ответ: 10,25 (м).
При вычитании десятичных дробей получился результат такой же, как при вычитании смешанных чисел, которые этим дробям соответствуют.
Операция вычитания десятичных дробей практически не отличается от вычитания натуральных чисел, важно только верно расположить разряды и десятичные запятые уменьшаемого и вычитаемого.
Вычитание десятичной дроби из натурального числа.
Вычитание десятичной дроби из натурального числа удобней выполнять в столбик.
Натуральное число в таком случае лучше представить в виде десятичной дроби, заменив дробную часть нулями.
Рассмотрим пример.
Периметр треугольника равен 34 см.
Сумма двух его сторон равна 23,1 см.
Найдите длину его третьей стороны.
Сделаем условный рисунок.
Эта информация доступна зарегистрированным пользователям
Пусть a, b, c– стороны треугольника, Р– это периметр треугольника- сумма длин трех его сторон.
Эта информация доступна зарегистрированным пользователям
Представим натуральное число 34 в виде десятичной дроби.
Вычитаемая дробь имеет один знак в дробной части, поэтому после натурального числа 34 поставим десятичную запятую, а после нее запишем один нуль, получим число 34,0 (тридцать четыре целых ноль десятых).
Выполним вычитание десятичных дробей 34,0 и 23,1 столбиком.
Эта информация доступна зарегистрированным пользователям
Так как из нуля единица не вычитается, займем десяток единиц из старшего разряда, при этом в нем на один десяток единиц станет меньше.
В итоге получаем:
c = 34 – 23,1 = 10,9 (см)- длина третьей стороны треугольника.
Ответ: с = 10,9 (см).
Вычитание натурального числа из десятичной дроби.
Чтобы вычесть натуральное число из десятичной дроби, необходимо это натуральное число вычесть из целой части уменьшаемой десятичной дроби, при этом дробную часть десятичной дроби необходимо оставить без изменений.
Пример.
Решим уравнение 59,3 – х = 18.
Найдем значение неизвестного х, при котором данное уравнение обратиться в верное равенство.
В заданном уравнении неизвестное является вычитаемым.
Чтобы найти вычитаемое (х), необходимо из уменьшаемого вычесть разность.
59,3 – х = 18
х = 59,3 – 18
Вычтем из десятичной дроби натуральное число по правилу: из целой части десятичной дроби 59,3 вычтем число 18, получим число 41, а дробную часть оставим без изменений.
х = 41,3
Проверка:
В исходное уравнение 59,3 – х = 18 вместо неизвестного х подставим найденное число х = 41,3.
59,3 – 41,3 = 18
Выполним вычитание столбиком двух десятичных дробей 59,3 и 41,3.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
Эта информация доступна зарегистрированным пользователям
18,0 = 18 (получили верное равенство, значит корень уравнения найден верно).
Ответ: х = 41,3.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и наоборот.
Первый способ.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и обыкновенной (смешанного числа) из десятичной можно свести к разности двух обыкновенных дробей (к разности двух смешанных чисел).
Для этого десятичную дробь нужно представить в виде обыкновенной дроби (смешанного числа) и выполнить вычитание двух обыкновенных дробей (смешанных чисел).
Второй способ.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и обыкновенной (смешанного числа) из десятичной можно свести к разности двух десятичных дробей.
Для этого обыкновенную дробь (смешанное число) нужно представить в виде десятичной дроби и выполнить вычитание двух десятичных дробей.
Рассмотрим пример.
Найдите значение выражения (mathbf{27frac{35}{100} – 6,11}).
Решение №1.
Переведем десятичную дробь 6,11 в смешанное число.
(mathbf{6,11 = 6frac{11}{100}})
Подставим в исходное выражение вместо десятичной дроби 6,11 полученное смешанное число (mathbf{6frac{11}{100}}).
Найдем разность двух смешанных чисел.
(mathbf{27frac{35}{100} – 6frac{11}{100} = (27 – 6) + (frac{35}{100} – frac{11}{100}) = 21 + frac{24}{100} = 21frac{24}{100}})
Решение №2.
Представим смешанное число (mathbf{27frac{35}{100}}) в виде десятичной дроби.
(mathbf{27frac{35}{100} = 27,35})
Подставим в исходное выражение вместо смешанного числа (mathbf{27frac{35}{100}}) соответствующую ему десятичную дробь 27,35.
Найдем разность двух десятичных дробей: 27,35 – 6,11.
Выполним вычитание столбиком.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
Эта информация доступна зарегистрированным пользователям
В результате получили десятичную дробь 21,24.
Находя значение выражения (mathbf{27frac{35}{100} – 6,11}) первым и вторым способом, получили один и тот же ответ, что доказывает равенство этих двух способов вычисления.
Эта информация доступна зарегистрированным пользователям
Математические операции сложения и вычитания часто приходятся использовать при решении уравнений и различных задач.
Для одной и той же задачи может существовать несколько верных способов ее решения.
Эта информация доступна зарегистрированным пользователям
Выбрав верную логику рассуждения, можно значительно упростить и ускорить процесс решения текстовой задачи.
Попробуем решить составную текстовую задачу на сложение и вычитание десятичных дробей арифметическим и алгебраическим способом.
При решении задач тем и другим способом необходимо учитывать и соблюдать основные свойства и правила математических операций, применять известные правила упрощения и преобразования выражений.
Задача.
В трехкомнатной квартире, площадью 51,5 м2, первая комната имеет площадь 10,5 м2, площадь второй комнаты на 12,3 м2 больше площади первой.
Какова площадь третьей комнаты?
Эта информация доступна зарегистрированным пользователям
Решим данную задачу арифметическим способом (составлением выражения).
Запишем кратко условие задачи.
Площадь первой комнаты- 10,5 м2
Площадь второй комнаты- 10,5 + 12,3 м2
Площадь третьей комнаты- ? м2
Общая площадь квартиры- 51,5 м2.
Чтобы найти площадь третьей комнаты, необходимо из общей площади трехкомнатной квартиры вычесть площадь первой и второй комнаты.
Составим выражение:
Эта информация доступна зарегистрированным пользователям
Найдем значение полученного выражения.
Данное выражение содержатся сразу несколько арифметических операций и скобки.
Определим порядок действий в данном выражении, используя правила, которые определяют порядок выполнения действий в математических выражениях.
1) Это выражение содержит скобки, следовательно, первым делом выполним действия в них.
Найдем сумму двух десятичных дробей 10,5 и 12,3 столбиком.
Количество десятичных знаков в десятичных дробях одинаково, поэтому сразу запишем дроби в столбик так, чтобы одноименные разряды находились друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Поразрядно выполним сложение, в полученной сумме поставим десятичную запятую так, чтобы она находилась под запятыми слагаемых.
Эта информация доступна зарегистрированным пользователям
Оставшиеся за скобками действия- это действия первой ступени (сложение и вычитание), они выполняются по порядку следования слева направо.
2) Найдем разность десятичных дробей 51,5 и 10,5.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
Эта информация доступна зарегистрированным пользователям
3) Найдем разность значений, которые были получены во втором и первом действии, т.е. из десятичной дроби 41,0 вычтем десятичную дробь 22,8.
Эта информация доступна зарегистрированным пользователям
В результате получим:
51,5 – 10,5 – (10,5 + 12,3) = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Эту же задачу можно решить арифметическим способом, но по действиям.
Запишем кратко условие задачи.
Эта информация доступна зарегистрированным пользователям
Площадь третьей комнаты- ? м2
Общая площадь квартиры- 51,5 м2.
В этом случае решение заданной задачи будет состоять из следующих этапов:
- Найдем площадь второй комнаты (данное действие мы выполняли, решая задачу первым способом).
- Сложив результат, полученный в первом действии, с площадью первой комнаты, определим общую площадь двух комнат- первой и второй вместе.
- Из площади всей трехкомнатной квартиры вычтем общую площадь первой и второй комнат.
1. 10,5 + 12,3 = 22,8 (м2) площадь второй комнаты.
2. Чтобы высчитать площадь второй комнаты, выполним сложение двух десятичных дробей столбиком:
Эта информация доступна зарегистрированным пользователям
10,5 + 22,8 = 33,3 (м2) площадь первой и второй комнат вместе.
3. Чтобы высчитать площадь третьей комнаты, выполним вычитание двух десятичных дробей столбиком:
Эта информация доступна зарегистрированным пользователям
51,5 – 33,3 = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Решим задачу алгебраическим способом.
Кратко запишем условие задачи.
Площадь первой комнаты- 10,5 м2
Площадь второй комнаты- 10,5 + 12,3 м2
Пусть х м2 площадь третьей комнаты
Зная, что площадь всей квартиры равна 51,5 м2, составим уравнение.
10,5 + (10,5 + 12,3) + х = 51,5
Упростим уравнение: выполним действие в скобках, т.е. найдем сумму чисел 10,5 и 12,3, полученный результат сложим с первым слагаемым. (данные действия мы уже выполняли, решая задачу арифметическим способом).
10,5 + (10,5 + 12,3) = 10,5 + 22,8 = 33,3
В итоге получаем, что целое выражение 10,5 + (10,5 + 12,3) тождественно равно 33,3.
Подставим в исходное уравнение вместо суммы трех десятичных дробей результат их суммы: 33,3.
Получим простое уравнение с неизвестным слагаемым.
33,3 + х = 51,5
х = 51,5 – 33,3
х = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Все три способа решения задачи равноправны и дают одинаковый результат.
Эта информация доступна зарегистрированным пользователям
Читайте также
Сложение и вычитание десятичных дробей
15 августа 2011
Чтобы найти сумму или разность двух чисел, записанных в десятичной форме, надо выполнить три шага:
- Записать числа в столбик таким образом, чтобы соответствующие разряды совпадали. Главный ориентир — десятичные точки. Они не являются отдельным разрядом, но должны стоять на одной вертикали;
- Сложить или вычесть полученные дроби столбиком — подобно тому, как мы складываем и вычитаем обычные числа. Не забудьте «внедрить» десятичную точку между соответствующими разрядами;
- Полученное число и будет ответом — больше ничего делать не надо.
Как видите, сложение десятичных дробей почти ничем не отличается от сложения обычных чисел. Самое сложное — правильно сопоставить разряды слагаемых, чтобы десятичные точки находились на вертикальной прямой, друг под другом.
Задача. Найдите значение выражений: 8,125 + 17,4; 3,5 + 121,048.
Для каждого выражения приведем правильную запись и две неправильные (самые распространенные). Сначала — правильные:
Теперь рассмотрим неправильные решения. В первом случае все числа «прижаты» к левому краю, во втором — к правому. Ответы получатся совсем другие:
Как видите, ничего общего с тем, что должно получиться на самом деле.
Если в одном из слагаемых нет десятичной точки, ее ставят справа от всего числа. Например, возьмем числа 5,83 и 72. В этом случае операция сложения будет выглядеть так:
Кто-то скажет, что все эти отступы, сдвиги и запятые — ненужные сложности, и лучше работать «по старинке». Что ж, я никого не собираюсь переубеждать. Отмечу лишь, что новая технология всегда требуют более высокой квалификации от тех, кто собирается ее использовать. В этом плане десятичные дроби — следующий уровень развития после обычных.
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25; 11,3 − 4,128; 5,21 − 11.
Эти примеры показывают, насколько упрощаются вычисления, когда дроби записаны в десятичной форме. Никаких дополнительных множителей, никаких общих знаменателей.
Чтобы почувствовать разницу, решим ту же задачу традиционным методом. Для этого переведем все десятичные дроби в обычные. Взгляните:
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25; 11,3 − 4,128; 5,21 − 11.
Итак, переводим все десятичные дроби в обычные и считаем по классической схеме:
Мы специально не стали выполнять обратный переход — от обычной дроби к десятичной — чтобы немного сократить вычисления.
Видно, что длина решения выросла многократно. Поэтому старайтесь работать с десятичными дробями везде, где это возможно.
Смотрите также:
- Умножение и деление десятичных дробей
- Как представить обычную дробь в виде десятичной
- Локальная теорема Муавра — Лапласа
- Вебинар по заданию 13: тригонометрия
- Задача B4: тарифы на сотовую связь
- Логарифмические неравенства, сводящиеся к квадратным
Содержание:
- Определение суммы чисел
- Свойства суммы чисел
Определение суммы чисел
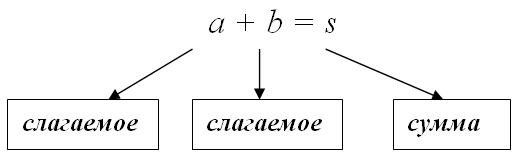
Суммой $s$ (лат. summa – итог, общее количество) чисел $a_{1}, a_{2}, dots, a_{n}$ называется результат
суммирования этих чисел: $s=a_{1}+a_{2}+ldots+a_{n}$ . В частности, если складывается два числа $a$ и $b$, то
Пример
Задание. Найти сумму чисел:
1) $12$ и $15$ 2) $1,1 ; 2,2 ; 3,3$ и $4,4$
Ответ.
$12+15=27$
$1,1+2,2+3,3+4,4=11$
Свойства суммы чисел
- Коммутативность: $n+m=m+n$
-
Ассоциативность: $(n+m)+k=n+(m+k)$
На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.
-
Дистрибутивность по отношению к умножению
$$(n+m) cdot k=n cdot k+m cdot k$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму чисел удобным способом:
1) $15+17+13$ ; 2) $34+22+16+18$
Решение. По свойствам сложения имеем
$$15+17+13 =15+(17+13)=15+30=45 $$
$$34+22+16+18 =(34+16)+(22+18)=50+40=90 $$
Ответ. 1) $15+17+13=45$
2) $34+22+16+18=90$
При сложении больших чисел или
десятичных дробей используется сложение в столбик.
Пример
Задание. Найти сумму чисел удобным способом:
1) $1562+13827$ ; 2) $34,71+356,161$
Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом.
В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем
числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном
столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:
Ответ. 1) $1562+13827=15389$
2) $34,71+356,161=390,871$
Сложение рациональных дробей производится по правилу
$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$
Пример
Задание. Найти сумму чисел:
1) $frac{1}{4}+frac{1}{6}$ ; 2) $frac{2}{3}+1 frac{1}{2}$
Решение. Вычислим первую сумму используя правило сложения рациональных чисел
$$frac{1}{4}+frac{1}{6}=frac{1 cdot 6+1 cdot 4}{4 cdot 6}=frac{6+4}{24}=frac{10}{24}$$
Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим
$$frac{1}{4}+frac{1}{6}=frac{5}{12}$$
Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого
умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим
правило сложение рациональных дробей
$$frac{2}{3}+1 frac{1}{2}=frac{2}{3}+frac{3}{2}=frac{2 cdot 2+3 cdot 3}{3 cdot 2}=frac{4+9}{6}=frac{13}{6}$$
Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком.
Полученное частное запишем в целую часть, а остаток от деления в числитель.
$$frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$$
Ответ. 1) $frac{1}{4}+frac{1}{6}=frac{5}{12}$ ;
2) $frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$
Читать дальше: что такое произведение чисел.