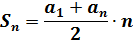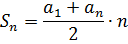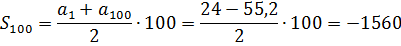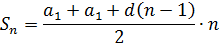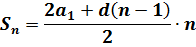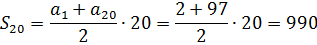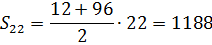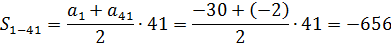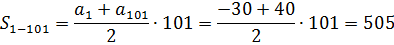Как найти сумму всех элементов последовательности

Download Article

An arithmetic sequence is a series of numbers in which each term increases by a constant amount. To sum the numbers in an arithmetic sequence, you can manually add up all of the numbers. This is impractical, however, when the sequence contains a large amount of numbers. Instead, you can quickly find the sum of any arithmetic sequence by multiplying the average of the first and last term by the number of terms in the sequence.

1
Make sure you have an arithmetic sequence. An arithmetic sequence is an ordered series of numbers, in which the change in numbers is constant.^[1] This method only works if your set of numbers is an arithmetic sequence.
- To determine whether you have an arithmetic sequence, find the difference between the first few and the last few numbers. Ensure that the difference is always the same.
- For example, the series 10, 15, 20, 25, 30 is an arithmetic sequence, because the difference between each term is constant (5).
2
Identify the number of terms in your sequence. Each number is a term. If there are only a few terms listed, you can count them. Otherwise, if you know the first term, last term, and common difference (the difference between each term) you can use a formula to find the number of terms. Let this number be represented by the variable .
- For example, if you are calculating the sum of the sequence 10, 15, 20, 25, 30, , since there are 5 terms in the sequence.
Advertisement
3

Identify the first and last terms in the sequence. You need to know both of these numbers in order to calculate the sum of the arithmetic sequence. Often the first numbers will be 1, but not always. Let the variable $a_{{1}}$ equal the first term in the sequence, and $a_{{n}}$ equal the last term in the sequence.

1
Set up the formula for finding the sum of an arithmetic sequence. The formula is $S_{{n}}=n({frac {a_{{1}}+a_{{n}}}{2}})$ , where $S_{{n}}$ equals the sum of the sequence.^[2]
- Note that this formula is indicating that the sum of the arithmetic sequence is equal to the average of the first and last term, multiplied by the number of terms.^[3]
2
3

Calculate the average of the first and second term. To do this, add the two numbers, and divide by 2.^[5]
4

Multiply the average by the number of terms in the series. This will give you the sum of the arithmetic sequence.^[6]

1

Find the sum of numbers between 1 and 500. Consider all consecutive integers.
2

Find the sum of the described arithmetic sequence. The first term in the sequence is 3. The last term in the sequence is 24. The common difference is 7.
3

Solve the following problem. Mara saves 5 dollars the first week of the year. For the rest of the year, she increases her weekly savings by 5 dollars every week. How much money does Mara save by the end of the year?

Add New Question

Question

How can I determine whether the sequence is arithmetic?

A sequence is arithmetic if there is a constant difference between any term and the terms immediately before and after it: for example, if each term is 7 more than the term before it.
Question

Why do I need to divide by 2?

You do this so that you can find the average of the two numbers. For example, if you were finding the average between 7, 12, and 8, you would add them up (27) and divide them by the number of values you have. In this case, you have three numbers, so you’d divide 27 by 3 to get an average of 9. In the case of the sum of an arithmetic sequence, you have two numbers that you are finding the average of, so you divide it by the amount of values you have, which is two.
Question

What is the sum of all integers from 1 to 50?

LyKaxandra Caimoy

Community Answer

You will find that 1 + 50 = 2 + 49 = 3 + 48 (and so on). Multiply the sum, which is 51, by half of the last term. You have the equation 51 × 25 = 1275. The sum is therefore 1275.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To find the sum of an arithmetic sequence, start by identifying the first and last number in the sequence. Then, add those numbers together and divide the sum by 2. Finally, multiply that number by the total number of terms in the sequence to find the sum. To see example problems, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 604,662 times.

Did this article help you?

Источник

Задача «Сумма последовательности»

Условие

Определите сумму всех элементов последовательности, завершающейся числом 0. В этой и во всех следующих задачах числа, следующие за первым нулем, учитывать не нужно.

Решение задачи от разработчиков на Python:

Другое решение задачи на Python:

Смотреть видео — Задача «Сумма последовательности» решение на Python

Делитесь с друзьями ссылкой на ответ и задавайте вопросы в комментариях! 👇

Посмотреть все комментарии

у меня показывает что неправильно так что 1 звезда

wpDiscuz

Оставьте комментарий! Напишите, что думаете по поводу статьи.x

Источник

Последовательность — высокоупорядоченный числовой набор, образованный по заданному закону. Термин «ряд» обозначает результат сложения членов соответствующей ему последовательности. Для различных числовых последовательностей мы можем найти сумму всех ее членов или общее число элементов до заданного предела.

Последовательность

Под этим термином понимается заданный набор элементов числового пространства. Каждый математический объект задается определенной формулой для определения общего элемента последовательности, а для большинства конечных числовых наборов существуют простые формулы определения их суммы. Наша программа представляет собой сборник из 8 онлайн-калькуляторов, созданных для вычисления сумм наиболее популярных числовых наборов. Начнем с самого простого — натурального ряда, которым мы пользуемся в повседневной жизни для пересчета предметов.

Натуральная последовательность

Когда школьники изучают числа, они первым делом учатся считать предметы, например, яблоки. Натуральные числа естественным образом возникают при счете предметов, и каждый ребенок знает, что 2 яблока — это всегда 2 яблока, не больше и не меньше. Натуральный ряд задается простым законом, который выглядит как n. Формула гласит, что n-ный член числового набора равен n: первый — 1, второй — 2, четыреста пятьдесят первый — 451 и так далее. Результат суммирования n первых натуральных чисел, то есть начинающихся от 1, определяется по простой формуле:

∑ = 0,5 n × (n+1).

Благодаря этому выражению легко рассчитать конечную сумму натурального ряда от 1 до n. Очевидно, что натуральная последовательность стремится в бесконечность, поэтому, чем больше n, тем больше конечный результат.

Расчет суммы натурального ряда

Для вычислений вам потребуется выбрать в меню калькулятора формулу натурального ряда n и ввести количество членов последовательности. Давайте вычислим сумму натурального ряда от 1 до 15. Указав n = 15, вы получите результат в виде самой последовательности:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

и суммы натурального ряда, равной 120.

Легко проверить корректность вычислений при помощи выше приведенной формулы. Для нашего примера результат сложения будет равен 0,5 × 15 × 16 = 0,5 × 240 = 120. Все верно.

Последовательность квадратов

Квадратичная последовательность образуется из натуральной, путем возведения каждого члена в квадрат. Ряд квадратов формируется по закону n², следовательно, n-ный член последовательности будет равняться n²: первый — 1, второй — 2² = 4, третий — 3² = 9 и так далее. Результат суммирования начальных n элементов квадратичной последовательности вычисляется по закону:

∑ = (n × (n+1) × (2n+1)) / 6.

При помощи этой формулы вы легко можете высчитать сумму квадратов от 1 до n для сколько угодно большого n. Очевидно, что эта последовательность также бесконечна и с ростом n будет расти и общее значение числового набора.

Расчет суммы квадратного ряда

В этом случае вам потребуется выбрать в меню программы закон квадратной последовательности n², после чего выбрать значение n. Давайте рассчитаем сумму первых десяти членов последовательности (n= 10). Программа выдаст саму последовательность:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100

а также сумму, равную 385.

Кубический ряд

Ряд кубов представляет собой последовательность натуральных чисел, возведенных в куб. Закон образования общего элемента последовательности записывается как n³. Таким образом, первый член ряда равен 1³ = 1, второй — 2³ = 8, третий — 3³ = 27 и так далее. Сумма первых n элементов кубического ряда определяется по формуле:

∑ = (0,5 n × (n+1))²

Как и в предыдущих случаях, элементы числового пространства стремятся в бесконечность, и чем больше количество слагаемых, тем больше результат суммирования.

Расчет суммы кубического ряда

Для начала выберите в меню калькулятора закон кубического ряда n³ и задайте любое значение n. Давайте определим сумму ряда из 13 членов. Калькулятор выдаст нам результат в виде последовательности:

1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197

и суммы соответствующего ей ряда, равного 8281.

Последовательность нечетных чисел

Множество натуральных чисел содержит подмножество нечетных элементов, то есть тех, которые не делятся на 2 без остатка. Последовательность нечетных чисел определяется выражением 2n — 1. Согласно закону, первый член последовательности будет равен 2×1 − 1 = 1, второй — 2×2 − 1 = 3, третий — 2×3 − 1 = 5 и так далее. Сумма начальных n элементов нечетного ряда вычисляется по простой формуле:

∑ = n².

Рассмотрим пример.

Вычисление суммы нечетных чисел

Сначала выберете в меню программы закон образования нечетного ряда 2n−1, после чего введите n. Давайте узнаем первые 12 членов нечетной ряда и его сумму. Калькулятор мгновенно выдаст результат в виде набора чисел:

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23,

а также суммы нечетного ряда, который равен 144. И действительно, 12² = 144. Все верно.

Прямоугольные числа

Прямоугольные числа относятся к классу фигурных чисел, которые представляют собой класс числовых элементов, необходимых для построения геометрических фигур и тел. К примеру, чтобы построить треугольник необходимо 3, 6 или 10 точек, квадрат — 4, 9 или 16 точек, а для выкладывания тетраэдра потребуется 4, 10 или 20 шаров или кубов. Прямоугольники легко построить при помощи двух последовательных чисел, например, 1 и 2, 7 и 8, 56 и 57. Прямоугольные же числа выражаются в виде произведения двух последовательных натуральных чисел. Формула для общего члена ряда выглядит какn × (n+1). Первые десять элементов такого числового набора выглядят как:

2, 6, 12, 20, 30, 42, 56, 72, 90, 110…

С увеличением n растет и значение прямоугольных чисел, следовательно, сумма такого ряда также будет расти.

Обратная последовательность

Для прямоугольных чисел существует обратная последовательность, определяемая формулой 1 / (n × (n+1)). Числовой набор трансформируется в набор дробей и выглядит как:

1/2 , 1/6, 1/12, 1/20, 1/30, 1/42, 1/56, 1/72, 1/90, 1/110…

Сумма ряда дробей определяется по формуле:

∑ = 1 — 1/(n+1).

Очевидно, что при увеличении количества элементов ряда значение дроби 1/(n+1) стремится к нулю, а результат сложения приближается к единице. Рассмотрим примеры.

Сумма прямоугольного и обратного ему ряда

Давайте рассчитаем значение прямоугольной последовательности для n = 20. Для этого выберете в меню онлайн-калькулятора закон задания общего члена числового набора n × (n+1) и укажите n. Программа выдаст мгновенный результат в виде 3080. Для вычислений обратного ряда измените закон на 1 / (n × (n+1)). Сумма обратных числовых элементов будет равна 0,952.

Ряд произведений трех последовательных чисел

Прямоугольный числовой набор можно изменить, добавив к нему еще один последовательный множитель. Следовательно, формула для вычисления n-ного члена набора преобразится в n × (n+1) × (n+2). Согласно этой формуле элементы ряда образуются в виде произведения трех последовательных чисел, например, 1 × 2 × 3 или 10 × 11 × 12. Первые десять элементов такого ряда выглядят как:

6, 24, 60, 120, 210, 336, 504, 720, 990, 1320

Это быстрорастущий числовой набор, а сумма соответствующего ряда при росте n уходит в бесконечность.

Обратная последовательность

Как и в предыдущем случае, мы можем обратить формулу n-ного члена и получить выражение 1 / (n × (n+1) × (n+2)). Тогда набор целых значений преобразится в ряд дробей, в знаменателе которых будут стоять произведения трех последовательных чисел. Начало такого набора имеет следующий вид:

1/6, 1/24, 1/60, 1/120, 1/210, 1/336…

Сумма соответствующего ряда определяется по формуле:

∑ = 0,5 × (0,5 — 1 / (n+1) × (n+2)).

Очевидно, что при росте количества элементов дробь 1 / ((n+1) × (n+2)) стремится к нулю, а сумма ряда приближается к значению 0,5 × 0,5 = 0,25. Рассмотрим примеры.

Ряд произведений трех последовательных чисел и обратный ему

Для работы с этим набором требуется выбрать закон определения общего элемента n × (n+1) × (n+2) и задать n, к примеру, 100. Калькулятор выдаст вам саму последовательность, а также значение результата сложения сотни чисел, равный 26 527 650. Если выбрать обратный закон 1 / (n × (n+1) × (n+2)), сумма ряда из 100 членов будет равна 0,250.

Заключение

Сборник калькуляторов позволяет рассчитать сумму восьми наиболее популярных последовательностей. Пользуйтесь нашим сервисом для решения учебных заданий по математике или программированию.

Источник

Здравствуйте.

Начал изучать питон, иногда нападают жуткие тупняки. Ряд задач с этим циклом, вроде, решен и понятен, тут не могу никак понять, как формулировать решение.

Определите сумму всех элементов последовательности, завершающейся числом 0. В этой и во всех следующих задачах числа, следующие за первым нулем, учитывать не нужно.
def по этому курсу еще не было, не знаю, что это. Т.е. задачу нужно решить, исходя из того, что материал был по

Занятие 1. Ввод-вывод, арифметические операции

Занятие 2. Условная инструкция

Занятие 3. Операции с целыми и вещественными числами

Занятие 4. Цикл for

Занятие 5. Строки

Занятие 6. Цикл while

Вот просто чего не понял.

i = 0
while int(input()) > 0:
    i += int(input())
print(i)

Но в этом случае суммируются элементы без первого, т.е. в том порядке, как входят, если делаю

i = 0
a = 0
while int(input()) >0:
    i += 1 
for j in range(0:a):
    a += int(input())
print(a)

то говорит, что закончились числа для ввода. Т.е. в целом я понимаю, что вообще что-то не то делаю.

Источник

Сумма n первых членов арифметической прогрессии — штука довольно простая и понятная. Как по смыслу, так и по формуле. Но задания на эту тему встречаются самые разные. От примитивных до вполне себе серьёзных. Имеет смысл разобраться, правда?)

Очень часто во всевозможных задачках на арифметическую прогрессию требуется найти сумму некоторого количества её членов. Если этих самых членов мало, то складывать, конечно, и безо всяких формул можно. А вот если много, то сложение “вручную” уже напрягает, да… В этих случаях и выручает формула.)

Итак, вот она, формула суммы n первых членов арифметической прогрессии:

Для начала, как водится, разберёмся с названием и со смыслом формулы суммы. А потом и задачки порешаем. В своё удовольствие.)

Ключевыми словами в названии формулы являются слова “n первых членов”. Эти слова всего лишь означают, что берётся последовательность

(a_n): a₁, a₂, a₃, a₄, a₅, …, a_n

и аккуратно суммируются (т.е. складываются) все её члены. С первого члена (a₁) по последний (a_n). Причём складываются именно все члены подряд, без пропусков! Это важно.

Смысл формулы суммы прост до неприличия. Эта формула позволяет легко и быстро находить сумму любого количества членов любой арифметической прогрессии с первого по n-й. Не складывая все числа по порядочку.)

А теперь, традиционно, разбираемся со всеми буковками и символами, сидящими в формуле. Это очень многое прояснит.

S_n — та самая сумма n первых членов, которую мы ищем. Результат сложения всех членов арифметической прогрессии с первого по последний. Ещё раз напоминаю, что сумма считается именно (и только) с первого члена. Дело всё в том, что частенько встречаются задачки типа: “найти сумму пятого и восьмого членов”. Или: “найти сумму всех членов с десятого по тридцатый”. В таких задачках прямое применение формулы суммы не катит, да…)

a₁ — первый член прогрессии. Здесь, думаю, комментарии излишни.)

a_n — последний член прогрессии. Под номером n. Да, не очень привычное название, но для работы с суммой — очень удобное.) Что это такое — об этом ниже.

n — номер последнего члена.

Вот и всё. Все обозначения расшифрованы. Осталось лишь разобраться, что же такое последний член.

Для начала задам такой хитрый вопрос: как вы думаете, какой член будет последним, если нам дана бесконечная арифметическая прогрессия? Ответ очевиден: никакой.) Какой бы член a_n и с каким бы номером n мы ни взяли, для него всегда найдётся следующий, (n+1)-й член.

Поэтому говорить о конкретной конечной сумме для бесконечной арифметической прогрессии (с бесконечным числом членов) попросту нету никакого смысла. Не существует такой суммы. Бесконечная она… Кстати, в отличие от геометрической прогрессии, сумму бесконечного числа членов которой, в некоторых случаях, найти… можно.) Но о геометрической прогрессии и о такой интересной бесконечной сумме — в соответствующих уроках.)

Короче говоря, когда мы имеем дело с суммой арифметической прогрессии, то нам всегда требуется некоторый конечный член. Тот член, на котором следует остановиться. Которым следует ограничиться. Чтобы не складывать все члены до бесконечности.) Вот именно этот граничный член a_n — и есть последний член прогрессии. И все дела.)

Номер этого самого последнего члена (т.е. n) определяется исключительно заданием. Либо он указан в условии прямым текстом, либо же косвенно, в зашифрованном виде.) А составители заданий, порой, шифруют эту ценную информацию (последний член и номер последнего члена) с безграничной фантазией, да…) Для грамотной расшифровки надо, во-первых, понимать смысл арифметической прогрессии, во-вторых, не бояться и думать головой и… внимательно читать задание.) Иначе — никак. Чуть ниже, в конкретных задачках мы все эти секреты пораскрываем.

Как выводится формула суммы?

Вывод формулы суммы n первых членов арифметической прогрессии хоть и прост, но весьма оригинален по сравнению с выводом формулы n-го члена.) Для этого придётся нам запустить машину времени и плавно переместиться… нет, не в будущее.) Мы переместимся в Германию конца XVIII века. Жил-был в то время великий немецкий математик Карл Фридрих Гаусс. Король математики! Одарённость его просто не знала границ!

Так вот, согласно легенде, когда Гаусс был ещё школьником, учитель дал детям задание. Скучно им, видите ли, было на уроке… А именно — посчитать сумму всех натуральных чисел от 1 до 100. Для всего класса это задание и впрямь оказалось работёнкой не из лёгких. На целый урок.) Но… только не для юного вундеркинда Гаусса с его нестандартным мышлением.) Как он выкрутился? Он заметил, что попарные суммы чисел с противоположных концов всегда одинаковы: 1+100=101, 2+99=101, 3+98=101 и так далее.) Всего таких попарных сумм, очевидно, будет 50. Рассуждая таким образом, Гаусс, к удивлению учителя, дал верный ответ за полминуты:

1+2+3+…+100 = 50·101 = 5050

И всё! Здорово, правда?)

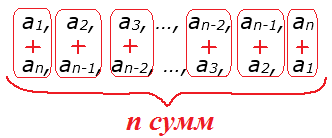
Для вывода нашей формулы, мы поступим так же мудро, как и Гаусс. По такому же принципу. Смотрите, сейчас интересно будет! Запишем сначала нашу прогрессию (a_n) в виде прямой последовательности:

a₁, a₂, a₃, …, a_n_-2, a_n_-1, a_n.

А теперь запишем эту же прогрессию, но в виде обратной последовательности. Член a_n будет на первом месте, а a₁ — на последнем.

Вот так:

a_n, a_n-1, a_n-2, …, a₃, a₂, a₁.

А теперь (внимание!) берём и попарно складываем между собой члены обеих последовательностей — прямой и обратной.

Вот так:

Получаем ровно “n” попарных сумм. Как вы думаете, что в итоге мы получим, если сложим между собой все эти n сумм? Очевидно, нужную нам сумму n первых членов арифметической прогрессии S_n, но… удвоенную. Что правда то правда: сначала мы складываем все члены с 1-го по n-й, а затем — наоборот. И, если сложить оба результата, то получим, как раз, удвоенную сумму членов с 1-го по n-й. То есть, 2S_n.

Можно смело записать:

2S_n = (а₁+a_n)+(a₂+a_n-1)+(a₃+a_n-2)+…+(a_n-2+a₃)+(a_n-1+a₂)+(a_n+a₁)

А теперь разберёмся со всеми “лишними” скобочками и буковками. Сейчас будет ещё интереснее!

Как вы уже, возможно, заметили, скобки, стоящие в сумме на одинаковых местах с начала и с конца, совершенно одинаковые! Только слагаемые переставлены местами.) Первые и последние скобки мы трогать не будем. Посмотрим, что получается во вторых и предпоследних скобках. Для этого представим a₂ как a₁+d, а a_n_-1 представим как a_n–d. Прямо по смыслу арифметической прогрессии:

a₂ = a₁ + d

a_n_-1 = a_n — d

Подставим это добро во вторую (и предпоследнюю) скобки. Что получим:

(a₂+a_n-1) = (a_n-1+a₂) = a₁ + d + a_n — d = a₁ + a_n

Рассуждая аналогичным образом, для третьих скобок с начала и с конца мы получим:

(a₃+a_n-2) = (a_n-2+a₃) = a₁ + 2d + a_n — 2d = a₁ + a_n

Ну как? Улавливаете идею? Да! Каждая из попарных сумм членов, стоящих на одинаковых местах с начала и с конца в нашей общей сумме 2S_n, всегда будет одна и та же. И равна a₁ + a_n. То есть, сумме первого и последнего членов. А всего таких попарных сумм у нас сколько? Правильно, “n” штук! Столько же, сколько и членов в прогрессии, да…) Не зря же я картинки рисую иногда.

Вот и пишем:

2S_n = (а₁+a_n)·n

Выражая из этого равенства S_n, получаем требуемую формулу:

Вот и всё.)

Ну что, со смыслом формулы разобрались. С выводом — тоже. Я вижу, вам уже не терпится начать решать задачки. Что ж, поехали!

Решение задач на сумму арифметической прогрессии.

Начнём с несложной задачки. Безо всяких фокусов.)

1. Дана арифметическая прогрессия:

24; 23,2; 22,4; 21,6; …

Найти сумму первых ста её членов.

Прогрессия нам задана в виде последовательности. Можно, конечно, уловить закономерность, продлить эту последовательность, выписать первые сто её членов, сложить их да посчитать, но… как-то тупо и долго получается, не находите? Но мы же с вами народ учёный. Формулу суммы знаем.) Вот и запустим её в дело.

Сразу пишем формулу суммы:

А теперь смотрим на формулу и соображаем, какие элементы формулы нам даны, а чего не хватает.

Первый член a₁ известен? Да! Это 24. А последний член a_n? Пока нет… Но… зато нам известен его номер n! Это 100 (n = 100). В задании прямым текстом сказано: найти сумму первых ста членов. Стало быть, последним членом прогрессии будет сотый член a₁₀₀. И как его отыскать? Считать и выписывать сто членов? Зачем!?) Ведь мы же не слепые, глазками последовательность видим, а смысл арифметической прогрессии – понимаем.

Стало быть, можем посчитать разность прогрессии и затем найти интересующий нас сотый член по формуле n-го члена:

a_n = a₁ + (n-1)·d

Вот и трудимся. Для разности d берём любой член последовательности (кроме первого) и отнимаем предыдущий.

ЕЩЁ РАЗ ВНИМАНИЕ!!! Не просто считаем разницу между большим и меньшим соседними членами (типа 23,2-22,4), а именно от выбранного члена (23,2) отнимаем предыдущий (24)!

Почему ругаюсь? Потому что это весьма и весьма распространённые грабли, на которые наступает значительная часть учеников, теряя драгоценные баллы на контрольных и экзаменах и получая заслуженные минусы. Особенно часто этот косяк встречается в убывающих прогрессиях и в прогрессиях с отрицательными членами.

Вот и считаем правильно. Например, так:

d = 23,2 — 24 = -0,8

Вот так. Разность — отрицательна. Прогрессия — убывает. Как и в задании.)

Считаем сотый член по формуле n-го члена:

a₁₀₀ = a₁ + (-0,8)·(100-1) = 24-0,8·99 = -55,2

Есть. Мы выяснили все интересующие нас параметры в формуле суммы. Осталось подставить их да посчитать:

Ответ: -1560

Кстати сказать, если подставить в формулу суммы вместо a_n его выражение через формулу n-го члена, то получим:

Или, если привести подобные в числителе:

Эта формула — тоже формула суммы n первых членов арифметической прогрессии. Только записанная в другом виде — через первый член и разность прогрессии. В некоторых задачках эта модифицированная формула здорово выручает, да.) Имеет смысл запомнить. Или, в случае чего, уметь вывести, как здесь. Ведь формулу n-го члена в любом случае надо помнить.)

Следующая задачка. На основе реального варианта ОГЭ:

2. Арифметическая прогрессия задана условием: a_n = -3 + 5n. Найдите сумму первых двадцати её членов.

Хорошая задачка. Лёгкая.) Настолько лёгкая, что народ тут же косячит… НЕ НАДО писать сразу, что первый член — минус три! Это фатальное заблуждение, да… Ибо прогрессия нам задана видоизменённой формулой n-го члена. Как работать с такой формулой, подробно рассказано по ссылке. Кто не в курсе — кликаем и читаем.) Кто в курсе, делаем всё как положено. А именно — подставляем в формулу вместо n единичку и считаем:

a₁ = -3+5·1 = 2

Вот так вот. Первый член — двойка, а не минус три…

Что там нам ещё нужно для суммы? Последний член и номер последнего члена? Пожалуйста! Нас спрашивают про сумму двадцати первых членов. Стало быть, в качестве последнего члена у нас будет выступать a₂₀, а номером n последнего члена будет, знамо дело, двадцатка.

Вот и считаем a₂₀ подставляя n = 20 в формулу n-го члена:

a₂₀ = -3+5·20 = 97

А теперь уже считаем нужную нам сумму:

Ответ: 990

А теперь задачка более творческая. 🙂

3. Найти сумму всех натуральных двузначных чисел, кратных четырём.

Во! Ни первого члена нет, ни последнего, ни номера n, ни прогрессии вообще… Что делать?!

Что-что… Головой думать, да.) И вытаскивать из условия задачи все элементы формулы суммы арифметической прогрессии. Ибо здесь, как раз, тот самый случай, когда ключевые параметры прогрессии в условии ловко зашифрованы.

Вот и начинаем расшифровку. Что такое натуральные числа — знаем. То есть, целые положительные. Что такое двузначные числа — тоже знаем. Ну, те, что из двух циферок состоят.) Какое же двузначное число будет первым? 10, ясное дело.) А последнее двузначное число? Очевидно, 99. За ним уже трёхзначные числа пойдут…

Идём дальше. Кратные четырём… Это что значит? Это значит, делящиеся на четыре нацело! Десятка делится на четыре? Не делится! 11 — тоже не делится. 12… делится! Если ещё немного подумать, то можно сообразить, что последнее такое число будет 96. Отлично! Очень многое проясняется! Теперь уже можно записать последовательность по условию задачки:

12, 16, 20, …, 92, 96.

Будет эта последовательность арифметической прогрессией? А как же! Каждый член отличается от предыдущего строго на четвёрку. Если к члену прибавить, скажем, 3 или 5, то новое число уже не поделится нацело на 4.

Сразу же можем и разность прогрессии посчитать:

d = 4

Пригодится.)

Ну вот. Теперь мы уже с вами знаем кое-какие параметры прогрессии:

a₁ = 12

d = 4

a_n = 96

А каков будет номер n последнего члена 96? А вот тут два пути решения. Первый путь — для сверхтрудолюбивых, но некультурных. Можно расписать всю прогрессию да посчитать пальчиком количество членов. А второй путь — для ленивых, зато культурных.) Я отношусь к ленивым, поэтому выберу второе. А именно — распишу последний член прогрессии (т.е. 96) по формуле n-го члена, подставляя уже известные нам данные:

96 = a₁ + d(n-1)

96 = 12 + 4(n-1)

4(n-1) = 84

n-1 = 21

n = 22

Вот так. Значит, число 96 — это двадцать второй член нашей прогрессии.

А теперь смотрим на формулу суммы:

Смотрим и… прыгаем от радости!) Ибо мы вытащили из условия задачи все необходимые данные для подсчёта требуемой суммы. Незаметно для себя. Вот они:

a₁ = 12

a₂₂ = 96

n = 22

S_n = S₂₂

Осталось лишь подставить да посчитать:

Ответ: 1188

Рассмотрим теперь ещё один тип популярных задачек. На первый взгляд, всё очень похоже, да не совсем…)

4. Дана арифметическая прогрессия:

-30; -29,3; -28,6; …

Найдите сумму членов с 42-го по 101-й.

И как вам? Прямое применение формулы суммы разочарует. Напоминаю, что формула считает сумму только с первого члена. А в нашей задаче надо считать сумму с сорок второго… Тупик? Ну да, щас!)

Можно, конечно, расписать всю прогрессию до 101-го члена и посчитать столбиком на бумажке все члены с 42-го по 101-й. Но возьмутся за это увлекательное занятие только откровенные мазохисты, да…)

Мы же поступим просто и элегантно.) А именно – разобьём нашу прогрессию на две части. Первая часть будет с первого члена по 41-й. А вторая часть — с 42-го члена по 101-й. Ясно, что если мы посчитаем сумму членов первой части S_1-41 и сложим её с суммой членов второй части S_42-101, то получим сумму членов прогрессии с первого по сто первый S_1-101.

В математической записи:

S_1-41 + S_42-101 = S_1-101

Из этого равенства видно, что найти нужную нам сумму S_42-101 можно простым вычитанием:

S_42-101 = S_1-101 – S_1-41

Вот теперь всё встало на свои места! Обе суммы справа считаются с первого члена. Стало быть, к ним уже применима наша стандартная формула суммы. Ну что, начнём?

Первым делом вытаскиваем из условия задачи ключевые параметры прогрессии:

a₁ = -30

d = 0,7

Кроме того, для расчёта сумм S_1-41 и S_1-101 нам понадобятся 41-й и 101-й члены. Считаем их по формуле n-го члена:

a₄₁ = a₁+40d = -30+40·0,7 = -30+28 = -2

a₁₀₁ = a₁+100d = -30+100·0,7 = -30+70 = 40

Теперь считаем суммы S_1-41 и S_1-101 по формуле:

Остались сущие пустяки. От суммы 101 члена отнять сумму 41 члена:

S_42-101 = S_1-101 – S_1-41 = 505 — (-656) = 1161

Ответ: 1161

Вот и всё.) Обратите внимание на одну очень полезную фишку. Вместо прямого расчёта того что нам нужно (S_42-101), мы вычислили то, что, казалось бы, совершенно не нужно (S_1-41). А уже потом посчитали и S_42-101, отбросив от полного результата ненужное. В злых задачках такой искусный манёвр очень часто спасает.)

В этом небольшом уроке мы рассмотрели задачки, для успешного решения которых достаточно понимать смысл суммы n первых членов арифметической. Ну и парочку формул знать надо, да.)

Подытожим наш урок практическим советом:

При решении любой задачи на сумму членов арифметической прогрессии настоятельно рекомендую выписать две ключевые формулы.

Формулу n-го члена:

a_n = a₁ + (n-1)·d

Формулу суммы n первых членов арифметической прогрессии:

Эти две формулы обязательно подскажут, что именно надо делать, в каком направлении двигаться, чтобы справиться с задачей. Проверено! Помогает.

А теперь решаем самостоятельно.

1. Найти сумму всех натуральных двузначных чисел, которые не делятся нацело на четыре.

Что, круто, да?) Подсказка спрятана в комментарии к последней разобранной задаче №4. Ну и результат предпоследней задачки №3 поможет.)

2. Арифметическая прогрессия задана условиями:

a₁ = -3,1

a_n+1 = a_n+0,9

Найдите сумму первых 19 её членов.

Да-да, это рекуррентная формула, которую многие так не любят. Задачки с такой формулой мы в этом уроке не рассматривали. А чего их рассматривать? Их решать надо.) Материала этого урока вполне достаточно, чтобы справиться с заданием. Про рекуррентную формулу и как именно с ней работать можно прочитать в предыдущем уроке. Не пренебрегайте этой задачкой, такие частенько встречаются в ОГЭ!

3. Марфуша была сладкоежкой и очень любила пирожные с кремом и шоколадной глазурью. Каждое пирожное стоит 60 рублей. Накопив 2700 рублей, Марфуша решила устроить себе сладкую жизнь: в первый день купить и съесть всего одно пирожное, а в каждый последующий день покупать и съедать на одно пирожное больше. Пока не истратит всю накопленную заначку.

а) сколько пирожных в итоге купила и съела Марфуша?

б) сколько дней сладкой жизни получилось у Марфуши?

Сложно? Поможет дополнительная формула суммы из разобранной задачи №1. Ну и решение квадратных уравнений тоже надо вспомнить, да.)

Ответы (в беспорядке): 9; 95; 45; 3717.

Источник

Video

About This Article

Did this article help you?

Задача «Сумма последовательности»

Условие

Решение задачи от разработчиков на Python:

Другое решение задачи на Python:

Related Posts

Последовательность

Натуральная последовательность

Расчет суммы натурального ряда

Последовательность квадратов

Расчет суммы квадратного ряда

Кубический ряд

Расчет суммы кубического ряда

Последовательность нечетных чисел

Вычисление суммы нечетных чисел

Прямоугольные числа

Обратная последовательность

Сумма прямоугольного и обратного ему ряда

Ряд произведений трех последовательных чисел

Обратная последовательность

Ряд произведений трех последовательных чисел и обратный ему

Заключение

Добавить комментарий Отменить ответ

Video

About This Article

Did this article help you?

Задача «Сумма последовательности»

Условие

Решение задачи от разработчиков на Python:

Другое решение задачи на Python:

Related Posts

Последовательность

Натуральная последовательность

Расчет суммы натурального ряда

Последовательность квадратов

Расчет суммы квадратного ряда

Кубический ряд

Расчет суммы кубического ряда

Последовательность нечетных чисел

Вычисление суммы нечетных чисел

Прямоугольные числа

Обратная последовательность

Сумма прямоугольного и обратного ему ряда

Ряд произведений трех последовательных чисел

Обратная последовательность

Ряд произведений трех последовательных чисел и обратный ему

Заключение

Вам также может понравиться

Как составить карты хронометража

Как найти log2 cos

Принтер canon g1411 ошибка 5b00 как исправить ошибку

Добавить комментарий Отменить ответ