Ольга Копотева
Знаток
(493)
7 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
Юрий Гринькин
Знаток
(327)
6 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Панкратова Татьяна
Знаток
(260)
4 года назад
как найти сумму длин всех ребер параллелепипеда
Кариночка Ученик (158), Вопрос решён 5 лет назад
11 Нравится Ответить
ЛУЧШИЙ ОТВЕТ
Анна Храпко 7 лет назад
Знаток (276)
L=4(a+b+c)
26 Нравится Пожаловаться
16 ОТВЕТОВ
ЛИЛИЯ Шевченко 3 года назад
Ученик (103)
L=4a+4b+4c
8 Нравится Пожаловаться
Ян Серебряков 3 года назад
Ученик (136)
L=4a+4b+4
2 Нравится Пожаловаться
Артём Фризен 3 года назад
Знаток (309)
L=4(a+b+c)
2 Нравится Пожаловаться
Ольга Копотева 2 года назад
Ученик (230)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
5 Нравится Пожаловаться
Юлия Моисеева 2 года назад
Ученик (133)
L=4(a+b+c)
2 Нравится Пожаловаться
katja maslova 2 года назад
Ученик (204)
L=4(a+b+c)
1 Нравится Пожаловаться
Eekler 2 года назад
Профи (633)
L=4(a+b+c)
Нравится Пожаловаться
Яна Подосенова 2 года назад
Ученик (166)
L=4(a+b+c)
Нравится Пожаловаться
Юрий Гринькин 2 года назад
Знаток (302)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение з
Как найти сумму длин всех рёбер параллелепипеда
У вас возникло затруднение в решении геометрической задачи, связанной с параллелепипедом. Принципы решения таких задач, основанные на свойствах параллелепипеда, изложены в простой и доступной форме. Понять – значит решить. Подобные задачи больше не будут вызывать у вас затруднений.
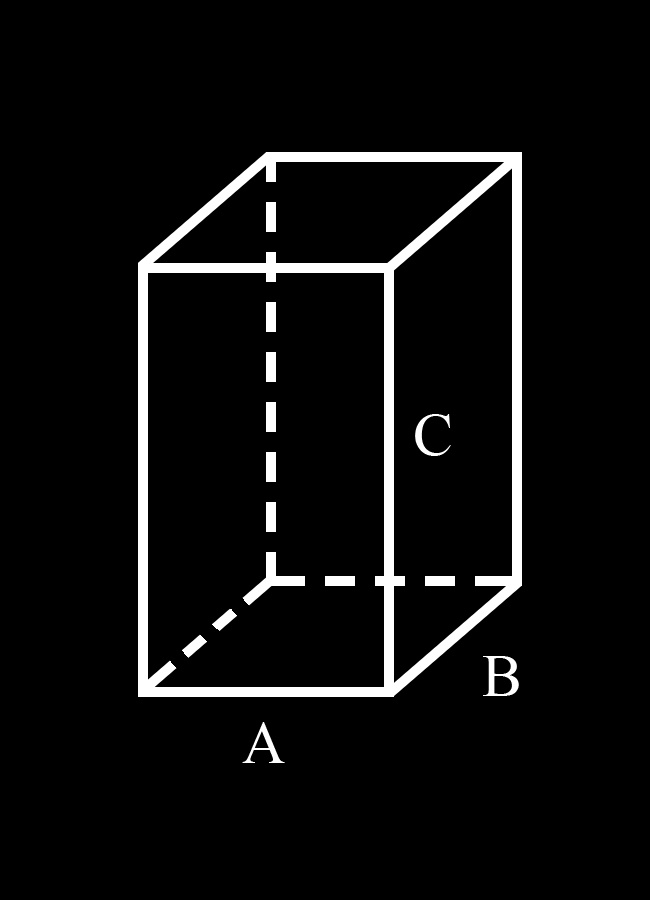
Инструкция
Для удобства введем обозначения:А и В стороны основания параллелепипеда; С – его боковая грань.
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Нужно просто хорошо усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.
Параллелепипед – это призма, основанием которой является параллелограмм.
Параллелепипед имеет 6 граней, и все они являются параллелограммами.
Противоположные грани равны и параллельны. Это важно.
Источники:
- сумма длин ребер прямоугольного параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)
Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)
Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc
У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tanα=a/d_3 =a/√(b^2+c^2 )
Вновь поступил вопрос про прямоугольный параллелепипед. И вопрос этот не простой, смотрите сами:
Рёбра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. Подскажите, как это переварить?
Вопрос, конечно, не простой — что такое прямоугольный параллелепипед, как и с чем его едят? В частности, как найти рецепт приготовления площади поверхности этого то ли фрукта, то ли овоща? Так, для начала давайте посмотрим, что это вообще такое — прямоугольный параллелепипед? Вот картинка прямоугольного параллелепипеда.
Как видите, прямоугольный параллелепипед — это, собственно, обыкновенный кирпич. Кстати, если бы Ньютону на голову упала не сфера в виде яблока, а прямоугольный параллелепипед в виде кирпича, то в школе мы вряд ли бы учили его законы. Прямоугольная комната — это тоже прямоугольный параллелепипед, который позволяет вам совершить обзорную экскурсию по его достопримечательностям прямо изнутри. Если вы хотите произвести внешний осмотр достопримечательностей сего математического чуда, тогда возьмите в руки коробку из-под обуви и можете вертеть её, сколько душе угодно.
И так, прямоугольный параллелепипед на картинке дает нам возможность увидеть вершины, ребра и диагонали. Вершины мы можем потрогать пальцем, ребра мы можем измерять, диагональ можем высчитать. Нам сейчас диагональ не нужна. Закон движения учеников в классе знаете? Если леди-учитель покидает класс, класс движется быстрее. Закон решения задач очень похож: чем меньше всякой ерунды нам нужно искать, тем проще задача.
Первая проблема, с которой мы сталкиваемся в задаче, это проблема сленга. Задача сформулирована на бытовом сленге, а все формулы и определения в математике формулируются на математическом сленге. Поэтому нам самим предстоит выполнить перевод. Приступаем к поэтапному переводу, по фразам.
«Рёбра прямоугольного параллелепипеда, выходящие из одной вершины …» — собственно, здесь говорится о тех ребрах, которые позволяют нам определить размеры прямоугольного параллелепипеда и на основании этих размеров выполнить все необходимые вычисления. На картинке это ребра a, b и c. Кто бы сомневался, что именно эти три ребра нам дадут по условию, но только не я. Ни один математик вам этого не скажет (не потому, что они этого не знают, а из боязни нарваться на очень неудобные вопросы), но если в условии задачи дать две длины параллельных ребер и одного перпендикулярного им, то нашу задачу в принципе решить будет невозможно. В прямоугольном параллелепипеде из любой вершины всегда выходит три взаимно перпендикулярных ребра. Вот по этому в нашей задаче прямо говорится об этом. Если верить Священным Писаниям разных религий, то именно из одного такого ребра сотворены все прямоугольные параллелепипеды, задачи о которых решает вся прекрасная половина человечества.
Следующая фраза «… равны 1, 2, 3» обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Тот, кто эту задачу придумал, уже сам всё измерил (или выдумал эти размеры, что в данном случае принципиального значения не имеет). Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Нам это без разницы. Как бы мы этот прямоугольный параллелепипед не крутили, площадь его поверхности всегда будет оставаться неизменной. Предыдущие поколения математиков этот факт не единожды проверили. Когда мы доберемся до решения, мы сами в этом убедимся.
Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? В каких единицах измерения? Ответ довольно прост — в любых единицах измерения длины. Англичане и американцы любят дюймы, футы, мили. Мы предпочитаем сантиметры, метры, километры. В чем измеряют длину инопланетяне? Мы вообще не знаем. Да нам эти единицы измерения и не важны. В чем бы мы не измеряли длину граней, циферки возле длин и площади будут одинаковыми. Циферки остаются, единицы измерения меняются. Вот два способа получения результата в математике.
разные числа + одинаковые единицы измерения = разный результат
одинаковые числа + разные единицы измерения = разный результат
Приблизительно, как в этом счетчике. Крутим одно колесико — меняются числа. Крутим другое колесико — меняются единицы измерения. Так устроена настоящая математика, маленький кусочек которой мы сейчас рассматриваем.
Это уже не детская математика, придуманная специально для того, чтобы мучить нас задачками. Это взрослая математика, одинаковая для всех.
В нашей задаче мы измеряем всё в абстрактных единицах измерения длины. Соответственно, полученная нами площадь будет измеряться в этих же единицах измерения, возведенных в квадрат.
Теперь нам осталось только достать из глубокого кармана шпаргалку с формулами для прямоугольного параллелепипеда и посмотреть, чего полезного для нас там имеется.
Что вообще есть в этой шпаргалке? Формула диагонали прямоугольного параллелепипеда, формула объема. Есть несколько формул для площади поверхности: полная, основания, боковая. Вот одна из этих формул нам как раз нужна. Разберемся в площадях на примере коробки для обуви. Площадь основания — это площадь донышка или крышки коробки. Площадь боковой поверхности — это боковые стеночки коробки без донышка и крышки. Полная площадь — это боковые стеночки вместе с донышком и крышкой.
Теперь смотрим в условие задачи и определяем, «чё тебе надобно, старче?». А надобно ему (ей, им) «площадь поверхности». Если уточнений типа «боковой» или «основания» нет, значит искать нужно полную площадь поверхности прямоугольного параллелепипеда. Длины трех граней у нас есть, формула тоже, можно произвести расчет. Заморачиваться с основаниями и боками нам нет смысла.
Как видим, полная площадь поверхности нашего прямоугольного параллелепипеда получилась равной 22 единицы в квадрате. Какие именно единицы? А какие вам не жалко или какие вы больше всего любите.
По просьбе учащихся добавляю картинку про сумму длин ребер прямоугольного параллелепипеда.
 |
| Сумма ребер прямоугольного параллелепипеда |
Сумму длин всех ребер параллелепипеда я обозначил через букву «P», поскольку она очень похожа на периметр прямоугольника. Кстати, в формуле длин всех ребер я этого не записал, но если мы возьмем три фигурообразующие грани прямоугольного параллелепипеда, которыми являются прямоугольники, то сумма длин всех ребер параллелепипеда будет равна сумме периметров этих прямоугольников.
Как обнаружить сумму длин всех рёбер параллелепипеда
У вас появилось затруднение в решении геометрической задачи, связанной с параллелепипедом. Тезисы решения таких задач, основанные на свойствах параллелепипеда , высказаны в примитивный и доступной форме. Осознать – значит решить. Сходственные задачи огромнее не будут вызывать у вас сложностей.

Инструкция
1. Для комфорта введем обозначения:А и В стороны основания параллелепипеда ; С – его боковая грань.
2. Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что супротив стороны А лежит равная ей сторона А. От того что противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3. То же дозволено сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4. Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда ). Ребро С единовременно является стороной 2-х соседних граней параллелепипеда . От того что противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5. Таким образом, сумма всех ребер параллелепипеда : 4А+4В+4С либо 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.Таким образом, решение задачи касательно пространственного тела неизменно дозволено свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Надобно примитивно отменно усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.Параллелепипед – это призма, основанием которой является параллелограмм. Параллелепипед имеет 6 граней, и все они являются параллелограммами. Противоположные грани равны и параллельны. Это главно.





