Как найти сумму всех ребер поверхности куба

Как найти сумму всех ребер поверхности куба

  1. Учебники
  2. 5 класс
  3. Математика 👍
  4. Мерзляк
  5. №603

ГДЗ Математика 5 класс Мерзляк, Полонский, Якир

авторы: Мерзляк, Полонский, Якир.

издательство: Вентана-Граф, 2018 г.

Посмотреть глоссарий

Математика 5 класс Мерзляк. Номер №603

  • Предыдущее
  • Следующее

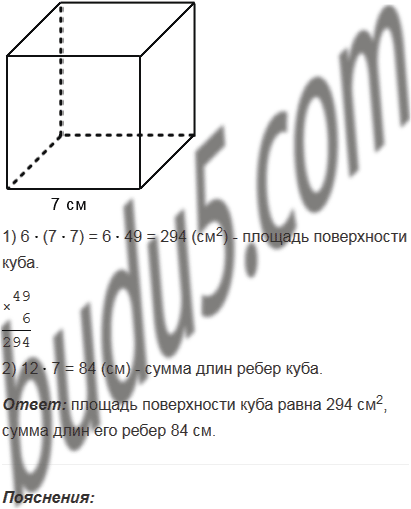
Найдите сумму длин всех ребер и площадь поверхности куба, если его ребро равно 7 см.

reshalka.com

Математика 5 класс Мерзляк. Номер №603

Решение

Получай решения и ответы с помощью нашего бота

Посмотреть калькулятор Натуральные числа

7 * 12 = 84 см сумма длин всех ребер;

S = 7 * 7 * 6 = 294

с

м

2

площадь поверхности.

  • Предыдущее
  • Следующее

Нашли ошибку?

Посмотреть глоссарий

Нашли ошибку?

Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

Источник

Номер № 603

603. Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.

Решение:

603. Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.

1) Всего 12 рёбер по 7 см.

7 • 12  = 84 (см) – сумма длин всех рёбер.

2) 6 граней по: 7 • 7 = 49 см²

49 • 6 = 294 (см²) – площадь поверхности куба

Ответ: длина всех рёбер 84 см, площадь поверхности 294 см².

<< № 602№ 603№ 604 >>

Выбрать другой номер

Если вам понравился сайт, поделитесь страничкой в соцсетях, чтобы не потерять его:

Источник

  1. Главная

  2. ГДЗ

  3. 5 класс
  4. Математика

  5. Мерзляк учебник

  6. 603

Вернуться к содержанию учебника

Страница 151

598
599
600
601
602
603
604
605
606
607
608

Вопрос

Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.

Подсказка

Вспомните:

  1. Что такое прямоугольный параллелепипед и какие у него элементы.
  2. Что называют измерениями прямоугольного параллелепипеда.
  3. Что такое куб.
  4. Как найти площадь поверхности прямоугольного параллелепипеда.

Ответ

598
599
600
601
602
603
604
605
606
607
608

598
599
600
601
602
603
604
605
606
607
608

Вернуться к содержанию учебника

Источник

ГДЗ и решебники
вип уровня

  1. ГДЗ
  2. 5 класс
  3. Математика
  4. Мерзляк
  5. Упражнение 603

Условие

Найдите сумму длин всех ребер и площадь поверхности куба, если его ребро равно 7 см.

Решение 1

Фото ответа 4 на Задание 603 из ГДЗ по Математике за 5 класс: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.

Решение 2

Фото ответа 1 на Задание 603 из ГДЗ по Математике за 5 класс: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.

Решение 3

Фото ответа 5 на Задание 603 из ГДЗ по Математике за 5 класс: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.

Решение 4

Фото ответа 3 на Задание 603 из ГДЗ по Математике за 5 класс: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.

Популярные решебники

Источник

В данной задаче нам необходимо найдите сумму длин всех ребер и площадь поверхности куба если его ребро равно 7 см.

Куб

  • Определение: Куб – это трехмерная фигура, которая состоит из шести одинаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов.
  • Элементы куба: грань (куб имеет 6 граней), ребро (их 12), вершина (8 вершин).
  • Площадь поверхности куба – это совокупность плоскостей всех граней. Площадь поверхности куба через длину ребра a можно определить, как S = 6a^2.

Вычисление площади поверхности куба

Используем формулу S = 6a^2. По условию задачи ребро куба равно 7 см. Подставляем эту величину в формулу. Получаем: S = 6a^2 = 6 * 7^2 = 6 * 49 = 294 см^2.

Сумма длин всех ребер

Куб имеет 12 ребер, поэтому, для того, чтобы узнать сумму длин всех его ребер, достаточно 12 умножить на длину одного ребра, по условию задачи это 7 см. получаем 12 * 7 = 84 см.

Ответ: S = 294 см^2; 84 см – сумма длин всех ребер куба.

Источник

Добавить комментарий