Как найти сумму всех сторон параллелепипеда прямоугольного - Сайт, где вы сможете решить свои вопросы

Как найти сумму длин всех рёбер параллелепипеда

У вас возникло затруднение в решении геометрической задачи, связанной с параллелепипедом. Принципы решения таких задач, основанные на свойствах параллелепипеда, изложены в простой и доступной форме. Понять – значит решить. Подобные задачи больше не будут вызывать у вас затруднений.

Инструкция

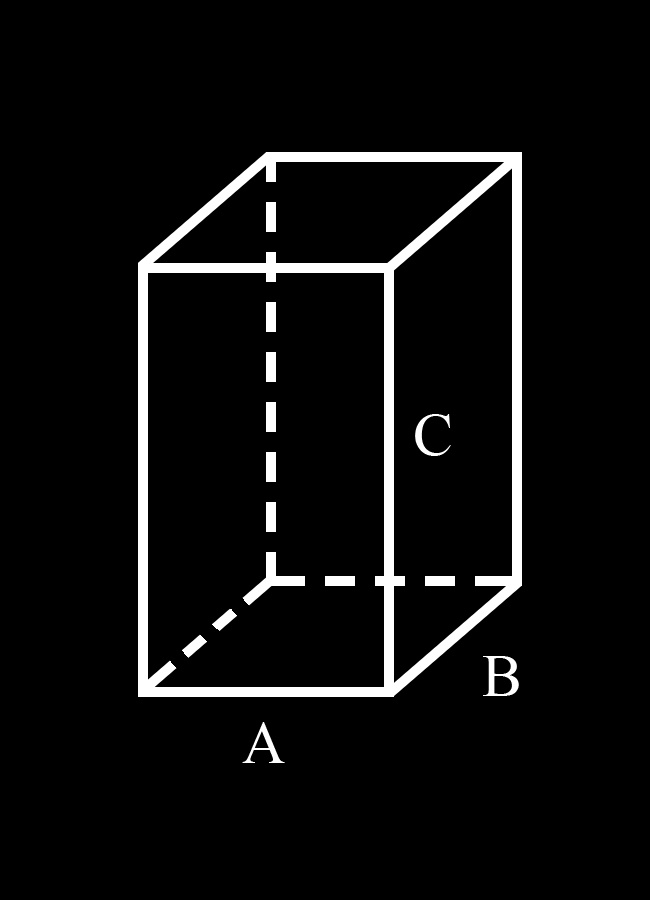
Для удобства введем обозначения:А и В стороны основания параллелепипеда; С – его боковая грань.

Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.

То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.

Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.

Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.

Полезный совет

Вычислить сумму всех ребер параллелепипеда – задача несложная. Нужно просто хорошо усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.

Параллелепипед – это призма, основанием которой является параллелограмм.

Параллелепипед имеет 6 граней, и все они являются параллелограммами.

Противоположные грани равны и параллельны. Это важно.

Источники:

сумма длин ребер прямоугольного параллелепипеда

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Ольга Копотева

Знаток

(494)

7 лет назад

1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.

Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u

Юрий Гринькин

Знаток

(327)

6 лет назад

Панкратова Татьяна

Знаток

(260)

4 года назад

как найти сумму длин всех ребер параллелепипеда
Кариночка Ученик (158), Вопрос решён 5 лет назад
11 Нравится Ответить
ЛУЧШИЙ ОТВЕТ
Анна Храпко 7 лет назад
Знаток (276)
L=4(a+b+c)
26 Нравится Пожаловаться
16 ОТВЕТОВ
ЛИЛИЯ Шевченко 3 года назад
Ученик (103)
L=4a+4b+4c
8 Нравится Пожаловаться

Ян Серебряков 3 года назад
Ученик (136)
L=4a+4b+4
2 Нравится Пожаловаться
Артём Фризен 3 года назад
Знаток (309)
L=4(a+b+c)
2 Нравится Пожаловаться
Ольга Копотева 2 года назад
Ученик (230)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.

Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
5 Нравится Пожаловаться
Юлия Моисеева 2 года назад
Ученик (133)
L=4(a+b+c)
2 Нравится Пожаловаться
katja maslova 2 года назад
Ученик (204)
L=4(a+b+c)
1 Нравится Пожаловаться
Eekler 2 года назад
Профи (633)
L=4(a+b+c)
Нравится Пожаловаться
Яна Подосенова 2 года назад
Ученик (166)
L=4(a+b+c)
Нравится Пожаловаться
Юрий Гринькин 2 года назад
Знаток (302)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение з

Источник

Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Рисунок 1

Определение

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

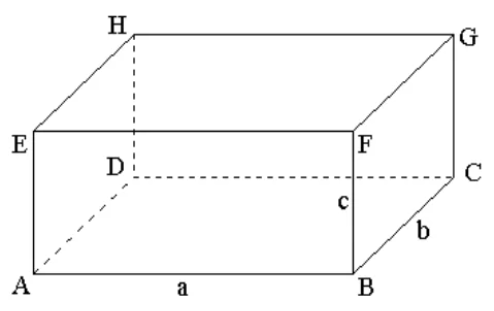
Рисунок 2

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

Длина, ширина, высота

Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

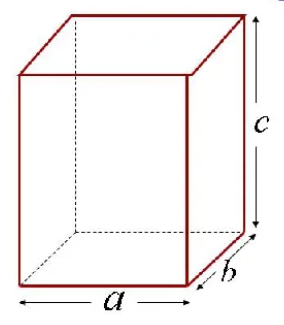
Рисунок 3

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

Куб

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

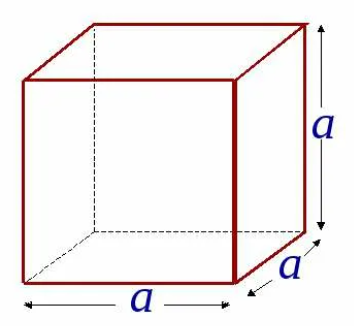
Рисунок 4

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a². Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a²

Объем прямоугольного параллелепипеда

Рисунок 5

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

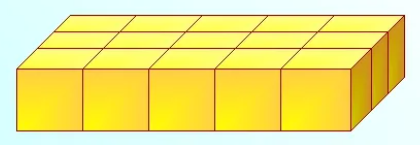
Рисунок 6

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм³; с ребром 1 см – кубическим сантиметром (см³) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

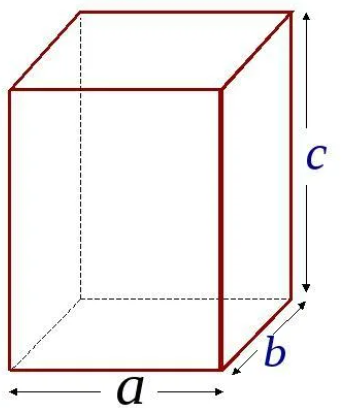
Рисунок 7

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a³

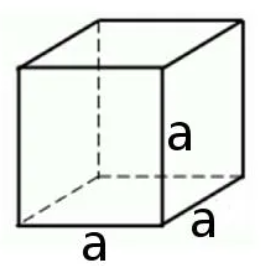
Рисунок 8

Пирамида

Рисунок 9

Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

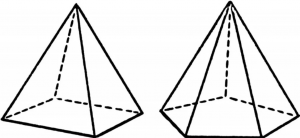
Рисунок 10

Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

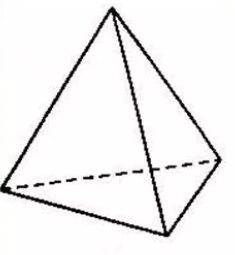
Рисунок 11

Даниил Романович | Просмотров: 993

Источник

Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)

Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)

Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc

У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )

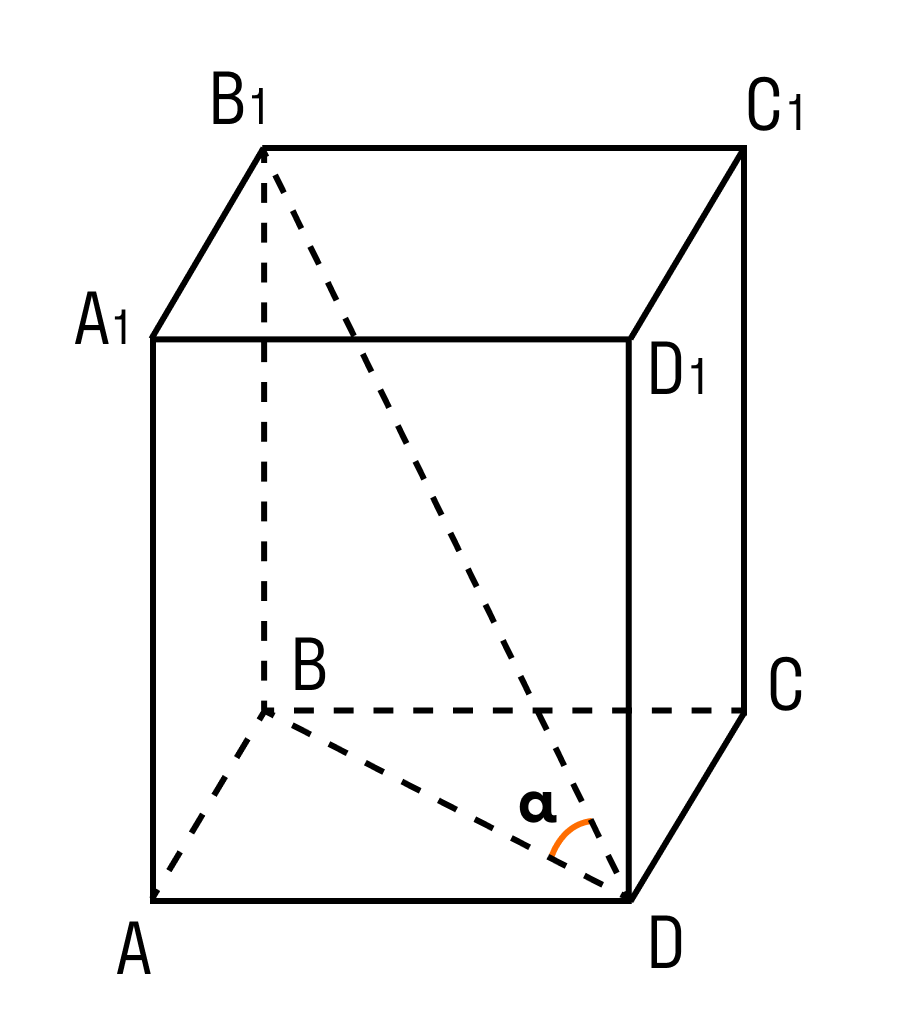
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tan⁡α=a/d_3 =a/√(b^2+c^2 )

Источник

Ниже приведены основные формулы, которые могут пригодиться при решении задач с прямоугольным параллелепипедом на ЕГЭ.

Прямоугольный параллелепипед. Формулы:

Чертеж:

Обозначения:

Формулы:

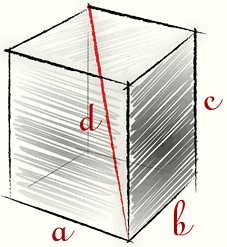V — Объем.

S_полн — площадь
полной поверхности.

d — диагональ.

a,b,c — ребра.

V = a * b * c

S_полн = 2(ab + bc + ac)

d² = a² + b² + c²

Рейтинг: 2.5 из 5.0
Проголосовало: 16

Комментарии

Всего комментариев: 0

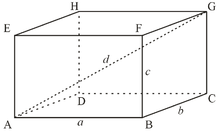
Прямоугольный параллелепипед

Прямоуго́льный параллелепи́пед (кубоид) — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником.

Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине, взаимно перпендикулярны.

Примерами тел, имеющих форму прямоугольного параллелепипеда, служат классная комната, кирпич, спичечный коробок или системный блок компьютера.

Длины трёх рёбер прямоугольного параллелепипеда, принадлежащих одной вершине, иногда называют измерениями. Например, распространённый спичечный коробок имеет измерения 15, 35, 50 мм.

Правильным или квадратным параллелепипедом называют параллелепипед, у которого два измерения равны, у такого параллелепипеда две (из шести) противолежащие грани представляют собой квадраты.

Объём прямоугольного параллелепипеда можно найти по формуле:

где — его измерения.

Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:

соответственно, длина диагонали равна:

Площадь поверхности прямоугольного параллелепипеда равна

Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба — равные квадраты.

См. также[править | править код]

Совершенный кубоид

Ссылки[править | править код]

uztest.ru Прямоугольный параллелепипед
Прямоугольный параллелепипед, учебный фильм

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

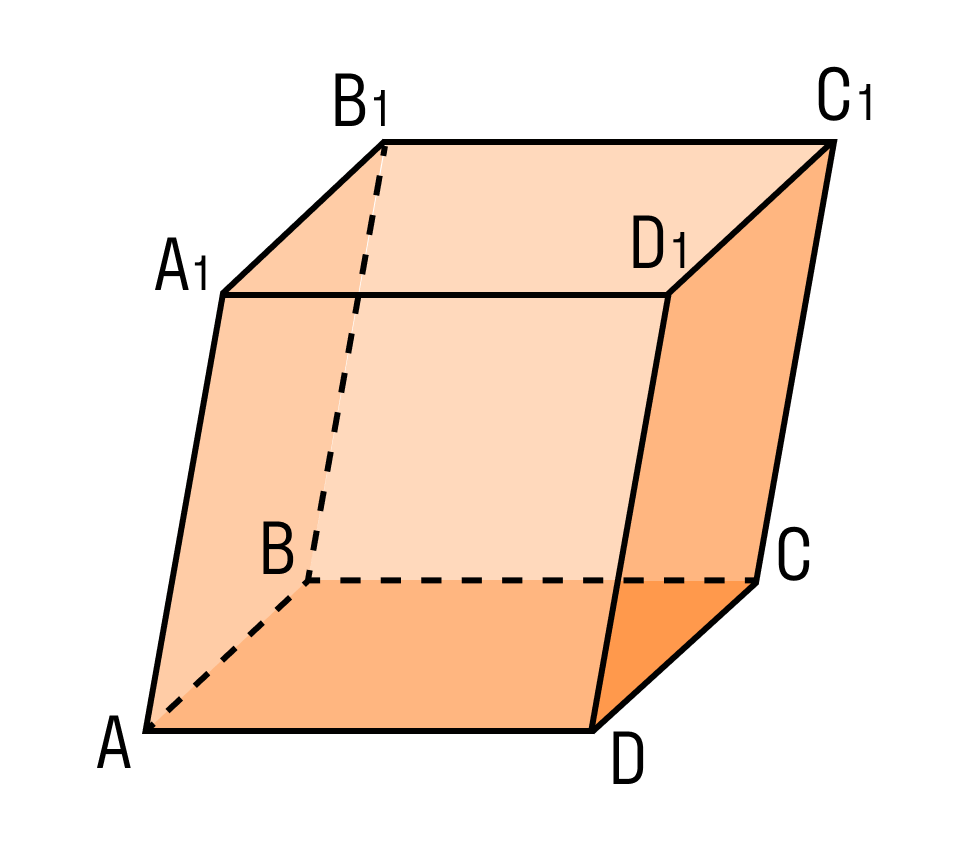
На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

основание;
грани;
ребра;
диагонали;
диагонали граней;
высота.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Противолежащие грани параллелепипеда равны и параллельны друг другу.
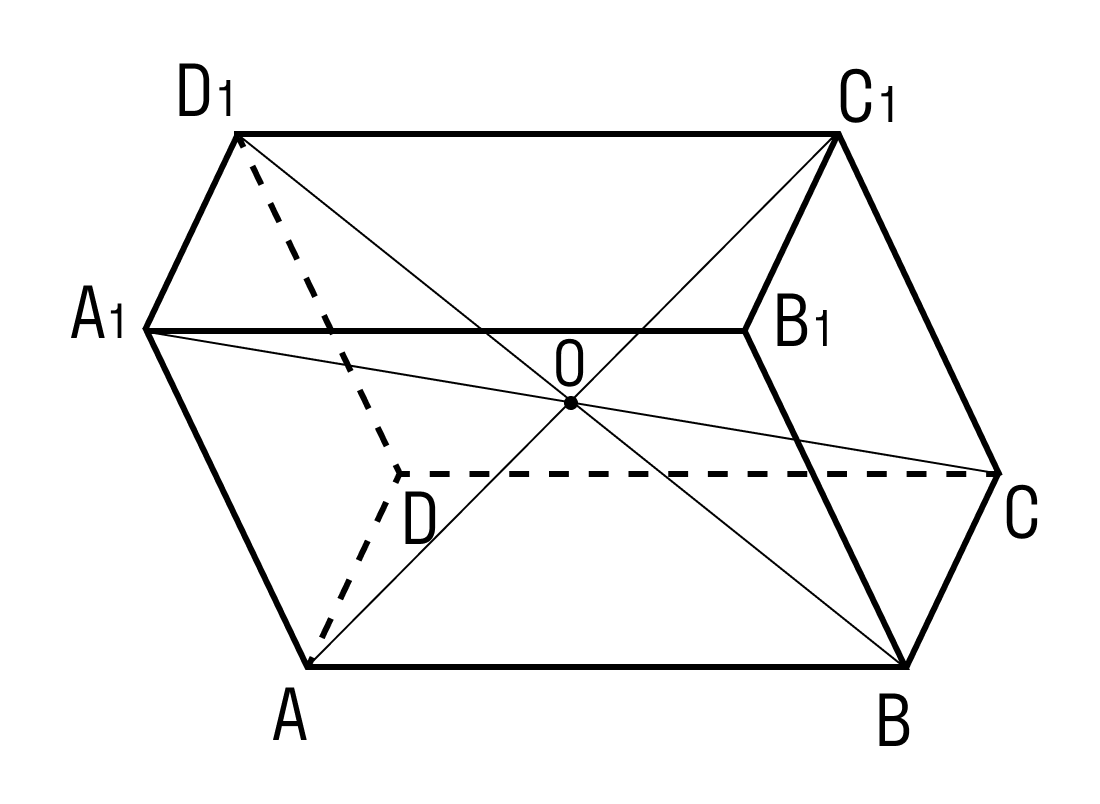
Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Параллелепипед симметричен относительно середины его диагонали.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

На рисунке: ребро АА1 перпендикулярно основанию ABCD. АА1 перпендикулярна прямым АB и АD, которые лежат в плоскости основания

Свойства прямого параллелепипеда:

Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
Высота прямого параллелепипеда равна длине бокового ребра.
Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота
Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания
Объем прямого параллелепипеда
V = Sо*h

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

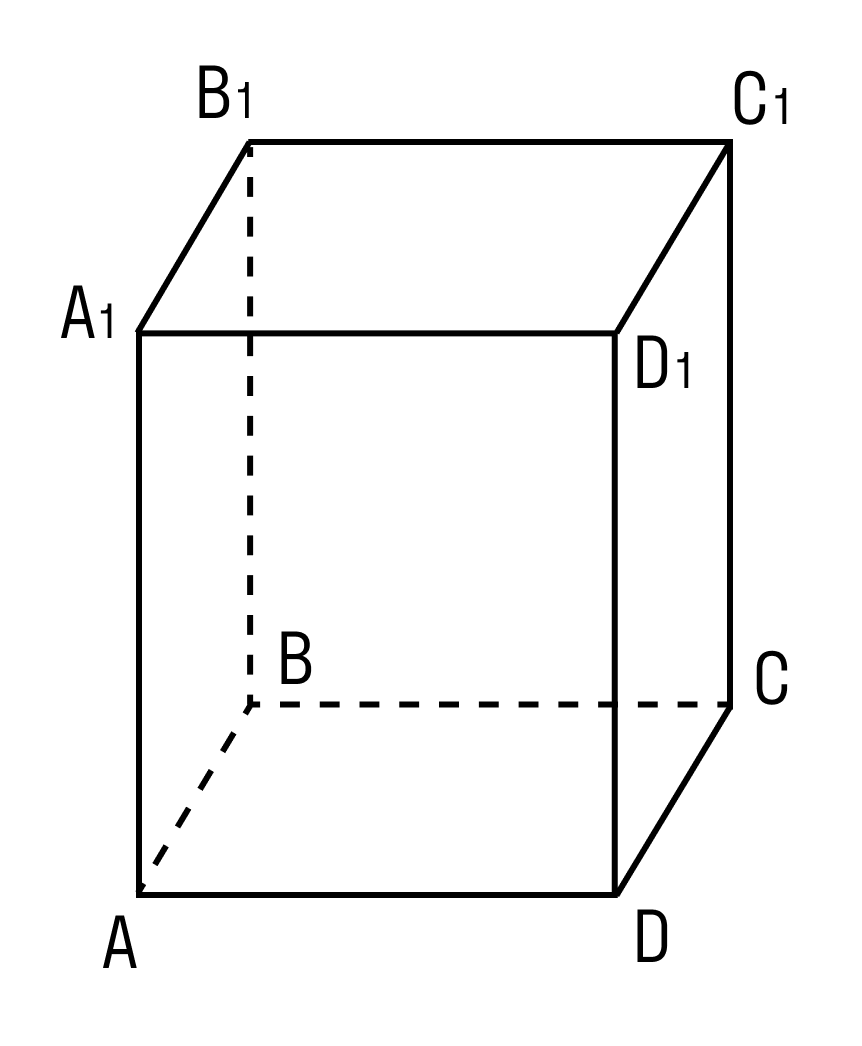
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

На рисунке: основание прямоугольного параллелепипеда ABCD; боковое ребро АА1 перпендикулярно АВСD; угол BAD = 90°

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
Противолежащие грани параллелепипеда попарно параллельны и равны.
Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
Диагонали прямоугольного параллелепипеда равны.
В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
Любая грань прямоугольного параллелепипеда может быть принята за основание.
Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота
Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро
Площадь поверхности
Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

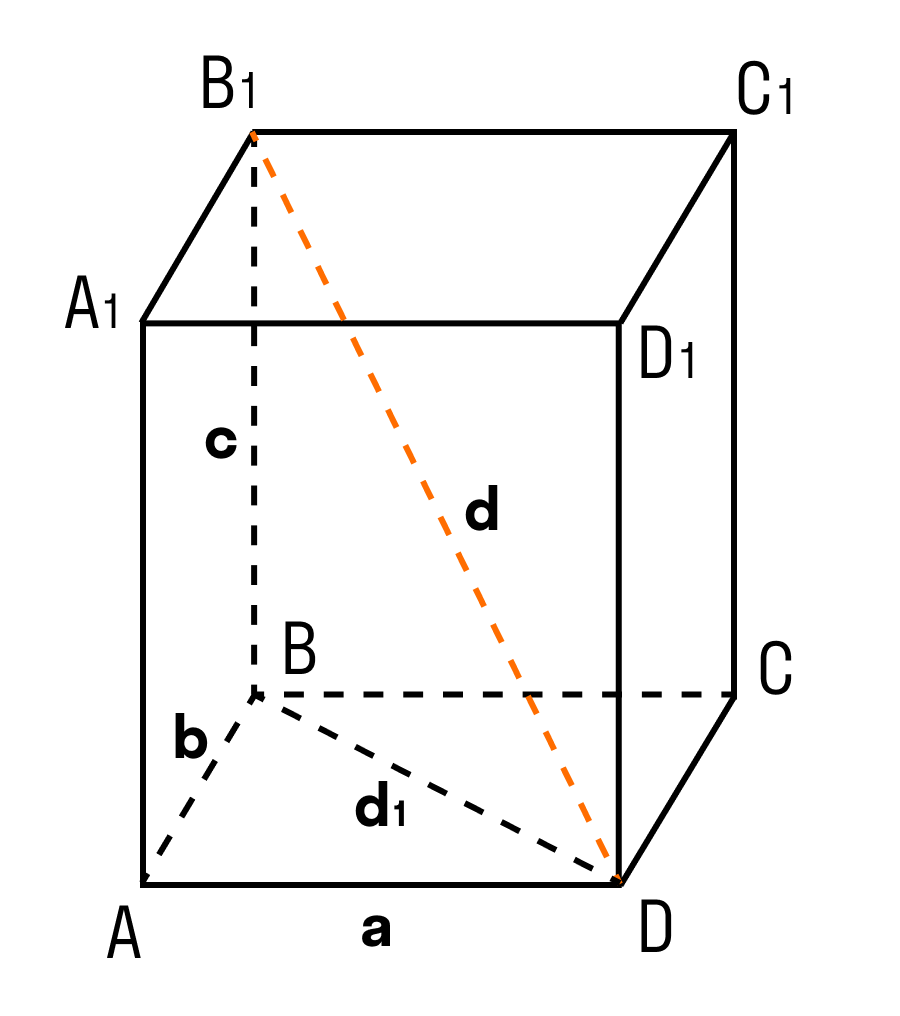
Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Применяем формулу:

d² = a² + b² + c²

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

d₁² = a² + b²

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Куб

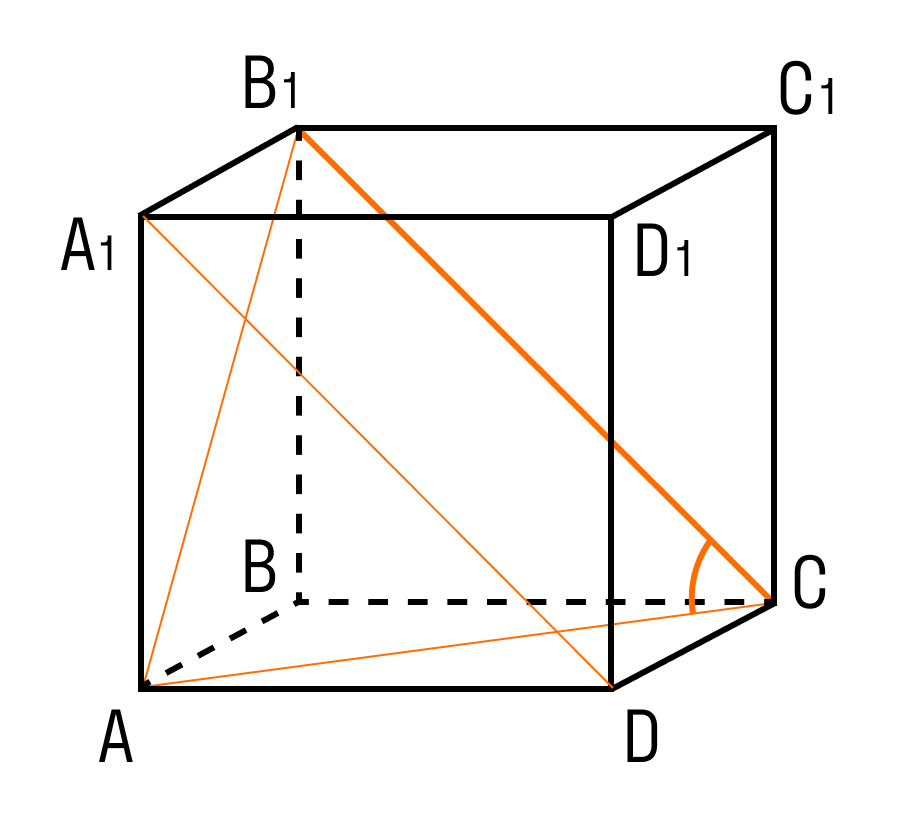
Свойства куба:

В кубе 6 граней, каждая грань куба — квадрат.
Противолежащие грани параллельны друг другу.
Все углы куба, образованные двумя гранями, равны 90°.
У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
Диагонали куба равны.
Диагональ куба в √3 раз больше его ребра.
Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Объем куба через длину ребра a
V = a3
Площадь поверхности куба
S = 6a2
Периметр куба
P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

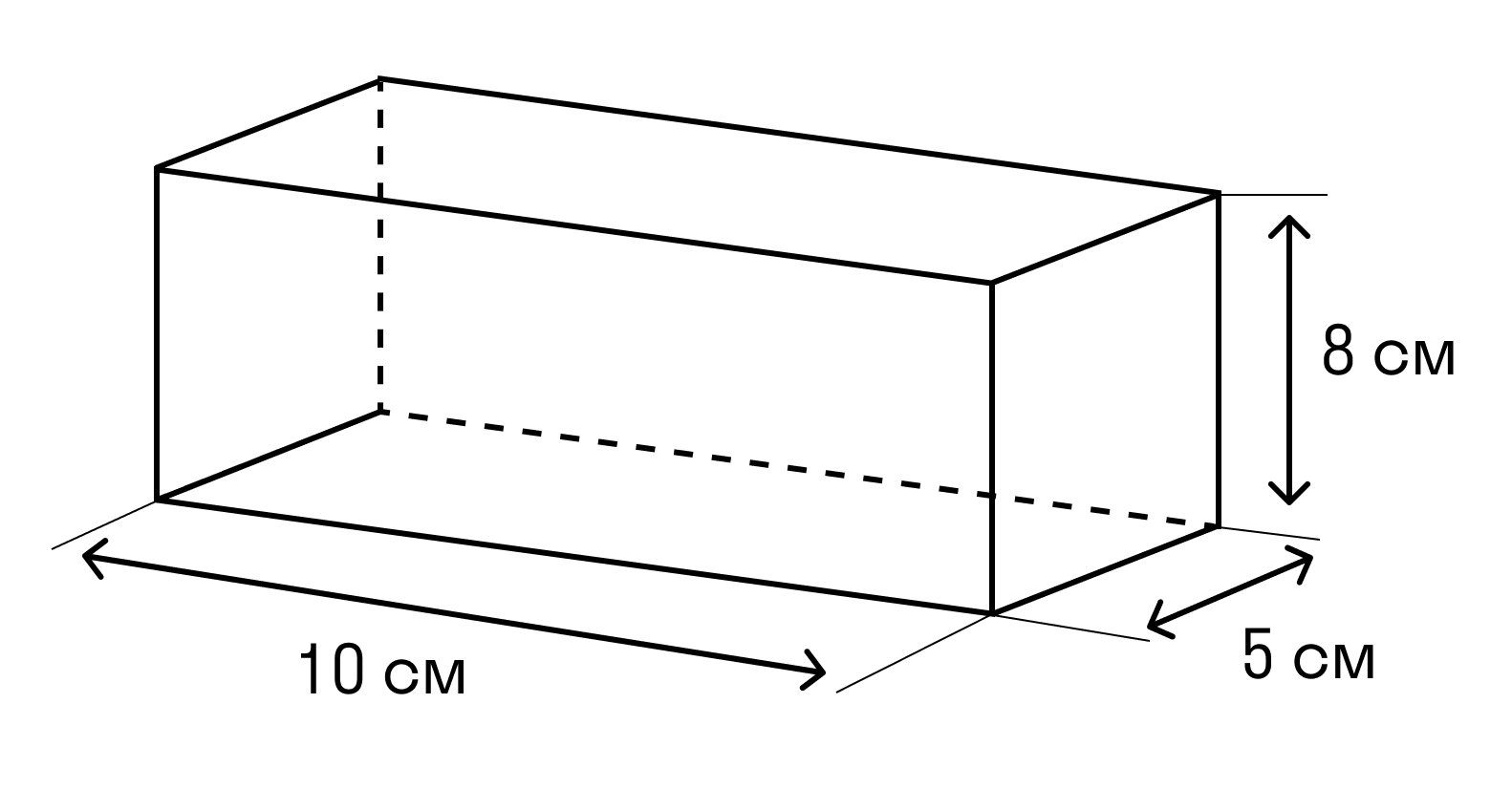
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

D₁B = √26
BB₁ = 3
A₁D₁ = 4

Нужно найти длину ребра A₁B₁.

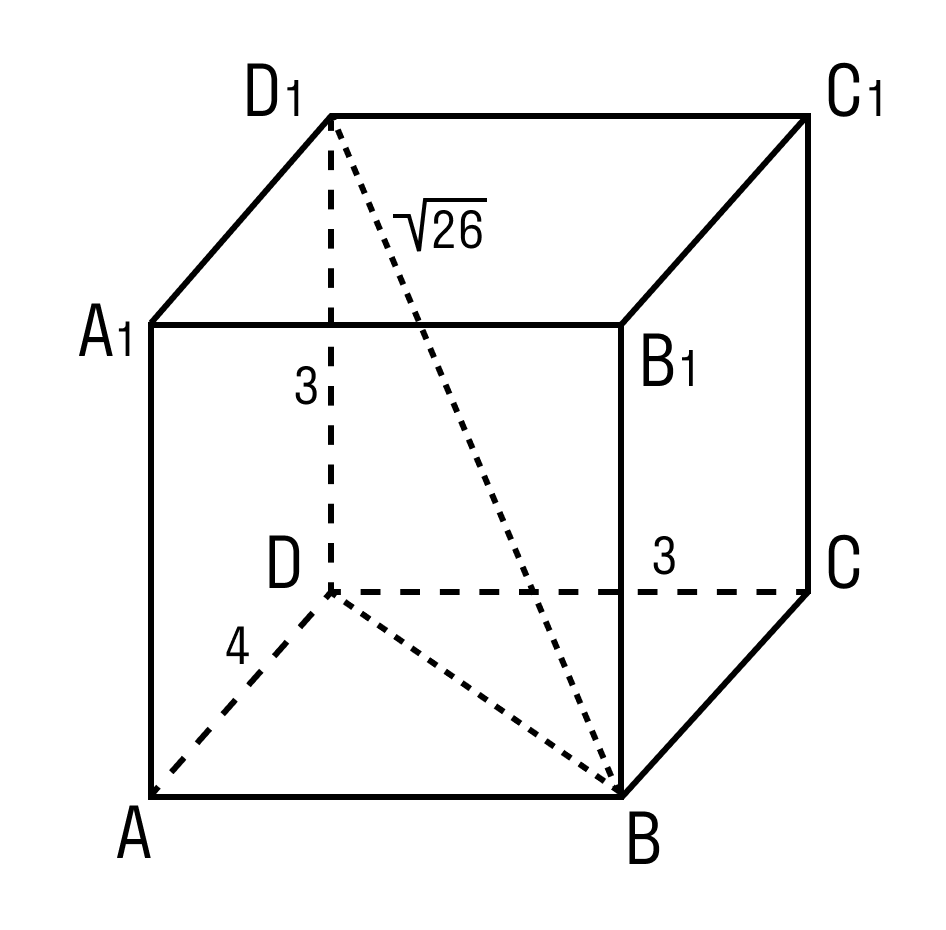
В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁² = DD₁² + BD²
BD² = BD₁² – DD₁²
BD² = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD² = AD² + AB²
AB² = BD² — AD² = (√17)2 — 4² = 1
A₁B₁ = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

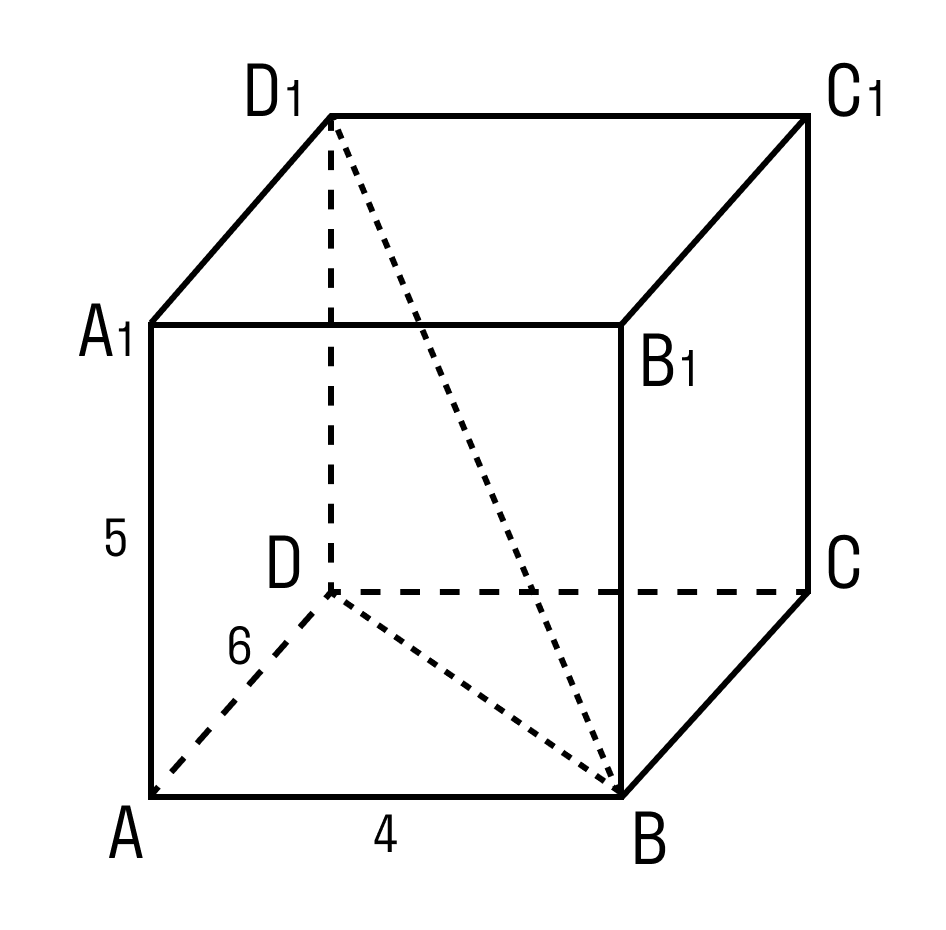
В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD² = AB²+AD²
BD² = 4² + 6² = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁² = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AC₁= 15
C₁D₁ = 3
B₁C₁= 12

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
основание прямоугольного параллелепипеда — прямоугольник;
три измерения прямоугольного параллелепипеда: длина, ширина, высота;
диагональ параллелепипеда равна сумме квадратов его измерений.

Решение задачи

В видео уроке представлено решение геометрической задачи из ЕГЭ (В13) про прямоугольный параллелепипед. При решении задачи вспоминается формула нахождения длины диагонали: квадрат диагонали равен сумме квадратов трёх её измерений (измерения параллелепипеда — это рёбра выходящие из одной вершины). Задача сводится к нахождению неизвестного ребра параллелепипеда. Отмечается, что в прямоугольнике противоположные стороны равны. При вычислении искомой величины используется арифметическая операция возведение в степень.

Видео урок предназначен для учащихся 10 класса при изучении темы : «Параллельность прямых и плоскостей» (Прямоугольный параллелепипед). Решение данной задачи будет полезным учащимся 11 класса при подготовке к ЕГЭ.

Отзывы учеников

Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.

Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.

Источник

Как найти сумму длин всех рёбер параллелепипеда

Длина, ширина, высота

Куб

Объем прямоугольного параллелепипеда

Формула объема прямоугольного параллелепипеда

Объем куба

Пирамида

См. также[править | править код]

Ссылки[править | править код]

Определение параллелепипеда

Свойства параллелепипеда

Прямой параллелепипед

Прямоугольный параллелепипед

Свойства прямоугольного параллелепипеда

Диагонали прямоугольного параллелепипеда: теорема

Куб: определение, свойства и формулы

Решение задач

Самопроверка

Решение задачи

Отзывы учеников

Вам также может понравиться

Как найти квартиль в питоне

Как найти иглы чертополоха

Как в симс 3 найти звезду

Добавить комментарий Отменить ответ