![]()
Сумма углов квадрата , как и любого другого не правильного четырёхугольника , всегда равна 360 градусам.И сумма углов любого n – угольника вычисляется по общей для определённого n – угольника формуле :
Сумма углов n – угольника = 180 * ( n – 2 ),
И для квадрата (четырёхугольника) эта формула превращается в :
180 * (4 – 2 )=180 * 2 = 360 градусов.
Ещё можно подсчитать эту сумму через 2 треугольника , на которые квадрат делится диагональю , а сумма углов любого треугольника = 180 гр. И (180гр.) * 2 =360 гр.
Ну и самое простое подсчитать сумму всех 4-х углов,каждый из которых равен 90 градусам :4 * 90 гр.= 360 гр.
Сумма углов любого 4-угольника (квадрата) равна 360 градусам.
модератор выбрал этот ответ лучшим
![]()
88SkyWalker88
[428K]
6 лет назад
У любого квадрата четыре угла. Как известно, у квадрата все углы равны, и они прямые, то есть равны девяносто градусов.
Путем нехитрых вычислений получаем: 90 умножить на 4 равно 360 градусов.
Это будет касаться и любого прямоугольника.
Пашенька
[189K]
6 лет назад
Как известно, углов у квадрата всего четыре.
Также в качестве аксиомы известно, что любой из них по определению является 90-тоградусным.
Поэтому перемножаем 4 на 90 и имеем 360.
А можно сложить 90 и 90 – это 180. Снова 90 и 90 – это 180. Вместе – 180+180= 360.
Ответ – 360.
![]()
Vika Neko
[34.1K]
7 лет назад
У квадрата все углы одинаковые и равны 90 градусов. У квадрата четыре угла. Чтобы узнать сумму углов квадрата, нужно сложить все четыре угла и получим результат.
90 град. + 90 град. + 90 град. + 90 град. = 360 градусов.
Сумма углов квадрата равна 360 градусов.
Сумма углов квадрата – 360 градусов.
У квадрата углы прямые. Прямой угол – это угол в 90 градусов.
У квадрата четыре угла.
Вот и получается: 90 Х 4 = 360.
Да и не только у квадрата.
Квадрат – это прямоугольник с равными сторонами.
У прямоугольника то же самое, сумма углов 360 градусов.
И не только у них.
Прямоугольник – это прямоугольный параллелограмм.
Но и у обычного (не прямоугольного) параллелограмма тоже сумма углов равна 360 градусов.
![]()
Ninaarc
[481K]
6 лет назад
Квадрат — это один из видов четырехугольника, в котором все стороны и углы равны. В квадрате внутренние углы прямые, то есть равные 90°. С помощью простейших вычислений определяем сумму углов квадрата. Поскольку в нем четыре угла, то умножаем 90° на 4, получая 360°.
Кстати, не только сумма углов в квадрате равна 360°. Это утверждение касается любого четырехугольника, будь то прямоугольник, ромб или трапеция.
![]()
Oleg74
[202K]
6 лет назад
Вопрос очень простой, если вы хорошо понимаете всю суть вопроса.
Геометрическая фигура под названием квадрат имеет 4 угла, каждый из которых всегда равен 90 °, а из этого следует, что сумма углов квадрата будет равняться 360 °.
360 ° = 90 ° х 4 = 90 ° + 90 ° + 90 ° + 90 °
![]()
Shipo3
[33.1K]
6 лет назад
Все видели квадрат, и все знают, что у него ровно 4 угла и , кстати 4 стороны. Каждый угол прямой, а это значит, что он имеет 90°. Тогда 90°•4=360°.
Также можно сказать, что по формуле суммы углов n-угольника:
сумма углов=(n-2)•180, то есть сумма углов=(4-2)•180=360°.
Анна Васюкова
[1.1K]
7 лет назад
В квадрате, как известно, имеется четыре угла, каждый из которых по отдельности равен девяносто градусов. Таким образом, сумма всех четырёх углов квадрата равна 4*90 градусов = 360 градусов. В принципе у прямоугольников и ромбов сумма углов также равна 360 градусов.
FERICITA
[1.7K]
7 лет назад
Самое простое подсчитать сумму углов квадрата. как и любого другого четырёхугольника это просуммировать все углы , а это :
1 ) сумма углов = 90 + 90 + 90 + 90 = 360 градусов.
2 ) сумма углов = 2 * 180 градусов = 360 градусов.Такой вывод делается потому , квадрат , как любой четырёхугольник состоит из двух треугольников , сумма углов которого равна 180 градусов.
Знаете ответ?
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы квадрата
Для расчёта всех основных параметров квадрата воспользуйтесь калькулятором.
Свойства квадрата
- Длины сторон квадрата равны.
- Все углы квадрата прямые, равны 90°.
- Противолежащие стороны квадрата параллельны друг другу.
- Сумма всех углов квадрата равна 360°.
- Величина угла между диагональю и стороной равна 45°.
- Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
- Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
- Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
- Пересечение диагоналей является центром вписанной и описанной окружности.
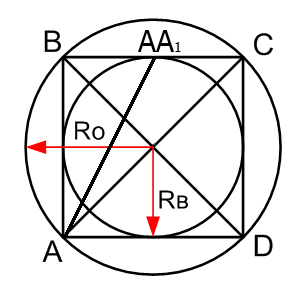
Сторона квадрата
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата | |
| RВ – радиус вписанной окружности | |
| RO – радиус описанной окружности | |
| AA1 – линия выходящая из угла на середину стороны квадрата |
Стороны квадрата через диагональ
$$
AB = {AC over sqrt{2}}
$$
Стороны квадрата через радиус вписанной окружности
$$
AB = 2 * R_В
$$
Стороны квадрата через радиус описанной окружности
$$
AB = {2 * R_О over sqrt{2} }
$$
Стороны квадрата через площадь, S
$$
AB = sqrt{S}
$$
Стороны квадрата через периметр, P
$$
AB = {P over 4}
$$
Стороны квадрата через линию выходящую из угла на середину стороны квадрата, AA1
$$
AB = {2 * AA_1 over sqrt{5}}
$$
Площадь квадрата
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата |
Площадь квадрата через сторону
$$
S = AB^2
$$
Площадь квадрата через диагональ
$$
S = {1 over 2} * AC^2
$$
Периметр квадрата
| Где: | AB – сторона квадрата |
$$
P = 4 * AB
$$
Диагональ квадрата
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата | |
| S – площадь квадрата | |
| P – периметр квадрата |
Диагональ квадрата через сторону
$$
AC = sqrt{2} * AB
$$
Диагональ квадрата через площадь
$$
AC = sqrt{2 * S}
$$
Диагональ квадрата через периметр
$$
AC = {P over 2 * sqrt{2}}
$$
Вписанная окружность
| Где: | AB – сторона квадрата |
Радиус вписанной окружности
$$
R = {AB over 2}
$$
Длина окружности, L
$$
L = 2 * pi * R
$$
Площадь окружности, S
$$
S = pi * R^2
$$
Описанная окружность
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата |
Радиус описанной окружности через сторону
$$
R = {AB over sqrt{2}}
$$
Радиус описанной окружности через диагональ
$$
R = {AC over 2}
$$
Длина окружности, L
$$
L = 2 * pi * R
$$
Площадь окружности, S
$$
S = pi * R^2
$$
Квадрат, свойства и формулы, площадь и периметр.
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат (понятие, определение), диагональ квадрата
Свойства квадрата
Формулы квадрата. Площадь квадрата. Периметр квадрата
Квадрат (понятие, определение), диагональ квадрата:
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат – это четырехугольник, имеющий равные стороны и углы.

Рис. 1. Квадрат
Все углы квадрата прямые. Каждый из них прямой и равен 90°.
Таким образом, все квадраты отличаются друг от друга только длиной стороны.

Рис. 2. Квадрат и диагонали квадрата
Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.
Квадрат является одновременно частным случаем других фигур: параллелограмма, ромба и прямоугольника. Поэтому квадрату присущи все свойства параллелограмма, ромба и прямоугольника.
Квадрат – это равносторонний прямоугольник.
Квадрат – это ромб с прямыми углами.
Свойства квадрата:
1. Длины всех сторон равны.

Рис. 3. Квадрат
AB = BC = CD = AD
2. Противоположные стороны квадрата параллельны.

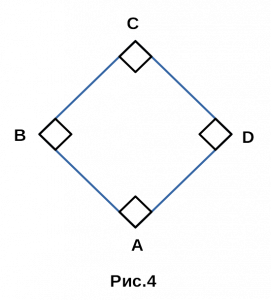
Рис. 4. Квадрат
AB||CD, BC||AD
3. Все углы квадрата прямые. Каждый из них равен 90°.

Рис. 5. Квадрат
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусам.
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
5. Диагонали квадрата равны между собой.

Рис. 6. Квадрат
AC = BD
6. Диагонали квадрата взаимно перпендикулярны. 
Рис. 7. Квадрат
AC ┴ BD
7. Диагонали квадрата точкой пересечения делятся пополам.

Рис. 8. Квадрат
BO = OD = AO = OC
8. Угол между диагональю и стороной квадрата равен 45 градусам.

Рис. 9. Квадрат
∠BCA = ∠ACD = ∠DAC = ∠CAB = 45°
9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

Рис. 10. Квадрат
∠ABD = ∠DBC = ∠BCA = ∠ACD = ∠CDB = ∠BDA = ∠DAC = ∠CAB = 45°
10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.
Обе диагонали делят квадрат на 4 равных равнобедренных прямоугольных треугольника.

Рис. 11. Квадрат
△ABD = △CBD = △ABC = △ACD,
△AOB = △BOC = △COD = △AOD
11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Рис. 12. Квадрат
Формулы квадрата. Площадь квадрата. Периметр квадрата:
Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.
Формула диагонали квадрата:
![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() .
.
Формула радиуса вписанной окружности квадрата:
Радиус вписанной окружности квадрата равен половине его стороны.
 .
.
Формула радиуса описанной окружности квадрата:
 .
.
Формула периметра квадрата:
![]() ,
, ![]() ,
, ![]() .
.
Формула площади квадрата:
![]() ,
,  ,
,  ,
, ![]() ,
, ![]() .
.
Квадрат
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
3 808
Сумма углов четырехугольника

Обновлено 01.02.2022
Свойства
- Сумма углов четырехугольника равна 360°.
∠A + ∠B + ∠C + ∠D = 360°.
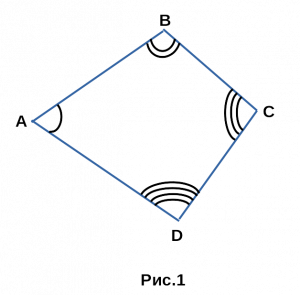
- Если четырехугольник правильный, то каждый угол по 90°
и этот четырехугольник является квадратом.
∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
ABCD — квадрат.
- Сумма противоположных углов четырехугольника равна 180°,
если около четырехугольника описана окружность.
∠A + ∠С = ∠В + ∠D = 180°.
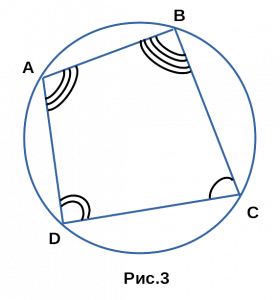
Такие четырехугольники называют вписанными.
- Если сумма трех углов четырехугольника равна 270°,
то четвертый угол прямой — 90°.
∠A + ∠B + ∠С = 270°, ⇒ ∠D = 90°(прямой угол).
- Виды четырехугольников: квадрат, прямоугольник,
параллелограмм, ромб, трапеция.
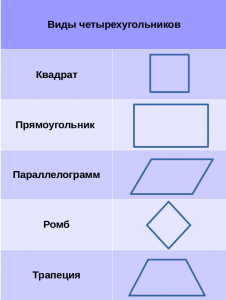
Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии. - Сумма внутренних углов любого четырехугольника равна 360°.
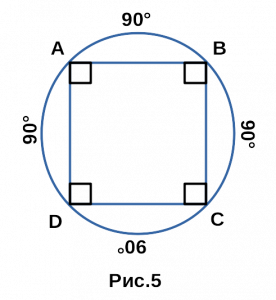
α + β + γ + δ = 360°. - Все углы вписанного четырёхугольника являются вписанными
в окружность, а также, равны половине дуг, на которые опираются.
◡ABC = 180°, ⇒ ∠ADC = 90°.
◡BCD = 180°, ⇒ ∠BAD = 90°.
- Формула суммы углов четырехугольника:
∠A + ∠B + ∠C + ∠D = (n-2) · 180°,
где n — количество сторон четырехугольника. - Сумма трех углов четырехугольника равна 300°,
значит четвертый угол равен 60 градусам. - Сумма внешних и внутренних углов четырехугольника равна 720°.
- Все углы имеют одинаковую градусную меру — 90°,
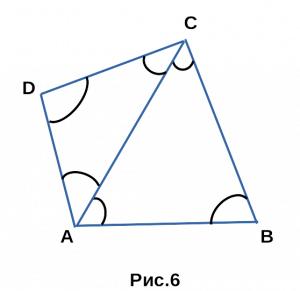
только у квадрата и у прямоугольника. - Сумма углов четырехугольника равна сумме углов фигур,
из которых состоит четырехугольник.
∠DCA + ∠ADC + ∠CAD + ∠ACB + ∠CBA + ∠BAC = 360°.
Следствия
- Если в четырехугольнике известны три угла,
но неизвестен четвертый угол, то его можно найти,
так: вычесть из 360 сумму всех трех известных углов,
так мы найдем четвертый угол.
∠A = 360° — (∠B + ∠C + ∠D). - Если три угла четырехугольника равны
90 градусов, то четвертый угол равен тоже 90. - Чтобы на рисунке измерить углы,
и найти их градусную меру, нужно
воспользоваться транспортиром. - Сумма углов четырехугольника
не может быть равна 180 градусам.
∠A + ∠B + ∠C + ∠D ≠ 180°. - Чтобы найти сумму углов
четырехугольника, нужно сложить все углы. - Сумма двух углов четырехугольника равна 180 градусам,
только, в том случае, если этот четырехугольник вписан в окружность.
Геометрия,
вопрос задал albinaaruniva3,
4 месяца назад
Вычисли сумму всех углов квадрата
siestarjoki:
сумма внутренних углов любого выпуклого четырехугольника равна 360
Ответы на вопрос
Ответил tiktakbobrovskiy
0
Ответ:
360
Объяснение:
каждый угол квадрата равен 90 градусов
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Литература,
29 дней назад
Вспомните дату рождения А.С. Пушкина. Напишите небольшой очерк о поэте…
Русский язык,
29 дней назад
Морфемный разбор слов: разноцветных, деревянные, знает, деревья ?
Литература,
4 месяца назад
Ребят срочно помогите!!!!! Нужно выполнить задание которое на фотке Помогите!!!(((…
Математика,
4 месяца назад
решите по действиям …
Математика,
5 лет назад
помогите люди добрые…
Математика,
5 лет назад
Срочно решите пжжжжжжжжж
– 7/12х+11/12=13/18…