Как найти сумму всех углов выпуклого семиугольника

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Семиугольник, виды, свойства и формулы.

Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.

Семиугольник, выпуклый и невыпуклый семиугольник

Правильный семиугольник (понятие и определение)

Свойства правильного семиугольника

Формулы правильного семиугольника

Семиугольник в природе, технике и культуре

Шестиугольник, семиугольник, восьмиугольник

Семиугольник, выпуклый и невыпуклый семиугольник:

Семиугольник – это многоугольник с семью углами.

Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.

Семиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый семиугольник – это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Звёздчатый семиугольник – семиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого семиугольника могут пересекаться между собой.

Рис. 1. Выпуклый семиугольник

Рис. 2. Невыпуклый семиугольник

Сумма внутренних углов любого выпуклого семиугольника равна 900°.

Правильный семиугольник (понятие и определение):

Правильный семиугольник – это правильный многоугольник с семью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

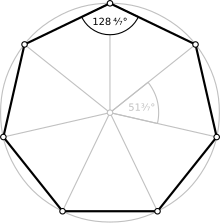
Правильный семиугольник – это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈ 128,571°.

Рис. 3. Правильный семиугольник

Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.

Углы правильного семиугольника образуют семь равнобедренных треугольников.

Правильный семиугольник невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).

Свойства правильного семиугольника:

1. Все стороны правильного семиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆ = a₇. 

2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = α₇ = 128 4/7° ≈ 128,571°.

Рис. 4. Правильный семиугольник

3. Сумма внутренних углов любого правильного семиугольника равна 900°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.

Рис. 5. Правильный семиугольник

5. Количество диагоналей правильного семиугольника равно 14.

Рис. 6. Правильный семиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный семиугольник

Формулы правильного семиугольника:

Пусть a – сторона семиугольника, r – радиус окружности, вписанной в семиугольник, R – радиус описанной окружности семиугольника, P – периметр семиугольника, S – площадь семиугольника.

Формулы стороны правильного семиугольника:

Формулы периметра правильного семиугольника:

Формулы площади правильного семиугольника:

Формулы радиуса окружности, вписанной в правильный семиугольник:

Семиугольник в природе, технике и культуре:

В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.

Некоторые виды кактусовых имеют форму звездчатого семиугольника.

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Восьмиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
2 371

Семиуго́льник, называемый иногда гептагон^[1] — многоугольник с семью углами. Семиугольником также называют всякий предмет такой формы.

Площадь семиугольника без самопересечений[править | править код]

Площадь семиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.

Выпуклый семиугольник[править | править код]

Выпуклым семиугольником называется такой семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Сумма внутренних углов выпуклого семиугольника равна 900°.

Известно, что существуют сколь угодно большие множества точек в общем положении, в которых нет выпуклого пустого семиугольника^[2].

Правильный семиугольник[править | править код]

Правильным называется семиугольник, у которого все стороны равны, а все внутренние углы равны .

Семиугольные звёзды в природе[править | править код]

Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника называется звёздчатым. Примером такого семиугольника в природе может являться один из видов кактусовых.

Примечания[править | править код]