Как найти сумму значений функции на отрезке - Сайт, где вы сможете решить свои вопросы

1. Понятие функции

Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.

x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).

График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).

Четная функция: f(-x)=f(x) для всех ;

Нечетная функция: f(-x)=-f(x) для всех ;

График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.

Периодическая функция с периодом T>0: f(x+T)=f(x) для всех .

Нули функции – значения x такие, что f(x)=0. Интервалы знакопостоянства – множества значений аргумента, при которых значения функции только положительны или только отрицательны.

На рисунке изображена функция с областью определения [a, e]. Нули функции: x=b, x=c, x=d; интервалы знакопостоянства: y>0 при ; y<0 при .

Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых , если x₁<x₂, то f(x₁)<f(x₂). Функция убывает на множестве X, если большему значению аргумента соответствует меньшее значение функции. Т.е. для любых , если x₁<x₂, то f(x₁)>f(x₂).

2. Основные элементарные функции

а) степенная функция .

б) показательная функция .

в) логарифмическая функция .

г) тригонометрические функции

y=sinx, y=cosx

y=tgx

y=ctgx

д) обратные тригонометрические функции

y=arcsin x, y=arccos x, y=arctg x, y=arcctg x

3. Некоторые алгебраические функции

а) линейная .

График функции – прямая линия, проходящая через точки (0, b) и .

Функция возрастает при a>0, убывает при a<0.

Частные случаи: y=b – прямая, параллельная оси OX;

y=ax – прямая, проходящая через начало координат.

б) квадратичная .

График функции – парабола. Ветви параболы направлены вверх при a>0, вниз при a<0. Вершина параболы:

Точки пересечения с осями координат:

с осью OX – (x₁, 0) и (x₂, 0),

где , D=b²-4ac – корни квадратного трехчлена;

с осью OY – (0, c).

Пример 1. График какой функции является возрастающим:

а) ; б) у = х³ – 27; в) y=2^-x?

Решение:

Рассмотрим каждую из функций в отдельности:

а) – степенная функция. Область определения этой функции: . На всей области определения функция монотонна.

Возьмём два значения х₁ = 1 и х₂ = 4. Им соответствует у₁ = – 1, у₂ = – 2. Видим, что если х₁ < x₂ , то у₁ > у₂. Функция убывающая.

б) у = х³ – 27 – алгебраическая функция. Область определения – множество всех действительных чисел. На всей области определения функция монотонна. Возьмём два значения х₁ = 3, х₂ = 4. Им соответствует у₁ = 0, у₂ = 37.

Видим, что если х₁ < x₂ , то и у₁ < у₂. Функция возрастающая.

в) y=2^-x – показательная функция. Областью определения является множество всех действительных чисел. На всей области определения функция монотонна. Пусть х₁ = 0, х₂ = 1. Им соответствуют у₁ = 1, у₂ = 0,5.

Видим, что если х₁ < x₂ , то у₁ > у₂. Функция убывающая.

Ответ: б) у = х³ – 27.

Пример 2. Парабола у = 2х² – (а – 3)х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.

Решение:

Найдём значение параметра а. Т.к. парабола проходит через начало системы координат, то координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 0² – (а – 3) ∙ 0 + а + 3; а = – 3.

Уравнение параболы примет вид: у = 2х² + 6х.

Абсцисса вершины параболы находится по формуле: . Получаем .

Ответ: – 1, 5.

Пример 3. В каких точках график функции f(x) = x² – 3 пересекает прямую у(х) = х – 1?

Решение:

Ответом на данный вопрос является решение системы

х² – 3 = х – 1; х² – х – 2 = 0; х₁= – 1, или х₂ = 2.

Соответственно, у₁ = – 2, у₂ = 1.

Ответ: (– 1; – 2), (2; 1).

Пример 4. При каких значениях k прямые – kх + 7у = – 13 и 14у – 3х + 5 = 0 параллельны?

Решение:

Две различные прямые у = k₁х + b₁ и у = k₂х + b₂ параллельны, если k₁ = k₂, но при этом b₁ ≠ b₂.

В обоих уравнениях выразим у через х.

. Следовательно, . При этом .

Ответ: при k = – 1,5.

Пример 5. Найти точки пересечения прямой у = 5 + х с осями координат.

Решение:

Когда график функции пресекает ось ОХ, значение у = 0.

Получаем уравнение 5 + х = 0, х = – 5.

Когда график функции пересекает ось OY, значение х = 0, т.е. у = 5.

Ответ: (– 5; 0), (0; 5).

Пример 6. Найти нули функции у = (х + 1)∙(х – 2).

Решение:

Решаем уравнение (х + 1)∙(х – 2) = 0.

х + 1 = 0 или х – 2 = 0; х₁ = – 1, х₂ = 2.

Ответ: (– 1; 0), (2; 0).

Пример 7. Найти область значений функции .

Решение:

Оцениваем последовательно:

Ответ: .

Пример 8. Найдите сумму целых значений функции у = 3 – 2 sin x.

Решение:

Оценим значение 3 – 2 sin x.

Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.

Ответ: 15.

Пример 9. Найти область определения функции .

Решение:

Функция задана аналитически, следовательно, область определения совпадает с областью допустимых значений выражения .

х² + х ≠ 0, т.к. на нуль делить нельзя.

х (х + 1) ≠ 0; х ≠ 0 или х ≠ – 1.

Ответ: .

Пример 10. Найдите область определения функции .

Решение:

Допустимые значения выражения :

Ответ: .

Пример 11. Найдите область определения функции .

Решение:

Допустимые значения выражения: .

Ответ: (– 1; + ∞).

Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А(0; 2), проходящая через точку В(2; – 6). Задайте эту функцию формулой.

Решение:

Уравнение квадратичной функции у = ах² + bх + с.

1) точка А является вершиной параболы, следовательно .

Уравнение примет вид: у = ах² + с.

2) точка А принадлежит графику, следовательно её координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.

Уравнение примет вид: у = ах² + 2.

3) график проходит через точку В. Её координаты также удовлетворяют уравнению: – 6 = а ∙ 2² + 2, – 8 = 4 ∙ а, а = – 2.

Получили уравнение у = – 2х² + 2.

Ответ: у = – 2х² + 2.

Пример 13. Найдите g (x) , если f (x) = 2x – 3, g (f (x)) = x. Вычислите g (1).

Решение:

Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.

2x – 3 = 1, х = 2.

Следовательно, g (f (x)) = 2, т.е. g (1) = 2.

Ответ: g (1) = 2.

Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y=5^2x, y=5^3x-1 и через точку параболы y=(2x-1)², в которой производная функции, задающей параболу, равна 8.

Решение:

1) найдём точку пересечения кривых:

2) найдём точку параболы, в которой производная равна 8:

3) прямая проходит через две точки (1; 25) и (1,5; 4). Согласно уравнению прямой, проходящей через две точки, имеем:

– 21х + 21 = 0,5у – 12,5; – 42х + 42 = у – 25; у = – 42х + 47.

Ответ: у = – 42х + 47.

Задания для самостоятельного решения

Базовый уровень

1) Вычислите значение функции в точке х₀ = 1.

2) Найдите значение функции при х = 4.

3) Для функции вычислите f(-1)-f(1).

4) Найдите g(f(x)), если Вычислите g(f(2)).

Найдите области определения функций:

5) .

6) .

7) .

8) .

9) .

10) .

11) .

12)

13) .

14) y=log₅(x+3).

15) y=log₅(x²-4).

16) .

При каких значениях х функции не определены?

17) .

18) .

19) .

20) .

21) y=ctgx+tgx.

22) .

23) .

Укажите длину интервала области определения для функций:

24) .

25) y=log₄(5x+6-x²)

26) y=log₆(x²+3).

Укажите области значения функций:

27) y=-3sinx.

28) y=0,7cos3x.

29) .

Решите задачи:

30) Сколько натуральных значений может принять функция y=log₂(4-x²) на всей области определения?

31) Найдите сумму целых значений функции y=3cosx-5.

32) Укажите функцию, областью значений которой является множество .

33) Укажите график функции, возрастающей на отрезке [-3; 2].

34) Укажите функцию, которая возрастает на всей области определения.

1) y=-x^0,5; 2) y=1-e^-x; 3) y=ctg2x; 4) y=|-x|.

35) Найдите нули функции .

36) Найдите нули функции

37) Найдите наименьшее значение функции f(x)=3^2x-1 на промежутке [-3; 1].

38) Вычислите координаты точек пересечения графика функции у = – 2х² + 4х + 6 с осью OY.

39) Вычислите ординату точки пересечения прямой у = 5 – 2х с осью ОY.

40) Укажите точки пересечения графиков функций у = 2х + 4 и у = – 2х.

41) В каких точках график функции f (x) = 3x² + 6x пересекает прямую у = 6 – х?

42) Укажите промежутки возрастания функции y=sin3x на интервале .

43) Укажите промежутки убывания функции y=-2cosx на интервале .

Повышенный уровень

44) При каких значениях а графики функций у = 3х – 4х³ и у = а имеют единственную общую точку?

45) Найдите длину промежутка области значений функции .

46) Найдите середину промежутка области значений функции y=cosx+|cosx|.

47) Найдите наибольшее целое значение выражения 2t, где t – число, принадлежащее области значений функции y=cos2x•tg2x.

48) Найдите наименьшее значение функции .

49) Укажите наименьшее значение функции y=log₂(x²-4x+12).

50) Укажите наибольшее значение функции .

51) Вычислите значение функции y=4•sin7x при , если при функция принимает значение – 2.

52) Вычислите значение функции y=|tg2x| при , если значение данной функции при равно 1.

53) Найдите значение 2sint, где t – сумма точек максимума функции на промежутке .

54) Укажите наибольшее значение функции y=cos(tgx) на промежутке .

Источник

Вычисление значений функции

Онлайн калькулятор поможет найти значения функции в заданном интервале, построить таблицу значений функции онлайн, табулировать функцию.
Вычисляет значения функции одной переменной y для заданных значений переменной x. Функция задается при помощи формулы, пример:
Построить таблицу значений функции f(x)=x/(x+1) на отрезке от 0 до 6 с шагом в единицу.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

Зачастую в рамках решения задач по тригонометрии нам приходится искать множество значений функции на области определения или отрезке. Например, такой поиск нужно делать, если приходится решать разные типы неравенств, при оценке выражений и др.

В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми можно вычислить область значения и область определения функции, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графически. Прочитав эту статью, вы получите исчерпывающее представление о том, что такое область значения функции.

Начнем с базовых определений.

Определение 1

Множество значений функции y = f(x) – это множество всех значений на некотором интервале x, которые данная функция принимает при переборе всех значений x∈X.

Определение 2

Область значений функции y=f(x) – это множество всех ее значений, которые она может принять при переборе значений x из области x∈(f).

Область значений некоторой функции обычно принято называть и обозначать E(f).

Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.

Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y=f(x). Область допустимых значений x для выражения f(x) и будет областью определения данной функции.

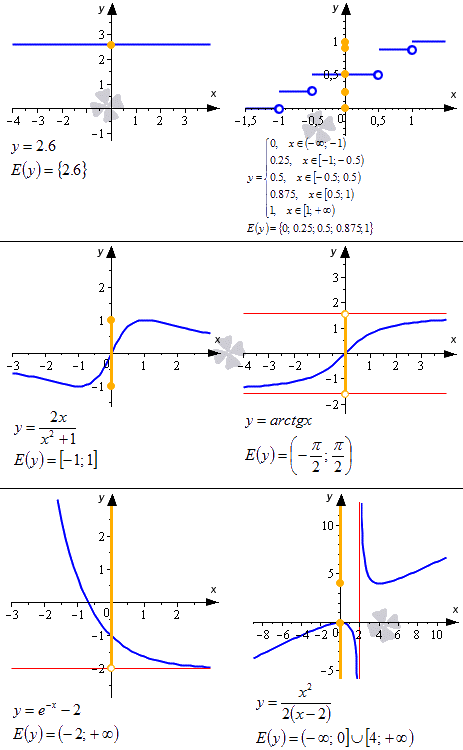
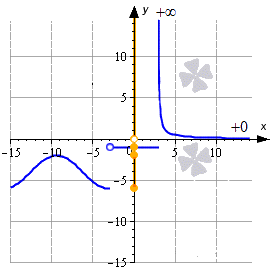
Ниже приводится иллюстрация, на которой показаны некоторые примеры, как построить графики функций и их построение. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.

Как найти область значения функции? Очевидно, что область или множество значений функции можно найти или получить при проецировании графика функции на ось Oy. При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.

Рассмотрим основные способы, как определить область значения функции.

Первый этап – определить тип функции. Функция может быть квадратичной, а также содержать дроби и корни.

Начнем с определения множества значений непрерывной функции y = f(x) на некотором отрезке, обозначенном [a; b]. Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего maxx∈a; bf(x) и наименьшего значения minx∈a; bf(x). Значит, у нас получится отрезок minx∈a; bf(x); maxx∈a; bf(x), в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Возьмем задачу, в которой нужно определить область значений арксинуса.

Пример 1

Условие: найдите область значений y = arcsin x.

Решение

В общем случае область определения арксинуса располагается на отрезке [-1; 1]. Нам надо определить наибольшее и наименьшее значение указанной функции на нем.

y’ = arcsin x’=11-x2

Мы знаем, что производная функции будет положительной для всех значений x, расположенных в интервале [-1; 1], то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x, равном -1, а самое большое – при x, равном 1.

minx∈-1; 1arcsin x=arcsin-1=-π2maxx∈-1; 1arcsin x=arcsin 1=π2

Таким образом, область значений функции арксинус будет равна E(arcsin x)=-π2; π2.

Ответ: E(arcsin x)=-π2; π2

Пример 2

Условие: вычислите область значений y=x4-5×3+6×2 на заданном отрезке [1; 4].

Решение

Как найти значение функции? Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.

Для определения точек экстремума надо произвести следующие вычисления:

y’=x4-5×3+6×2’=4×3+15×2+12x=x4x2-15x+12y’=0⇔x(4×2-15x+12)=0x1=0∉1; 4 или 4×2-15x+12=0D=-152-4·4·12=33×2=15-338≈1.16∈1; 4; x3=15+338≈2.59∈1; 4

Теперь найдем значения заданной функции в концах отрезка и точках x2=15-338; x3=15+338:

y(1)=14-5·13+6·12=2y15-338=15-3384-5·15-3383+6·15-3382==117+16533512≈2.08y15+338=15+3384-5·15+3383+6·15+3382==117-16533512≈-1.62y(4)=44-5·43+6·42=32

Как найти множество значений функции? Значит, множество значений функции будет определяться отрезком 117-16533512; 32.

Ответ: 117-16533512; 32.

Перейдем к нахождению множества значений непрерывной функции y = f(x) в промежутках (a; b), причем a; +∞, -∞; b, -∞; +∞.

Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведение функции в заданных условиях. Для этого у нас есть все необходимые данные.

Пример 3

Условие: вычислите область значений функции y=1×2-4 на интервале (-2; 2).

Решение

Определяем наибольшее и наименьшее значение функции на заданном отрезке

y’=1×2-4’=-2x(x2-4)2y’=0⇔-2x(x2-4)2=0⇔x=0∈(-2; 2)

У нас получилось максимальное значение, равное 0, поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:

То есть, y(0)=102-4=-14 будет максимальным значением функции.

Теперь определим поведение функции при таком x, который стремится к -2 с правой стороны и к +2 с левой стороны. Иными словами, найдем односторонние пределы:

limx→-2+01×2-4=limx→-2+01(x-2)(x+2)==1-2+0-2-2+0+2=-14·1+0=-∞limx→2+01×2-4=limx→2+01(x-2)(x+2)==12-0-22-0+2=14·1-0=-∞

У нас получилось, что значения функции будут возрастать от минус бесконечности до -14 тогда, когда аргумент изменяется в пределах от -2 до 0. А когда аргумент меняется от 0 до 2, значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет (-∞; -14].

Ответ: (-∞; -14].

Пример 4

Условие: укажите множество значений y=tg x на заданном интервале -π2; π2.

Решение

Нам известно, что в общем случае производная тангенса в -π2; π2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:

limx→π2+0tg x=tg-π2+0=-∞limx→π2-0tg x=tgπ2-0=+∞

Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от -π2 до π2,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.

Ответ: -∞; +∞.

Пример 5

Условие: определите, какова область значений функции натурального логарифма y = ln x.

Решение

Нам известно, что данная функция является определенной при положительных значениях аргумента D(y)=0; +∞. Производная на заданном интервале будет положительной: y’=ln x’=1x. Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:

limx→0+0ln x=ln(0+0)=-∞limx→∞ln x=ln+∞=+∞

Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.

Ответ: множество всех действительных чисел – область значений функции натурального логарифма.

Пример 6

Условие: определите, какова область значений функции y=9×2+1.

Решение

Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:

y’=9×2+1’=-18x(x2+1)2y’=0⇔x=0y’≤0⇔x≥0y’≥0⇔x≤0

В итоге мы определили, что данная функция будет убывать, если x≥0; возрастать, если x≤0; она имеет точку максимума y(0)=902+1=9 при переменной, равной 0.

Посмотрим, как же ведет себя функция на бесконечности:

limx→-∞9×2+1=9-∞2+1=9·1+∞=+0limx→+∞9×2+1=9+∞2+1=9·1+∞=+0

Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.

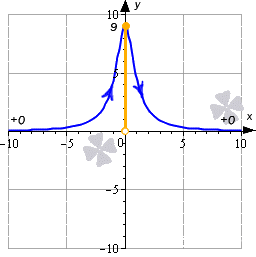
Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9. Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0. Мы отобразили это на рисунке:

На нем видно, что областью значений функции будет интервал E(y)=(0; 9]

Ответ: E(y)=(0; 9]

Если нам надо определить множество значений функции y = f(x) на промежутках [a; b), (a; b], [a; +∞), (-∞; b], то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.

А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.

Пример 7

Условие: определите, какой будет область значений y=xx-2.

Решение

Поскольку знаменатель функции не должен быть обращен в 0, то D(y)=-∞; 2∪2; +∞.

Начнем с определения множества значений функции на первом отрезке -∞; 2, который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.

limx→2-0xx-2=2-02-0-2=2-0=-∞limx→-∞xx-2=limx→-∞x-2+2x-2=limx→-∞1+2x-2=1+2-∞-2=1-0

Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1. Если же значения x меняются от минус бесконечности до 2, то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала -∞; 1. Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.

Для открытого луча 2; +∞ производим точно такие же действия. Функция на нем также является убывающей:

limx→2+0xx-2=2+02+0-2=2+0=+∞limx→+∞xx-2=limx→+∞x-2+2x-2=limx→+∞1+2x-2=1+2+∞-2=1+0

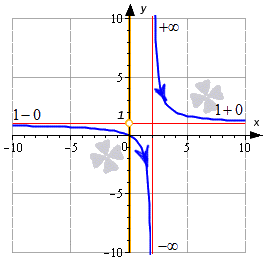
Значения функции на данном отрезке определяются множеством 1; +∞. Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств -∞; 1 и 1; +∞.

Ответ: E(y)=-∞; 1∪1; +∞.

Это можно увидеть на графике:

Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.

Пример 8

Условие: определите область значений синуса y = sin x.

Решение

Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0; 2π и смотрим, каким будет множество значений на нем.

y’=(sin x)’=cos xy’=0⇔cos x=0⇔x=π2+πk, k∈Z

В рамках 0; 2π у функции будут точки экстремума π2 и x=3π2. Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.

y(0)=sin 0=0yπ2=sin π2=1y3π2=sin3π2=-1y(2π)=sin(2π)=0⇔minx∈0; 2πsin x=sin3π2=-1, maxx∈0; 2πsin x=sinπ2=1

Ответ: E(sin x)=-1; 1.

Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения (или указать). Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.

Пример 9

Условие: определите область значения y=3arccosx3+5π7-4.

Решение

Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E(arccos x)=0; π или 0≤arccos x≤π. Мы можем получить функцию arccosx3+5π7 из арккосинуса, сдвинув и растянув ее вдоль оси Ox, но такие преобразования нам ничего не дадут. Значит, 0≤arccosx3+5π7≤π.

Функция 3arccosx3+5π7 может быть получена из арккосинуса arccosx3+5π7 с помощью растяжения вдоль оси ординат, т.е. 0≤3arccosx3+5π7≤3π. Финалом преобразований является сдвиг вдоль оси Oy на 4 значения. В итоге получаем двойное неравенство:

0-4≤3arccosx3+5π7-4≤3π-4⇔-4≤3arccosx3+5π7-4≤3π-4

Мы получили, что нужная нам область значений будет равна E(y)=-4; 3π-4.

Ответ: E(y)=-4; 3π-4.

Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.

Пример 10

Условие: вычислите, какова будет область значений функции y=22x-1+3.

Решение

Перепишем функцию, заданную в условии, как y=2·(2x-1)-12+3. Для степенной функции y=x-12 область значений будет определена на промежутке 0; +∞, т.е. x-12>0. В таком случае:

2x-1-12>0⇒2·(2x-1)-12>0⇒2·(2x-1)-12+3>3

Значит, E(y)=3; +∞.

Ответ: E(y)=3; +∞.

Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.

Пример 11

Условие: дана функция y=2sinx2-4, x≤-3-1, -3<x≤31x-3, x>3. Вычислите область ее значений.

Решение

Данная функция является определенной для всех значений x. Проведем ее анализ на непрерывность при значениях аргумента, равных -3 и 3:

limx→-3-0f(x)=limx→-32sinx2-4=2sin-32-4=-2sin32-4limx→-3+0f(x)=limx→-3(1)=-1⇒limx→-3-0f(x)≠limx→-3+0f(x)

Имеем неустранимый разрыв первого рода при значении аргумента -3. При приближении к нему значения функции стремятся к -2sin32-4, а при стремлении x к -3 с правой стороны значения будут стремиться к -1.

limx→3-0f(x)=limx→3-0(-1)=1limx→3+0f(x)=limx→3+01x-3=+∞

Имеем неустранимый разрыв второго рода в точке 3. Когда функция стремится к нему, ее значения приближаются к -1, при стремлении к той же точке справа – к минус бесконечности.

Значит, вся область определения данной функции является разбитой на 3 интервала (-∞; -3], (-3; 3], (3; +∞).

На первом из них у нас получилась функция y=2sinx2-4. Поскольку -1≤sin x≤1, получаем:

-1≤sinx2<1⇒-2≤2sinx2≤2⇒-6≤2sinx2-4≤-2

Значит, на данном промежутке (-∞; -3] множество значении функции – [-6;2].

На полуинтервале (-3; 3] получилась постоянная функция y =-1. Следовательно, все множество ее значений в данном случае будет сводится к одному числу -1.

На втором промежутке 3; +∞ у нас есть функция y=1x-3. Она является убывающей, потому что y’=-1(x-3)2<0. Она будет убывать от плюс бесконечности до 0, но самого 0 не достигнет, потому что:

limx→3+01x-3=13+0-3=1+0=+∞limx→+∞1x-3=1+∞-3=1+∞+0

Значит, множество значений исходной функции при x > 3 представляет собой множество 0; +∞. Теперь объединим полученные результаты: E(y)=-6; -2∪-1∪0; +∞.

Ответ: E(y)=-6; -2∪-1∪0; +∞.

Решение показано на графике:

Пример 12

Условие: есть функция y=x2-3ex. Определите множество ее значений.

Решение

Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:

y’=x2-3ex’=2xex-ex(x2-3)e2x=-x2+2x+3ex=-(x+1)(x-3)ex

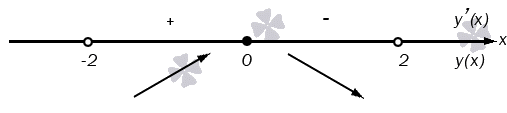
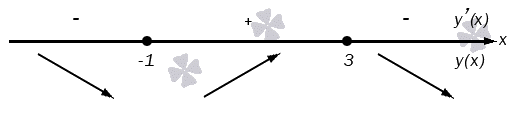
Мы знаем, что производная обратится в 0, если x=-1 и x=3. Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.

Функция будет убывать на (-∞; -1]∪[3; +∞) и возрастать на [-1; 3]. Точкой минимума будет -1, максимума –3.

Теперь найдем соответствующие значения функции:

y(-1)=-12-3e-1=-2ey(3)=32-3e3=6e-3

Посмотрим на поведение функции на бесконечности:

limx→-∞x2-3ex=-∞2-3e-∞=+∞+0=+∞limx→+∞x2-3ex=+∞2-3e+∞=+∞+∞==limx→+∞x2-3’ex’=limx→+∞2xex=+∞+∞==limx→+∞2x'(ex)’=2limx→+∞1ex=2·1+∞=+0

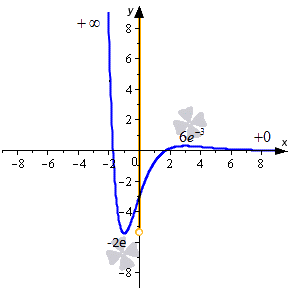
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.

На нем видно, что значения функции будут убывать от плюс бесконечности до -2e тогда, когда аргумент меняется от минус бесконечности до -1. Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6e-3 до 0, но при этом 0 достигнут не будет.

Таким образом, E(y)=[-2e; +∞).

Ответ: E(y)=[-2e; +∞)

Источник

0 / 0 / 0

Регистрация: 24.12.2018

Сообщений: 2

24.12.2018, 12:21. Показов 2734. Ответов 1

Найти сумму значений функции, определенной на отрезке [-5,5] с шагом 0,5
Y = х3 – cosx + sin2x

Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782	24.12.2018, 12:21
1

TrollHammer

1192 / 692 / 329

Регистрация: 22.02.2018

Сообщений: 2,001

Записей в блоге: 2

24.12.2018, 13:13

Если правильно понял формулу, то так

#include <stdio.h>
#include <math.h>
 
float f_y(float x)
{
   return (x*x*x)-cos(x)+sin(x)*sin(x);
}
 
main()
{
    float x;
 
    for(x = -5.; x<=5; x+=.5)
     printf("X = %2.2f  Y = %fn", x, f_y(x));
 
     system("pause");
}

Источник

КАК НАЙТИ МНОЖЕСТВО ЗНАЧЕНИЙ
ФУНКЦИИ

Сильвестров
В.В.

д.ф.-м.н.,
профессор кафедры
естественнонаучных дисциплин

Чувашского
республиканского института образования

Единый государственный
экзамен (ЕГЭ) внес новое веяние в
экзаменационные задания по математике.
Наряду с задачами традиционного
характера, предлагающимися на выпускных
экзаменах за курс средней школы и
вступительных экзаменах в вузы, задания
ЕГЭ неизменно содержат 2-3 задачи на
нахождение множества значений функции
или сводящиеся к ним задачи. Такие задачи
вызывают у учащихся немалые затруднения,
и особенно, если требуется оформление
решения с обоснованием всех моментов.

В данной статье на
конкретных примерах раскрываются методы
нахождения множества значений функции.
Более подробно с этими методами, теорией
и типовыми примерами можно ознакомиться
по книге [1].

Приведем свойства непрерывных,
монотонных и дифференцируемых функций,
наиболее часто используемые при
нахождении множества значений функции.

Если функция

непрерывна на отрезке

и

– ее наименьшее и наибольшее значения
на этом отрезке, то множество значений
функции

на

есть отрезок

Если

непрерывная и возрастающая
функция на отрезке
,
то множество значений функции на этом
отрезке есть отрезок
.
При этом каждое значение

функция принимает ровно при одном
значении
,
т.е. уравнение

имеет единственный корень
на отрезке
.
Если

– непрерывная и убывающая функция на
отрезке
,
то ее множество значений на

есть отрезок
.

Если функция непрерывна
на отрезке

и дифференцируема (имеет
производную) в интервале

то наибольшее и наименьшее
значения функции на этом отрезке
существуют и достигаются либо на концах
отрезка, либо в критических точках
функции, расположенных на отрезке.

К основным методам и
приемам нахождения множества значений
функции относятся:

последовательное нахождение
значений сложных аргументов функции;
метод оценок;
использование свойств непрерывности
и монотонности функции;
использование производной;
графический метод;
метод введения параметра;
метод обратной функции.

Рассмотрим эти методы на конкретных
примерах.

Пример 1.
Найдите область значений

функции

Решим пример методом
последовательного нахождения значений
сложных аргументов функции.

Так как

принимает все неотрицательные
значения, и только их, то

Обозначим

Тогда

где

Функция

определена лишь при

поэтому ее множество значений при

совпадает с множеством значений функции
на промежутке (0; 10], где функция
непрерывна и возрастает. При

она стремится к
,
а при

принимает значение 1. Следовательно,
множество значений

на (0; 10] есть луч

Тем самым,
.
Тогда у функции

область значений
.

Через сложный аргумент
z
исходная функция выражается
формулой

где
.
Эта функция определена при

поэтому множество значений функции у
при

совпадает с ее множеством значений при
.
На промежутке (0; 2] функция

непрерывна и убывает. Так
как логарифмирование по основанию 0,1
меняет характер монотонности, то у
– непрерывная и возрастающая
функция на (0; 2]. При

дробь

стремится к
,
значит, функция у
стремится к
.
При

она равна

Следовательно, множество значений
функции у при

есть луч
.
Это и есть

Ответ:
.

Пример 2.
Найдите область значений

функции

Решим пример методом
оценок.

Из неравенств

складывая второе и
последнее по частям, получим

При

и

функция принимает значения

и

Эта функция, как линейная комбинация
непрерывных функций

и

непрерывна на всей числовой оси, поэтому
она принимает все значения с (– 7) до
7 включительно, причем только их, так
как в силу неравенств

другие значения у нее
невозможны.

Ответ:
.

Наиболее распространенная
ошибка при нахождении множества значений
функции методом оценок состоит в
следующем. На основании полученных
оценок, например, неравенств

делается ошибочно заключение,
что множество значений функции есть
отрезок [А; В],
в то время, как такое заключение
можно сделать лишь тогда, когда функция
непрерывна на рассматриваемом промежутке
и на нем имеются точки, в которых функция
принимает значения А
и В (достигает
нижней А и
верхней В
границы оценки). В общем
случае оценка

лишь означает, что множество
значений функции на рассматриваемом
промежутке принадлежит
отрезку [А; В],
и вовсе не означает, что оно
совпадает со
всем отрезком [А; В].
Например, функция

как и функция в примере 2, удовлетворяет
неравенствам

Однако нет таких значений
x,
при которых функция принимала бы значения
(– 7) и 7, поэтому на основании неравенств

можно лишь утверждать о
принадлежности множества значений
функции отрезку
.
На самом деле,
,
что найдем в следующем примере, используя
производную.

Пример 3.

Решение. По формуле синуса
тройного угла

Обозначим

Тогда

Так как

принимает все значения с
(– 1) до 1 включительно, и только их,
то область значений функции у
совпадает с множеством
значений функции

на отрезке
.

На этом отрезке функция

дифференцируема, так как ее
производная

существует при всех
.
Из уравнения

находим критические точки функции

которые принадлежат отрезку
.
В этих точках и на концах отрезка

Так как

то

и по свойству дифференцируемой функции
наименьшее значение функции

на отрезке

равно
,
а наибольшее значение равно
.
На отрезке

функция
,
как многочлен, непрерывна
(это следует также из дифференцируемости
функции), поэтому ее множество значений
на этом отрезке есть и область значений
.

Ответ:
.

Пример 4.
Найдите множество значений
функции

на отрезке
.

Решим пример, используя
свойство непрерывности и
монотонности функции.

На отрезке

функция

а значит, и функция

убывают и непрерывны. Кроме того,

так как

для всех х.
Так как

имеет другой характер монотонности,
чем t,
и

то функция

непрерывна, возрастает и положительна
при
.
Функция

непрерывна и возрастает на
всей числовой оси, в частности, и на
отрезке
,
где она, кроме того, положительна.
Следовательно, функция

как произведение двух непрерывных,
возрастающих и положительных функций

и
,
также непрерывна и возрастает на отрезке
,
поэтому искомое множество значений
функции

есть отрезок

Ответ:
.

Задача нахождения области
(множества) значений функции

тесно связана с вопросом о разрешимости
уравнения

Действительно, число а
является одним из значений
функции

тогда и только тогда, когда
найдется хотя бы одно значение аргумента
х такое,
что

Последнее означает, что
уравнение

имеет хотя бы один корень х.
Следовательно, область
значений

функции

совпадает с множеством значений параметра
а, для которых уравнение

имеет хотя бы один корень.

Пример 5.

Решение. Найдем множество
значений параметра а,
для которых уравнение

имеет хотя бы один корень.

При

уравнение является линейным

с ненулевым коэффициентом при неизвестной
x,
поэтому имеет решение.

При

уравнение является квадратным,
поэтому оно разрешимо тогда и только
тогда, когда его дискриминант

Так как точка

принадлежит заштрихованному отрезку,
то искомым множеством значений параметра
а, значит, и
областью значений

будет весь этот отрезок.

Ответ:
.

Как продолжение метода
введения параметра
можно рассматривать метод обратной
функции, для нахождения
которой надо решать относительно х
уравнение

считая у
параметром. Если это уравнение
имеет единственное решение

то область
значений

исходной функции

совпадает с областью
определения
обратной
функции

Пример 6.

Решение. Найдем обратную
функцию

из уравнения

Теперь найдем область
определения
:

Так как

то

Ответ:

При нахождении множества
значений функции во многих случаях
помогает схематический график функции.

Пример 7.
Из уравнения

нашли всевозможные у
через х.
Найдите множество всех
значений, которые может принимать у.

Решим пример графически.

В системе координат Оху
построим график уравнения

Им будет окружность
радиуса 2 с центром в точке (0; 1). С
другой стороны, этот график представляет
собой совокупность графиков всевозможных
функций у,
определяемых из заданного
уравнения, поэтому у
может принимать все те
значения, которые являются координатами
проекций точек графика на ось Оу.
Из рисунка видно, что искомое
множество есть отрезок
.

Ответ:
.

Пример 8.
Найдите все те значения функции

каждое из которых она принимает только
при одном значении аргумента х
(ровно один раз).

Решение. По свойствам
степеней
.
Обозначим

Тогда

Так как

и

– возрастающая
функция на числовой оси, то различным
значениям х
соответствуют различные
положительные значения t,
поэтому задача равносильна
задаче нахождения таких значений а
функции

каждое из которых она принимает ровно
при одном положительном значении
аргумента t.

Последнее означает, что
график функции

при

(часть параболы с вершиной в точке

ветви которой направлены вверх) и
прямая

имеют единственную общую
точку (пересечения или касания). Из
рисунка, на котором изображены нужные
нам часть параболы и прямые, видно,
что указанному условию удовлетворяют
значения

Это и есть искомые значения функции
у.

Ответ:

Приведенные примеры не
исчерпывают все многообразие задач,
связанных с нахождением множества
значений функции. Большое число таких
задач, с решениями и без них, имеется в
книге [1]. Приведем некоторые из них,
рекомендуя читателям самостоятельно
решить их.

А1. Найдите области (множества)
значений функций:

1) 2) 3)