|
Как проверить, существует ли треугольник, если известны три его стороны?
Необходимым и достаточным условием существования треугольника является выполнение следующих неравенств: a+b>c, a+c>b, b+c>a, (a>0, b>0, c>0), где a, b и с – длины сторон треугольника. Другими словами, треугольник существует тогда и только тогда, когда сумма любых двух его сторон больше третьей стороны.
автор вопроса выбрал этот ответ лучшим
Kuzmich291192 9 лет назад Условие существования треугольника можно представить в следующем виде: пусть a b c стороны треугольника. Тогда, что бы треугольник существовал необходимо, что бы сумма двух любых его сторон была больше третьей стороны a+b>c или a+c>b или b+c>a (если сумма будет равна какой-либо стороне, то такой треугольник называется вырожденным). Рассмотрим пример: пусть дан треугольник со сторонами 3, 6, 5. Возьмём две любые стороны, например, 3 и 6. Проверим условие существования: 3+6=9>5, следовательно треугольник существует. Так же условие сущесвтвования треугольника можно представить в виде векторной суммы. Пусть вектора a b c задают стороны треугольника(и эти вектора не равны нуль-вектору), тогда треугольник существует, если векторная сумма a+b+c=0.
Mefody66 9 лет назад Kuzmich291192 написал в общем, все правильно, но с одним маленьким уточнением: нужно взять самую большую сторону, и проверить, что сумма двух других сторон больше, чем эта большая сторона. Возьмем, например, числа 1, 2 и 10. Если мы сложим 1 + 10 > 2, 2 + 10 > 1, значит, треугольник существует? НЕТ! 1 + 2 < 10. Поэтому треугольник не существует.
У м к а 6 лет назад В геометрии есть теорема под названием “Неравенство треугольника”, которая гласит о том, что любая из сторон треугольника не будет превосходить по своему значению сумму двух других его сторон. Примечательно, что данная теорема также имеет доказательство.
Таким образом, вам необходимо всего лишь поочерёдно просуммировать по две стороны треугольника и сравнить полученное значение с размером третьей стороны, которая не участвовала с сложении.
Galina7v7 4 года назад Когда такой вопрос конкретно задаётся, причём, в цифрах, то нужно проверить величину каждой стороны, чтобы на была меньше суммы двух других сторон. Вот треугольник со сторонами 3,4, и 5 существует, а изменив только одну из сторон, например, 5 см на 7 см, то такого треугольника не существует, так 3 + 4 = 7, а не больше, как положено для существования треугольника. Начинать проверку нужно для большей стороны, и если она меньше суммы двух меньших сторон, то этот треугольник существует. Требование к углам треугольника тоже не маловажное, потому что если даны углы треугольника, и сумма их не равна 180 градусам, то треугольник не существует.
Если известны длины трех сторон треугольника, то еще до его построения можно определить может ли такой треугольник существовать реально. Есть даже простенькая программа для вычисления этого на компьютере, но все что нам надо это найти самую длинную сторону из заданных и проверить является ли сумма двух других сторон больше. Примерно так: заданы три сторона а, в, с, причем в сторона самая длинная. Условием возможности существования треугольника будет выполнение неравенства в<а+с. Если большая сторона будет равна сумме двух других сторон, то это случай вырожденного треугольника, когда все вершины лежат на одной прямой:
Azamatik 6 лет назад Имеем треугольник АВС, где АВ, ВС и СА – это три его стороны. Треугольник существует в тех случаях, когда АВ + ВС > СА; АВ + СА > ВС; ВС + СА > АВ, то есть в том случае, если сложить любые две стороны любого треугольника, сумма должна быть больше третьей его стороны. Например, АВ = 5 см, ВС = 6 см, СА = 8 см – треугольник существует. И другой пример: АВ = 4 см, ВС = 3 см, СА = 9 см. Получается, что одна сторона больше суммы двух других – треугольник не существует.
moreljuba 6 лет назад Чтобы проверить существование треугольника нужно сложить все три угла треугольника ивот если они в сумме не дадут 180-ти градусов, то такого треугольника просто как раз не существует. А также треугольника не существует в том случае, когда одна сторона будет по длине больше чем длина в сумме двух других сторон.
Помощни к 6 лет назад Если одна из сторон треугольника будет больше (по длине), чем две других стороны, то из этих катетов не получится сделать один треугольник. Получится фигура, напоминающая флажок, состоящая из треугольника и присоединенной линии. Любая сторона не может быть больше сумму двух оставшихся сторон треугольника.
Smiledimasik 6 лет назад Самое главное во всех правилах существования треугольника то, что сума двух меньших сторон треугольника или как называются они “катеты” должна быть больше самой большой стороны треугольника. Если сума этих сторон совпадет с самой большой стороной, то это будет обычная прямая с точками на ней.
MarkTolkien 6 лет назад Длина каждой из сторон треугольника должна быть меньше сумы остальных двух сторон, иначе этот треугольник не сложится. Углы треугольника в сумме дают 180 градусов, это еще один критерий для проверки, позволяющий вычислить, существует ли треугольник.
Roxrite 9 лет назад Если одна сторона треугольника окажется больше суммы двух остальных сторон, то такого треугольника не существует. Если сумма всех 3-х углов треугольника не будет равна 180°, то такого треугольника не существует. Знаете ответ? |
Онлайн калькулятор поможет проверить существование треугольника.
Чтобы треугольник существовал, сумма двух сторон треугольника всегда должна быть больше третей стороны.
a + b > c, b + c > a, a + c > b.
Определить существование треугольника |
|
| Сторона треугольника A | |
| Сторона треугольника B | |
| Сторона треугольника C | |
|
|
|
Скачать калькулятор
Рейтинг: 3.4 (Голосов 76)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Сторона квадрата |
| Стороны ромба | Стороны параллелограмма | Ребро куба | Боковое ребро параллелепипеда |
Существующие треугольники
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.
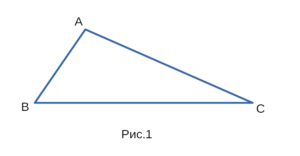
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы
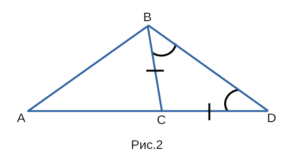
- Проведем отрезок CD равный отрезку CB.
- △BCD — равнобедренный, значит ∠ CBD=∠CDB.
- Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB
Треугольник — определение и основные свойства и виды треугольника
Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.
Определение треугольника
Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.
Посмотрите на треугольник на рисунке.

У него три вершины —  ,
,  ,
,  и три стороны
и три стороны  ,
,  и
и  . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут
. У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут  ([а-бэ-цэ]). А треугольник на вот этом рисунке
([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать  ([эм-эн-ка]).
([эм-эн-ка]).
По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.
В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.
Высота треугольника
В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.
Например, в треугольнике  , высотой будет отрезок
, высотой будет отрезок  .
.

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты  ,
,  ,
,  .
.
Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.
Виды треугольника
Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.
Виды треугольников по углам
В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный
, треугольник бывает остроугольным, тупоугольным или прямоугольным.
Посмотрите на рисунки — перед вами три основных вида треугольника:



Виды треугольников по сторонам
Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.
На рисунке показаны равносторонний и равнобедренный треугольники.


Свойства сторон треугольника
Треугольник имеет важные свойства и характеристики.
Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.
Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.
Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:
Например, пусть наш треугольник имеет длины двух сторон  , а
, а  см. В каком диапазоне будет размер третьей стороны треугольника?
см. В каком диапазоне будет размер третьей стороны треугольника?
Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.
Правило существования треугольника
Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.
Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.
Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?
Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.
Свойство углов в треугольнике
Сумма всех углов в треугольнике равна  .
.
Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна  .
.
Например, пусть известно, что в треугольнике  ,
,  ,
,  , нужно найти
, нужно найти  .
.

Так как сумма углов в треугольнике равна  , то находим:
, то находим:
 .
.
Ответ:  .
.
Элементы композиции
Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.
Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры – треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Определение треугольника
Треугольник – это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом – △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)
- Точки A, B и C – вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА – стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b – β, с – γ.
Углы треугольника, также, можно обозначать специальным символом – ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Свойства треугольника
1.Свойства углов и сторон треугольника.

- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника
Формулы медиан треугольника через стороны:
[spoiler title=”источники:”]
http://repetitor-mathematics.ru/treugolnik-vidy-treugolnika-svoistva/
http://binary2hex.ru/triangle.html
[/spoiler]
Существующие треугольники

Обновлено 28.02.2022
Содержание
- Определение
- Теорема
- Доказательство теоремы
- Следствия из теоремы
- Признаки существования треугольника
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы

- Проведем отрезок CD равный отрезку CB.
- △BCD — равнобедренный, значит ∠CBD = ∠CDB.
- Рассмотрим △ABD: ∠ABD > ∠CBD, следовательно ∠ABD > ∠CDB, то AB < AD.
- Но AD = AC + CD = AC + CB, поэтому AB < AC + CB, ч.т.д.
Следствия из теоремы
- Для любых точек А, В, С, не лежащих на
одной прямой справедливы неравенства:
AB < AC + BC
AC < AB + BC
BC < AC + AB
- Каждая сторона треугольника меньше суммы двух других сторон.
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним углов.
- Теорема о неравенстве треугольника для разности сторон.
Признаки существования треугольника
- Если каждая сторона треугольника меньше суммы двух других сторон, значит треугольник существует.
- Если большая сторона треугольника меньше суммы двух других сторон,
значит треугольник существует. - Если сумма углов треугольника равна 180°, значит треугольник существует.
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b , b + c , a + c . Первую сумму сравниваем с оставшейся стороной c , вторую — с a и третью — с b . Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
Содержание
- 1 Как по сторонам узнать какой треугольник?
- 2 В каком случае существует треугольник?
- 3 Как определить какой треугольник?
- 4 Какие существуют виды треугольников?
- 5 Что такое острый треугольник?
- 6 Как определить прямоугольный треугольник или нет?
- 7 Как проверить существует ли треугольник с данными сторонами?
- 8 В каком случае нельзя построить треугольник?
- 9 Как узнать можно ли построить треугольник со сторонами?
- 10 Какие бывают треугольники 4 класс?
- 11 Какие бывают треугольники 3 класс?
- 12 Какие виды треугольников бывают по углам и сторонам?
- 13 Какие виды треугольников ты знаешь?
- 14 Какие бывают разносторонние треугольники?
Как по сторонам узнать какой треугольник?
Если выполняется теорема Пифагора: с²=a²+b² , где с — наибольшая сторона, а и b две других, – треугольник прямоугольный. Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² треугольник остроугольный.
В каком случае существует треугольник?
Треугольник существует только тогда, когда сумма двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше либо равна сумме двух других, то треугольника с такими сторонами не существует.
Как определить какой треугольник?
Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла, т. е. как часть плоскости, ограниченную тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Какие существуют виды треугольников?
Существует три вида треугольников по углам:
- остроугольные;
- прямоугольные;
- тупоугольные.
Что такое острый треугольник?
Остроугольный треугольник — это треугольник, у которого все углы острые. Прямоугольный треугольник — это треугольник, у которого есть прямой угол. Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Как определить прямоугольный треугольник или нет?
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов). Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Как проверить существует ли треугольник с данными сторонами?
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b , b + c , a + c . Первую сумму сравниваем с оставшейся стороной c , вторую — с a и третью — с b . Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
В каком случае нельзя построить треугольник?
Если большая сторона меньше суммы двух других сторон, то треугольник построить можно. 1) а = 1 см; b = 2 см; с = 3 см, 3 треугольник построить нельзя.
Как узнать можно ли построить треугольник со сторонами?
По свойству треугольников: «Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше или равна сумме двух других, то треугольника с такими сторонами не существует.»
Какие бывают треугольники 4 класс?
Мы знали, что треугольники бывают разносторонние, равносторонние и равнобедренные. Мы узнали, что треугольники еще бывают остроугольные, прямоугольные и тупоугольные.
Какие бывают треугольники 3 класс?
По сторонам различают 3 вида треугольников: разносторонние, равнобедренные и равносторонние.
Какие виды треугольников бывают по углам и сторонам?
Виды треугольников по углам
- Остроугольный треугольник – это треугольник, у которого все углы острые, то есть меньше 90°.
- Прямоугольный треугольник – это треугольник, у которого один из углов является прямым, то есть равен 90°. …
- Тупоугольный треугольник – это треугольник, у которого один из углов является тупым, то есть больше 90°.
Какие виды треугольников ты знаешь?
Какие виды треугольников ты знаешь
- прямоугольный,равносторонний,равнобедренный,тупоугольный, остроугольный, прямоугольный
- Треугольник называется РАВНОБЕДРЕННЫМ, если у него две стороны равны.
- Треугольник, у которого все стороны равны, называется РАВНОСТОРОННИМ или ПРАВИЛЬНЫМ.
2 февр. 2014 г.
Какие бывают разносторонние треугольники?
Разносторонним называется треугольник, у которого все стороны имеют разную длину. Против большего угла лежит большая сторона, а против меньшего угла — меньшая сторона.




