
Пример параллакса (видео)
Паралла́кс (греч. παράλλαξις, от παραλλαγή, «смена, чередование») — изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя.
Зная расстояние между точками наблюдения L (базис) и угол смещения α, можно определить расстояние до объекта:
Для малых углов (α — в радианах)

Измерение расстояния при помощи параллакса
Параллакс используется в геодезии и астрономии для измерения расстояния до удалённых объектов (в частности в специальных единицах — парсеках). На явлении параллакса основано бинокулярное зрение.
Астрономия[править | править код]
Суточный параллакс[править | править код]
Суточный параллакс (геоцентрический параллакс) — разница в направлениях на одно и то же светило из центра масс Земли (геоцентрическое направление) и из заданной точки на поверхности Земли (топоцентрическое направление).
Этот угол зависит от высоты светила над горизонтом, максимальное его значение достигается при нулевой высоте (когда светило наблюдается прямо на горизонте).
Такая величина называется горизонтальным параллаксом[1]. База параллакса при этом равна радиусу Земли (около 6400 км).
Из-за вращения Земли вокруг своей оси положение наблюдателя относительно центра Земли и, соответственно, параллактический угол циклически изменяются.
При наблюдении Луны её кажущиеся смещения на фоне звёзд (по сравнению с расчётным орбитальным движением) достигают 2° (соответственно, параллакс равен 1°) и были замечены уже древнегреческими астрономами, что позволило им довольно точно определить расстояние до Луны[2].
Суточный параллакс планет довольно мал (для Марса 24″ во время великого противостояния), но тем не менее был единственным способом измерения абсолютных расстояний в Солнечной системе до появления радиолокации: наиболее удобными для этого были прохождения Венеры по диску Солнца и близко подходящие к Земле астероиды (относительные же расстояния легко определяются на основе законов Кеплера, так что достаточно абсолютного измерения какого-то одного расстояния, чтобы определить все).
Годичный параллакс[править | править код]
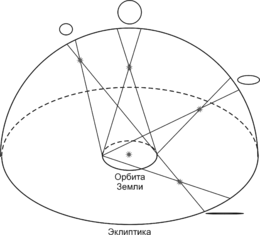
Параллактические эллипсы звёзд при различных расстояниях от плоскости эклиптики
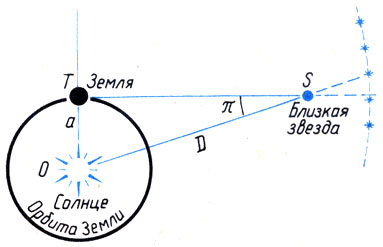
Годичный параллакс — изменение направления на объект (например, звезду), связанное с движением Земли вокруг Солнца. Величина параллакса равна углу, под которым со звезды видна большая полуось земной орбиты (перпендикулярная лучу зрения).
Годичные параллаксы являются показателями расстояний до звёзд. Расстояние до объекта, годичный параллакс которого равен 1 угловой секунде, называется парсек (1 парсек = 3,085678⋅1016 м). Ближайшая к нам звезда Проксима Центавра имеет параллакс 0,7687±0,0003″, следовательно, расстояние до неё составляет 1,3009±0,00015 пк.
Вековой параллакс[править | править код]
Вековым параллаксом обычно называется изменение видимого положения объекта на небесной сфере в результате комбинаций собственных движений этого объекта и Солнечной системы в галактике.
Параллакс в фотографии[править | править код]

Отражение солнца в воде находится на отражении фонаря, хотя в неотражённом виде оно находится на заметном удалении над фонарём
Параллакс видоискателя[править | править код]
Параллакс видоискателя — несовпадение границ изображения, видимых в оптическом видоискателе, с границами изображения, получаемого в кадровом окне[3]. Параллакс почти незаметен в случае съёмки удалённых объектов, и весьма значителен на небольших конечных дистанциях[4]. Он возникает из-за наличия расстояния (базиса) между оптическими осями съёмочного объектива и видоискателя. Величина параллакса 
где 


Параллакс прицела[править | править код]
Частным случаем является параллакс прицела.
Параллакс прицела — это угол между осью ствола и осью прицела с вершиной на цели. Чем ближе цель к стрелку, тем больше этот угол, тем больше надо корректировать прицел. Если прицел пристрелян на расстояние в 100 метров, а цель находится на расстоянии 50 метров, то пуля пролетит ниже цели. И чем ближе цель будет приближаться к 100 метрам от стрелка, тем ближе будет попадание к цели. При нахождении цели дальше 100 метров пуля пролетит выше цели. Баллистика в данном вопросе не учитывается.
Параллакс дальномера[править | править код]
Параллакс дальномера — угол, под которым виден объект во время наводки на резкость с помощью оптического дальномера.
Стереоскопический параллакс[править | править код]
Стереоскопический (бинокулярный) параллакс — это угол, под которым рассматривают объект двумя глазами или когда его фотографируют стереоскопическим фотоаппаратом.
Временно́й параллакс[править | править код]
Временной параллакс — искажение формы быстро движущихся объектов, возникающее при съёмке фотоаппаратом со шторно-щелевым фокальным затвором или видеокамерой со строчным переносом. Так как экспозиция происходит не единовременно по всей площади светочувствительного элемента, а последовательно по мере движения щели, то при съёмке быстро движущихся объектов их форма может искажаться. Например, если объект движется в ту же сторону, что и щель затвора, его изображение будет растянуто, а если в обратную, то сужено.
Примечания[править | править код]
- ↑ Параллакс Архивная копия от 26 апреля 2016 на Wayback Machine (Глоссарий astronet.ru)
- ↑ Еремеева А. И., Цицин Ф.А. История астрономии. — М.: Изд-во МГУ, 1989. — С. 89. — 349 с.
- ↑ Техника фотографии, 1973, с. 40.
- ↑ Выбор фотоаппарата, 1962, с. 26.
Литература[править | править код]
- Бунимович Д. З. Выбор фотоаппарата / Е. А. Иофис. — М.: «Искусство», 1962. — 128 с.
- Иофис Е. А. Техника фотографии. — М.: «Искусство», 1973. — 349 с.
- Яштолд-Говорко В. А. Фотосъёмка и обработка. Съёмка, формулы, термины, рецепты. Изд. 4-е, сокр. — М.: «Искусство», 1977.
- Hirshfeld, Alan w. Parallax: The Race to Measure the Cosmos. — New York: W.H. Freeman (англ.) (рус., 2001. — ISBN 978-0-7167-3711-7.
- Whipple, Fred L. Earth Moon and Planets. — Read Books, 2007. — ISBN 978-1-4067-6413-0.
- Zeilik, Michael A.; Gregory, Stephan A. Introductory Astronomy & Astrophysics. — 4th. — Saunders College Publishing (англ.) (рус., 1998. — ISBN 978-0-03-006228-5.
Ссылки[править | править код]
- The ABC’s of Distances — обзор об измерении расстояний до астрономических объектов (англ.)
Координаты небесных тел, определенные
из наблюдений на поверхности Земли,
называются топоцентрическими.
Топоцентрические координаты одного и
того же светила в один и тот же момент,
вообще говоря, различны для различных
точек на поверхности Земли. Различие
это заметно лишь для тел Солнечной
системы и практически не ощутимо для
звезд (меньше 0″,00004). Из множества
направлений, по которым светило видно
из разных точек Земли, основным считается
направление из центра Земли. Оно дает
геоцентрическое положение светила и
определяет его геоцентрические
координаты. Угол между направлениями,
по которым светило М’ было бы видно из
центра Земли и из какой-нибудь точки на
ее поверхности, называется суточным
параллаксом светила (рис. 20). Иными
словами, суточный параллакс есть угол
![]() ‘,
‘,
под которым со светила был бы виден
радиус Земли в месте наблюдения.

Для светила, находящегося в момент
наблюдения в зените, суточный параллакс
равен нулю. Если светило М наблюдается
на горизонте, то суточный параллакс его
принимает максимальное значение и
называется горизонтальным параллаксом
![]() .
.
Из соотношения между сторонами и углами
треугольников ТОМ’ и ТОМ (рис. 20) имеем
![]()
и
![]()
Отсюда получаем
sin ![]() ‘
‘
= sin ![]()
sin ![]() ‘.
‘.
Горизонтальный параллакс у всех тел
Солнечной системы — величина небольшая
(у Луны в среднем
![]() = 57′, у Солнца
= 57′, у Солнца![]() = 8″,79, у планет меньше 1’).
= 8″,79, у планет меньше 1’).
Поэтому синусы углов
![]() и
и![]() ‘
‘
в последней формуле можно заменить
самими углами и написать
![]() ‘
‘
=![]() sin z’. (1.40)
sin z’. (1.40)
Вследствие суточного параллакса светило
кажется нам ниже над горизонтом, чем
это было бы, если бы наблюдение проводилось
из центра Земли; при этом влияние
параллакса на высоту светила пропорционально
синусу зенитного расстояния, а максимальное
его значение равно горизонтальному
параллаксу
![]() .
.
Так как Земля имеет форму сфероида, то
во избежание разногласий в определении
горизонтальных параллаксов необходимо
вычислять их значения для определенного
радиуса Земли. За такой радиус принят
экваториальный радиус Земли R0=
6378 км, а горизонтальные параллаксы,
вычисленные для него, называются
горизонтальными экваториальными
параллаксами![]() 0. Именно эти параллаксы тел Солнечной
0. Именно эти параллаксы тел Солнечной
системы приводятся во всех справочных
пособиях.
4.5. Вычисление моментов времени и азимутов восхода и захода светил
Часовой угол светила определяется из
первой формулы (1.37), а именно:
![]() (1.41)
(1.41)
Если какая-нибудь точка небесного свода
восходит или заходит, то она находится
на горизонте и, следовательно, ее видимое
зенитное расстояние z’ = 90°. Ее истинное
зенитное расстояние z в этот момент
вследствие рефракции будет больше
видимого на величину
![]() = 35′. Суточный параллакс понижает светило
= 35′. Суточный параллакс понижает светило
над горизонтом, т. е. увеличивает видимое
зенитное расстояние z’ на величину
горизонтального параллакса![]() .
.
Следовательно, истинное зенитное
расстояние точки в момент ее восхода
или захода
z = z’ +![]() 90
90
—![]() = 90° +
= 90° +![]() 90
90
—![]() .
.
Кроме того, для Солнца и Луны, имеющих
заметные размеры, координаты относятся
к центру их видимого диска, а восходом
(или заходом) этих светил считается
момент появления (пли исчезновения) на
горизонте верхней точки края диска.
Следовательно, истинное зенитное
расстояние центра диска этих светил в
момент восхода или захода будет больше
зенитного расстояния верхней точки
края диска на величину видимого углового
радиуса R диска. (У Солнца и Луны их
видимые угловые радиусы приблизительно
одинаковы и в среднем равны 16’.)
Таким образом, при вычислении часового
угла светила в момент его восхода и
захода в формуле (1.41), в самом общем
случае, z = 90°+![]() 90—
90—![]() +R,
+R,
и она напишется тогда в следующем виде:
![]() (1.42)
(1.42)
По формуле (1.42) часовые углы восхода и
захода вычисляются только для Луны. В
этом случае RR= 16’, рR= 57’ и![]() 90= 35′. и формула (1.42) принимает вид
90= 35′. и формула (1.42) принимает вид
![]()
При вычислении часовых углов восхода
и захода Солнца его горизонтальным
параллаксом можно пренебречь, и при R ¤
= 16′ и
![]() 90= 35′ формула (1.42) принимает вид
90= 35′ формула (1.42) принимает вид
![]() (1.43)
(1.43)
Для звезд и планет можно пренебречь
также и их видимыми радиусами и вычислять
часовые углы восхода и захода по формуле
![]()
Наконец, если пренебречь и рефракцией,
то часовой угол восхода и захода
вычисляется по формуле
cost= —tg
![]() tg
tg![]() . (1.44)
. (1.44)
Каждое из приведенных уравнений дает
два значения часового угла: t1= t и
t2= — t. Положительное значение
соответствует заходу, отрицательное —
восходу светила. Местное звездное время
восхода и захода, согласно формуле
(1.15), получается таким:
sвосх =
![]() —
—
t.
sзах=
![]() +t.
+t.
Затем можно вычислить моменты восхода
и захода светила по местному среднему
солнечному времени и по декретному
времени.
Если вычисляется восход и заход Солнца,
то нет необходимости вычислять звездное
время явлений, так как, увеличив часовые
углы t1и t2на 12h, мы сразу
получаем моменты по местному истинному
солнечному времени Т¤= t¤+ 12h. Тогда местное среднее время
Tвосх= 12h — t¤+ h,
Тзах= 12h + t¤+ h,
где h — уравнение времени, которое
берется, так же как
![]() и
и![]() Солнца, из Астрономического Ежегодника.
Солнца, из Астрономического Ежегодника.
Азимуты точек восхода и захода светил
(без учета рефракции, параллакса и
углового радиуса) получим, если в первой
формуле (1.36) положим z = 90°; тогда cos z = 0,
sin z =1 и
![]() (1.45)
(1.45)
По формуле (1.45) получаем два значения
азимута: А1= A и A2= 360° — A.
Первое значение является азимутом точки
захода, второе — азимутом точки восхода
светила.
Представим теперь формулы (1.45) и (1.44) в
виде
![]()
и (1.46)
![]()
Так как косинус не может быть больше 1,
то из этих формул следует, что восход и
заход светила возможны только при
условии
|
![]() | < (90° — |
| < (90° — |
![]() | )
| )
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Stellar parallax motion from annual parallax. Half the apex angle is the parallax angle.
Parallax is an angle subtended by a line on a point. In the upper diagram, the Earth in its orbit sweeps the parallax angle subtended on the Sun. The lower diagram shows an equal angle swept by the Sun in a geostatic model. A similar diagram can be drawn for a star except that the angle of parallax would be minuscule.
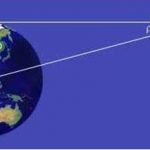
The most important fundamental distance measurements in astronomy come from trigonometric parallax, as applied in the stellar parallax method. As the Earth orbits the Sun, the position of nearby stars will appear to shift slightly against the more distant background. These shifts are angles in an isosceles triangle, with 2 AU (the distance between the extreme positions of Earth’s orbit around the Sun) making the base leg of the triangle and the distance to the star being the long equal length legs. The amount of shift is quite small, even for the nearest stars, measuring 1 arcsecond for an object at 1 parsec’s distance (3.26 light-years), and thereafter decreasing in angular amount as the distance increases. Astronomers usually express distances in units of parsecs (parallax arcseconds); light-years are used in popular media.
Because parallax becomes smaller for a greater stellar distance, useful distances can be measured only for stars which are near enough to have a parallax larger than a few times the precision of the measurement. In the 1990s, for example, the Hipparcos mission obtained parallaxes for over a hundred thousand stars with a precision of about a milliarcsecond,[1] providing useful distances for stars out to a few hundred parsecs. The Hubble telescope WFC3 now has the potential to provide a precision of 20 to 40 microarcseconds, enabling reliable distance measurements up to 5,000 parsecs (16,000 ly) for small numbers of stars.[2][3] The Gaia space mission provided similarly accurate distances to most stars brighter than 15th magnitude.[4] Distances can be measured within 10% as far as the Galactic center, about 30,000 light years away.
Stars have a velocity relative to the Sun that causes proper motion (transverse across the sky) and radial velocity (motion toward or away from the Sun). The former is determined by plotting the changing position of the stars over many years, while the latter comes from measuring the Doppler shift of the star’s spectrum caused by motion along the line of sight. For a group of stars with the same spectral class and a similar magnitude range, a mean parallax can be derived from statistical analysis of the proper motions relative to their radial velocities. This statistical parallax method is useful for measuring the distances of bright stars beyond 50 parsecs and giant variable stars, including Cepheids and the RR Lyrae variables.[5]


Hubble precision stellar distance measurement has been extended 10 times further into the Milky Way.[7]
The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 AU per year, while for halo stars the baseline is 40 AU per year. After several decades, the baseline can be orders of magnitude greater than the Earth–Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of observed stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the uncertainty is inversely proportional to the square root of the sample size.[8]
Moving cluster parallax is a technique where the motions of individual stars in a nearby star cluster can be used to find the distance to the cluster. Only open clusters are near enough for this technique to be useful. In particular the distance obtained for the Hyades has historically been an important step in the distance ladder.
Other individual objects can have fundamental distance estimates made for them under special circumstances. If the expansion of a gas cloud, like a supernova remnant or planetary nebula, can be observed over time, then an expansion parallax distance to that cloud can be estimated. Those measurements however suffer from uncertainties in the deviation of the object from sphericity. Binary stars which are both visual and spectroscopic binaries also can have their distance estimated by similar means, and don’t suffer from the above geometric uncertainty. The common characteristic to these methods is that a measurement of angular motion is combined with a measurement of the absolute velocity (usually obtained via the Doppler effect). The distance estimate comes from computing how far the object must be to make its observed absolute velocity appear with the observed angular motion.
Expansion parallaxes in particular can give fundamental distance estimates for objects that are very far, because supernova ejecta have large expansion velocities and large sizes (compared to stars). Further, they can be observed with radio interferometers which can measure very small angular motions. These combine to provide fundamental distance estimates to supernovae in other galaxies.[9] Though valuable, such cases are quite rare, so they serve as important consistency checks on the distance ladder rather than workhorse steps by themselves.
Parsec[edit]
This section is an excerpt from Parsec.[edit]

The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to 3.26 light-years or 206,265 astronomical units (au), i.e. 30.9 trillion kilometres (19.2 trillion miles).[a] The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 au subtends an angle of one arcsecond[10] (1/3600 of a degree). This corresponds to 648000/π astronomical units, i.e. 1 pc = 1 au/tan(1 arcsec).[11] The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun.[12] Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand.[13]
The word parsec is a portmanteau of “parallax of one second” and was coined by the British astronomer Herbert Hall Turner in 1913[14] to make calculations of astronomical distances from only raw observational data easy for astronomers. Partly for this reason, it is the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and common usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs (kpc) for the more distant objects within and around the Milky Way, megaparsecs (Mpc) for mid-distance galaxies, and gigaparsecs (Gpc) for many quasars and the most distant galaxies.
In August 2015, the International Astronomical Union (IAU) passed Resolution B2 which, as part of the definition of a standardized absolute and apparent bolometric magnitude scale, mentioned an existing explicit definition of the parsec as exactly
648000/π au, or approximately 30.856775814913673×1015 metres (based on the IAU 2012 exact SI definition of the astronomical unit). This corresponds to the small-angle definition of the parsec found in many astronomical references.[15][16]
Stellar parallax[edit]

Stellar parallax created by the relative motion between the Earth and a star can be seen, in the Copernican model, as arising from the orbit of the Earth around the Sun: the star only appears to move relative to more distant objects in the sky. In a geostatic model, the movement of the star would have to be taken as real with the star oscillating across the sky with respect to the background stars.
Stellar parallax is most often measured using annual parallax, defined as the difference in position of a star as seen from the Earth and Sun, i.e. the angle subtended at a star by the mean radius of the Earth’s orbit around the Sun. The parsec (3.26 light-years) is defined as the distance for which the annual parallax is 1 arcsecond. Annual parallax is normally measured by observing the position of a star at different times of the year as the Earth moves through its orbit. Measurement of annual parallax was the first reliable way to determine the distances to the closest stars. The first successful measurements of stellar parallax were made by Friedrich Bessel in 1838 for the star 61 Cygni using a heliometer.[17] Stellar parallax remains the standard for calibrating other measurement methods. Accurate calculations of distance based on stellar parallax require a measurement of the distance from the Earth to the Sun, now based on radar reflection off the surfaces of planets.[18]
The angles involved in these calculations are very small and thus difficult to measure. The nearest star to the Sun (and thus the star with the largest parallax), Proxima Centauri, has a parallax of 0.7687 ± 0.0003 arcsec.[19] This angle is approximate that subtended by an object 2 centimeters in diameter located 5.3 kilometers away.

The fact that stellar parallax was so small that it was unobservable at the time was used as the main scientific argument against heliocentrism during the early modern age. It is clear from Euclid’s geometry that the effect would be undetectable if the stars were far enough away, but for various reasons such gigantic distances involved seemed entirely implausible: it was one of Tycho’s principal objections to Copernican heliocentrism that for it to be compatible with the lack of observable stellar parallax, there would have to be an enormous and unlikely void between the orbit of Saturn (then the most distant known planet) and the eighth sphere (the fixed stars).[21]
In 1989, the satellite Hipparcos was launched primarily for obtaining improved parallaxes and proper motions for over 100,000 nearby stars, increasing the reach of the method tenfold. Even so, Hipparcos was only able to measure parallax angles for stars up to about 1,600 light-years away, a little more than one percent of the diameter of the Milky Way Galaxy. The European Space Agency’s Gaia mission, launched in December 2013, can measure parallax angles to an accuracy of 10 microarcseconds, thus mapping nearby stars (and potentially planets) up to a distance of tens of thousands of light-years from Earth.[22][23] In April 2014, NASA astronomers reported that the Hubble Space Telescope, by using spatial scanning, can precisely measure distances up to 10,000 light-years away, a ten-fold improvement over earlier measurements.[20]
Diurnal parallax[edit]
Diurnal parallax is a parallax that varies with the rotation of the Earth or with a difference in location on the Earth. The Moon and to a smaller extent the terrestrial planets or asteroids seen from different viewing positions on the Earth (at one given moment) can appear differently placed against the background of fixed stars.[24][25]
The diurnal parallax has been used by John Flamsteed in 1672 to measure the distance to Mars at its opposition and through that to estimate the astronomical unit and the size of the Solar System.[26]
Lunar parallax[edit]
Lunar parallax (often short for lunar horizontal parallax or lunar equatorial horizontal parallax), is a special case of (diurnal) parallax: the Moon, being the nearest celestial body, has by far the largest maximum parallax of any celestial body, at times exceeding 1 degree.[27]
The diagram for stellar parallax can illustrate lunar parallax as well if the diagram is taken to be scaled right down and slightly modified. Instead of ‘near star’, read ‘Moon’, and instead of taking the circle at the bottom of the diagram to represent the size of the Earth’s orbit around the Sun, take it to be the size of the Earth’s globe, and a circle around the Earth’s surface. Then, the lunar (horizontal) parallax amounts to the difference in angular position, relative to the background of distant stars, of the Moon as seen from two different viewing positions on the Earth: one of the viewing positions is the place from which the Moon can be seen directly overhead at a given moment (that is, viewed along the vertical line in the diagram); and the other viewing position is a place from which the Moon can be seen on the horizon at the same moment (that is, viewed along one of the diagonal lines, from an Earth-surface position corresponding roughly to one of the blue dots on the modified diagram).
The lunar (horizontal) parallax can alternatively be defined as the angle subtended at the distance of the Moon by the radius of the Earth[28][29]—equal to angle p in the diagram when scaled-down and modified as mentioned above.
The lunar horizontal parallax at any time depends on the linear distance of the Moon from the Earth. The Earth-Moon linear distance varies continuously as the Moon follows its perturbed and approximately elliptical orbit around the Earth. The range of the variation in linear distance is from about 56 to 63.7 Earth radii, corresponding to a horizontal parallax of about a degree of arc, but ranging from about 61.4′ to about 54′.[27] The Astronomical Almanac and similar publications tabulate the lunar horizontal parallax and/or the linear distance of the Moon from the Earth on a periodical e.g. daily basis for the convenience of astronomers (and of celestial navigators), and the study of how this coordinate varies with time forms part of lunar theory.

Diagram of daily lunar parallax
Parallax can also be used to determine the distance to the Moon.
One way to determine the lunar parallax from one location is by using a lunar eclipse. A full shadow of the Earth on the Moon has an apparent radius of curvature equal to the difference between the apparent radii of the Earth and the Sun as seen from the Moon. This radius can be seen to be equal to 0.75 degrees, from which (with the solar apparent radius of 0.25 degrees) we get an Earth apparent radius of 1 degree. This yields for the Earth-Moon distance 60.27 Earth radii or 384,399 kilometres (238,854 mi) This procedure was first used by Aristarchus of Samos[30] and Hipparchus, and later found its way into the work of Ptolemy.[31] The diagram at the right shows how daily lunar parallax arises on the geocentric and geostatic planetary model in which the Earth is at the center of the planetary system and does not rotate. It also illustrates the important point that parallax need not be caused by any motion of the observer, contrary to some definitions of parallax that say it is, but may arise purely from motion of the observed.
Another method is to take two pictures of the Moon at the same time from two locations on Earth and compare the positions of the Moon relative to the stars. Using the orientation of the Earth, those two position measurements, and the distance between the two locations on the Earth, the distance to the Moon can be triangulated:

Example of lunar parallax: Occultation of Pleiades by the Moon
This is the method referred to by Jules Verne in From the Earth to the Moon:
Until then, many people had no idea how one could calculate the distance separating the Moon from the Earth. The circumstance was exploited to teach them that this distance was obtained by measuring the parallax of the Moon. If the word parallax appeared to amaze them, they were told that it was the angle subtended by two straight lines running from both ends of the Earth’s radius to the Moon. If they had doubts about the perfection of this method, they were immediately shown that not only did this mean distance amount to a whole two hundred thirty-four thousand three hundred and forty-seven miles (94,330 leagues) but also that the astronomers were not in error by more than seventy miles (≈ 30 leagues).
Solar parallax[edit]
After Copernicus proposed his heliocentric system, with the Earth in revolution around the Sun, it was possible to build a model of the whole Solar System without scale. To ascertain the scale, it is necessary only to measure one distance within the Solar System, e.g., the mean distance from the Earth to the Sun (now called an astronomical unit, or AU). When found by triangulation, this is referred to as the solar parallax, the difference in position of the Sun as seen from the Earth’s center and a point one Earth radius away, i.e., the angle subtended at the Sun by the Earth’s mean radius. Knowing the solar parallax and the mean Earth radius allows one to calculate the AU, the first, small step on the long road of establishing the size and expansion age[32] of the visible Universe.
A primitive way to determine the distance to the Sun in terms of the distance to the Moon was already proposed by Aristarchus of Samos in his book On the Sizes and Distances of the Sun and Moon. He noted that the Sun, Moon, and Earth form a right triangle (with the right angle at the Moon) at the moment of first or last quarter moon. He then estimated that the Moon–Earth–Sun angle was 87°. Using correct geometry but inaccurate observational data, Aristarchus concluded that the Sun was slightly less than 20 times farther away than the Moon. The true value of this angle is close to 89° 50′, and the Sun is about 390 times farther away.[30] He pointed out that the Moon and Sun have nearly equal apparent angular sizes and therefore their diameters must be in proportion to their distances from Earth. He thus concluded that the Sun was around 20 times larger than the Moon; this conclusion, although incorrect, follows logically from his incorrect data. It does suggest that the Sun is larger than the Earth, which could be taken to support the heliocentric model.[33]

Measuring Venus transit times to determine solar parallax
Although Aristarchus’ results were incorrect due to observational errors, they were based on correct geometric principles of parallax, and became the basis for estimates of the size of the Solar System for almost 2000 years, until the transit of Venus was correctly observed in 1761 and 1769.[30] This method was proposed by Edmond Halley in 1716, although he did not live to see the results. The use of Venus transits was less successful than had been hoped due to the black drop effect, but the resulting estimate, 153 million kilometers, is just 2% above the currently accepted value, 149.6 million kilometers.
Much later, the Solar System was “scaled” using the parallax of asteroids, some of which, such as Eros, pass much closer to Earth than Venus. In a favorable opposition, Eros can approach the Earth to within 22 million kilometers.[34] During the opposition of 1900–1901, a worldwide program was launched to make parallax measurements of Eros to determine the solar parallax (or distance to the Sun), with the results published in 1910 by Arthur Hinks of Cambridge[35] and Charles D. Perrine of the Lick Observatory, University of California.[36] Perrine published progress reports in 1906[37] and 1908.[38] He took 965 photographs with the Crossley Reflector and selected 525 for measurement.[39] A similar program was then carried out, during a closer approach, in 1930–1931 by Harold Spencer Jones.[40] The value of the Astronomical Unit (roughly the Earth-Sun distance) obtained by this program was considered definitive until 1968, when radar and dynamical parallax methods started producing more precise measurements.
Also radar reflections, both off Venus (1958) and off asteroids, like Icarus, have been used for solar parallax determination. Today, use of spacecraft telemetry links has solved this old problem. The currently accepted value of solar parallax is 8.794143 arcseconds.[41]
Moving-cluster parallax[edit]
The open stellar cluster Hyades in Taurus extends over such a large part of the sky, 20 degrees, that the proper motions as derived from astrometry appear to converge with some precision to a perspective point north of Orion. Combining the observed apparent (angular) proper motion in seconds of arc with the also observed true (absolute) receding motion as witnessed by the Doppler redshift of the stellar spectral lines, allows estimation of the distance to the cluster (151 light-years) and its member stars in much the same way as using annual parallax.[42]
Dynamical parallax[edit]
Dynamical parallax has sometimes also been used to determine the distance to a supernova when the optical wavefront of the outburst is seen to propagate through the surrounding dust clouds at an apparent angular velocity, while its true propagation velocity is known to be the speed of light.[43]
Spatio-temporal parallax[edit]
From enhanced relativistic positioning systems, spatio-temporal parallax generalizing the usual notion of parallax in space only has been developed. Then, event fields in spacetime can be deduced directly without intermediate models of light bending by massive bodies such as the one used in the PPN formalism for instance.[44]
Statistical parallax[edit]
Two related techniques can determine the mean distances of stars by modelling the motions of stars. Both are referred to as statistical parallaxes, or individually called secular parallaxes and classical statistical parallaxes.
The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 AU per year, whereas for halo stars the baseline is 40 AU per year. After several decades, the baseline can be orders of magnitude greater than the Earth–Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of other stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the precision is inversely proportional to the square root of the sample size.[45]
The mean parallaxes and distances of a large group of stars can be estimated from their radial velocities and proper motions. This is known as a classical statistical parallax. The motions of the stars are modelled to statistically reproduce the velocity dispersion based on their distance.[45][46]
Other methods for distance measurement in astronomy[edit]
In astronomy, the term “parallax” has come to mean a method of estimating distances, not necessarily utilizing a true parallax, such as:
- Photometric parallax method
- Spectroscopic parallax
- Dynamical parallax
See also[edit]
- Cosmic distance ladder
- Lunar distance (astronomy)
Notes[edit]
- ^ One trillion here is short scale, ie. 1012 (one million million, or billion in long scale).
References[edit]
- ^
Perryman, M. A. C.; et al. (1999). “The HIPPARCOS Catalogue”. Astronomy and Astrophysics. 323: L49–L52. Bibcode:1997A&A…323L..49P. - ^ Harrington, J. D.; Villard, R. (10 April 2014). “NASA’s Hubble Extends Stellar Tape Measure 10 Times Farther Into Space”. NASA. Archived from the original on 17 February 2019. Retrieved 17 October 2014.
- ^
Riess, A. G.; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, A. V. (2014). “Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope”. The Astrophysical Journal. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ…785..161R. doi:10.1088/0004-637X/785/2/161. S2CID 55928992. - ^ Brown, A. G. A.; et al. (Gaia collaboration) (August 2018). “Gaia Data Release 2: Summary of the contents and survey properties”. Astronomy & Astrophysics. 616. A1. arXiv:1804.09365. Bibcode:2018A&A…616A…1G. doi:10.1051/0004-6361/201833051.
- ^
B., Baidyanath (2003). An Introduction to Astrophysics. PHI Learning Private Limited. ISBN 978-81-203-1121-3. - ^ “Hubble finds Universe may be expanding faster than expected”. Archived from the original on 11 September 2018. Retrieved 3 June 2016.
- ^ “Hubble stretches the stellar tape measure ten times further”. ESA/Hubble Images. Archived from the original on October 30, 2017. Retrieved April 12, 2014.
- ^
Popowski, P.; Gould, A. (1998). “Mathematics of Statistical Parallax and the Local Distance Scale”. arXiv:astro-ph/9703140. - ^
Bartel, N.; et al. (1994). “The shape, expansion rate and distance of supernova 1993J from VLBI measurements”. Nature. 368 (6472): 610–613. Bibcode:1994Natur.368..610B. doi:10.1038/368610a0. S2CID 4316734. - ^ “Cosmic Distance Scales – The Milky Way”. Retrieved 24 September 2014.
- ^ B. Luque; F. J. Ballesteros (2019). “To the Sun and beyond”. Nature Physics. 15 (12): 1302. Bibcode:2019NatPh..15.1302L. doi:10.1038/s41567-019-0685-3.
- ^ Benedict, G. F.; et al. “Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri” (PDF). Proceedings of the HST Calibration Workshop. pp. 380–384. Retrieved 11 July 2007.
- ^ “Farthest Stars”. StarDate. University of Texas at Austin. 15 May 2021. Retrieved 5 September 2021.
- ^ Dyson, F. W. (March 1913). “The distribution in space of the stars in Carrington’s Circumpolar Catalogue”. Monthly Notices of the Royal Astronomical Society. 73 (5): 342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334.
[paragraph 14, page 342] Taking the unit of distance R* to be that corresponding to a parallax of 1″·0 [… Footnote:]
* There is need for a name for this unit of distance. Mr. Charlier has suggested Siriometer, but if the violence to the Greek language can be overlooked, the word Astron might be adopted. Professor Turner suggests Parsec, which may be taken as an abbreviated form of “a distance corresponding to a parallax of one second”. - ^ Cox, Arthur N., ed. (2000). Allen’s Astrophysical Quantities (4th ed.). New York: AIP Press / Springer. Bibcode:2000asqu.book…..C. ISBN 978-0387987460.
- ^ Binney, James; Tremaine, Scott (2008). Galactic Dynamics (2nd ed.). Princeton, NJ: Princeton University Press. Bibcode:2008gady.book…..B. ISBN 978-0-691-13026-2.
- ^ Zeilik & Gregory 1998, p. 44.
- ^ Zeilik & Gregory 1998, § 22-3.
- ^ Benedict, G. Fritz, et al. (1999). “Interferometric Astrometry of Proxima Centauri and Barnard’s Star Using Hubble Space Telescope Fine Guidance Sensor 3: Detection Limits for Substellar Companions”. The Astronomical Journal. 118 (2): 1086–1100. arXiv:Astro-ph/9905318. Bibcode:1999AJ….118.1086B. doi:10.1086/300975. S2CID 18099356.
- ^ a b Harrington, J.D.; Villard, Ray (10 April 2014). “NASA’s Hubble Extends Stellar Tape Measure 10 Times Farther Into Space”. NASA. Archived from the original on 12 April 2014. Retrieved 11 April 2014.
- ^ Dobrzycki, J. (1973). Dobrzycki, Jerzy (ed.). The Reception of Copernicus’ Heliocentric Theory. p. 51. doi:10.1007/978-94-015-7614-7. ISBN 978-90-481-8340-1.
- ^ “Soyuz ST-B successfully launches Gaia space observatory”. nasaspaceflight.com. 19 December 2013. Archived from the original on 19 December 2013. Retrieved 19 December 2013.
- ^ Henney, Paul J. “ESA’s Gaia Mission to study stars”. Astronomy Today. Archived from the original on 2008-03-17. Retrieved 2008-03-08.
- ^ Seidelmann, P. Kenneth (2005). Explanatory Supplement to the Astronomical Almanac. University Science Books. pp. 123–125. ISBN 978-1-891389-45-0.
- ^ Barbieri, Cesare (2007). Fundamentals of astronomy. CRC Press. pp. 132–135. ISBN 978-0-7503-0886-1.
- ^ Van Helden, A. (2010). Measuring the universe: cosmic dimensions from Aristarchus to Halley. University of Chicago Press. Ch. 12.
- ^ a b “D”. The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981.
- ^ The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981. p. M10.
- ^ United States Naval Observatory. Nautical Almanac Office; Great Britain. Nautical Almanac Office (2006). Explanatory Supplement to the Astronomical Almanac. University Science Books. p. 125. ISBN 978-1-891389-45-0.
- ^ a b c Gutzwiller, Martin C. (1998). “Moon–Earth–Sun: The oldest three-body problem”. Reviews of Modern Physics. 70 (2): 589–639. Bibcode:1998RvMP…70..589G. doi:10.1103/RevModPhys.70.589.
- ^ Webb, Stephen (1999), “3.2 Aristarchus, Hipparchus, and Ptolemy”, Measuring the Universe: The Cosmological Distance Ladder, Springer, pp. 27–35, ISBN 9781852331061. See in particular p. 33: “Almost everything we know about Hipparchus comes down to us by way of Ptolemy.”
- ^ Freedman, W.L. (2000). “The Hubble constant and the expansion age of the Universe”. Physics Reports. 333 (1): 13–31. arXiv:astro-ph/9909076. Bibcode:2000PhR…333…13F. doi:10.1016/S0370-1573(00)00013-2. S2CID 413222.
- ^ Al-Khalili, Jim (2010), Pathfinders: The Golden Age of Arabic Science, Penguin UK, p. 270, ISBN 9780141965017, archived from the original on 2015-03-17,
Some have suggested that his calculation of the relative size of the earth and sun led Aristarchus to conclude that it made more sense for the earth to be moving around the much larger sun than the other way round.
- ^ Whipple 2007, p. 47.
- ^ Hinks, Arthur R. (1909). “Solar Parallax Papers No. 7: The General Solution from the Photographic Right Ascensions of Eros, at the Opposition of 1900”. Monthly Notices of the Royal Astronomical Society. 69 (7): 544–67. Bibcode:1909MNRAS..69..544H. doi:10.1093/mnras/69.7.544.
- ^ Perrine, Charles D. (1910). Determination of the solar parallax from photographs of Eros made with the Crossley reflector of the Lick Observatory University of California (First ed.). Washington, D. C.: Carnegie Institution of Washington. pp. 1–104.
- ^ Perrine, C. D. (1906). “The Measurement and Reduction of the Photographs of Eros Made With the Crossley Reflector in 1900”. Publications of the Astronomical Society of the Pacific. 18 (10): 226.
- ^ Perrine, Charles D. (1908). “Progress on the Crossley Eros Solar Parallax Work”. Publications of the Astronomical Society of the Pacific. 20 (120): 184. Bibcode:1908PASP…20..184P. doi:10.1086/121816. S2CID 121782316.
- ^ Campbell, W. W. (1906). “Reports of the Observatories: Lick Observatory”. Publications of the Astronomical Society of the Pacific. 19 (113): 92.
- ^ Jones, H. Spencer (1941). “The Solar Parallax and the Mass of the Moon from Observations of Eros at the Opposition of 1931”. Mem. Roy. Astron. Soc. 66: 11–66.
- ^ “Astronomical Constants” (PDF). US Naval Observatory. Archived from the original (PDF) on 2011-07-20.
- ^ Vijay K. Narayanan; Andrew Gould (1999). “A Precision Test of Hipparcos Systematics toward the Hyades”. The Astrophysical Journal. 515 (1): 256. arXiv:astro-ph/9808284. Bibcode:1999ApJ…515..256N. doi:10.1086/307021. S2CID 15351552.
- ^ Panagia, N.; Gilmozzi, R.; MacChetto, F.; Adorf, H.-M.; et al. (1991). “Properties of the SN 1987A circumstellar ring and the distance to the Large Magellanic Cloud”. The Astrophysical Journal. 380: L23. Bibcode:1991ApJ…380L..23P. doi:10.1086/186164.
- ^ Rubin, J.L. (2015). “Relativistic Pentametric Coordinates from Relativistic Localizing Systems and the Projective Geometry of the Spacetime Manifold”. Electronic Journal of Theoretical Physics. 12 (32): 83–112. Archived from the original on 2015-02-08.
- ^ a b Popowski, Piotr; Gould, Andrew (29 January 1998). “Mathematics of Statistical Parallax and the Local Distance Scale”. arXiv:astro-ph/9703140. Bibcode:1997astro.ph..3140P.
- ^ Layden, Andrew C; Hanson, Robert B; Hawley, Suzanne L; Klemola, Arnold R; Hanley, Christopher J (1996). “The Absolute Magnitude and Kinematics of RR Lyrae Stars Via Statistical Parallax”. The Astronomical Journal. 112: 2110. arXiv:astro-ph/9608108. Bibcode:1996AJ….112.2110L. doi:10.1086/118167. S2CID 8732647.
 Планета Земля не является стационарным объектом в космическом пространстве, а совершает один оборот вокруг своей оси каждые 24 часа (земные сутки), а так же обращается вокруг Солнца за 365 земных суток (один земной год).
Планета Земля не является стационарным объектом в космическом пространстве, а совершает один оборот вокруг своей оси каждые 24 часа (земные сутки), а так же обращается вокруг Солнца за 365 земных суток (один земной год).
Содержание:
- 1 Краткие сведения
- 2 История
- 3 Сравнение гелиоцентрической и геоцентрической системы мира
- 4 Василий Струве и Пулковская обсерватория в которой он работал
- 5 Основы геометрии и тригонометрии
- 6 Частные случаи использования суточного и годичного параллакса
- 7 Вековой и внегалактический параллакс
Краткие сведения
Радиус земной орбиты составляет одну астрономическую единицу или около 150 миллионов километров. В связи с этим все внеземные объекты на земном небе так же выписывают годичные “петли” (параллактическое движение). Чем дальше небесный объект находится от Земли, тем его параллактическое движение на земном небе является менее заметным (в переводе с греческого слово “параллакс” означает “смещение”).
Измерения углового диаметра параллактического движения небесных тел на земном небе позволяет проводить наиболее точные измерения расстояния до них (тригонометрическое расстояние). Кроме того, важным в истории астрономии оказался суточный (геоцентрический) и вековой параллакс. Первый из них обозначает половину от максимального различия в угловых координатах небесного тела на земном небе при различных географических положениях на поверхности Земли (относительно центра Земли), второй обозначает собственные движения звезд на небе нашей планеты по причине движения Солнечной Системы вокруг центра галактики.
История
Суточным (геоцентрическим) параллаксом называется угол, под которым виден земной радиус с определенного небесного тела. Кроме того, выделяют понятие горизонтального параллакса. Горизонтальным параллаксом называется угол, под которым виден экваториальный радиус Земли из центра определенного небесного тела при нахождении последнего на истинном горизонте (истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения). Различия понятий суточного и горизонтального параллакса связаны с несферичностью Земли (так полярный радиус Земли короче экваториального радиуса на 21 км).
Суточный параллакс сыграл очень важную роль в истории астрономии, как наиболее простой и достоверный способ определения расстояния до объектов Солнечной Системы. Фактически этот метод являлся единственным геометрическим методом измерения расстояний в Солнечной Системе вплоть до радиолокации, лазерной локации и методов радиоинтерференции сигналов межпланетных станций. Базой суточного параллакса является земной радиус. Самым большим суточный параллакс является у Луны (57 угловых минут) и у Солнца (9 угловых минут). У всех планет Солнечной Системы суточный параллакс подвержен регулярным изменениям и значительно меньше угловой минуты (у Венеры 0.1-0.6 угловых минут, у Марса 0.1-0.4 угловых минут, у Юпитера и Сатурна меньше 0.1 угловой минуты, а у Урана и Нептуна меньше одной угловой секунды).
Первыми параллакс Луны и Солнца определили древнегреческие астрономы на основе наблюдений лунных затмений, которые позволяли определять параллакс Луны из одного и того же места. Так древнегреческий астроном Гиппарх Никейский (180-125 годы до нашей эры) в 129 году до нашей эры оценил параллакс Солнца в 7 угловых минут (максимальная величина угла, который неразличим невооруженным глазом). Похожие расчеты выполнил до него другой древнегреческий астроном Аристарх Самосский (310-230 годы до нашей эры).
С другой стороны, александрийский астроном Клавдий Птолемей (100-170 годы нашей эры) полагал, что расстояние до Луны зависит от её фаз. Это говорит о больших разногласиях среди астрономов Древнего мира по поводу оценок параллаксов Луны и Солнца. Позже ошибка Птолемея о зависимости размера параллакса Луны от её фаз стала одним из основных объектом критики птолемевской системы мира. Так юный Николай Коперник (1473-1543 годы нашей эры) во время учебы в Италии проводил измерения параллакса Луны вместе со своим учителем Новарой. Наблюдения положения Луны во время затмения яркой звезды Альдебаран из Болоньи 9 марта 1497 года показали, что параллакс Луны не зависит от её фазы. В последующие века началось широкое использование одновременных наблюдений из северного и южного полушария для точного измерения параллаксов Луны, Солнца и Марса. К примеру, в 18 веке такие наблюдения осуществлялись в обсерватории мыса Доброй Надежды в южной части Африки и Берлинской обсерватории.
Сравнение гелиоцентрической и геоцентрической системы мира
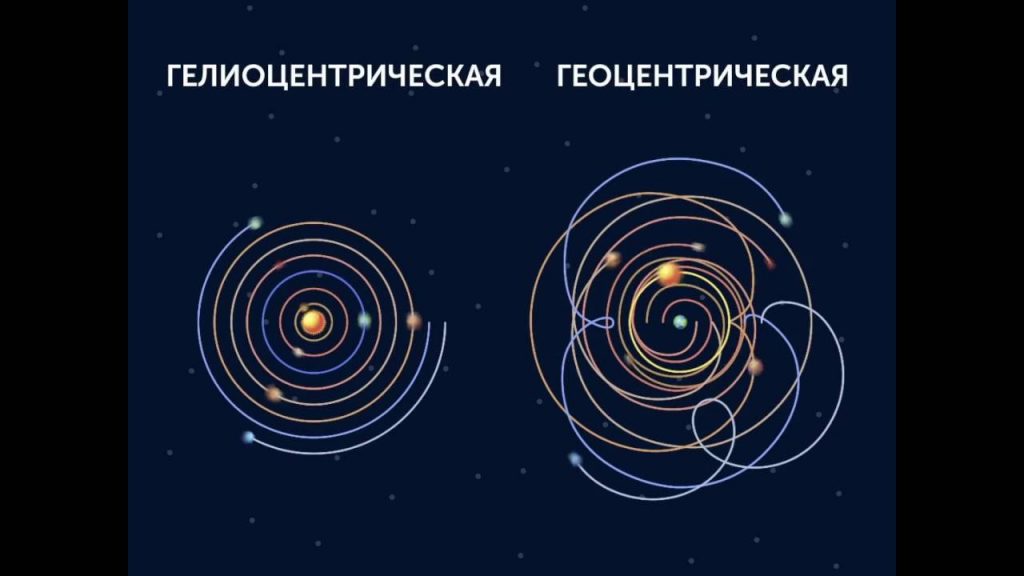
Сравнение гелиоцентрической и геоцентрической системы мира
Годичный параллакс (звездный параллакс) даже у ближайших звезд не превышает одной угловой секунды. В связи с этим его измерение стало возможным лишь после изобретения оптических инструментов – телескопов. Сама возможность существования этого явления стала причиной принципиальных разногласий между геоцентрической и гелиоцентрической системами мира – геоцентрическая система считала, что Солнце обращается вокруг Земли. В то же время сторонники гелиоцентрической системы в течение почти 2 тысяч лет объясняли ненаблюдаемость звездных параллаксов огромными расстояниями до звезд. Первые попытки измерения звездных параллаксов были предприняты древнегреческим астрономом Аристархом Самосским в 3-ем веке нашей эры (считается, что он первым выдвинул предположения о гелиоцентрической системе мира). Позже такие попытки были предприняты Н. Коперником, Т. Браге, Г. Галилео, У. Гершелем и т.д. Последний во время попыток обнаружения звездных параллаксов случайно открыл неизвестную планету Солнечной Системы – Уран. По иронии судьбы, к тому времени, когда в начале 19 века всё же удалось измерить первые параллаксы звезды, сомнений в справедливости гелиоцентрической системы мира уже не оставалось. Так в ходе безуспешных попыток измерить параллакс у звезды Гамма Дракона (Этамин) английский астроном Джеймс Бредли (1692-1762 годы) в 1727 году открыл явление аберрации света, которая вызвана орбитальным движением Земли вокруг Солнца. Аберрация света представляет собой изменение видимого положения звезд примерно на 50 угловых секунд по причине конечной скорости света (первооткрыватель годичной аберрация определил скорость света в 308 тысяч км в секунду). Одновременно Д.Бредли получил верхний предел для звездных параллаксов в 0.5 угловой секунды. С другой стороны в попытках измерить звездные параллаксы, другому английскому астроному Уильяму Гершелю (1738-1822 году) в 1803 году удалось впервые зарегистрировать орбитальное движение двойных звезд (ранее предполагалось, что визуальные двойные звезды являются результатом случайности). Кроме того У. Гершель первым определил на основе наблюдаемых собственных движений звезд, что Солнечная Система движется в сторону созвездия Геркулеса.
Впервые факт отсутствия неизменности положения звезд на земном небе был обнаружен ещё Гиппархом на основе сверки положения ярких звезд его каталога, состоящего из примерно тысячи звезд с более древними каталогами вавилонян и александрийских астрономов. Гиппарх обнаружил систематическое изменение долготы положения звезд примерно на один градус (в то время как широта звезд относительно эклиптики оставалась неизвестной). Ныне это явление называется прецессией земной оси с периодом в 26 тысяч лет. Истинное движение звезд было впервые обнаружено в 1718 году английским астрономом Эдмондом Галлеем (1656-1743). В процессе уточнения прецессии Э. Галилей сравнил положения звезд из каталога Гиппарха с современными звездными каталогами. Сравнение показало, что на фоне большинства звезд, у которых положение на земном небе менялось согласно прецессии, встречался ряд аномалий (для Сириуса, Арктура и Альдебарана). У этих звезд отклонения в положении в несколько раз превысили погрешность измерений.
Василий Струве и Пулковская обсерватория в которой он работал

Василий Струве
Первые достоверные измерения звездных параллаксов были опубликованы в 1837-1838 годах сразу тремя исследователями: Василий Струве (1793-1864 годы) для Веги, Фридрихом Бесселем (1784-1846 годы) для 61 Лебедя и Томасом Хендерсоном (1798-1844 годы) для Альфы Центавра. Хотя за много лет до этого – к 1822 году Фридрих Струве в Дерптской обсерватории на территории нынешней Эстонии получил достаточно точные измерения параллаксов нескольких ярких звезд (к примеру, для Альтаира).
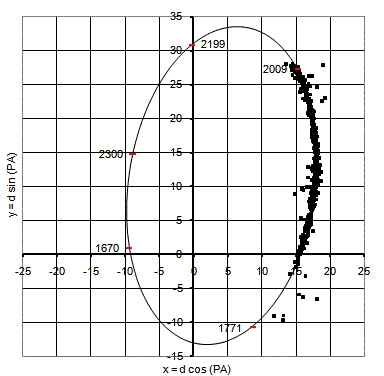
Орбитальное движение звезд системы 61 Лебедя (черным отметками отмечены измерения астрономов)
Кроме того французский астроном Доминик Араго (1786-1853) ещё за несколько лет до Ф. Бесселя опубликовал значение параллакса 61 Лебедя с большой погрешностью. Результат Ф. Бесселя был воспринят мировым сообществом как наиболее достоверный в связи с большим количеством астрометрических измерений (более 400).
Для сравнения у Ф. Струве для Веги было сделано только 17 астрометрических измерений. Кроме того работу Бесселя облегчил факт того, что двойная система 61 Лебедя обладает заметным орбитальным движением. Так можно было сравнить параллакс для обеих звезд системы.
Визуальные измерения параллаксов и собственных движений являлись крайне трудоемкими. К концу 19 века удалось измерить тригонометрические расстояния лишь до сотни звезд. Всё резко изменилось с использованием фотографии. Точность измерений выросла до 10 угловых микросекунд, а число измеряемых звезд достигло нескольких тысяч. Замена фотопластинок приборами с зарядовой связью (ПЗС-матрицами), широкое использование компьютеров для обработки данных, а также вынос телескопов за пределы атмосферы Земли позволил улучшить точность измерения положения звезд до миллионных долей угловой секунды, а размер астрометрических каталогов вырос до девятизначных цифр.

Прогресс в точности измерения положения звезд за последние 2.5 тысячи лет
Основы геометрии и тригонометрии
При вычислении лунного параллакса активно используются основы геометрии для прямоугольного треугольника. Прямоугольным треугольником называется такой треугольник, у которого один из углов равен 90 градусов.
В прямоугольном треугольнике стороны, которые образуют угол в 90 градусов, называются катетами, а сторона, лежащая напротив угла в 90 градусов гипотенузой. Сумма углов в прямоугольном треугольнике равна 180 градусов. Отсюда несложно определить, что при известном катете (радиусе Земли) и угле между гипотенузой и катетом (суточным параллаксом) гипотенуза (расстояние до небесного тела) будет равна отношению известного катета к синусу суточного параллакса.
Только в этом случае радиус Земли заменяется радиусом земной орбиты вокруг Солнца, а суточный параллакс заменяется годичным параллаксом
Синусом в прямоугольном треугольнике называют отношение катета противолежащего угла к гипотенузе.
Аналогичный принцип вычислений существует для расчетов тригонометрических расстояний до звезд.
По причине огромных расстояний до звезд (ближайшая звезда находится в 270 тысячах астрономических единиц от Солнца), для вычисления тригонометрических расстояний чаще всего используют отношение 206265 угловых секунд и измеренного годичного параллакса, который так же представлен в угловых секундах. Число 206265 означает число угловых секунд в одном радиане. Радиан – это угол, соответствующий дуге окружности, длина которой равна радиусу этой окружности.
Частные случаи использования суточного и годичного параллакса
Многие тысячи лет число известных объектов в Солнечной Системе было постоянным и было равно девяти (Земля, Луна, Солнце, Меркурий, Венера, Земля, Марс, Юпитер и Сатурн). Это постоянство нарушали лишь кометы, которые периодически появлялись во внутренних областях Солнечной Системы. В 18 веке в Солнечной Системе начались открытия новых планет и астероидов (к примеру, Урана и Цереры). Шквал новых открытий вынудил астрономов разрабатывать методики по вычислению орбит небесных тел Солнечной Системы по минимальному числу измерений. В 1801 году 24-летний немецкий математик Фридрих Гаусс (1777-1855 годы) с целью обнаружения потерянной Цереры разработал математический метод, по которому было возможно определить орбиту небесного тела на основе всего трех его наблюдений.
В то же время примерное расстояние до небесного тела в Солнечной Системе, возможно, определить лишь по двум наблюдениям. Особенно, это актуально в случае открываемых объектов за орбитой Нептуна (ТНО). У таких объектов скорость движения является минимальной по сравнению с орбитальной скоростью Земли (несколько сотен метров в секунду против 30 км в секунду). В результате этого наблюдаемое расстояние от Солнца (гелиоцентрическое расстояние) до ТНО в астрономических единицах можно определить простым соотношением 150/q, где q – это угловая скорость объекта в угловых секундах за один час.
С другой стороны в последние годы астрометрические наблюдения мигрируют из оптического диапазона в более длинноволновые диапазоны электромагнитного спектра: инфракрасные лучи и радиоволны. Первый диапазон является очень перспективным для астрометрии красных и коричневых карликов во Вселенной (наиболее распространенной популяции массивных объектов в галактике, чей максимум теплового излучения приходится на инфракрасный диапазон). Второй диапазон является уникальным во всем электромагнитном спектре по проникающей способности.
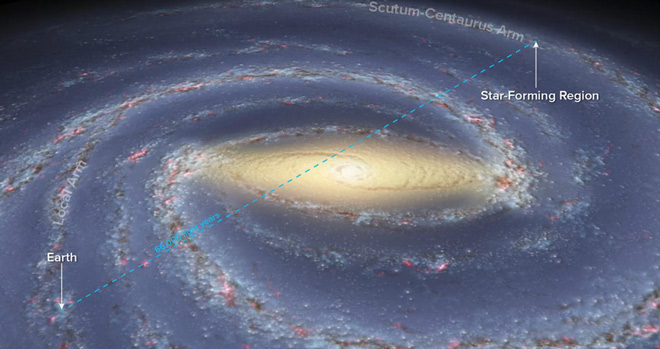
Так недавно радиоастрономы с помощью радиоинтерферометра VLBA смогли установить рекорд самого далекого измеренного параллакса: расстояние до межзвездного облака G007.47+00.05 (внешний рукав Щита – Центавра) составило 20 тысяч парсек или 67 тысяч световых лет
Вековой и внегалактический параллакс
Солнечная Система, как сотни миллиардов планетных систем нашей галактики обращается вокруг центра галактики в созвездии Стрельца. Один оборот Солнечной Системы вокруг центра галактики (галактический год) равен 225-250 миллионов лет (средняя скорость движения Солнечной Системы в межзвездном пространстве около 220 км в секунду). По причине различий в галактических орбитах другие звезды на земном небе движутся по различным траекториям, с различной угловой и пространственной скоростью.
Как говорилось выше, собственные движения звезд были впервые обнаружены в 1718 году английским астрономом Эдмондом Галлеем (1656-1743). Так как это открытие случилось за столетие до первых измерений параллаксов, звезды с высоким собственным движением стали потенциально интересными для измерения параллаксов. Из трех первых опубликованных параллаксов в 1837-1838 годах, два приходятся на звезды с высоким собственным движением (61 Лебедя и Альфа Центавра). Собственное движение этих систем составляет около 4 угловых секунд в год. Для сравнения, у третьей звезды – Веги собственное движение в 20 раз меньше (Ф. Бессель выбрал эту звезду для измерения параллакса по причине её околорекордной видимой яркости на северном небе). В дальнейшем поиск неизвестных близких звезд в большинстве случаев проходил через первоначальное обнаружение звезд с высоким собственным движением (к примеру, так были обнаружены в 20 веке звезды Проксима Центавра и Летящая Барнарда). В результате этого в последние годы астрономы открывают близкие звездные системы только с минимальным собственным движением (0.15 угловых секунд в год и меньше). Исключением из этого правила могут стать лишь плотные звездные поля или области вблизи очень ярких звезд.
Естественно и наша галактика в космическом пространстве Вселенной не является неподвижным объектом. Сегодня астрономы полагают, что наша галактика с соседними галактиками (Местная группа галактик) входят в состав сверхскопления галактик созвездия Девы. Исследования реликтового излучения в конце 20 века показали, что Солнечная Система движется относительно реликтового излучения со скоростью 368 ± 2 км/с (или 78 астрономических единиц в год). В результате этого движения, объект, который находится в миллионе парсек от нас, и расположен перпендикулярно внегалактическому апексу будет обладать на земном небе собственным движением в 78 угловых микросекунд в год (миллионных долей угловой секунды). Подобная точность измерений является вполне достижимой в последние десятилетия. В ходе измерения собственных движений близких галактик широко используются снимки крупнейших наземных телескопов и космических телескопов Хаббл и Гаяй, а так же данные радиоинтерферометров. К примеру, измерение собственного движения галактики М31 привело к прогнозу её столкновения с нашей галактикой через несколько миллиардов лет.
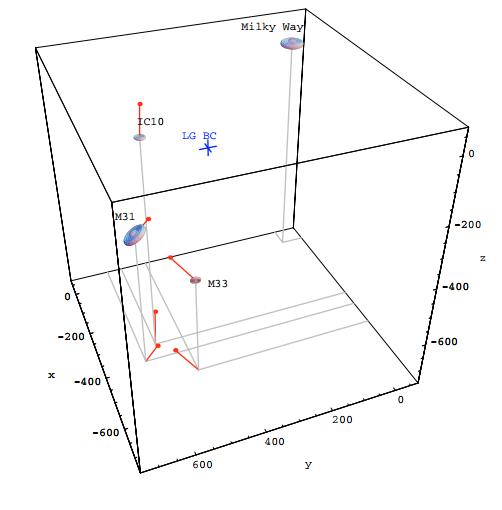
Схема движения галактик в Местной группе относительно нашей галактики взята из работы A. Brunthaler et al. 2007 года
Измеренное собственное движение галактики Андромеды с расстоянием в 0.8 миллионов парсек составило около 50 угловых микросекунд в год. Для сравнения современные радиоинтерферометры способны регистрировать собственные движения галактик на основе наблюдения мазеров до удаления в 20 миллионов парсек за 10-летние наблюдения. Сложности измерения собственных движений галактик заключаются в необходимости разграничения общего движения всей галактики от орбитального движения отдельных звездных скоплений или межзвездных туманностей в ней. Решением этой проблемы является измерение собственного движения ядер галактик. В связи с этим удобным источником для измерения внегалактических собственных движений являются галактики с активными ядрами (квазары) – одни из ярчайших радиоисточников на земном небе. В работе 2005 года с названием “Quasar Apparent Proper Motion Observed by Geodetic VLBI Networks” сообщается, что геодезическим радиоинтерферометрам в период с 1980 по 2002 годы удалось измерить или ограничить собственное движение 580 квазаров.
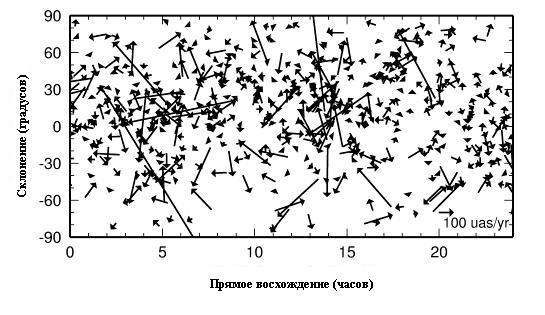
У многих из них собственное движение составляет несколько сотен угловых микросекунд
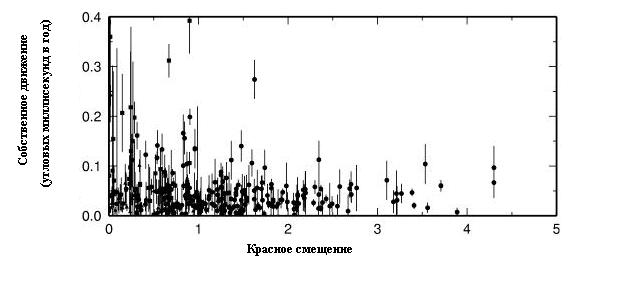
Большинство этих источников находились на огромных расстояниях в многие миллиарды световых лет
В работе 2017 года был опубликован каталог собственных движений 713 внегалактических радиоисточников, которые наблюдались в среднем около 22 лет. Средняя погрешность этих измерений составила 24 угловых микросекунд в год. Эти наблюдения позволили зарегистрировать ускорение движения Солнечной Системы по галактической орбите (статистический уровень значимости 6.3 сигм). Это явление приводит к систематическому изменению угловой скорости внегалактических объектов на несколько микросекунд в год.
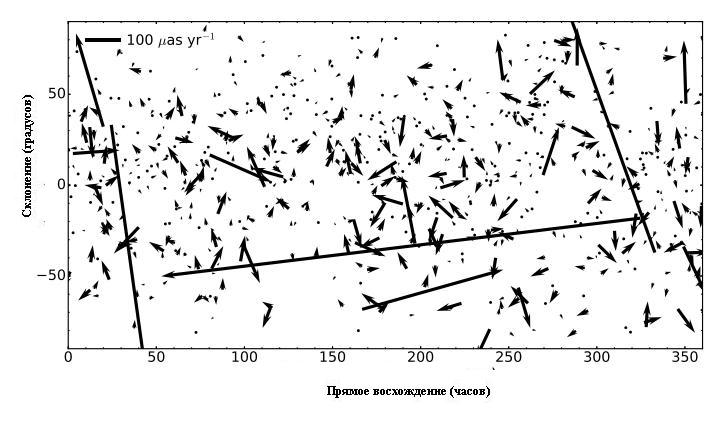
Карта собственных движений из нового каталога
Самое большое наблюдаемое собственное движение в вышеназванном каталоге (около 1.5 угловых миллисекунд в год) наблюдается у радиогалактики SDSS J213836.38+001241.8, у которой наблюдаемый блеск в оптическом диапазоне составляет примерно 23 звездных величины (её красное смещение равно 0.6). Для сравнения у одной ближайшей галактики (Большое Магелланово облако) собственное движение равно 2 угловым миллисекундам.
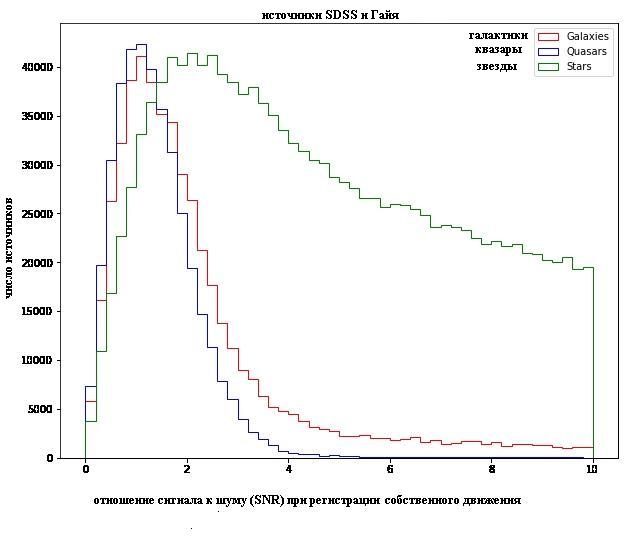
Публикация первых (предварительных) релизов космического телескопа GAIA, который работает в оптическом диапазоне, так же смогла зарегистрировать собственные движения некоторых галактик и квазаров
Актуальность регистрации собственных движений внегалактических объектов в последние годы возрастает в связи с поисками темной (скрытной материи). Как известно темная материя была заподозрена на основе аномально высоких лучевых скоростей движения внешних областей многих галактик. В этих случаях лучевые скорости были измерены через анализ спектров. Измерение собственного движения этих аномальных областей позволило бы лучше прояснить этот вопрос.
Представим себе «новую звезду» или иной астрономический объект, который неподвижен относительно звезд или очень незначительно перемещается по отношению к ним в течение суток. Допустим, что он находится гораздо ближе к Земле, чем звезды. Далее можно либо принять точку зрения, что Земля делает один оборот вокруг своей оси с востока на запад, либо что звезды вместе с этим объектом вращаются вокруг неподвижной Земли раз в сутки с запада на восток. В любом случае, поскольку мы видим объект в слегка разных направлениях в различное время ночи, его видимая позиция на фоне звезд будет смещаться. Это явление называется суточным параллаксом объекта. Измерение суточного параллакса позволяет определить расстояние до объекта, а в случае, если он так мал, что его не удается измерить, определяется минимальное расстояние, ближе которого астрономический объект находиться не может.
Для расчета величины этого углового сдвига необходимо для фиксированной наблюдательной площадки на Земле определить видимое расположение объекта среди звезд два раза: первый раз – когда он лишь появляется над горизонтом и второй раз – когда он находится выше всего на небе. Для того чтобы показать примерный расчет, рассмотрим простейший в геометрическом отношении случай: обсерватория расположена на экваторе, и объект находится в одной плоскости с экватором Земли. Конечно, это было не так в том случае, когда Тихо Браге измерял параллакс сверхновой звезды, но так мы тоже можем получить величину того же порядка.
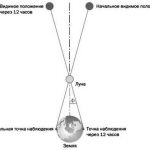
Луч зрения от наблюдателя, направленный в сторону объекта, проходит по касательной к поверхности Земли в тот момент, когда он восходит над горизонтом, поэтому угол между этим лучом и направлением от обсерватории в центр Земли – прямой. Отрезки, соединяющие наблюдателя, центр Земли и объект, таким образом, образуют прямоугольный треугольник (см. рис. 14). Синус угла ? в этом треугольнике равен отношению противолежащего катета, радиуса Земли rз, к гипотенузе, расстоянию d от центра Земли до объекта, которое мы измеряем. Как видно из чертежа, этот же угол равен видимому смещению объекта на фоне удаленных звезд между моментом его появления над горизонтом и кульминацией. Полное смещение за время от восхода объекта до его захода составит 2?.
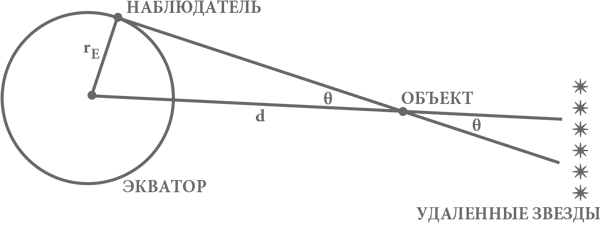
Рис. 14. Использование суточного параллакса для определения расстояния d от Земли до астрономического объекта. Здесь показан вид в плане со стороны южного полюса Земли. Для простоты примера наблюдатель расположен на экваторе, а наблюдаемый объект находится в той же самой плоскости, что и экватор. Две прямые, пересекающиеся под углом ?, – это направления от наблюдателя к объекту в моменты его восхода над горизонтом и шесть часов спустя, во время его кульминации прямо в зените для наблюдателя.
Например, если мы предположим, что наблюдаемый объект находится от нас так же далеко, как Луна, то d ? 400 000 км, rз ? 6400 км, поэтому sin ? ? 6,4/400, и, таким образом, ? ? 0,9°, а полный суточный параллакс составляет 1,8°. При наблюдении объекта из иной произвольной точки на Земле, такой как остров Вен (например, сверхновой 1572 г.), ожидаемый суточный параллакс должен быть меньше, но все равно того же порядка величины – около 1°. Этого более чем достаточно, чтобы такой опытный астроном, как Браге, измерил бы его и без увеличительных инструментов. Однако Тихо Браге не удалось, наблюдая сверхновую, заметить наличие у нее какого-либо суточного параллакса, из чего он заключил, что звезда находится гораздо дальше Луны. Кроме того, надо отметить, что и параллакс самой Луны был измерен без труда, что стало способом измерения расстояния между Землей и Луной.





