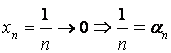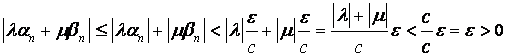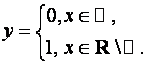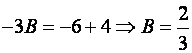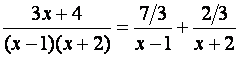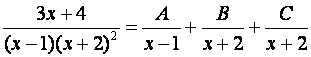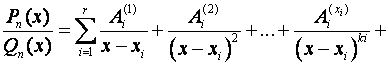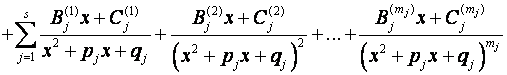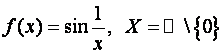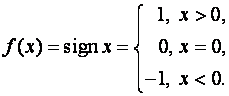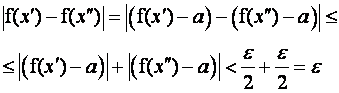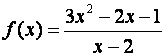85
-
Числовая функция: определение , способы задания, график Содержание
§ 7. Числовая функция: определение , способы задания, график 70
6.1.
Определение числовой функции 70
7.1.
Сужение функции 72
7.2.
Способы задания функции 73
7.3.
Явно или неявно заданные функции 73
7.4.
Параметрически заданные функции 75
7.5.
График функции 77
7.6.
Примеры построения графиков функций 78
7.7.
Упражнения для самостоятельной работы 83
Вопросы
для самопроверки 85
Глоссарий 85
-
Определение числовой функции
|
Определение |
|
Переменная |
Обозначения:
или
или
или
или
.
где x— это независимая
переменная, или аргумент;y— это зависимая переменная, или функция.
Если обозначить через
X– множество числовых
значений, которые может принимать
переменнаяx,
Y– множество числовых
значений, которые принимает переменнаяy,
то
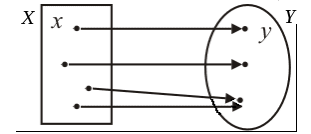
функциональная зависимость между
переменными xиyздесь задает отображение числового
множестваXна числовое
множествоY, при котором
каждому элементу
ставится в соответствие единственный
элемент множестваY(рис. 40).
Рис.
40
В отличие
от более общего определения функции
как отображения множеств, состоящих из
элементов любой природы, числовая
функция задает отображение множества
X, элементами которого
являются числа, на множествоY,
элементами которого тоже являются
числа. Кроме того, далее будем считать,
что множествоY —
это есть множество значений функции,
так что отображениеявляется сюръекцией.
МножествоXзадания
функции и множествоYзначений функции для числовых функций
традиционно называютобластью
определения функции(ООФ)иобластью
значений функции(ОЗФ).
Значение функции в точке
Если задано отображение множеств
функцией
,
то элементы множествXиYназываются точками.
Символомобозначается при этом как сама функция,
так и элемент,
соответствующий элементуx
при этой функциональной зависимости.
Если
x0— это
фиксированное значение аргументаx,
то значение функции в точкеx0обозначается следующими символами:
или
или
или
.
Например, ;
,
.
-
Сужение функции
Если есть функцияи рассматривается некоторое подмножествоЕ множестваХ, то отображение
называетсясужением
функции f на множество Е.
Пример
1 (сужение
функций)
1) ,
— это есть
сужение функции,
на множество
;
2) любая
последовательность
есть сужение функции
на множество натуральных чисел
;
например,– это есть сужение функции
,
на множество
.
Наряду с понятием
сужения функции существует и понятие
расширения функции.
Пример
2 (расширение
функций)
1) ;
от
этой функции можно перейти к её расширению
на множество:
;
2) от функции
можно перейти к её расширению на множество
,
если рассматривать её значения на
множестве комплексных чисел, где возможно
извлечение корня квадратного из
отрицательного числа.
-
Способы задания функции
1.Аналитический
способ задания функции
— функция задается математической
формулой, связывающей аргумент и функцию.
По этой формуле для каждого возможного
значения аргумента можно вычислить
соответствующее значение функции. При
этом нужно различать:
-
явное задание функции,
-
неявное задание функции,
-
параметрическое задание функции.
2.Табличный
способ задания функции— используется для функций, заданных
на дискретном конечном множестве
значений аргумента; записывается обычно
в виде следующей таблицы:
|
x |
x1 |
x2 |
… |
xn |
|
y |
y1 |
y2 |
… |
yn |
3.Графический
способ задания функции— задается множество точек координатной
плоскости, координаты которых являются
соответствующими друг другу значениями
аргумента и функции.
4.Описательный
способ задания функции– функциональная зависимость описывается
словами. Например,,
где— этоцелая
часть x, которая
определяется как наибольшее целое
число, не превышающееx.
Сужение функции на множество[]
– множества,
– подмножество множества,
– функция.
Множество 









Обозначим 
Сужение алгебраической структуры до сигнатуры[]
– множества,
– сигнатуры,
– подмножество алфавита отношений,
– подмножество алфавита операций,
– объединение алфавита отношений и
алфавита операций,– сужение функции местности,
– алгебраические структуры.
Алгебраическая структура 










Обозначим 
Сужение функции на подмножество 



Сужение функции 



Так, для 





Определение[править | править код]
Пусть дано отображение 

Функция 




Вариации и обобщения[править | править код]
Продолжение[править | править код]
Если функция 




Имея некоторую функцию 




|
№ гр. |
Дата |
Время |
Аудитория |
|
Э18 |
18.11.08 |
10:20 |
Г-104 |
|
25.11.08 |
10:20 |
Г-104 |
|
|
Э28 |
18.11.08 |
8:30 |
Г-309 |
|
25.11.08 |
8:30 |
Г-309 |
|
|
Э38 |
18.11.08 |
8:30 |
Г-309 |
|
25.11.08 |
8:30 |
Г-309 |
|
|
Э48 |
19.11.08 |
8:30 |
Г-309 |
|
26.11.08 |
8:30 |
Г-309 |
|
|
Э58 |
19.11.08 |
8:30 |
Г-309 |
|
26.11.08 |
8:30 |
Г-309 |
|
|
Э18 |
29.11.08 |
8:30 |
И-119 |
7.5. Свойства пределов, связанные с арифметическими
действиями над числовыми последовательностями
О п р е д е л е н и е. Числовая последовательность называется бесконечно
малой, если предел этой последовательности равен нулю.
Если – числовые последовательности, то – бесконечно малые числовые последовательности.
Итак, если (предел равен нулю)
при , то
– бесконечно ма
лая последовательность.
П р и м е р.
Другое определение бесконечно малой последовательности.
Псоледовательность – бесконечно малая
последовательность, если для любого существует такой номер
, что при
выполняется условие
.
О п р е д е л е н и е. Суммой (разностью), произведением и частным числовые
последовательностей и
называются
последовательности
,
,
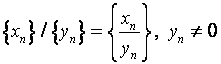
В частном случае при
получаем
.
Как видим, арифметические операции с числовыми
последовательностями переносятся на элементы этих последовательностей.
Если – последовательность,
в которой все элементы одинаковы, то такая последовательность называется стационарной
последовательностью.
Если , то числовая
последовательность будет бесконечно малой
последовательностью.
Пусть
при
, т.е.
– бесконечно малая последовательность. Если
, то это значит, что для любого
,
, что при
выполняется условие
. Поэтому последовательность
– бесконечно малая
последовательность.
Справедливо и обратное утверждение: если последовательность – бесконечно малая
последовательность, то .
Итак, сходящуюся последовательность можно представить в виде суммы предела
этой последовательности и бесконечно малой
последовательности , те в виде
О
п р е д е л е н и е. Числовая
последовательность называется бесконечно
большой последовательностью, если,
для любого , существует такой номер
, что при
выполняется условие
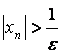
Другое определение бесконечно большой последовательности. Последовательность называется бесконечно
большой, если для любого положительного числа (как бы велико оно ни было), существует такой номер
, что все члены последовательности при
превосходят это число.
Считается, что предел бесконечно большой
последовательности равен бесконечности .
П
р и м е р .
Последовательность является бесконечно
большой, так как для любого 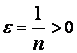
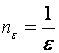
выполняется условие
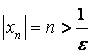
Пример
. Последовательность ,
– бесконечно большая.
Бесконечно большая последовательность – последовательность
неограниченная.
Если последовательность – бесконечно большая,
то последовательность 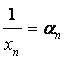
Рассмотрим основные свойства пределов числовых последовательностей, связанные с арифметическими действиями над
числовыми последовательностями
1°. Линейная комбинация любого конечного числа
бесконечно малых последовательностей
есть последовательность бесконечно малая.
Пусть
,
,
. Из определения предела последовательности следует, что для
существует такое число
,
и существует такой
номер , что при
выполняется условие
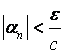
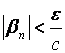
Примечание. Линейными комбинациями называются выражения вида .
Нужно доказать, что . Используя свойства абсолютной величины, получаем
Значит, для существует такой номер
, что при
выполняется
условие , т.е.
– бесконечно малая
величина.
2°. Произведение ограниченной и
бесконечно малой последовательности есть последовательность бесконечно малая.
Пусть
– ограниченная
последовательность. Это значит, что для заданного существует такое число
, что для всех
. Пусть
– бесконечно
малая последовательность. Тогда для
любого , существует такой номер
, что при
выполняется условие
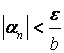
при
и
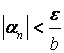
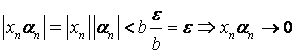
3°. Произведение конечного числа
бесконечно малых последовательностей есть последовательность бесконечно малая. (Это свойство следует из предыдущего).
Замечание. Что касается отношений бесконечно малых
последовательностей, то однозначного ответа здесь нет. Дробь может являться
бесконечно малой, бесконечно большой или в зависимости от скорости стремления к
нулю этих последовательностей.
Свойства бесконечно больших последовательностей аналогичны свойствам
бесконечно малых последовательностей, за исключением разности , которая может быть бесконечно большой или ограниченной в
зависимости от скорости стремления к бесконечности этих последовательностей.
4°. Если последовательность имеет предел равный
, то последовательность из абсолютных величин
будет стремиться к
.
Т.к.
, то это значит, что для любого
, существует такой номер
, что при
выполняется условие
. Воспользуемся свойством абсолютной величины
– бесконечно малая
последовательность .
5°. Пусть последовательность имеет предел равный
,
– предел равный
, тогда последовательность
будет иметь предел
равный .
Очевидно,
,
. Тогда
.
6°. Пусть ,
. Тогда
.
,
,
где
.
7°. Если ,
и ,
,
, то
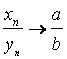
Пусть последовательность
,
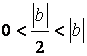
такой, что при
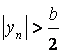
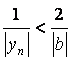
,
, то
,
,
где ,
. В этом случае
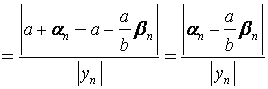
Так как 
– ограниченная
последовательность и
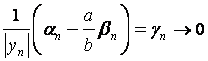
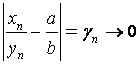
Значит, 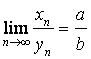
ГЛАВА
8. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§ 8.1. Понятие функции
Определение. Пусть и
– два каких-либо
множества. Соответствие, с помощью которого каждому элементу соответствует
единственный элемент , называется функцией, заданной (определенной) на
множестве со значениями в
множестве . Символическое
обозначение .
Эквивалентные
названия: преобразование, отображение (), морфизм.
Определение. Подмножество (
) называется множеством значений функции
, если каждый элемент
этого множества
ставится в соответствие хотя бы одному
элементу .
Пример 8.1. ,
(множества
вещественных чисел), . Тогда область задания множества будет совпадать со всей
вещественной числовой осью..
Элемент называется независимой
переменной или аргументом, а соответствующий ему элемент называют зависимой
переменной или функцией. Если функцию рассматривать как
отображение , то элемент
называют образом
элемента . Элемент же
в этом случае называют
прообразом
элемента . Множество
называется множеством
задания (определения) функции , множество
– множеством значений
функции.
Возможны
следующие четыре типа отображения:
1)Если , то это будет отображением
на
или сюръекция.
2)Если различным и
соответствуют
различные элементы ,
,
то – это инъекция (взаимно однозначное отображение
в
).
3)Если отображение является одновременно
сюръекцией и инъекцией, то – это биекция (взаимно однозначное
отображение на
).
4)Пусть и существует подмножество
множества
, тогда отображение
называется сужением
функции на множество
, если для
.
В
определении функции подчеркивается, что каждому элементу ставится в
соответствие единственный элемент . Если это условие не выполняется, т.е. одному элементу может
ставиться в соответствие несколько элементов, то такая функция называется многозначной.
Пример 8.2.
– двузначная функция.
Определение. Функция , определённая на множестве
значений функции
и ставящая в
соответствие каждому элементу его прообраз
, называется обратной функцией к
и обозначается:
.
Определение. Сложной функцией называется функция,
являющаяся наложением нескольких функций или, по-другому, суперпозицией
функций:
.
Определение. Числовая функция – это функция, у
которой область задания и множество значений являются числовыми множествами.
График
функции – это множество точек , т.е. некоторая
линия.
Способы
задания функции:
1)Аналитический
(задание функции в виде формул).
2)Графический.
3)Табличный.
Примеры.1), 2)
§ 8.2. Элементарные функции
Основными элементарными функциями называются следующие функции:
1) (
– константа),
2) – степенная (
– вещественное число),
3) – показательная (
),
4) – логарифмическая (
,
),
5) тригонометрические ,
6) обратные тригонометрические
.
Элементарными называются функции , которые содержат конечное число арифметических операций над
основными элементарными функциями и конечное число композиций (суперпозиций)
основных элементарных функций.
Элементарные функции подразделяются на следующие
классы:
1)Многочлены (полиномы) – функции вида
,
– старшая степень
полинома.
2)Рациональные (функции, представляющие собой
отношение двух полиномов):
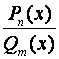
При
этом, если , то дробь называется неправильной, если
– правильной.
Пример 8.4.
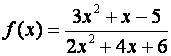
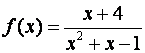
Простейшими
(элементарными) рациональными функциями называются следующие функции:
I. ,
II. 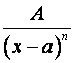
III. 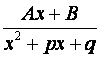
IV 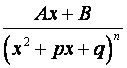
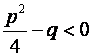
не имеет вещественных
нулей.
В курсе
алгебры доказывается, что всякую правильную рациональную дробь можно
представить в виде суммы простейших при
помощи метода неопределенных коэффициентов.
Пример 8.5. 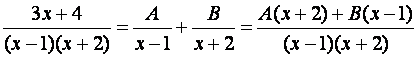
,
При
При
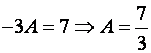
Пример 8.6.
(сколько сомножителей, столько дробей)
В общем случае
при 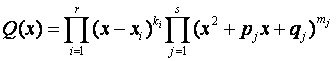
.
– нули многочлена
.
Пример 8.7.
.
,
,
,
;
,
,
,
Всякую правильную дробь можно представить в виде суммы
элементарных дробей с неопределенными коэффициентами.
3)Иррациональные
функции – функции, которые получаются с помощью суперпозиции
рациональных функций, а также степенных функций с рациональными показателями и четырёх
арифметических действий.
4)Трансцендентные
функции – функции, которые не являются рациональными или
иррациональными. Это тригонометрические, показательные, обратные
тригонометрические, логарифмические,
гиперболические функции.
5)Гиперболические функции:
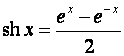
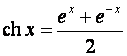
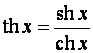
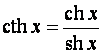
,
.
Гиперболические функции можно выразить через
тригонометрические и наоборот.
§ 8.3. Предел функции
8.3.1. Первое
определение предела
функции (определение по Гейне)
Определение. Число называется пределом
функции , в точке
, если для любой последовательности
,
, сходящейся к
, соответствующая последовательность значений функции
сходится к
.
Символическое обозначение или
при
.
Определение. Точка называется точкой прикосновения множества
, если существует последовательность
, предел которой
равен , т.е.
.
Все точки являются точками прикосновения множества
. Могут существовать точки прикосновения, не принадлежащие
множеству .
Пример 8.8.
а) Множество – множество точек интервала
. Точками прикосновения в данном случае будут точки
.
б) – множество точек
и
, для которых
.
Точками
прикосновения множества будут точки
(,
), для которых
.
Из
определения точки прикосновения следует, что точка будет точкой
прикосновения множества тогда и только тогда,
когда любая окрестность этой точки пересекается с множеством .
Понятие
предела функции в точке очевидно имеет смысл
тогда и только тогда, когда точка является точкой прикосновения множества (области определения
функции). Поэтому будем предполагать, специально не оговаривая, что точка является точкой
прикосновения множества .
Пример8.9.Найдите предел
функции
в точке , если
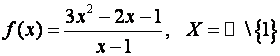
Решение.
Строим любую последовательность , сходящуюся к нулю.
Тогда
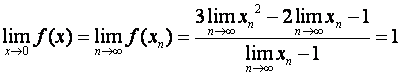
Пример8.10.
Найдите предел функции в точке
, если
Решение. Для 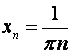
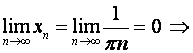
.
Для 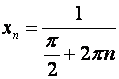
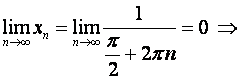
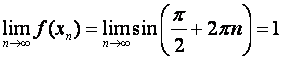
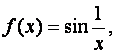
предела не имеет.
Определение. Пусть задана функция ,
, тогда
называется пределом
сужения функции.
Очевидно
для всякой функции, имеющей предел, существуют и пределы сужения функции.
Обратное в общем случае неверно. Так в примере 8.10 предел функции 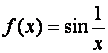
равен
, а по сужению
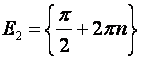
, хотя в этой точке предел функции
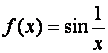
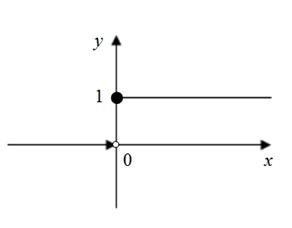
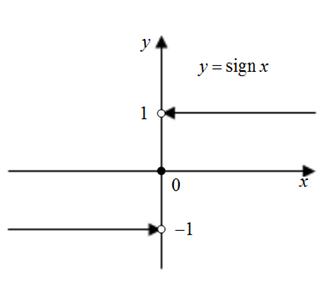
Пример 8.11.Существует ли предел в точке функции
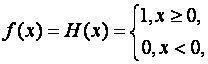
функцией Хевисайда (единичной функцией).
Решение.
Пределы по сужению
и по сужению
,
как видим, различны. Поэтому предел функции Хевисайда
в точке не существует.
Определение. Проколотой окрестностью точки называется всякая
окрестность этой точки, из которой исключена точка .
,
,
.
Зачастую рассматривается предел функции не по всему
множеству , а по пересечению его с выколотой окрестностью
.
Пример 8.12. Функция Дирихле 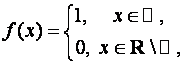
единице в рациональных точках и нулю в иррациональных точках, не имеет предела ни в одной точке, так
как ,
.
Пример 8.13.
Предел по сужению
.
Предел по сужению
.
Предел по сужению
– не существует.
Пример 8.14. .
Предел по сужению
– не существует.
Предел по сужению
.
8.3.2. Второе
определение предела
функции (определение по Коши)
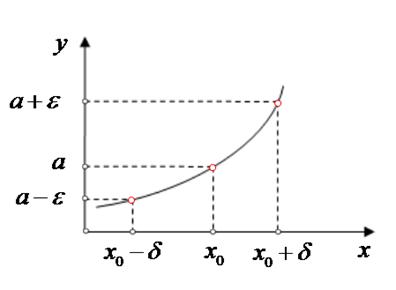
Определение. Число называется пределом
функции , в точке
, если для любого
существует такое
, что при
выполняется условие
. Символическое
обозначение
.
Данные два определения эквивалентны, так как
условие эквивалентно
условию , а условие
эквивалентно условию
.
Определение можно представить в виде окрестности точки
.
§ 8.4. Односторонние пределы
Пусть – область определения
или задания функции . Введём обозначения
,
.
Очевидно,
что ,
.Тогда предел
называется пределом функции справа.
Аналогично предел
называется
пределом функции слева. Пределы справа
и слева являются односторонними пределами функции .
Замечание.
Если односторонние пределы функции рассматриваются на
множестве с выколотой точкой
, т.е. на сужении
множества
, то применяются следующие обозначения:
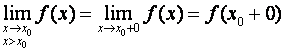
справа,
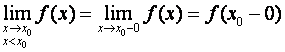
В том случае, когда запишем:
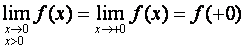
справа,
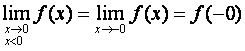
Если , то существует только предел функции слева
.
.
Если , то существует только предел функции слева
.
Пример 8.15. ,
.
Односторонние пределы на множестве равны
,
.
Односторонние пределы на множестве не существуют.
В символической форме
,
.
Теорема.
Функция имеет в точке
предел тогда и только тогда, когда в этой
точке существуют односторонние пределы функции. При этом .
Необходимость.
, тогда существуют пределы по любому сужению, тоже равные
. Следовательно,
.
Достаточность. Существуют односторонние пределы
.
Тогда для существует такое
, что при
выполняется условие
(или
)
и существует такое , что при
выполняется условие
(или
). Выберем
. Тогда
при будут одновременно
выполняться условия
и
(или
и
),
т.е. условия или
, откуда следует, что
.
§ 8.5. Свойства предела функции
Свойства
аналогичны свойствам предела последовательности:
1) ,
;
2) ;
3) ;
4) 
5) 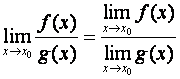
;
6) ,
,
, при
,
.
Теорема. Если имеет в точке
предел, то существует
некоторая окрестность , в которой функция ограничена.
Согласно одному из определений предела функций
при
, то при
существует
, что при
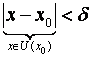
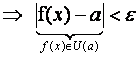
. При
– это и означает
ограниченность функции.
§ 5.6. Предел монотонной функций
Функция называется монотонно возрастающей (убывающей), если для
, выполняется условие
.
Пусть – множество значений
, тогда
,
.
Теорема. Пусть функция монотонно возрастает
(убывает) на интервале , тогда в точках
и
существуют
соответствующие односторонние пределы, при этом предел справа в точке равен нижней грани.
,
–для монотонно
возрастающей.
,
– для монотонно
убывающей.
Пусть
монотонно возрастает на интервале
и
,
тогда для существует такое
, что
.
Положим ,
. Выберем точку
, следовательно,
.
и ,следовательно,
,
,
.
Аналогично доказывается, что
§ 8.7.
Критерий Коши существования предела функции
Теорема.
Необходимым и достаточным условием
существования предела в точке
является условие:
, для
,
.
(Функция имеет в точке
предел тогда и только
тогда, когда для существует такая
окрестность точки
, что для
выполняется условие
).
Необходимость. В
точке существует предел
.
Из определения предела функции в точке следует, что в
этом случае для существует окрестность
, такая что для
выполняется
условие 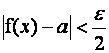
для любых
точек. Поэтому выбираем две точки , принадлежащие этой окрестности.
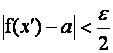
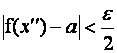
Достаточность. Предположим, что выполняется условие:
,
для ,
.
,
.
,
, где
и
– некоторые числа,
удовлетворяющие условию: ,
.
выбирается из
заданного .
, а т.к.
, то, следовательно,
и
.
Соответственно
– условие Коши существования предела для
последовательности .
Значит, предел последовательности существует, а
.
ЛЕКЦИЯ 14
§ 8.8. Бесконечно малые и
бесконечно большие функции
Определение. Функция называется бесконечно
малой в точке , если предел функции в этой точке равен нулю. Будем
обозначать: …
Определение. Функция называется бесконечно
большой в точке , если для любого положительного числа можно указать такаю
окрестность в точке , что
.
Окрестность , если
, если
.
Если при
, то, следовательно,
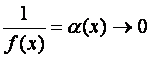
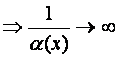
Одна и та же функция в одних точках может быть
бесконечно малой, а в других бесконечно большой.
Пример 5.17.
Очевидно в точке ,
, а
.
,
.
Основные
свойства бесконечно малых функций (аналогичны свойствам бесконечно малых
последовательностей).
1°. Если
, то
.
2°.Если и
, то
при
.
3°.Сумма
конечного числа бесконечно малых функций есть функция бесконечно малая.
4°.Произведение
ограниченной функции на бесконечно малую есть функция бесконечно малая.
, если
– ограниченная,
при
.
5°.Произведение
бесконечно малых функций есть функция бесконечно малая.
, если
,
при
.
Это свойство можно распространить на конечное число
бесконечно малых функций.
Доказательства аналогичны доказательствам свойств
бесконечно малых последовательностей.
Сужение функции
Bardaro
Ученик
(147),
закрыт
8 лет назад
AnVass
Просветленный
(21423)
8 лет назад
Иными словами, сужение функции f— это та же самая функция f, но рассматриваемая не на всей области определения D(f), а только на её части P.
Источник: Основы арифметики