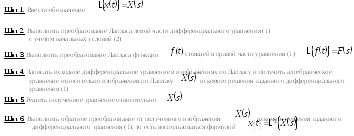Как найти свертку двух функций - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Свёртка.

Свёртка, конволюция — операция в функциональном анализе, которая при применении к двум функциям и возвращает третью функцию, соответствующую взаимнокорреляционной функции f(x) и . Операцию свёртки можно интерпретировать как «схожесть» одной функции с отражённой и сдвинутой копией другой. Понятие свёртки обобщается для функций, определённых на произвольных измеримых пространствах, и может рассматриваться как особый вид интегрального преобразования. В дискретном случае свёртка соответствует сумме значений с коэффициентами, соответствующими смещённым значениям , то есть

Свёртка двух прямоугольных импульсов: в результате даёт треугольный импульс.

Свёртка прямоугольного импульса (входного сигнала) с импульсным откликом RC цепи

Определение[править | править код]

Пусть ${displaystyle f,g:mathbb {R} ^{n}to mathbb {R} }$ — две функции, интегрируемые относительно меры Лебега на пространстве $mathbb {R} ^{n}$ . Тогда их свёрткой называется функция ${displaystyle f*g:mathbb {R} ^{n}to mathbb {R} }$ , определённая формулой

В частности, при n=1 формула принимает вид

Свёртка определена при почти всех ${displaystyle xin {mathbb {R} ^{n}}}$ и интегрируема.

В случае, когда , а функции определены на промежутке , свёртку можно записать в виде

Впервые интегралы, являющиеся свёрткой двух функций, встречаются в трудах Леонарда Эйлера (1760-е годы); позднее свёртка появляется у Лапласа, Лакруа, Фурье, Коши, Пуассона и других математиков. Обозначение свёртки функций при помощи звёздочки впервые предложил Вито Вольтерра в 1912 году на своих лекциях в Сорбонне (опубликованы годом позже)^[1].

Свойства[править | править код]

Коммутативность:

Ассоциативность:

Линейность (дистрибутивность по сложению и ассоциативность с умножением на скаляр):

${displaystyle (f_{1}+f_{2})*g=f_{1}*g+f_{2}*g}$

${displaystyle f*(g_{1}+g_{2})=f*g_{1}+f*g_{2}}$

{displaystyle (af)*g=a(f*g)=f*(ag),quad forall ain mathbb {R} }

Правило дифференцирования:

{displaystyle mathrm {D} (f*g)=mathrm {D} f*g=f*mathrm {D} g}

где обозначает производную функции по любой переменной.

Преобразование Лапласа:

{displaystyle {mathcal {L}}{f(x)*g(x)}={mathcal {L}}{f(x)}cdot {mathcal {L}}{g(x)}}

Свойство фурье-образа:

{displaystyle {mathfrak {F}}[f*g]={mathfrak {F}}[f]cdot {mathfrak {F}}[g]}

где обозначает преобразование Фурье функции.

Если является матрицей дискретного преобразования Фурье, то:

${displaystyle {mathcal {W}}(C^{(1)}xast C^{(2)}y)=({mathcal {W}}C^{(1)}bullet {mathcal {W}}C^{(2)})(xotimes y)={mathcal {W}}C^{(1)}xcirc {mathcal {W}}C^{(2)}y}$

где — символ торцевого произведения матриц^[2]^[3]^[4]^[5]^[6], обозначает произведение Кронекера, — символ произведения Адамара (тождество является следствием свойств отсчётного скетча^[7]).

Пример[править | править код]

График функции — количество выпавшего снега в килограммах на начало часа.

Пусть стоит задача вычислить, как будет изменяться количество снега на каком-либо участке земли в зависимости от времени. Решение этой задачи можно разделить на два этапа:

построить модель выпадения снега и модель таяния снега.
каким-то образом соединить эти две модели в одну.

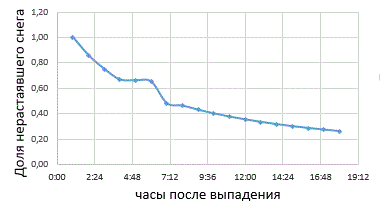
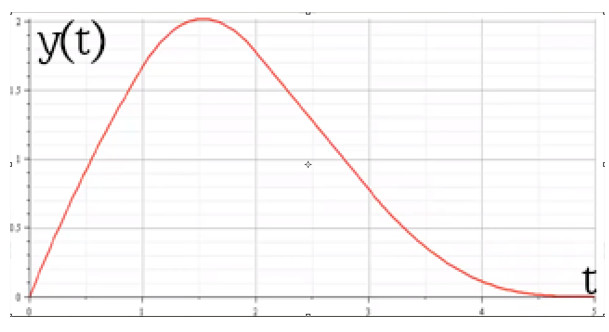
График зависимости количества нерастаявшего снега от времени прошедшего с момента его выпадения.

Задачи первого этапа решаются путём наблюдений и опытов, а задачи второго этапа — свёрткой получившихся на первом этапе моделей.

Пусть в результате решения задачи на первом этапе было построено две зависимости (математические модели):

зависимость количества выпавшего снега от текущего времени ,
зависимость доли нерастаявшего снега от времени, прошедшего с момента его выпадения .

Если бы снег не начинал таять, количество всех выпавших осадков можно было бы посчитать путём сложения в дискретном случае:

${displaystyle G=sum _{t=0}^{T}g(t)}$

или путём интегрирования в случае непрерывном:

${displaystyle G=int limits _{0}^{T}g(t),dt}$

Но в данном случае таяние снега имеет место и, более того, оно зависит не только от текущего общего количества снега, но и от того, в какой момент времени выпал этот конкретный объём снега. Так снег, выпавший две недели назад, может уже испариться, в то время как снег, выпавший полчаса назад, ещё будет лежать и даже не начнёт подтаивать.

Получается, что для снега, выпавшего в разное время, нужно построить свою модель таяния и как-то сложить все эти модели вместе.

Для этих целей и можно использовать понятие математической свёртки. Пусть в момент времени рассматривается снег, который выпал в момент времени tau , тогда

Нужно для каждого количества снега, выпавшего в момент времени tau , сложить множество моделей в одну функцию. Если это сделать, получится сумма в дискретном случае:

${displaystyle w(t)=sum limits _{tau =0}^{t}g(tau )f(t-tau ),}$

или интеграл в непрерывном:

${displaystyle w(t)=int limits _{tau =0}^{t}g(tau )f(t-tau )dtau .}$

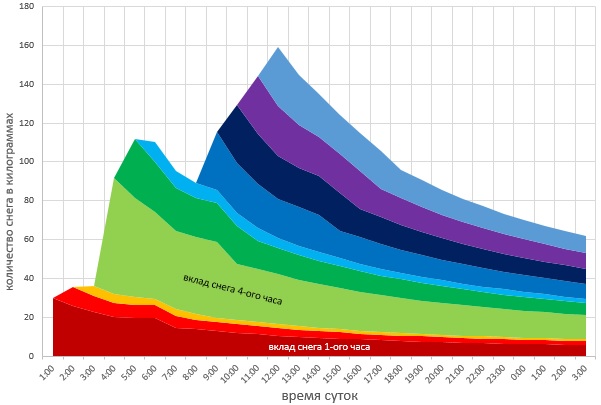
Графически функция w(t) изображена ниже, где разными цветами представлены вклады каждой кучи снега из графика .

График функции w(t) , где разным цветом представлен вклад каждой кучи снега (цвета вкладов соответствуют цветам куч выпавшего снега на графике выше)

Функция w(t) полностью моделирует поведение снега, выпавшего согласно модели . Так, на графике выше видно, что общее количество снега увеличивается тремя скачками, но снег начинает таять сразу, не дожидаясь выпадения других осадков.

Свёртка на группах[править | править код]

Пусть — группа, оснащённая мерой , и — две функции, определённые на . Тогда их свёрткой называется функция^{[источник не указан 1280 дней]}

${displaystyle (f*g)(x)=int limits _{G}f(y),gleft(xy^{-1}right),m(dy),quad forall xin G.}$

Свёртка мер[править | править код]

Пусть есть борелевское пространство и две меры . Тогда их свёрткой называется мера^{[источник не указан 1280 дней]}

${displaystyle mu *nu (A)=mu otimes nu left({(x,y)in mathbb {R} ^{2}mid x+yin A}right),quad forall Ain {mathcal {B}}(mathbb {R} ),}$

где обозначает произведение мер и .

Свойства[править | править код]

${displaystyle f_{mu }={frac {dmu }{dm}},quad f_{nu }={frac {dnu }{dm}}.}$

Тогда mu * nu также абсолютно непрерывна относительно , и её производная Радона — Никодима $f_{mu * nu} = frac{d mu * nu}{dm}$ имеет вид^{[источник не указан 1280 дней]}

${displaystyle f_{mu *nu }=f_{mu }*f_{nu }.}$

Свёртка распределений[править | править код]

Если $mathbb{P}^X,mathbb{P}^Y$ — распределения двух независимых случайных величин и , то^{[источник не указан 1280 дней]}

${displaystyle mathbb {P} ^{X+Y}=mathbb {P} ^{X}*mathbb {P} ^{Y},}$

где $mathbb{P}^{X+Y}$ — распределение суммы X+Y . В частности, если X,Y абсолютно непрерывны и имеют плотности f_X,f_Y , то случайная величина X+Y также абсолютно непрерывна и её плотность имеет вид:

${displaystyle f_{X+Y}=f_{X}*f_{Y}.}$

См. также[править | править код]

Обратная свертка (деконволюция)
Взаимнокорреляционная функция
Автокорреляционная функция
Свёртка последовательностей

Примечания[править | править код]

↑ Domínguez A. A History of the Convolution Operation // IEEE Pulse. — 2015. — Vol. 6, no. 1. — P. 38—49. Архивировано 3 февраля 2016 года.
↑ Slyusar, V. I. (December 27, 1996). “End products in matrices in radar applications” (PDF). Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50—53. Архивировано (PDF) из оригинала 2020-07-27. Дата обращения 2020-08-01.
↑ Slyusar, V. I. (1997-05-20). “Analytical model of the digital antenna array on a basis of face-splitting matrix products” (PDF). Proc. ICATT-97, Kyiv: 108—109. Архивировано (PDF) из оригинала 2020-01-25. Дата обращения 2020-08-01.
↑ Slyusar, V. I. (1997-09-15). “New operations of matrices product for applications of radars” (PDF). Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73—74. Архивировано (PDF) из оригинала 2020-01-25. Дата обращения 2020-08-01.
↑ Slyusar, V. I. (March 13, 1998). “A Family of Face Products of Matrices and its Properties” (PDF). Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz.- 1999. 35 (3): 379—384. DOI:10.1007/BF02733426. Архивировано (PDF) из оригинала 2020-01-25. Дата обращения 2020-08-01.
↑ Slyusar, V. I. (2003). “Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels” (PDF). Radioelectronics and Communications Systems. 46 (10): 9—17. Архивировано (PDF) из оригинала 2020-09-20. Дата обращения 2020-08-01.
↑ Ninh, Pham; Rasmus, Pagh (2013). Fast and scalable polynomial kernels via explicit feature maps. SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. DOI:10.1145/2487575.2487591.

Литература[править | править код]

Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, — М.: Наука, 2004 (7-е изд.).
Ширяев А. Н. Вероятность, — М.: Наука. 1989.
Напалков В. В. Уравнения свертки в многомерных пространствах. — М., Наука, 1982. — Тираж 3500 экз. — 240 с.

Ссылки[править | править код]

Java-Applet
Java-Applet
Линейная и циклическая свертка. Дата обращения: 15 ноября 2010.

Источник

Inclab
Scilab для продвинутых
Анимируем свёртку функций

Анимируем свёртку функций

Свёртка это математическая операция, применимая к ( f(t) ) и ( g(t) ), которая порождает третью функцию и определяется формулой:

( y(t) = (f * g)(t) = displaystyleint_{-infty}^{infty}f(tau)g(t-tau)dtau ) (1)

Рассмотрим реализацию свёртки двух сигналов на примере. Пусть сигналы ( f(t) ) и ( g(t) ) задаются в следующем виде:

begin{matrix}
f(t) = begin{cases}
2, quad 0 leq t < 1 \
-2t+4, quad 1 leq t < 2 \
0, quad t<0 text{ or } t geq 2 \
end{cases}
&
g(t) = begin{cases}
1, quad t = 0 \
1 – frac{1}{3}t, quad 0 < t < 3 \
0, quad t<0 text{ or } t geq 3 \
end{cases}
end{matrix}

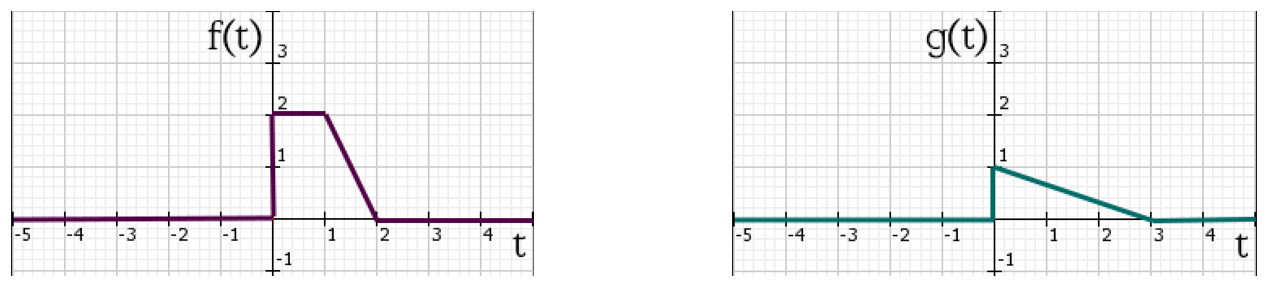
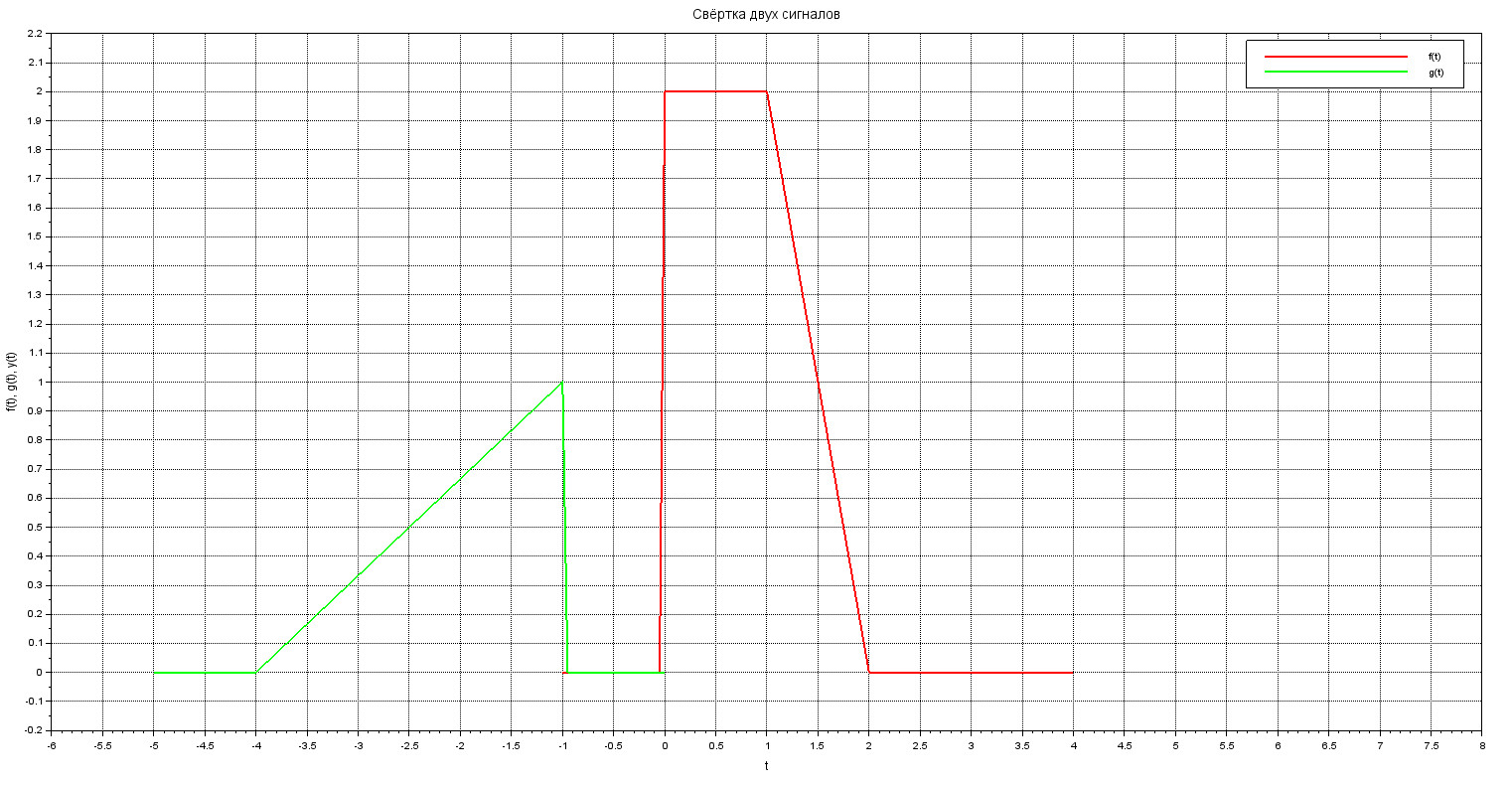
Их графики, соответственно будут представлять собой ломаные, как показано ниже

Графики сигналов f(t) и g(t)

Пример свёртки двух функций пошагово

Проведём пошаговую операцию свёртки двух сигналов, чтобы детально разобраться в смысле данной математической операции.

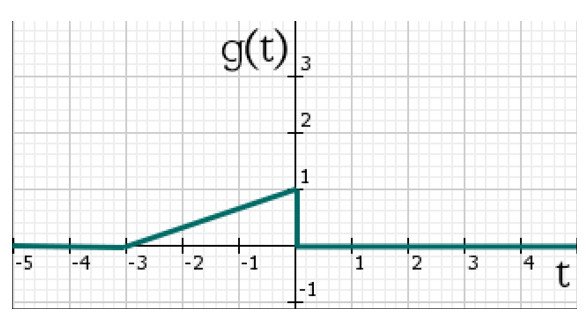
Итак, начнём с того, что в интегральном выражении у функции ( g(t-tau) ) по переменной, которой производится интегрирование, стоит знак “-“, а значит график нужно отразить по горизонтальной оси относительно оси ординат, как показано на рисунке ниже:

Отражённый сигнал g(t)

Выражение ( (t-tau) ) означает, что движение будет происходить оси ( t ). Причём, если ( t<0 ), то график функции ( g(t) ) будет двигаться влево, при ( t geq 0 ) движение будет происходить вправо.

Далее необходимо вычислить произведение ( g(t)(t-tau) ) для каждого значения ( t ) и посчитать площадь получившейся в результате произведения двух графиков фигуры.

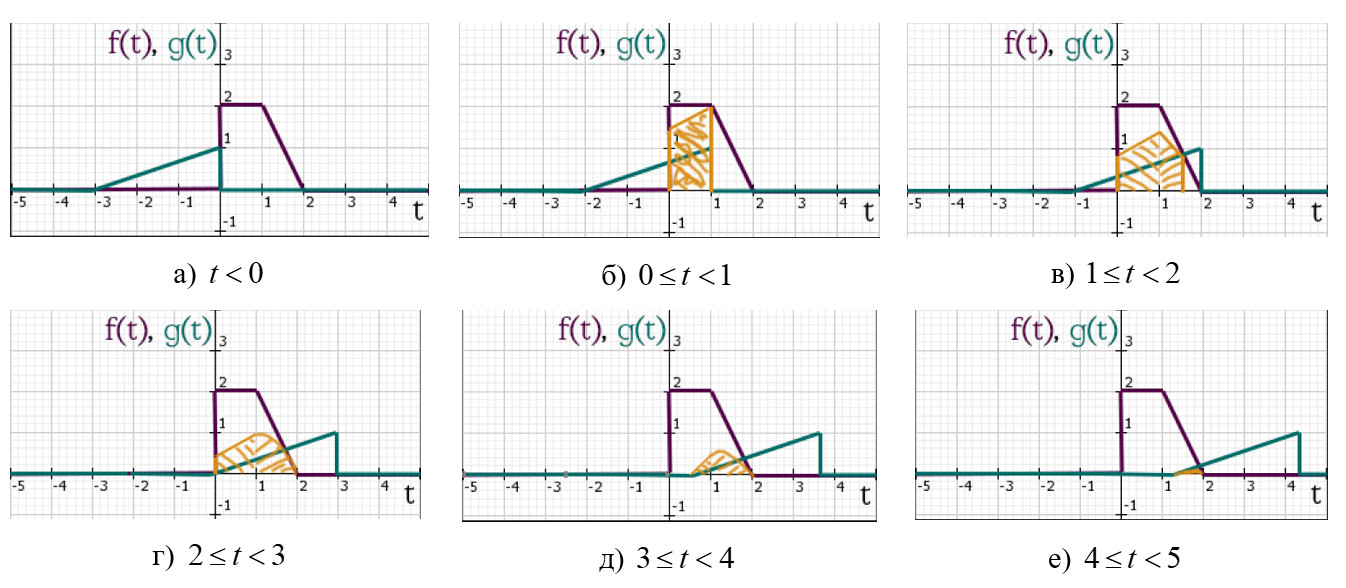
На рисунке ниже показано, какие случаи пересечений нам необходимо просчитать по мере движения графика по оси ( t ) .

Графичекая пошаговая интерпретация свёртки сигналов f(t) и g(t)

Остановимся на каждом из 6-ти случаев и произведём расчёты площадей получившихся фигур.

При ( t<0 ) графики сигналов не пересекаются, а значит и площадь фигуры их пересечения нулевая, то есть, результирующий интеграл примет вид:

( displaystyleint_{-infty}^{0}f(tau)g(t-tau)dtau=0 )
На интервале ( 0 leq t < 1 ) сигнал ( f(t) ) представляет собой константу: ( f(t)=2 ) , а график сигнала ( g(t) ) – есть прямая (1 – frac{1}{3}t). Исходя из вышесказанного, результатом сворачивания двух функций будет функция ( y(t) ) вида:

( y(t) = displaystyleint_{0}^{t} 2 left(1 – frac{1}{3}(t-tau)right) dtau = 2t – frac{t^2}{3} )
На интервале ( 1 leq t < 2 ) результирующий интеграл можно разбить на 2 интеграла: первый вида, описанного в пункте b). Второй интеграл будет представлять собой площадь фигуры, имеющей стороны, описываемые прямыми (1 – frac{1}{3}t) и ( -2t+4 ) . В результате, функция ( y(t) ) примет вид:

( y(t) = displaystyleint_{0}^{1} 2 left(1 – frac{1}{3}(t-tau)right) dtau + displaystyleint_{1}^{t} left( 4 – 2tau right) left(1 – frac{1}{3}(t-tau)right) dtau = frac{t^3}{9} -frac{5}{3}t^2 + frac{13}{3}t – frac{10}{9} )
На интервале ( 2 leq t < 3 ) результатом свёртки будет функция ( y(t) ):

( y(t) = displaystyleint_{0}^{1} 2 left(1 – frac{1}{3}(t-tau)right) dtau + displaystyleint_{1}^{2} left( 4 – 2tau right) left(1 – frac{1}{3}(t-tau)right) dtau = frac{34}{9} -t )
Предпоследним, дающим непустое пересечение графиков, будет интервал ( 3 leq t < 4 ), который породит функцию ( y(t) ):

( y(t) = displaystyleint_{t-3}^{1}2 left(1 – frac{1}{3}(t-tau)right) dtau + displaystyleint_{1}^{2}left( 4 – 2tau right) left(1 – frac{1}{3}(t-tau)right) dtau = frac{1}{3}t^2 -3t + frac{61}{9} )
Результирующей функцией на интервале ( 4 leq t < 5 ) будет второе слагаемое из предыдущего случая со своими пределами интегрирования:

( y(t) = displaystyleint_{t-3}^{2} left( 4 – 2tau right) left(1 – frac{1}{3}(t-tau)right) dtau = frac{1}{9}t^3 + frac{5}{3}t^2 – frac{25}{3}t + frac{125}{9} )

Таким образом, результатом свёртки игналов ( f(t) ) и ( g(t) ) будет функция ( y(t) ), задаваемая совокупностью уравнений:

begin{matrix}
y(t) = begin{cases}
0, quad t<0 text{ or } t geq 5 \
2t – frac{t^2}{3}, quad 0 leq t < 1 \
frac{t^3}{9} -frac{5}{3}t^2 + frac{13}{3}t – frac{10}{9}, quad 1 leq t < 2 \
frac{34}{9} -t, quad 2 leq t < 3 \
frac{1}{3}t^2 -3t + frac{61}{9}, quad 3 leq t < 4 \
frac{1}{9}t^3 + frac{5}{3}t^2 – frac{25}{3}t + frac{125}{9}, quad 4 leq t < 5 \
end{cases}
end{matrix}

На рисунке ниже приведена функция являющаяся результатом сворачивания двух сигналов на каждом из смысловых промежутков.

Функция y(t) – результат свёртки сигналов f(t) и g(t)

Реализация свёртки на Scilab

Для реализации в численных методах, рассматривается дискретный случай свертки двух функций ( f(j) ) и ( g(j) )

( z(k) = displaystylesum_{j=max(1, k+1-L_g)}^{min(k,L_f)} f(j)cdot g(k+1-j), quad k=1,..,L_f+L_g quad (3) )

где ( L_f, L_g) – количество элементов функций ( f(j) ) и ( g(j) ) соответственно.

Прежде всего, зададим функции ( f(j) ) и ( g(j) ) с помощью условных операторов в Scilab:


function ft = f(t)
    ft = zeros(t);
    
    for j = 1:length(t)   
        if ( t(j) >= 0 && t(j) < 1 ) then
            ft(j) = 2;
        elseif ( t(j) >= 1 && t(j) < 2 )  then
            ft(j) = -2*t(j) + 4;  
        end;
    end;
endfunction

Задание сигнала f(t)


function gt = g(t)  
    gt = zeros(t);
    
    for j = 1:length(t)   
        if ( t(j) == 0 ) then
            gt(j) = 1;
        elseif ( t(j) >= 0 && t(j) < 3 )  then
            gt(j) = -1/3*t(j) + 1;  
        end;
    end;
endfunction

Задание сигнала g(t)

Далее на пишем функцию, реализующую свёртку, согласно формулы (3)


function cnv = myconv(f_, g_)
    Lf = length(f_);
    Lg = length(g_);
    
    L = Lf + Lg - 1;
    cnv = zeros(1,L);
    
    for k = 1:L 
        jmin = max(1, k + 1 - Lg);
        jmax = min(k, Lf);
      
        for j = jmin:jmax      
            cnv(k) = cnv(k) + f_(j) * g_(k + 1 - j);
        end        
    end
endfunction

Задание сигнала g(t)

И посмотрим, сойдётся ли результат, полученный с помощью нашей функции ( myconv() ) с результатом, полученным при использовании встроенной функции ( conv() )


d = 1e-1;
Tmin = -1; Tmax = 4;
t = Tmin:d:Tmax;
  
plot( conv(f(t), g(t)), 'r' );
plot( myconv(f(t), g(t)), 'b--' );
xgrid();xtitle("Свёртка двух сигналов","t", "y(t)");
legend("Встроенная свёртка", "Своя свёртка");
gca().children.children.thickness  = 2;

Вывод графиков двух функций с настройкой толщины в Scilab

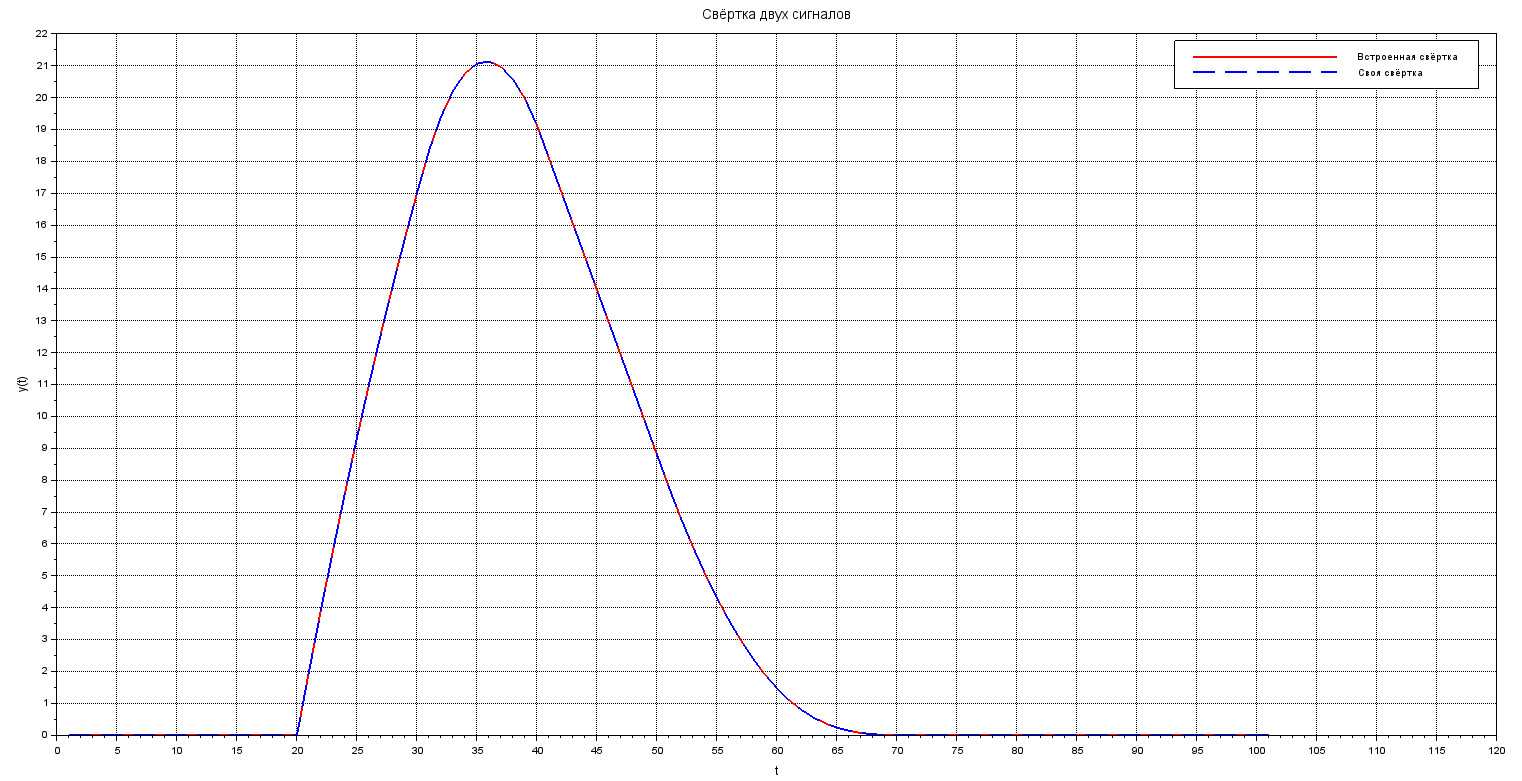
Глядя на изображение ниже, можно с уверенностью сказать, что результаты совпадают 🙂

Результат наложения встроенной и самописной функции свёртки

Вот только масштаб и отсчёты не похожи на наши задынные промежутки. Поэтому, проведём масштабирование результатов.

Корректировка результатов свёртки

Для корректного отображения результирующего графика нам потребуется несколько модифицировать функцию ( myconv() ). Прежде всего, заведём переменную, отвечающую за сдвиг результата по горизонтальной оси:


N = (2*abs(Tmin))/d;

Переменная сдвига

И изменим функцию ( myconv() ) следующим образом:


function cnv = myconv(f_, g_, shift)
    Lf = length(f_);
    Lg = length(g_);
    
    L = Lf + Lg - 1;
    cnv = zeros(2,L);
    
    for k = 1:L 
        jmin = max(1, k + 1 - Lg);
        jmax = min(k, Lf);
        cnv(1,k) = k - shift;
        for j = jmin:jmax      
            cnv(2,k) = cnv(2,k) + f_(j) * g_(k+1-j);
        end        
    end
endfunction

Обновлённая функция свёртки

Посмотрим, как теперь будет выглядеть результат:


myconv_scalled = d * myconv(f(t), g(t), N);
plot(myconv_scalled(1,:), myconv_scalled(2,:), 'b--' );
xgrid();xtitle("Свёртка двух сигналов","t", "y(t)");
legend("Своя свёртка");
gca().children.children.thickness  = 2;

Рисум график масштабированной свёртки

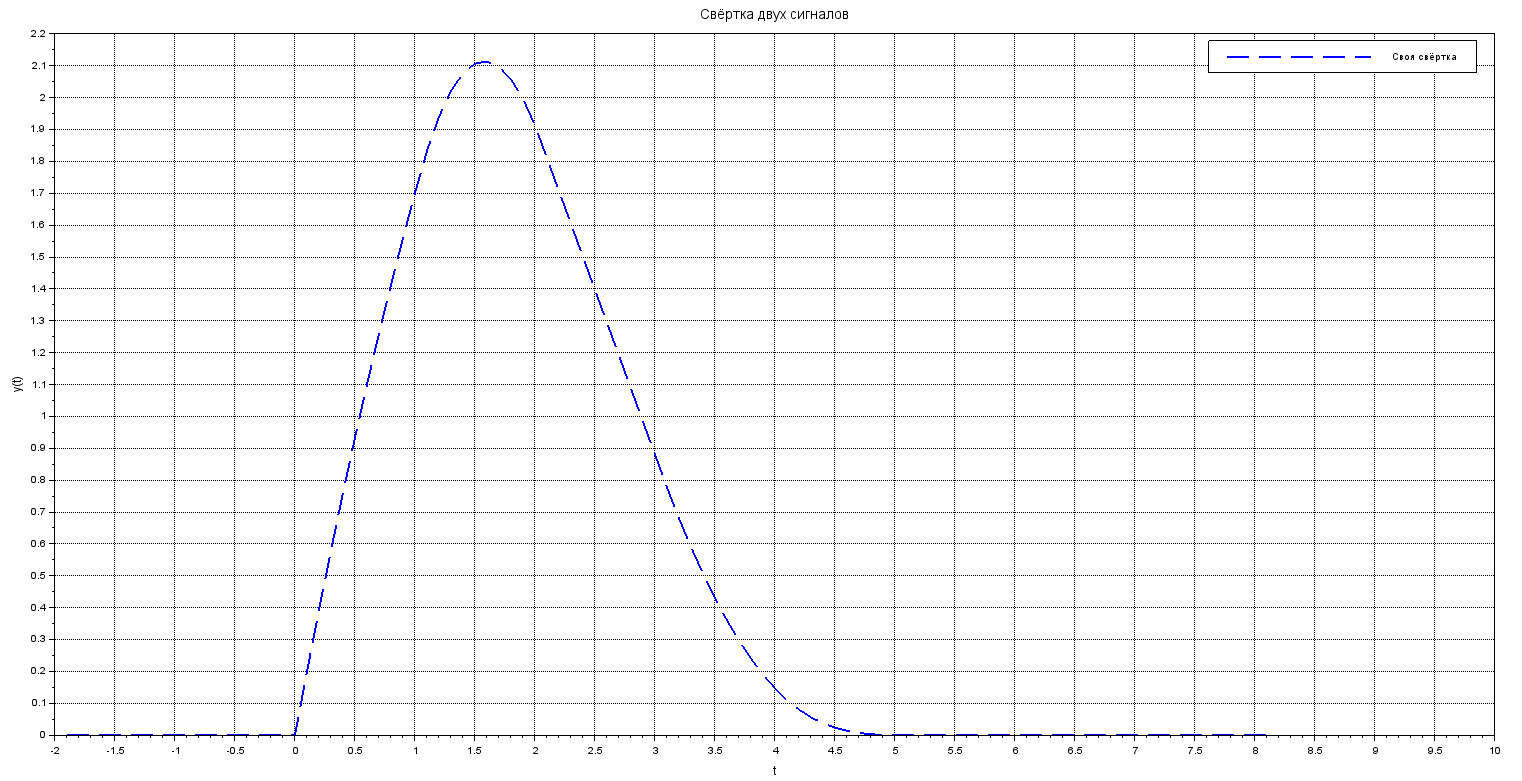
Результат модификации свёртки

Стало значительно лучше: мы укладываемся в интервал и стартуем из нуля.

Реализация анимации свёртки двух сигналов

Прежде всего, выведем графики сигналов, которые сворачиваем:


shift = 2*abs(Tmin);
plot(t, f(t), "r" ); 
plot(-t - shift, g(t), "g" );
xgrid();xtitle("Свёртка двух сигналов","t", "f(t), g(t), y(t)");
legend("f(t)", "g(-t)");

conv_axes = gca();
conv_axes.data_bounds=[-5 -0.1; 8 max(myconv_scalled(2,:))];
conv_axes.children.children.thickness  = 2;

Рисуем графики функций f(t) и отражённой и сдвинутой g(t)

Чтобы графики выглядели поприличнее, нужно уменьшить шаг дискретизации, например до ( d=0,01 ) и настроить их толщину с помощью ( gca().children.children.thickness )

Графики функций f(t) и g(t)

Осталось лишь реализовать анимационный цикл.

В статьедано описание основ анимации в Scilab.

Здесь на каждом шагу цикла мы рисуем i-ю точку свёртки, а зелёный график рисуем и стираем, что имитирует его движение.


i = 1; t_ = Tmin; g_inv = g(t);
while ( (i <= length(myconv_scalled(2,:))) && (t_ < 2*Tmax)  )
    drawlater();    
        sca(conv_axes);           
                      
        plot(myconv_scalled(1,i), myconv_scalled(2,i), '.-b');
        plot(-t - shift + i*d, g_inv, 'g');
        conv_axes.children.children.thickness  = 2;
        
        realtime(i);
        delete(conv_axes.children.children(3));
    drawnow();    
    
   i = i+1;
   t_ = i*d;
end

Эффект движущегося графика в Scilab

В результате получим такую анимированную картинку движения графика и построения результирующего интеграла-свёртки:

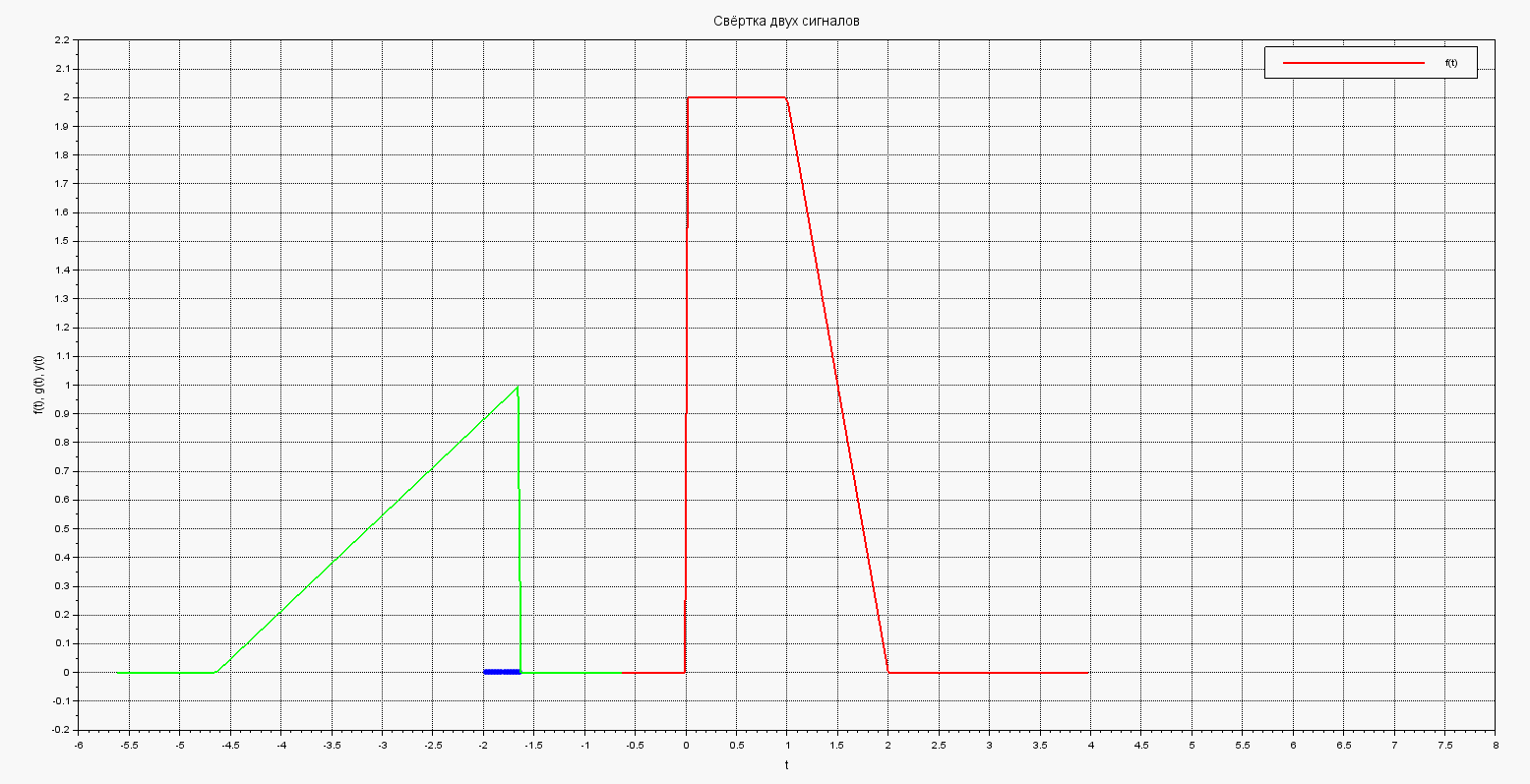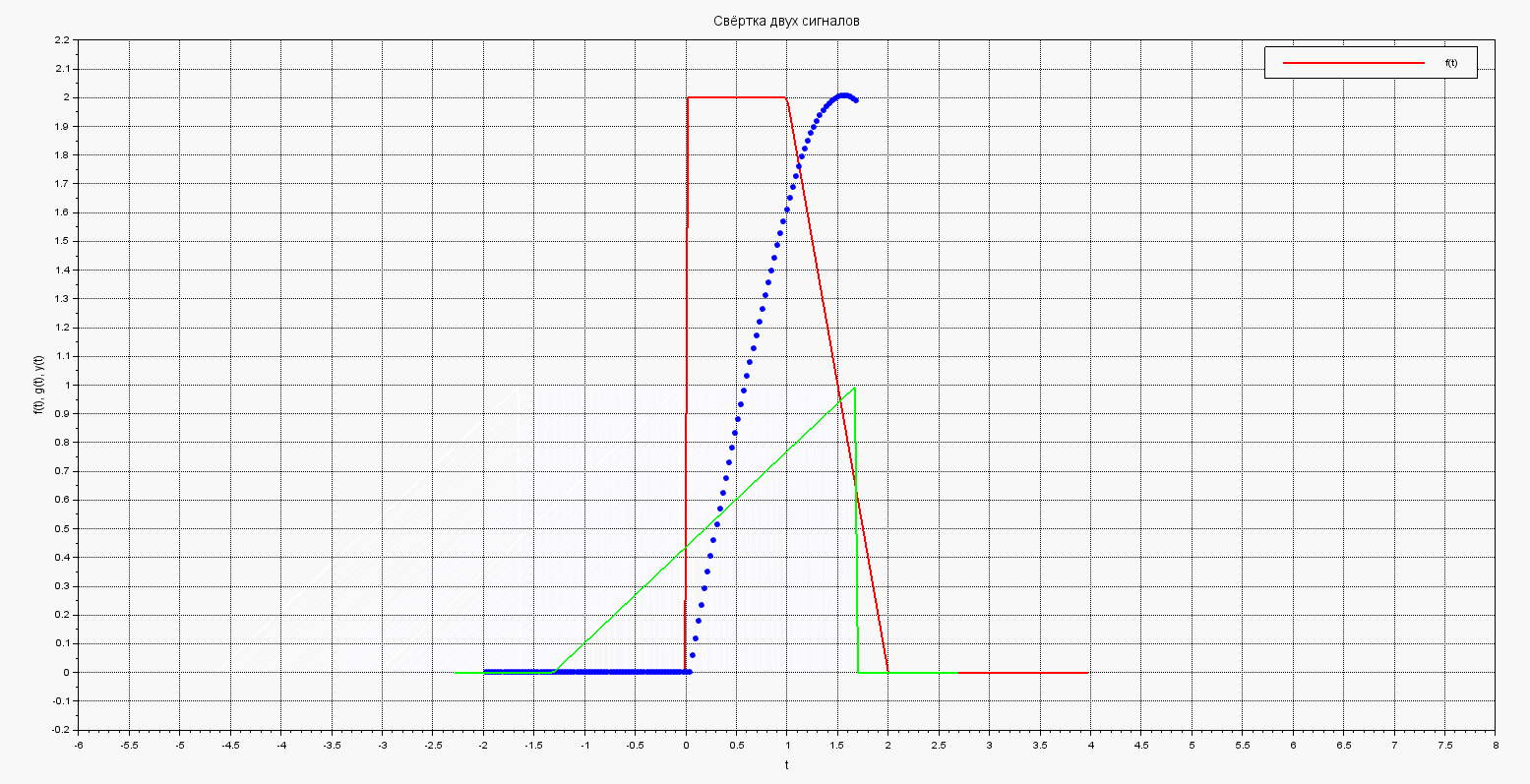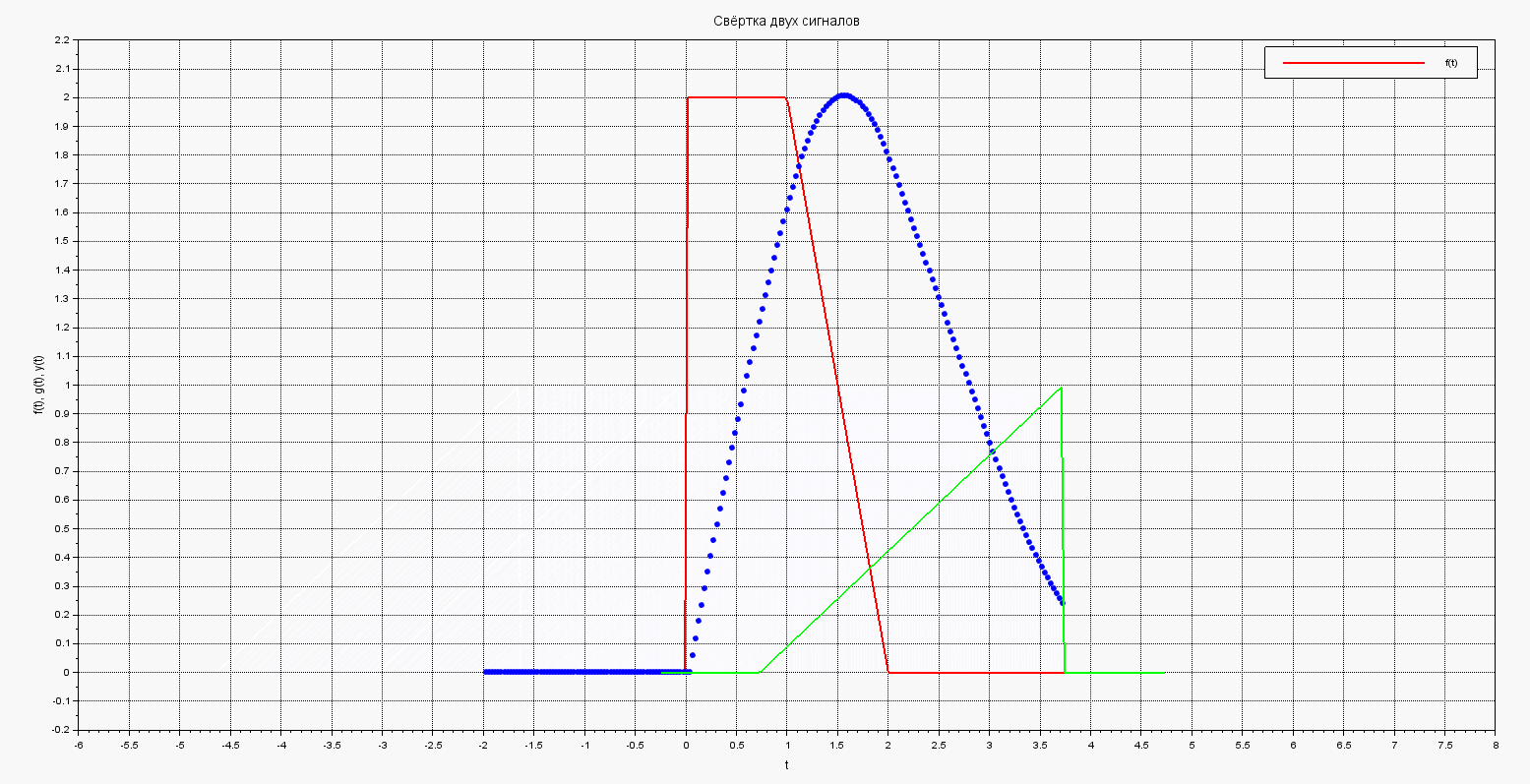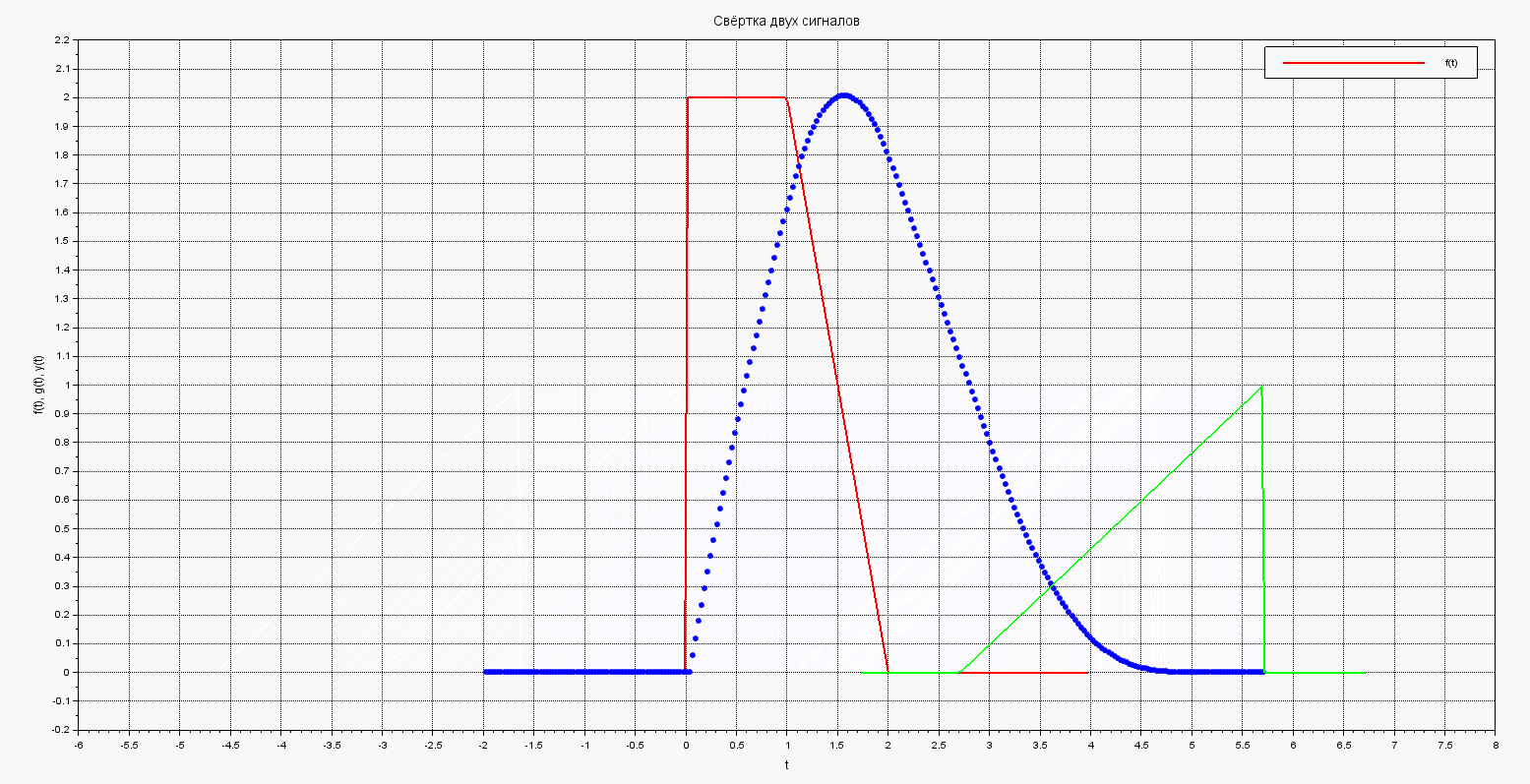
Анимация свёртки

Нравится
55
(лайкай без регистрации)

Источник

Пусть заданы две функции
и,
определенные на всей действительной
оси. Времяtменяется отдо.

(1)

Введем новую функцию, которую назовем
сверткой двух функций
и.

(2)

Считается это следующим образом:

– свернутая с функцией.
Для получения сверткииследует заменить переменнуюtна,
затем в функцииаргументзаменить на,
то есть образовать,
перемножить две функции, а затем взять
интеграл.

Основные свойства свертки функций:

Свертывание двух функций обладает
свойством коммутативности. То есть:

(3)

Доказательство

Докажем, что

Обозначим
и
запишем:

Свойство коммутативности свертки
аналогично свойству коммутативности
двух чисел.

Свойство ассоциативности.

Если заданы
,
то справедливо следующее соотношение:

(4)

Введем обозначения:

Свойство (4) будет доказано, если будет
установлено следующее равенство:

(5)

Подставим
в функцию:

Вводим
и получаем:

Меняем порядок интегрирования и получаем:

Так как значение интеграла не зависит
от наименования переменной интегрирования,
то правая часть этого равенство совпадает
с правой частью равенства (5).

3) Свойство дистрибутивности.

Заданы 3 функции
и,
для них справедливо следующее равенство:

(6)

Доказательство

Имеем

Следовательно, формула (6) справедлива.
Если
ипри,
то,
когда.
И,
когда.

Следовательно,
,
когда.Тогда
свертка функций выглядит так:

(7)

21. Определение оригинала по изображению.

(1)

Обратное преобразование Лапласа
определяется по формуле (1). Установим
однозначное соответствие между
изображением и оригиналом в точках
непрерывности f(t).

Пусть F(s)
является изображением, и пусть, когда,
имеет конечное число полюсов.F(s)
удовлетворяет условиям леммы Жордана.

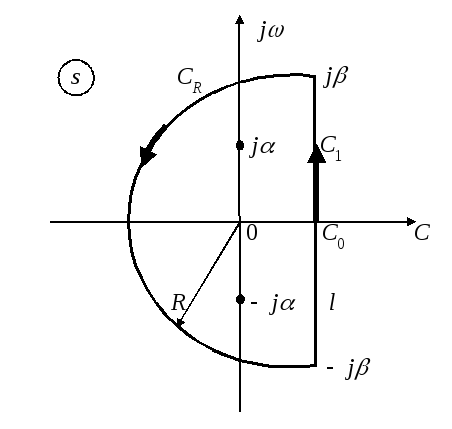
Лемма Жордана.

При F(s),
стремящейся на дугек нулю приравномерно относительноargsпри любом положительном
значенииt, имеем:

(2)

Где
– часть окружности с радиусомR,
находится в полуплоскости.

А теперь, применяя теорему о вычете,
получаем:

(3)

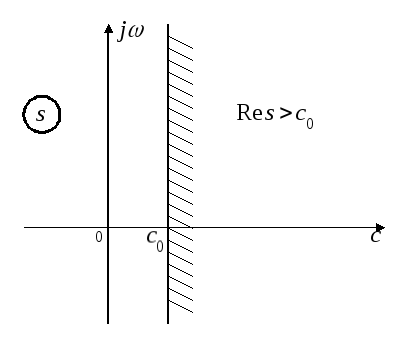
Так как изображение F(s)
является оригиналом, где,
то все полюсы находятся на прямой,
параллельной мнимой оси и проходящее
через точку.

При
следует
положить, чтоf(t)
тождественно равна нулю. Следовательно,
присогласно
лемме Жордана справедливо:

(4)

При этом
– часть окружностиCс
радиусомR, который
находится в полуплоскости.
Следовательно, присправедливо:

Так как изображение F(s)
– аналитическая функция, для которой
сумма вычетов равна нулю.

22. Решение линейных дифференциальных уравнений с постоянными коэффициентами с помощью преобразования Лапласа.

Имеется линейное дифференциальное
уравнение:

(1)

Заданы начальные условия:

Алгоритм нахождения обыкновенных
линейных неоднородных дифференциальных
уравнений.

Алгоритм решения дифференциальных
уравнений второго порядка.

(2)

23. Прямое и обратное преобразование Фурье.

Совокупность операций, которые позволяют
по f(t) найти
соответствующую ей спектральную
характеристикуназывается
преобразованием Фурье.

Преобразование Фурье задается формулой:

(1)

Символически преобразование Фурье
будет обозначаться следующим образом:

(2)

Интеграл правой части уравнения (1)
понимается как главное значение:

Равенство (1) устанавливает связь между
функцией f(t),
аргументом которой является действительное
числоtи комплексная
функция,
в качестве аргумента которой играет
частота.

Пример

Найти спектральную характеристику
.
При этоми
это действительное число.

Решение

Заданная функция на всей оси времени tкусочно – непрерывна и абсолютно
непрерывна, поэтому она преобразуема
по Фурье.

Покажем, что интеграл (1) абсолютно и
равномерно по отношению к параметру
сходится.
Для этого надо оценить интеграл по
модулю:

Соседние файлы в папке лекции

Источник

Основной метод нахождения ряда Фурье для заданной функции

состоит в том, чтобы вычислить коэффициенты по интегралам

Эти вычисления можно производить каждый раз или воспользоваться таблицей для наиболее употребительных функций.

Возможно ли из известных (сравнительно простых) разложений вывести другие разложения?

Очевидно, если известны

то известно и

А как выглядит разложение произведения двух функций? Для действительных функций имеем

Подставляя и переставив члены, получим

Следовательно, коэффициент в разложении произведения двух функций будет

Это выражение называется сверткой последовательности с последовательностью Таким образом, чтобы получить коэффициенты для разложения произведения двух функций, нужно вычислить свертки коэффициентов.

Для комплексных функций обычно используют произведение одной функции на комплексно-сопряженную другую.

Свертка, которая является результатом перемножения двух функций, одновременно наталкивает на мысль о нахождении функции, которая соответствует перемножению соответствующих коэффициентов из двух разложений, т. е. функции, которой соответствует ряд

Чтобы найти ее, введем свертку двух периодических функций

которая симметрична относительно двух функций. Вычислим коэффициенты Фурье для этой свертки. Получим (применяя временно обозначение для коэффициентов Фурье)

Поскольку предполагается периодической, то можно сдвинуть интервал интегрирования, переходя от переменной к и при этом убедиться, что второй интеграл есть а первый интеграл, так как не зависит от есть Следовательно, мы показали, что что и можно было ожидать. Из этой формы ряда Фурье следует, что сглаживание Ланцоша свертывает данную функцию с окном непрерывной прямоугольной формы (с единичной площадью) и вызывает в области коэффициентов появления соответствующих умножающих окон, сигма-факторов. Полученный результат есть обобщение известного положения о том, что, благодаря линейности, эффект свертки одной функции с другой заключается в перемножении коэффициентов соответствующих разложений Фурье.

Если в свертке двух последовательностей

предположить, что все равны нулю, за исключением одного, например то сумма превращается в один член, а именно, Вычисляя последовательные значения свертки можно определить по одному все члены Следовательно, свертка с одиночным импульсом, т. е. с указанным рядом имеющим только один ненулевой член, дает импульсную характеристику — просто члены другой последовательности.

Обращаясь к определению нерекурсивного фильтра

отметим, что если использовать импульсную функцию за исключением то будут получены значения являющиеся коэффициентами фильтра по порядку. Здесь импульс на входе вызывает отклик, который определяет коэффициенты фильтра.

Обратно, если известна импульсная характеристика нерекурсивного фильтра, то известны и коэффициенты,

а следовательно, и сам фильтр. Таким образом, импульсная характеристика играет фундаментальную роль в теории.

Источник

Определение[править | править код]

Свойства[править | править код]

Пример[править | править код]

Свёртка на группах[править | править код]

Свёртка мер[править | править код]

Свойства[править | править код]

Свёртка распределений[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Анимируем свёртку функций

Пример свёртки двух функций пошагово

Реализация свёртки на Scilab

Корректировка результатов свёртки

Реализация анимации свёртки двух сигналов

21. Определение оригинала по изображению.

22. Решение линейных дифференциальных уравнений с постоянными коэффициентами с помощью преобразования Лапласа.

23. Прямое и обратное преобразование Фурье.

Вам также может понравиться

Как найти маску по фотографии

Как найти линейку на айфоне

Как найти телефон по серийному номеру онлайн

Добавить комментарий Отменить ответ