Как найти свертку матрицы

Магия тензорной алгебры: Часть 5 — Действия над тензорами и некоторые другие теоретические вопросы

Введение

Прежде чем продолжать рассказ о прикладных аспектах применения тензорного исчисления, совершенно необходимо затронуть ещё тему, обозначенную заголовком. Эти вопросы всплывали в неявной форме во всех предыдущих частях частях цикла. Однако, мной были допущены некоторые неточности, в частности тензорные формы записи скалярного и векторного произведения в статьях 1 и 2 были названы мною «сверткой», хотя на деле они являются комбинацией свертки и умножения тензоров. О сложении, умножение тензоров на число, о тензорном произведении упоминалось только вскользь. О симметричных, антисимметричных тензорах вообще речи не шло.

В этой заметке мы поговорим о тензорных операциях более подробно. Для дальнейших упражнений нам потребуется хорошо в них ориентироваться.

Кроме того, важным является представление о симметричных и антисимметричных тензорах. Мы узнаем о том, что любой тензор можно разложить на симметричную и антисимметричную части, а также познакомимся с тем фактом, что антисимметричной части тензора можно поставить в соответствие псевдовектор. Многие физические величины (к примеру угловая скорость) являются псевдовекторами. И именно тензорный подход к описанию физических явлений позволяет выявить истинную природу некоторых величин.

1. Четыре основных действия над тензорами

1.1. Умножение тензора на скаляр и сложение тензоров (линейная комбинация)

Под умножением на число понимают умножение на это число каждой компоненты исходного тензора. В результате получается тензор того же ранга, что и исходный.

Складывать же, можно только тензоры, имеющие одинаковый ранг. В бескомпонентной записи линейная комбинация тензоров выглядит так

где — скаляры. Если перейти к компонентной записи, то, например, для тензоров второго ранга данная операция выглядит следующим образом

1.2. Умножение тензоров

Умножение выполняется над тензорами любого ранга. Результатом является тензор суммарного ранга. Пусть, например — тензор ранга (0,1), а — тензор ранга (0,2). Тогда результатом их умножения будет тензор ранга (0,3)

или, в компонентной форме

С тензорным произведением мы уже сталкивались во второй статье, рассматривая диаду. Вернемся к этому ещё раз, перемножив два вектора

что в компонентной форме

дает матричное представление полученной диады

Из последних примеров, в частности видно, что в общем случае тензорное произведение не коммутативно

что очень легко проверить, выписав умножение в компонентной форме и выписав матричное представление диады

Очевидно, что , но так же очевидно и то, что

Это является следствием выполнения другого действия над тензорами

1.3. Перестановка индексов тензора

При этом из компонент исходного тензора образуется новая совокупность величин, с другим порядком индексов. Ранг тензора при этом не изменяется. Например, из тензора ранга (0,3) можно получить три других тензора , и , таких что

Для тензоров второго ранга возможно лишь одна перестановка, называемая транспонированием

Выше, когда мы рассмотрели не коммутативность тензорного произведения и переставили векторы, образующие диаду мы как раз и выполнили перестановку индексов, ведь перестановка множителей ведет к перестановке индексов результирующего тензора

1.4. Свертка

Сверткой называется суммирование компонент тензора по какой-либо паре индексов. Это действие выполняется над одним тензором и на выходе дает тензор с меньшим на два. Скажем, для тензора второго ранга, свертка дает скаляр, называемый, первым главным инвариантом или следом тензора

Свертка всегда производится по паре разновариантных индексов (один индекс должен быть верхним, а другой нижним).

Очень часто свертку комбинируют с произведением тензоров. Иногда такую комбинацию называют внутренним произведением тензоров. При этом тензоры сначала перемножают, а потом сворачивают получившийся тензор суммарного ранга. Примером может служить, использованная нами ранее запись скалярного произведения

что эквивалентно безиндексной записи

Точка, напоминающая скалярное произведение, в безиндексной записи как раз и означает совмещение умножения со сверткой. Свертка производится по соседей с точкой паре индексов. Покажем весь процесс развернуто. Из ковектора и вектора умножением образуем тензор ранга (1,1)

Свернем получившийся тензор по его единственной паре индексов

Однако не стоит считать эту точку скалярным произведением, поскольку, например вот такая операция

так же умножение совмещенное со сверткой

но по смыслу производимых действий оно эквивалентно произведению матриц, которыми представлены компоненты тензоров.

2. Симметричные и антисимметричные тензоры

Тензор называется симметричным по паре индексов, если он не изменяется при перестановке этих индексов

Если тензор не меняется при перестановке любых двух индексов, то он является абсолютно симметричным

Тензор называют антисимметричным по паре индексов, если при их перестановке тензор меняет знак

Если тензор меняет знак при перестановке любых двух индексов, то он является абсолютно антисимметричным

Любой тензор можно разложить на симметричную и антисимметричную, по выбранной паре индексов, части. Доказать это очень легко, пусть дан тензор . Проведем над ним эквивалентные преобразования

где симметричная часть тензора

а его антисимметричная часть

Чтобы не оставалось сомнений, докажем, для полученных нами тензоров, симметричность

Если говорить о тензорах второго ранга, то если таковой тензор симметричен, то он же и абсолютно симметричен. Это же касается и антисимметричного тензора второго ранга. Эти свойства следуют непосредственно из данных нами определений — у тензора второго ранга всего одна пара индексов.

Антисимметричный тензор обладает любопытным свойством. Пусть тензор второго ранга — антисимметричный. Тогда его компоненты удовлетворяют условию

данное условие выполнимо только в том случае, если диагональные компоненты тензора — нули, так как при перестановке индексов (и транспонировании матрицы компонент) диагональные компоненты переходят сами в себя. А единственное число, противоположное самому себе это ноль. Компоненты симметричные относительно главной диагонали имеют противоположные знаки.

Таким образом, из девяти компонент антисимметричного тензора второго ранга только три являются независимыми (речь идет, разумеется, о трехмерном пространстве). Три независимые компоненты образуют вектор (или ковектор). Логично предположить, что может существовать некий вектор, который однозначно зависит от данного антисимметричного тензора. Попробуем найти такой вектор.

3. Сопутствующий вектор тензора второго ранга

Для того чтобы разобраться с этим вопросом я хорошенько, до перегрева клавиш на клавиатуре, «погуглил». Толкового и вместе с тем элегантного ответа на сформулированный параграфом вопрос я не нашел, поэтому предлагаю свой ответ, являющийся в некотором роде компиляцией и переработкой полученных мною сведений.

Вспомним о тензоре Леви-Чивиты, о котором я уже подробно писал тут, и построим такой тензор

Докажем, что тензор (1) — антисимметричный. Переставим в нем индексы

Минус в (2) вылез из-за того, что тензор Леви-Чивиты — абсолютно антисимметричный тензор третьего ранга. Перестановка индексов в нем, ведет к перестановке векторов базиса, на смешанном произведении которых построен данный тензор. Таким образом тензор (1) действительно антисимметричный. Тогда мы можем легко найти вектор

Примечание: о том, откуда взялись в (3) две дельты Кронекера можно прочитать в восьмой статье цикла.

соответствующий антисимметричному тензору . Тензор третьего ранга в (3), это контравариантный тензор Леви-Чивиты, который повторяет свойства ковариантного собрата с той лишь разницей, что

– для правой системы координат (для левой надо изменить знак ненулевых компонент на противоположный). Компоненты вектора (3), с учетом свойств тензора (4) определяются однозначным образом

или, если представить матрицу компонент антисимметричного тензора , то перед нами предстанет такая запись

Заметим ещё один факт, не упомянуть который нельзя, но оставив строгое доказательство за рамками данной статьи (к этому мы вернемся несколько позже). Если тензор /> является истинным тензором, то соответствующий ему вектор (3) является псевдовектором или аксиальным вектором. Псевдовектор преобразуется как и вектор при повороте координатных осей, но при смене базиса с правого на левый (или с левого на правый) — меняет своё направление на противоположное (все его компоненты меняют знак).

Если же в (1) вектор — истинный вектор, то образованный из него антисимметричный тензор является псевдотензором — компоненты такого тензора преобразуются так же как и компоненты истинного тензора при повороте осей системы координат, но меняют знак на противоположный при смене ориентации базиса.

Таким образом, любому антисимметричному тензору можно поставить в соответствии псевдовектор, получаемый в соответствии с выражением (3).

Теперь покажем, что симметричный тензор не имеет соответствующего ему псевдовектора, вернее этот псевдовектор — нулевой. Допустим, нам дан симметричный тензор , то есть справедливо равенство

Предположим, что существует вектор

Переставим индексы в (6) учитывая симметричность (5)

Выражение (7) справедливо только в одном случае, если

То есть, если мы умножим симметричный тензор на тензор Леви-Чивиты с последующей сверткой по двум парам индексов, мы получим нулевой вектор. Если мы проделаем аналогичное с произвольным тензором второго ранга

на выходе получится псевдовектор, соответствующий его антисимметричной части.

Заключение

Получилось еще одно погружение в теорию тензорного исчисления. Но погружение несомненно нужное, ибо результаты, собранные в данной статье мы используем в дальнейших статьях цикла. Спасибо читателям за проявленное внимание!

Наглядно объясняем операцию свертки в моделях глубокого обучения

При помощи анимированных изображений и визуализаций слоев CNN-сетей раскрываем широко применяемое в моделях глубокого обучения понятие свертки.

В современных фреймворках глубокого обучения сверточные слои в моделях нередко представляются в виде однострочного кода. Само же понятие свертки обычно остается для начинающих аналитиков труднодоступным, как и лежащие в его основе понятия ядра, фильтра, канала и т. д. Тем не менее, свертка представляет собой мощный и расширяемый инструмент, позволяющий разреживать взаимодействия нейронов, находить общие параметры, работая одинаковым образом со входными данными различного размера. Сравним механики операции свертки и полносвязной нейросети.

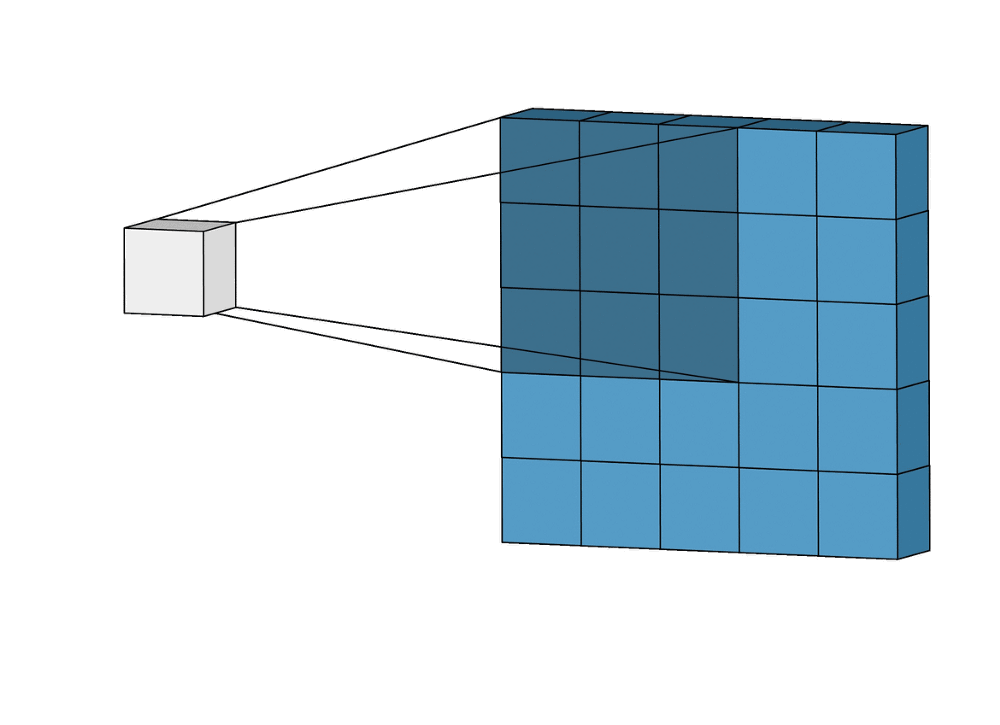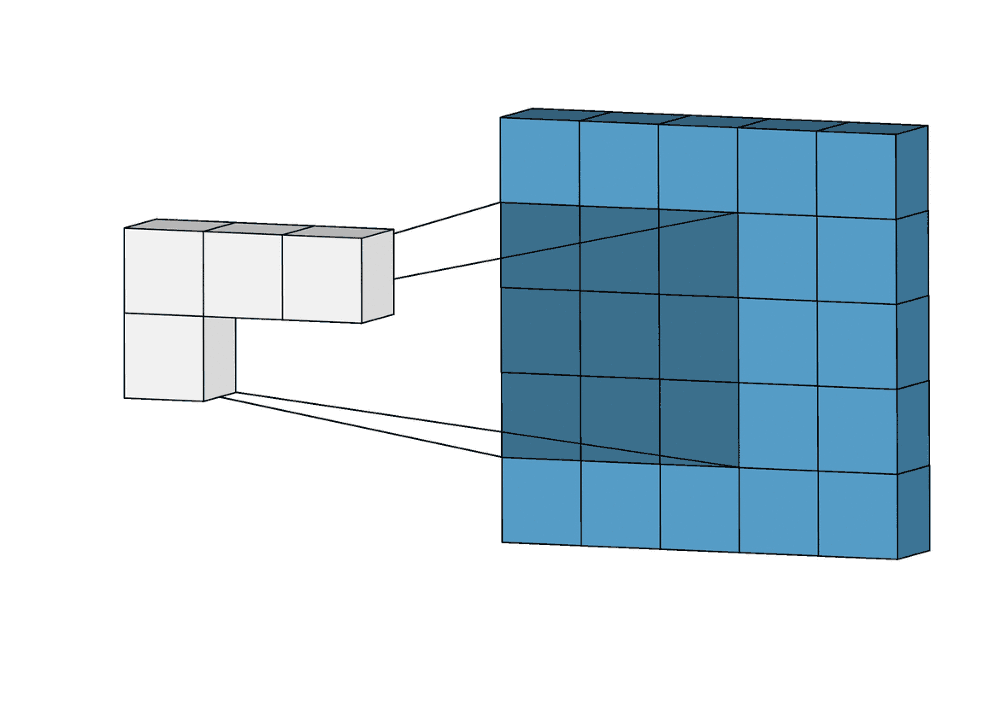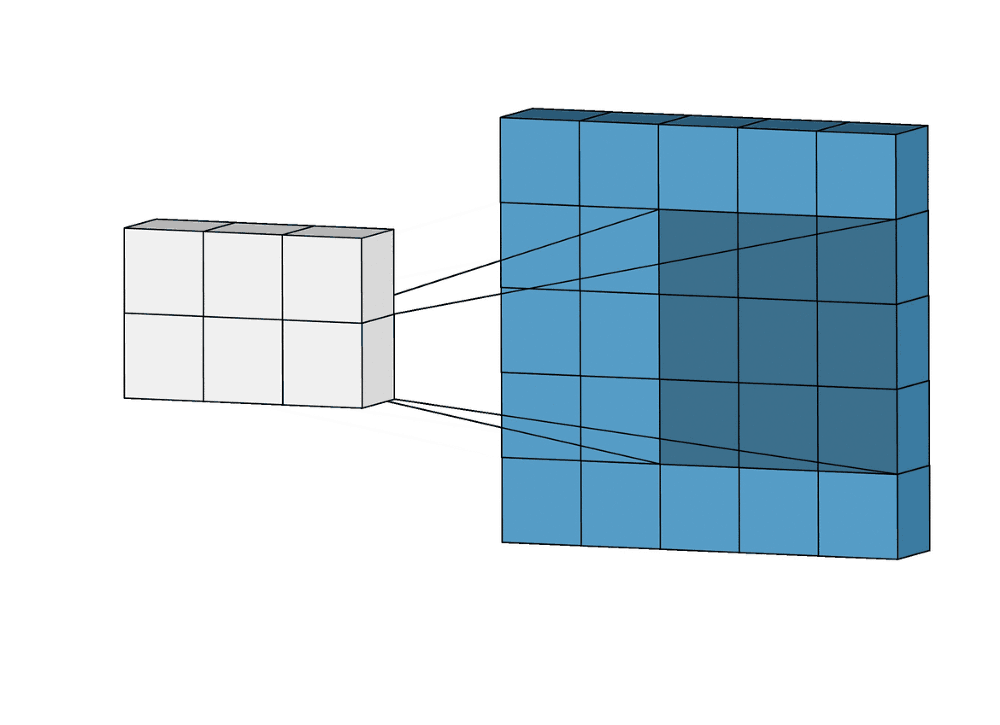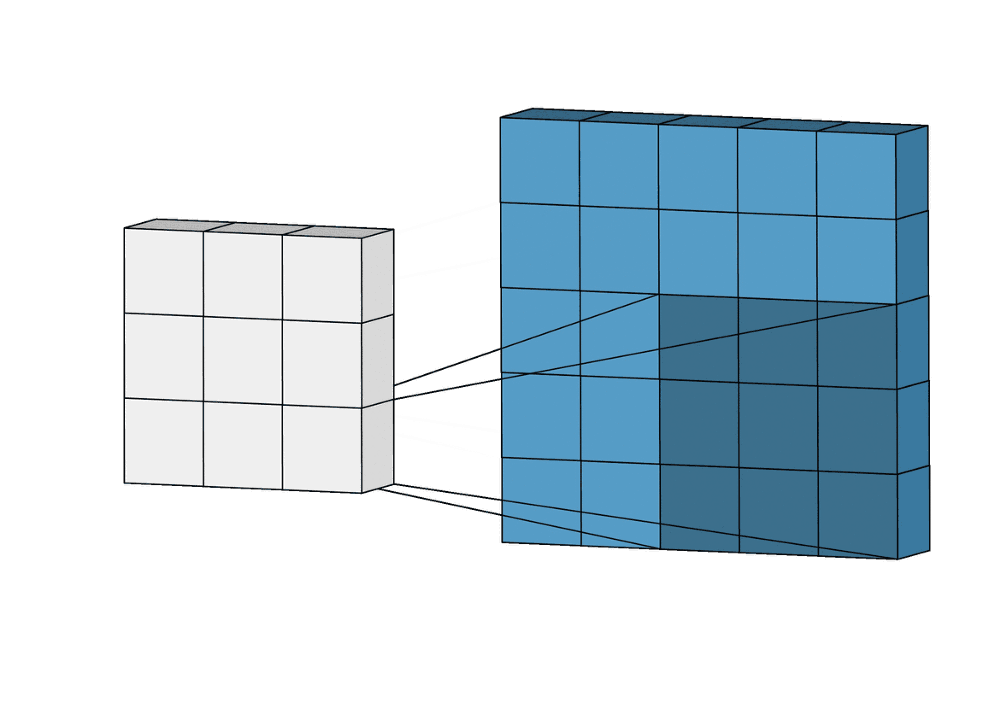
Суть операции свертки на примере черно-белых изображений

В математическом отношении в двумерной свертке нет ничего сложного. Имеется ядро – небольшая матрица весов. Это ядро «скользит» по двумерным входным данным, выполняя поэлементное умножение для той части данных, которую сейчас покрывает. Результаты перемножений ячеек суммируются в одном выходном пикселе. В случае сверточных нейросетей ядро определяется в ходе обучения сети. Начальные веса, аналогично случаю перцептрона, могут иметь рандомные значения, и корректируются в процессе обучения.

Перемножение и суммирование повторяются для каждой локации, по которой проходит ядро. Двумерная матрица входных признаков преобразуется в двумерную матрицу выходных. Выходные признаки, таким образом, являются взвешенными суммами входных признаков. Число входных признаков в комбинации для одного выходного признака определяет размер ядра.

Такой подход контрастирует с полносвязными сетями. Так, в приведенном выше примере имеется 5×5=25 входных признаков и 3×3=9 выходных. Если бы это были два полносвязных слоя, весовая матрица состояла бы из 25×9=225 весовых параметров. При этом каждая функция вывода была бы взвешенной суммой всех входов. В случае свертки, взвешенная сумма берется только по числу весов ядра. И в рассмотрении одновременно участвуют только близлежащие элементы.

Свертка соответствует модели иерархий абстрактных представлений: совокупность пикселей обобщается до ребер, те – до паттернов, и, наконец, до самого объекта. Малозначимые детали отфильтровываются в процессе перехода к более абстрактным образам.

Некоторые распространенные методы

Обратим внимание на два характерных метода, связанных с операцией свертки: дополнение отступа (padding) и выбор шага (strides).

Нулевой отступ

В вышеприведенном примере скольжение ядра «обрезает» исходный двумерный массив по краю, преобразуя матрицу 5×5 в 3×3. Краевые пиксели теряются из-за того, что ядро не может распространяться за пределы края. Однако иногда необходимо, чтобы размер выходного массива был тем же, что и у входных данных.

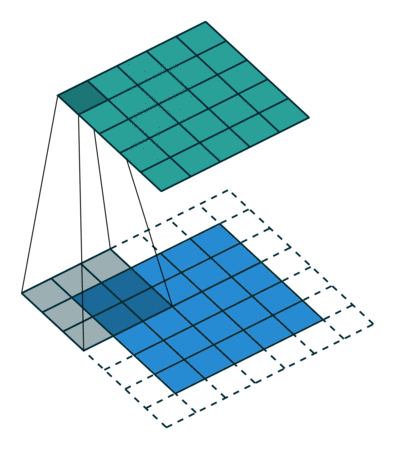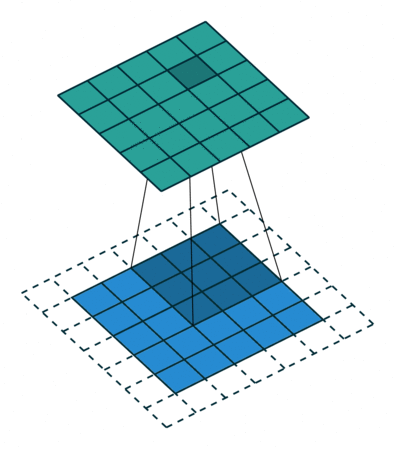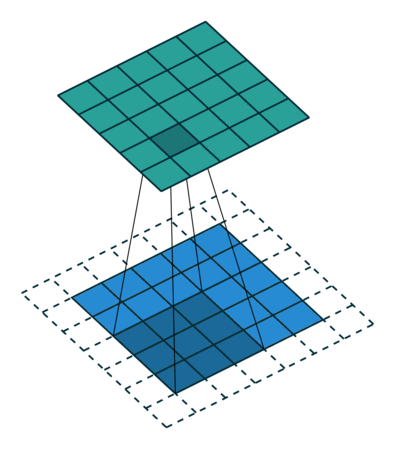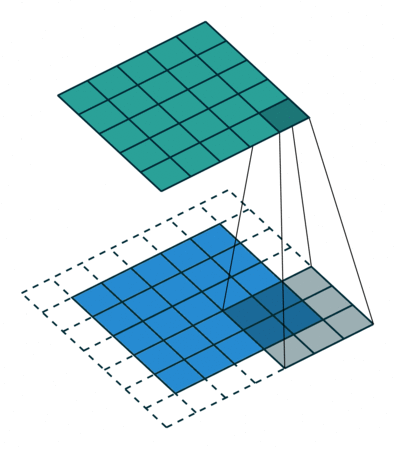
Чтобы решить эту задачу, исходный массив можно дополнить «поддельными» пикселями. Например, в виде краевого поля, окружающего массив. Если в качестве значений берутся нули, говорят о «нулевом отступе» (zero padding).

Еще чаще стоит задача субдискретизации – уменьшения размерности выходного сигнала в сравнении с исходным. Это обычное явление в сверточных нейросетях, где размер пространственных измерений уменьшается при увеличении количества каналов. Одним из способов является применение объединяющего (pooling) слоя. За счет отбора средних/максимальных значений из каждых соседствующих счетверенных ячеек 2×2 можно уменьшить размерность исходной сетки вдвое. Другой подход – использовать шаг свертки.

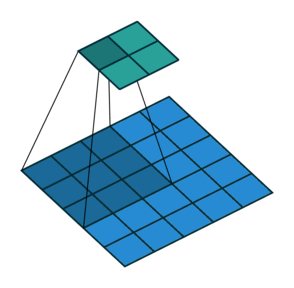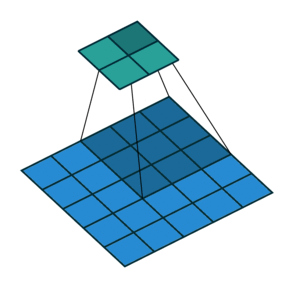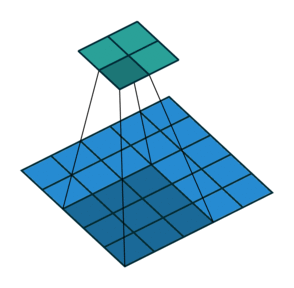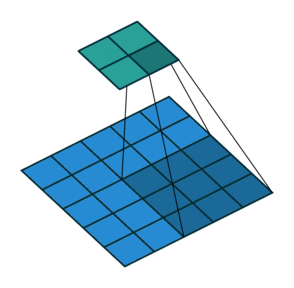
Идея шага состоит в том, чтобы при скольжении ядра пропускать часть позиций массива. Значения шага 1 означает выбор каждого пикселя сетки. Шаг 2 означает отбор пикселей на расстоянии в два пикселя с пропуском одного промежуточного, и так далее.

Многоканальная версия – цветные изображения

Вышеприведенные диаграммы соответствуют лишь изображениям с одним входным каналом. На практике большинство изображений имеют три канала: красный, зеленый и синий.

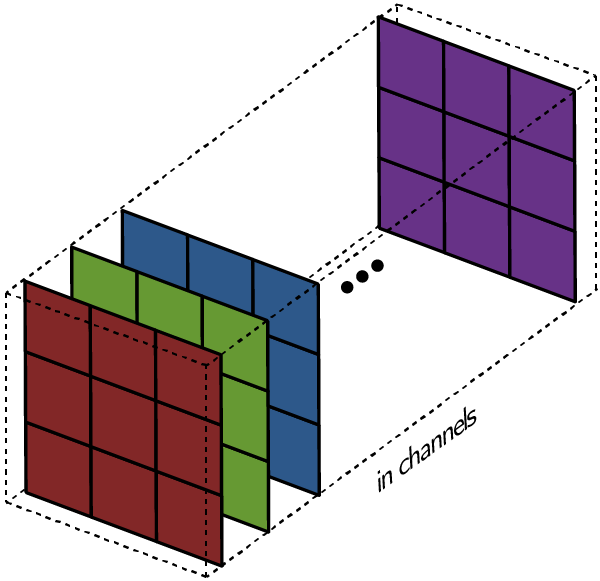
В случае с одним каналом термины фильтр и ядро взаимозаменяемы. Для цветного изображения они различны. Фильтр – это коллекция ядер, каждое из которых соответствует одному каналу. Ядро фильтра скользит по данным канала, создавая их обработанную версию. Значимость ядер определяется взаимным отношением их весов. Например, ядро для красного канала может быть более значимым в модели, чем другие ядра фильтра, тогда будут больше и соответствующие веса.

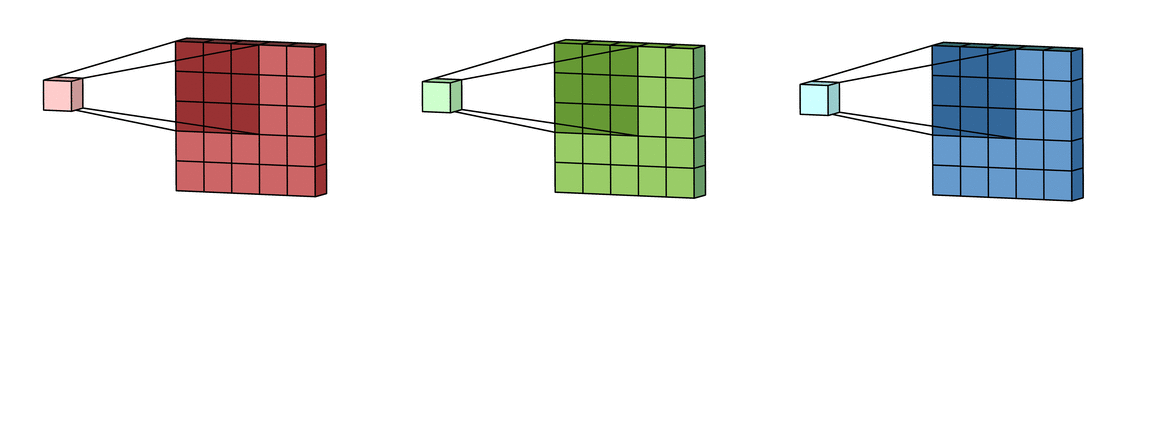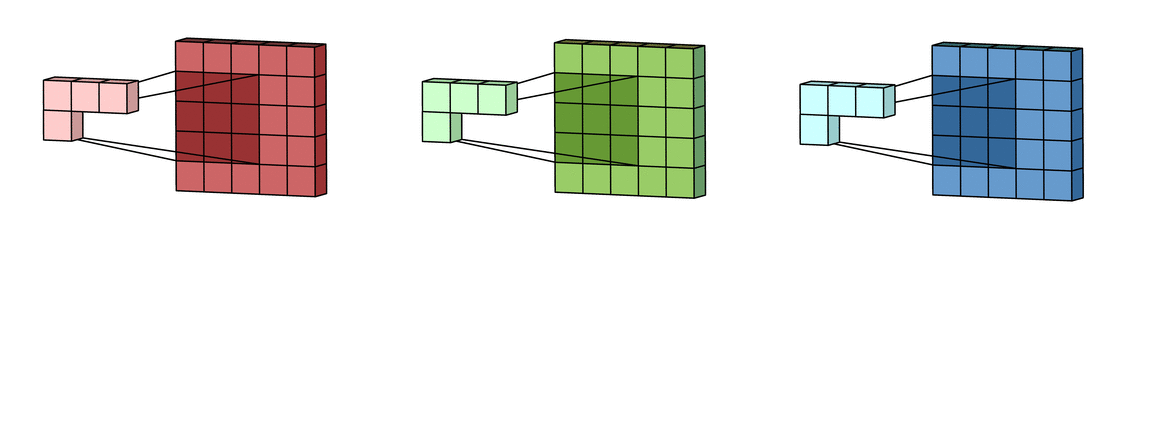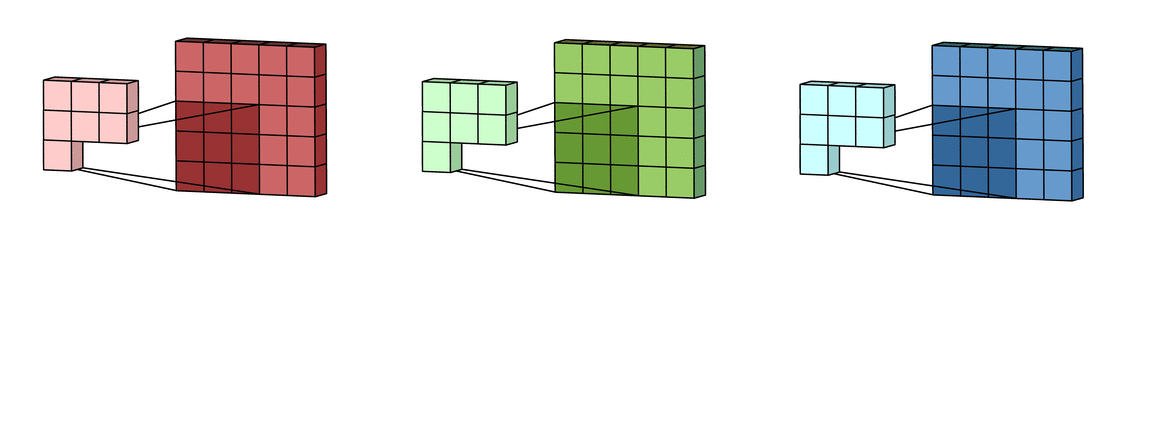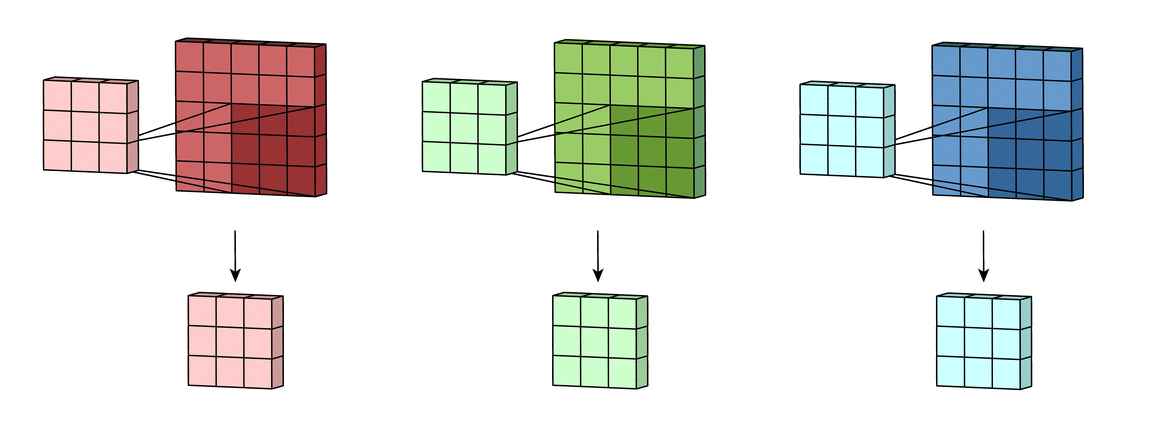
Каждая из обработанных в своих каналах версий суммируется для формирования общего канала.

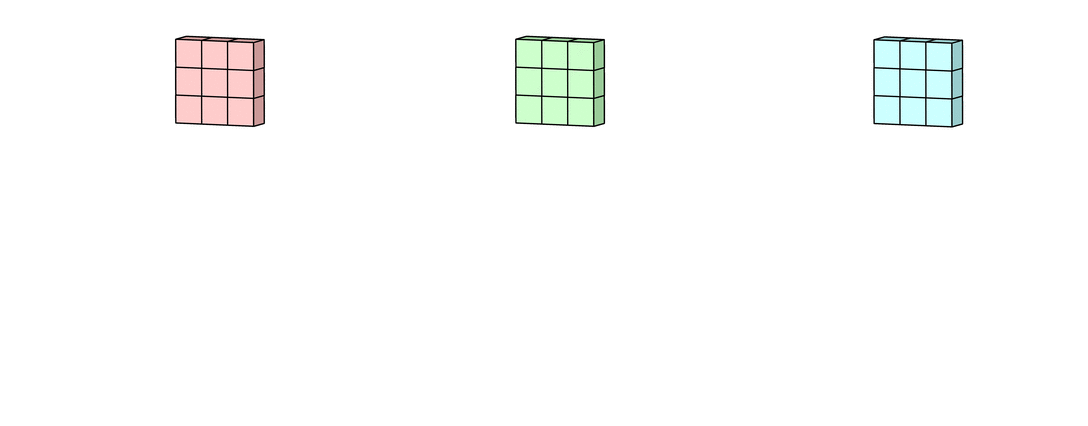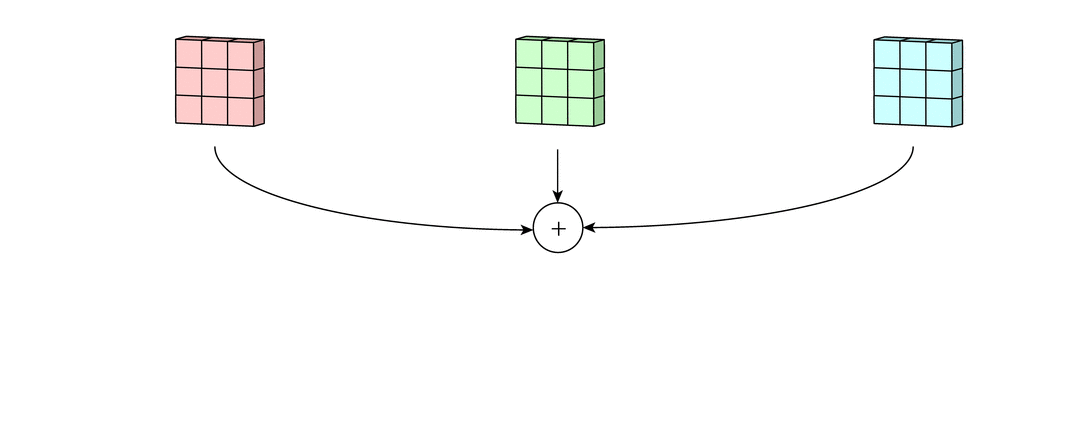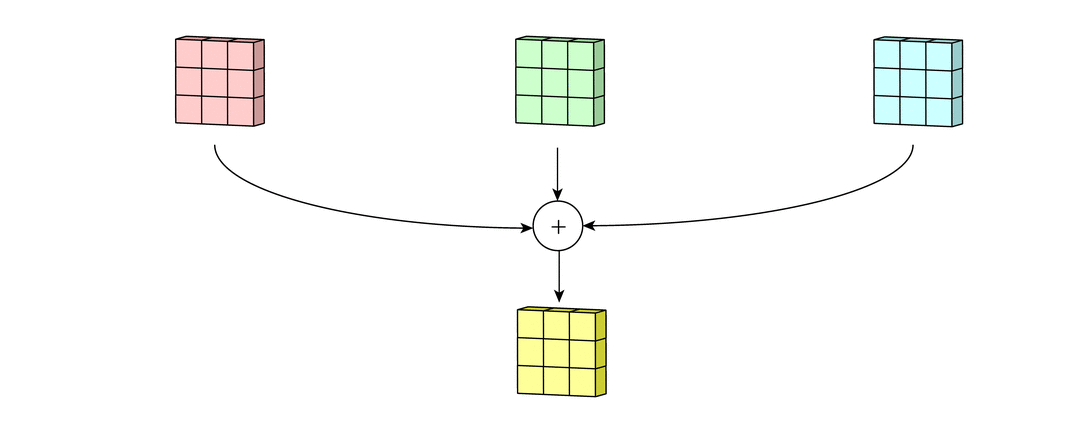
В выходном терминале может присутствовать линейное смещение, независимое от функций каждого из ядер и свойственное лишь выходному каналу.

Математическая подоплека свертки – особенности линейного преобразования

Предположим, что у нас есть вход 4×4. Мы хотим преобразовать его в сетку 2×2. Если мы используем сеть прямого распространения, потребуется входной вектор из 16 нейронов, полностью связанных с 4 выходными нейронами. Такую ситуацию можно визуализировать весовой матрицей w.

Хотя операция ядерной свертки может показаться вначале немного странной, она является линейным преобразованием. Если бы мы использовали ядро K размера 3 для тех же размеров входа и выхода, эквивалентная матрица линейного преобразования выглядела бы следующим образом:

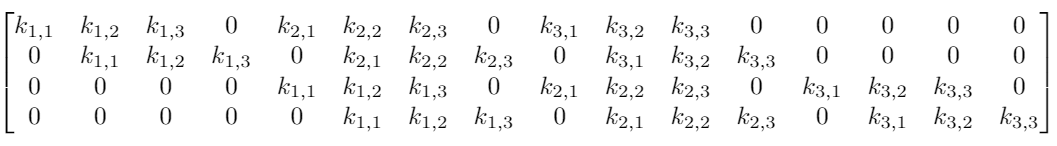
Для матрицы с 16×4=64 элементами имеется всего 9 нетривиальных параметров, подлежащих оптимизации вместо 64 весовых параметров для полносвязной двухслойной нейронной сети. Обнуление значительной части параметров обусловлено локальностью применяемой операции. Помимо ускорения расчетов, свертка приводит и к лучшей инвариантности относительно размеров входных данных.

Впрочем это не объясняет, почему такой подход может быть не менее эффективным, чем полносвязная сеть. Ядро, формирующее выходной сигнал, представляет взвешенную комбинацию небольшой области близкорасположенных пикселей. Но в то же время операция взаимодействия с ядром применяется одинаково ко всему изображению.

Локальность свертки

Если бы это был какой-то другой тип данных, а не изображения (например, набор категориальных данных), обобщение, осуществляемое сверткой, могло бы привести к катастрофе. В выходных признаках появлялась бы отсутствовавшая исходно корреляция.

В то же время любое изображение с точки зрения математики представляет собой совокупность правил взаимного расположения элементов. Использование фильтров для поиска элементов изображений – это одна из старых идей компьютерного зрения. Например, для обнаружения контуров можно использовать фильтр Собеля. В отличие от обучаемых ядер сверточных нейронных сетей, ядро этого фильтра имеет фиксированные веса:

Для фонового неба, не содержащего краевых элементов большинство пикселей на изображении имеют одинаковые значения. Суммарные значения выхода ядра в этих местах равны нулю. Для части изображения с вертикальными границами в местах границ существует разница между пикселями слева и справа от края. Ядро, вычисляя эту ненулевую разницу, определяет положение контуров. Повторимся, ядро работает каждый раз только с локальными областями 3×3, обнаруживая аномалии в локальном масштабе.

Применяя один и тот же подход ко всему изображению, можно получить результат для всего массива. Аналогично свертка с транспонированным ядром позволяет выделить горизонтальные края.

Визуализация признаков при помощи оптимизации

Целая отрасль исследований в сфере глубокого обучения посвящена тому, чтобы сделать модели нейронных сетей интерпретируемыми. Одним из мощных инструментов для подобного рода задач является предложенная в работе 2017 года визуализация признаков при помощи оптимизации. Идея в корне простая: оптимизировать изображение, инициализированное шумом, так, чтобы активировать фильтр как можно сильнее.

На трех изображениях ниже представлены визуализации трех различных каналов для первого сверточного слоя GoogleNet. Хотя слои детектируют различные типы контуров, все они являются низкоуровневыми детекторами.

На двух следующих изображениях представлены примеры визуализации фильтров сверточных слоев второго и третьего уровней.

Одна из важных вещей: изображения после операции свертки – это все еще изображения. Операция действует эквивариантно: если изменяется вход, то выход изменяется так же.

Элементы, находившиеся в левом верхнем углу, после свертки имеют соответствующие отображения также в левом верхнем углу. Как бы глубоко ни заходили детекторы признаков, они все равно будут работать на очень маленьких ядерных участках. Неважно, насколько глубоко происходит свертка, но вы не можете обнаружить лица из сеток размером 3х3. Здесь возникает идея локальной зоны восприимчивости (receptive field).

Зона восприимчивости свертки

Существенной составляющей архитектуры сверточной нейронной сети является уменьшение объема данных от входа к выходу модели с одновременным увеличением глубины канала. Как упоминалось ранее, обычно это делается при помощи выбора шага свертки или pooling-слоев. Зона восприимчивости определяет, какая площадь оригинальных входных данных из исходной сетки обрабатывается на выходе. На изображениях ниже представлен пример шагающей свертки с выкидыванием промежуточных пикселей.

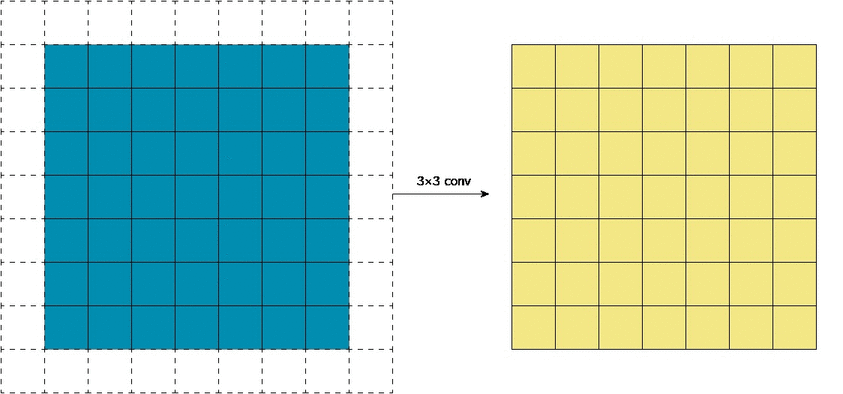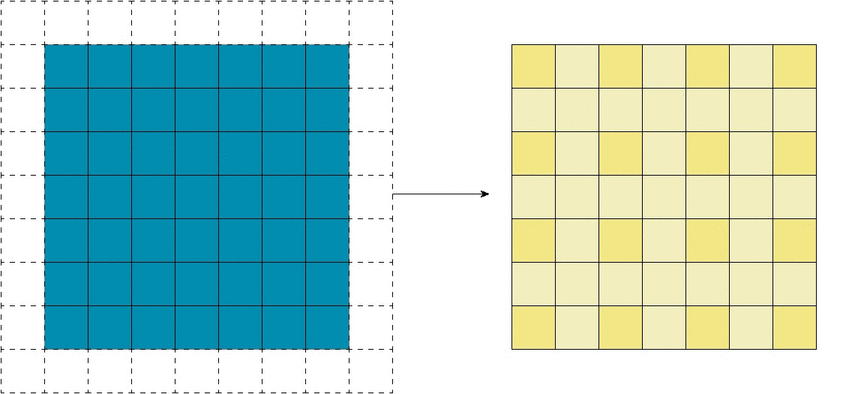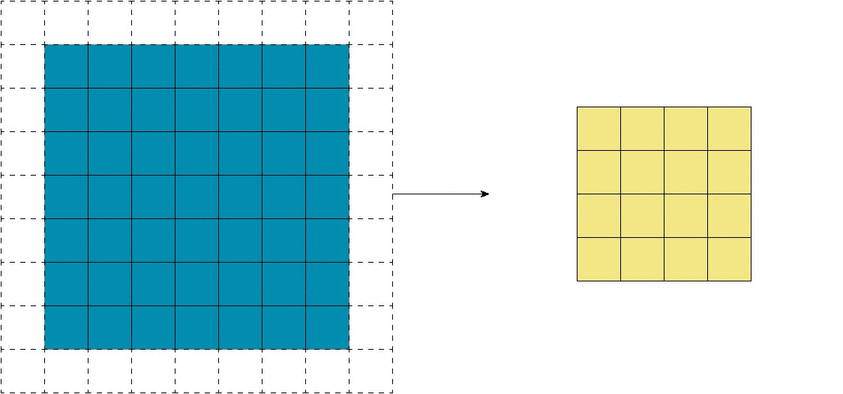
Ниже представлены примеры визуализации признаков набора блоков свертки, показывающие постепенное увеличение сложности. Расширение поля восприимчивости позволяет сверточным слоям комбинировать низкоуровневые признаки (линии, края) в более высокоуровневые (кривые, текстуры).

Сеть развивается от небольшого количества низкоуровневых фильтров на начальных этапах (64 в случае GoogleNet) до очень большого количества фильтров (1024 в финальной свертке), каждый из которых находит специфичный высокоуровневый признак. Переход от уровня к уровню обеспечивает иерархию распознавания образов.

Обобщающие процессы свертки имеет свою оборотную сторону – возможность подделки изображений под удовлетворение особенностей распознающих фильтров. На изображениях ниже человек в обоих случаях узнает фотографии панды. А сверточные нейросети можно запутать, добавив шум, подстроенный под фильтры распознавания других образов.

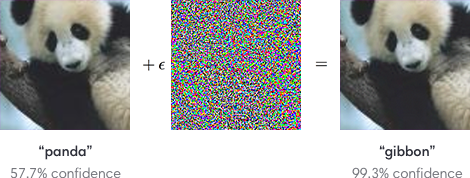
Однако именно сверточные нейронные сети позволили компьютерному зрению пройти путь от простых приложений до сложных продуктов и услуг, таких как распознавание лиц и улучшение качества медицинских диагнозов.

ML: Тензоры в Numpy

Введение

Тензор – это множество упорядоченных чисел ( элементов), пронумерованных при помощи d целочисленных индексов: $mathrm[i_0,, i_1,. , i_]$. Число индексов d называется размерностью тензора.
Каждый индекс меняется от 0, до $d_i-1$, где $d_i$ называется размерностью индекса.
Перечисление размерностей всех индексов: $(d_0,,d_1. d_)$ называется формой тензора.

Существующие фреймворки машинного обучения работают с тензорами примерно одинаковым образом.
Ниже мы рассмотрим универсальную библиотеку numpy. Это не справочник по numpy, для этого см. scipy.org.
Мы сосредоточимся на понятиях размерности и формы тензора, а также на том, как они изменяются при различных операциях (что собственно и требуется при анализе нейронных сетей).

Размерность и форма тензора

В библиотеке numpy у каждого тензора t есть четыре базовых свойства (атрибута):

• t. ndim – размерность = сколько у тензора индексов;
• t. shape – форма = кортеж с размерностью каждого индекса;
• t. size – количество элементов тензора (если shape=(a,b,c), то size=a*b*c);
• t. dtype – тип тензора ( float32, int32. ) одинаковый для всех элементов.

Если тензор имеет один индекс: t[i] – то это вектор ( ndim=1), а если у него два индекса: t[i,j] – то это матрица ( ndim=2). Индексы нумеруются начиная с нуля.

Метод np. array(lst) преобразует список lst (список чисел или список других списков) в тензор numpy:

Обратим внимание, что:

• форма одномерного тензора (вектора) это (n,) , а не (n) , т.к. для Python (n) – это число, а не кортеж.
• t = np.array( [[[1]]] ) – это тензор из одного числа, с shape=(1,1,1) и t.ndim==3, t[0,0,0]==1.

Тензоры принято изображать в табличной форме: вектор ( ndim=1) – это строка чисел, матрица формы (rows,cols) – это прямоугольная таблица с rows строчками и cols колонками. Трёхмерный тензор (три индекса, ndim=3) изображают в виде стопки матриц:

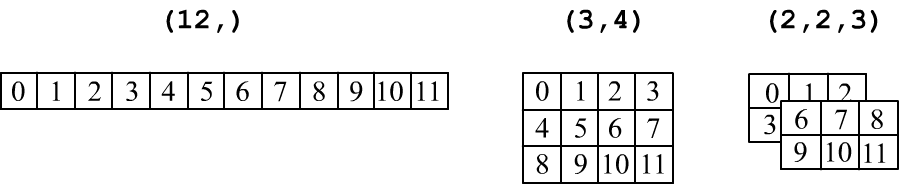
Важно не путать вектор (n,) и матрицу, состоящую из одной строки (1,n) или одной колонки (n,1):

Ниже матрицы из одной строчки или одной колонки окружены двойной линией, чтобы отличить их от вектора:

$$ begin <|c|c|>hline 1 & 2\ hline end

begin <|c|>hline begin <|c|c|>hline 1 & 2\ hline end \ hline end

begin <|c|>hline begin <|c|>hline 1 \ hline 2\ hline end \ hline end $$

Последовательность элементов

Тензор формы shape = (a,b,c) состоит из size = a*b*c упорядоченных чисел (элементов).
Форму тензора можно изменить (с сохранением количества элементов size) при помощи метода reshape или прямого изменения атрибута shape:

$$ begin <|c|c|c|c|c|c|>hline 1 & 2 & 3 & 4 & 5 & 6 \ hline end

begin <|c|>hline begin <|c|c|c|c|c|c|>hline 1 & 2 & 3 & 4 & 5 & 6 \ hline end\ hline end

begin <|c|c|c|>hline 1 & 2 & 3 \ hline 4 & 5 & 6 \ hline end $$

При изменении формы тензора методом reshape, результат возвращается по ссылке (не создаётся новой копии множества чисел). Поэтому, если поменять значение элемента в m16, то он поменяется и в v:

Элементы в памяти идут в порядке увеличения индексов, начиная с конца. Например, для трёхмерного тензора с формой (2,1,3) это 6 чисел в следующем порядке:

Менять форму тензора можно произвольным образом, сохраняя неизменным число элементов. Ниже метод arange создаёт вектор (одномерный тензор) из 12 целых чисел от 0 до 11. Затем получаются ссылки на матрицу и трёхмерный тензор. В последнем случае значение -1 в размерности первого индекса, просит numpy самостоятельно высчитать эту размерность (исходя из числа элементов и размерностей остальных индексов):

Оси тензора

Индексы – это оси ( axis) тензора. Первый индекс – это axis=0, второй axis=1 и т.д. У многих методов есть параметр axis. Например, суммирование по данной оси уменьшает размерность ndim на 1.

Аналогично работают функции min, max, mean, median, var, std, argmin, argmax и т.п.

Из тензора можно вырезать подмножество его элементов. Ниже вырезается нулевая строчка и нулевая колонка, а затем квадратная матрица 2×2:

Подмножества элементов, находящиеся в v1, v2, v3 получаются по по ссылке, а не по значению, поэтому:

Менять можно не только значение одного элемента, но и всех элементов (ниже, стоящих в первой колонке):

Сложение, умножение и broadcasting

При поэлементном сложении и умножении тензоров одинаковой формы результат имеет ту же форму: $$ (x+y)_:

x_*y_. $$ Например (ниже np. arange(beg=0, end) – вектор целых чисел от beg до end, исключая end):

Аналогично работают функции от тензоров : $T’_=F(T_)$. Например: np. exp( ), np. log( ), np. sin( ), np. tanh( ), полный список см. на scipy.org.

При добавлении к матрице (n, m) вектора (n,) или матрицы, состоящей из одной строки (1,n), у последней дублируются строки и затем происходит сложение (или умножение) матриц одинаковой формы. При добавлении к матрице (n, m) матрицы, состоящей из одной колонки (m,1), у последней дублируются колонки: $$ begin <|c|c|>hline 0 & 1 \ hline 2 & 3 \ hline end

begin <|c|c|>hline mathbf <4>& mathbf <5>\ hline end

begin <|c|c|>hline 0 & 1 \ hline 2 & 3 \ hline end

begin <|c|c|>hline mathbf <4>& mathbf <5>\ hline mathbf <4>& mathbf <5>\ hline end,

begin <|c|c|>hline 0 & 1 \ hline 2 & 3 \ hline end

begin <|c|>hline begin <|c|>hline mathbf <4>\ hline mathbf <5>\ hline end \ hline end

begin <|c|c|>hline 0 & 1 \ hline 2 & 3 \ hline end

begin <|c|c|>hline mathbf <4>& mathbf <4>\ hline mathbf <5>& mathbf <5>\ hline end $$

Например: В общем случае, для тензоров с различными shape, работает алгоритм расширения ( broadcasting):

• выравнивается число индексов ( ndim), добавляя к меньшему в shapeспереди единицы;
• размерности индексов считаются сравнимыми если они равны или один из них 1;
• размерность единичного индекса увеличиваем до большего, дублируя значения по этой оси:

Например, сложим матрицу из одной колонки и вектора $(3,1) + (2,) = (3,1) + (underline<1,>2) = (3,2)$: $$ begin<|c|>hline begin<|c|>hline 1\ hline 2\ hline 3\ hline end \ hline end

begin <|c|c|>hline 4 & 5 \ hline end

begin <|c|>hline begin <|c|>hline 1\ hline 2\ hline 3\ hline end \ hline end

begin <|c|>hline begin <|c|c|>hline 4 & 5 \ hline end \ hline end

begin <|c|c|>hline 1 & 1 \ hline 2 & 2 \ hline 3 & 3 \ hline end

begin <|c|c|>hline 4 & 5 \ hline 4 & 5 \ hline 4 & 5 \ hline end

begin <|c|c|>hline 5 & 6 \ hline 6 & 7 \ hline 7 & 8 \ hline end $$

Свёртка векторов и матриц

В numpy обе операции выполняются при помощи метода dot. Так, для векторов:

Для матриц: Представим последнее умножение в табличном виде:

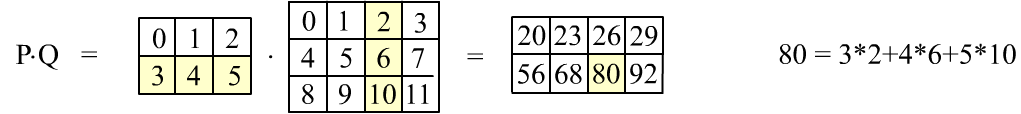
При матричном умножении сворачиваются строки первой матрицы со столбцами второй.
На рисунке выше приведено вычисление элемента $80$, закрашенного желтым цветом.
Чтобы получить все элементы, сначала первая строка первой матрицы должна 4 раза свернуться с 4-я колонками второй матрицы. Это даёт первую строку результирующей матрицы. Затем то-же делает вторая строка, что приводит ко второй строке результата.

Свёртка матриц возможна только, когда число колонок первой матрицы равно числу строк второй.
Выполняется следующая важная формула для форм исходных матрицы и результата свёртки:

$$ (n,, underline) cdot (underline, m)

Если первая матрица состоит из одной строчки, а вторая из одного столбика, то их произведение будет по-прежнему матрицей, но с одним элементом $(1,,underline<2>)cdot(underline<2>,,1)=(1,,1)$:

$$ begin <|c|>hline begin <|c|c|>hline 1 & 2\ hline end \ hline end

begin <|c|>hline begin <|c|>hline 3\ hline 4\ hline end \ hline end

Свёртка по единственному индексу: $(2,,underline<1>) cdot (underline<1>,,2) = (2,,2)$ равна попарному перемножению элементов (по тому же правилу “строка на столбец”): $$ begin <|c|>hline begin <|c|>hline 1\ hline 2\ hline end \ hline end

begin <|c|>hline begin <|c|c|>hline 3 & 4\ hline end \ hline end

begin <|c|c|>hline 3 & 4 \ hline 6 & 8 \ hline end = c_r_ <1j>$$

Транспонирование матриц

Операция транспонирования переставляет элементы таким образом, что столбцы и строчки меняются местами. Если форма исходной матрицы была $(n,,m)$, то у транспонированной она будет $(m,,n)$:

begin <|c|c|c|>hline 0 & 1 & 2 \ hline 3 & 4 & 5 \ hline end

begin <|c|c|c|>hline 0 & 3 \ hline 1 & 4 \ hline 2 & 5 \ hline end $$

В numpy транспонирование осуществляется методом transpose() или при помощи атрибута .T:

Подчеркнём что транспонирование и перестановка размерностей при помощи reshape приводят к различному порядку элементов:

Транспонирование не создаёт новой матрицы (возвращается ссылка, а не значения). Поэтому:

Не квадратную матрицу можно умножить саму на себя, только предварительно транспонировав её (иначе не выполнится правило совпадение числа колонок и числа строк):

Для тензоров произвольной размерности операция транспонирования переставляет все индексы в противоположном порядке $t^T_=t_<. kji>$: Как и в случае с матриц, такая перестановка индексов приводит иному порядку элементов, чем просто изменение атрибута shape.

Перемножение тензоров со свёрткой

Произведение вектора $mathbf$ и тензора $mathbf$, независимо от ndim последнего, интерпретируется следующим образом.
У тензора берутся последние два индекса и делаются такие свёртки (второй случай – по принципу “последний с предпоследним”):

mathbf cdot mathbf

Если у тензора ndim=2 (матрица), то вектор справа превращается в столбик, а слева – в строчку:

$$ begin <|c|c|>hline 1 & 1 \ hline end cdot begin <|c|c|c|>hline 1 & 1 & 1\ hline 1 & 1 & 1\ hline end cdot begin <|c|c|c|>hline 1 \ hline 1 \ hline 1 \ hline end

6 $$ В этом случае для форм имеем: $underline<(2,),. (2,3)>,. (3,) = (3,),. (3,) = $ скаляр или $(2,),. underline <(2,3),. (3,)>= (2,),. (2,) = $ тот же скаляр.

Другие операции свёртки

Существует ещё один метод свёртки matmul (и @ – операция для него). Для ndim = 2 результат такой свёртки не отличается от свёртки dot. Различия начинаются при ndim > 2.

В этом случае тензоры интерпретируются как стопки 2D матриц по последним двум индексам.
Эти 2D матрицы перемножаются независимо в каждой “плоскости стопки”.
Последние два индекса тензоров фиксируются, а по остальным тензоры расширяются (broadcasting).
Для векторов индекс добавляется, а потом убирается. $$ (overline<1,>, 2, 3)

(3, 2, 2, underline<3>)

(3, 2, underline<3>, 5)

(3, 2, 2, 5) $$ Перемножить $(mathbf<3>,

5)$ нельзя, т.к. они нерасширяемы по “жирным” индексам (по последним двум индексам должно быть матричное умножение и их не трогаем). Как и в dot, размерность последнего индекса первого тензора и предпоследнего второго должны совпадать.

Универсальная свёртка np. tensordot(A, B, axes = (axes_A, axes_B)) проводит свёртку вдоль указанных индексов тензоров A и B:

Если axes = 1, то это стандартное dot – произведение. Если axes = 0, то это прямое произведение $Aotimes B$.

Инициализация элементов

Инициализация элементов тензора может быть самой разнообразной. Для следующих методов элементы будут иметь тип float64: Следующие функции приводят к целочисленным элементам int32: Тип элементов этих тензоров зависит от аргументов методов инициализации:

Тип элементов можно менять в процессе инициализации:

Случайные тензоры

Разные полезности

Пусть надо отобрать элементы, удовлетворяющие условию: Ещё одна возможность: numpy.where(condition, x[, y]) – из x или y:

Пусть есть два массива, элементы которых нужно синхронно перемешать:

Число значащих цифр и другие свойства вывода тензоров на печать задаются методом:

[spoiler title=”источники:”]

http://proglib.io/p/convolution

http://qudata.com/ml/ru/NN_Base_Numpy.html

[/spoiler]

Матричные фильтры обработки изображений

Данная статья рассказывает не только о наиболее распространённых фильтрах обработки изображений, но в понятной форме описывает алгоритмы их работы. Статья ориентирована, прежде всего, на программистов, занимающихся обработкой изображений.

Матрица свёртки

Фильтров использующих матрицу свёртки много, ниже будут описаны основные из них.

Матрица свёртки – это матрица коэффициентов, которая «умножается» на значение пикселей изображения для получения требуемого результата.
Ниже представлено применение матрицы свёртки:

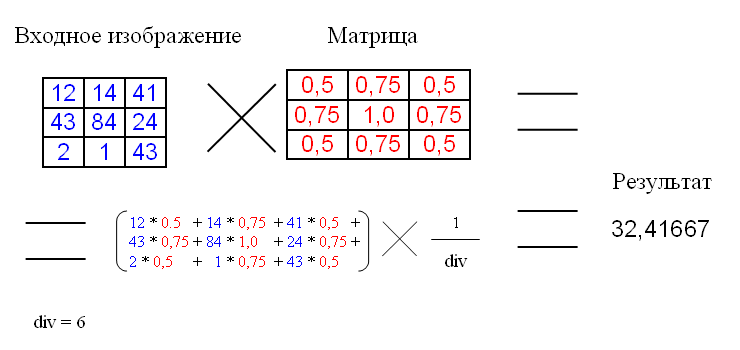
div – это коэффициент нормирования, для того чтобы средняя интенсивность оставалась не изменой.

В примере матрица имеет размер 3×3, хотя размер может быть и больше.

Фильтр размытия

Наиболее часто используемым фильтром, основанным на матрице свёртки, является фильтр размытия.

Обычно матрица заполняется по нормальному (гауссовому закону). Ниже приведена матрица размытия 5×5 заполненная по закону Гауссовского распределения.

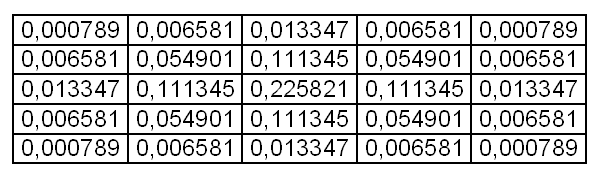
Коэффициенты уже являются нормированными, так что div для этой матрицы равен одному.

От размера матрицы зависит сила размытия.

Стоит упомянуть о граничных условиях (эта проблема актуальна для всех матричных фильтров). У верхнего левого пикселя не существует «соседа» с права от него, следовательно, нам не на что умножать коэффициент матрицы.

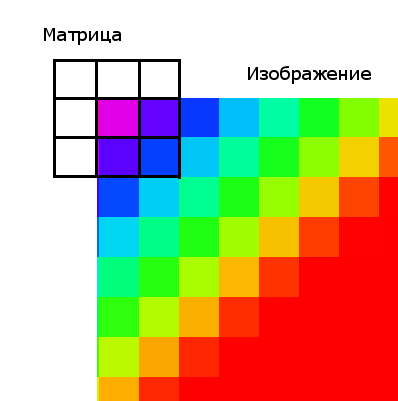
Существует 2 решения этой проблемы:

1. Применение фильтра, только к «окну» изображения, которое имеет координаты левого верхнего угла [kernelSize / 2, kernelSize / 2], а для правого нижнего [width — kernelSize / 2, height — kernelSize / 2]. kernelSize – размер матрицы; width, height – размер изображения.

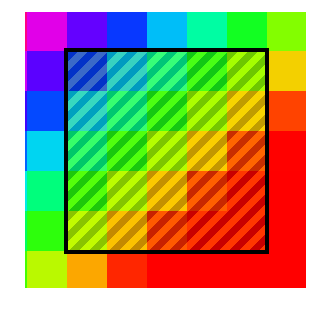
Это не лучший способ, так как фильтр не применяется ко всему изображению. Качество при этом довольно сильно страдает, если размер фильтра велик.

2. Второй метод (дополнение) требует создания промежуточного изображения. Идея в том, чтобы создавать временное изображение с размерами (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). В центр изображения копируется входная картинка, а края заполняются крайними пикселями изображения. Размытие применяется к промежуточному буферу, а потом из него извлекается результат.

Данный метод не имеет недостатков в качестве, но необходимо производить лишние вычисления.

Фильтр размытия по Гауссу имеет сложность O(hi * wi * n *n), где hi, wi – размеры изображения, n – размер матрицы (ядра фильтра). Данный алгоритм можно оптимизировать с приемлемым качеством.

Квадратное ядро (матрицу) можно заменить двумя одномерными: горизонтальным и вертикальным. Для размера ядра 5 они будут иметь вид:

Фильтр применяется в 2 прохода: сначала горизонтальный, а потом к результату вертикальный (или на оборот).

Сложность данного алгоритма будет O(hi * wi * n) + O(hi * wi * n) = 2 * O(hi * wi * n), что для размера ядра больше двух, быстрее, чем традиционный метод с квадратной матрицей.

Фильтр улучшения чёткости

Для улучшения четкости необходимо использовать следующую матрицу:

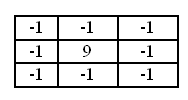
Эта матрица увеличивает разницу значений на границах. Div для этой матрицы равен 1.

В программе GIMP есть фильтр «Матрица свёртки», который упрощает поиск необходимого Вам матричного преобразования.

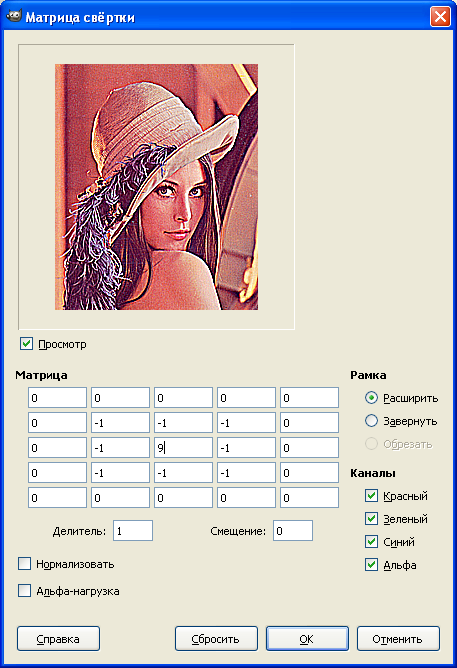
Более подробную информацию о фильтрах основанных на матрице свёртки вы можете найти в статье «Графические фильтры на основе матрицы скручивания».

Медианный фильтр

Медианный фильтр обычно используется для уменьшения шума или «сглаживания» изображения.

Фильтр работает с матрицами различного размера, но в отличие от матрицы свёртки, размер матрицы влияет только на количество рассматриваемых пикселей.

Алгоритм медианного фильтра следующий:

Для текущего пикселя, пиксели, которые «попадают» в матрицу, сортируются, и выбирается средние значение из отсортированного массива. Это значение и является выходным для текущего пикселя.

Ниже представлена работа медианного фильтра для размера ядра равного трём.

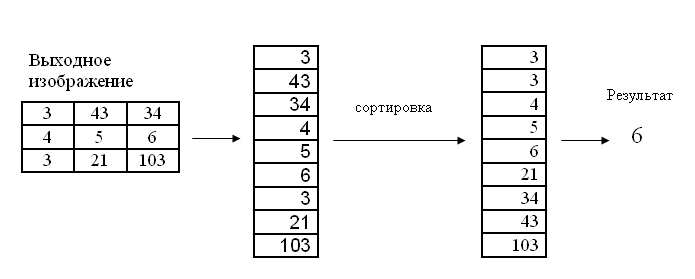
Фильтры эрозия и наращивание

Фильтры наращивание и эрозия служат для получения морфологического расширения или сужения соответственно. Проще говоря, для изображений это значит выбор пикселя с максимальной или минимальной интенсивностью из окрестности.

В результате наращивания происходит увеличение ярких объектов, а эрозии – увеличение тёмных объектов.

Фильтр использует входное изображение и бинарную матрицу. Бинарная матрица определяет форму окрестности. Обычно окрестность имеет круглую форму.

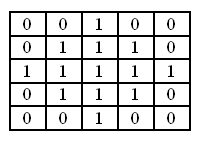
Фильтр наращивание может быть использован для увеличения бликов, ярких отражений.

Заключение

В статье были описаны некоторые из фильтров обработки изображения, описаны их алгоритмы и особенности применения.

ru.wikipedia.org/wiki/Медианный_фильтр
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
ru.wikipedia.org/wiki/Математическая_морфология
habrahabr.ru/post/43895

У этого термина существуют и другие значения, см. Свёртка.

Свёртка в тензорном исчислении — операция понижения валентности тензора на 2, переводящая тензор валентности в тензор валентности .

Определение[править | править код]

В простейшем случае, свёртка для простого тензора типа , определяется как скаляр .
Эта операция продолжается линейно на все тензоры типа .

В общем случае, тензор типа можно рассматривать как линейное отображение из пространства тензоров валентности в пространство тензоров валентности ;
для выбора такого представления надо выбрать ко- контравариантный индекс.
Свёртка образа даёт отображение из пространства тензоров валентности в скаляры, то есть тензор валентности .
Он и называется свёрткой тензора по двум данным индексам.

Обозначения[править | править код]

В координатах она записывается следующим образом:

где применено правило суммирования Эйнштейна по повторяющимся разновариантным (верхнему и нижнему) индексам, то есть в данном случае по .

Часто операцию свёртки проводят над тензорами, являющимися произведениями тензоров, или, короче, производят свёртку двух или нескольких тензоров.

Например, есть запись обыкновенного перемножения матрицы A на матрицу B, то есть, в обычной матричной записи, записывая индексы внизу и не опуская знак суммы, это

.

В принципе свёртка всегда проводится по верхнему и нижнему индексам, однако
в случае если задан метрический тензор, ко- и контравариантные индексы можно однозначно переводить друг в друга (поднимать и опускать), поэтому свёртку можно вести по любой паре индексов, используя метрический тензор, если оба индекса верхние или нижние. Например:

Замечание: операция свёртки определена и имеет смысл не только для тензорных объектов. Во всяком случае, в компонентах совершенно та же операция применяется для свертки с матрицами преобразования координат (матрицами Якоби) и с компонентами аффинной связности, не являющимися представлениями тензоров. Эти свёртки имеют так же ясный геометрический смысл и играют важную роль в тензорном анализе, к тому же используются для построения представления настоящих тензорных объектов, таких как тензор кривизны.

Примеры[править | править код]

• Свёртка тензора по паре индексов, по которым он анти(косо)симметричен, даёт нулевой тензор.
• Свёртка вектора v с тензором A ранга (1,1) представляет умножение вектора на линейный оператор, каковым такой тензор является по отношению к вектору.
• Свёртка векторов a и b с тензором B ранга (0,2) является билинейной формой; так свёртка двух векторов с метрическим тензором дает их скалярное произведение.
• В том числе  — квадратичная форма; именно таким образом свертка с метрическим тензором дает квадрат нормы вектора.
• Свёртка ковариантного и контравариантного вектора дает действие 1-формы на вектор, или, если считать ковариантные компоненты просто дуальным представлением настоящего вектора, то это скалярное произведение двух векторов, один из которых представлен в дуальном базисе.
• Свёртка тензора A ранга (1,1) (с собой) является следом матрицы . Это простейший случай построения (скалярного) инварианта из тензора.
• Действие линейного оператора на пространстве тензоров некоторого определенного ранга есть свёртка с тензором вдвое большего ранга, столько же раз ковариантного, сколько контравариантного, например (в координатной записи):

Свойства[править | править код]

• Свёртка (корректная) одного или нескольких тензоров (в том числе векторов и скаляров) всегда дает тензор (в том числе, возможно, вектор или скаляр).

Литература[править | править код]

• Винберг Э. Б. Курс алгебры. — 2. — Москва: МЦНМО, 2014. — С. 347. — 590 с. — ISBN 978-5-4439-2013-9.

Типы ядер свертки: упрощенный

  Перевод

  Ссылка на автора

Интуитивное введение в различные вариации гламурного слоя CNN

Просто краткое вступление

Convolution использует «ядро» для извлечения определенных «функций» из входного изображения, Позволь мне объяснить. Ядро – это матрица, которая скользит по изображению и умножается на входные данные, так что выходные данные улучшаются определенным желаемым образом. Смотрите это в действии ниже.

Например, ядро, использованное выше, полезно для повышения резкости изображения. Но что такого особенного в этом ядре ?? Рассмотрим два расположения входных изображений, как показано в примере ниже. Для первого изображения центральное значение равно 3 * 5 + 2 * -1 + 2 * -1 + 2 * -1 + 2 * -1 = 7. Значение 3 увеличено до 7. Для второго изображения вывод равно 1 * 5 + 2 * -1 + 2 * -1 + 2 * -1 + 2 * -1 = -3. Значение 1 уменьшилось до -3. Очевидно, что контраст между 3 и 1 увеличен до 7 и -3, что, в свою очередь, сделает изображение более четким.

Вместо использования ядер, созданных вручную, для извлечения функций через Deep CNN мы можем узнать эти значения ядра, которые могут извлечь скрытые функции. Для дальнейшего изучения работы обычных CNN я бы предложил этот блог.

Интуитивно понятное понимание сверток для глубокого обучения

Изучение сильных визуальных иерархий, которые заставляют их работать

towardsdatascience.com

Ядро против фильтра

Прежде чем мы углубимся в это, я просто хочу провести четкое различие между терминами «ядро» и «фильтр», потому что я видел, что многие люди используют их взаимозаменяемо. Ядро, как описано ранее, представляет собой матрицу весов, которые умножаются на входные данные для извлечения соответствующих признаков. Размеры матрицы ядракак свертка получает свое имя, Например, в двумерных свертках матрица ядра является двумерной матрицей.

Однако фильтр представляет собой объединение нескольких ядер, каждое из которых назначено определенному каналу ввода. Фильтры всегда на одно измерение больше, чем ядра. Например, в двумерных свертках фильтры являются трехмерными матрицами (что по существу является объединением двумерных матриц, то есть ядер). Таким образом, для слоя CNN с размерами ядра h * w и входными каналами k размеры фильтра k * h * w.

Общий слой свертки фактически состоит из нескольких таких фильтров.Для простоты в последующем обсуждении предположим наличие только одного фильтра, если он не указан, поскольку одинаковое поведение реплицируется во всех фильтрах.

1D, 2D и 3D свертки

1D свертки обычно используются для анализа данных временных рядов (поскольку в таких случаях вводится 1D). Как упоминалось ранее, ввод данных 1D может иметь несколько каналов. Фильтр может двигаться только в одном направлении, и, следовательно, выходной сигнал равен 1D. Ниже приведен пример одноканальной свертки 1D.

Мы уже видели пример одноканальной двухмерной свертки в начале публикации, поэтому давайте представим многоканальную двухмерную свертку и попытаемся обернуть ее вокруг. На диаграмме ниже размеры ядра 3 * 3, и в фильтре несколько таких ядер (помечено желтым). Это потому, что на входе есть несколько каналов (отмечены синим), и у нас есть одно ядро, соответствующее каждому каналу на входе. Очевидно, что здесь фильтр может двигаться в 2 направлениях, и, таким образом, конечный результат является 2D. 2D-свертки являются наиболее распространенными и часто используются в Computer Vision.

Трудно визуализировать 3D-фильтр (поскольку это 4-мерная матрица), поэтому мы обсудим здесь одноканальную 3D-свертку. Как видно из изображения ниже, в трехмерных свертках ядро ​​может двигаться в 3 направлениях, и, таким образом, полученный результат также является трехмерным.

Большая часть работы, проделанной в модификации и настройке слоев CNN, была сфокусирована только на двухмерных свертках, и поэтому с этого момента я буду обсуждать только эти вариации в контексте двухмерных сверток.

Транспонированная Свертка (Деконволюция)

GIF ниже хорошо показывает, как двумерная свертка уменьшает размеры входных данных. Но иногда нам нужно выполнять обработку ввода, например, чтобы увеличить ее размеры (также называемые «повышающей дискретизацией»).

Чтобы достичь этого с помощью свертки, мы используем модификацию, известную как транспонированная свертка или деконволюция (хотя это не совсем «обратная» операция свертки, поэтому многие люди не предпочитают использовать этот термин). Пунктирные блоки в GIF ниже представляют отступы.

Я думаю, что эти анимации дают хорошее представление о том, как различные выходные данные с повышенной частотой дискретизации могут быть созданы из одного и того же входа на основе шаблона заполнения. Такие свертки очень часто используются в современных сетях CNN, главным образом из-за их способности увеличивать размеры изображения.

Отделимая свертка

Разделяемая свертка относится к разбиению ядра свертки на ядра более низкой размерности. Отделимые свертки бывают двух основных типов Во-первых, это пространственно отделимые свертки, см., Например, ниже.

Однако пространственно отделимые свертки не так часто встречаются в Deep Learning. С другой стороны, отделимые глубиной извилины широко используются в облегченных моделях CNN и обеспечивают действительно хорошие характеристики. Смотрите ниже, например.

Но почему делим извилины?Эффективность !!Использование отделимых сверток может значительно уменьшить количество требуемых параметров. С растущей сложностью и огромным размером сетей глубокого обучения, которые мы имеем сегодня, возможность обеспечить аналогичную производительность с меньшим количеством параметров, безусловно, является требованием.

Дилатационная (злокачественная) свертка

Как вы видели во всех вышеупомянутых слоях свертки (без исключения), они обрабатывают все соседние значения вместе. Тем не менее, иногда в интересах конвейера было бы пропустить определенные входные значения, и именно так были введены расширенные свертки (также называемые сверточными свертками). Такая модификация позволяет ядру увеличить егодальность обзора,без увеличения количества параметров.

Из приведенной выше анимации ясно видно, что ядро ​​способно обрабатывать более широкие окрестности с теми же 9 параметрами, что и ранее. Это также означает потерю информации из-за невозможности обработать детализированную информацию (поскольку она пропускает определенные значения). Тем не менее, общий эффект представляется положительным в некоторых приложениях.

Деформируемая свертка

Свертки очень жесткие с точки зрения формы выделения признаков. То есть формы ядра – это только квадрат / прямоугольник (или какая-то другая форма, которую необходимо определить вручную), и, таким образом, они могут работать только с такими шаблонами.Что, если форма свертки сама по себе была обучаемой?Это основная идея введения деформируемых извилин.

Реализация деформируемой свертки на самом деле очень проста. Каждое ядро ​​фактически представлено двумя разными матрицами. Первая ветвь учится предсказывать «смещение» от источника. Это смещение указывает на то, какие входные данные вокруг источника будут обрабатываться. Поскольку каждое смещение прогнозируется независимо, им не нужно формировать какую-либо жесткую форму между собой, что позволяет деформируемому характеру. Вторая ветвь – это просто ветвь свертки, вход которой теперь является значениями этих смещений.

Что дальше?

Было несколько вариантов слоев CNN, которые использовались независимо или в комбинации друг с другом для создания успешных и сложных архитектур. Каждый вариант был основан на интуиции о том, как должно работать извлечение признаков. Таким образом, я считаю, что хотя эти сети Deep CNN изучают веса, которые мы не можем объяснить, интуиция, связанная с их формированием, очень важна для их работы, и дальнейшая работа в этом направлении важна для успеха очень сложных CNN.

---

Этот блог является частью усилий по созданию упрощенного введения в области машинного обучения. Следуйте за полной серией здесь

Машинное обучение: упрощенное

Знай это, прежде чем погрузиться в

towardsdatascience.com

Или просто прочитайте следующий блог в серии

Распределенное векторное представление: упрощенное

Возможно, самый важный метод представления функций в машинном обучении

towardsdatascience.com

---

Ссылки

[1] Крижевский, Алекс, Илья Суцкевер и Джеффри Э. Хинтон. «Классификация Imagenet с глубокими сверточными нейронными сетями». Достижения в системах обработки нейронной информации. 2012.
[2] Думулин, Винсент и Франческо Висин. «Руководство по арифметике свертки для глубокого обучения». Препринт arXiv arXiv: 1603.07285 (2016).
[3] Чен, Лян-Цзе и др. «Deeplab: семантическая сегментация изображений с помощью глубоких сверточных сетей, атомной свертки и полностью связанных crfs». IEEE-транзакции по анализу образов и машинному интеллекту 40.4 (2017): 834–848.
[4] Dai, Jifeng, et al. «Деформируемые сверточные сети». Материалы международной конференции IEEE по компьютерному зрению. 2017.
[5] Говард, Эндрю Дж. И соавт. «Мобильные сети: эффективные сверточные нейронные сети для приложений мобильного зрения». Препринт arXiv arXiv: 1704.04861 (2017).
[6] https://github.com/vdumoulin/conv_arithmetic