Как найти сводный индекс физического объема

Основные формулы исчисления сводных или общих индексов

Наименование индекса	Формула	Что показывает индекс	Что показывает значение индекса, уменьшенное на 100%	Что показывает разность числителя и знаменателя
Индекс физического объема продукции (по цене)		Во сколько раз изменилась стоимость продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения ее физического объема	На сколько процентов изменилась стоимость продукции в результате изменения объема ее производства	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) объема ее производства
Индекс цен		Во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен	На сколько процентов изменилась стоимость продукции в результате изменения цен	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) цен
Индекс стоимости продукции (товарооборота)		Во сколько раз изменилась стоимость продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным	На сколько процентов изменилась стоимость продукции в текущем периоде по сравнению с базисным	На сколько рублей изменилась стоимость продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции (по себестоимости)		Во сколько раз изменились издержки производства продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения объема ее производства	На сколько процентов изменились издержки производства продукции в результате изменения объема ее производства	На сколько рублей изменились издержки производства продукции в результате изменения объема ее производства
Индекс себестоимости продукции		Во сколько раз изменились издержки производства продукции в результате изменения себестоимости продукции, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения себестоимости продукции	На сколько процентов изменились издержки производства продукции в результате изменения себестоимости продукции	На сколько рублей изменились издержки производства продукции в результате изменения себестоимости продукции
Индекс издержек производства		Во сколько раз изменились издержки производства продукции, или сколько процентов составил рост (снижение) издержек производства продукции в текущем периоде по сравнению с базисным	На сколько процентов изменились издержки производства продукции в текущем периоде по сравнению с базисным	На сколько рублей изменились издержки производства продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции (по трудоемкости)		Во сколько раз изменились затраты времени на производство продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменения ее физического объема	На сколько процентов изменились затраты времени на производство продукции в результате изменения объема ее производства	На сколько человеко-часов изменились затраты времени на производство продукции в результате роста (уменьшения) объема ее производства
Индекс трудоемкости		Во сколько раз изменились затраты времени на производство продукции в результате изменения ее трудоемкости, или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменения ее трудоемкости	На сколько процентов изменились затраты времени на производство продукции в результате изменения ее трудоемкости	На сколько человеко-часов изменились затраты времени на производство продукции в результате роста (уменьшения) ее трудоемкости
Индекс затрат времени на производство продукции		Во сколько раз изменились затраты времени на производство продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным	На сколько процентов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным	На сколько человеко-часов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным

18.
Индексы –
это относительные показатели, которые
характеризуют средние измерения во
времени, пространстве по сравнению с
планом или нормативом отдельных или
сложных общественных явлений, элементы
которых не поддаются непосредственному
суммированию.

Для
удобства работы с индексами будем
использовать следующие обозначения:

g₁ и
g₀ –
это физический объем (количество)
произведенной или реализованной
продукции в отчетном (g₁)
и базисном (g₀)
периодах соответственно;

р₁ и
р₀ –
цена единицы продукции;

р₁g₁ и
р₀g₀ –
стоимость (товарооборот) произведенной
или реализованной продукции;

z₁ и
z₀ –
себестоимость произведенной продукции.

Различают
индексы объемных (количественных) и
качественных показателей.

К
индексам объемных показателей относятся
индексы физического объема продукции,
валового сбора и т.д.

К
индексам качественных показателей относятся
индексы цен, себестоимости, производительности
труда и т.д.

В
зависимости от охвата единиц совокупности
индексы подразделяют на индивидуальные
и общие.

Индивидуальные
индексы –
это отношение уровня показателя в
текущем (отчетном) периоде к такому же
показателю в базисном периоде (i). 

Общие
индексы используются для сопоставления
непосредственно несоизмеримых разнородных
явлений.

Агрегатные
индексы состоят из двух элементов:
индексируемой величины и признака-веса.

Индексируемая
величина – это показатель изменения,
который отражает индекс.

Признак-вес
(соизмеритель) – это показатель, который
позволяет перейти от несоизмеримых
элементов к соизмеримым.

В
статистике существует правило построения
агрегатных индексов, согласно которому
веса в индексах объемных показателей
берутся на уровне базисного периода, а
веса в индексах качественных показателей
берутся на уровне отчетного периода.

–
агрегатный индекс физического объема
продукции (товарооборота) 

–
агрегатный индекс цен 

–
агрегатный индекс стоимости произведенной
или реализованной продукции (товарооборота)

 Связь
этих индексов I_pg =
I_p·I_g

–
агрегатный индекс себестоимости
произведенной продукции 

–
агрегатный индекс физического объема
произведенной продукции 

–
агрегатный индекс затрат на производство
продукции Связь
этих индексовI_zg =
I_z·I_g

Для
правильного составления общего индекса
необходимо учитывать следующие
требования:

1)   в
числителе и знаменателе общего индекса
всегда будут суммы произведений
индексируемой величины на показатель,
принятый в качестве веса индекса;

2)   выбор
весов индексов определяется экономическим
содержанием изучаемого явления. При
индексировании качественных показателей
взвешивание производят по отчетным
весам; при индексировании объемных
(количественных) показателей взвешивание
производят по базисным весам;

3)   при
индексировании двух показателей, таких
как товарообо­рот – pq; затраты
на выпуск продукции – zq и др.

Общий
индекс строится как относительная
величина динамики: в числителе –
отчетный период – p₁ ×
q; в знаменателе базисный – p₀ ×
q₀ (сравниваемый
период);

4) при
составлении системы взаимосвязанных
индексов сначала устанавливают
взаимосвязи между исходными показателями,
затем переходят к системе взаимосвязанных
индексов.

Например:

pq
= p × q; Jpq = J_р ×
J_q.

Построение
агрегатной формы индекса рассмотрим
на примере.

Известны
цены и количество проданного товара на
ранке города.

Таблица
6.1

Товар	Продано, кг.	Цена за кг в руб.
Базисный период (q0)	Отчетный период (q1)	Базисный период (p0)	Отчетный период (p1)
Картофель Капуста Помидоры	5000 2000 10000	6000 2500 12000	6,0 7,0 8,0	8,0 10,0 15,0

Определить
изменение цен и количества товаров в
целом по всем товарам в отчетном периоде
по сравнению с базисным.

Индивидуальные
индексы для отдельных видов овощей
рассчитываются следующим образом: для
картофеля количество продаж составило – ,
т.е. количество проданного картофеля
увеличилось в 1,2 раза или на
20% = 120 – 100.  по
картофелю 8,0 : 6,0 = 1,333, таким
образом, цена увеличилась в 1,333 раза или
на 33% = 133 – 100.

Итак,
нам надо построить общие индексы цен и
количества проданного товара – J_р;
J_q.

Согласно
вышеизложенному правилу индекс цены
равен

.

В
качестве веса берем количество проданного
товара, но так как индексируемая
величина – качественный показатель,
то веса берем в отчетном периоде.

.

Таким
образом, цены по всем трем товарам
увеличились на 69,2% = 169,2 – 100. Это в
относительном выражении, а в абсолютных
величинах они увеличились на 103 500
руб. = 253 000 – 149 500.

Экономический
эффект или иначе сумма сэкономленных
или перерасходованных денег за счет
изменения цен исчисляется по данным
общего индекса цен и равна разности
числителя и знаменателя индекса:
Σр₁q_1 – Σp₀q₀;
следовательно, в связи с ростом цен на
69,8% население в отчетном периоде
дополнительно израсходовало 103 500
руб. на покупку данных товаров.

Определим
общий индекс физического объема

так
как физический объем – количественный
показатель, то веса берется в базисном
периоде.

.

Следовательно,
не только цены увеличились, но и количество
проданных овощей увеличилось на 20,5% =
120,5 – 100, что в абсолютном выражении
составляет: 25 500 руб. = 149 500 –
124 000.

Если
абсолютная величина, т.е. разница между
числителем и знаменателем получается
с плюсом, то эффект от продаж получает
продавец. Если же абсолютная величина
получается с минусом, то сумму экономии
получает покупатель.

А
теперь посмотрим, а что же получил
продавец от продажи этих товаров.  согласно
третьему правилу построения общих
индексов, когда влияют одновременно
два фактора, т.е. на динамику товарооборота.

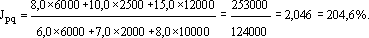
Следовательно,
товарооборот увеличится в 2,04 раза, а в
абсолютном отношении это составило
129 000 руб.

Итак,
мы проследили, как повлиял каждый фактор
в отдельности в относительном и абсолютном
выражениях на цену и количество проданных
овощей, а также выявили влияние сразу
двух факторов.

А
теперь посмотрим, как взаимосвязаны
общие индексы. В математике p × q = pq; в
индексах точно так

J_pq =J_p ×
J_q,

согласно
нашему примеру: 1,692 × 1,205 = 2,046.

Следовательно,
индексы составлены правильно.

Любой
агрегатный индекс может быть представлен
как взвешенная величина из индивидуальных
индексов

 найдем 

.

Подставим
в общий индекс цены

,

тогда
получим среднегармонический взвешенный
индекс

.

,

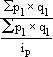отсюда
q₁ =
iq ×q₀,
подставим в агрегатную форму общего
индекса физического объема

Получили
средневзвешенный индекс. Вот для каких
целей используется индивидуальный
индекс, т.е. расширяет возможности
агрегатной формы индекса.

Использование
исходной формы агрегатного индекса или
среднегармонического, средневзвешенного
индекса зависит от исходных данных,
имеющихся в распоряжении исследователя.

19
 зависимости
от методологии расчета индивидуальных
и сводных индексов различают средние
арифметические и средние
гармонические индексы. Другими
словами, общий индекс, построенный на
базе индивидуального индекса, принимает
форму среднего арифметического или
гармонического индекса, т. е. он может
быть преобразован в средний арифметический
и средний гармонический индексы.

Идея
построения сводного индекса в виде
средней величины из индивидуальных
(групповых) индексов вполне объяснима:
ведь сводный индекс является общей
мерой, характеризующей среднюю величину
изменения индексируемого показателя,
и, конечно, его величина должна зависеть
от величин индивидуальных индексов. А
критерием правильности построения
сводного индекса в форме средней величины
(среднего индекса) является его
тождественность агрегатному индексу.

Преобразование
агрегатного индекса в средний из
индивидуальных (групповых) индексов
производится следующим образом: либо
в числителе, либо в знаменателе агрегатного
индекса индексируемый показатель
заменяется его выражением через
соответствующий индивидуальный
индекс. Если
такую замену сделать в числителе, то
агрегатный индекс будет преобразован
в средний арифметический, если же в
знаменателе – то в средний гармонический
из индивидуальных индексов.

Например,
известен индивидуальный индекс
физического объема IQ
у = К1/значении q0 и
стоимость продукции каждого вида в
базисном периоде (д0р0). Исходной
базой построения среднего из индивидуальных
индексов служит сводный индекс физического
объема:

 

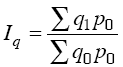
(агрегатная
форма индекса Ласпейреса).

Из
имеющихся данных непосредственно
суммированием можно получить только
знаменатель формулы. Числитель же может
быть получен перемножением стоимости
отдельного вида продукции базисного
периода на индивидуальный индекс:

 

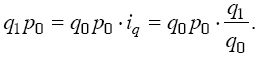
Тогда
формула сводного индекса примет вид:

 

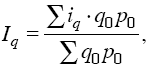
т.
е. получим средний арифметический индекс
физического объема, где весами служит
стоимость отдельных видов продукции в
базисном периоде.

Допустим,
что в наличии имеется информация о
динамике объема выпуска каждого вида
продукции (г^) и стоимости каждого вида
продукции в отчетном периоде (p1q1). Для
определения общего изменения выпуска
продукции предприятия в этом случае
удобно воспользоваться формулой Пааше:

 

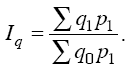
Числитель
формулы можно получить суммированием
величин q1P1, а
знаменатель – делением фактической
стоимости каждого вида продукции на
соответствующий индивидуальный индекс
физического объема продукции, т. е.
делением: p1q1/на
IQ ,
тогда:

 

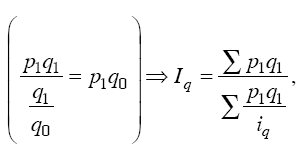
таким
образом, получаем формулу среднего
взвешенного гармонического индекса
физического объема.

Применение
той или иной формулы индекса физического
объема (агрегатного, среднего
арифметического и среднего гармонического)
зависит от имеющейся в распоряжении
информации. Также нужно иметь в виду,
что агрегатный индекс может быть
преобразован и рассчитан как средний
из индивидуальных индексов только при
совпадении перечня видов продукции или
товаров (их ассортимента) в отчетном и
базисном периодах, т. е. когда агрегатный
индекс построен посравнимому
кругу единиц
(агрегатные индексы качественных
показателей и агрегатные индексы
объемных показателей при условии
сравнимого ассортимента).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  22.02.201663.49 Кб91.doc

• #

  22.02.2016240.09 Кб221.docx

• #
• #
• #
• #
• #
• #
• #
• #
• #

Имеются следующие данные о реализации молочных продуктов на городском рынке:

Рассчитайте сводные индексы цен, товарооборота и физического объема реализации.

Решение:

Дополним таблицу ещё одной графой: индивидуальный индекс цен.

Сводный индекс цен определяется по формуле:

 

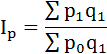
Значения цен в ноябре по условию задачи не известны, однако известно их изменение. Выразим из формулы индивидуального индекса значение цены за ноябрь:

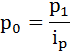
Преобразуем формулу индекса цен:

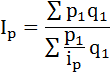
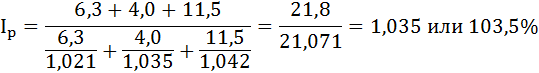
Цены на все продукты возросли на 3,5%.

Индекс товарооборота определяется по формуле:

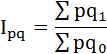
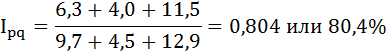
Товарооборот за декабрь снизился на 19,6%.

Индекс физического объёма продукции:

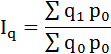
Преобразуем формулу индекса физического объёма:

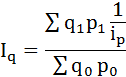
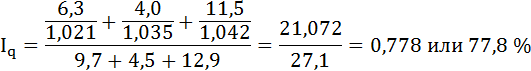
Физический объём трёх продуктов уменьшился на 22,2%.

Можно воспользоваться взаимосвязью трёх индексов:

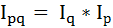
Отсюда

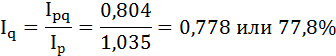
Ответ:

Цены на три продукта в целом возросли на 3,5%.

Товарооборот в декабре уменьшился по сравнению с товарооборотом за ноябрь на 19,6%.

Физический объём трёх продуктов уменьшился на 22,2%.

Тема 8. Экономические индексы

8.1. Понятие об индексах в
статистике. 

8.2. Индивидуальные индексы.

8.3. Сводные (общие) индексы.

8.1.Понятие об
индексах в статистике

Индекс – это показатель
сравнений двух состояний одного и того же явления (простого или сложного,
состоящих из соизмеримых или несоизмеримых элементов, во времени и в
пространстве).

Каждый индекс включает два вида данных:

•             
оцениваемые данные, которые принято называть отчетными и

обозначать значком «1»;

•             
данные, которые используются в качестве базы сравнения, –
базисные, обозначаются значком «0».

 Индекс чаще всего выражается как
отношение, но может быть выражен в разностной форме, как разность между
числителем и знаменателем отношения: Отношения = Отчетные данные : Базисные
данные  Индекс как отношение может быть выражен в виде:

•             
коэффициентов (когда базисный уровень принят за 1);

•             
процентов (когда базисный уровень принят за 100)

  Если индекс больше 1 (100%) – уровень
изучаемого явления растёт. Например,  индекс потребительских цен, равный 112%,
означает, что цены на потребительские товары или услуги выросли на 12% в
отчетном периоде по сравнению с базисным периодом.

  Если индекс меньше 1 (100%) – уровень
изучаемого явления снижается. Например, индекс товарооборота магазина, равный
97%, означает, что в отчетном период, по сравнению с базисным, выручка от
продажи товаров снизилась на 3%. 

Классификация индексов

ИНДЕКСЫ
В зависимости от базы сравнения	 В зависимости от масштабов обобщения
Цепные	Базисные	Индивидуальные	Сводные (общие)

Обозначения, применяемые в теории индексного метода:

•             
p – цена за единицу товара или услуги,  руб.;

•             
q – количество единиц (произведенной, выпущенной, реализованной
продукции), шт.;

•             
1 – подстрочное обозначение отчетного периода;

•             
0 – подстрочное обозначение базисного периода;

•             
i – индивидуальный индекс;

•             
I – сводный (общий) индекс.

8.2. Индивидуальные
индексы

                            Индивидуальный индекс – даёт
сравнительную оценку отдельных

элементов той или иной
совокупности (или отдельной единицы совокупности)

1.                 
Индивидуальный индекс цены – показывает, как изменилась цена на
товар в отчетном периоде по сравнению с базисным периодом.

i_p = p₁
: p₀

 Например, цена яблок в январе 2020 года
68 руб., а в декабре 2019 года 61 руб. Рассчитать, индивидуальный индекс цены
яблок.

i_p = 68 :
61 = 1,115 ∙ 100 = 111,5%

           Вывод. Цена на яблоки в январе выросла на 11,5% по
сравнению с декабрем.

2.                 
Индивидуальный индекс физического объёма производства
(реализации) – показывает, как изменился объём производства (реализации)
конкретного товара в натуральных единицах измерения в отчетном периоде по
сравнению с базисным периодом.

i_q = q₁
: q₀

 Например, количество проданных  яблок в
январе 2020 года 780 кг., а в декабре 2019 года 850 кг. Рассчитать,
индивидуальный индекс количества проданных яблок.

                                     i_q = 780 : 850
= 0,918 i_p 100 = 91,8%

          Вывод. Количество проданных 
яблок в январе уменьшилась на 8,2% по сравнению с декабрем.

3.                 
Индивидуальный индекс товарооборота – показывает, как изменился
объём товарооборота в отчетном периоде по сравнению с базисным периодом.

i_pq = p₁q₁
: p₀q₀

          Например, рассчитать,
индивидуальный индекс товарооборота яблок.  i_pq = (68 ∙ 780) : (61∙
850) = 1,023 ∙ 100 = 102,3%

 Вывод. Товарооборот яблок в январе
увеличился на 2,3% по сравнению с декабрем.

Взаимосвязь
индивидуальных индексов:

ipq= ip∙ iq

8.3. Сводные (общие)
индексы

 Общие (сводные) индексы – характеризуют
изменение совокупности в целом по какому-либо признаку. Сводные индексы
вычисляются по товарным группам или нескольким видам продукции.

1.                
Общий (сводный) индекс цены – показывает, как повлияло изменение
цен на реализуемые товары на изменение объёма товарооборота в отчетном периоде
по сравнению с базисным периодом.

I_p = ∑ p₁q₁
: ∑ p₀q₁

                   Абсолютное
влияние изменения цен на изменение товарооборота:

                                                   ∑ p₁q₁
– ∑ p₀q₁

2.                
Общий (сводный) индекс физического объёма – показывает, как
повлияло изменение количества реализуемых товаров на изменение объёма
товарооборота в отчетном периоде по сравнению с базисным периодом.

I_q = ∑ p₀q₁
: ∑ p₀q₀

              Абсолютное влияние изменения
физического объёма на изменение товарооборота:

                                                   ∑ p₀q₁
– ∑ p₀q₀

3.                
Общий (сводный) индекс товарооборота – показывает, как изменился
объём товарооборота в отчетном периоде по сравнению с базисным периодом, под
влиянием двух факторов сразу: цены и физического объёма.

I_pq = ∑ p₁q₁
: ∑ p₀q₀

Абсолютное изменение
товарооборота:

                                                   ∑ p₁q₁
– ∑ p₀q₀

Взаимосвязь общих
(сводных) индексов:

I_pq= I_p
∙ I_q

Наприме, рассчитать индивидуальные и
общие индексы товарооборота, физического объёма и цен по следующим данным о
ценах и реализации товаров за 2 месяца.

Товары		Март		Апрель		Индексы %
Цена, руб.	Реализация	Цена, руб.	Реализация	Цены	Физического объёма	Товарооборота
кг.	руб.	кг.	руб.
А	10	800	8 000	8	750	6 000	80	93,8	75
Б	5	400	2 000	5	540	2 700	100	135	135
В	6	150	900	7	200	1 400	116,7	133,3	155,6
Итого	–	–	10 900			10 100	88,6	104,6	92,7

Решение.

1.  
Рассчитаем индивидуальный индекс цены товаров:

товар
А 8 : 10 = 0,8 или 80% товар Б  5 : 5 = 1 или 100% товар В 7 : 6 = 1,167 или
116,7%

2.  
Рассчитаем индивидуальный индекс физического объёма  товаров:

товар
А 750 : 800 = 0,938 или 93,8% товар Б  540 : 400 = 1,35 или 135% товар В 200 :
150 = 1,333 или 133,3%

3.  
Рассчитаем индивидуальный индекс товарооборота:

товар
А 6 000 : 8000 = 0,75 или 75% товар Б  2 700 : 2 000 = 1,35 или 135% товар В 1
400 : 900 = 1,556 или 155,6%

4.  
Рассчитаем общий (сводный) индекс цены товаров:

10 100 : (10 ∙ 750 + 5 ∙ 540 + 6 ∙ 200) =
10 100 : 11 400 = 0,886 или 88,6 %.  Цены на товары снизились на 11,4%

Абсолютное изменение цены 10 100
– 11 400 = – 1 300 руб.

5. Рассчитаем общий (сводный)
индекс физического объёма товаров:

11400 : 10900 = 1,046 или 104,6%.
Физический объём продаж товаров возрос на 4,6%

Абсолютное изменение физического
объёма 11400 – 10900 = 500 руб.

6. Рассчитаем общий (сводный)
индекс товарооборота:

10 100 : 10900 = 0,927 или 92,7%.
Товарооборот трёх товаров снизился  на 7,3% Абсолютное изменение товарооборота
10 100 – 10900 = – 800 руб.

Взаимосвязь индексов 0,886  ∙
1,046 = 0,927

Абсолютное изменение -1300 + 500
= – 800 руб.

Вывод. В целом по трем товарам
товарооборот снизился на 7,3% или 800 руб. Это произошло за счет снижения цен
на 11,4 % или 1300 руб., и роста объёмов продаж на 4,6% или 500 руб.

Контрольные вопросы:

1.      
Что такое индекс в статистике?

2.      
Из каких данных состоит индекс?

3.      
В каких видах может быть выражен индекс?

4.      
Какие вы знаете виды индексов?

5.      
Как определить индивидуальный индекс цены?

6.      
Как определить индивидуальный индекс физического объёма?

7.      
Как определить индивидуальный индекс товарооборота?

8.      
Как определить общий (сводный) индекс цены?

9.      
Как определить общий (сводный) индекс физического объёма?

10.  
Как определить общий (сводный) индекс товарооборота?

11.  
Как определить абсолютное изменение с помощью индексов?

Практическое занятие
№ 4

Тема занятия: Расчёт
индивидуальных и общих индексов

Задача № 1

Имеются следующие
данные о производстве продукции на предприятии:

Товары		1 квартал		2 квартал
Цена единицы, руб.	Физический объём шт.	Производство, тыс. руб.	Цена единицы, руб.	Физический объём шт.	Производство, тыс. руб.
А	400		800	370		400
Б	470		700	450		500
В	540		500	520		800

1.           
Определить индивидуальные индексы:     цены;          физического
  объёма;

товарооборота;

2.           
Определить общие индексы: цены; физического объёма;
товарооборота; 3. Установить степень влияния изменения цен и количества
произведённой продукции в отдельности на динамику товарооборота. Задача № 2

Имеются следующие
данные о реализации продукции на предприятии:

Товары	Реализация т.	Цена за 1 кг.
Базисный период	Отчётный период	Базисный период	Отчётный период
А	200	220	8	9,5
Б	300	280	6	8
В	250	260	8	16

1.           
Определить индивидуальные индексы:     цены;          физического
  объёма;

товарооборота;

2.           
Определить общие индексы: цены; физического объёма;
товарооборота; 3. Установить степень влияния изменения цен и количества
произведённой продукции в отдельности на динамику товарооборота.

Задача № 3

Имеются следующие данные о товарообороте
предприятия по группам товаров:

Товары	Количество проданных             товаров, кг.	Цена за единицу товара, руб.
1 квартал	2 квартал	1 квартал	2 квартал
Капуста	1860	1827	25	30
Лук	7027	8728	40	35
Чеснок	258	333	120	130

1.           
Определить индивидуальные индексы:     цены;          физического
        объёма;

товарооборота;

2.           
Определить общие индексы: цены; физического объёма;
товарооборота;

3.           
Установить степень влияния изменения цен и количества проданной
продукции в отдельности на динамику товарооборота.

Задача № 4

Имеются следующие данные о товарообороте
предприятия по группам товаров:

Товар	1 квартал	2 квартал
Продано шт.	Цена руб.  за ед.	Продано шт.	Цена  руб. за ед.
Молоко	427	23	445	24
Сметана	169	45	163	49
Кефир	131	31	120	32

1.           
Определить индивидуальные индексы:     цены;          физического
        объёма;

товарооборота;

2.           
Определить общие индексы: цены; физического объёма;
товарооборота;

3.           
Установить степень влияния изменения цен и количества проданной
продукции в отдельности на динамику товарооборота.

Задача № 5

Имеются следующие данные о товарообороте предприятия по
группам товаров:

Товар	Продано (кг)	Цена за кг (руб.)
1 квартал	2 квартал	1 квартал	2 квартал
Печенье «Кокос»	1342	1380	164	181
Пряники «Заря»	1841	1620	134	128
Сушка «Малютка»	1920	2000	162	166

1.           
Определить индивидуальные индексы:     цены;          физического
        объёма;

товарооборота;

2.           
Определить общие индексы: цены; физического объёма;
товарооборота;

3.           
Установить степень влияния изменения цен и количества проданной
продукции в отдельности на динамику товарооборота.

Рассчитать сводные индексы цен, физического объема реализации и товарооборота, а также величину перерасхода населения от роста цен