Циркуляция векторного поля. Ротор вектора. Теорема Стокса
Содержание:







По этой ссылке вы найдёте полный курс лекций по математике:
Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь
Пример 1. вычислить циркуляцию векторного поля вдоль эллипса L: По определению циркуляции имеем Параметрические уравнения данного эллипса имеют вид: , и, значит, . Подставляя эти выражения в формулу (2), найдем Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора 8.1.
Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.
Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что , и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде: Рассмотрим сначала случай, когда гладкая поверхность Е и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур А соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура А. Для определенности будем считать, что контур L ориентирован так, что поверхность Е остается слева, так что веетор нормали п к поверхности Е составдя етсосью Oz острый угол 7 (cos 7 >0).
Возможно вам будут полезны данные страницы:
Пусть — уравнение поверхности Е и функция ф(х>у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.
Рассмотрим интеграл Линия L лежит на поверхности Е. Поэтому, пользуясь уравнением этой поверхности , мы можем заменить г под знаком интеграла на ^(ж, у). Координаты перемсннойточки кривой А равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по А, Применим к интегралу, стоящему справа, формулу Грина.
Имеем Перейдем теперь от интеграла по области D к интегралу по поверхности Е. Так как dS = cos 7 • da, то из формулы (8) получим, что Вектор нормали п° к поверхности Е определяется выражением к. Отсюда видно, что . Поэтому равенсгво (9) можно переписать так: Считая Е гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул Циркуляция векторного поля.
Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример 3:
Вычислить циркуляцию вектора по линии 1) пользуясь определением; 2) по теореме Стокса. 4 1) Зададим линию L параметрически: Тогда 2) Найдем rota: Натянем на контур L кусок плосхости Тогда . Инвариантное определение ротора поля Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат. Теорема 8.
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4
Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.
Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.
Физический смысл ротора поля Пустьтвердое
тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.
Правила вычисления ротора
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и<М) на векторную а(М) вычисляется по формуле
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Ротор векторного поля. Формула Стокса

Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
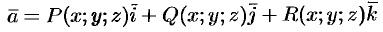
называется вектор, обозначаемый 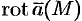 и определяемый формулой
и определяемый формулой
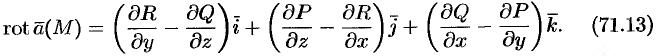
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
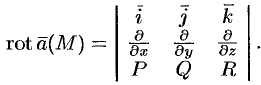
Отметим некоторые свойства ротора.
- Если
 — постоянный вектор, то
— постоянный вектор, то 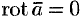 .
. 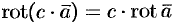 , где
, где 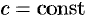 .
.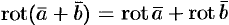 , т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.- Если
 — скалярная функция, а
— скалярная функция, а 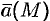 — векторная, то
— векторная, то
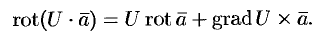
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
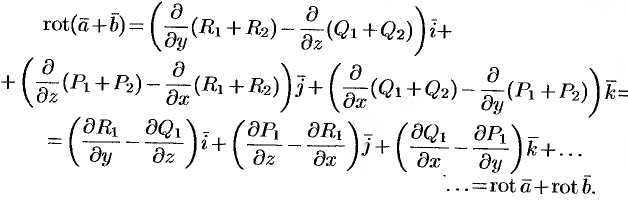
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
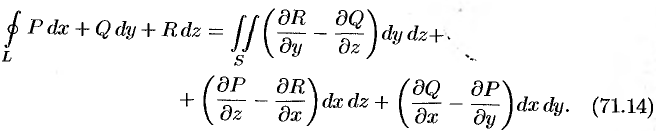
Левая часть формулы (71.14) представляет собой циркуляцию вектора  по контуру
по контуру  , т. е.
, т. е. 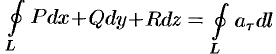 (см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора
(см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора 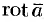 через поверхность
через поверхность  , ограниченную контуром
, ограниченную контуром  (см. (71.3)), т. е.
(см. (71.3)), т. е.
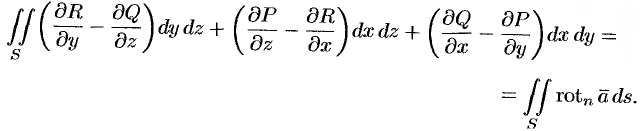
Следовательно, формулу Стокса можно записать в виде
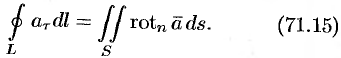
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре  и выбор стороны у поверхности
и выбор стороны у поверхности  согласованы между собой так же, как в теореме Стокса.
согласованы между собой так же, как в теореме Стокса.
Формула (71.15) показывает, что циркуляция вектора  вдоль замкнутого контура
вдоль замкнутого контура  равна потоку ротора этого вектора
равна потоку ротора этого вектора  через поверхность
через поверхность  , лежащую в поле вектора
, лежащую в поле вектора  и ограниченную контуром
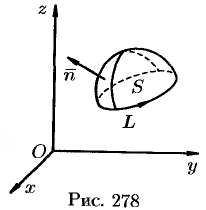
и ограниченную контуром  (натянутую на контур) (см. рис. 278).
(натянутую на контур) (см. рис. 278).
Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки  с контуром
с контуром  , содержащей точку
, содержащей точку  .
.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
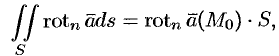
где 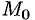 — некоторая (средняя) точка площадки
— некоторая (средняя) точка площадки  (см. рис. 279).
(см. рис. 279).
Тогда формулу (71.15) можно записать в виде
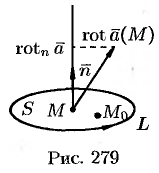
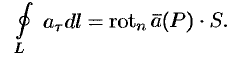
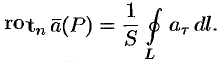
Пусть контур  стягивается в точку
стягивается в точку  . Тогда
. Тогда 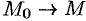 , a
, a 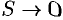 . Перейдя к пределу, получаем:
. Перейдя к пределу, получаем:
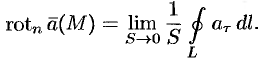
Ротором вектора  в точке
в точке  называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора
называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора  по контуру
по контуру  плоской площадки
плоской площадки  , перпендикулярной этому направлению, к площади этой площадки.
, перпендикулярной этому направлению, к площади этой площадки.
Как видно из определения, ротор вектора 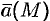 есть векторная величина, образующая собственное векторное поле.
есть векторная величина, образующая собственное векторное поле.
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси 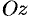 с постоянной угловой скоростью (пример 69.2)
с постоянной угловой скоростью (пример 69.2) 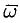 , т. е. ротор вектора
, т. е. ротор вектора 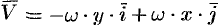 .
.
По определению ротора
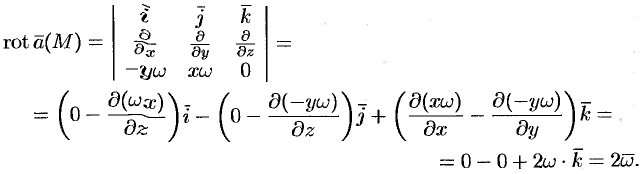
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 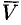 представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке  .
.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline$
Задача 4. Вычислить потенциальную функцию векторного поля
Поток поля через поверхность
Циркуляция векторного поля
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ overline = (3x-1) overline+ (y-x+z)overline+4z overline, $$ $L$ – контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline = xz overline -overline+y overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline = z overline+ (x+y)overline+y overline, quad (p): 2x+y+2z=2. $$
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.
[spoiler title=”источники:”]
http://lfirmal.com/rotor-vektornogo-polya/
http://www.matburo.ru/ex_ma.php?p1=mafield
[/spoiler]
Понятие дивергенции как локального свойства векторного поля было введено при рассмотрении потока векторного поля на замкнутой поверхности. Аналогично можно ввести соответствующую характеристику при рассмотрении циркуляции векторного поля.
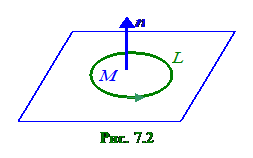 Рассмотрим некоторую точку M и векторное поле a. Выберем некоторое направление, характеризуемое единичным вектором n и плоскость, перпендикулярную к вектору n и проходящую через точку M. Окружим точку M контуром L, лежащим в заданной плоскости. Вычислим циркуляцию векторного поля по этому контуру и возьмем отношение этой циркуляции к площади S, ограниченной контуром L:
Рассмотрим некоторую точку M и векторное поле a. Выберем некоторое направление, характеризуемое единичным вектором n и плоскость, перпендикулярную к вектору n и проходящую через точку M. Окружим точку M контуром L, лежащим в заданной плоскости. Вычислим циркуляцию векторного поля по этому контуру и возьмем отношение этой циркуляции к площади S, ограниченной контуром L:
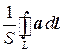
Найдем теперь предел этого отношения при S®0, при условии, что контур L стягивается в точку M, не выходя из плоскости. Этот предел называется ротором векторного поля a в точке M:
 . (7.6)
. (7.6)
Замечание 3. Ротор есть характеристика “вращательной составляющей” векторного поля, поэтому его обозначают как rot. Однако иногда вместо слова ротор используют термин “вихрь” и обозначают символом curl.
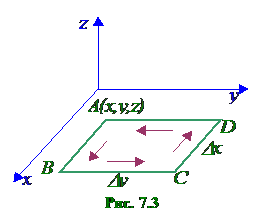 Выведем теперь формулу для ротора в декартовой системе координат. Пусть n совпадает с направлением оси Oz, а контуром L является прямоугольник со сторонами Dx и Dy, при этом контур обходится против часовой стрелки (см. рис. 7.3). Тогда получим
Выведем теперь формулу для ротора в декартовой системе координат. Пусть n совпадает с направлением оси Oz, а контуром L является прямоугольник со сторонами Dx и Dy, при этом контур обходится против часовой стрелки (см. рис. 7.3). Тогда получим
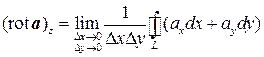 .
.
Для первого слагаемого получаем
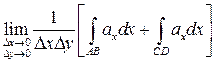
(отрезки DA и BC можно не учитывать, поскольку здесь x=const и dx=0). Далее
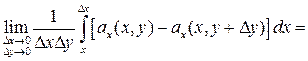
 .
.
Аналогично получаем для второго слагаемого
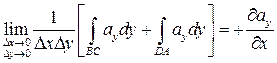 .
.
В результате, находим
 .
.
Аналогично вычисляем проекции на другие оси координат:
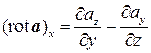 ,
, 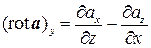 .
.
В векторной форме это можно следующим образом:
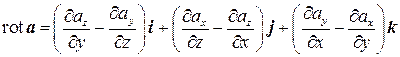 . (7.7)
. (7.7)
Эту формулу можно записать более компактно в символической форме:
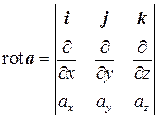 . (7.8)
. (7.8)
Формула (7.7) получается из (7.8) путем разложения определителя по первой строке.
Пример 7.4. Вычислить ротор векторного поля a=x 2 y 3 i+j+zk в точке M(1;1;1).
Решение. Записываем
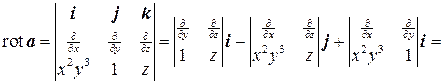
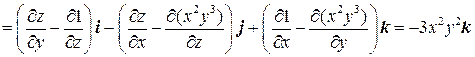 .
.
 .
.
Пример 7.5. Найти ротор поля скоростей вращающего тела v=–wyi+wxj.
 .
.
Итак, ротор скоростей твердого тела в любой его точке равен удвоенной угловой скорости. Найденный механический смысл ротора имеет более широкое значение. Например, колесо с лопастями в потоке жидкости будет иметь максимальную скорость вращения, если ось вращения будет направлена вдоль rota, при этом скорость вращения будет равна 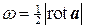 .
.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10573 —  | 7332 —
| 7332 —  или читать все.
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Расчет ротора
Конвертация времени центрифугирования с использованиемk-факторов
Инструкции:
- Выберите ротор для текущего протокола и укажите скорость и продолждительность центрифугирования.
(Для роторов, не указанных в списке используйте пользовательский ротор, и укажите его максимальный и минимальный радиус и максимальную скорость вращения) - Затем, укажите ротор и скорость вращения для нового протокола.
- Используйте кнопку “Рассчитать” для отображения новой продолжительности центрифугирования.
- Для указания десятичных дробей, пожалуйста, используйте точку в качестве разделителя.
(k-факторы будут отображены автоматически.)
© 2000- Beckman Coulte, Inc. Все права защищены.
НЕ ВСЕ ПРОДУКТЫ ДОСТУПНЫ ВО ВСЕХ СТРАНАХ.
ДОСТУПНОСТЬ И РЕГУЛЯТОРНЫЙ СТАТУС ПРОДУКЦИИ ЗАВИСИТ ОТ РЕГИСТРАЦИИ ПРОДУКТА В СООТВЕТСТВИИ С МЕСТНЫМ ЗАКОНОДАТЕЛЬСТВОМ
Указанные регуляторные статусы продукции соответствуют следующему:
IVD: In Vitro Diagnostic. Данная продукция предназначена для клинической диагностики in vitro.
ASR: Analyte Specific Reagents. Специфические аналитические реагенты. Аналитические и технические характеристики не установлены.
CE: Продукция, предназначенная для клинической диагностики in vitro и соответствующая директиве Европейского союза (98/79/EC). (Примечание: Оборудование может соответствовать другим директивам Европейского союза, и иметь соответствующую маркировку.)
RUO: Research Use Only. Данная продукция предназначена только для научных исследований и не предназначена для клинической диагностики in vitro.
LUO: Laboratory Use Only. Продукция предназначены только для лабораторного использования.
Без регуляторного статуса: немедицинские изделия и изделия, не подлежащие обязательной регистрации в регуляторных органах. Данная продукция не предназначена для клинического применения.
Важнейшими характеристиками векторного поля являются ротор и дивергенция. В этом параграфе мы рассмотрим математическое описание этих характеристик векторных поле и методы их вычисления с помощью дифференциальных операций. При этом мы будем использовать только декартову систему координат. Более полное определение дивергенции и ротора и их физический смысл рассмотрим в следующей главе. Вычисление этих величин в криволинейных системах координат рассмотрим позже.
Рассмотрим векторное поле , заданное в трехмерном пространстве.
Определение 1. Дивергенцией векторного поля называется число, которое определяется выражением

При этом предполагается, что соответствующие частные производные существуют в рассматриваемой точке. Дивергенцию векторного поля, так же, как и градиент, можно записать, используя оператор набла

Здесь дивергенция представлена как скалярное произведение векторов и F. Отметим без доказательства, что дивергенция описывает плотность источников, создающих поле .
Пример 1. Вычислить дивергенцию векторного поля в точке .




Определение 2. Ротором векторного поля называется вектор, который определяется выражением

Отметим, что в представленной сумме индексы в соседних слагаемых изменяются согласно правилу круговой перестановки с учетом правила .

Ротор векторного поля можно записать с помощью оператора набла


Ротор характеризует тенденцию к вращению или завихрению векторного поля , поэтому иногда его называют вихрем и обозначают curlF.
Пример 1. Вычислить ротор векторного поля в точке .




Иногда возникает необходимость вычисления градиента векторного поля . В этом случае вычисляется градиент от каждой компоненты векторного поля. В результате получается тензор второго ранга, которым и определяется градиент вектора. Этот тензор можно описать матрицей

Для описания таких объектов удобно использовать тензорные обозначения


полагая . Использование тензорных методов упрощает математические операции над такими объектами. Детальное изложение аппарата тензорного исчисления дается в курсе «Основы тензорного анализа», который читается параллельно курсу «Дополнительные главы высшей математики».

Пример 1. Вычислить градиент векторного поля .
Решение. Для вычислений используем тензорные обозначения. Имеем

Здесь символ Кронекера, — единичная матрица.


Пример 2. Вычислить градиент скалярного поля и сравнить выражения и .

Ранее мы ввели оператор векторного дифференцирования

С помощью этого оператора мы записали основные дифференциальные операции в тензорных полях:



Оператор является обобщением оператора дифференцирования и обладает соответствующими свойствами производной:
1) производная суммы равна сумме производных

2) постоянный множитель можно выносить за знак оператора

В переводе на язык векторных функций эти свойства имеют вид:






Выводятся эти формулы так же, как и соответствующие формулы для производных функции одной переменной.
Использование оператора Гамильтона позволяет упростить многие операции, связанные с дифференцированием в тензорных полях. Однако следует иметь в виду, что этот оператор векторный и с ним надо обращаться аккуратно. Рассмотрим некоторые применения этого оператора. При этом соответствующие формулы записываются как с помощью оператора Гамильтона, так и в обычных обозначениях.









Доказательство этих равенств можно произвести как непосредственным вычислением соответствующих функций, так и с помощью оператора «набла». Рекомендуется самостоятельно проверить справедливость записанных равенств двумя методами.

В качестве примера, показывающего необходимость аккуратного обращения с оператором Гамильтона, вычислим градиент скалярного произведения двух векторных функций . Формально, используя свойства оператора дифференцирования, можно записать


Если считать , , то получим неправильный результат



Ошибка здесь заключается в том, что выражение следует понимать как , т.е. как градиент векторной функции (специального обозначения для этого объекта нет). Правильным будет выражение

где точка означает свертку тензора с вектором (свертка является обобщением понятия скалярного произведения). Более удобной здесь является тензорная форма записи

Здесь по повторяющимся индексам производится суммирование от 1 до 3.
Пусть поле
![]() –
–
дифференцируемое поле (то есть проекции
вектора поля на оси координат являются
дифференцируемыми функциями).
Определение.Вихрем векторного поля![]() (обозначаетсяrot
(обозначаетсяrot![]() )
)
называется вектор, проекция которого
на произвольный вектор![]() определяется как предел отношения
определяется как предел отношения
циркуляции поля![]() по некоторому контуру (L),
по некоторому контуру (L),
содержащему точкуM,
и лежащему в плоскости, перпендикулярной
вектору![]() ,
,
к площади области, ограниченной этим
контуром, при условии, что этот контур
стягивается в точкуM,
а площадь области (S)
стремится к нулю:
 .
.
(1.13)
В трехмерном
пространстве
![]() через декартовы прямоугольные координаты
через декартовы прямоугольные координаты
вектора![]() выражается следующим образом:
выражается следующим образом:
![]() ,
,
(1.14)
или в удобной для
запоминания символической форме
 .
.
(1.15)
Теорема Стокса.Пусть координаты вектора![]() +
+![]()
![]() непрерывны и имеют непрерывные частные
непрерывны и имеют непрерывные частные
производные. Тогда циркуляция векторного
поля![]() по замкнутому контуру (L)
по замкнутому контуру (L)
равна потоку вихрей поля через произвольную
поверхность (S),
натянутую на этот контур:
![]() .
.
(1.16)
Предполагается,
что ориентация контура (L)
и поверхности (S)
согласованы: при положительном обходе
контура нормаль направлена от “ног к
голове”.
Свойства ротора:
1)
![]() ;
;
2)
![]() .
.
Определение.Векторное поле![]() называется безвихревым в данной области
называется безвихревым в данной области
(V), если![]() .
.
Пример 1.Найти
ротор поля вектора напряженности
магнитного поля![]() .
.
Решение. Вектор![]() в координатной форме:
в координатной форме: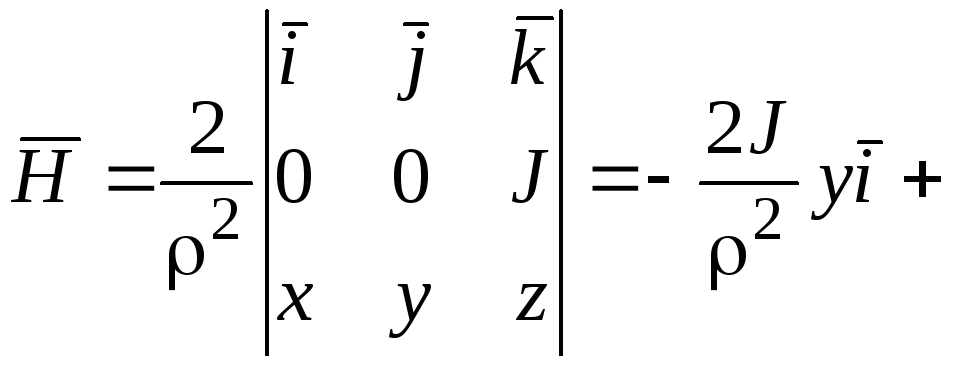
![]()
![]() .
.
Вычислим ротор по формуле (1.15):

+![]() –
–
– поле напряженности
![]() – безвихревое поле.
– безвихревое поле.
Пример 2.Вычислить циркуляцию вектора![]() по контуру
по контуру![]() 1)непосредственно, 2)по теореме Стокса.
1)непосредственно, 2)по теореме Стокса.
Р
Рис.5.
ешение. 1)Контур (L)
– окружность радиуса![]() ,
,
лежащая в плоскостиz=3 (см. рис.5). Выберем ориентацию на ней,
как указано на рисунке. Параметрические
уравнения линии![]()
![]() ,
,
так что![]() ,
,![]() .
.
Для циркуляции вектора![]() имеем:
имеем:![]() .
.
2)Для вычисления циркуляции по теореме
Стокса выберем какую-нибудь поверхность
(S), натянутую на контур
(L).Естественно в
качестве (S) взять
круг, имеющий линию (L)
своей границей. Согласно выбранной
ориентации контура нормаль![]() к кругу необходимо взять равной
к кругу необходимо взять равной![]() .
.
Вычислим ротор: .
.
По теореме Стокса![]()
![]() .
.
Задачи для самостоятельного решения
Найти векторные
линии плоских векторных полей:
1.![]() ;2.
;2.
![]() ;3.
;3.
![]() ;4.
;4.![]() ;
;
5.![]() .
.
Найти векторные
линии:
6.
![]() ;
;
7.
![]() ,
,
где![]() ;
;
8.
![]() ;
;
9.![]() ,
,
![]() ;
;
10.![]() ;
;
11.![]() ;
;
12.![]() ;
;
13.![]() ,
,
где
![]() –постоянные векторы.
–постоянные векторы.
Найти векторные
линии, проходящие через заданную точку:
14.![]() ,
,![]() ;15.
;15.![]() ,
,![]() .
.
Вычислить поток
векторного поля, используя поверхностный
интеграл первого рода:
16.![]() ,
,
(S): верхняя сторона
треугольника, ограниченного плоскостями![]() ,
,![]() .
.
17.
![]() ,
,
(S): внешняя сторона
параболоида![]() ,
,
ограниченного плоскостью![]() ;
;
18.![]() ,
,![]() :
:
боковая поверхность кругового цилиндра![]() ,
,
ограниченного плоскостями![]() ;
;
19.
![]() ,
,
(S): внешняя сторона
части параболоида![]() ,
,
расположенной в первом октанте;
20.![]() ,
,
(S): полная поверхность
конуса![]() ,
,
ограниченного плоскостью![]() ;
;
21.
![]() ,
,
(S): замкнутая поверхность,
ограниченная параболоидом![]() и плоскостьюz= 0;
и плоскостьюz= 0;
22.
![]() ,
,
(S): полная поверхность
пирамиды, ограниченной плоскостями![]() ,
,![]() ,
,![]() ,
,![]() ;
;
23.![]() ,
,
(S): сфера![]() .
.
Вычислить поток,
используя метод проектирования на все
три координатные плоскости.
24.![]() ,
,
(S): верхняя сторона
круга, вырезанного конусом![]() на плоскости
на плоскости![]()
25.![]() ,
,
(S): верхняя сторона
треугольника, полученного пересечением
плоскости![]() с координатными плоскостями;
с координатными плоскостями;
26.
![]() ,
,
(S): часть плоскости![]() ,
,
ограниченная окружностью![]() ,
,
в направлении орта![]() .
.
Определить поток
поля, используя формулу Гаусса-Остроградского:
27.![]() ,
,
(S): произвольная
кусочно гладкая замкнутая поверхность;
28.
![]() ,
,
(S): поверхность куба![]() ,
,![]() ,
,![]() ;
;
29.![]() ,
,
(S): сфера![]() ;
;
30.
![]() ,
,
(S): часть параболоида![]() ,
,
отсекаемая плоскостью![]() ;
;
в отрицательную сторону осиOx;
31.![]() ,
,
(S): поверхность тела![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
32.
![]() ,
,
(S): поверхность тела![]() ,
,![]() ;
;
33.
![]() ,
,
(S):![]() ;
;
34.![]() ;
;
35.
![]() .
.
Найти линейный
интеграл вектора на плоскости:
36.
![]() верхняя половина эллипса
верхняя половина эллипса![]() от точкиA(a,0),
от точкиA(a,0),
до точкиB(-a,0);
37.![]() а) отрезок прямойOB;
а) отрезок прямойOB;
б) дуга параболы![]() ;
;
в) дуга параболы![]() ;
;
г) ломанаяOAB, гдеA(1,0); д) ломанаяOCB,
гдеC(0,1);
38.
![]()
39.![]() от точки (-1, 1) до точки (2, 2).
от точки (-1, 1) до точки (2, 2).
Вычислить линейный
интеграл:
40.![]()
41.![]() ,
,![]() отрезок прямой от точки (1,1,1) до точки
отрезок прямой от точки (1,1,1) до точки
(4,4,4);
42.
![]()
43.![]()
44.
![]() отрезок прямой от точки (0,0,0) до точки
отрезок прямой от точки (0,0,0) до точки
(1,1,1).
45.Дана
напряженность![]() силового поля. Найти работу поля при
силового поля. Найти работу поля при
перемещении массыmвдоль одного витка винтовой линии![]()
![]() ,
,![]() из точки
из точки![]() в точкуB(t=2);
в точкуB(t=2);
46.Силовое поле
образовано силой, равной по величине
расстоянию от начала координат до точки
ее приложения и направленной к началу
координат. Найти работу поля по перемещению
единицы массы вдоль дуги параболы![]() от точки с абсциссой
от точки с абсциссой![]() до точки с абсциссой
до точки с абсциссой![]() .
.
В задачах 47- 51 найти
циркуляцию поля:
47.
![]() в отрицательном направлении;
в отрицательном направлении;
48.
![]() замкнутая
замкнутая
линия, образованная отрезками осей
координатOxиOyи другой астроиды![]() ,
,![]() ,
,
лежащей в первом квадранте;
49.![]()
50.![]()
51.![]() линия пересечения параболоида
линия пересечения параболоида![]() с координатными плоскостями (в первом
с координатными плоскостями (в первом
октанте);
52.Твердое тело
вращается с постоянной угловой скоростью![]() вокруг осиOz. Вычислить
вокруг осиOz. Вычислить
циркуляцию поля линейных скоростей
вдоль окружности радиусаR,
центр которой лежит на оси вращения,
если плоскость окружности перпендикулярна
оси вращения (циркуляция рассматривается
в направлении вращения).
53.Найти работу
поля![]() при перемещении точки единичной массы
при перемещении точки единичной массы
вдоль замкнутой линии, состоящей из
трех прямолинейных отрезков, лежащих
в координатных плоскостях, отсекающих
на осях координат отрезки, равные
единице.
Найти дивергенцию
нижеследующих полей:
54.![]() .
.
При какой функции![]() будет
будет![]() ?
?
55.
![]() ;56.
;56.
![]() – линейная скорость точек вращающейся
– линейная скорость точек вращающейся
жидкости![]() – угловая скорость);
– угловая скорость);
57.![]() напряженность магнитного поля,J,
напряженность магнитного поля,J,![]() – постоянные;
– постоянные;
58.![]() ; 59.
; 59.
 ;
;
60.Вычислить![]() в точке (1,-1,1).
в точке (1,-1,1).
Найти поток
векторного поля через указанные замкнутые
поверхности: 1) непосредственно, 2) по
теореме Гаусса-Остроградского в векторной
формулировке:
61.![]()
62.![]()
63.![]()
64.![]()
![]() ;
;
65.
![]()
66.
![]()
67.
![]()
68.
![]()
69.
![]()
70.
![]()
71.
![]()
72.
![]()
В задачах 73 и 74
вычислить ротор указанных векторных
полей:
73.![]() 74.
74.![]()
75.Показать,
что если координаты вектора![]() имеют непрерывные частные производные
имеют непрерывные частные производные
второго порядка, то![]() .
.
76.Показать,
что если![]() и
и![]() –
–
постоянные векторы, то![]() .
.
77.Показать,
что![]() .
.
78.Показать,
что![]() .
.
79.Показать,
что векторное поле![]() является безвихревым.
является безвихревым.
80.Показать,
что ротор поля линейных скоростей![]() точек вращающегося твердого тела есть
точек вращающегося твердого тела есть
постоянный вектор, направленный
параллельно оси вращения, модуль которого
равен удвоенной угловой скорости
вращения:![]() .
.
81.Какова должна
быть функция![]() ,
,
чтобы ротор векторного поля![]() совпадал с вектором
совпадал с вектором![]() ?
?
Найти циркуляцию
поля по указанным контурам 1)непосредственно,
2)по теореме Стокса в векторной
формулировке:
82.![]()
83.![]()
84.![]() по контуру, образованному пересечением
по контуру, образованному пересечением
плоскости![]() с координатными плоскостями;
с координатными плоскостями;
85.
![]()
86.
![]()
87.
![]()
88.
![]()
89.
![]()
90.
![]()
15.2. Частные случаи
векторных полей. Операции второго
порядка
15.2.1. Потенциальное
векторное поле
Определение.Векторное поле![]() называется потенциальным полем, если
называется потенциальным полем, если
существует некоторая скалярная функция![]() ,
,
градиент которой образует это поле:
![]() .
.
(2.1)
Функция uназывается потенциалом векторного поля![]() .
.
Теорема.Для
того, чтобы поле было потенциальным,
необходимо и достаточно, чтобы оно было
безвихревым:
![]() .
.
(2.2)
Формула (2.2) есть
критерий потенциальности векторного
поля
![]() .
.
Свойства
потенциальных полей.
1)
в области непрерывности потенциала
поля u
линейный интеграл не зависит от пути
интегрирования и равняется приращению
потенциала
![]() (2.3)
(2.3)
2)
циркуляция (1.9) вектора
![]() по любому замкнутому контуру, целиком
по любому замкнутому контуру, целиком
лежащему в области непрерывности поля,
равна нулю:
![]() .
.
(2.4)
3)
потенциал
![]() находится по формуле (2.3):
находится по формуле (2.3):
![]() ,
,
(2.5)
где
(AM)
– произвольная кривая, стягивающая
точки A
и M.
Если путь (AM)
взять в виде ломаной, состоящей из
отрезков, параллельных осям координат
(количество таких ломаных равно шести),
то для нахождения потенциала может быть
применена одна из формул, выражающая
потенциал
![]() через определенные интегралы
через определенные интегралы![]() ;
;![]() ):
):
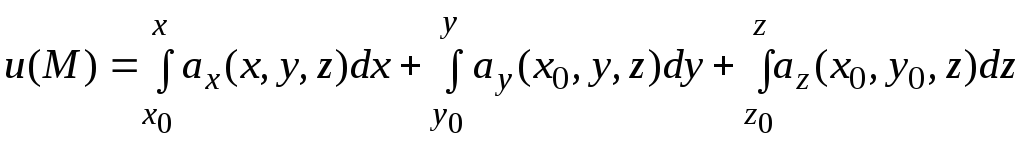 .
.
(2.6)
Пример.
Проверить, что поле вектора
![]() является потенциальным и найти его
является потенциальным и найти его
потенциал.
Решение.
Составим для данного поля критерий
потенциальности (2.2):
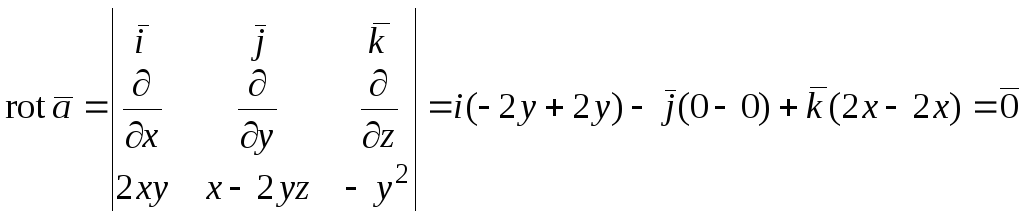
–
поле потенциально. Найдем потенциал
![]() по формуле (2.6): за начальную точку удобно
по формуле (2.6): за начальную точку удобно
взять точкуA(0,0,0):
![]()
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Пример 3:
- Правила вычисления ротора







По этой ссылке вы найдёте полный курс лекций по математике:
Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь
Пример 1. вычислить циркуляцию векторного поля вдоль эллипса L: По определению циркуляции имеем Параметрические уравнения данного эллипса имеют вид: , и, значит, . Подставляя эти выражения в формулу (2), найдем Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора 8.1.
Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.
Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что , и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде: Рассмотрим сначала случай, когда гладкая поверхность Е и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур А соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура А. Для определенности будем считать, что контур L ориентирован так, что поверхность Е остается слева, так что веетор нормали п к поверхности Е составдя етсосью Oz острый угол 7 (cos 7 >0).
Возможно вам будут полезны данные страницы:
Пусть — уравнение поверхности Е и функция ф(х}у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.
Рассмотрим интеграл Линия L лежит на поверхности Е. Поэтому, пользуясь уравнением этой поверхности , мы можем заменить г под знаком интеграла на ^(ж, у). Координаты перемсннойточки кривой А равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по А, Применим к интегралу, стоящему справа, формулу Грина.
Имеем Перейдем теперь от интеграла по области D к интегралу по поверхности Е. Так как dS = cos 7 • da, то из формулы (8) получим, что Вектор нормали п° к поверхности Е определяется выражением к. Отсюда видно, что . Поэтому равенсгво (9) можно переписать так: Считая Е гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул Циркуляция векторного поля.
Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример 3:
Вычислить циркуляцию вектора по линии 1) пользуясь определением; 2) по теореме Стокса. 4 1) Зададим линию L параметрически: Тогда 2) Найдем rota: Натянем на контур L кусок плосхости Тогда . Инвариантное определение ротора поля Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат. Теорема 8.
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4
Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.
Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.
Физический смысл ротора поля Пустьтвердое
тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.
Правила вычисления ротора
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и{М) на векторную а(М) вычисляется по формуле
Лекции:
- Векторное произведение векторов
- Таблица производных полная: для студентов
- Функции двух переменных. Действия над случайными величинами
- Найти значение выражения
- Исследование графика функции
- Нормальное распределение
- Ранг матрицы: примеры решения
- Найдите объем тела ограниченного
- Разложение вектора по базису
- Умножение матрицы на вектор

Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
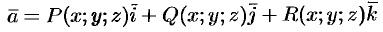
называется вектор, обозначаемый 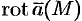 и определяемый формулой
и определяемый формулой
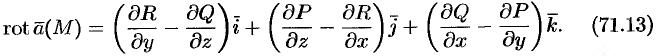
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
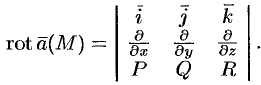
Отметим некоторые свойства ротора.
- Если
 — постоянный вектор, то
— постоянный вектор, то 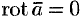 .
. 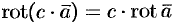 , где
, где 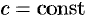 .
.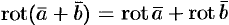 , т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.- Если
 — скалярная функция, а
— скалярная функция, а 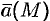 — векторная, то
— векторная, то
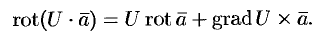
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
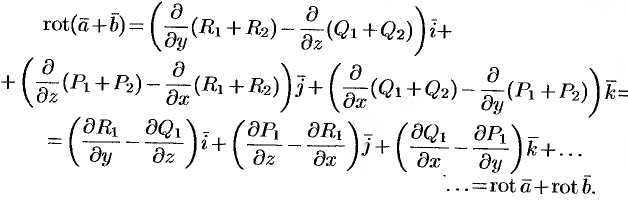
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
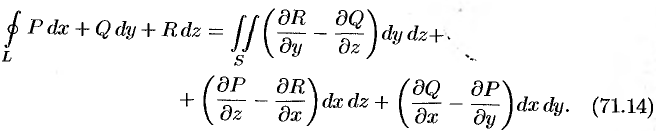
Левая часть формулы (71.14) представляет собой циркуляцию вектора  по контуру
по контуру  , т. е.
, т. е. 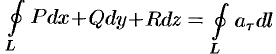 (см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора
(см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора 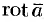 через поверхность
через поверхность  , ограниченную контуром
, ограниченную контуром  (см. (71.3)), т. е.
(см. (71.3)), т. е.
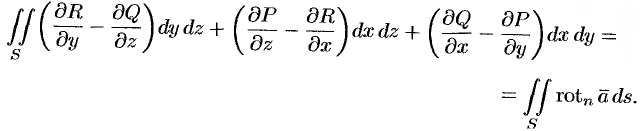

Следовательно, формулу Стокса можно записать в виде
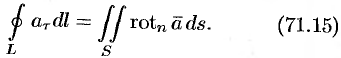
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре  и выбор стороны у поверхности
и выбор стороны у поверхности  согласованы между собой так же, как в теореме Стокса.
согласованы между собой так же, как в теореме Стокса.
Формула (71.15) показывает, что циркуляция вектора  вдоль замкнутого контура
вдоль замкнутого контура  равна потоку ротора этого вектора
равна потоку ротора этого вектора  через поверхность
через поверхность  , лежащую в поле вектора
, лежащую в поле вектора  и ограниченную контуром
и ограниченную контуром  (натянутую на контур) (см. рис. 278).
(натянутую на контур) (см. рис. 278).
Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки  с контуром
с контуром  , содержащей точку
, содержащей точку  .
.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
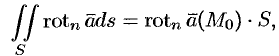
где 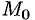 — некоторая (средняя) точка площадки
— некоторая (средняя) точка площадки  (см. рис. 279).
(см. рис. 279).
Тогда формулу (71.15) можно записать в виде

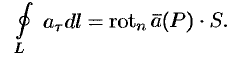
Отсюда:
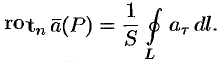
Пусть контур  стягивается в точку
стягивается в точку  . Тогда
. Тогда 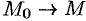 , a
, a 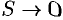 . Перейдя к пределу, получаем:
. Перейдя к пределу, получаем:
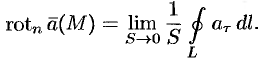
Ротором вектора  в точке
в точке  называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора
называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора  по контуру
по контуру  плоской площадки
плоской площадки  , перпендикулярной этому направлению, к площади этой площадки.
, перпендикулярной этому направлению, к площади этой площадки.
Как видно из определения, ротор вектора 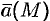 есть векторная величина, образующая собственное векторное поле.
есть векторная величина, образующая собственное векторное поле.
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси 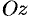 с постоянной угловой скоростью (пример 69.2)
с постоянной угловой скоростью (пример 69.2) 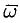 , т. е. ротор вектора
, т. е. ротор вектора 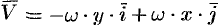 .
.
По определению ротора
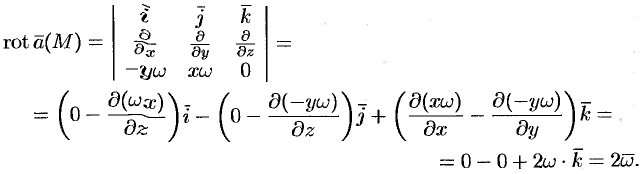
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 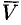 представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке  .
.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:

