Загрузить PDF
Загрузить PDF
Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).
-
1
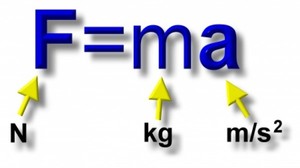
Для вычисления веса используйте формулу
. Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула
.[1]
-
2
Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
-
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с2. В других местах Вселенной эта величина меняется.[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с2 (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).[5]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
-
4
Подставьте значения в формулу
. Теперь, когда вы знаете массу
и ускорение свободного падения
, подставьте их значения в формулу
. Так вы найдете вес тела (измеряется в ньютонах, Н).
Реклама
-
1
Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
-
2
Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
-
3
Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.
Реклама
-
1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
-
2
Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с2), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.
Реклама
Приложение: вес, выраженный в кгс
- Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
Советы
- Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
- Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с2.
- Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
- Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.
Реклама
Предупреждения
- Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».
Реклама
Об этой статье
Эту страницу просматривали 113 683 раза.
Была ли эта статья полезной?
Вес тела. Калькулятор онлайн.
Калькулятор вычисления веса тела, вычислит вес тела, массу, ускорение свободного падения и даст подробное решение.
Калькулятор содержит:
Калькулятор вычисления веса тела, если известны масса тела и ускорение свободного падения.
Калькулятор вычисления массы тела, если известны вес тела и ускорение свободного падения.
Калькулятор вычисления ускорения свободного падения, если известны вес тела и его масса.
В данной таблице приведены значения ускорения свободного падения для планет Солнечной системы и их спутников.
Калькулятор вычисления веса тела, если известны масса тела и ускорение свободного падения.
Вес тела P, которое покоится в инерциальной системе отсчета равен произведению массы m этого тела и ускорения свободного падения g над поверхностью космического тела.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Единицей измерения силы – Ньютон (Н, N)
Масса m =
Ускорение свободного падения g =
Единица измерения веса P
Калькулятор вычисления массы тела, если известны вес тела и ускорение свободного падения.
Масса тела m равна отношению веса P к ускорению свободного падения g над поверхностью космического тела.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Единица массы – килограмм, но также можно использовать и другие единицы, например грамм, тонна, миллиграмм и т.д.
Вес P =
Ускорение свободного падения g =
Единица измерения массы m
Калькулятор вычисления ускорения свободного падения, если известны вес тела и его масса.
Ускорение свободного падения g равно отношению веса тела P к его массе m.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Ускорение свободного падения — это ускорение, которое тело приобретает под действием гравитационной силы около поверхности небесных тел в космическом пространстве.
Единица ускорения – метр в секунду в квадрате.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §28. Вопросы. Номер №4
Решение
Получай решения и ответы с помощью нашего бота
Вес тела равен силе тяжести.
P
=
F
т
я
ж
, если тело и опора неподвижны или движутся равномерно и прямолинейно. Следовательно, вес тела можно определить по формуле
P=gm, где:
m − масса тела,
g − ускорение свободного падения (g= 9,8 Н/кг).
Мы часто употребляем фразы наподобие: «Пачка конфет весит 250 грамм» или «я вешу 52 килограмма». Использование таких предложений происходит автоматический. Но что такое вес? Из чего он складывается и как его посчитать?
Для начала нужно понять, что неправильно говорить: «Этот предмет весит Х килограмм». В физике существует два разных понятия – масса и вес. Масса измеряется в килограммах, граммах, тонах и так далее, а вес тела рассчитывается в ньютонах. Поэтому, когда мы говорим, например, что мы весим 52 килограмма, мы на самом деле имеем в виду массу, а не вес.
Вес в физике
Масса – это мера инертности тела. Чем тело обладает большей инертностью, тем больше времени понадобится, чтобы придать ему скорость. Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;
- унция;
- фунт;
- стоун;
- американская тонна;
- английская тонна;
- грамм;
- миллиграмм и так далее.
Когда мы говорим один, два, три килограмма, мы сравниваем массу с эталонной массой (прообраз которой находится во Франции в МБМВ). Масса обозначается m.
Вес – это сила, которая действует на подвес или опору за счёт предмета, притягиваемого силой тяжести. Это векторная величина, а значит у него есть направление (как и у всех сил), в отличие от массы (скалярная величина). Направление всегда идёт в центр Земли (из-за силы тяжести). Например, если мы сидим на стуле, сиденье которого располагается параллельно Земле, то вектор силы направлен строго вниз. Вес обозначается P и рассчитывается в ньютонах [Н].
Если тело находится в движении или покое, то сила тяжести (Fтяж), действующая на тело, равна весу. Это справедливо, если движение происходит вдоль прямой линии относительно Земли, и оно имеет постоянную скорость. Вес действует на опору, а сила тяжести на само тело (которое располагается на опоре). Это разные величины, и независимо от того, что они равны в большинстве случаев, не стоит их путать.
Сила тяжести – это результат притяжения тела к земле, вес – воздействие тела на опору. Так как тело изгибает (деформирует) опору своим весом, возникает ещё одна сила, она называется сила упругости (Fупр). Третий закон Ньютона гласит, что тела взаимодействуют друг с другом с одинаковыми по модулю силами, но разными по вектору. Из этого следует, что для силы упругости должна быть противоположная сила, и эта она называется – сила реакции опоры и обозначается N.
По модулю |N|=|P|. Но так как эти силы разнонаправленные, то, раскрывая модуль, мы получим N= – P. Именно поэтому вес можно измерить динамометром, который состоит из пружинки и шкалы. Если подвесить груз на это устройство, пружинка растянется до определённой отметки на шкале.
Как измерить вес тела
Второй закон Ньютона гласит, что ускорение равно силе, делённой на массу. Таким образом, F=m*a. Так как Fтяж равна P (если тело находится в покое или движется по прямой (относительно Земли) с одинаковой скоростью), то и Р тела будет равняться произведению массы и ускорения (P=m*a).
Мы знаем, как найти массу, и знаем, что такое вес тела, осталось разобраться с ускорением. Ускорение – это физическая векторная величина, которая обозначает изменение скорости тела за единицу времени. Например, объект движется первую секунду со скоростью 4 м/с, а на второй секунде его скорость увеличивается до 8 м/с, значит, его ускорение равняется 2. По международной системе единиц ускорение рассчитывается в метрах на секунду в квадрате [м/с2].
Если поместить тело в специальную среду, где будет отсутствовать сила сопротивления воздуха – вакуум, и убрать опору, то объект начнёт лететь равноускоренно. Название этого явления — ускорение свободного падения, которое обозначается g и рассчитывается в метрах на секунду в квадрате [м/с2].
Интересно, что ускорение не зависит от массы тела, а значит если мы кинем листок бумажки и гирю на Земле в специальных условиях, при которых отсутствует воздух (вакуум), то эти предметы приземлятся в одно и то же время. Так как листок имеет большую площадь поверхности и относительно маленькую массу, то для того чтобы упасть, ему приходятся сталкиваться с большим сопротивлением воздуха. В вакууме такого не происходит, и поэтому перо, листок бумаги, гиря, пушечное ядро и другие предметы будут лететь с одной и той же скоростью и упадут в одно время (при условии, что они начнут лететь в одно и то же время, и их первоначальная скорость будет равняться нулю).
Так как Земля имеет форму геоида (или по-другому эллипсоида), а не идеального шара, то и ускорение свободного падения в разных участках Земли разное. Например, на экваторе оно равно 9,832 м/с2, а на полюсах 9,780 м/с2. Это происходит потому, что на некоторых участках Земли расстояние до ядра больше, а на некоторых меньше. Чем ближе объект находится к центру, тем сильнее он притягивается. Чем объект дальше, тем сила тяжести меньше. Обычно, в школе округляют это значение до 10, это делается для удобства расчётов. Если же необходимо измерить более точно (в инженерном или военном деле и так далее), то берут конкретные значения.
Таким образом, формула для расчёта веса телу будет выглядеть следующим образом P=m*g.
Примеры задач для расчёта веса тела
Первая задача. На стол положили груз массой 2 килограмма. Каков вес груза?
Для решения этой задачи нам понадобится формула по расчёту веса P=m*g. Мы знаем массу тела, а ускорение свободного падения примерно составляет 9,8 м/с2. Подставляем эти данные в формулу и получим P=2*9,8=19,6 Н. Ответ: 19,6 Н.
Вторая задача. На стол положили парафиновый шарик, объёмом 0,1 м3. Каков вес шарика?
Эту задачу необходимо решать в следующей последовательности;
- Для начала нам надо вспомнить формулу веса P=m*g. Ускорение нам известно – 9,8 м/с2. Осталось найти массу.
- Масса рассчитывается по формуле m=p*V, где p – это плотность, а V – объём. Плотность парафина можно посмотреть в таблице, объём нам известен.
- Необходимо подставить значения в формулу, для нахождения массы. m=900*0,1=90 кг.
- Теперь подставляем значения в первую формулу, для нахождения веса. P=90*9,9=882 Н.
Ответ: 882 Н.
Видео
В этом видео уроке разбирается тема – сила тяжести и вес тела.
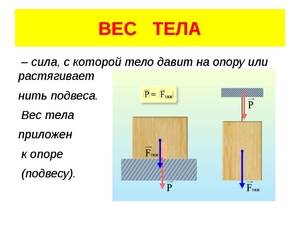
Определение Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.
Вес тела имеет электромагнитную природу (не путать с силой тяжести — она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.
Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:
P = T; P = N; P = Fупр.
Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:
P0 = Fтяж = mg
Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.
Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:
P = mg = 16,38∙10 = 163,8 (Н)
История понятия
Понятия тяжести и лёгкости в качестве неотъемлемых свойств физических тел упоминаются ещё древнегреческими философами. Платон описывал вес как естественную тенденцию предметов к поиску себе подобных. Для Аристотеля лёгкость была свойством в восстановлении порядка основных элементов: воздуха, земли, огня и воды. Архимед рассматривал вес как качество, противоположное плавучести. Первое контактное определение было дано Евклидом, описывающее величину как лёгкость одной вещи по сравнению с другой, измеряемую балансом.
Когда средневековые учёные обнаружили, что на практике скорость падающего предмета со временем возрастала. Они изменили концепцию веса для сохранения причинно-следственных связей между явлениями. Понятие было разделено для тел в состоянии покоя и находящихся в гравитационном падении.
Значительных результатов в теории добился Галилей, пришедший к выводу, что величина пропорциональна количеству вещества в объекте, а не скорости его движения, как предполагала Аристотелева физика. Открытие Ньютоном закона всемирного тяготения привело к принципиальному отделению веса от фундаментального свойства объектов, связанных с инерцией. Факторы окружающей среды и плавучесть учёный считал искажением условий измерения. Для подобных обстоятельств он ввёл термин кажущийся вес.
В XX веке ньютоновские концепции абсолютного времени и пространства были поставлены под сомнение работами Эйнштейна. Теория относительности поставила всех наблюдателей, движущихся и ускоряющихся, в разные условия. Это привело к двусмысленности относительно того, что именно подразумевается под массой, которая вместе с гравитационной силой стала по существу зависящей от системы отсчёта величиной.
Неоднозначности, порождённые относительностью, привели к серьёзным дебатам в педагогическом сообществе о том, как определять вес для учеников и что им должно называться. Выбор стал лежать между пониманием его как силы, вызванной гравитацией Земли, и контактным определением, вытекающим из акта взвешивания.
Единицы измерения веса в других системах единиц
Иногда в физике применяют систему единиц, называемую СГС (сантиметр, грамм, секунда). В этой системе единица длины – сантиметр (см), единица массы – грамм (г), единица времени секунда (с). В системе СГС единицу веса, как и любой силы, называют дина (обозначение: дин). 1 дин – это сила, которая сообщает телу массой 1 г ускорение, равное 1$frac<�см><�с^2>$. Дина в сравнении с ньютоном очень маленькая единица силы. Ньютон и дина соотносятся как:
При технических расчетах можно встретить еще одну единицу измерения веса, которую называют килограмм – сила (кгс). 1 кгс – это сила, с которой Земля действует на эталонную массу в один килограмм, притягивая ее.
[1Нapprox 0,10197162 кгс.]
В России килограмм-силу используют как внесистемную единицу измерения силы.
Получаем, дин, кгс – единицы измерения веса.
Различия с массой
Путаница в понимании того, чем отличается масса от веса, свойственна для людей, не изучающих физику подробно. Этому есть простое объяснение — как правило, эти термины используются в повседневной жизни взаимозаменяемо. В общем случае, если тело находится на поверхности земли и неподвижно, значение массы будет равно скаляру веса в килограммах. Таблица, проясняющая разницу между понятиями, выглядит так:
| Масса | Вес |
| Является свойством материи. Постоянна всегда. | Зависит от действия силы тяжести. |
| У материального объекта никогда не бывает равна нулю. | Может быть равен нулю при определённых условиях. |
| Не меняется в зависимости от местоположения. | Уменьшается или увеличивается в разных местах Земли или в зависимости от высоты над её поверхностью. |
| Является скалярной величиной. | Вектор с направлением к центру земли или к другому гравитационному центру. |
| Может быть измерена с помощью баланса | Измеряется с помощью пружинных весов. |
| Как правило, измеряется в граммах и килограммах. | Единица у силы и веса одна — Ньютон (обозначается как Н) |
Главное отличительное свойство массы заключается в том, что для классической динамики она является конкретной инвариантной величиной для каждого тела. Общая теория относительности описывает переход массы в энергию и наоборот.
Обычно численное значение между m и P на Земле строго пропорционально. На бытовом уровне чтобы узнать вес тела с известной массой, достаточно помнить, что объекты обычно весят в ньютонах приблизительно в 10 раз больше значения m в килограммах.
Вес в физике
Масса – это мера инертности тела. Чем тело обладает большей инертностью, тем больше времени понадобится, чтобы придать ему скорость. Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;
- унция;
- фунт;
- стоун;
- американская тонна;
- английская тонна;
- грамм;
- миллиграмм и так далее.
Когда мы говорим один, два, три килограмма, мы сравниваем массу с эталонной массой (прообраз которой находится во Франции в МБМВ). Масса обозначается m.
Способы измерения
Фактически вес можно измерить как силу реакции опоры на массу, появляющуюся в точке приложения. Величина возникновения этой силы по значению равна искомому P. Определить её можно с помощью пружинных весов. Поскольку сила тяжести, вызывающая фиксируемое отклонение на шкале, может варьироваться в разных местах, значения также будут отличаться. Для стандартизации измерительные приборы такого типа всегда калибруются на 9,80665 м/с2 в заводских условиях, а затем повторно в том месте, где будут использоваться.
Для измерения массы применяют рычажный механизм. Поскольку любые изменения в гравитации будут одинаково воздействовать на известные и неизвестные массы, балансный способ позволяет иметь в результате одинаковые значения в любом месте Земли. Весовые коэффициенты в этом случае калибруются и маркируются в единицах массы, поэтому балансировочный рычаг позволяет найти массу, сравнивая воздействие притяжения на искомый объект с воздействием на эталон.
При отсутствии гравитационного поля вдали от крупных астрономических тел, баланс рычага работать не будет, но, например, на Луне он покажет те же значения, что и на Земле. Некоторые подобные инструменты могут быть размечены в единицах веса, но, поскольку они калибруются на заводе-изготовителе для стандартной гравитации, то будут показывать P для условий, под которые они настроены.
Это значит, что рычажные весы не предназначены для измерения локальной силы тяжести, воздействующей на объект. Точный вес можно определить расчётным путём, умножив массу на значение локальной гравитации из соответствующих таблиц.
Ньютон – единица измерения веса в Международной системе единиц
В настоящее время в физике в большем масштабе, чем остальные, используют Международную систему единиц (СИ) в которой ньютон – единица измерения веса, как разновидности силы. Один ньютон (1Н) – это сила, сообщающая телу, имеющему массу в 1 килограмм, ускорение равное 1 метру, деленному на секунду в квадрате в направлении действия силы:
Ньютон не является основной единицей в СИ. С такой единицей как ньютон используют кратные и дольные единицы силы, применяя стандартные приставки системы СИ, например: $1кН=<10>^3Н;; 1нН=<10>^<-9>Н;; 1МН=<10>^6Н.$
И так, ньютон и $frac<�кгcdot м><�с^2>.$ – единицы измерения веса, как силы в системе СИ.
На других планетах
В отличие от массы, вес тела в разных местах варьируется в зависимости от изменения значения гравитационного ускорения. Величина силы притяжения на других планетах, как и на Земле, зависит не только от их массы, но и от того, насколько удалена поверхность от центра тяжести.
В таблице ниже приведены сравнительные гравитационные ускорения на других планетах, Солнце и Луне. Под поверхностью для газовых гигантов (Юпитер, Сатурн, Уран и Нептун) подразумеваются их внешние облачные слои, для Солнца — фотосфера. Значения в таблице указаны без учёта центробежного вращения и отражают фактическую гравитацию, наблюдаемую вблизи полюсов.
| Астрономический объект | Насколько гравитация превышает земную | Поверхностное ускорение м/с2 |
| Солнце | 27,9 | 274,1 |
| Меркурий | 0,377 | 3,703 |
| Венера | 0,9032 | 8,872 |
| Земной шар | 1 | 9,8226 |
| Луна | 0,1655 | 1,625 |
| Марс | 0,3895 | 3,728 |
| Юпитер | 2,64 | 25,93 |
| Сатурн | 1,139 | 11,19 |
| Уран | 0,917 | 9,01 |
| Нептун | 1,148 | 11,28 |
Для того чтобы получить собственный вес на другой планете, необходимо просто умножить его на число кратности из соответствующего столбика. Чем ближе к центру планеты делать замер, тем значение будет выше, и наоборот. Поэтому, несмотря на то что сила притяжения Юпитера из-за огромной массы в 316 раз превышает земную, вес на уровне облаков, из-за большой их удалённости от центра масс, выглядит не таким впечатляющим, как можно было бы ожидать.
Ещё один интересный эффект, называемый невесомостью, характерный не только для космоса. Его можно наблюдать при различных обстоятельствах и на Земле. Например, при свободном падении нет опоры, к которой была бы приложена сила, а значит вес будет равен нулю, несмотря на присутствие ускорения силы тяжести и массы.
Подобный феномен происходит с космонавтами Международной космической станции на орбите Земли. Фактически она всегда падает вместе со своими обитателями на поверхность планеты, поэтому её обитатели постоянно находятся в состоянии невесомости.
Таким образом, главное правило, объясняющее наблюдаемые феномены и позволяющее избежать путаницы с массой, выглядит так: значение P всегда измеряется с помощью контактных весов, помещённых между объектом и опорной поверхностью. Именно поэтому тело, размещённое на весах и падающее вместе с ними, не будет давить на прибор, а шкала, соответственно, покажет нулевое значение.
Примеры задач для расчёта веса тела
Первая задача. На стол положили груз массой 2 килограмма. Каков вес груза?
Для решения этой задачи нам понадобится формула по расчёту веса P=m*g. Мы знаем массу тела, а ускорение свободного падения примерно составляет 9,8 м/с 2 . Подставляем эти данные в формулу и получим P=2*9,8=19,6 Н. Ответ: 19,6 Н.
Вторая задача. На стол положили парафиновый шарик, объёмом 0,1 м 3 . Каков вес шарика?
Эту задачу необходимо решать в следующей последовательности;
- Для начала нам надо вспомнить формулу веса P=m*g. Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу.
- Масса рассчитывается по формуле m=p*V, где p – это плотность, а V – объём. Плотность парафина можно посмотреть в таблице, объём нам известен.
- Необходимо подставить значения в формулу, для нахождения массы. m=900*0,1=90 кг.
- Теперь подставляем значения в первую формулу, для нахождения веса. P=90*9,9=882 Н.
Явление гравитации
Чтобы понять, что в физике означает g (в 7 классе общеобразовательных школ проходят эту тему), следует познакомиться с явлением гравитации. В конце XVII века Исаак Ньютон опубликовал свой знаменитый научный труд, в котором сформулировал основные положения механики. В этом труде особое место он выделил для так называемого закона Всемирного тяготения. Согласно нему все тела, которые обладают конечной массой, притягиваются друг к другу независимо от расстояния между ними. Сила притяжения между телами с массами m1, m2 вычисляется по следующей формуле:
F = G*m1*m2/r2.
Здесь G — универсальная гравитационная константа, r — расстояние между центрами масс тел в пространстве. Сила F называется гравитационным взаимодействием, которое, как и кулоновское, убывает с квадратом расстояния, однако в отличие от кулоновского гравитация носит только притягивающий характер.
Наше время
Сейчас люди практически не видят разницу массы и веса. Типичным примером этого является любая покупка в магазине, когда покупатель спрашивает у продавца информацию о весе продукта. С точки зрения науки, правильно было бы поинтересоваться его массой. Тем не менее на упаковках производитель указывает все как нужно.
Мы можем увидеть там такие надписи, как «масса нетто» (то есть масса чистого продукта) и «масса брутто» (масса продукта вместе с упаковкой). В результате этого масса и вес стали практически синонимами в потребительской сфере, и большинство людей искренне удивляются, когда кто-то пытается им доказать, что есть разница в массе и весе.
В настоящее время нет особых требований в том, чтобы каждый человек умел различать данные понятия. Скорее, это больше необходимо тем, кто занимается научной деятельностью.
Источник
Рассчитать вес по росту
Простой способ известный больше как формула Брокка. Упрощенная версия выглядит так:
- Для женщин: Идеальный вес = Рост (см) — 110
- Для мужчин: Идеальный вес = Рост (см) — 100
Пример: нормальный вес мужчины с ростом 180 см равен 80 кг, а женщины с ростом 170 см – 60 кг
Современный вариант этой же формулы выглядит немного иначе, но считается более точным:
- Для женщин: Идеальный вес = (Рост (см) — 110)*1,15
- Для мужчин: Идеальный вес = (Рост (см) — 100)*1,15
Пример: нормальный вес мужчины с ростом 180 см равен 92 кг, а женщины с ростом 170 см – 69 кг