Как найти свойства квадратного корень 8 класс

Здравствуйте, читатели. В этой статье рассмотрим свойства арифметического квадратного корня и примеры решений из ОГЭ задания №8 для каждого из свойств.

Все свойства представим в виде таблица и распределим для каждого задания, которые встречаются на ФИПИ. Вам остается только по аналогии натренироваться в решении. Только тренировка приведет к результату.

Свойство №1. Квадратный корень из произведения

1) Что бы раскрыть скобку, нужно число, стоящее за скобкой, умножить на каждое число, стоящее в скобке.

2) Числа стоящие перед корнем, перемножаются отдельно, а числа стоящие под корнем, вносятся под единый корень.

3) Если числа из-под корня не извлекаются, то необходимо разложить числа. Старайтесь раскладывать так, чтобы какой-либо множитель можно было вынести из-под корня.

Свойство №2. Квадратный корень из дроби

Рассмотрим примеры.

Редко, когда в выражении применяется только одно свойство. Ниже приведу решение, где нужно применить свойство квадратного корня из произведения и из дроби.

В числителе применено свойство квадратного корня из произведения.

В следующем примере помимо свойств квадратного корня, применено свойство деления степеней с одинаковым основанием. Напомню его: при делении степеней с одинаковым основанием, основание остается прежним, показатели степени вычитаются.

Свойство №3

Рассмотрим решение следующего выражения:

Часто встречаются задания, в которых нужно применять формулы сокращенного умножения.

Зеленым цветом выделены противоположные числа, сумма которых равна нулю.

Свойство №4. Квадратный корень из степени

Приведу решение нескольких выражений:

Задание №1

Задание №2

Задание №3 (дополнение от 16.10.2022)

а) Найти значение выражения:

Воспользуемся формулой сокращенного умножения:

Решение:

б) Найти значение выражения:

Задание №4 Найдите значение выражения:

Задание №5 Найдите значение выражения:

Если вам было что-то не понятно, вы всегда можете задать уточняющий вопрос в комментариях.

Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Все что было представлено выше, вы можете посмотреть в видео

Арифметический квадратный корень и его свойства

Арифметическим квадратным корнем из числа a называют такое неотрицательное число b (b ≥ 0), вторая степень которого равна a.

Запишем это определение на математическом языке:

Убедимся в правильности данной записи на примере. Пусть а = 16, b = 4, тогда

Всё верно: если 4 в квадрате равно 16, значит корень из 16 равен 4.

Извлечем парочку корней:

√0 = 0;

√1 = 1;

√4 = 2;

√256 = 16 и т.д.

Обратите внимание, что подкоренное выражение неотрицательно! Извлечение корней из отрицательных чисел – это уже совсем другая история и в школьной математике не рассматривается.

Свойства арифметического квадратного корня (далее корень).

1. Корень произведения равен произведению корней (а ≥ 0, b ≥ 0).

 Примеры:

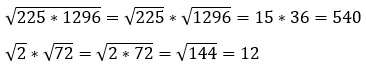
2. Корень частного равен частному корней (а ≥ 0, b > 0).

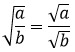
Примеры:

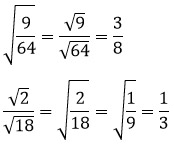
3. Корень в квадрате равен подкоренному выражению (а ≥ 0).

Примеры:

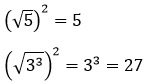
4. Корень из квадрата числа равен модулю этого числа (а – любое).

Примеры:

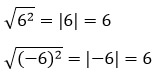
5. Корень из степени с основанием а и показателем n равен корню из числа а в степени n (а ≥ 0, n – натуральное). 

Пример:

Свойство работает в обе стороны.

6. Квадратный корень числа в четной степени равен этому числу в степени, деленной на 2.

Пример:

Вынесение множителя за знак корня.

Рассмотрим вынесение множителя на примере: возьмем число √12.

Число 12 можно разложить на два множителя – 3 и 4; один из них извлекается. Значит, из-под корня выносится двойка (корень из 4), а под корнем остается 3.

То же самое запишу на математическом языке:

Возьмем число побольше: √845.

Очевидно, что подкоренное выражение делится на 5, т.е. один из множителей равен 5, тогда второй равен 169 (169 · 5 = 845). Корень из 169 извлекается, значит из-под корня выносится множитель 13, а под корнем остается 5.

И возьмем число √28800.

Оно делится на 100, значит его можно представить в виде произведения чисел 100 и 288. Но 288 тоже можно разложить на произведение чисел 144 и 2. Это значит, что под корнем остается число 2, а выносятся сразу два множителя – 10 и 12, которые в дальнейшем нужно перемножить.

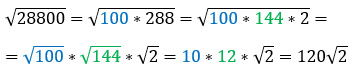
Еще есть второй способ – он короче. Здесь важно заметить, что 28800 – это произведение 14400 и 2. Результат не меняется.

Внесение множителя под знак корня.

Как в случае с вынесением рассмотрим внесение множителя под знак корня на примерах.

Возьмем число 2√3. Для внесения необходимо множитель перед корнем возвести в квадрат и умножить на подкоренное выражение. Получившееся число записываем под корнем. 

Специально взяла пример из раздела “Вынесение множителя за знак корня” для того, чтобы вы убедились в правильности данного решения. Второй этап решения (произведение корней √2² и √3), кстати говоря, всегда пропускают.

Следующий пример: 5√7.

Пятерку возводим в квадрат и умножаем на 7. Результат записываем под знаком “корня”.

Успехов в учебе!

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  «Свойства квадратных корней».
  П.2.6 стр.93
  √

• 

  2 слайд

  Девиз урока:
  8 класс
  «Дорогу
  осилит идущий,
  а математику – мыслящий».

• 

  3 слайд

  Задание: проверьте, верны ли данные равенства и ответьте на вопрос «почему?»

  = 4;
  = 9;
  = 3;

  = 3;
  = 0;
  = 5.

• 

  4 слайд

  21.06.2022
  4
  Цель урока: способствовать организации продуктивной деятельности учащихся, направленной на достижение ими следующих результатов:
  предметные:
  понимание сути основных свойств квадратного корня;
  понимание смысла формулировок и умение формулировать основные свойства квадратного корня;
  овладение навыками вычисления выражений, содержащих знак квадратного корня, упрощение такого рода выражений; нахождение рациональных путей решения;
  овладение опытом творческой деятельности при решении заданий на нахождение выражений через использование формул сокращённого умножения (формулы разности квадратов);
  понимать смысл математических терминов « квадратный корень из произведения», «квадратный корень из дроби», «вычисление корней» и умение правильно употреблять их в устной и письменной речи;

• 

  5 слайд

  Образовательные
  Закрепить и систематизировать знания учащихся по теме «Свойства арифметического квадратного корня»

  Сформировать умение применять их для преобразования выражений, содержащих квадратные корни

  Научить вычислять значения квадратных корней

• 

  6 слайд

  21.06.2022
  6
  метапредметные:
  в познавательной деятельности:
  определять структуру объекта познания, выполнять поиск и выделять значимые функциональные связи и отношения между частями целого;
  уметь разделять процессы на этапы, шаги;
  выделять соответствующие причинно-следственные связи;
  сравнение, сопоставление, классификация, ранжирование объектов по одному или нескольким предложенным основаниям, критериям;
  исследование несложных практических ситуаций, выдвижение предложений, понимание необходимости их проверки на практике.
  в информационно-коммуникативной деятельности:
  умения формулировать вопросы, задачи;
  умение разделять процессы на этапы, звенья;
  умение перефразировать мысль (объяснить иными словами)
  умение вступать в речевое общение, участвовать в диалоге (понимать точку зрения собеседника, признавать право на иное мнение);
  умение выдвигать гипотезу и аргументировано доказывать её;
  умение отражать в устной или письменной форме результаты своей деятельности;
  в рефлексивной деятельности:
  самостоятельно организовать учебную деятельность (постановка цели, планирование, определение оптимального соотношения цели и средств);
  осуществлять поиск и устранять причины возникших трудностей в ходе решения задач;
  овладеть умением совместной деятельности, направленным на сотрудничество;
  объективное оценивание своей деятельности на уроке;
  Объективное оценивание своей деятельности на уроке

• 

  7 слайд

  21.06.2022
  7
  личностные
  получать удовольствие от уроков математики;
  умение читать и учиться самостоятельно
  выражать свои мысли в письменной форме
  овладеть умение хорошо говорить и легко выражать свои мысли;
  уверенно и легко выполнять математические операции;
  умение вступать в речевое общение, участвовать в диалоге;
  овладеть умением применять полученные знания в нестандартных ситуациях;
  формирование характера и личности.

• 

  8 слайд

  Вопрос:
  Что называется квадратным корнем ?
  Как обозначается арифметический квадратный корень из числа а?

  Как читается выражение
  При каких значениях а оно имеет смысл?

• 

• 

  10 слайд

  Изучение нового материала
  1. Найдите значение выражения
  Вывод:
  Если а ≥ 0, b ≥ 0, то
  Корень из произведения неотрицательных множителей равен произведению корней из этих множителей

• 

  11 слайд

  21.06.2022
  11
  Работаем с учебником стр.93

• 

  12 слайд

  Решите самостоятельно
  Если а ≥ 0, b ≥ 0, то

• 

  13 слайд

  Вывод:
  2. Найдите значение выражения
  Если а ≥ 0, b > 0, то
  Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя

• 

  14 слайд

  21.06.2022
  14
  Работаем с учебником стр.94.

• 

  15 слайд

  Если а ≥ 0, b > 0, то
  Решите самостоятельно

• 

• 

  17 слайд

  Математика настолько серьезный предмет, что полезно не упускать случая сделать его немного занимательным.
  Б. Паскаль

• 

  18 слайд

  Составь карточку – памятку из фрагментов формул левой и правой части и условий при которых эти равенства верны.

• 

  19 слайд

  Карточка – памятка «Свойства арифметического квадратного корня».

• 

  20 слайд

  21.06.2022
  20
  3
  6
  0,2

• 

  21 слайд

  21.06.2022
  21
  =
  =
  =
  =
  3
  =
  =
  =
  0,2
  = 6
  =3

• 

  22 слайд

  Вычислите
  Вычислите

• 

  23 слайд

  21.06.2022
  23
  Работаем с учебником стр.94

• 

• 

  25 слайд

  Какие свойства арифметического квадратного корня
  вы сегодня узнали?
  Вопрос ?

• 

  26 слайд

  Корень из произведения неотрицательных множителей равен произведению корней из этих множителей:
  √ а·в = √ а ·√ в, где а≥0, в≥0

  Пример: √144·25=√ 144 · √ 25 = 12·5 = 60

  Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя

  √а/в= √а/√в , где а≥0, в>0

  Пример: √ 36/169 = √ 36/√ 169 = 6/13

• 

• 

• 

• 

  30 слайд

  Закончите предложения.
  Арифметическим квадратным корнем из числа а, называется
  неотрицательное число, квадрат которого равен а.
  Знак √ называется
  радикал
  Корень из произведения неотрицательных множителей равен
  произведению корней из этих множителей.
  Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен
  корню из числителя, деленному на корень из знаменателя.

• 

  31 слайд

  Вариант 1
  Вариант 2
  Самостоятельная работа
  2.Решите уравнение

• 

• 

  33 слайд

  К математике способность проявляйте,
  Не ленитесь, а ежедневно развивайтесь.
  Умножайте, делите, трудитесь, соображайте,
  С математикой дружить не забывайте.

  Пожелание

• 

  34 слайд

  п.2.6 стр.93-95 ,фрагмент 1,2,3
  свойства учить
  №318(б, г),
  №319(в, г),
  №320(б, г),
  №321(г, д, е),
  №323(г, д)

  Домашнее задание:

• 

  35 слайд

  Теорема.
  При любом значении х верно
  равенство √ х² =|х|

  Пример: √ (1,7)²=|1,7|= 1,7
  √ (-19)²=|-19|=19
  √ а²=|а|=а, если а≥0 ;
  √ в²=|в|= -в , если в<0

  Квадратный корень из степени

• 

  36 слайд

  1. Докажите, что верно равенство: =
  Творческие задания
  –
  2.Упростите выражения:
  =
  +
  5

  а) у
  , где у
  0,
  , где а < 0,
  б)7а
  , где а > 0,
  в)

  г)

• 

  37 слайд

  21.06.2022
  37
  Преобразовать

  при х < 0

• 

  38 слайд

  Интеллектуальная разминка
  Знание – самое превосходное из владений. Все стремятся к нему, само оно не приходит

  Творческие задания

• 

  39 слайд

  Урок окончен.
  Спасибо
  за работу.

• 

  40 слайд

  1) √16 = 4

  2) √25 = -5

  3) √8 = 3

  4) √-9 = -3

  5) √ 9 = 3

  6) √64 = 4

  Верны ли данные равенства?
  Почему?

• 

  41 слайд

  Вариант 1
  Вариант 2
  Самостоятельная работа
  2.Решите уравнение
  3. Упростите выражение

• 

  42 слайд

  Физкультминутка
  Вы на славу потрудились,
  И немного утомились,
  Дружно стать нам всем пора:
  Начинается игра!

• 

• 

  44 слайд

  21.06.2022
  44
  Корень из дроби, числитель
  которой неотрицателен,
  а знаменатель положителен,
  равен корню из числителя,
  деленному на корень из знаменателя

• 

  45 слайд

  21.06.2022
  45
  Корень из произведения
  неотрицательных
  множителей равен
  произведению корней из
  этих множителей

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 263 105 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»

• Курс профессиональной переподготовки «Организация логистической деятельности на транспорте»

• Курс повышения квалификации «Введение в сетевые технологии»

• Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»

• Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»

• Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»

Свойства арифметического квадратного корня

1 октября 2020

• Домашняя работа

0. Кратная вводная

Перед любыми манипуляциями с корнями полезно вспомнить свойства степеней с натуральным показателем. Я группирую эти свойства в три блока.

1. Умножаем и делим степени с одинаковым основанием — меняется только показатель:

[begin{align} & {{a}^{x}}cdot {{a}^{y}}={{a}^{x+y}} \ & frac{{{a}^{x}}}{{{a}^{y}}}={{a}^{x-y}} \ & {{left( {{a}^{x}} right)}^{y}}={{a}^{xcdot y}} \ end{align}]

2. Умножаем и делим степени с одинаковым показателем — меняется основание:

[begin{align} & {{left( acdot b right)}^{x}}={{a}^{x}}cdot {{b}^{x}} \ & {{left( frac{a}{b} right)}^{x}}=frac{{{a}^{x}}}{{{b}^{x}}} \ end{align}]

3. Чётные степени «сжигают» минусы, нечётные — нет:

[begin{align} & {{left( -a right)}^{2n}}={{a}^{2n}} \ & {{left( -a right)}^{2n+1}}=-left( {{a}^{2n+1}} right) \ end{align}]

Мы будем использовать эти свойства на всю катушку в третьей части урока. А пока начнём с более простых вещей.

1. Корни из точных степеней

При работе с корнями многие ученики допускают одну и ту же ошибку. Они пытаются подменить чёткие правила алгебры интуитивными размышлениями. И на первый взгляд всё выглядит хорошо. Взгляните на примеры:

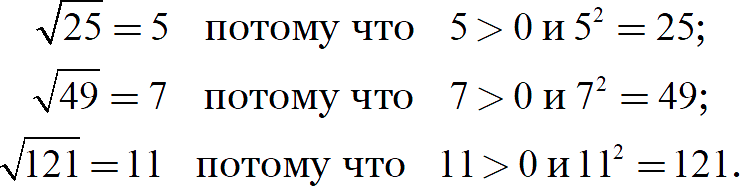
Во всех трёх случаях мы видим, что под корнем стоят точные квадраты. Их можно переписать так:

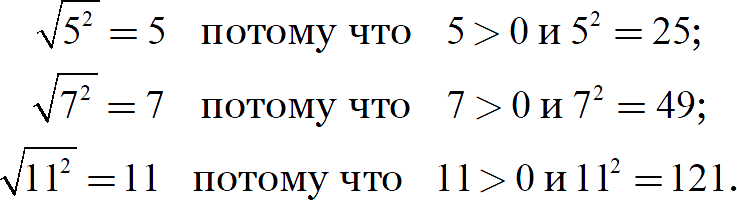
Может показаться, что для упрощения выражения достаточно убрать степень и знак корня. На практике это не так:

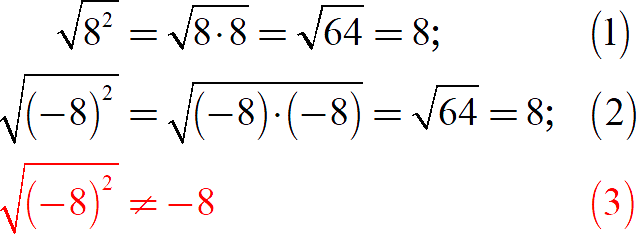
Из третьей строки видно, что просто убрать степень и корень с отрицательного основания нельзя, ведь корень не может быть отрицательным! Вторая строка объясняет нам, что именно происходит: квадрат делает число под корнем положительным, а дальше мы извлекаем этот самый корень и вновь получаем положительное число. В итоге строки 1 и 2 ведут к извлечению корня из одного и того же числа — 64.

Вывод?

1.1. Корень из точного квадрата

А вывод такой: корень из квадрата не меняет положительные числа, а отрицательные меняет на противоположные. Это в точности совпадает с определением модуля:

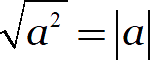
Для удобства дальнейших размышлений предлагаю взять на вооружение вот такое определение модуля:

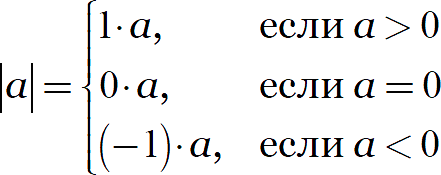
Это определение чрезвычайно полезно для решения сложных задач с параметрами. Об этом как-нибудь в следующий раз. А пока давайте потренируемся:

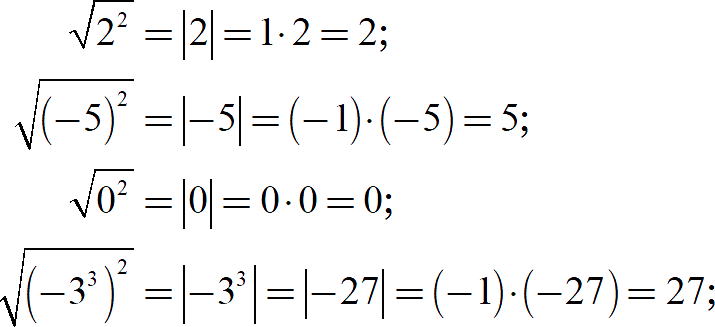
Опыт моих учеников: поначалу довольно непривычно выписывать эти множители (1, 0 и −1), но затем человек привыкает и пишет всё на автомате. А затем и вовсе перестаёт писать — всё происходит в его голове, но навык добавления множителей остаётся (и очень пригодится, когда мы считаем коэффициенты многочленов).

Потренируйтесь самостоятельно:

Задание. Найдите значение выражения:

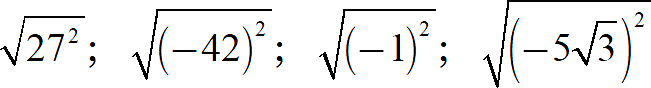
[Показать ответы]

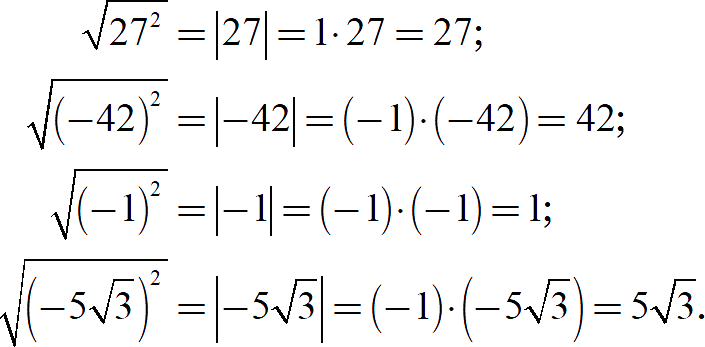
Отдельное внимания заслуживают двойные корни, вложенные друг в друга:

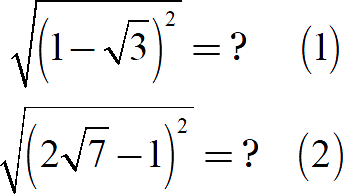
Для них замена корня модулем тоже работает, но возникает вопрос: как корректно раскрыть модуль? Придётся сравнивать корни:

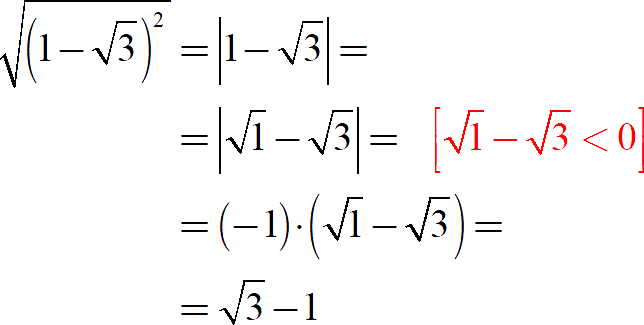
Откуда такое смелое утверждение во второй строке? Существует два способа доказать неравенство в красных скобках:

• 1.Использовать свойства корней;
• 2.Составить цепочку неравенств.

Я приведу оба:

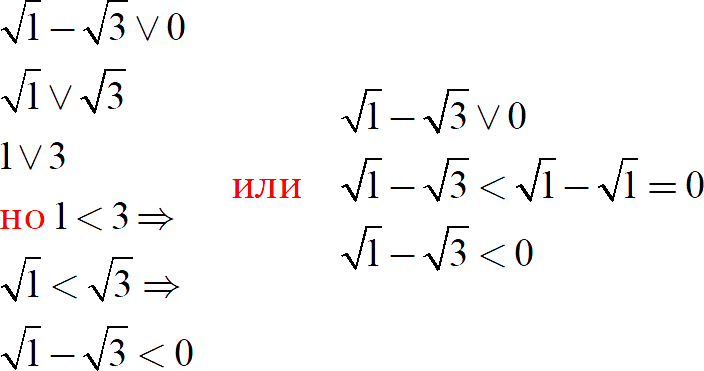
Сравнение корней — отдельная серьёзная тема. Ей посвящён целый урок. Поэтому давайте просто решим второе задание:

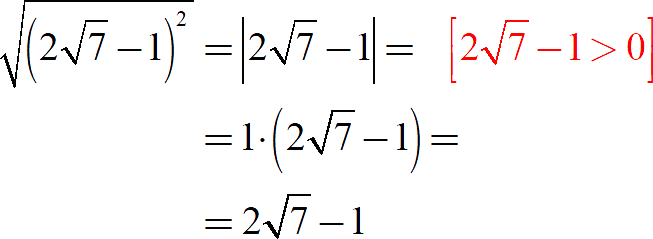
Задание. Вычислите значение выражения:

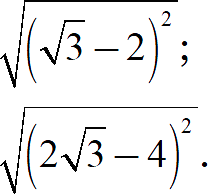
[показать ответ]

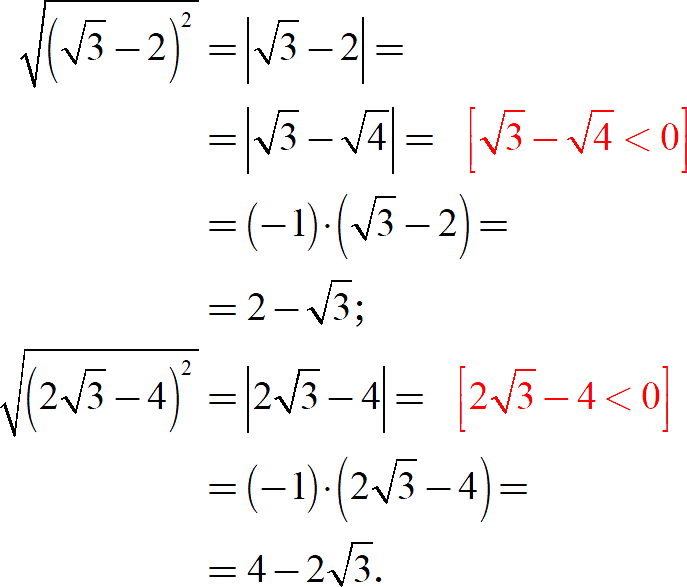
1.2. Корень из чётной степени

Идём дальше. Вновь запишем нашу волшебную формулу:

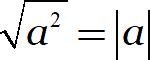
Капитан очевидность как бы намекает: эта формула верна не только для квадратов, но и для всех чётных степеней:

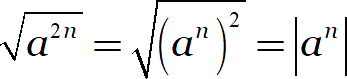
Другими словами, корень из любой чётной степени понижает эту степень ровно в два раза, но взамен навешивает на неё модуль! Рассмотрим примеры:

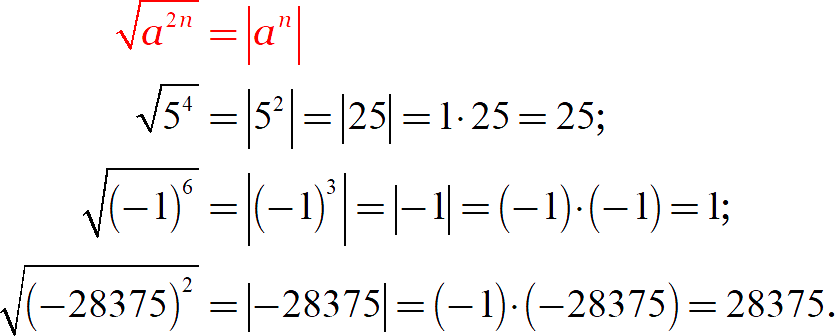
Обратите внимание на последнюю строку: изначально под корнем стоит довольно громоздкое число. Вычислять его напролом — возводить в квадрат, а затем извлекать корень — безумие. Но формула понижения степени редуцирует задачу до устной — отличная экономия времени на экзамене.:)

Попробуйте сами:

Задание 2. Найдите значение выражения:

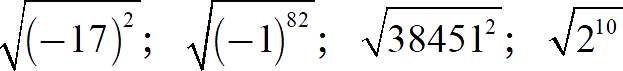
[Показать ответы]

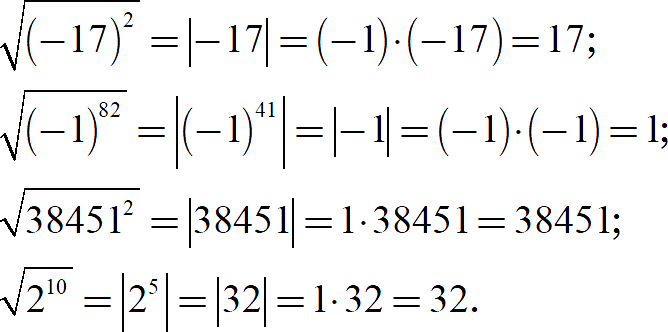
Вывод: если видите корень из степени, то смело понижайте степень вдвое, убирайте корень, но взамен ставьте модуль. Всегда. Обязательно. Ок? Переходим ко второй части урока.

2. Корни из произведения и частного

Перед тем как давать какие-либо новый формулы, напомню важный факт. Корень из суммы не равен сумме корней:

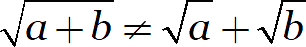
Иначе мы бы получили вот такие бредовые выкладки:

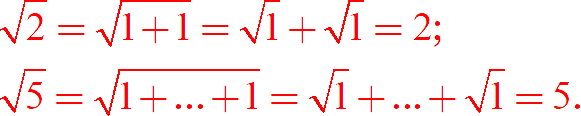
Вроде бы, капитаноочевидно, но многие даже в старших классах допускают такие ошибки.

А теперь разберём ещё два свойства корней.

2.1. Умножение и деление корней

Корни можно умножать и делить. Правила просты:

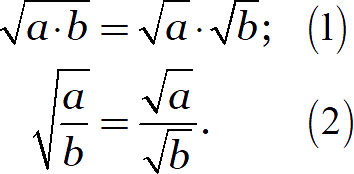
Примеры:

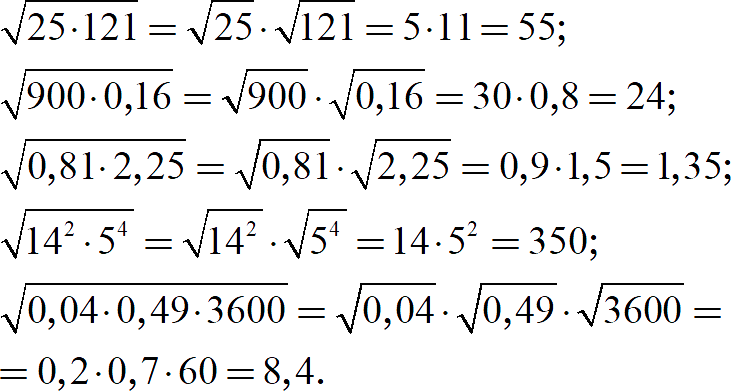
Попробуйте сами:

Задание 3. Найдите значение выражения:

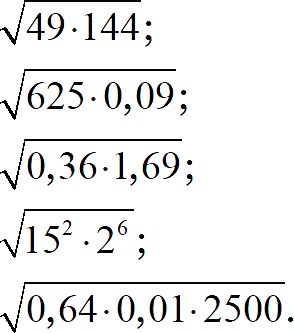
[показать ответы]

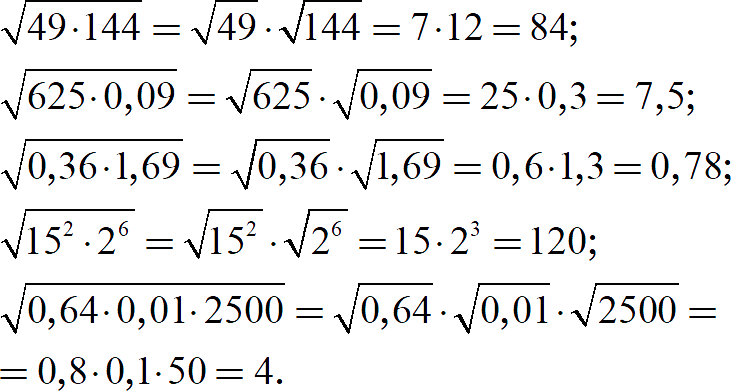
Как видите, с помощью формул мы разбиваем сложный корень на несколько простых.

Мы знаем, то все формулы работают как слева-направо, так и справа-налево, поэтому корни можно «склеивать». При этом новый корень может легко вычисляться, хотя исходные части — не вычисляются вообще. Например:

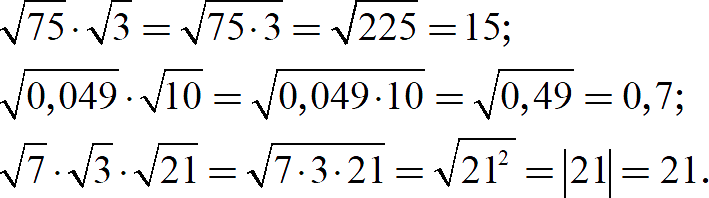
Попробуйте повторить этот трюк:

Задание 4. Найдите значение выражения:

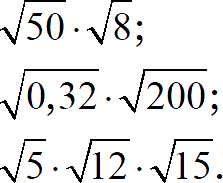
[показать ответы]

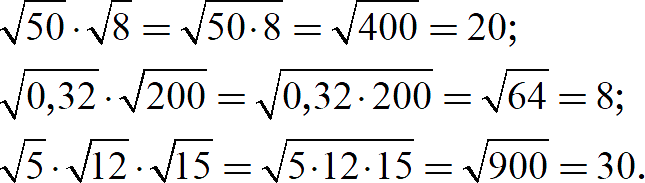
2.2. Проблемы с областью определения

Но есть одна тонкость. Взгляните, например, на формулу произведения корней:

Напомню: знак радикала обозначает арифметический квадратный корень, который извлекается только из неотрицательных чисел и сам является числом неотрицательным.

С левой стороны от знака равенства стоит один корень, а справа — целых два. Поэтому области определения левой и правой части этого равенства различны:

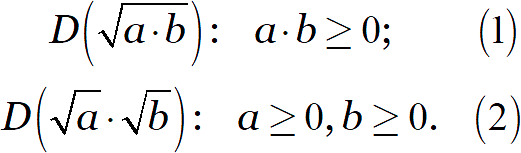
В чём конкретно состоит различие?

В первой строке мы видим произведение, поэтому неравенство (1) верно всякий раз, когда знаки множителей совпадают. В частности, оба множителя могут быть отрицательными, но их произведение всё равно будет положительным.

Вторая строка — система из двух неравенств, и здесь отрицательные числа нас уже не устроят. Вывод:

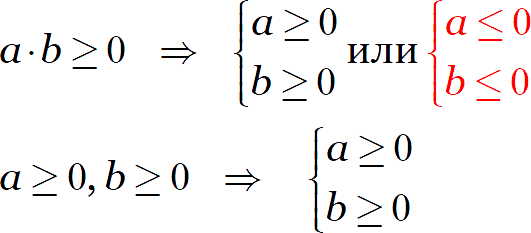
Красным я выделил ситуацию, которая допустима для корня из произведения, но становится недопустимой для произведения корней.

Поскольку любое равенство определено лишь тогда, когда определена и левая, и правая его части, дополним исходные правила специальными требованиями:

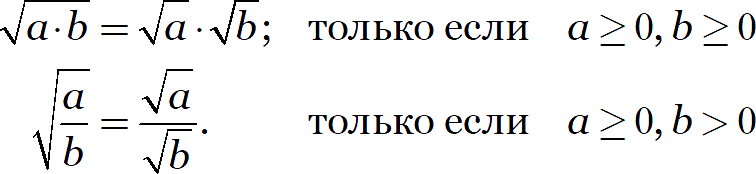
И вот в таком виде их уже можно использовать — везде и всегда!

Может показаться, что эти ограничения несущественны. Или искусственны. Чуть выше мы никак их не учитывали и всё прекрасно посчитали. Поэтому вопрос: когда ограничения области определения становятся существенным?

Ответ: когда под корнями стоят не конкретные числа, а переменные. К примеру, пусть даны числа:

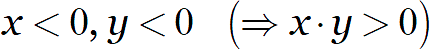
Очевидно, что произведение двух отрицательных чисел будет положительным. И хотя корень из произведения будет определён, извлекать корни из отдельных множителей нельзя:

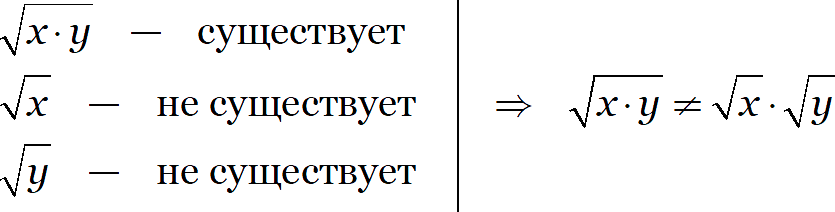
Значит, нужно сделать так, чтобы множители под корнем стали положительными. И тут нам на помощь приходит старое доброе число −1:

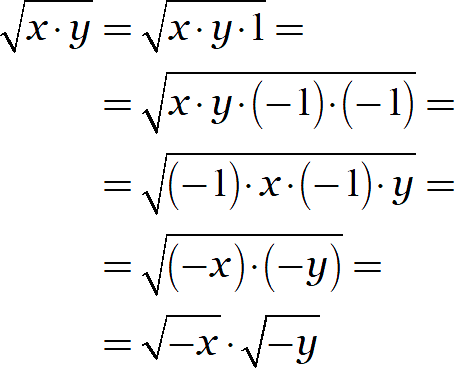
Добавление минусов к каждому из двух множителей нисколько не повлияло на произведение, но привело к возникновению двух новых множителей, каждый из которых уже точно положителен:

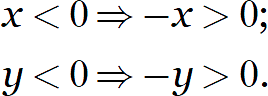
Помните об этом преобразовании, когда сталкиваетесь с произведением отрицательных выражений под знаком корня. Источником такой отрицательности могут быть условия задачи, либо следствия из области определения (такое часто встречается в логарифмических уравнениях и неравенствах, которые изучаются в 10—11 классах).

Ну а мы немного потренируемся и пойдём к третьей части урока — работе с переменными.

Задание 5. Найдите значение выражения:

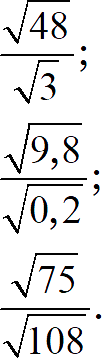
[показать ответы]

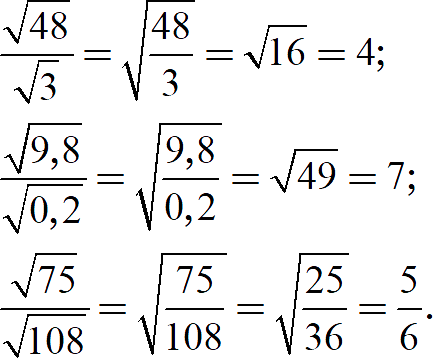
Переходим к самому весёлому.:)

3. Работа с переменными

Если не считать определения, то мы знаем о корнях две вещи. Во-первых, корни понижают степени, но добавляют модули:

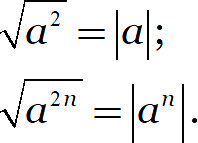
Во-вторых, корни можно умножать и делить. Но не всегда:

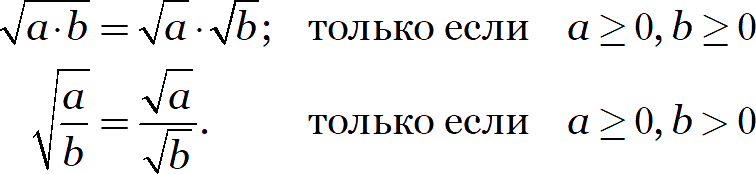
До сих пор мы тренировались лишь на конкретных числах. И многие могут удивляться: зачем все эти рассуждения про модули и ограничения?

Сейчас мы заменим числа буквами — и задача резко усложнится. Или не усложнится — если вы внимательно изучите то, что написано дальше.:)

3.1. Раскрытие модуля через свойства степеней

Начнём с простого. Мы уже знаем, как избавляться от точной степени:

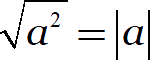
Попробуем применить эту формулу к двум различным выражениям:

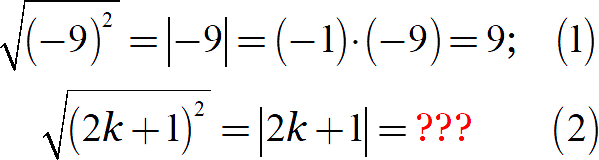
В первой строке мы без труда раскрыли модуль, поскольку знаем, что число под модулем отрицательно. Затем посчитали — получили ответ.

Но как раскрыть модуль во второй строке? Ведь правила раскрытия будут меняться в зависимости от того, какое значение принимает переменная. И если никаких дополнительных ограничений на переменную нет, то модуль так и останется нераскрытым. Взгляните:

Замените выражение тождественно равным, не содержащим знака корня:

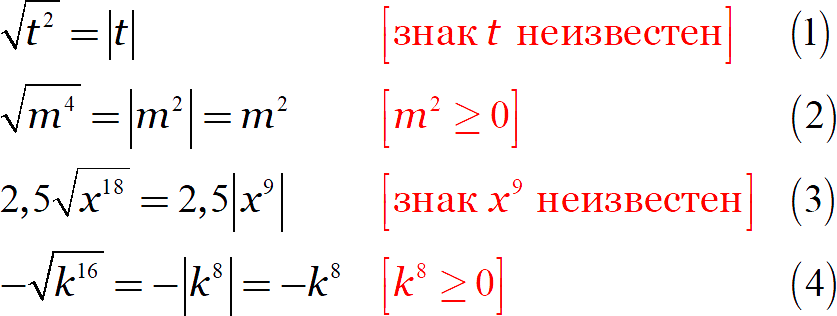
Из приведённых примеров видно:

• В строках (2) и (4) мы можем раскрыть модуль, ничего не зная о переменной;
• В строках (1) и (3) раскрыть модуль не удалось.

Почему? Чётные степени в строках (2) и (4) при любом значении переменной будут положительным числом или нулём. Поэтому модуль однозначно раскрывается со знаком «плюс».

Нечётная степень в строках (1) и (3) таким свойством не обладает: она может оказаться как положительным числом, так и отрицательным. Поэтому модуль раскрыть нельзя.

Попробуйте сами:

Задание. Замените выражение тождественно равным, не содержащим знака корня:

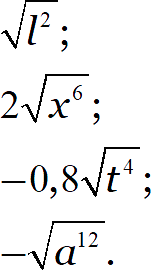
[показать ответ]

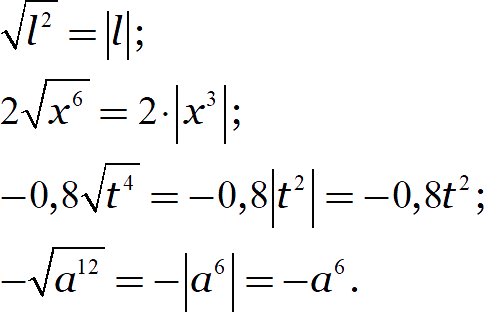
Чётные степени всегда неотрицательны, нечётные степени могут принимать любой знак:

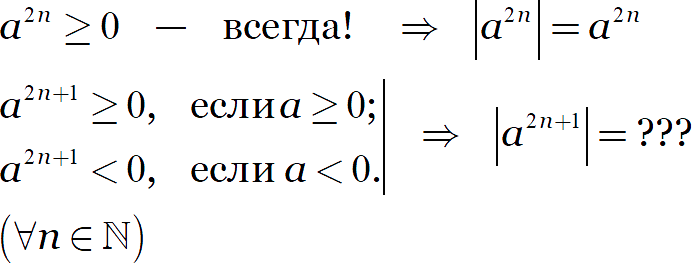
Тем не менее, модуль нечётной степени тоже можно раскрыть. Если в задаче есть дополнительные условия.

3.2. Учёт дополнительных ограничений

Зачастую в самом условии задачи содержатся ограничения на переменную, которые помогают однозначно раскрыть модуль. Пример:

Упростите выражение:

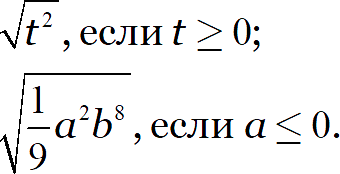
Работаем по тем правилам, которые изучали выше:

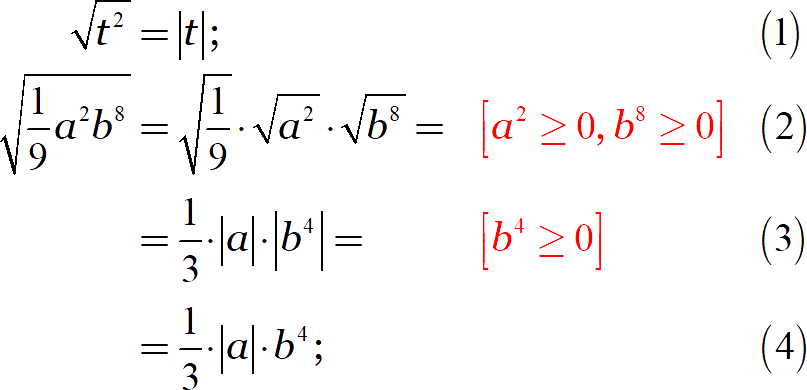
Обратите внимание: в строке (2) чётные степени под корнем дают три неотрицательных числа, поэтому корень можно разбить на три изолированных множителя — область определения при этом не поменяется; затем в строке (3) мы видим чётную степень под модулем и раскрываем его.

Ещё раз запишем результат и дополним его исходными условиями:

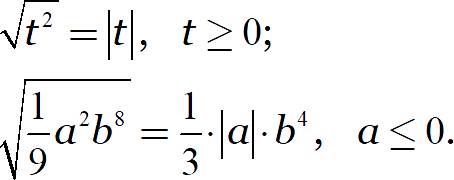
В первом случае выражение под модулем положительно или ноль, поэтому модуль однозначно раскрывается со знаком «плюс». Во втором — отрицательно или ноль, поэтому модуль раскрывается со знаком «минус»:

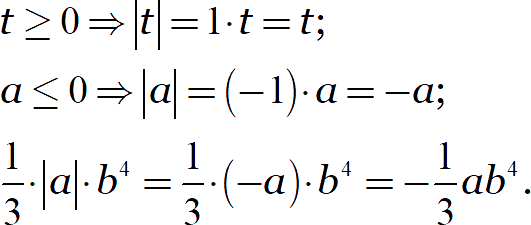
Возможно, у вас возникает вопрос: почему мы пишем множитель 1 или −1, но не рассматриваем отдельно множитель 0? В этом фишка модуля:

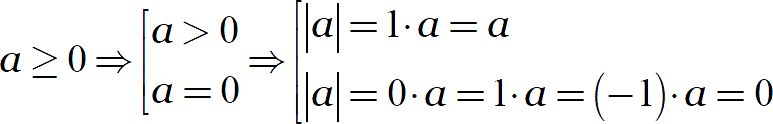
Таким образом, в нуле модуль можно раскрывать любым удобным способом.

Попробуйте самостоятельно:

Задание. Упростите выражение:

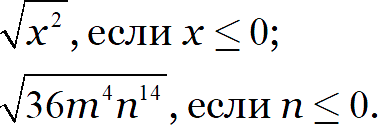
[показать ответ]

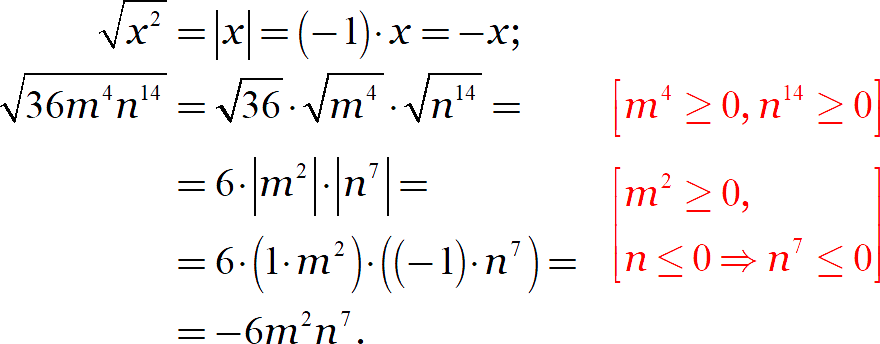
Это были весьма примитивные выражения, сводящиеся к раскрытию модуля. На них мы отработали важный новый навык. Теперь воспользуемся этим навыком для решения более интересных задач.

3.3. Упрощение выражений

Последний и самый интересный раздел этого урока.

Откуда берутся дополнительные ограничения на переменные? Существует ровно два источника таких ограничений:

• 1.Условие задачи. Например, если переменная — это длина отрезка на чертеже, то можно без ущерба для здоровья полагать, что она неотрицательна (а если всё-таки отрицательна, то у вас неправильный чертёж).
• 2.Неявные следствия из исходного выражения / уравнения / неравенства. Тут всё намного интереснее: анализ следствий из исходного условия — увлекательный процесс, доступный лишь хорошо подготовленным ученикам.

Начнём с первого пункта — ограничений, явно указанных в условии задачи. Примеры:

Упростите выражение:

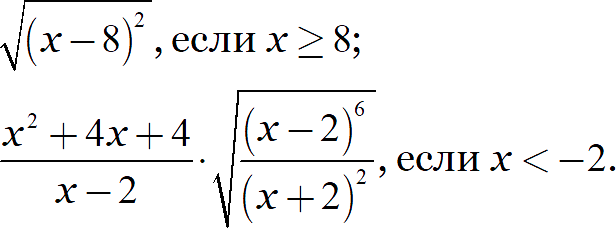
С первым выражением всё просто:

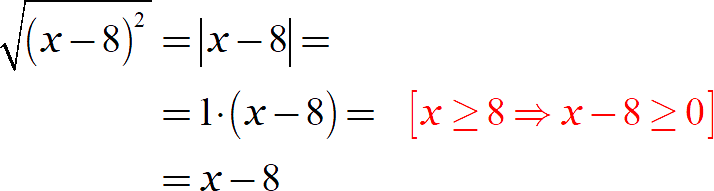
Со вторым уже интереснее. Заметим, что в первом числителе стоит формула сокращённого умножения, а дробь под корнем гарантированно имеет неотрицательный числитель и знаменатель:

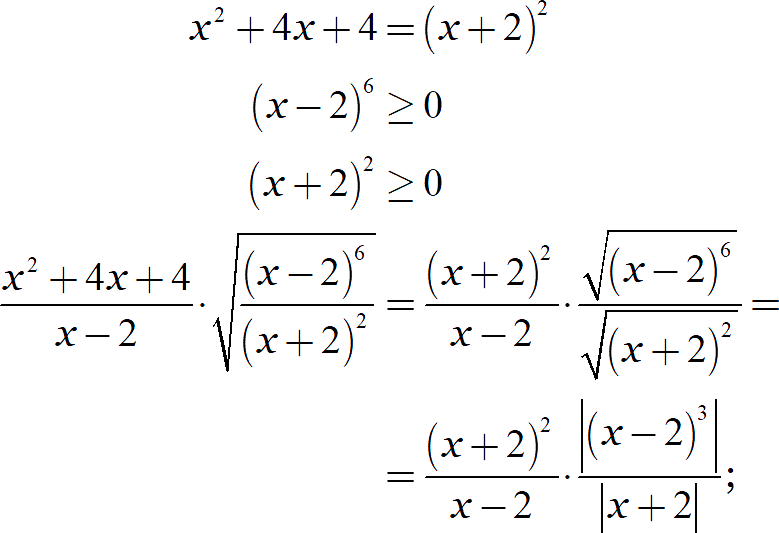
Вспомним исходные ограничения:

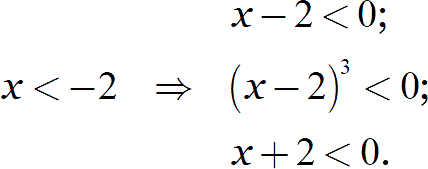
И раскроем модули:

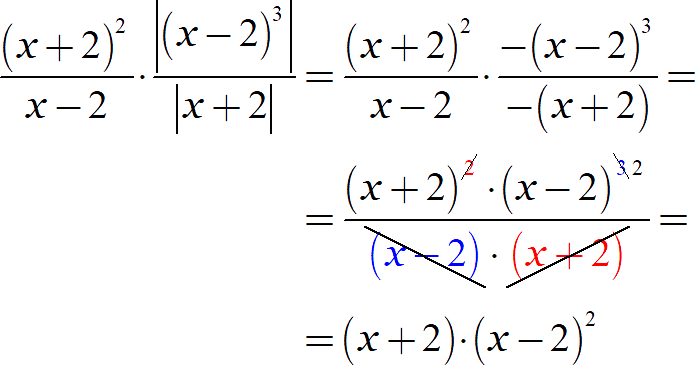
Как видите, нам удалось избавиться не только от модулей, но и от дробей.:)

Обратите внимание

Материал, представленный дальше, относится скорее к следующему уроку — «Внесение и вынесение множителей из-под знака корня». Его изучение прямо сейчас не является обязательным, но может оказаться весьма полезным для сильных учеников.

Наконец, разберёмся с неявными ограничениями. Ещё раз запишем самую первую формулу:

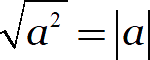
Пусть известно, что подмодульное выражение неотрицательно. Тогда модуль можно убрать:

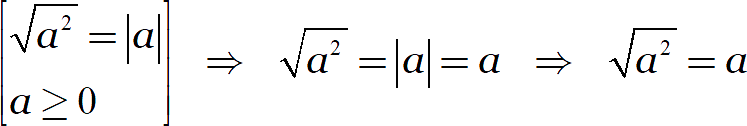
С отрицательными величинами тоже можно провернуть такой трюк:

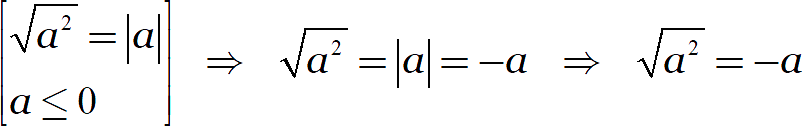
Но любое равенство работает как слева-направо, так и справа-налево. Следовательно, если нам известен знак переменной, мы можем внести её под знак корня:

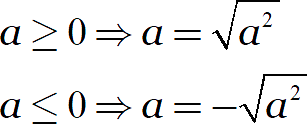
Это замечание позволит упрощать выражения, которые неподготовленному ученику покажутся неприступными.

Остаётся лишь один вопрос: где взять знак переменной? Ответ: ограничения на переменную часто скрыты в области определения. Например:

Упростите выражения:

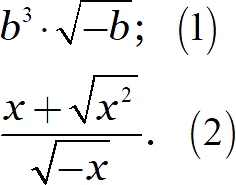
Решение:

В первой строке мы видим корень, поэтому выпишем область определения. Это даст нам ограничения на переменную и поможет внести её под знак корня:

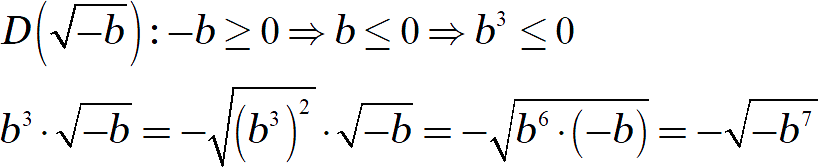
То же самое со вторым выражением:

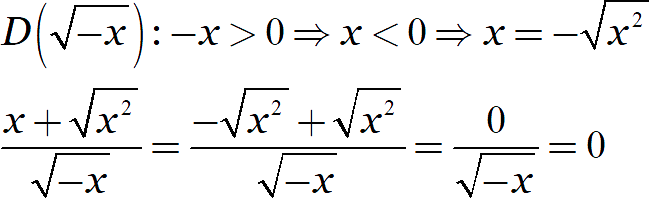
В итоге мы получили выражение, тождественно равное нулю. Однако помните: это равенство сохраняется только для отрицательных значений переменной! Для положительных значений исходное выражение вообще не определено.

Операция, которую мы только что провернули, как раз и называется внесением переменной под знак радикала.

В заключение хотел бы рассмотреть типичную ситуацию для сложных алгебраических задач, когда под корнем стоят, на первый взгляд, противоположные числа.

Упростите выражение:

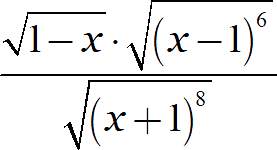
Заметим, что самый первый корень накладывает жёсткие ограничения на переменную:

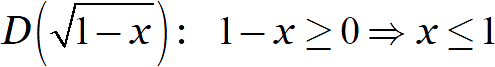
Под остальными корнями стоят неотрицательные выражения, поэтому дальше всё просто:

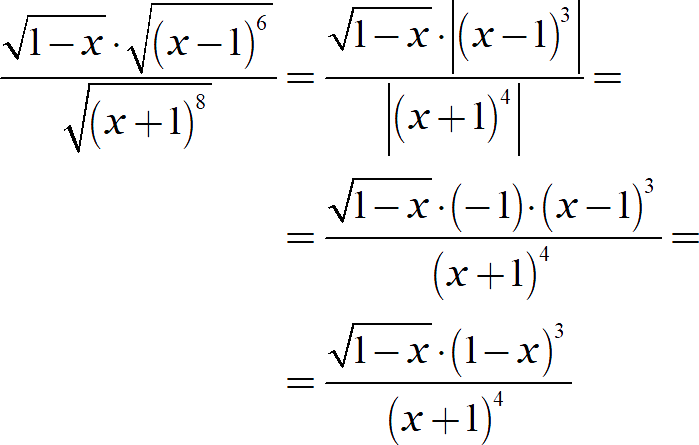
Наличие неявного ограничения позволило нам раскрыть модуль даже у нечётной степени. Обратите внимание на этот переход:

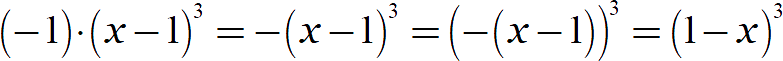
Как мы помним из краткой вводной, минусы можно выносить (и вносить) из основания нечётной степени. Это можно сделать как после раскрытия модуля, так и в самом начале — прямо под корнем:

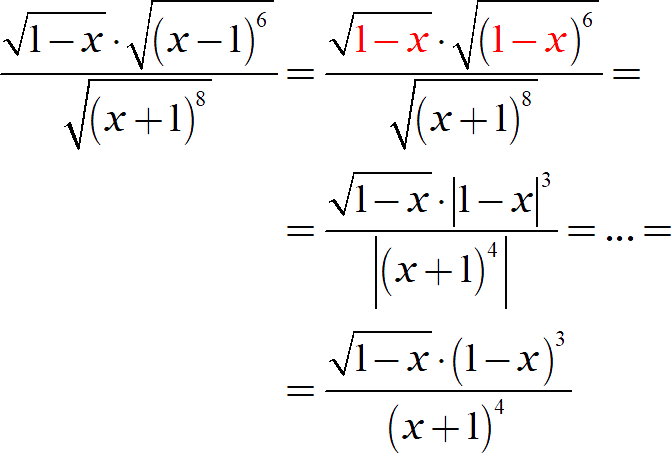
Красным я отметил одинаковые выражения, стоящие под корнем и в основании степени. Именно такая форма записи (а не игра с минусами) является предпочтительной, например, в логарифмических уравнениях и неравенствах.

Но это тема совсем другого урока. А на сегодня хватит.:)

Смотрите также:

1. Умножение корней n-й степени
2. Корень степени N
3. Следствия из теоремы Виета
4. Задача B3 — работа с графиками
5. C2: расстояние между двумя прямыми
6. Задача B2 на проценты: вычисление полной стоимости покупки

Что такое арифметический квадратный корень

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа (a) называется такое неотрицательное число, квадрат которого равен (a). (  (sqrt{a}=x, {{x}^{2}}=a; x, age 0)).

А почему же число  ( a) (число под корнем) должно быть обязательно неотрицательным?

Например, чему равен ( sqrt{-9})?

Так-так, попробуем подобрать. Может, три?

Проверим: ( {{3}^{2}}=9), а не ( -9).

Может, ( left( -3 right))? 

Опять же, проверяем: ( {{left( -3 right)}^{2}}=9).

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!

Число или выражение под знаком корня должно быть неотрицательным!

Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!

 Ведь в определении сказано, что «квадратным корнем из числа( a)называется такое неотрицательное число, квадрат которого равен( a)».

Но подождите!  В самом начале мы разбирали пример ( {{x}^{2}}=4) и один из ответов был отрицательным числом! 

 Мы подбирали числа, которые можно возвести в квадрат и получить при этом ( displaystyle 4). Ответом были ( displaystyle 2) и ( displaystyle -2)

А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?

Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.

К примеру, ( displaystyle {{x}^{2}}=4) (квадратное уравнение) не равносильно выражению ( x=sqrt{4}) (арифмитический квадратный корень).

Из ( {{x}^{2}}=4) следует, что

( left| x right|=sqrt{4}), то есть ( x=pm sqrt{4}=pm 2) или ( {{x}_{1}}=2); ( {{x}_{2}}=-2)

(не помнишь почему так? Почитай тему «Модуль числа»!)

А из ( x=sqrt{4}) следует, что ( x=2).

Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как ( 2), так и ( x=-2).

Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

Запись иррациональных чисел с помощью квадратного корня

А теперь попробуй решить такое уравнение ( {{x}^{2}}=3).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: ( {{0}^{2}}=0) – не подходит.

Двигаемся дальше ( displaystyle x=1); ( displaystyle {{1}^{2}}=1) – меньше трех, тоже отметаем.

А что если ( displaystyle x=2)? 

Проверим: ( displaystyle {{2}^{2}}=4) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между ( displaystyle 1) и ( displaystyle 2), а также между ( displaystyle -2) и ( displaystyle -1).

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции ( displaystyle y={{x}^{2}}) и отметим на нем решения.

Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!

Извлечем корень из ( displaystyle 3), делов-то!

Ой-ой-ой, выходит, что ( sqrt{3}=1,732050807568ldots ) Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. ( sqrt{3}) и ( -sqrt{3}) уже сами по себе ответы.

Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.

Деление корней

С умножением корней разобрались, теперь приступим к свойству деления.

Напомню, что формула в общем виде выглядит так:

( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b>0).

А значит это, что корень из частного равен частному корней.

Ну что, давай разбираться на примерах:

( displaystyle   frac{sqrt{12}}{sqrt{3}}=sqrt{frac{12}{3}}=sqrt{4}=2)

Вот и вся наука. А вот такой пример:

( displaystyle   frac{sqrt{12}}{3}=frac{sqrt{12}}{sqrt{9}}=sqrt{frac{12}{9}}=sqrt{frac{4}{3}}=frac{2}{sqrt{3}})

Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.

А что, если попадется такое выражение:

( displaystyle   sqrt{frac{144}{225}}=?)

Надо просто применить формулу в обратном направлении:

( displaystyle   sqrt{frac{144}{225}}=frac{sqrt{144}}{sqrt{225}}=frac{12}{15}=frac{4}{5}=0,8)

А вот такой примерчик:

( displaystyle   sqrt{0,16}=sqrt{frac{16}{100}}=frac{4}{10}=0,4)

Еще ты можешь встретить такое выражение:

( displaystyle   sqrt{5frac{19}{25}}=?)

Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!

( displaystyle   sqrt{5frac{19}{25}}=sqrt{frac{144}{25}}=frac{12}{5}=2,4)

Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.

Возведение в степень

А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа ( displaystyle a) – это число, квадратный корень которого равен ( displaystyle a).

Так вот, если мы возводим число, квадратный корень которого равен ( displaystyle a), в квадрат, то что получаем?

Ну, конечно, ( displaystyle a)!

Рассмотрим на примерах:

Все просто, правда? А если корень будет в другой степени? Ничего страшного!

Придерживайся той же логики и помни свойства и возможные действия со степенями.

Забыл?

Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.

Вот, к примеру, такое выражение:

( displaystyle   {{left( sqrt{5} right)}^{6}}={{left( {{left( sqrt{5} right)}^{2}} right)}^{3}}={{5}^{3}}=125)

В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:

( displaystyle   {{left( sqrt{5} right)}^{7}}={{left( sqrt{5} right)}^{6}}cdot sqrt{5}=125sqrt{5})

С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:

( displaystyle   sqrt{{{3}^{2}}}=sqrt{9}=3)

Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:

Ну как, все понятно? Тогда реши самостоятельно примеры:

• ( displaystyle   sqrt{{{left( -3 right)}^{2}}})
• ( displaystyle   sqrt{{{6}^{6}}})
• ( displaystyle   {{left( sqrt{8} right)}^{7}})

А вот и ответы:

Извлечение корней из больших чисел

До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!

( displaystyle   sqrt{98}=sqrt{49cdot 2}=sqrt{49}cdot sqrt{2}=7sqrt{2})

Можно было пойти по иному пути и разложить на другие множители:

( displaystyle   sqrt{98}=sqrt{7cdot 14})

Что дальше? А дальше раскладываем на множители до самого конца:

( displaystyle   sqrt{98}=sqrt{7cdot 14}=sqrt{7cdot 7cdot 2}=sqrt{{{7}^{2}}cdot 2}=7sqrt{2})

Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.

Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:

( displaystyle   sqrt{15}cdot sqrt{180}cdot sqrt{12})

Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:

А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):

( displaystyle   sqrt{15}cdot sqrt{180}cdot sqrt{12}=sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6})

Разве это конец? Не останавливаемся на полпути!

( displaystyle   begin{array}{l}sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6}=sqrt{5cdot 3}cdot sqrt{3cdot 12cdot 5}cdot sqrt{2cdot 3cdot 2}=\=sqrt{5cdot 3}cdot sqrt{3cdot 2cdot 2cdot 3cdot 5}cdot sqrt{2cdot 3cdot 2}end{array})

На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:

( displaystyle   begin{array}{l}sqrt{5cdot 3cdot 3cdot 2cdot 2cdot 3cdot 5cdot 2cdot 3cdot 2}=sqrt{5cdot 5cdot 3cdot 3cdot 3cdot 3cdot 2cdot 2cdot 2cdot 2}=\=sqrt{25}cdot sqrt{81}cdot sqrt{16}=5cdot 9cdot 4=180end{array})

Вот и все, не так все и страшно, правда?

( displaystyle   sqrt{15}cdot sqrt{54}cdot sqrt{10}=?)

Получилось ( displaystyle   90)? Молодец, все верно!

А теперь попробуй вот такой пример решить:

( displaystyle   sqrt{4225}=?)

А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.