Одинаковое расстояние можно проехать за разное время.
Например, спортивная машина один километр может проехать быстрее, чем тяжело нагруженная грузовая машина. Одна и та же машина может ехать как быстрее, так и медленнее.

Обрати внимание!
Чтобы сравнить различные движения, необходимо знать скорость движения.
Скоростью движения называется величина, численно равная пути, проходимому телом в единицу времени.
Скорость вычисляется по формуле
v=st
, где
(s) — пройденный путь;
(t) — время.
Чем больше скорость, тем больший путь проходит тело за единицу времени. Если путь измеряется в метрах (м), а время движения в секундах (с), то скорость тела измеряется в (м/с).
Метр в секунду (м/с) — единица скорости в международной системе единиц.
Скорость можно выражать и в других единицах, например в км/с или в км/ч.
Различные примеры скорости:
1. скорость реактивного самолета — 3000 км/ч.
2. Скорость спринтера на дистанции — 37 км/ч.
3. Скорость звука в воздухе — 1224 км/ч.
4. Средняя скорость ходьбы — 6 км/ч.
5. Максимальная скорость гепарда — 114 км/ч.
6. Скорость улитки — 0,02 км/ч.
Средняя скорость. Решение задач по физике
- Подробности
- Обновлено 02.09.2018 15:56
- Просмотров: 2375

Задачи по физике – это просто!
Среднюю скорость движения иначе называют путевой скоростью.

где
Sобщ – общий путь, т.е. сумма всех отрезков пути
t общ – общее время, т.е. время, за которое был пройден весь путь
При решении задач очень помогает простенький чертеж, на котором надо показать все отрезки пути.
Около каждого отрезка для наглядности укажите буквенные обозначения скорости, времени, пути (с нужным индексом) и формулы для их расчета (если это необходимо).
Переходим к решению задач.
От простых к сложным!
Элементарные задачи из курса школьной физики
Задача 1
Автомобиль проехал 100 метров за 25 секунд, а следующие 300 метров за 1 минуту.
Определить среднюю скорость движения автомобиля.

Задача 2
Автомобиль ехал 2 минуты со скоростью 10 м/с, а затем проехал еще 500 метров за 30 секунд.
Определить среднюю скорость движения.

Задача
3
Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 20 м/c.
Определить среднюю скорость автомобиля.

Задача 4
Автомобиль проехал первую половину пути со скоростью 10 м/с, а вторую половину пути со скоростью 20 м/с. Определить среднюю скорость автомобиля на всем пути.
Пусть S – общий пройденный путь.

Задача 5
Автомобиль одну треть времени движения ехал со скоростью 10 м/с, а остальное время со скоростью 20 м/с. Определить среднюю скорость за все время движения.
Пусть t – общее время движения.

Скорость, путь и время являются важными характеристиками любого механического движения. Они связаны между собой формулами:
- $upsilon = frac{S}{t}$
- $S = upsilon t$
- $t = frac{S}{upsilon}$
Данные формулы описывают равномерное движение. При неравномерном движении мы говорим о средней скорости: $upsilon_{ср} = frac{S}{t}$.
Чтобы полноценно научиться использовать вышеупомянутые определения и величины, в данном уроке мы рассмотрим решение разнообразных задач. Вы научитесь вычислять скорость, среднюю скорость, время и путь, переводить единицы измерения скорости из одних в другие, узнаете, как использовать графики этих величин.
Задача №1
Выразите в метрах в секунду ($frac{м}{с}$) скорости: $60 frac{км}{ч}$; $90 frac{км}{ч}$; $300 frac{км}{ч}$; $120 frac{м}{мин}$.
Дано:
$upsilon_1 = 60 frac{км}{ч}$
$upsilon_2 = 90 frac{км}{ч}$
$upsilon_3 = 300 frac{км}{ч}$
$upsilon_4 = 120 frac{м}{мин}$
Показать решение и ответ
Скрыть
Решение:
Для перевода скорости в метры в секунду нам нужно:
- перевести километры в метры ($1 space км = 1000 space м$)
- выразить часы или минуты в секундах ($1 space мин = 60 space с$; $1 space ч = 60 space мин = 3600 space с$)
Тогда,
$upsilon_1 = 60 frac{км}{ч} = 60 frac{1000 space м}{3600 space c} = frac{1000 space м}{60 space c} approx 16.7 frac{м}{с}$.
При вычислениях старайтесь увидеть величины, которые можно сократить (как 60 и 3600).
Если мы вычислим множитель $frac{1000 space м}{3600 space c}$, то получим, что $1 frac{км}{ч} = frac{}{3.6} frac{м}{с}$.
Вы можете каждый раз последовательно переводить величины (километры в метры и часы в секунды) или просто разделить скорость, выраженную в километрах в час на $3.6$ и получить скорость в метрах в секунду. Рекомендуется идти первым путем, потому что второй способствует потере точности.
Переведем следующие две скорости в единицы СИ:
$upsilon_2 = 90 frac{км}{ч} = 90 frac{1000 space м}{3600 space c} = 1000 cdot 0.025 frac{м}{с} = 25 frac{м}{с}$,
$upsilon_3 = 300 frac{км}{ч} = 300 frac{1000 space м}{3600 space c} = frac{1000 space м}{12 space c} approx 83.3 frac{м}{с}$.
Теперь переведем скорость, выраженную в метрах в минуту в метры в секунду:
$upsilon_4 = 120 frac{м}{мин} = 120 frac{м}{60 space c} = 2 frac{м}{с}$.
Ответ: $upsilon_1 approx 16.7 frac{м}{с}$; $upsilon_2 = 25 frac{м}{с}$; $upsilon_1 approx 83.3 frac{м}{с}$; $upsilon_4 = 2 frac{м}{с}$.
Задача №2
Пуля, выпущенная из винтовки, долетела до цели, находящейся на расстоянии $1 space км$, за $2.5 space с$. Найдите скорость пули.
Дано:
$S = 1 space км$
$t = 2.5 space с$
СИ:
$S = 1000 space м$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета скорости:
$upsilon = frac{S}{t}$.
Перед вычислениями не забывайте переводить единицы измерения величин в СИ!
Рассчитаем скорость:
$upsilon = frac{1000 space м}{2.5 space с} = 400 frac{м}{с}$.
Ответ: $upsilon = 400 frac{м}{с}$.
Задача №3
Пароход, двигаясь против течения со скоростью $14 frac{км}{ч}$, проходит расстояние между двумя пристанями за $4 space ч$. За какое время он пройдет то же расстояние по течению, если его скорость в этом случае равна $5.6 frac{м}{с}$?
Дано:
$upsilon_1 = 14 frac{км}{ч}$
$t_1 = 4 space ч$
$upsilon_2 = 5.6 frac{м}{с}$
$t_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Найдем расстояние между двумя пристанями:
$S = upsilon_1 t_1$,
$S = 14 frac{км}{ч} cdot 4 space ч = 56 space км = 56 space 000 space м$.
Обратите внимание, что мы изначально не перевели единицы измерения в СИ (километры в час в метры в секунду и часы в секунды), потому что удобнее это сделать после расчета расстояния $S$. Таким образом мы сохраняем более высокую точность вычислений.
Итак, мы знаем расстояние и скорость движения парохода по течению. Теперь мы можем рассчитать время движения парохода по течению:
$t_2 = frac{S}{upsilon_2}$,
$t_2 = frac{56 space 000 space м}{5.6 frac{м}{с}} = 10 space 000 space с$.
Ответ: $t_2 = 10 space 000 space с$.
Задача №4
Автомобиль проехал равномерно участок дороги длиной $3.5 space км$ за $3 space мин$. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак “скорость не более $50 frac{км}{ч}$”?
Дано:
$S = 3.5 space км$
$t = 3 space мин$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
После того, как мы рассчитаем скорость движения автомобиля, нам нужно будет сравнить ее со скоростным ограничением в $50 frac{км}{ч}$. Для того чтобы это сделать, нужно, чтобы скорость тоже была выражена в километрах в час.
Так как водитель двигался равномерно, рассчитывать скорость его движения мы будем по формуле:
$upsilon = frac{S}{t}$.
Путь $S$ у нас и так выражен в километрах, а время — в минутах. Поэтому, перед рассветом скорости переведем время из минут в часы:
$t = 3 space мин = frac{3}{60} cdot ч = 0.05 space ч$.
Теперь мы можем рассчитать скорость движения автомобиля:
$upsilon = frac{3.5 space км}{0.05 space ч} = 70 frac{км}{ч}$.
Получается, что водитель нарушил правила дорожного движения, ведь $70 frac{км}{ч} > 50 frac{км}{ч}$.
Ответ: нарушил.
Задача №5
Росток бамбука за сутки вырастает на $86.4 space см$. На сколько он вырастает за $1 space мин$?
Дано:
$S = 86.4 space см$
$t = 1 space сут$
$t_1 = 1 space мин$
$S_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Переведем сутки в минуты:
$t = 1 space сут = 24 space ч = 24 cdot 60 space мин = 1440 space мин$.
Рассчитаем скорость роста бамбука, выраженную в сантиметрах в минуту:
$upsilon = frac{86.4 space см}{1440 space мин} = 0.06 frac{см}{мин}$.
Понятие скорости в физике определяет расстояние, которое тело проходит в единицу времени. В нашем случае полученную скорость роста мы можем описать так:
бамбук вырастает на расстояние, равное $0.06 space см$, за $1 space мин$.
Значит,
$S_1 = 0.06 space см = 0.6 space мм$.
Ответ: $S_1 = 0.6 space мм$.
Задача №6
Самолет, летящий со скоростью $300 frac{км}{ч}$, в безветренную погоду пролетел расстояние между аэродромами A и B за $2.2 space ч$. Обратный полет из-за встречного ветра он совершил за $2.5 space ч$. Определите скорость ветра.
Дано:
$upsilon_1 = 300 frac{км}{ч}$
$t_1 = 2.2 space ч$
$t_2 = 2.5 space ч$
$upsilon_в — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала вычислим расстояние между аэродромами, которое пролетает самолет:
$S = upsilon_1 t_1$,
$S = 300 frac{км}{ч} cdot 2.2 space ч = 660 space км$.
Теперь рассчитаем скорость, с которой самолет совершил обратный полет:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{660 space км}{2.5 space ч} = 264 frac{км}{ч}$
Если бы ветра не было, то скорость самолета составила бы $300 frac{км}{ч}$. Но ветер направлен противоположно движению самолеты, вектор его скорости противоположно направлен вектору скорости самолета. Поэтому мы можем записать, что скорость самолета, летящего при встречном ветре, равна разности скорости самолета в безветренной обстановке и скорости ветра:
$upsilon_2 = upsilon_1 — upsilon_в$.
Рассчитаем скорость ветра:
$upsilon_в = upsilon_1 — upsilon_2$,
$upsilon_в = 300 frac{км}{ч} — 264 frac{км}{ч} = 36 frac{км}{ч}$,
или в СИ $upsilon_в = 36 cdot frac{1000 space м}{3600 space с} = 10 frac{м}{с}$.
Ответ: $upsilon_в = 10 frac{м}{с}$.
Определите по графику равномерного движения, изображенному на рисунке 1:
- скорость движения
- путь, пройденный телом в течение $4.5 space с$
- время, в течение которого пройден путь, равный $15 space м$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитывается по формуле:
$upsilon = frac{S}{t}$.
Выберем на графике такую точку, данные которой мы можем точно определить. Например, в момент времени, равный $4 space с$, был пройден путь, равный $16 space м$.
Используя эти данные, рассчитаем скорость:
$upsilon = frac{16 space м}{4 space с} = 4 frac{м}{с}$.
Найдем путь, пройденный телом в течение $4.5 space с$. Если мы взглянем на график, то в этот момент времени тело прошло путь, приблизительно равный $18 space м$. Давайте проверим точность этих данных с помощью вычислений:
$S = upsilon t$,
$S = 4 frac{м}{с} cdot 4.5 space с = 18 space м$.
Используя график, мы не можем точно определить время, в течение которого пройден путь, равный $15 space м$. Поэтому вычислим его:
$t = frac{S}{upsilon}$,
$t = frac{15 space м}{4 frac{м}{с}} = 3.75 space с$.
Ответ: $4 frac{м}{с}$, $18 space м$, $3.75 space с$.
Задача №8
Средняя скорость велосипедиста на всем пути равна $40 frac{км}{ч}$. Первую половину пути он ехал со скоростью $60 frac{км}{ч}$. С какой скоростью велосипедист проехал остаток пути?
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$upsilon_1 = 60 frac{км}{ч}$
$S_1 = S_2 = frac{1}{2}S$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу средней скорости при неравномерном движении:
$upsilon_{ср} = frac{S}{t}$.
Общее время движения $t$ мы можем представить в виде суммы $t_1 + t_2$, где $t_1$ — это время движения на первой половине пути, а $t_2$ — время движения на второй половине пути:
$upsilon_{ср} = frac{S}{t_1 + t_2}$.
Время мы можем выразить через скорость на данном участке пути и пройденный за это время путь:
$t_1 = frac{S_1}{upsilon_1} = frac{frac{1}{2}S}{upsilon_1} = frac{S}{2 upsilon_1}$,
$t_2 = frac{S_2}{upsilon_2} = frac{frac{1}{2}S}{upsilon_2} = frac{S}{2 upsilon_2}$,
$upsilon_{ср} = frac{S}{frac{S}{2 upsilon_1} + frac{S}{2 upsilon_2}} = frac{S}{frac{S(upsilon_1 + upsilon_2)}{2 upsilon_1 upsilon_2}} = frac{2 upsilon_1 upsilon_2}{upsilon_1 + upsilon_2}$.
Теперь выразим отсюда скорость $upsilon_2$, с которой велосипедист двигался вторую половину пути:
$2 upsilon_1 upsilon_2 = upsilon_{ср} upsilon_1 + upsilon_{ср} upsilon_2$,
$2 upsilon_1 upsilon_2 — upsilon_{ср} upsilon_2 = upsilon_{ср} upsilon_1$,
$upsilon_2 cdot (2 upsilon_1 — upsilon_{ср}) = upsilon_{ср} upsilon_1$,
$upsilon_2 = frac{upsilon_{ср} upsilon_1}{2 upsilon_1 — upsilon_{ср}}$.
Рассчитаем эту скорость:
$upsilon_2 = frac{40 frac{км}{ч} cdot 60 frac{км}{ч}}{2 cdot 60 frac{км}{ч} — 40 frac{км}{ч}} = frac{2400 frac{км}{ч}}{80} = 30 frac{км}{ч}$.
Ответ: $upsilon_2 = 30 frac{км}{ч}$.
Задача №9
На рисунке 2 дан график пути движения поезда. Определите скорости движения на участках, изображенных отрезками графика OA, AB и BC. Какой путь пройден поездом в течении $3 space ч$ с начала его движения?
Дано:
$t = 3 space ч$
$upsilon_1 — ?$, $upsilon_2 — ?$, $upsilon_3 — ?$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы определить скорость на каждом участке пути, мы будем выбирать удобную нам точку на графике и проводить вычисления.
Определим скорость движения поезда на участке OA. В момент времени, равный $1 space ч$, пройденный поездом путь составил $40 space км$:
$upsilon_1 = frac{S_1}{t_1}$,
$upsilon_1 = frac{40 space км}{1 space ч} = 40 frac{км}{ч}$.
Участок графика AB параллелен оси времени, пройденный путь не изменяется. Значит скорость здесь равна нулю: $upsilon_2 = 0 frac{км}{ч}$.
Определим скорость движения поезда на участке BC. По наклону прямой графика мы видим, что скорость после остановки изменилась. За время с $2 space ч$ до $3 space ч$, пройденный путь изменился с $60 space км$ до $80 space км$. Значит, за $1 space ч$ поезд прошел путь, равный $20 space км$:
$upsilon_3 = frac{S_3}{t_3}$,
$upsilon_3 = frac{20 space км}{1 space ч} = 20 frac{км}{ч}$.
Теперь нам нужно найти путь, пройденный поездом за $3 space ч$ с момента начала движения. Этот путь будет складываться из трех составляющих на разных участках:
$S = S_1 + S_2 + S_3$.
Путь $S_2$, соответствующий участку AB будет равен нулю, так как на нем скорость движения равна нулю.
Тогда, используя данные графика и рассчитанные значения скоростей, мы можем записать:
$S = S_1 + S_3 = upsilon_1 t_1 + upsilon_3 t_3$,
$S = 40 frac{км}{ч} cdot 1.5 space ч + 20 frac{км}{ч} cdot 1 space ч = 80 space км$.
Ответ: $upsilon_1 = 40 frac{км}{ч}$, $upsilon_2 = 0 frac{км}{ч}$, $upsilon_3 = 20 frac{км}{ч}$, $S = 80 space км$.
Задача №10
От одной и той же станции в одном и том же направлении отправляются два поезда. Скорость первого $30 frac{км}{ч}$, второго $40 frac{км}{ч}$. Второй поезд отправляется через $10 space мин$ после первого. После сорокаминутного движения первый поезд делает пятиминутную остановку, потом продолжает двигаться дальше с прежней скоростью.
Определите графически, когда и на каком расстоянии от станции второй поезд догонит первый. Графическое решение проверьте вычислением.
Дано:
$upsilon_1 = 30 frac{км}{ч}$
$upsilon_2 = 40 frac{км}{ч}$
$t_{01} = 0 space мин$
$t_{02} = 10 space мин$
$t_1 = 40 space мин$
$t_{1о} = 5 space мин$
$t — ?$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала займемся построением графика движения поездов.
По оси $x$ мы будем откладывать время, а по оси $y$ — расстояние. Время оставим в $мин$, а расстояние будем отмечать в $км$.
Построим график движения первого поезда (рисунок 3). Он начинает свое движение в момент времени $t_{01} = 0 space мин$.
Движется он со скоростью $30 frac{км}{ч}$ в течение $t_1 = 40 space мин$. Переведем эту скорость в $frac{км}{мин}$ и вычислим, какое расстояние этот поезд пройдет за указанное время:
$upsilon_1 = 30 frac{км}{ч} = 30 frac{км}{60 space мин} = 0.5 frac{км}{мин}$,
$S_1 = upsilon_1 t_2$,
$S = 0.5 frac{км}{мин} cdot 40 space мин = 20 space км$.
Поставим эту точку на графике и соединим с началом координат.
Далее поезд сделал остановку. Этот участок графика будет параллелен оси времени — значение пройденного пути остается постоянным, ведь поезд никуда не двигается.
Далее поезд продолжает движение с прежней скоростью. Без вычислений мы можем провести из точки, соответствующей концу остановки, прямую параллельную первой части графика.
Теперь построим тут же график движения для второго поезда (рисунок 4).
Он начинает свое движение не из начала координат, а из точки, соответствующей времени $t_{02} = 10 space мин$.
Он движется со скоростью $40 frac{км}{ч}$. Это означает, что за $1 space ч = 60 space мин$ он проходит путь, равный $40 space км$. Отметим эту точку на координатной плоскости и соединим с точкой начала движения.
Итак, графически мы получили, что
- Второй поезд догонит первый в момент времени $t = 40 space мин$
- Поезда встретятся на расстоянии $S = 20 space км$ от места отправления
Теперь подтвердим полученные данные вычислениями. Поезда встретятся друг с другом, пройдя определенный путь $S$. Это случится через определенное время $t$:
$S = S_1 = S_2$,
$S_1 = upsilon_1 t$,
$S_2 = upsilon_2 (t — t_{02})$.
Найдем это время:
$upsilon_1 t = upsilon_2 (t — t_{02})$,
$upsilon_2 t — upsilon_1 t = upsilon_2 t_{02}$,
$t (upsilon_2 — upsilon_1) = upsilon_2 t_{02}$,
$t = frac{upsilon_2 t_{02}}{upsilon_2 — upsilon_1}$.
Перед расчетом переведем $мин$ в $ч$: $t_{02} = 10 space мин = frac{10}{60} space ч = frac{1}{6} space ч$.
Теперь рассчитаем время встречи двух поездов:
$t = frac{40 frac{км}{ч} cdot frac{1}{6} space ч}{40 frac{км}{ч} — 30 frac{км}{ч}} = frac{4}{6} space ч = frac{2}{3} space ч = 40 space мин$.
Используя полученное значение времени и скорость движения первого поезда, рассчитаем расстояние, на котором встретятся поезда:
$S = upsilon_1 t$,
$S = 30 frac{км}{ч} cdot frac{2}{3} space ч = 20 space км$.
Ответ: $t = 40 space мин$, $S = 20 space км$.
Задача №11
Поезд прошел $25 space км$ за $35 space мин$, причем первые $10 space км$ он прошел в течение $18 space мин$, вторые $10 space км$ в течение $12 space мин$, а последние $5 space км$ за $5 space мин$. Определите среднюю скорость поезда на каждом участке и на всем пути.
Дано:
$S = 25 space км$
$t = 35 space мин$
$S_1 = 10 space км$
$t_1 = 18 space мин$
$S_2 = 10 space км$
$t_2 = 12 space мин$
$S_3 = 5 space км$
$t_3 = 5 space мин$
$upsilon_{1ср} — ?$, $upsilon_{2ср} — ?$, $upsilon_{3ср} — ?$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Переведем время из $мин$ в $ч$:
- $t = 35 space мин = frac{35}{60} space ч = frac{7}{12} space ч$
- $t_1 = 18 space мин = frac{18}{60} space ч = frac{3}{10} space ч = 0.3 space ч$
- $t_2 = 12 space мин = frac{12}{60} space ч = frac{1}{5} space ч = 0.2 space ч$
- $t_3 = 5 space мин = frac{5}{60} space ч = frac{1}{12} space ч$
Теперь рассчитаем среднюю скорость на каждом участке пути:
- $upsilon_{1ср} = frac{S_1}{t_1}$,
$upsilon_{1ср} = frac{10 space км}{0.3 space ч} approx 33.3 frac{км}{ч}$ - $upsilon_{2ср} = frac{S_2}{t_2}$,
$upsilon_{2ср} = frac{10 space км}{0.2 space ч} = 50 frac{км}{ч}$ - $upsilon_{3ср} = frac{S_3}{t_3}$,
$upsilon_{3ср} = frac{5 space км}{frac{1}{12} space ч} = 60 frac{км}{ч}$
Рассчитаем среднюю скорость на на всем пути:
$upsilon_{ср} = frac{S}{t}$,
$upsilon_{ср} = frac{25 space км}{frac{7}{12} space ч} approx 42.9 frac{км}{ч}$
Ответ: $upsilon_{1ср} approx 33.3 frac{км}{ч}$, $upsilon_{2ср} = 50 frac{км}{ч}$, $upsilon_{3ср} = 60 frac{км}{ч}$, $upsilon_{ср} approx 42.9 frac{км}{ч}$.
Задали вычислить собственную скорость движения.
[Кристя]
Знаток
(304),
закрыт
5 лет назад
По физике задали вычислить собственную скорость движение. Знаю U=s:t,но, проблема в том, я не могу найти расстояние, т. к ходить по улице и вычислять очень трудно и долго. Как можно найти расстояние?
Сказали по шагам. Выяснила свой шаг в длину, и сколько шагов по улице .Что делать дальше? Помогите, пожалуйста!
Дивергент
Высший разум
(1537079)
10 лет назад
Ну, так засеки время и посчитай сколько шагов ты делаешь за минуту. Или наоборот, сколько секунд тебе потребуется, чтобы пройти 100 шагов. Затем умножь количество шагов на длину одного шага и подели на измеренное время. Получишь свою скорость.
Средняя скорость


4.6
Средняя оценка: 4.6
Всего получено оценок: 164.
Обновлено 13 Июля, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 164.
Обновлено 13 Июля, 2021
Важнейшей характеристикой тела в кинематике является скорость, с которой оно движется. Движение с нулевой скоростью фактически вообще не является движением. Однако скорость можно измерять различными методами и получать различные значения. Например, можно находить среднюю скорость. Рассмотрим эту тему подробнее: дадим определение средней скорости, приведем формулу средней скорости.
Движение и его скорость
Движение — это изменение координаты материальной точки со временем. Для вычисления быстроты изменения координаты используется такая физическая величина, как скорость (для обозначения используется символ $v$):
$$v={Delta x over Delta t}$$
Если движение происходит равномерно, то это отношение всегда будет одинаковым, независимо от выбора момента времени.
Например, если автомобиль движется со скоростью 36 км/ч, то за время $Delta t = 5c$ он пройдет расстояние $Delta x = 50м$, а за время $Delta t = 60c$ он пройдет расстояние $Delta x = 600м$.
Отношение пройденного расстояния ко времени перемещения в обоих случаях будет одинаковым и равным $v=10$м/с. Это и есть скорость движения автомобиля в данном примере.

Равномерное и неравномерное движение
Заметим, что автомобиль в приведенном примере на рассматриваемом промежутке времени $Delta t$ двигается равномерно. Но такое движение встречается довольно редко.
Тот же автомобиль когда-то стоял на месте, затем начал разгон и лишь потом двигался равномерно. А если рассмотреть ситуацию дальше — то рано или поздно автомобиль начнет замедление и остановится.
Получается, что скорость движения в рассматриваемом промежутке времени может изменяться. Движение с изменяемой скоростью называется неравномерным.
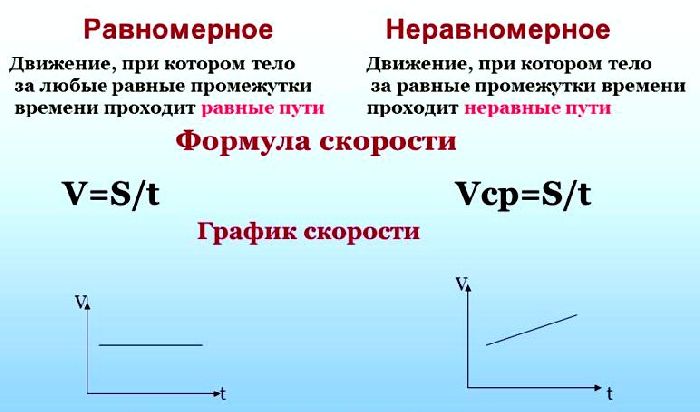
Средняя скорость
Как можно сравнивать скорости неравномерных движений?
Один из способов решения этой задачи — использование в физике такого понятия, как средняя скорость.
Идея состоит в том, чтобы пренебречь изменением скорости во время рассматриваемого промежутка времени, а рассматривать только начальный и конечный момент. Такое измерение удобно, если нам необходимо оценить общий результат движения.
В самом деле, как правило, целью движения является прибытие в конечный пункт к необходимому моменту времени. Как именно это достигнуто, зачастую неважно. Тело могло начать движение сразу и равномерно достигнуть конечного пункта. Могло, как автомобиль, сперва разогнаться, а потом затормозить в конечном пункте к тому же моменту времени. Наконец, тело могло двигаться «рывками», делая ряд остановок во время перемещения, но прибыть в конечный пункт, опять же, к тому же моменту времени.
Во всех трех приведенных случаях важно то, что тело начало и закончило движение в одни и те же моменты и переместилось за время движения на одно и то же расстояние. Что происходило во время движения, не рассматривается.
Скорость, рассчитываемая только по начальному и конечному моменту движения, называется средней. Для нахождения средней скорости необходимо найти отношение общего перемещения материальной точки ко времени, за которое это перемещение произошло.
$$v_{ср}={Delta x_{общ} over Delta t_{общ}}$$
Например, если автомобиль начал разгон в нулевой момент времени с нулевой скорости, разогнался до 50 км/ч, потом притормозил до 40 км/ч, и потом, через минуту, остановился в 600 м от начального пункта, то для нахождения средней скорости его движения необходимо 600 м поделить на 60 с. Средняя скорость составит 10 м/с.


Что мы узнали?
Одним из способов оценки скорости неравномерного движения является средняя скорость. При расчете средней скорости исходят только из начального и конечного моментов движения. А изменениями скорости между этими моментами пренебрегают. Средняя скорость удобна, если необходимо оценить общий результат движения, не обращая внимания на мелкие детали.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 164.
А какая ваша оценка?
