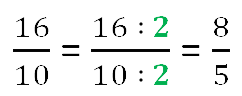Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Отношение чисел
Поддержать сайт
Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.
Если вам знакомо понятие отношение чисел, можете смело переходить к теме
пропорции.
Что называют отношением двух чисел
Запомните!
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Покажем на примере, где используется понятие отношение двух чисел.
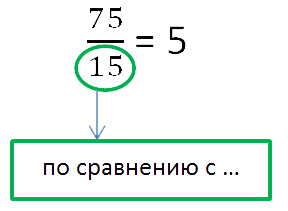
В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15.
В этом году — 75. Во сколько раз увеличилось количество участников в этом году по
сравнению с предыдущим годом?
Прежде чем решать задачу, подчёркиваем важные данные.
Запишем отношение количества участников в этом году к количеству участников в предыдущем.
Запомните!
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».
Запомните!
Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.
При внимательном изучении правила выше, можно подметить, что правило записанное выше,
есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.
Отношение 16 к 10:
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 апреля 2023 в 20:44
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
Вот задачка, которую дал на экзамене один из моих преподавателей. Студентам-первокурсникам нужно было найти связь между двумя рядами чисел. На всё про всё 30 секунд. Ещё 30 секунд на то, чтобы на листочке коротко написать ответ и сдать. Вас я во времени ограничивать не буду, думайте.
Задача на самом деле детская. Не решить её можно было только из-за стресса перед экзаменом и неожиданности. 30 секунд вполне достаточно, чтобы догадаться и написать ответ одним предложением.
Конечно, студенты рассчитывали на “отлично” автоматом для тех, кто решил, но нет… Преподаватель предлагал только тройку по 10-балльной шкале (это как три с большим минусом по пятибалльной системе). Впрочем, были те, кто соглашался.
Пока вы думаете, расскажу ещё один случай, который у нас в институте старшекурсники передавали младшекурсникам из уст в уста как легенду. Никто уже точно не знает, что это был за предмет, и что за преподаватель, и было ли это вообще в нашем институте или нет, но история следующая.
Приходят студенты в лекционную аудиторию на экзамен. Весь поток. Разумеется, отличники садятся на первые парты, а двоечники, прогульщики и оболтусы подальше, чтобы можно было списать. Заходит преподаватель, рисует на центральной доске большую окружность мелом, мочит тряпку, отжимает её, отдает первому студенту в первом ряду и просит бросить тряпку так, чтобы она попала в круг.
Тем, кто попал — отлично, остальным отвечать по всей строгости экзаменатора. Понятно, что почти все отличники, сидевшие на первом ряду, быстренько получили свои отлы и счастливые пошли отмечать. А вот оболтусы с последних парт остались сдавать и в большинстве своем ушли на пересдачу, потому что списать уже возможности не было..
Ну да ладно, это все легенды. Вернемся к нашей задаче. В ней, как я и говорил, все просто.
Первый ряд чисел — это просто числа, записанные в произвольном порядке. А второй ряд чисел — это количество букв в слове, которое обозначает число из первого ряда. Под единичкой написано 4, потому что в слове “ОДИН” четыре буквы. Под двойкой написано 3, потому что в слове “ДВА” три буквы и так далее. Вот и вся задачка.
Пишите в комментариях, кто решил, а кто не решил. Приглашаю всех на мой Ютуб канал и рекомендую посмотреть вот эти задачи: Чему равны круг, треугольник и квадрат? Детская задачка, которую взрослые решают слишком сложно
Задача из американского теста. Какое число должно быть следующим в последовательности и 4 варианта ответа
Вьетнамская задача для 3-классников. Расставь цифры от 1 до 9
Соотношение 1: упростить
:
Соотношение 2: сравнить
:
Результат упрощения
Результат сравнения
Вы можете использовать этот инструмент для получения наиболее упрощенного соотношения или для сравнения двух одинаковых соотношений.
Соотношение
Соотношение в математике — это термин, который используется для сравнения двух или более чисел. Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом». Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».
Что такое соотношение?
Соотношение определяется как сравнение двух величин в одних и тех же единицах измерения, которое показывает, сколько одного количества присутствует в другом количестве. Коэффициенты можно разделить на два типа. Одно из них — соотношение части к части, а другое — соотношение части к целому. Соотношение частей к частям показывает, как связаны две различные сущности или группы. Например, соотношение мальчиков и девочек в классе составляет 12: 15, тогда как соотношение частей к целому обозначает соотношение между определенной группой и целым. Например, из каждых 10 человек 5 любят читать книги. Таким образом, соотношение части к целому составляет 5: 10, что означает, что каждые 5 человек из 10 любят читать книги.
Формула соотношения
Мы используем формулу соотношения при сравнении соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b».
Форма дроби, представляющая это соотношение, — a/b. Чтобы еще больше упростить соотношение, мы следуем той же процедуре, которую используем для упрощения дроби. a:b = a/b. Давайте разберемся в этом на примере.
Пример. В классе из 50 учеников 23 девочки, а остальные мальчики. Найдите соотношение количества мальчиков к количеству девочек.
Общее количество студентов = 50; Количество девушек = 23.
Общее количество мальчиков = Общее количество учеников — Общее количество девочек
= 50 — 23
= 27
Таким образом, желаемое соотношение (Количество мальчиков: Количество девочек) равно 27:23.
Расчет коэффициентов
Для того чтобы рассчитать соотношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления пышных блинов необходимо 15 стаканов муки и 20 стаканов сахара, давайте рассчитаем соотношение муки и сахара, используемых в рецепте.
- Шаг 1: Найдите величины обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
- Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 15/20.
- Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 может быть упрощено до 3/4.
- Шаг 4: Поэтому соотношение муки к сахару можно выразить как 3:4.
Используйте бесплатный онлайн-калькулятор коэффициентов, чтобы проверить свои ответы при расчете коэффициентов.
Как упростить соотношения?
Соотношение выражает, сколько требуется одного количества по сравнению с другим количеством. Два термина в соотношении могут быть упрощены и выражены в их низшей форме. Соотношения, выраженные в их наименьших выражениях, легко понять и могут быть упрощены так же, как мы упрощаем дроби. Чтобы упростить соотношение, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, давайте упростим соотношение 18:10.
- Шаг 1: Запишите заданное соотношение a:b в виде дроби a/b. Записав соотношение в виде дроби, мы получим 18/10.
- Шаг 2: Найдите наибольший общий коэффициент ‘a’ и ‘b’. В этом случае GCF из 10 и 18 равен 2.
- Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, мы получаем, (18÷2)/(10÷2) = 9/5.
- Шаг 4: Представьте эту дробь в форме соотношения, чтобы получить результат. Таким образом, упрощенное соотношение составляет 9:5.
Используйте бесплатный онлайн-калькулятор коэффициентов упрощения, чтобы проверить свои ответы.
Советы и рекомендации по соотношению:
- В случае, если оба числа «a» и «b» равны в соотношении a: b, то a: b = 1.
- Если a > b в соотношении a : b, то a : b > 1.
- Если a < b в соотношении a : b, то a : b < 1.
- Перед их сравнением необходимо убедиться в том, что единицы измерения двух величин одинаковы.
Эквивалентные Соотношения
Эквивалентные соотношения аналогичны эквивалентным дробям. Если предшествующий (первый член) и последующий (второй член) данного соотношения умножаются или делятся на одно и то же число, отличное от нуля, это дает эквивалентное соотношение. Например, когда антецедент и следствие соотношения 1:3 умножаются на 3, мы получаем, (1 × 3) : (3 × 3) или 3: 9. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Аналогично, когда оба члена соотношения 20:10 делятся на 10, это дает 2:1. Здесь 20:10 и 2:1 являются эквивалентными соотношениями. Бесконечное число эквивалентных соотношений любого заданного соотношения может быть найдено путем умножения предшествующего и последующего на положительное целое число.
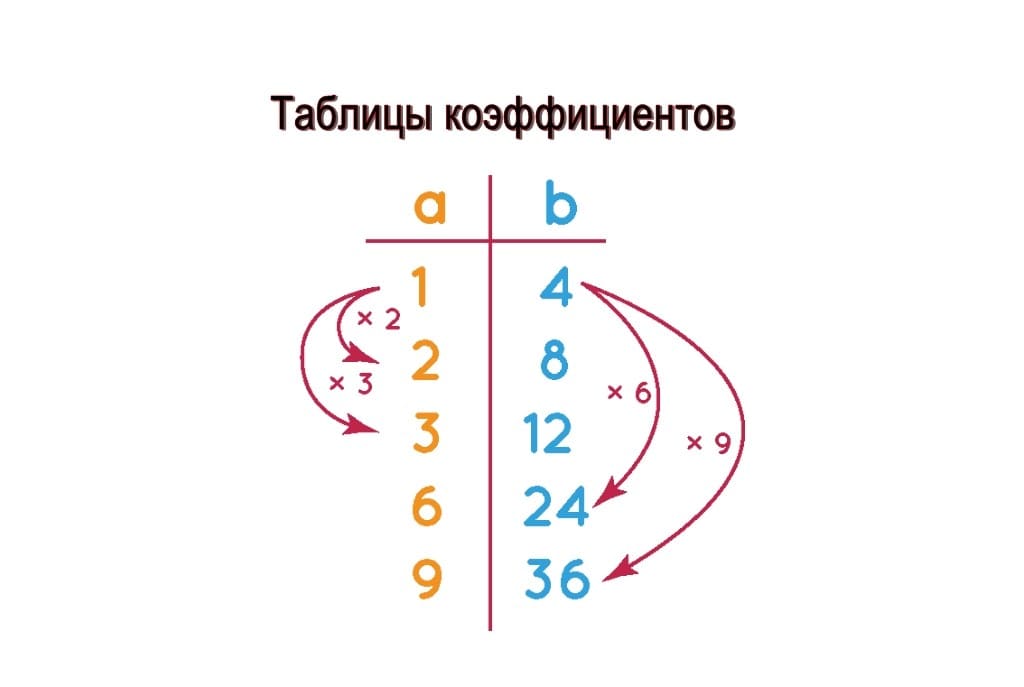
Таблица коэффициентов
Таблица коэффициентов — это список, содержащий эквивалентные коэффициенты любого заданного соотношения в структурированном виде. В следующей таблице соотношений приведено соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные соотношения связаны друг с другом умножением числа. Эквивалентные соотношения получаются путем умножения или деления двух членов соотношения на одно и то же число. В примере, показанном на рисунке, давайте возьмем соотношение 1:4 и найдем четыре эквивалентных соотношения, умножив оба члена соотношения на 2, 3, 6 и 9. В результате мы получаем 2:8, 3:12, 6:24, и 9:36.
Используйте бесплатный онлайн-калькулятор эквивалентных коэффициентов, чтобы проверить свои ответы.
Примеры соотношения
-
Пример 1. В школьном зале 49 мальчиков и 28 девочек. Выразите соотношение числа мальчиков к числу девочек.
Решение:
Учитывая, что количество мальчиков = 49, а количество девочек = 28. GCF 49 и 28 равен 7. Теперь, для упрощения, разделите два термина на их GCF, который равен 7. Это означает, (49 ÷ 7)/(28 ÷ 7) = 7/4. Следовательно, соотношение числа мальчиков к числу девочек = 7:4.
-
Пример 2: В музыкальном классе 30 учеников. 10 из них были взрослыми, а остальные — детьми. Каково соотношение числа детей к общему числу учащихся в музыкальном классе?
Решение:
Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно 20. Отношение общего числа детей к общему числу учащихся в музыкальном классе = 20: 30, что в упрощенном виде дает 2:3.
-
Пример 3: Упростите заданное соотношение, 87:75.
Решение:
Чтобы упростить данное соотношение, мы сначала найдем GCF 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшей форме равно 29:25.
Как ваш ребенок может овладеть математическими понятиями?
Математическое мастерство приходит с практикой и пониманием того, «Почему» стоит за «Что». Почувствуйте разницу в математике.
FAQ по соотношению
Что такое соотношение в математике?
Соотношение может быть определено как соотношение или сравнение между двумя числами одной и той же единицы измерения, чтобы проверить, насколько одно число больше другого. Например, если количество баллов, набранных в тесте, равно 7 из 10, то отношение полученных баллов к общему количеству баллов записывается как 7:10.
Каковы способы написания соотношения?
Соотношение может быть записано путем разделения двух величин с помощью двоеточия (:) или оно может быть записано в дробной форме. Например, если есть 4 яблока и 8 дынь, то соотношение яблок и дынь можно записать как 4: 8 или 4/8, что может быть дополнительно упрощено как 1: 2.
Как рассчитать Соотношение между двумя числами?
Для того чтобы рассчитать соотношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления крема для глазури необходимо 14 чашек сливочного масла и 28 чашек сахара, каково соотношение масла и сахара?
- Шаг 1: Обратите внимание на количество обоих ингредиентов, для которых мы определяем соотношение. В данном случае это 14 и 28.
- Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 14/28.
- Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 14/28 может быть упрощено до 1/2.
- Шаг 4: Поэтому соотношение сливочного масла к сахару можно выразить как 1:2.
Как найти эквивалентные соотношения?
Два коэффициента считаются эквивалентными, если при упрощении они представляют одно и то же значение. Эта концепция аналогична эквивалентным дробям. Например, когда соотношение 1: 4 умножается на 2, это означает умножение обоих членов в соотношении на 2. Таким образом, мы получаем, (1 × 2)/ (4 × 2) = 2/8 или 2: 8. Здесь 1:4 и 2:8 являются эквивалентными соотношениями. Аналогично, соотношение 30: 10 при делении на 10 дает соотношение 3:1. Здесь 30:10 и 3:1 являются эквивалентными соотношениями. Таким образом, эквивалентные соотношения можно найти с помощью операции умножения или деления в зависимости от чисел.
Что такое Таблица коэффициентов?
Таблица коэффициентов показывает список эквивалентных коэффициентов, которые получаются либо путем умножения, либо деления обеих величин на одно и то же значение. Например, если таблица коэффициентов начинается с соотношения 1 : 3, то последующие строки будут иметь 2:6, 3:9, 4:12, и так далее. Когда эти соотношения упрощены, они представляют одно и то же значение, то есть 1:3.
Что такое Золотое сечение?
Золотое сечение — это отдельное число, значение которого приблизительно равно 1,618. Символом для этого является греческая буква «phi», представленная как ϕ. Это особый атрибут, который используется в искусстве, геометрии и архитектуре, потому что считается, что золотое сечение создает наиболее приятную и красивую форму.Это также известно как божественная пропорция, которая существует между двумя величинами, и соотношение для расчета золотого сечения представлено как ϕ = a /b = (a + b)/a = 1,61803398875… где a и b — размеры двух величин, а a — большее между ними.
Почему важны Коэффициенты?
Соотношения важны, потому что они позволяют нам выражать величины таким образом, чтобы их было легче интерпретировать. Это инструмент, который используется для сравнения размеров двух или более величин по отношению друг к другу. Например, если в классе 30 девочек и 20 мальчиков. Мы можем представить количество девочек к числу мальчиков с помощью соотношения, которое в данном случае равно 3: 2.
Какова формула соотношения?
Формула соотношения используется для сравнения соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b».
Что такое Соотношение и Пропорция?
Соотношение — это соотношение или сравнение между двумя величинами одной и той же единицы измерения, чтобы проверить, насколько одно число больше другого. Он записывается как a/b или a: b, где b не равно нулю. Пропорция — это равенство двух соотношений. Пропорции используются для записи эквивалентных соотношений, которые помогают решить неизвестные величины. Например, пропорция выражается следующим образом: a: b = c: d
Как сравнить коэффициенты?
Существуют различные методы сравнения коэффициентов. Например, давайте сравним 1: 2 и 2: 3 с помощью метода LCM.
- Шаг 1: Запишите соотношения в виде дроби. Здесь это означает 1/2 и 2/3.
- Шаг 2: Уменьшите фракции по отдельности. Здесь обе фракции 1/2 и 2/3 уже находятся в их уменьшенной форме.
- Шаг 3: Теперь сравните 1/2 и 2/3, найдя LCM (наименьшее общее кратное) знаменателей. LCM 2 и 3 равно 6.
- Шаг 4: Сделайте знаменатели равными, умножив числитель и знаменатель первой дроби на 3, то есть, (1 × 3)/(2 × 3) = 3/6. Затем умножьте числитель и знаменатель второй дроби на 2, то есть, (2 × 2)/(3 × 2) = 4/6.
- Шаг 5: Теперь 3/6 и 4/6 можно легко сравнить. Это показывает, что 4/6 больше, чем 3/6. Следовательно, 2:3 > 1:2.
Как преобразовать соотношения в дроби?
Соотношения могут быть записаны в виде дробей очень простым способом. Предшествующее записывается как числитель, а последующее записывается как знаменатель. Например, если мы возьмем соотношение 3: 5. Здесь 3 — это предшествующее, а 5 — последующее. Итак, мы можем записать это как 3/5.
Как преобразовать дроби в соотношения?
Дроби могут быть записаны в виде соотношений после упрощения. Это означает, что мы сначала уменьшаем данную дробь до ее наименьших членов, а затем записываем числитель в качестве предшествующего, а знаменатель — в качестве последующего. Например, доля 16/48 сначала будет уменьшена до 1/3, а затем она может быть выражена в виде соотношения 1:3.
Как перевести коэффициенты в десятичные дроби?
Соотношения можно легко преобразовать в десятичные дроби, записав соотношение в виде дроби, а затем дробь преобразуется в десятичную дробь путем деления числителя на знаменатель. Например, 3:7 может быть записано как 3/7. Теперь 3/7 = 0,428.
Как преобразовать коэффициенты в проценты?
Коэффициенты можно преобразовать в проценты, выполнив следующие действия. Например, давайте преобразуем 5: 6 в виде процента.
- Шаг 1: Запишите соотношение в виде дроби. Здесь 5: 6 может быть записано как 5/6.
- Шаг 2: Умножьте эту дробь на 100 и добавьте символ процента. В этом случае 5/6 × 100 = 83,33%.
Как решать IQ задачи? Многие IQ задачи подчинены общим закономерностям. Уже само по себе прохождение iq теста раз за разом ведет к улучшению результата. Решая iq-задачи, вы вырабатываете iq навыки и умение правильно распределять время.
Существуют несколько основных типов задач. Попробуем их систематизировать. В большинстве задач на iq надо найти зависимость чисел, даже если это задание на связь букв. Зависимость между числами может быть подчинена не одной, а нескольким закономерностям.
Найти пропущенное число:
1) 2 6 10 … 18
Показать решение
Заменить вопрос числом:
2 3 6 15 42 ?
Показать решение
Определить закономерность и найти число:
2 3 8 27 112 ?
Показать решение
Найти недостающее число:
1) 17; 13; 11; ?; 5; 3; 2
Показать решение
2) 81; 49; 25; ?; 1
Показать решение
Как научить ребенка решать iq задачи? Для начала предложите ему поискать решение самостоятельно. Если найти зависимость между числами ему не удается, обсудите, какая числовая закономерность была использована в каждом конкретном случае. Постарайтесь не просто рассказывать ребенку решение, но, задавая наводящие вопросы, подводите его к самостоятельным выводам. Теперь попросите ребенка придумать для вас подобные задания. Отнеситесь к их разгадке со всей серьезностью. Расскажите ему, что зависимость чисел в каждом тесте может быть самая разная и надо пробовать использовать различные подходы, чтобы найти верное решение.
Регулярная IQ-тренировка — один из действенных способов развития логического мышления.
Если зависимость может быть любая (например, числа фиббоначи) – то никак. Можно поискать последовательность на oeis.org
Если же возможна только зависимость вида +a_0, +a_1, +a_2,…, +a_k, +a_0, +a_1… т.е. повторяющийся фиксированный паттерн приращений, то есть быстрое и простое решение.
Во первых, если вам дано 10 чисел, то всегда можно сказать, что есть паттерн длиной в 9 приращений.
Но можно найти кратчайший паттерн с помощью алгоритма поиска периода в строке. Буквально, по определению, нужный вам кратчайший паттерн (типа {+3, -2} для второго примера) будет периодом строки. Правда, тут не строка, а массив чисел, но это вообще никак не меняет алгоритмы. Просто у вас алфавит нестандартный.
Сначала от массива чисел перейдите к массиву приращений.
Потом можно применить жадное наивное решение – просто перебираете все возможные значения периода от 1 до n/2 и проверяете, что a[i] == a[i+str] для всех i. Как только все совпало – вы нашли период. Это решение за квадрат. Если чисел вам задано много, то можно применить префикс функцию: найдите значение префикс функции (p) для всей строки и, если ее значение больше половины длины строки, то у строки есть период n-p. Это будет линейное решение.
Еще можно применить алгоритм Дюваля. Тоже линейное решение, но более сложное в реализации и понимании.