Анализ связи между двумя переменными
Хотя результаты одномерного
анализа данных часто имеют самостоятельное
значение, большинство исследователей
уделяют основное внимание анализу
связей между переменными. Самым простым
и типичным является случай анализа
взаимосвязи (сопряженности) двух
переменных. Используемые здесь методы
задают некоторый логический каркас,
остающийся почти неизменным и при
рассмотрении более сложных моделей,
включающих множество переменных.
Устойчивый интерес социологов к
двумерному и многомерному анализу
данных объясняется вполне понятным
желанием проверить гипотезы о причинной
зависимости двух и более переменных.
Ведь утверждения о причинных взаимосвязях
составляют фундамент не только социальной
теории, но и социальной политики (по
крайней мере, так принято считать). Так
как возможности социологов проверять
причинные гипотезы с помощью эксперимента,
как уже говорилось, ограниченны, основной
альтернативой является статистический
анализ неэкспериментальных данных. В
общем случае для демонстрации
причинно-следственного отношения между
двумя переменными, скажем, X
и Y,
необходимо выполнить следующие
требования:
1) показать, что существует эмпирическая
взаимосвязь между переменными;
2) исключить возможность
обратного влияния Y
на X;
3) убедиться, что взаимосвязь между
переменными не может быть объяснена
зависимостью этих переменных от какой-то
дополнительной переменной (или
переменных).
Первым шагом к анализу
взаимоотношений двух переменных является
их перекрестная
классификация, или
построение таблицы
сопряженности. Речь
идет о таблице, содержащей информацию
о совместном распределении переменных.
Допустим, в результате одномерного
анализа данных мы установили, что люди
сильно различаются по уровню заботы о
своем здоровье: некоторые люди регулярно
делают физические упражнения, другие
– полностью пренебрегают зарядкой. Мы
можем предположить, что причина этих
различий – какая-то другая переменная,
например, пол, образование, род занятий,
доход и т. п.
Пусть мы располагаем
совокупностью данных о занятиях
физзарядкой и образовании для выборки
горожан. Для простоты мы предположим,
что обе переменные имеют лишь два уровня:
высокий и низкий. Так как данные об
образовании исходно разбиты на большее
количество категорий, нам придется их
перегруппировать, разбив весь диапазон
значений на два класса. Предположим, мы
выберем в качестве граничного значения
10 лет обучения, так что люди, получившие
неполное среднее и среднее образование,
попадут в «низкую» градацию, а остальные
– в «высокую». (Это, конечно, большое
огрубление, но мы используем его из
соображений простоты.) Для занятий
физическим^ упражнениями мы соответственно
воспользуемся двумя категориями –
«делают физзарядку» и «не делают
физзарядку». Таблица
8.3 показывает, как могло
бы выглядеть совместное распределение
этих двух переменных.
Таблица 8.3 Взаимосвязь
между уровнем образования и занятиями
физкультурой
-
Уровень
образованияВсего
Высокий
Низкий
Делают
зарядку50
200
250
Не делают
зарядку205
45
250
Всего
255
245
500
В таблице 8.3
два столбца (для образования) и две
строки (для занятий физкультурой),
следовательно, размерность этой таблицы
2х2. Кроме того, имеются дополнительные
крайний столбец и крайняя строка
(маргиналы таблицы), указывающие общее
количество наблюдений в данной строке
или в столбце. В правом нижнем углу
указана общая сумма, т. е. общее число
наблюдений в выборке. Не давшие ответа
уже исключены (для реальных данных их
число также стоит указать, но не в
таблице, а в подтабличной сноске). Заметим
здесь, что многие исследователи при
построении таких таблиц пользуются
неписаным правилом: для той переменной,
которую полагают независимой, отводится
верхняя строка (горизонталь), а зависимую
располагают «сбоку», по вертикали
(разумеется, соблюдение этого правила
не является обязательным и ничего с
точки зрения анализа не меняет).
Обычно характер взаимоотношений
между переменными в небольшой таблице
можно определить даже «на глазок»,
сравнивая числа в столбцах или строках.
Еще легче это сделать, если вместо
абсолютных значений стоят проценты.
Чтобы перевести абсолютные частоты,
указанные в клетках таблицы, в проценты,
нужно разделить их на маргинальные
частоты и умножить на 100. Если делить на
маргинал столбца, мы получим процент
по столбцу. Например,
50/255х100 = 19,6%, т. е. 19,6% имеющих
низкий уровень образования делают
зарядку (но не наоборот!). Если делить
на маргинал строки, то мы получим другую
величину –процент по
строке. В частности,
можно заметить, что 80% делающих зарядку,
составляют люди с высоким уровнем
образования(200/250х100). Деление на общую
численность выборки дает общий процент.
Так, всего в выборке 50% людей, делающих
зарядку.
Так как вывод о наличии
взаимосвязи между переменными требует
демонстрации различий между подгруппами
по уровню зависимой
переменной, при анализе
таблицы сопряженности можно
руководствоваться простыми правилами.
Во-первых, нужно определить независимую
переменную и, в соответствии с принятым
определением, пересчитать абсолютные
частоты в проценты. Если независимая
переменная расположена по горизонтали
таблицы, мы считаем проценты по столбцу;
если независимая переменная расположена
по вертикали, проценты берутся от сумм
по строке. Далее сравниваются процентные
показатели, полученные для подгрупп с
разным уровнем независимой переменной,
каждый раз внутри
одной категории зависимой переменной
(например, внутри категории делающих
зарядку). Обнаруженные различия
свидетельствуют о существовании
взаимосвязи между двумя переменными.
(В качестве упражнения примените
описанную процедуру к таблице
8.3, чтобы убедиться в
наличии связи между уровнем образования
и занятиями физкультурой.)
Отметим специально, что
элементарная таблица сопряженности
размерности 2х2 – это минимально необходимое
условие для вывода о наличии взаимосвязи
двух переменных. Знания о распределении
зависимой переменной недостаточно.
Нельзя, например, утверждать, будто из
того, что 75% детей-первенцев имеют
интеллект выше среднего, а 25% – средний
и более низкий, следует зависимость
между порядком рождения и интеллектом.
Необходимо проанализировать и
распределение показателей интеллекта
для детей-непервенцев. Варьировать
должна не только зависимая, но и
независимая переменная.
Таблица 8.4 Oбщая
форма таблицы сопряженности размерности
2х2
-
Переменная
ХВсего
0
1
Переменная
У0
а
б
А+б
1
с
д
С+д
Всего
А+с
Б+д
n

довольно ясно показывает, что всякое
приращение в размерах партийной кассы
(сдвиг вправо по оси Х)влечет за
собой увеличение парламентского
представительства (сдвиг вверх по
оси ординат). Между переменнымиХиYсуществуетлинейное отношение:если одна переменная возрастает по
величине, то это же происходит и с другой.
Помимо указания на природу отношения
двух переменных, диаграмма нарисунке
21позволяет также сделать некоторые
предположения обинтенсивности,силе этого отношения. Очевидно, что чем
более компактно, «скученно»
располагаются точки-наблюдения вокруг
пунктирной прямой линии (описывающейидеальное линейное отношение Х иY), тем сильнее зависимость. Нарисунке
22приведены еще три диаграммы
рассеивания.
Очевидно, что на рисунке 22акакая-либо
связь между x
и
y попросту
отсутствует. Нарисунке
22бвоображаемая прямая линия
(отмечена пунктиром) пересекла бы
диаграмму сверху вниз, из левого верхнего
в правый нижний угол. Иными словами,
линейная связь в этом случае имеет
обратное направление:
чем больше X,тем меньше зависимая переменная У.
Заметим также, что «кучность»
расположения точек вдоль воображаемой
прямойна рисунке 226не очень велика, а значит и связь
(корреляция) между переменными не только
обратная, отрицательная, но еще и не
очень сильная, умеренная. Наконец,на
рисунке 22в зависимую и независимую
переменную связывает явно нелинейное
отношение: воображаемый график
нисколько не похож на прямую линию и
напоминает скорее параболу12.
Отметим, что методы анализа, о которых
сейчас пойдет речь, не годятся для этого
нелинейного случая, так как обычная
формула для подсчета коэффициента
корреляции даст нулевое значение, хотя
связь между переменными существует.
Существует обобщенный показатель,
позволяющий оценить, насколько связь
между переменными приближается к
линейному функциональному отношению,
которое на диаграмме рассеивания
выглядит как прямая линия. Это коэффициент
корреляции,измеряющий тесноту связи
между переменными, т. е. их тен-денцию
изменяться совместно. Как и в рассмотренных
выше мерах связи каче-ственных признаков,
коэффициент корреляции позволяет
оценить возможность предсказания
значений зависимой переменной по
значениям независимой. Общая формула
для вычислениякоэффициента корреляции
Пирсонавключает в себя величинуковариациизначенийXиY.
Эта величина (sxy)характеризует совместное изменение
значений двух переменных. Она задается
как сумма произ-
12
Именно так обычно выглядит зависимость
между благожелательностью установки
по отношению к некоторому объекту
(X)
и интенсивностью установки (Y):
люди, занимающие крайне благожелательную
или крайне неблагожелательную позицию
в каком-то вопросе, обычно оценивают
свои убеждения как более выраженные и
интенсивные, чем те люди, чьи установки
лежат в области середины, «нейтральных»
значений шкалы.ведений отклонений
наблюдаемых значений Х
и У от средних X
и Y
соответственно, т. е. Ei=1n
(Xi
– Х )(Yi
–
Y
),
деленная на количество наблюдений.
Чтобы понять «физический смысл»
ковариации, достаточно обратить внимание
на следующее ее свойство: если для
какого-то объекта
i
в выборке оба значения
—X,
и
Y,—
окажутся высокими, то и произведение
(Хi
– Х)
на (Yi
– Y)
будет большим и положительным. Если
оба значения (по Х
и по Y)
низки, то произведение двух отклонений,
т. е. двух отрицательных чисел, также
будет положительным. Таким образом,
если линейная связь Х
и Y
положительна и велика, сумма таких
произведений для всех наблюдений также
будет положительна. Если связь между Х
и У обратная,
томногимположительным
отклонениям по Х
будут
соответствовать отрицательные
отклонения по Y,
т. е. сумма отрицательных произведений
отклонений будет отрицательной.
Наконец, при
отсутствии систематической связи
произведения будут иногда положительными,
иногда отрицательными, а их сумма (и,
следовательно, ковариация Х
и Y)
будет, в пределе, равна нулю. Таким
образом, ко вариация показывает
величину и направление связи, совместного
изменения Х
и У. Если разделить ковариацию
sxy
на стандартные отклонения
sx
и sy
(чтобы избавиться от влияния масштаба
шкал, в которых измеряются X
и Y),
то мы получим искомую формулу коэффициента
корреляции Пирсона
(rxy):
![]()
Более удобная для практических вычислений
расчетная формула выглядит так:

Несмотря на несколько устрашающий вид,
расчетная формула очень проста. Для
«ручного» вычисления rxy,вам понадобятся лишь пять величин: суммы
значений поXиY(Ei=1nХiиEi=1nYi),
суммы квадратов значений поХ и
Y (Ei=1nХ2иEi=1nY2),
суммы произведенийХ иYпо всем
объектам-«случаям» (Ei=1n
XiYi).
В таблице 8.11приведены данные о максимальных дневных
и ночных температурах, зарегистрированных
в 10городах13.
Просуммировав значения в столбцах, мы
получим E10 i=1Хi
=258иE10 i=1 Yi=156.
Возведя каждое из значений Х и
Yв квадрат и просуммировав, мы
найдем, чтоE10 i=1Хi2
= 7180иE10 i=1
Yi2
= 2962.Сумма попарных произведенийХiиYi(E10
i=1 XiYi)
составит 4359.Вы можете
самостоятельно убедиться в том, что
подстановка всех значений в расчетную
формулу даст (надеюсь) величинуrxy=0,91.
Иными словами, корреляция между дневными
и ночными температурами воздуха очень
высока, но все же отлична от
1,0(коэффициент корреляции может
меняться в пределах от-1,0 до
+1,0).Это отличие, вероятно, объясняется
влиянием других факторов (продолжительность
дня и ночи, облачность, географическое
положение и т. п.). Судя по полученной
величине корреляции, знание дневных
температур позволяетпредсказыватьночные температуры с очень высокой
точностью, но не безошибочно.
13Погода (Гидрометцентр
РФ) //Сегодня.
1994. 23авг.
|
Таблица 8.11 |
||
|
Город |
Дневная температура воздуха |
Ночная температура воздуха |
|
Лондон |
16 |
11 |
|
Париж |
21 |
12 |
|
Стокгольм |
20 |
12 |
|
Варшава |
25 |
14 |
|
Бонн |
25 |
16 |
|
Рим |
36 |
23 |
|
Тель-Авив |
31 |
23 |
|
Анкара |
32 |
15 |
|
Каир |
36 |
22 |
|
Москва |
16 |
8 |
|
N=10 |
Величина, которая равна квадрату
коэффициента корреляции Пирсона, т. е.
г, имеет ряд интересных статистических
свойств. Отметим сейчас, что r2является ПУО-мерой связи, подобной
обсуждавшимся выше (см. с.
176—179).Можно показать, что она
характеризует ту долю дисперсии значенийY, которая объясняется наличием
корреляции междуХ и Y.(Естественно, величинаr2будет
всегда положительной и не может
превзойти по абсолютной величине
коэффициент корреляции.)14Та
часть разброса в значенияхY, которая
не может быть предсказана по значениям
X,—этодисперсия
ошибки нашего прогноза,т. е.
1 –r2.Необъясненный
разброс в значенияхУприсутствует
в том случае, когда при равных уровнях
Х (ср., например, дневные температуры
в Варшаве и Бонне изтаблицы
8.11) сохраняются различия в
значенияхY.
Коэффициент корреляции позволяет
оценить степень связи между переменными.
Однако этого недостаточно для того,
чтобы непосредственно преобразовывать
информацию, относящуюся к одной
переменной, в оценки другой переменной.
Допустим, мы выяснили, что коэффициент
корреляции между переменными «величина
партийного бюджета» и «число мест в
парламенте» равен 0,8.Можем ли мы теперь предсказать, сколько
мест в парламенте получит партия,
годовой бюджет которой равен
100млн рублей? Похоже, что знание
величины коэффициента корреляции нам
здесь не поможет. Однако мы можем
вспомнить, что коэффициент корреляции
—это еще и оценка соответствия
разброса наших наблюдений той
идеальной модели линейного функционального
отношения, которое на рассмотренных
выше диаграммах рассеивания (см.рис.
21—22)представлено пунктирными
прямыми. Эти линии называютлиниями
регрессии.
Если бы все наблюдения аккуратно
«укладывались» на линию регрессии, то
для предсказания значения зависимой
переменной достаточно было бы восстано
вить перпендикуляр к оси
Y из той точки прямой, которая
соответствует известному значению
X.
14Подробный анализ
можно найти в большинстве руководств
по прикладной статистике. Здесь
мы ограничимся обсуждением общей логикиоценки объясненной дисперсии.
На рисунке 23показано, как можно было бы графически
определить ожидаемые значенияYдля гипотетического примера с партийной
кассой и местами в парламенте. (Разумеется,
найти искомое значение У можно и без
линейки, с помощью вычислений, если
известен угол наклона регрессионной
прямой и точка пересечения с осью
ординат.)
Как говорилось выше, линия регрессии
не обязательно должна быть прямой, но
мы ограничимся рассмотрением самого
простого случая линейной зависимости(нелинейные связи во многих случаях
также могут быть приближенно описаны
линейными отношениями).
Существуют специальные статистические
процедуры, которые позволяют найти
регрессионную прямую, максимально
соответствующую реальным данным.
Регрессионный анализ, таким образом,
дает возможность предсказывать
значенияYпо значениям Х с
минимальным количеством ошибок.В
общем виде уравнение, описывающее прямую
линию регрессии Y
no X,выглядит
так:
Y=ayx
+byx
X,
где Y—то предсказываемое значение по переменнойY(в только что рассмотренном
примере —количество
мест в парламенте),а —это точка, в которой прямая пересекает
осьY(т. е. значение Y для случая,
когдаX=0), и b—коэффициент
регрессии, т. е. наклон прямой. Часто
удобно измерять обе переменные не в
«сырых» шкалах, а в единицах отклонения
от среднего. Процедурастандартизации,т. е. перевода исходной шкалы в стандартные
Z-оценки,вам уже известна (см. с.
169).Преимущество использования
стандартизированных переменных в
регрессионном анализе заключается в
том, что линия регрессии в этом случае
проходит через начало координат.
Стандартизованный коэффициент
регрессии (наклон прямой) обозначают
обычно греческой буквой b(либо лат. b*).Правда, в отличие от b-коэффициента,
bне позволяет
прямо заключить, на какое количество
исходных единиц возрастет У при увеличенииХна одну единицу (например, насколько
увеличится число депутатских мандатов
при увеличении бюджета на 1млн рублей или насколько увеличивается
заработная плата при увеличении
стажа работы на один год). С другой
стороны, bпозволяет сопоставить
влияние на независимую переменную
контрольных переменных, измеренных в
разных шкалах.

Социологи обычно осуществляют
регрессионный анализ, используя
возможности распространенных
прикладных пакетов компьютерных программ
(например, SPSS).В этом
случае для нахождения линии регрессии,
лучше всего соответствующей данной
выборке наблюдений, которая представлена
точками на диаграмме рассеивания,
используют метод минимизации взвешенной
суммы квадратов расстояний между этими
точками и искомой прямой15.
Хотя здесь не место для обсуждения
статистических деталей, мы все же
сделаем несколько замечаний,
относящихся к осмысленному (или
бессмысленному) использованию техники
линейной регрессии.
Во-первых, как и в ранее обсуждавшихся
примерах анализа связи, наличие
координации, согласованности в
изменениях двух переменных еще не
доказывает, что обнаруженное отношение
носит собственно каузальный характер.
Проверка альтернативных причинных
моделей, иначе объясняющих эмпирическую
сопряженность переменных-признаков,
может основываться только на содержательных
теоретических представлениях.
Далее, нужно помнить о том, что регрессионные
коэффициенты в общем случае
асимметричны.Если мы решим, что это
У, а неХявляется независимой
переменной, то вполне можем рассчитать
другую по величине пару коэффициентов
—аxуиbxу.(Заметьте, что порядок букв в подстрочном
индексе значим: первой всегда идет
предсказываемая переменная, а второй
—предсказывающая.) Разумеется,
при выборе кандидатов в зависимые и
независимые переменные также важны
не статистические, а содержательные
соображения.
Если вернуться к затронутой выше
взаимосвязи между линейной регрессией
и корреляцией,то здесь мы можем
сделать следующие дополнения. Пусть
все точки-наблюдения аккуратно
размещены на регрессионной прямой.
Перед нами почти невероятный случай
абсолютной линейной зависимости. Зная,
например, что коэффициентb(нестандартизованный) равен
313,мы можем утверждать, что именно
такова величина воздействия переменнойXна зависимую переменнуюY.
Кроме того, мы можем точно сказать, что
единичная прибавка в величинеXвызовет увеличениеYна ту же величину,
313(если, допустим,Х—стаж работы, а У —зарплата,
то с увеличением стажа на год зарплата
растет на313рублей). В
этом случае коэффициент корреляции
будет равен в точности 1,0, что
свидетельствует о сильном, «абсолютном»,
характере связи переменных. Различие
между предсказанными и наблюдаемыми
значениями в этом случае отсутствует.
Корреляция как мера точности прогноза
показывает, что ошибок предсказания
просто нет.
15Более детальные
сведения можно найти в статистической
литературе. Очень доступно проблема
излагается, в частности, в кн.:Гласе
Дж., Стенли Дж.Указ. соч. С.
123—141.Для тех же, кто захочет
осуществить «ручную» регрессию для
какого-либо из использованных примеров,
просто приведем формулы для вычисления
нестандартизированных коэффициентов
(обозначения те же, что и выше):

В действительности, однако, из-за влияния
других переменных и случайной выборочной
ошибки точки-наблюдения обычно лежат
выше или ниже прямой, которая, как
говорилось, является лишь наилучшим
приближением реальных данных. Коэффициент
корреляции Пирсона rи величинаr2по-прежнему служат оценкой точности
прогноза, основанного на линии регрессии.
Вполне возможны ситуации, когда
коэффициент регрессии очень велик,
воздействиеXнаYпросто громадно, но корреляция низка
и, следовательно, точность прогноза
невелика. Нет ничего необычного и в
обратной ситуации: воздействиеХ на
Y относительно мало, а коэффициент
корреляции и объясненная дисперсия
очень велики. Посмотрев на приведенные
выше диаграммы рассеивания, можно легко
уяснить себесмысл отношения между
корреляцией и регрессией:первая
имеет прямое отношение к «разбросанности»
точек наблюдения (чем выше «разбросанность»,
тем нижеr2и ненадежнее
прогноз), тогда как коэффициент регрессии
описывает наклон, «крутизну» линии.
Однако существующее здесь различие
не стоит и преувеличивать: регрессионный
коэффициент (наклон прямой) для
стандартизованных данных в точности
равен коэффициенту корреляции Пирсонаr16. 16
Легко понять, что при измерении в единицах
стандартного отклонения максимальная
связь (Р=
1,0)
соответствует ситуации, когда сдвигу
от начала координат в
1 ед.
стандартного отклонения по Х
соответствует увеличение У также на
1 ед.
стандартного отклонения. Важно
заметить, что в случае стандартизированных
переменных (и только в этом случае)
коэффициенты регрессии
Y
no
X и
X noY
будут совпадать.
Предположим, что исследователь изучает
зависимость между образованием матери
(X)и образованием
детей (Y). Обе переменные измерены
как количество лет, затраченных на
получение образования. Найдя достаточно
высокую корреляцию междуХи У—скажем, равную 0,71, —он
также находит коэффициенты регрессииаиbи устанавливает, чтоr2(называемый также коэффициентом
детерминации) в данном случае приближенно
равен 0,5.Это значит, что
доля вариации в значениях переменнойY(образование детей), объясненная
воздействием переменной-предиктораХ(материнское образование), составляет
около 50%общей дисперсии
предсказываемой переменной. Коэффициент
корреляции между переменными достаточно
велик и статистически значим даже для
не очень большой выборки. Следовательно,
обнаруженная взаимосвязь переменных
не может быть объяснена случайными
погрешностями выборки. В пользу
предложенной исследователем причинной
гипотезы говорит и то обстоятельство,
что альтернативная гипотеза
—образование детей влияет на
образовательный статус родителей
—крайне неправдоподобна и может
быть отвергнута на основании
содержательных представлений о временной
упорядоченности событий. Однако все
еще не исключены те возможности, которые
мы обсуждали в параграфе, посвященном
методу уточнения. Иными словами, нам
следует считаться с вероятностью того,
что какая-то другая переменная (или
несколько переменных) определяют и
образование родителей и образование
детей (например, финансовые возможности
либо интеллект). Чтобы проверить такую
конкурирующую гипотезу, следует
рассчитать так называемуючастную
корреляцию.Логика расчета частной
корреляции совпадает с логикой построения
частных таблиц сопряженности при
использовании метода уточнения.
Построить частные таблицы сопряженности
для различных уровней контрольной
переменной в случае, когда переменные
измерены на интервальном уровне,—
это практически неразрешимая задача.
Чтобы убедиться в этом, достаточно
подсчитать, каким должно быть количество
таблиц уже при десяти-двенадцати
категориях каждой переменной. Расчет
коэффициента частной корреляции—
это простейшее средство уточнения
исходной причинной модели при введении
дополнительной переменной. Интерпретация
коэффициента частной корреляции не
отличается от интерпретации частных
таблиц сопряженности:частной
корреляцией называют корреляцию между
двумя переменными, когда статистически
контролируется, или «поддерживается
на постоянном уровне», третья
переменная (набор переменных).
Если, предположим, при изучении корреляции
между образованием и доходом нам
понадобится «вычесть» из полученной
величины эффект интеллекта, предположительно
влияющего и на образование, и на доход,
достаточно воспользоваться процедурой
вычисления частной корреляции. Полученная
величина будет свидетельствовать о
чистом влиянии образования на доход,
из которого «вычтена» линейная
зависимость образования от интеллекта.
Мюллер и соавторы 17приводят
интересный пример использования
коэффициента частной корреляции. В
исследовании П. Риттербэнда и Р.
Силберстайна изучались студенческие
беспорядки 1968—1969гг. Одна
из гипотез заключалась в том, что
число нарушений дисциплины и демонстраций
протеста в старших классах учебных
заведений связано с различиями показателей
академической успеваемости учащихся.
Корреляция между частотой «политических»
беспорядков и средней успеваемостью
оказалась отрицательной (хуже успеваемость
—больше беспорядков) и статистически
значимой(r = -0,36).Однако
еще более высокой была корреляция между
частотой беспорядков и долей чернокожих
учащихся (r=0,54). Исследователи решили
проверить, сохранится ли связь между
беспорядками и успеваемостью, если
статистически проконтролировать
влияние расового состава учащихся.
Коэффициент частной корреляции частоты
беспорядков и успеваемостипри контролерасового состава учащихся оказался
равным нулю. Исходная корреляция между
беспорядками и успеваемостью в данном
случае может быть описана причинной
моделью«ложной взаимосвязи» (см. рис.
19):наблюдаемые значения этих двух
переменных скор-релированы лишь потому,
что обе они зависят от третьей переменной
—доли чернокожих в общем количестве
учащихся. Чернокожие студенты, как
заметили исследователи, оказались
восприимчивее к предложенным самыми
активными «политиканами» образцам
участия в политических беспорядках.
Кроме того, их успеваемость, помимо
всяких политических событий, была
устойчиво ниже, чем средняя успеваемость
белых.
Коэффициент частной корреляции между
переменными Х и. Y
при контроле дополнительной переменной
Z(т. е. при поддержании Z«на постоянном уровне») обозначают
какrxy.z.Для его
вычисления достаточно знать, величины
наблюдаемых попарных корреляций
между переменнымиX, Yи Z
(т. е.простых корреляций —rxy, ryz, rxz):

Как всякая выборочная статистика,
коэффициент корреляции подвержен
выборочному разбросу. Существует
некоторая вероятность того, что для
данной вы-
17 Mueller
J., Schuessler К., Costner
H. Statistical Reasoning in Sociology.
3rd ed. Boston:
Haighton Mifflin Co,
1977. P. 279—281.
борки будет получено ненулевое значение
коэффициента корреляции, тогда как
истинное его значение для генеральной
совокупности равно нулю. Иными словами,
существует задача оценки значимостиполученных значений корреляций и
коэффициентов регрессии, относящаяся
к области теории статистического вывода.
Описание соответствующих статистических
методов выходит за рамки этой книги,
поэтому мы рассмотрим лишь самые общие
принципы, позволяющие решать описанную
задачу в простых случаях и интерпретировать
соответствующие показатели при
использовании стандартных компьютерных
программ.
Прежде всего вероятностная оценка
коэффициента корреляции подразумевает
оценку отношения к его случайной ошибке.
Удобная, хотя и не вполне надежная
формула для вычисления ошибки коэффициента
корреляции (тr),выглядит
так18:
![]()
Всегда полезно вычислить отношение
полученной величины rк его ошибке
(т. е.r/тi).В использовавшемся
нами примере данных о погоде коэффициент
корреляции оказался равен
0,91,а его выборочная ошибка составляет:
![]()
Отношение rк mrобозначаемое как t,составит (0,91/0,573)= 15,88.Разумеется, коэффициент, превосходящий
свою случайную ошибку почти в
16раз, может быть признан значимым
даже без построения доверительных
интервалов.
Когда значение г не столь близко к
единице и выборка невелика, нужно все
же проверить статистическую гипотезу
о равенстве rнулю в генеральной
совокупности. Для этого нужно
определить tпо формуле:

где t —это величина так называемого
t-критерияСтьюдента (см. также главу
4),г —выборочный
коэффициент корреляции,п
—объем выборки. Для установления
значимости вычисленной величины
t-критерияпользуются таблицами
t-распределениядля (n – 2)степеней свободы (см.табл.
4.1).Во многих пособиях по статистике
можно найти и готовые таблицы критических
значений коэффициента корреляцииrдля данного уровня значимостиа. В
этом случае отпадает необходимость
в каких-либо вычислениях t:достаточно сравнить полученную величину
коэффициента корреляции с табличным
значением19. (Например, величина
коэффициента корреляцииr
= 0,55будет существенной на уровне
значимостир = 0,01даже
для выборки объемом 105,так как критическое значение составляет
0,254.)
18См.:Дружинин Н.
К.Логика оценки статистических
гипотез. М.: Статистика, 1973.
С. 112—114.
“См., в частности:Ликеш
И., Ляга И.Основные таблицы математической
статистики. М.: Финансы и статистика,
1985.(Табл. 14.)
Множественная регрессия
и путевой анализ
Выше описывалась модель линейной
регрессии для двух переменных. В
действительности социолог довольно
редко сталкивается со столь простыми
моделями данных. Влияние одного
фактора обычно может объяснить лишь
часть разброса наблюдаемых значений
независимой переменной. Метод частной
корреляции позволяет нам проконтролировать
эффекты воздействия любых других
контрольных переменных, которые мы в
состоянии измерить. (Стоит снова
подчеркнуть здесь, что статистические
методы изучения причинных взаимосвязей,
в отличие от экспериментальных,позволяют нам контролировать лишь те
источники вариации, которые мы способны
концептуализировать и измерить.) Однако
еще более интересной задачей является
контроль одновременного воздействиянесколькихнезависимых наоднузависимую переменную, а также сравнение
эффекта воздействия разных независимых
переменных и предсказание «отклика»
независимой переменной. Именно эти
задачи решают методы анализа, о
которых пойдет речь в данном параграфе.
Наше изложение будет неполным, так
как более детальное обсуждение требует
дополнительной математической
подготовки. Мы будем ориентироваться
на сравнительно скромные цели понимания
общей логики и интерпретации результатов
соответствующих статистических
процедур.
Уравнение множественной регрессии
—это определенная модельпорождения
данных.Важные допущения, принимаемые
в этой модели, касаются уже известного
вам требованиялинейности,а такжеаддитивностисуммарного эффекта
независимых переменных. Последнее
означает, что воздействия разных
независимых переменных просто
суммируются, а не, скажем, перемножаются
(мультипликативный эффект, в отличие
от аддитивного, имеет место тогда, когда
величина воздействия одной независимой
переменной на зависимую, в свою очередь,
находится под влиянием другой независимой
переменной, т. е. независимые переменные
взаимодействуют друг с другом).
Множественная регрессия во многом
аналогична простой (бивариантной)
регрессии. Отличие состоит в том, что
регрессия осуществляется по двум и
более независимым переменным одновременно,причем каждая из них входит в регрессионное
уравнение с коэффициентом, позволяющим
предсказать значения зависимой переменной
с минимальным количеством ошибок
(критерием здесь снова является метод
наименьших квадратов). Частные коэффициенты
в уравнении множественной регрессии
показывают, какой будет величина
воздействия соответствующей независимой
переменной на зависимуюпри контролевлияния других независимых переменных.
Если воспользоваться простейшей
системой обозначений, то уравнение
множественной регрессии для трех
независимых переменных можно записать
как:
![]()
где Y—это предсказываемое
значение зависимой переменной,X1
… Х3,—независимые переменные, аb,
…b3,
—частные коэффициенты регрессии
для каждой из зависимых переменных.
Коэффициенты bмогут быть
интерпретированы как показатели влияния
каждой из независимых переменных на
зависимую при контроле всех других
независимых переменных в уравнении.
В отличие от коэффициентов частной
корреляции коэффициенты регрессии
обладают размерностью. Они показывают,на
сколько единиц изменится зависимая
переменная при увеличении независимой
на одну единицу (при контроле всех
остальных переменных модели). Пусть,
например, мы построили уравнение
множественной регрессии, описывающее
зависимость дохода от интеллекта(Х1)и стажа работы(Х2).Если величинаb1оказалась
равной 100,это означает,
что каждый дополнительный балл по шкале
интеллекта увеличивает доход на
100рублей. Значениеb2=
950 говорит нам, что год стажа прибавляет
950рублей. Однако «сырые» оценки
интеллекта и стажа измерены в разных
единицах. Для определениясравнительной
значимостинезависимых переменных,
входящих в уравнение множественной
регрессии, мы должны подвергнуть все
переменныестандартизации(т. е.
перевести их в Z-оценки,см. выше). Стандартизованные коэффициенты
множественной регрессии, которые удобнее
всего обозначать какb*(либо греч.
«бета» — B),меняются в пределах от -1,0до +1,0.Они сохраняют свою
величину при изменении масштаба шкалы:
переход от измерения возраста в годах
к измерению в днях не изменит
соответствующийb*.
Стандартизованные коэффициенты позволяют
оценить «вклад» каждой из
переменных-предикторов в предсказание
значений независимой переменной.
Если в примере с влиянием интеллекта и
стажа работы на доход окажется, что
b1*= 0,25,
a b2*=0,30,то можно заключить, что сравнительная
значимость «веса» интеллекта и стажа
в предсказании дохода различаются
незначительно. Если же для одной
переменнойb1*
=0,80,тогда какb2*
=0,40, мы можем сказать, что эффект
воздействия второй переменной в два
раза меньше эффекта первой.
Чтобы определить ожидаемые значения
зависимой переменной для отдельных
индивидов, достаточно подставить в
уравнение множественной регрессии
соответствующие значения
переменных-предикторов и вычисленных
коэффициентов Ь.Пусть, например,
мы хотим рассчитать прогнозное значение
величины дохода для человека, чей
коэффициент интеллекта равен
110,а стаж работы — 20годам. Еслиb1,
как в вышеприведенном примере,
составляет 100,
b2
= 950, а слагаемое а
= 50000,то мы получим:
ожидаемый доход = 50000 +100х 110 + 950х 20 =
80000руб.
Множественную регрессию можно использовать
и для предсказания средних групповых
значений,например среднего дохода
мужчин-врачей. Единственное различие
в данном случае заключается в использованиисредних значений независимых
переменныхдля подстановки в уравнение
множественной регрессии. В качестве
независимой переменной множественной
регрессии могут использоваться и
дихотомические переменные, которым
приписывают значения 0и
1 (например, пол). Для того чтобы
включить в уравнение номинальную
переменную с более чем двумя
категориями, нужно создать соответствующее
число новых,«фиктивных» переменных,каждая из которых будет кодироваться
как О или 1в зависимости
от наличия или отсутствия категории-признака.
Скажем, состоящую из трех категорий
переменную «цвет глаз» можно представить
с помощью трех переменных:Х1
—«голубые глаза»,Х2
—«карие глаза»,Х3,
— «зеленые глаза». (Человек с
голубыми глазами получит 1поХ1и 0по
двум другим переменным.)
|
Таблица 8.12 Множественный |
|||
|
Независимая переменная |
Коэффициент b |
Коэффициент b* |
p< |
|
Индекс совокупного тиража порнографических |
6,99 |
0,52 |
0,001 |
|
Показатель числа убийств и непредумышленных |
1,70 |
0,55 |
0,001 |
|
Показатель числа публичных оскорблений |
0,04 |
0,32 |
0,001 |
|
Индекс положения женщин |
0,43 |
0,27 |
0,014 |
|
Число грабежей |
-0,03 |
-0,25 |
0,052 |
|
Процент черного населения |
-0,41 |
-0,38 |
0,001 |
|
Процент живущих ниже федерального |
1,11 |
0,29 |
0,011 |
Метод множественной регрессии очень
популярен среди социологов. Вот,
например, как выглядели результаты
его применения в исследовании Л. Бэрона
и М. Строса, изучавших факторы, влияющие
на статистику изнасилований20.
Использованная в планировании этого
исследования матрица данных включала
в себя в качестве объектов («случаев»)
различные штаты США. Признаками, по
которым описывались штаты, служили
около десятка независимых и собственно
контрольных переменных, предположительно
воздействующих на зависимую
переменную,—количество
зарегистрированных полицией изнасилований
на 100000населения в год
для данного штата (по данным ежегодных
статистических отчетов ФБР). Предполагалось,
что существующие различия между штатами
в уровне изнасилований можно будет
объяснить различиями в уровнях независимых
переменных. Нужно отметить, что разброс
«случаев» по зависимой переменной был
весьма велик —от
71,9на Аляске до 8,2в
Северной Дакоте (1979).Из десятка переменных, включенных в
уравнение множественной регрессии,
девять оказались статистически значимы.
Основные результаты регрессионного
анализа для семи переменных представлены
втаблице 8.12.
Из таблицы видно, что индекс совокупного
тиража порнографических журналов
(интегральный показатель, учитывающий
уровни продаж восьми популярных
изданий) имеет коэффициент регрессии
6,99.Это означает, что рост индекса
на единицу в среднем увеличивает
количество изнасилований почти на7случаев (в расчете на 100000населения). Весьма значительно и влияние
числа убийств, что особенно заметно
при сравнении стандартизованных
коэффициентов (b*), не зависящих
от шкалы измерения признака. Фактически
количество убийств вносит самый
значительный «вклад» в предсказание
значений зависимой переменной (b*
= 0,55).Интересно отметить, что одна
из независимых переменных в описываемом
исследовании —индекс
положения женщин, рассчитанный на
основании 22-х политических, экономических
и социальных индикаторов,—при
анализе простых взаимосвязей
продемонстрировала практически
нулевую корреляцию с количеством
изнасилований (г = 0,17),причем
20 Baron
L., Strauss M. A. Sexual
Stratification, Pornography, and Rape in the United States //
Malamuth
N.. Donnerstein E. (eds.)
Pornography and Sexual Aggression. Orlando etal.:
Academic Press, 1984.
P. 185—209.
21Таблица приводится
в сокращении по источнику:
Baron L, Strauss V. A.
Sexual Stratification, Pornography, and Rape…
результаты анализа диаграммы рассеивания
также не дали никаких свидетельств в
пользу гипотезы о нелинейной связи.
Множественная регрессия позволила
уточнить первоначальные выводы: при
контроле прочих переменных модели, чем
вышестатус женщин, темвышеуровень изнасилований (результат,
которому довольно трудно найти
теоретическое объяснение). Использование
девяти независимых переменных позволило
объяснить 83%дисперсии в
показателях количества изнасилований
(квадрат коэффициента множественной
корреляцииr2составил
0,83).
При интерпретации результатов
множественной регрессии стандартизованные
коэффициенты, как уже говорилось,
используют в качестве показателей
значимости, «вклада» соответствующих
переменных. Эта трактовка верна лишь в
определенных пределах. При нарушении
некоторых условий сравнение абсолютных
величин стандартизованных коэффициентов
может вести к неверным выводам. Дело в
том, что коэффициенты регрессии подвержены
влиянию случайных ошибок измерения(см. с. 116).Использованиененадежных индикаторов«сдвигает»
регрессионные коэффициенты к нулю22.
Иными. словами,более надежныеиндикаторы даютболее высокиеоценки
коэффициентов. Пусть, например, для
предсказания риска сердечно-сосудистых
заболеваний использовались две
независимые переменные индивидуального
уровня—«ориентация на
достижения» и «склонность подавлять
агрессию»,—причем
шкала для измерения первой обладалаболее высокимкоэффициентом
надежности. Если стандартизованный
коэффициент регрессии для достиженческой
мотивации окажетсявыше,чем для
подавления агрессии, это может
рассматриваться как следствие таких
содержательных различий между
переменными, которые важны с точки
зрения теории психосоциальных
факторов заболеваемости. Но нельзя
исключить и альтернативное объяснение,
связывающее более высокий регрессионный
коэффициент первой переменной с побочными
эффектами методов измерения: влияние
ориентации на достижения не превосходит
влияния, оказываемого на риск инфаркта
склонностью подавлять агрессию, а
наблюдаемые различия регрессионных
коэффициентов связаны лишь с ненадежностью
использованных индикаторов склонности
к подавлению.
Другая проблема, требующая некоторой
осторожности в интерпретации коэффициентов
регрессии, возникает вследствие того,
что модель множественной регрессии
не обязывает нас ни к каким строгим
предположениям о причинных связях
между независимыми переменными.Регрессионное уравнение, образно
говоря, не делает никаких различий между
собственно независимыми, т. е. теоретически
специфицированными, переменными и
дополнительными—контрольными,
опосредующими и т. п.—факторами,
вводимыми в модель с целью уточнения.
В тех случаях, когда теоретическая
гипотеза, проверяемая в ходе исследования,
допускает: 1)существование
взаимосвязей между независимыми
переменными, 2)наличие
прямых и косвенных (опосредованных)
влияний, а также 3)использование нескольких индикаторов
для каждого латентного фактора, могут
понадобиться более совершенные
статистические методы. Одна из возможностей
здесь—это использованиепутевого анализа.
22Это явление
называютаттенюацией.Существуют
специальные методы внесения поправок
на аттенюацию, но здесь они обсуждаться
не будут.
Путевой анализ —
один из основных способов построения
и проверки причинных моделей в
социологии.Многие более продвинутые
статистические техники основаны на
сходной исследовательской методологии.
Важным достоинством путевого анализа
является то, что он позволяет оценить
параметры каузальных моделей, причем
в расчет принимаются не только прямые,но инепрямые (опосредованные)влияния. Если, например, в результате
корреляционного или регрессионного
анализа мы обнаружили, что интеллект
(измеренный как IQ)лишь
умеренно влияет на доход, нам не следует
торопиться с общими выводами. Мы
оставили неучтенной возможность того,
что интеллект может иметь существенное
влияние на образование, которое, в свою
очередь, воздействует на последующий
доход. Таким образом, нам нужно принять
во внимание то, что интеллект
—помимо прямого эффекта
—может иметь еще и опосредованное,
непрямое влияние на доход посредством
влияния на образование. Методы,
рассматривавшиеся нами до сих пор,
описывали только прямые эффекты.
Путевой анализ включает в себя технику
представления прямых и косвенных
причинных влияний при помощи специальных
диаграмм (потоковых графов). Эти диаграммы
часто называют просто причинными
(структурными) моделями.
Последовательно «считывая» такую
модель, можно легко определить все пути
влияния одной переменной на другую и
соответственно оценить величину чистого
эффекта. Во многих разделах этой книги
причинные модели уже использовались
для представления сравнительно сложных
причинных гипотез (см., например, с.
122),поэтому общая логика их построения
не требует детального обсуждения.
Порядок представления переменных на
диаграмме отражает предполагаемое
направление причинной связи, а диапазон
включенных в диаграмму переменных
и отношения между ними зависят от
принятых исследователем теоретических
гипотез. Так называемыепутевые
коэффициенты,описывающие связи
между переменными (связям соответствуют
стрелочки на диаграмме),равны
стандартизованным коэффициентам
множественной регрессии (b*)23.
Обычно путевую диаграмму рисуют слева
направо —от самых «ранних»
по порядку следования независимых
переменных до зависимой. Путевые
коэффициенты часто обозначают
латинскими«р»с подстрочными
индексами(р21
— это путевой коэффициент для
связи между переменнымиX1
—>Х2).Нарисунке
24в качестве примера
изображена путевая диаграмма, отражающая
гипотетические отношения между
интеллектом(Х1),образованием(Х2),социально-экономическим статусом(Х3),доходом(Х4)и размерами сбережений(Х5).
Специальные правила позволяют перевести
отношения, изображенные на диаграмме,
в совокупность структурных уравнений,описывающих механизмы прямого и
опосредованного воздействия одних
переменных на другие. Нарисунке
24,в частности, видно, что не
существует пути дляпрямого воздействия
интеллекта на размеры сбережений,
однако общий эффект воздействия
интеллекта будет включать в себясовокупность непрямых эффектов:
X1воздействует наX5 и
через образование(Х2),и через достигнутый статус(Х3),и через доход(Х4).Иными
словами, хотя и нельзя утверждать, что
склонность откладывать деньги «в
кубышку» зависит от умственных
способностей, последние влияют
23В оценивании также
используется метод наименьших квадратов.
и на возможность получения образования,
и на статус, и на доход. В свою очередь,
люди с определенным социальным и
экономическим статусом обнаруживают
склонность иметь сбережения.
В общем случае, полный эффект влияния
переменной равен сумме ее непосредственного
эффекта и всех косвенных эффектов
влияния.Величины возмущений (е2
— e4)
Haрисунке позволяют оценить, насколько
хорошо работает модель, показывая,
какая часть дисперсии соответствующей
переменной осталась необъясненной. В
результате путевой анализ позволяет
пересматривать и уточнять исходную
теоретическую модель, сравнивать
«эффективность» нескольких
конкурирующих теорий для объяснения
существующей совокупности эмпирических
наблюдений. Существуют даже компьютерные
программы, осуществляющие автоматический
поиск наилучшей структурной модели, т.
е. процедуру, сходную с отбором из
нескольких существующих теорий такой,
которая максимально соответствовала
бы полученным в исследовании данным24.
Важно, однако, осознавать, что сами по
себе результаты применения регрессионных
методов и причинных моделей (регрессионные
коэфициенты, линии регрессии, путевые
диаграммы) решают прежде всего задачуобобщенного описанияуже полученных
эмпирических данных. Они могут служить
надежной основой для интерполяции,
оценки положения гипотетических «точек»
в пределах ряда наблюдавшихся значений,
однако их использование в целяхэкстраполяции и прогнозаможет
вести к существенным ошибкам в тех
случаях, когда такой прогноз не
подкреплен более широкой теорией, не
сводимой к отдельной модели для конечной
совокупности данных. (Достаточно указать
в качестве примера на многочисленные
ошибочные прогнозы в экономике
—на уке, где количество эмпирических
данных и описывающих их структурных
моделей многократно превзошло количество
существующих теорий.)
24Подробнее см.:И.
Ф. Девятко.Диагностическая процедура
в социологии: очерк истории и теории.
М.: Наука, 1993.С.121—136.
Путевой анализ, как и множественная
регрессия, сегодня является частью
большинства стандартных статистических
программ для компьютера. Не стоит,
однако, забывать о том, что при любом
уровне прогресса в компьютерном
обеспечении задать причинную модель,
т. е. совокупность содержательных
гипотез, подлежащих статистическому
оцениванию,может только сам
исследователь.
Дополнительная литература
Вайнберг Дж., Шумекер Дж..Статистика. М.: Финансы и статистика,
1979.
Гласе Дж., Стэнли Дж.Статистические
методы в педагогике и психологии.
М.: Прогресс, 1976.
Интерпретация и анализ данныхв
социологическом исследовании. М.: Наука,
1987.
Татарова Г. Г.Типологический анализ
в социологии. М.: Наука,
1993.
Типология и классификацияв
социологических исследованиях. М.:
Наука, 1982.
Толстова Ю. Н.Логика математического
анализа социологических
данных. М.: Наука, 1991.
Хейс Д.Причинный анализ в статистических
исследованиях. М.:
Финансы и статистика, 1981.
Флейс Дж.Статистические методы для
изучения таблиц долей и пропорций. М.:
Финансы и статистика, 1989.
Ядов В. А.Социологическое исследование:
методология, программа, методы. 2-е
изд. М.: Наука, 1987.Гл.
5.
Исследуем отношение между переменными¶
В этой главе исследуются отношения между переменными.
-
Мы будем визуализировать отношения с помощью диаграмм рассеяния (scatter plots), диаграмм размаха (box plots) и скрипичных диаграмм (violin plots),
-
И мы будем количественно определять отношения, используя корреляцию (correlation) и простую регрессию (simple regression).
Самый важный урок этой главы заключается в том, что вы всегда должны визуализировать взаимосвязь между переменными, прежде чем пытаться ее количественно оценить; в противном случае вас могут ввести в заблуждение.
In [1]:
from os.path import basename, exists def download(url): filename = basename(url) if not exists(filename): from urllib.request import urlretrieve local, _ = urlretrieve(url, filename) print('Downloaded ' + local) download('https://github.com/AllenDowney/' + 'ElementsOfDataScience/raw/master/brfss.hdf5')
Изучение отношений¶
В качестве первого примера мы рассмотрим взаимосвязь между ростом и весом.
Мы будем использовать данные из Системы наблюдения за поведенческими факторами риска (BRFSS), которая находится в ведении Центров по контролю за заболеваниями по адресу https://www.cdc.gov/brfss.
В опросе приняли участие более 400 000 респондентов, но, чтобы произвести анализ, я выбрал случайную подвыборку из 100 000 человек.
In [2]:
import pandas as pd brfss = pd.read_hdf('brfss.hdf5', 'brfss') brfss.shape
Out[3]:
| SEX | HTM4 | WTKG3 | INCOME2 | _LLCPWT | _AGEG5YR | _VEGESU1 | _HTMG10 | AGE | |
|---|---|---|---|---|---|---|---|---|---|
| 96230 | 2.0 | 160.0 | 60.33 | 8.0 | 1398.525290 | 6.0 | 2.14 | 150.0 | 47.0 |
| 244920 | 2.0 | 163.0 | 58.97 | 5.0 | 84.057503 | 13.0 | 3.14 | 160.0 | 89.5 |
| 57312 | 2.0 | 163.0 | 72.57 | 8.0 | 390.248599 | 5.0 | 2.64 | 160.0 | 42.0 |
| 32573 | 2.0 | 165.0 | 74.84 | 1.0 | 11566.705300 | 3.0 | 1.46 | 160.0 | 32.0 |
| 355929 | 2.0 | 170.0 | 108.86 | 3.0 | 844.485450 | 3.0 | 1.81 | 160.0 | 32.0 |
BRFSS включает сотни переменных. Для примеров в этой главе я выбрал всего девять.
Мы начнем с HTM4, который записывает рост каждого респондента в см, и WTKG3, который записывает вес в кг.
In [4]:
height = brfss['HTM4'] weight = brfss['WTKG3']
Чтобы визуализировать взаимосвязь между этими переменными, мы построим диаграмму рассеяния (scatter plot).
Диаграммы рассеяния широко распространены и понятны, но их на удивление сложно правильно построить.
В качестве первой попытки мы будем использовать функцию plot с аргументом o, который строит круг для каждой точки.
см. документацию по plot
In [5]:
import matplotlib.pyplot as plt %matplotlib inline plt.plot(height, weight, 'o') plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Похоже, что высокие люди тяжелее, но в этом графике есть несколько моментов, которые затрудняют интерпретацию.
Первый из них – перекрытие (overplotted), то есть точки данных накладываются друг на друга, поэтому вы не можете сказать, где много точек, а где только одна.
Когда это происходит, результаты могут вводить в заблуждение.
Один из способов улучшить график – использовать прозрачность (transparency), что мы можем сделать с помощью ключевого аргумента alpha. Чем ниже значение alpha, тем прозрачнее каждая точка данных.
Вот как это выглядит с alpha=0.02.
In [6]:
plt.plot(height, weight, 'o', alpha=0.02) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Уже лучше, но на графике так много точек данных, что диаграмма рассеяния все еще перекрывается. Следующим шагом будет уменьшение размеров маркеров.
При markersize=1 и низком значении alpha диаграмма рассеяния будет менее насыщенной.
Вот как это выглядит.
In [7]:
plt.plot(height, weight, 'o', alpha=0.02, markersize=1) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Уже лучше, но теперь мы видим, что точки строятся отдельными столбцами. Это потому, что большая часть высоты была указана в дюймах и преобразована в сантиметры.
Мы можем разбить столбцы, добавив к значениям некоторый случайный шум; по сути, мы заполняем округленные значения.
Такое добавление случайного шума называется дрожанием (jittering).
Дрожание – это добавление случайного шума к данным для предотвращения перекрытия статистических графиков. Если непрерывное измерение округлено до некоторой удобной единицы, может произойти перекрытие. Это приводит к превращению непрерывной переменной в дискретную порядковую переменную. Например, возраст измеряется в годах, а масса тела – в фунтах или килограммах. Если вы построите диаграмму разброса веса в зависимости от возраста для достаточно большой выборки людей, там может быть много людей, записанных, скажем, с 29 годами и 70 кг, и, следовательно, в этой точке будет нанесено много маркеров (29, 70).
Чтобы уменьшить перекрытие, вы можете добавить к данным небольшой случайный шум. Размер шума часто выбирается равным ширине единицы измерения. Например, к значению 70 кг вы можете добавить количество u , где u – равномерная случайная величина в интервале [-0,5, 0,5]. Вы можете обосновать дрожание, предположив, что истинный вес человека весом 70 кг с равной вероятностью находится в любом месте интервала [69,5, 70,5].
Контекст данных важен при принятии решения о дрожании. Например, возраст обычно округляется в меньшую сторону: 29-летний человек может праздновать свой 29-й день рождения сегодня или, возможно, ему исполнится 30 завтра, но ей все равно 29 лет. Следовательно, вы можете изменить возраст, добавив величину v , где v – равномерная случайная величина в интервале [0,1]. (Мы игнорируем статистически значимый случай женщин, которым остается 29 лет в течение многих лет!)
Источник: Jittering to prevent overplotting in statistical graphics
Мы можем использовать NumPy для добавления шума из нормального распределения со средним 0 и стандартным отклонением 2.
см. документацию NumPy
In [8]:
import numpy as np noise = np.random.normal(0, 2, size=len(brfss)) height_jitter = height + noise
Вот как выглядит график с дрожащими (jittered) высотами.
In [9]:
plt.plot(height_jitter, weight, 'o', alpha=0.02, markersize=1) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Столбцы исчезли, но теперь мы видим, что есть строки, в которых люди округляют свой вес. Мы также можем исправить это с помощью дрожания веса.
In [10]:
noise = np.random.normal(0, 2, size=len(brfss)) weight_jitter = weight + noise
In [11]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Наконец, давайте увеличим масштаб области, где находится большинство точек данных.
Функции xlim и ylim устанавливают нижнюю и верхнюю границы для осей $x$ и $y$; в данном случае мы наносим рост от 140 до 200 сантиметров и вес до 160 килограмм.
Вот как это выглядит.
In [12]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Теперь у нас есть достоверная картина взаимосвязи между ростом и весом.
Ниже вы можете увидеть вводящий в заблуждение график, с которого мы начали, и более надежный, которым мы закончили. Они явно разные, и они предлагают разные истории о взаимосвязи между этими переменными.
In [13]:
# Set the figure size plt.figure(figsize=(8, 3)) # Create subplots with 2 rows, 1 column, and start plot 1 plt.subplot(1, 2, 1) plt.plot(height, weight, 'o') plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height') # Adjust the layout so the two plots don't overlap plt.tight_layout() # Start plot 2 plt.subplot(1, 2, 2) plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height') plt.tight_layout()
Смысл этого примера в том, что для создания эффективного графика разброса требуются некоторые усилия.
Упражнение: Набирают ли люди вес с возрастом? Мы можем ответить на этот вопрос, визуализировав взаимосвязь между весом и возрастом.
Но прежде чем строить диаграмму рассеяния, рекомендуется визуализировать распределения по одной переменной за раз. Итак, давайте посмотрим на возрастное распределение.
Набор данных BRFSS включает столбец AGE, который представляет возраст каждого респондента в годах. Чтобы защитить конфиденциальность респондентов, возраст округляется до пятилетних интервалов. AGE содержит середину интервалов (bins).
-
Извлеките переменную
'AGE'из фрейма данныхbrfssи присвойте ееage. -
Постройте функцию вероятности (Probability mass function, PMF) для
ageв виде гистограммы, используяPmfизempiricaldist.
empiricaldist– библиотека Python, представляющая эмпирические функции распределения.
In [14]:
try: import empiricaldist except ImportError: !pip install empiricaldist
In [15]:
from empiricaldist import Pmf
Упражнение: Теперь давайте посмотрим на распределение веса.
Столбец, содержащий вес в килограммах, – это WTKG3. Поскольку этот столбец содержит много уникальных значений, отображение его как функции вероятности (PMF) работает плохо.
In [17]:
Pmf.from_seq(weight).bar() plt.xlabel('Weight in kg') plt.ylabel('PMF') plt.title('Distribution of weight');
Чтобы получить лучшее представление об этом распределении, попробуйте построить график функции распределения (Cumulative distribution function, CDF).
Вычислите функцию распределения (CDF) нормального распределения с тем же средним значением и стандартным отклонением и сравните его с распределением веса.
Подходит ли нормальное распределение для этих данных? А как насчет логарифмического преобразования весов?
Упражнение: Теперь давайте построим диаграмму разброса (scatter plot) для weight и age.
Отрегулируйте alpha и markersize, чтобы избежать наложения (overplotting). Используйте ylim, чтобы ограничить ось y от 0 до 200 килограммов.
Упражнение: В предыдущем упражнении возрасты указаны в столбцах, потому что они были округлены до 5-летних интервалов (bins). Если мы добавим дрожание (jitter), диаграмма рассеяния покажет взаимосвязь более четко.
- Добавьте случайный шум к
ageсо средним значением0и стандартным отклонением2.5. - Создайте диаграмму рассеяния и снова отрегулируйте
alphaиmarkersize.
Визуализация отношений¶
В предыдущем разделе мы использовали диаграммы разброса для визуализации взаимосвязей между переменными, а в упражнениях вы исследовали взаимосвязь между возрастом и весом. В этом разделе мы увидим другие способы визуализации этих отношений, в том числе диаграммы размаха и скрипичные диаграммы.
Я начну с диаграммы разброса веса в зависимости от возраста.
In [23]:
age = brfss['AGE'] noise = np.random.normal(0, 1.0, size=len(brfss)) age_jitter = age + noise plt.plot(age_jitter, weight_jitter, 'o', alpha=0.01, markersize=1) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.ylim([0, 200]) plt.title('Weight versus age');
В этой версии диаграммы разброса я скорректировал дрожание весов, чтобы между столбцами оставалось пространство.
Это позволяет увидеть форму распределения в каждой возрастной группе и различия между группами.
С этой точки зрения кажется, что вес увеличивается до 40-50 лет, а затем начинает уменьшаться.
Если мы пойдем дальше, то сможем использовать ядерную оценку плотности (Kernel Density Estimation, KDE) для оценки функции плотности в каждом столбце и построения графика. И для этого есть название – скрипичная диаграмма (violin plot).
Библиотека Seaborn предоставляет функцию, которая создает скрипичную диаграмму, но прежде чем мы сможем ее использовать, мы должны избавиться от любых строк с пропущенными данными.
Вот так:
In [24]:
data = brfss.dropna(subset=['AGE', 'WTKG3']) data.shape
dropna() создает новый фрейм данных, который удаляет строки из brfss, где AGE или WTKG3 равны NaN.
Теперь мы можем вызвать функцию violinplot.
см. документацию по violinplot
In [25]:
import seaborn as sns sns.violinplot(x='AGE', y='WTKG3', data=data, inner=None) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Аргументы x и y означают, что нам нужно AGE на оси x и WTKG3 на оси y.
data – это только что созданный фрейм данных, который содержит переменные для отображения.
Аргумент inner=None немного упрощает график.
На рисунке каждая фигура представляет собой распределение веса в одной возрастной группе. Ширина этих форм пропорциональна предполагаемой плотности, так что это похоже на две вертикальные ядерные оценки плотности (KDE), построенные вплотную друг к другу (и залитые красивыми цветами).
Другой, связанный с этим способ просмотра данных, называется диаграмма размаха (ящик с усами, box plot).
Код для создания диаграммы размаха очень похож.
см. документацию по boxplot
In [26]:
sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Я включил аргумент whis=10, чтобы отключить функцию, которая нам не нужна.
Каждый прямоугольник представляет распределение веса в возрастной группе. Высота каждого прямоугольника представляет собой диапазон от 25-го до 75-го процентиля. Линия в середине каждого прямоугольника – это медиана. Шипы, торчащие сверху и снизу, показывают минимальное и максимальное значения.
На мой взгляд, этот график дает лучшее представление о взаимосвязи между весом и возрастом.
-
Глядя на медианы, кажется, что люди в возрасте от 40 лет являются самыми тяжелыми; люди младшего и старшего возраста легче.
-
Глядя на размеры ящиков, кажется, что люди в возрасте от 40 также имеют наибольший разброс в весе.
-
Эти графики также показывают, насколько искажено распределение веса; то есть самые тяжелые люди намного дальше от медианы, чем самые легкие.
Для данных, которые склоняются к более высоким значениям, иногда полезно рассматривать их в логарифмической шкале.
Мы можем сделать это с помощью Pyplot-функции yscale.
In [27]:
sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10) plt.yscale('log') plt.xlabel('Age in years') plt.ylabel('Weight in kg (log scale)') plt.title('Weight versus age');
Чтобы наиболее четко показать взаимосвязь между возрастом и весом, я бы использовал этот рисунок.
В следующих упражнениях у вас будет возможность создать скрипичную диаграмму и диаграмму размаха.
Упражнение: Ранее мы рассмотрели диаграмму рассеяния (scatter plot) по росту и весу и увидели, что более высокие люди, как правило, тяжелее. Теперь давайте более подробно рассмотрим диаграмму размаха (box plot).
Фрейм данных brfss содержит столбец с именем _HTMG10, который представляет высоту в сантиметрах, разбитую на группы по 10 см.
-
Составьте диаграмму размаха, показывающую распределение веса в каждой группе роста.
-
Постройте ось Y в логарифмическом масштабе.
Предложение: если метки на оси x сталкиваются, вы можете повернуть их следующим образом:
plt.xticks(rotation='45')Упражнение: В качестве второго примера давайте посмотрим на взаимосвязь между доходом (income) и ростом.
В BRFSS доход представлен как категориальная переменная; то есть респондентов относят к одной из 8 категорий доходов. Имя столбца – INCOME2.
Прежде чем связывать доход с чем-либо еще, давайте посмотрим на распределение, вычислив функцию вероятности (PMF).
-
Извлеките
INCOME2изbrfssи присвойте егоincome. -
Постройте функцию вероятности (PMF) для
incomeв виде гистограммы (bar chart).
Примечание: вы увидите, что около трети респондентов относятся к группе с самым высоким доходом; лучше, если бы было больше лидирующих групп, но мы будем работать с тем, что у нас есть.
Упражнение: Создайте скрипичную диаграмму (violin plot), которая показывает распределение роста в каждой группе дохода.
Вы видите взаимосвязь между этими переменными?
Корреляция¶
В предыдущем разделе мы визуализировали отношения между парами переменных. Теперь мы узнаем о коэффициенте корреляции, который количественно определяет силу этих взаимосвязей.
Когда люди говорят “корреляция”, они имеют в виду любую связь между двумя переменными. В статистике обычно это означает коэффициент корреляции Пирсона, который представляет собой число от -1 до 1, которое количественно определяет силу линейной связи между переменными.
Для демонстрации я выберу три столбца из набора данных BRFSS:
In [31]:
columns = ['HTM4', 'WTKG3', 'AGE'] subset = brfss[columns]
Результатом является фрейм данных только с этими столбцами.
С этим подмножеством данных мы можем использовать метод corr, например:
Out[32]:
| HTM4 | WTKG3 | AGE | |
|---|---|---|---|
| HTM4 | 1.000000 | 0.474203 | -0.093684 |
| WTKG3 | 0.474203 | 1.000000 | 0.021641 |
| AGE | -0.093684 | 0.021641 | 1.000000 |
Результатом является корреляционная матрица. В первой строке корреляция HTM4 с самим собой равна 1. Это ожидаемо; корреляция чего-либо с самим собой равна 1.
Следующая запись более интересна; соотношение роста и веса составляет около 0.47. Коэффициент положительный, это означает, что более высокие люди тяжелее, и он умеренный по силе, что означает, что он имеет некоторую прогностическую ценность. Если вы знаете чей-то рост, вы можете лучше предположить его вес, и наоборот.
Корреляция между ростом и возрастом составляет примерно -0.09. Коэффициент отрицательный, это означает, что пожилые люди, как правило, ниже ростом, но он слабый, а это означает, что знание чьего-либо возраста не поможет, если вы попытаетесь угадать их рост.
Корреляция между возрастом и весом еще меньше. Напрашивается вывод, что нет никакой связи между возрастом и весом, но мы уже видели, что она есть. Так почему же корреляция такая низкая?
Помните, что зависимость между весом и возрастом выглядит так.
In [33]:
data = brfss.dropna(subset=['AGE', 'WTKG3']) sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Люди за сорок – самые тяжелые; люди младшего и старшего возраста легче. Итак, эта связь нелинейна.
Но корреляция измеряет только линейные отношения. Если связь нелинейная, корреляция обычно недооценивает ее силу.
Чтобы продемонстрировать, я сгенерирую несколько поддельных данных: xs содержит точки с равным интервалом между -1 и 1.
ys – это квадрат xs плюс некоторый случайный шум.
In [34]:
xs = np.linspace(-1, 1) ys = xs**2 + np.random.normal(0, 0.05, len(xs))
Вот диаграмма рассеяния для xs и ys.
In [35]:
plt.plot(xs, ys, 'o', alpha=0.5) plt.xlabel('x') plt.ylabel('y') plt.title('Scatter plot of a fake dataset');
Понятно, что это сильная связь; если вам дано x, вы можете гораздо лучше догадаться о y.
Но вот корреляционная матрица:
Out[36]:
array([[1. , 0.01135475],
[0.01135475, 1. ]])
Несмотря на то, что существует сильная нелинейная зависимость, вычисленная корреляция близка к 0.
В общем, если корреляция высока, то есть близка к
1или-1, вы можете сделать вывод, что существует сильная линейная зависимость.
Но если корреляция близка к0, это не означает, что связи нет; может быть связь нелинейная.
Это одна из причин, по которой я считаю, что корреляция не является хорошей статистикой.
В частности, корреляция ничего не говорит о наклоне. Если мы говорим, что две переменные коррелируют, это означает, что мы можем использовать одну для предсказания другой. Но, возможно, это не то, о чем мы заботимся.
Например, предположим, что нас беспокоит влияние увеличения веса на здоровье, поэтому мы строим график зависимости веса от возраста от 20 до 50 лет.
Я создам два поддельных набора данных, чтобы продемонстрировать суть дела. В каждом наборе данных xs представляет возраст, а ys – вес.
Я использую np.random.seed для инициализации генератора случайных чисел, поэтому мы получаем одни и те же результаты при каждом запуске.
In [37]:
np.random.seed(18) xs1 = np.linspace(20, 50) ys1 = 75 + 0.02 * xs1 + np.random.normal(0, 0.15, len(xs1)) plt.plot(xs1, ys1, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #1');
А вот и второй набор данных:
In [38]:
np.random.seed(18) xs2 = np.linspace(20, 50) ys2 = 65 + 0.2 * xs2 + np.random.normal(0, 3, len(xs2)) plt.plot(xs2, ys2, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #2');
Я построил эти примеры так, чтобы они выглядели одинаково, но имели существенно разные корреляции:
In [39]:
rho1 = np.corrcoef(xs1, ys1)[0][1] rho1
In [40]:
rho2 = np.corrcoef(xs2, ys2)[0][1] rho2
В первом примере сильная корреляция, близкая к 0.75. Во втором примере корреляция умеренная, близкая к 0.5. Поэтому мы можем подумать, что первые отношения более важны. Но посмотрите внимательнее на ось y на обоих рисунках.
В первом примере средняя прибавка в весе за 30 лет составляет менее 1 килограмма; во втором больше 5 килограммов!
Если нас беспокоит влияние увеличения веса на здоровье, второе соотношение, вероятно, более важно, даже если корреляция ниже.
Статистика, которая нас действительно волнует, – это наклон линии, а не коэффициент корреляции.
В следующем разделе мы увидим, как оценить этот наклон. Но сначала давайте попрактикуемся с корреляцией.
Упражнения: Цель BRFSS – изучить факторы риска для здоровья, поэтому в него включены вопросы о диете.
Столбец _VEGESU1 представляет количество порций овощей, которые респонденты ели в день.
Посмотрим, как эта переменная связана с возрастом и доходом.
- Во фрейме данных
brfssвыберите столбцы'AGE',INCOME2и_VEGESU1. - Вычислите корреляционную матрицу для этих переменных.
Упражнение: В предыдущем упражнении корреляция между доходом и потреблением овощей составляет около 0.12. Корреляция между возрастом и потреблением овощей составляет примерно -0.01.
Что из следующего является правильной интерпретацией этих результатов?
- A: люди в этом наборе данных с более высоким доходом едят больше овощей.
- B: Связь между доходом и потреблением овощей линейна.
- C: Пожилые люди едят больше овощей.
- D: Между возрастом и потреблением овощей может быть сильная нелинейная зависимость.
Упражнение: В общем, рекомендуется визуализировать взаимосвязь между переменными перед вычислением корреляции. В предыдущем примере мы этого не делали, но еще не поздно.
Создайте визуализацию взаимосвязи между возрастом и овощами. Как бы вы описали отношения, если они есть?
Простая регрессия¶
В предыдущем разделе мы видели, что корреляция не всегда измеряет то, что мы действительно хотим знать. В этом разделе мы рассмотрим альтернативу: простую линейную регрессию.
Давайте еще раз посмотрим на взаимосвязь между весом и возрастом. В предыдущем разделе я создал два фальшивых набора данных, чтобы доказать свою точку зрения:
In [44]:
plt.figure(figsize=(8, 3)) plt.subplot(1, 2, 1) plt.plot(xs1, ys1, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #1') plt.tight_layout() plt.subplot(1, 2, 2) plt.plot(xs2, ys2, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #2') plt.tight_layout()
Тот, что слева, имеет более высокую корреляцию, около 0,75 по сравнению с 0,5.
Но в этом контексте статистика, которая нас, вероятно, волнует, – это наклон линии, а не коэффициент корреляции.
Чтобы оценить наклон, мы можем использовать linregress из SciPy-библиотеки stats.
см. документацию по scipy.stats.linregress
In [45]:
from scipy.stats import linregress res1 = linregress(xs1, ys1) res1._asdict()
Out[45]:
{'slope': 0.018821034903244396,
'intercept': 75.08049023710964,
'rvalue': 0.7579660563439407,
'pvalue': 1.8470158725245546e-10,
'stderr': 0.002337849260560816,
'intercept_stderr': 0.08439154079040351}
Результатом является объект LinregressResult, содержащий пять значений: slope – наклон линии, наиболее подходящей для данных; intercept – это пересечение линии регрессии.
Для фальшивого набора данных 1 расчетный наклон составляет около 0,019 кг в год или около 0,56 кг за 30-летний период.
Вот результаты для фальшивого набора данных 2.
In [47]:
res2 = linregress(xs2, ys2) res2._asdict()
Out[47]:
{'slope': 0.17642069806488858,
'intercept': 66.60980474219305,
'rvalue': 0.47827769765763184,
'pvalue': 0.0004430600283776228,
'stderr': 0.046756985211216295,
'intercept_stderr': 1.6878308158080693}
Расчетный наклон почти в 10 раз выше: около 0,18 килограмма в год или около 5,3 килограмма за 30 лет:
То, что здесь называется rvalue, – это корреляция, которая подтверждает то, что мы видели раньше; первый пример имеет более высокую корреляцию, около 0,75 по сравнению с 0,5.
Но сила эффекта, измеренная по наклону линии, во втором примере примерно в 10 раз выше.
Мы можем использовать результаты linregress для вычисления линии тренда: сначала мы получаем минимум и максимум наблюдаемых xs; затем мы умножаем на наклон и добавляем точку пересечения.
Вот как это выглядит для первого примера.
In [49]:
plt.plot(xs1, ys1, 'o', alpha=0.5) fx = np.array([xs1.min(), xs1.max()]) fy = res1.intercept + res1.slope * fx plt.plot(fx, fy, '-') plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake Dataset #1');
То же самое и со вторым примером.
In [50]:
plt.plot(xs2, ys2, 'o', alpha=0.5) fx = np.array([xs2.min(), xs2.max()]) fy = res2.intercept + res2.slope * fx plt.plot(fx, fy, '-') plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake Dataset #2');
Визуализация здесь может ввести в заблуждение, если вы не посмотрите внимательно на вертикальные шкалы; наклон на втором рисунке почти в 10 раз больше.
Рост и вес¶
Теперь рассмотрим пример с реальными данными.
Вот еще раз диаграмма рассеяния для роста и веса.
In [51]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Теперь мы можем вычислить линию регрессии. linregress не может обрабатывать значения NaN, поэтому мы должны использовать dropna для удаления строк, в которых отсутствуют нужные нам данные.
In [52]:
subset = brfss.dropna(subset=['WTKG3', 'HTM4']) height_clean = subset['HTM4'] weight_clean = subset['WTKG3']
Теперь мы можем вычислить линейную регрессию.
In [53]:
res_hw = linregress(height_clean, weight_clean) res_hw._asdict()
Out[53]:
{'slope': 0.9192115381848256,
'intercept': -75.12704250330165,
'rvalue': 0.47420308979024434,
'pvalue': 0.0,
'stderr': 0.005632863769802997,
'intercept_stderr': 0.960886026543318}
Наклон составляет около 0,92 килограмма на сантиметр, а это означает, что мы ожидаем, что человек выше на один сантиметр будет почти на килограмм тяжелее. Это довольно много.
Как и раньше, мы можем вычислить линию тренда:
In [54]:
fx = np.array([height_clean.min(), height_clean.max()]) fy = res_hw.intercept + res_hw.slope * fx
In [55]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.plot(fx, fy, '-') plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Наклон этой линии соответствует диаграмме рассеяния.
Линейная регрессия имеет ту же проблему, что и корреляция; она только измеряет силу линейной связи.
Вот диаграмма рассеяния веса по сравнению с возрастом, которую мы видели ранее.
In [56]:
plt.plot(age_jitter, weight_jitter, 'o', alpha=0.01, markersize=1) plt.ylim([0, 160]) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Люди в возрасте от 40 – самые тяжелые; люди младшего и старшего возраста легче. Так что отношения нелинейные.
Если мы не посмотрим на диаграмму рассеяния и вслепую вычислим линию регрессии, мы получим вот что.
In [57]:
subset = brfss.dropna(subset=['WTKG3', 'AGE']) age_clean = subset['AGE'] weight_clean = subset['WTKG3'] res_aw = linregress(age_clean, weight_clean) res_aw._asdict()
Out[57]:
{'slope': 0.023981159566968686,
'intercept': 80.07977583683224,
'rvalue': 0.021641432889064033,
'pvalue': 4.3743274930078674e-11,
'stderr': 0.003638139410742186,
'intercept_stderr': 0.18688508176870167}
Расчетный уклон составляет всего 0,02 килограмма в год или 0,6 килограмма за 30 лет.
А вот как выглядит линия тренда.
In [58]:
plt.plot(age_jitter, weight_jitter, 'o', alpha=0.01, markersize=1) fx = np.array([age_clean.min(), age_clean.max()]) fy = res_aw.intercept + res_aw.slope * fx plt.plot(fx, fy, '-') plt.ylim([0, 160]) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Прямая линия плохо отражает взаимосвязь между этими переменными.
Давайте попрактикуемся в простой регрессии.
Упражнение: Как вы думаете, кто ест больше овощей, люди с низким доходом или люди с высоким доходом? Давайте выясним.
Как мы видели ранее, столбец INCOME2 представляет уровень дохода, а _VEGESU1 представляет количество порций овощей, которые респонденты ели в день.
Постройте диаграмму рассеяния порций овощей в зависимости от дохода, то есть с порциями овощей по оси y и группой доходов по оси x.
Вы можете использовать ylim для увеличения нижней половины оси y.
Упражнение: Теперь давайте оценим наклон зависимости между потреблением овощей и доходом.
-
Используйте
dropnaдля выбора строк, в которыхINCOME2и_VEGESU1не равныNaN. -
Извлеките
INCOME2и_VEGESU1и вычислите простую линейную регрессию этих переменных.
Каков наклон линии регрессии? Что означает этот наклон в контексте изучаемого нами вопроса?
Упражнение: Наконец, постройте линию регрессии поверх диаграммы рассеяния.
Постановка задачи
При статистическом анализе зависимостей между количественными переменными возникают ситуации, когда представляет интерес расчет и анализ такого показателя как корреляционное отношение (η).
Данный показатель незаслуженно обойден вниманием в большинстве доступных для пользователей математических пакетов.
В данном разборе рассмотрим способы расчета и анализа η средствами Python.
Не будем углубляться в теорию (про η достаточно подробно написано, например, в [1, с.73], [2, с.412], [3, с.609]), но вспомним основные свойства η:
-
η характеризует степень тесноты любой корреляционной связи (как линейной, так и нелинейной), в отличие от коэффициента корреляции Пирсона r, который характеризует тесноту только линейной связи. Условие r=0 означает отсутствие линейной корреляционной связи между величинами, но при этом между ними может существовать нелинейная корреляционная связь (η>0).
-
η принимает значения от 0 до 1; при η=0 корреляционная связь отсутствует, при η=1 связь считается функциональной; степень тесноты связи можно оценивать по различным общепринятым шкалам, например, по шкале Чеддока и др.
-
Величина η² характеризует долю вариации, объясненной корреляционной связью между рассматриваемыми переменными.
-
η не может быть меньше абсолютной величины r: η ≥ |r|.
-
η несимметрично по отношению к исследуемым переменным, то есть ηXY ≠ ηYX.
-
Для расчета η необходимо иметь эмпирические данные эксперимента с повторностями; если же мы имеем просто два набора значений переменных X и Y, то данные нужно группировать. Этот вывод, в общем-то, очевиден – если предпринять попытку рассчитать η по негруппированным данным, получим результат η=1.
Группировка данных для расчета η заключается в разбиении области значений переменных X и Y на интервалы, подсчет частот попадания данных в интервалы и формирование корреляционной таблицы.
Важное замечание: особенности методики расчета корреляционного отношения, особенно при форме связи, близкой к линейной, и η близком к единице, могут привести к результатам, в общем-то абсурдным, например:
-
когда нарушается условие η ≥ |r|;
-
когда r окажется значим, а η нет;
-
когда нижняя граница доверительного интервала для η окажется меньше 0 или верхняя граница – больше 1.
Это нужно учитывать при выполнении анализа.
Итак, перейдем к расчетам.
Формирование исходных данных
В качестве исходных данных рассмотрим зависимость расхода среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от среднемесячного пробега (км) (Mileage).
Загрузим исходные данные из csv-файла (исходные данные доступны в моем репозитории на GitHub):
fuel_df = pd.read_csv(
filepath_or_buffer='data/fuel_df.csv',
sep=';',
index_col='Number')
dataset_df = fuel_df.copy() # создаем копию исходной таблицы для работы
display(dataset_df.head())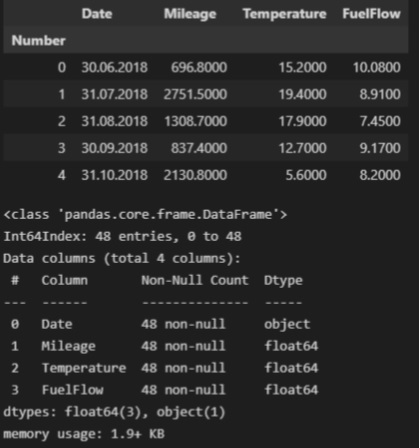
Загруженный DataFrame содержит следующие столбцы:
-
Month — месяц (в формате Excel)
-
Mileage – месячный пробег (км)
-
Temperature – среднемесячная температура (°C)
-
FuelFlow – среднемесячный расход топлива (л/100 км)
Сохраним нужные нам переменные Mileage и FuelFlow в виде numpy.ndarray.
X = np.array(dataset_df['Mileage'])
Y = np.array(dataset_df['FuelFlow'])Для удобства дальнейшей работы сформируем сформируем отдельный DataFrame из двух переменных – X и Y:
data_XY_df = pd.DataFrame({
'X': X,
'Y': Y})Настройка заголовков отчета (для дальнейшего формирования графиков):
# Общий заголовок проекта
Task_Project = "Расчет и анализ корреляционного отношения средствами Python"
# Заголовок, фиксирующий момент времени
AsOfTheDate = ""
# Заголовок раздела проекта
Task_Theme = "Анализ расхода топлива автомобиля"
# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"
# Наименования переменных
Variable_Name_X = "Среднемесячный пробег (км)"
Variable_Name_Y = "Среднемесячный расход топлива автомобиля (л/100 км)"Визуализация и первичная обработка данных
Предварительно отсеем аномальные значения (выбросы). Подробно не будем останавливаться на этой процедуре, она не является целью данного разбора.
mask1 = data_XY_df['X'] > 200
mask2 = data_XY_df['X'] < 2000
data_XY_df = data_XY_df[mask1 & mask2]
X = np.array(data_XY_df['X'])
Y = np.array(data_XY_df['Y'])Описательная статистика исходных данных:
data_XY_df.describe()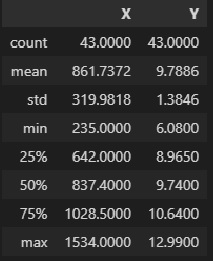
Выполним визуализацию исходных данных:
fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
fig.suptitle(Task_Theme)
axes.set_title('Зависимость расхода топлива от пробега')
data_df = data_XY_df
sns.scatterplot(
data=data_df,
x='X', y='Y',
label='эмпирические данные',
s=50,
ax=axes)
axes.set_xlabel(Variable_Name_X)
axes.set_ylabel(Variable_Name_Y)
#axes.tick_params(axis="x", labelsize=f_size+4)
#axes.tick_params(axis="y", labelsize=f_size+4)
#axes.legend(prop={'size': f_size+6})
plt.show()
fig.savefig('graph/scatterplot_XY_sns.png', orientation = "portrait", dpi = 300)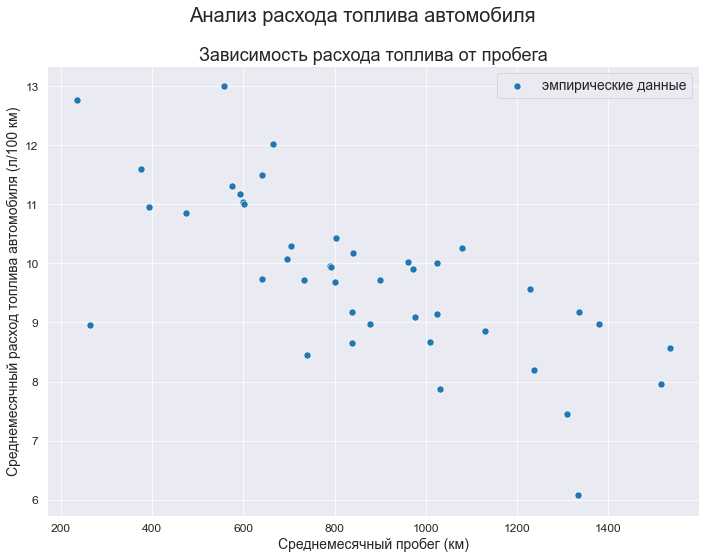
Для визуальной оценки выборочных данных построим гистограммы и коробчатые диаграммы:
fig = plt.figure(figsize=(420/INCH, 297/INCH))
ax1 = plt.subplot(2,2,1)
ax2 = plt.subplot(2,2,2)
ax3 = plt.subplot(2,2,3)
ax4 = plt.subplot(2,2,4)
fig.suptitle(Task_Theme)
ax1.set_title('X')
ax2.set_title('Y')
# инициализация данных
data_df = data_XY_df
X_mean = data_df['X'].mean()
X_std = data_df['X'].std(ddof = 1)
Y_mean = data_df['Y'].mean()
Y_std = data_df['Y'].std(ddof = 1)
bins_hist = 'sturges' # выбор числа интервалов ('auto', 'fd', 'doane', 'scott', 'stone', 'rice', 'sturges', 'sqrt')
# данные для графика плотности распределения X
xmin = np.amin(data_df['X'])
xmax = np.amax(data_df['X'])
nx = 100
hx = (xmax - xmin)/(nx - 1)
x1 = np.linspace(xmin, xmax, nx)
xnorm1 = sps.norm.pdf(x1, X_mean, X_std)
kx = len(np.histogram(X, bins=bins_hist, density=False)[0])
xnorm2 = xnorm1*len(X)*(xmax-xmin)/kx
# данные для графика плотности распределения Y
ymin = np.amin(Y)
ymax = np.amax(Y)
ny = 100
hy = (ymax - ymin)/(ny - 1)
y1 = np.linspace(ymin, ymax, ny)
ynorm1 = sps.norm.pdf(y1, Y_mean, Y_std)
ky = len(np.histogram(Y, bins=bins_hist, density=False)[0])
ynorm2 = ynorm1*len(Y)*(ymax-ymin)/ky
# гистограмма распределения X
ax1.hist(
data_df['X'],
bins=bins_hist,
density=False,
histtype='bar', # 'bar', 'barstacked', 'step', 'stepfilled'
orientation='vertical', # 'vertical', 'horizontal'
color = "#1f77b4",
label='эмпирическая частота')
ax1.plot(
x1, xnorm2,
linestyle = "-",
color = "r",
linewidth = 2,
label = 'теоретическая нормальная кривая')
ax1.axvline(X_mean, color='magenta', label = 'среднее значение')
ax1.axvline(np.median(data_df['X']), color='orange', label = 'медиана')
ax1.legend(fontsize = f_size+4)
# гистограмма распределения Y
ax2.hist(
data_df['Y'],
bins=bins_hist,
density=False,
histtype='bar', # 'bar', 'barstacked', 'step', 'stepfilled'
orientation='vertical', # 'vertical', 'horizontal'
color = "#1f77b4",
label='эмпирическая частота')
ax2.plot(
y1, ynorm2,
linestyle = "-",
color = "r",
linewidth = 2,
label = 'теоретическая нормальная кривая')
ax2.axvline(Y_mean, color='magenta', label = 'среднее значение')
ax2.axvline(np.median(data_df['Y']), color='orange', label = 'медиана')
ax2.legend(fontsize = f_size+4)
# коробчатая диаграмма X
sns.boxplot(
#data=corn_yield_df,
x=data_df['X'],
orient='h',
width=0.3,
ax=ax3)
# коробчатая диаграмма Y
sns.boxplot(
#data=corn_yield_df,
x=data_df['Y'],
orient='h',
width=0.3,
ax=ax4)
# подписи осей
ax3.set_xlabel(Variable_Name_X)
ax4.set_xlabel(Variable_Name_Y)
plt.show()
fig.savefig('graph/scatterplot_boxplot_X_Y_sns.png', orientation = "portrait", dpi = 300)
Перед тем, как приступать к дальнейшим расчетам, проверим исходные данные на соответствие нормальному закону распределения.
Выполнять такую проверку нужно обязательно, так как только для нормально распределенных данных мы можем в дальнейшем использовать общепринятые статистические процедуры анализа: проверку значимости корреляционного отношения, построение доверительных интервалов и т.д.
Для проверки нормальности распределения воспользуемся критерием Шапиро-Уилка:
# функция для обработки реализации теста Шапиро-Уилка
def Shapiro_Wilk_test(data):
data = np.array(data)
result = sci.stats.shapiro(data)
s_calc = result.statistic # расчетное значение статистики критерия
a_calc = result.pvalue # расчетный уровень значимости
print(f"Расчетный уровень значимости: a_calc = {round(a_calc, DecPlace)}")
print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
if a_calc >= a_level:
conclusion_ShW_test = f"Так как a_calc = {round(a_calc, DecPlace)} >= a_level = {round(a_level, DecPlace)}" +
", то гипотеза о нормальности распределения по критерию Шапиро-Уилка ПРИНИМАЕТСЯ"
else:
conclusion_ShW_test = f"Так как a_calc = {round(a_calc, DecPlace)} < a_level = {round(a_level, DecPlace)}" +
", то гипотеза о нормальности распределения по критерию Шапиро-Уилка ОТВЕРГАЕТСЯ"
print(conclusion_ShW_test)# проверка нормальности распределения переменной X
Shapiro_Wilk_test(X)
# проверка нормальности распределения переменной Y
Shapiro_Wilk_test(Y)
Итак, гипотеза о нормальном распределении исходных данных принимается, что позволяет нам в дальнейшем пользоваться статистическим инструментарием для интервального оценивания величины η, проверки гипотез и т.д.
Переходим собственно к расчету корреляционного отношения.
Переходим собственно к расчету корреляционного отношения.
Расчёт и анализ корреляционного отношения
1. Выполним группировку исходных данным по обоим признакам X и Y:
Создадим новую переменную matrix_XY_df для работы с группированными данными:
matrix_XY_df = data_XY_df.copy()Определим число интервалов группировки (воспользуемся формулой Стерджесса); при этом минимальное число интервалов должно быть не менее 2:
# объем выборки для переменных X и Y
n_X = len(X)
n_Y = len(Y)
# число интервалов группировки
group_int_number = lambda n: round (3.31*log(n_X, 10)+1) if round (3.31*log(n_X, 10)+1) >=2 else 2
K_X = group_int_number(n_X)
K_Y = group_int_number(n_Y)
print(f"Число интервалов группировки для переменной X: {K_X}")
print(f"Число интервалов группировки для переменной Y: {K_Y}")Выполним группировку данных средствами библиотеки pandas, для этого воспользуемся функцией pandas.cut. В результате получим новые признаки cut_X и cut_X, которые показывают, в какой из интервалов попадает конкретное значение X и Y. Полученные новые признаки добавим в DataFrame matrix_XY_df:
cut_X = pd.cut(X, bins=K_X)
cut_Y = pd.cut(Y, bins=K_Y)
matrix_XY_df['cut_X'] = cut_X
matrix_XY_df['cut_Y'] = cut_Y
display(matrix_XY_df.head())
Теперь мы можем получить корреляционную таблицу с помощью функции pandas.crosstab:
CorrTable_df = pd.crosstab(
index=matrix_XY_df['cut_X'],
columns=matrix_XY_df['cut_Y'],
rownames=['cut_X'],
colnames=['cut_Y'])
display(CorrTable_df)
# проверка правильности подсчета частот по интервалам
print(f"sum = {np.sum(np.array(CorrTable_df))}")
Функция pandas.crosstab также позволяет формировать более ровные и удобные для восприятия границы интервалов группировки путем задания их вручную. Для расчета η это принципиального значения не имеет, но в отдельных случаях может быть полезно.
Например, зададим вручную границы интервалов группировки для X и Y:
bins_X = pd.IntervalIndex.from_tuples([(200, 400), (400, 600), (600, 800), (800, 1000), (1000, 1200), (1200, 1400), (1400, 1600)])
cut_X = pd.cut(X, bins=bins_X)
bins_Y = pd.IntervalIndex.from_tuples([(6.0, 7.0), (7.0, 8.0), (8.0, 9.0), (9.0, 10.0), (10.0, 11.0), (11.0, 12.0), (12.0, 13.0)])
cut_Y = pd.cut(X, bins=bins_Y)
CorrTable_df2 = pd.crosstab(
index=pd.cut(X, bins=bins_X),
columns=pd.cut(Y, bins=bins_Y),
rownames=['cut_X'],
colnames=['cut_Y'])
display(CorrTable_df2)
# проверка правильности подсчета частот по интервалам
print(f"sum = {np.sum(np.array(CorrTable_df2))}")
Есть и другой способ получения корреляционной таблицы – с помощью pandas.pivot_table:
matrix_XY_df.pivot_table(
values=['Y'],
index='cut_X',
columns='cut_Y',
aggfunc=len,
fill_value=0)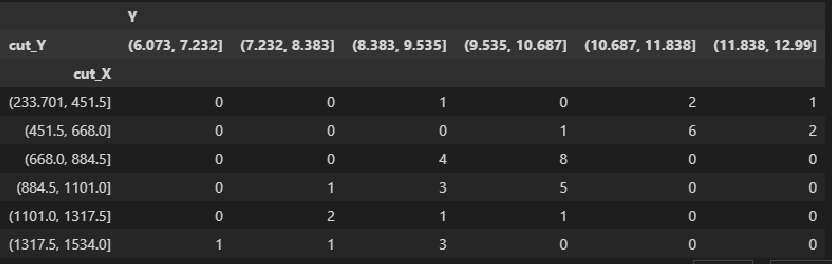
2. Выполним расчет корреляционного отношения:
Для дальнейших расчетов приведем корреляционную таблицу к типу numpy.ndarray:
CorrTable_np = np.array(CorrTable_df)
print(CorrTable_np, type(CorrTable_np))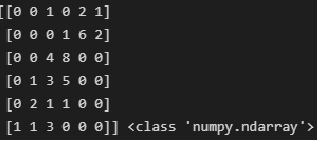
Итоги корреляционной таблицы по строкам и столбцам:
# итоги по строкам
n_group_X = [np.sum(CorrTable_np[i]) for i in range(K_X)]
print(f"n_group_X = {n_group_X}")
# итоги по столбцам
n_group_Y = [np.sum(CorrTable_np[:,j]) for j in range(K_Y)]
print(f"n_group_Y = {n_group_Y}")![]()
Также нам необходимо получить среднегрупповые значения X и Y для каждой группы (интервала). При этом нужно помнить, что функция pandas.crosstab при группировании расширяет крайние диапазоны на 0.1% с каждой стороны, чтобы включить минимальное и максимальное значения.
Для доступа к данным – границам интервалов, полученным с помощью pandas.cut – существуют методы right и left:
# Среднегрупповые значения переменной X
Xboun_mean = [(CorrTable_df.index[i].left + CorrTable_df.index[i].right)/2 for i in range(K_X)]
Xboun_mean[0] = (np.min(X) + CorrTable_df.index[0].right)/2 # исправляем значения в крайних интервалах
Xboun_mean[K_X-1] = (CorrTable_df.index[K_X-1].left + np.max(X))/2
print(f"Xboun_mean = {Xboun_mean}")
# Среднегрупповые значения переменной Y
Yboun_mean = [(CorrTable_df.columns[j].left + CorrTable_df.columns[j].right)/2 for j in range(K_Y)]
Yboun_mean[0] = (np.min(Y) + CorrTable_df.columns[0].right)/2 # исправляем значения в крайних интервалах
Yboun_mean[K_Y-1] = (CorrTable_df.columns[K_Y-1].left + np.max(Y))/2
print(f"Yboun_mean = {Yboun_mean}", 'n')![]()
Находим средневзевешенные значения X и Y для каждой группы:
Xmean_group = [np.sum(CorrTable_np[:,j] * Xboun_mean) / n_group_Y[j] for j in range(K_Y)]
print(f"Xmean_group = {Xmean_group}")
Ymean_group = [np.sum(CorrTable_np[i] * Yboun_mean) / n_group_X[i] for i in range(K_X)]
print(f"Ymean_group = {Ymean_group}")![]()
Общая дисперсия X и Y:
Sum2_total_X = np.sum(n_group_X * (Xboun_mean - np.mean(X))**2)
print(f"Sum2_total_X = {Sum2_total_X}")
Sum2_total_Y = np.sum(n_group_Y * (Yboun_mean - np.mean(Y))**2)
print(f"Sum2_total_Y = {Sum2_total_Y}")![]()
Межгрупповая дисперсия X и Y (дисперсия групповых средних):
Sum2_between_group_X = np.sum(n_group_Y * (Xmean_group - np.mean(X))**2)
print(f"Sum2_between_group_X = {Sum2_between_group_X}")
Sum2_between_group_Y = np.sum(n_group_X * (Ymean_group - np.mean(Y))**2)
print(f"Sum2_between_group_Y = {Sum2_between_group_Y}")![]()
Внутригрупповая дисперсия X и Y (возникает за счет других факторов – не связанных с другой переменной):
print(f"Sum2_within_group_X = {Sum2_total_X - Sum2_between_group_X}")
print(f"Sum2_within_group_Y = {Sum2_total_Y - Sum2_between_group_Y}")![]()
Эмпирическое корреляционное отношение:
corr_ratio_XY = sqrt(Sum2_between_group_Y / Sum2_total_Y)
print(f"corr_ratio_XY = {corr_ratio_XY}")
corr_ratio_YX = sqrt(Sum2_between_group_X / Sum2_total_X)
print(f"corr_ratio_YX = {corr_ratio_YX}")![]()
Итак, мы получили результат – значение корреляционного отношения.
Оценим тесноту корреляционной связи по шкале Чеддока, для удобства создадим пользовательскую функцию:
def Cheddock_scale_check(r, name='r'):
# задаем шкалу Чеддока
Cheddock_scale = {
f'no correlation (|{name}| <= 0.1)': 0.1,
f'very weak (0.1 < |{name}| <= 0.2)': 0.2,
f'weak (0.2 < |{name}| <= 0.3)': 0.3,
f'moderate (0.3 < |{name}| <= 0.5)': 0.5,
f'perceptible (0.5 < |{name}| <= 0.7)': 0.7,
f'high (0.7 < |{name}| <= 0.9)': 0.9,
f'very high (0.9 < |{name}| <= 0.99)': 0.99,
f'functional (|{name}| > 0.99)': 1.0}
r_scale = list(Cheddock_scale.values())
for i, elem in enumerate(r_scale):
if abs(r) <= elem:
conclusion_Cheddock_scale = list(Cheddock_scale.keys())[i]
break
return conclusion_Cheddock_scale![]()
Шкала Чеддока изначально предназначалась для оценки тесноты линейно корреляционной связи (на основе коэффициента корреляции Пирсона r), но мы ее применим и для корреляционного отношения η (не забывая про свойство η ≥ r!). В выводе функции Cheddock_scale_check можно указать символ, обозначающий величину – аргумент name=chr(951) выводит η вместо r.
В современных исследованиях шкала Чеддока теряет популярность, в последние годы все чаще применяется шкала Эванса (в психосоциальных, медико-биологических и др.исследованиях) ( более подробно про шкалы Чеддока, Эванса и др. – см.[4]). Оценим тесноту корреляционной связи по шкале Эванса, для удобства также создадим пользовательскую функцию:
def Evans_scale_check(r, name='r'):
# задаем шкалу Эванса
Evans_scale = {
f'very weak (|{name}| < 0.19)': 0.2,
f'weak (0.2 < |{name}| <= 0.39)': 0.4,
f'moderate (0.4 < |{name}| <= 0.59)': 0.6,
f'strong (0.6 < |{name}| <= 0.79)': 0.8,
f'very strong (0.8 < |{name}| <= 1.0)': 1.0}
r_scale = list(Evans_scale.values())
for i, elem in enumerate(r_scale):
if abs(r) <= elem:
conclusion_Evans_scale = list(Evans_scale.keys())[i]
break
return conclusion_Evans_scale
print(f"Оценка тесноты корреляции по шкале Эванса: {Evans_scale_check(corr_ratio_XY, name=chr(951))}")![]()
Итак, степень тесноты корреляционной связи может быть оценена как высокая (по шкале Чеддока), сильная (по шкале Эванса).
3. Проверка значимости корреляционного отношения:
Рассмотрим нулевую гипотезу:
H0: ηXY = 0
H1: ηXY ≠ 0Для проверки нулевой гипотезы воспользуемся критерием Фишера:
# расчетное значение статистики критерия Фишера
F_corr_ratio_calc = (n_X - K_X)/(K_X - 1) * corr_ratio_XY**2 / (1 - corr_ratio_XY**2)
print(f"Расчетное значение статистики критерия Фишера: F_calc = {round(F_corr_ratio_calc, DecPlace)}")
# табличное значение статистики критерия Фишера
dfn = K_X - 1
dfd = n_X - K_X
F_corr_ratio_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
print(f"Табличное значение статистики критерия Фишера: F_table = {round(F_corr_ratio_table, DecPlace)}")
# расчетный уровень значимости
a_corr_ratio_calc = 1 - sci.stats.f.cdf(F_corr_ratio_calc, dfn, dfd, loc=0, scale=1)
print(f"Расчетный уровень значимости: a_calc = {round(a_corr_ratio_calc, DecPlace)}")
print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
# вывод
if F_corr_ratio_calc < F_corr_ratio_table:
conclusion_corr_ratio_sign = f"Так как F_calc = {round(F_corr_ratio_calc, DecPlace)} < F_table = {round(F_corr_ratio_table, DecPlace)}" +
", то гипотеза о равенстве нулю корреляционного отношения ПРИНИМАЕТСЯ, т.е. корреляционная связь НЕЗНАЧИМА"
else:
conclusion_corr_ratio_sign = f"Так как F_calc = {round(F_corr_ratio_calc, DecPlace)} >= F_table = {round(F_corr_ratio_table, DecPlace)}" +
", то гипотеза о равенстве нулю корреляционного отношения ОТВЕРГАЕТСЯ, т.е. корреляционная связь ЗНАЧИМА"
print(conclusion_corr_ratio_sign)
4. Доверительный интервал для корреляционного отношения:
# число степеней свободы
f1 = round ((K_X - 1 + n_X * corr_ratio_XY**2)**2 / (K_X - 1 + 2 * n_X * corr_ratio_XY**2))
f2 = n_X - K_X
# вспомогательные величины
z1 = (n_X - K_X) / n_X * corr_ratio_XY**2 / (1 - corr_ratio_XY**2) * 1/sci.stats.f.ppf(p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
z2 = (n_X - K_X) / n_X * corr_ratio_XY**2 / (1 - corr_ratio_XY**2) * 1/sci.stats.f.ppf(1 - p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
# доверительный интервал
corr_ratio_XY_low = sqrt(z1) if sqrt(z1) >= 0 else 0
corr_ratio_XY_high = sqrt(z2) if sqrt(z2) <= 1 else 1
print(f"{p_level*100}%-ный доверительный интервал для корреляционного отношения: {[round(corr_ratio_XY_low, DecPlace), round(corr_ratio_XY_high, DecPlace)]}")![]()
Важное замечание: при значениях η близких к 0 или 1 левая или правая граница доверительного интервала может выходить за пределы отрезка [0; 1], теряя содержательный смысл (см. [1, с.80]). Причина этого – в аппроксимационном подходе к определению границ доверительного интервала. Подобные нежелательные явления возможны, и их нужно учитывать при выполнении анализа.
5. Проверка значимости отличия линейной корреляционной связи от нелинейной:
Оценим величину коэффициента линейной корреляции:
corr_coef = sci.stats.pearsonr(X, Y)[0]
print(f"Коэффициент линейной корреляции: r = {round(corr_coef, DecPlace)}")
print(f"Оценка тесноты линейной корреляции по шкале Чеддока: {Cheddock_scale_check(corr_coef)}")
print(f"Оценка тесноты линейной корреляции по шкале Эванса: {Evans_scale_check(corr_coef)}")
Проверим значимость коэффициента линейной корреляции:
# расчетный уровень значимости
a_corr_coef_calc = sci.stats.pearsonr(X, Y)[1]
print(f"Расчетный уровень значимости коэффициента линейной корреляции: a_calc = {a_corr_coef_calc}")
print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
# вывод
if a_corr_coef_calc >= a_level:
conclusion_corr_coef_sign = f"Так как a_calc = {a_corr_coef_calc} >= a_level = {round(a_level, DecPlace)}" +
", то гипотеза о равенстве нулю коэффициента линейной корреляции ПРИНИМАЕТСЯ, т.е. линейная корреляционная связь НЕЗНАЧИМА"
else:
conclusion_corr_coef_sign = f"Так как a_calc = {a_corr_coef_calc} < a_level = {round(a_level, DecPlace)}" +
", то гипотеза о равенстве нулю коэффициента линейной корреляции ОТВЕРГАЕТСЯ, т.е. линейная корреляционная связь ЗНАЧИМА"
print(conclusion_corr_coef_sign)
Теперь проверим значимость отличия линейной корреляционной связи от нелинейной. Для этого рассмотрим нулевую гипотезу:
H0: η² - r² = 0
H1: η² - r² ≠ 0Для проверки нулевой гипотезы воспользуемся критерием Фишера:
print(f"Корреляционное отношение: {chr(951)} = {round(corr_ratio_XY, DecPlace)}")
print(f"Коэффициент линейной корреляции: r = {round(corr_coef, DecPlace)}")
# расчетное значение статистики критерия Фишера
F_line_corr_sign_calc = (n_X - K_X)/(K_X - 2) * (corr_ratio_XY**2 - corr_coef**2) / (1 - corr_ratio_XY**2)
print(f"Расчетное значение статистики критерия Фишера: F_calc = {round(F_line_corr_sign_calc, DecPlace)}")
# табличное значение статистики критерия Фишера
dfn = K_X - 2
dfd = n_X - K_X
F_line_corr_sign_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
print(f"Табличное значение статистики критерия Фишера: F_table = {round(F_line_corr_sign_table, DecPlace)}")
# расчетный уровень значимости
a_line_corr_sign_calc = 1 - sci.stats.f.cdf(F_line_corr_sign_calc, dfn, dfd, loc=0, scale=1)
print(f"Расчетный уровень значимости: a_calc = {round(a_line_corr_sign_calc, DecPlace)}")
print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
# вывод
if F_line_corr_sign_calc < F_line_corr_sign_table:
conclusion_line_corr_sign = f"Так как F_calc = {round(F_line_corr_sign_calc, DecPlace)} < F_table = {round(F_line_corr_sign_table, DecPlace)}" +
f", то гипотеза о равенстве {chr(951)} и r ПРИНИМАЕТСЯ, т.е. корреляционная связь ЛИНЕЙНАЯ"
else:
conclusion_line_corr_sign = f"Так как F_calc = {round(F_line_corr_sign_calc, DecPlace)} >= F_table = {round(F_line_corr_sign_table, DecPlace)}" +
f", то гипотеза о равенстве {chr(951)} и r ОТВЕРГАЕТСЯ, т.е. корреляционная связь НЕЛИНЕЙНАЯ"
print(conclusion_line_corr_sign)
Создание пользовательской функции для корреляционного анализа
Для практической работы целесообразно все вышеприведенные расчеты реализовать в виде пользовательских функций:
-
функция corr_coef_check – для расчета и анализа коэффициента линейной корреляции Пирсона
-
функция corr_ratio_check – для расчета и анализа корреляционного отношения
-
функция line_corr_sign_check – для проверка значимости линейной корреляционной связи
Данные функции выводят результаты анализа в виде DataFrame, что удобно для визуального восприятия и дальнейшего использования результатов анализа (впрочем, способ вывода – на усмотрение каждого исследователя).
# Функция для расчета и анализа коэффициента линейной корреляции Пирсона
def corr_coef_check(X, Y, p_level=0.95, scale='Cheddok'):
a_level = 1 - p_level
X = np.array(X)
Y = np.array(Y)
n_X = len(X)
n_Y = len(Y)
# оценка коэффициента линейной корреляции средствами scipy
corr_coef, a_corr_coef_calc = sci.stats.pearsonr(X, Y)
# несмещенная оценка коэффициента линейной корреляции (при n < 15) (см.Кобзарь, с.607)
if n_X < 15:
corr_coef = corr_coef * (1 + (1 - corr_coef**2) / (2*(n_X-3)))
# проверка гипотезы о значимости коэффициента корреляции
t_corr_coef_calc = abs(corr_coef) * sqrt(n_X-2) / sqrt(1 - corr_coef**2)
t_corr_coef_table = sci.stats.t.ppf((1 + p_level)/2 , n_X - 2)
conclusion_corr_coef_sign = 'significance' if t_corr_coef_calc >= t_corr_coef_table else 'not significance'
# доверительный интервал коэффициента корреляции
if t_corr_coef_calc >= t_corr_coef_table:
z1 = np.arctanh(corr_coef) - sci.stats.norm.ppf((1 + p_level)/2, 0, 1) / sqrt(n_X-3) - corr_coef / (2*(n_X-1))
z2 = np.arctanh(corr_coef) + sci.stats.norm.ppf((1 + p_level)/2, 0, 1) / sqrt(n_X-3) - corr_coef / (2*(n_X-1))
corr_coef_conf_int_low = tanh(z1)
corr_coef_conf_int_high = tanh(z2)
else:
corr_coef_conf_int_low = corr_coef_conf_int_high = '-'
# оценка тесноты связи
if scale=='Cheddok':
conclusion_corr_coef_scale = scale + ': ' + Cheddock_scale_check(corr_coef)
elif scale=='Evans':
conclusion_corr_coef_scale = scale + ': ' + Evans_scale_check(corr_coef)
# формируем результат
result = pd.DataFrame({
'notation': ('r'),
'coef_value': (corr_coef),
'coef_value_squared': (corr_coef**2),
'p_level': (p_level),
'a_level': (a_level),
't_calc': (t_corr_coef_calc),
't_table': (t_corr_coef_table),
't_calc >= t_table': (t_corr_coef_calc >= t_corr_coef_table),
'a_calc': (a_corr_coef_calc),
'a_calc <= a_level': (a_corr_coef_calc <= a_level),
'significance_check': (conclusion_corr_coef_sign),
'conf_int_low': (corr_coef_conf_int_low),
'conf_int_high': (corr_coef_conf_int_high),
'scale': (conclusion_corr_coef_scale)
},
index=['Correlation coef.'])
return result # Функция для расчета и анализа корреляционного отношения
def corr_ratio_check(X, Y, p_level=0.95, orientation='XY', scale='Cheddok'):
a_level = 1 - p_level
X = np.array(X)
Y = np.array(Y)
n_X = len(X)
n_Y = len(Y)
# запишем данные в DataFrame
matrix_XY_df = pd.DataFrame({
'X': X,
'Y': Y})
# число интервалов группировки
group_int_number = lambda n: round (3.31*log(n_X, 10)+1) if round (3.31*log(n_X, 10)+1) >=2 else 2
K_X = group_int_number(n_X)
K_Y = group_int_number(n_Y)
# группировка данных и формирование корреляционной таблицы
cut_X = pd.cut(X, bins=K_X)
cut_Y = pd.cut(Y, bins=K_Y)
matrix_XY_df['cut_X'] = cut_X
matrix_XY_df['cut_Y'] = cut_Y
CorrTable_df = pd.crosstab(
index=matrix_XY_df['cut_X'],
columns=matrix_XY_df['cut_Y'],
rownames=['cut_X'],
colnames=['cut_Y'])
CorrTable_np = np.array(CorrTable_df)
# итоги корреляционной таблицы по строкам и столбцам
n_group_X = [np.sum(CorrTable_np[i]) for i in range(K_X)]
n_group_Y = [np.sum(CorrTable_np[:,j]) for j in range(K_Y)]
# среднегрупповые значения переменной X
Xboun_mean = [(CorrTable_df.index[i].left + CorrTable_df.index[i].right)/2 for i in range(K_X)]
Xboun_mean[0] = (np.min(X) + CorrTable_df.index[0].right)/2 # исправляем значения в крайних интервалах
Xboun_mean[K_X-1] = (CorrTable_df.index[K_X-1].left + np.max(X))/2
# среднегрупповые значения переменной Y
Yboun_mean = [(CorrTable_df.columns[j].left + CorrTable_df.columns[j].right)/2 for j in range(K_Y)]
Yboun_mean[0] = (np.min(Y) + CorrTable_df.columns[0].right)/2 # исправляем значения в крайних интервалах
Yboun_mean[K_Y-1] = (CorrTable_df.columns[K_Y-1].left + np.max(Y))/2
# средневзевешенные значения X и Y для каждой группы
Xmean_group = [np.sum(CorrTable_np[:,j] * Xboun_mean) / n_group_Y[j] for j in range(K_Y)]
Ymean_group = [np.sum(CorrTable_np[i] * Yboun_mean) / n_group_X[i] for i in range(K_X)]
# общая дисперсия X и Y
Sum2_total_X = np.sum(n_group_X * (Xboun_mean - np.mean(X))**2)
Sum2_total_Y = np.sum(n_group_Y * (Yboun_mean - np.mean(Y))**2)
# межгрупповая дисперсия X и Y (дисперсия групповых средних)
Sum2_between_group_X = np.sum(n_group_Y * (Xmean_group - np.mean(X))**2)
Sum2_between_group_Y = np.sum(n_group_X * (Ymean_group - np.mean(Y))**2)
# эмпирическое корреляционное отношение
corr_ratio_XY = sqrt(Sum2_between_group_Y / Sum2_total_Y)
corr_ratio_YX = sqrt(Sum2_between_group_X / Sum2_total_X)
try:
if orientation!='XY' and orientation!='YX':
raise ValueError("Error! Incorrect orientation!")
if orientation=='XY':
corr_ratio = corr_ratio_XY
elif orientation=='YX':
corr_ratio = corr_ratio_YX
except ValueError as err:
print(err)
# проверка гипотезы о значимости корреляционного отношения
F_corr_ratio_calc = (n_X - K_X)/(K_X - 1) * corr_ratio**2 / (1 - corr_ratio**2)
dfn = K_X - 1
dfd = n_X - K_X
F_corr_ratio_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
a_corr_ratio_calc = 1 - sci.stats.f.cdf(F_corr_ratio_calc, dfn, dfd, loc=0, scale=1)
conclusion_corr_ratio_sign = 'significance' if F_corr_ratio_calc >= F_corr_ratio_table else 'not significance'
# доверительный интервал корреляционного отношения
if F_corr_ratio_calc >= F_corr_ratio_table:
f1 = round ((K_X - 1 + n_X * corr_ratio**2)**2 / (K_X - 1 + 2 * n_X * corr_ratio**2))
f2 = n_X - K_X
z1 = (n_X - K_X) / n_X * corr_ratio**2 / (1 - corr_ratio**2) * 1/sci.stats.f.ppf(p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
z2 = (n_X - K_X) / n_X * corr_ratio**2 / (1 - corr_ratio**2) * 1/sci.stats.f.ppf(1 - p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
corr_ratio_conf_int_low = sqrt(z1) if sqrt(z1) >= 0 else 0
corr_ratio_conf_int_high = sqrt(z2) if sqrt(z2) <= 1 else 1
else:
corr_ratio_conf_int_low = corr_ratio_conf_int_high = '-'
# оценка тесноты связи
if scale=='Cheddok':
conclusion_corr_ratio_scale = scale + ': ' + Cheddock_scale_check(corr_ratio, name=chr(951))
elif scale=='Evans':
conclusion_corr_ratio_scale = scale + ': ' + Evans_scale_check(corr_ratio, name=chr(951))
# формируем результат
result = pd.DataFrame({
'notation': (chr(951)),
'coef_value': (corr_ratio),
'coef_value_squared': (corr_ratio**2),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_corr_ratio_calc),
'F_table': (F_corr_ratio_table),
'F_calc >= F_table': (F_corr_ratio_calc >= F_corr_ratio_table),
'a_calc': (a_corr_ratio_calc),
'a_calc <= a_level': (a_corr_ratio_calc <= a_level),
'significance_check': (conclusion_corr_ratio_sign),
'conf_int_low': (corr_ratio_conf_int_low),
'conf_int_high': (corr_ratio_conf_int_high),
'scale': (conclusion_corr_ratio_scale)
},
index=['Correlation ratio'])
return result # Функция для проверка значимости линейной корреляционной связи
def line_corr_sign_check(X, Y, p_level=0.95, orientation='XY'):
a_level = 1 - p_level
X = np.array(X)
Y = np.array(Y)
n_X = len(X)
n_Y = len(Y)
# коэффициент корреляции
corr_coef = sci.stats.pearsonr(X, Y)[0]
# корреляционное отношение
try:
if orientation!='XY' and orientation!='YX':
raise ValueError("Error! Incorrect orientation!")
if orientation=='XY':
corr_ratio = corr_ratio_check(X, Y, orientation='XY', scale='Evans')['coef_value'].values[0]
elif orientation=='YX':
corr_ratio = corr_ratio_check(X, Y, orientation='YX', scale='Evans')['coef_value'].values[0]
except ValueError as err:
print(err)
# число интервалов группировки
group_int_number = lambda n: round (3.31*log(n_X, 10)+1) if round (3.31*log(n_X, 10)+1) >=2 else 2
K_X = group_int_number(n_X)
# проверка гипотезы о значимости линейной корреляционной связи
if corr_ratio >= abs(corr_coef):
F_line_corr_sign_calc = (n_X - K_X)/(K_X - 2) * (corr_ratio**2 - corr_coef**2) / (1 - corr_ratio**2)
dfn = K_X - 2
dfd = n_X - K_X
F_line_corr_sign_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
comparison_F_calc_table = F_line_corr_sign_calc >= F_line_corr_sign_table
a_line_corr_sign_calc = 1 - sci.stats.f.cdf(F_line_corr_sign_calc, dfn, dfd, loc=0, scale=1)
comparison_a_calc_a_level = a_line_corr_sign_calc <= a_level
conclusion_null_hypothesis_check = 'accepted' if F_line_corr_sign_calc < F_line_corr_sign_table else 'unaccepted'
conclusion_line_corr_sign = 'linear' if conclusion_null_hypothesis_check == 'accepted' else 'non linear'
else:
F_line_corr_sign_calc = ''
F_line_corr_sign_table = ''
comparison_F_calc_table = ''
a_line_corr_sign_calc = ''
comparison_a_calc_a_level = ''
conclusion_null_hypothesis_check = 'Attention! The correlation ratio is less than the correlation coefficient'
conclusion_line_corr_sign = '-'
# формируем результат
result = pd.DataFrame({
'corr.coef.': (corr_coef),
'corr.ratio.': (corr_ratio),
'null hypothesis': ('ru00b2 = ' + chr(951) + 'u00b2'),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_line_corr_sign_calc),
'F_table': (F_line_corr_sign_table),
'F_calc >= F_table': (comparison_F_calc_table),
'a_calc': (a_line_corr_sign_calc),
'a_calc <= a_level': (comparison_a_calc_a_level),
'null_hypothesis_check': (conclusion_null_hypothesis_check),
'significance_line_corr_check': (conclusion_line_corr_sign),
},
index=['Significance of linear correlation'])
return resultdisplay(corr_coef_check(X, Y, scale='Evans'))
display(corr_ratio_check(X, Y, orientation='XY', scale='Evans'))
display(line_corr_sign_check(X, Y, orientation='XY'))
Сделаем выводы по результатам расчетов:
-
Между величинами существует значимая (acalc<0.05) корреляционная связь, корреляционное отношение η = 0.7936 (т.е. связь сильная по Эвансу).
-
Линейная корреляционная связь между величинами также значимая (acalc<0.05), отрицательная, коэффициент корреляции r = -0.7189 (связь сильная по Эвансу); линейная корреляция между переменными объясняет 51.68% вариации.
-
Гипотеза о равенстве корреляционного отношения и коэффициента корреляции отвергается (acalc<0.05), то есть отличие линейной формы связи от нелинейной значимо.
ИТОГИ
Итак, мы рассмотрели способы построения корреляционной таблицы, расчета корреляционного отношения, проверки его значимости и построения для него доверительных интервалов средствами Python. Также предложены пользовательские функции, уменьшающие размер кода.
Исходный код находится в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods).
ЛИТЕРАТУРА
-
Айвазян С.А. и др. Прикладная статистика: исследование зависимостей. – М.: Финансы и статистика, 1985. – 487 с.
-
Айвазян С.А., Мхитарян В.С. Прикладная статистика. Основы эконометрики: В 2 т. – Т.1: Теория вероятностей и прикладная статистика. – М.: ЮНИТИ-ДАНА, 2001. – 656 с.
-
Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. – М.: ФИЗМАТЛИТ, 2006. – 816 с.
-
Котеров А.Н. и др. Сила связи. Сообщение 2. Градации величины корреляции. – Медицинская радиология и радиационная безопасность. 2019. Том 64. № 6. с.12–24 (https://medradiol.fmbafmbc.ru/journal_medradiol/abstracts/2019/6/12-24_Koterov_et_al.pdf).
Все курсы > Оптимизация > Занятие 3
Как мы уже говорили, исследуя изменения случайных величин, мы зачастую обнаруживаем, что между этими изменениями существует взаимосвязь (bivariate relationship, association).
Откроем ноутбук к этому занятию⧉
Возьмем вот такой простой набор данных.
|
toy_df = pd.DataFrame({ ‘a’:[1, 4, 5, 6, 9], ‘b’:[2, 3, 5, 6, 8], ‘c’:[6, 5, 4, 3, 2], ‘d’:[7, 4, 3, 4, 6] }) toy_df |

Посмотрим на распределения величин с помощью boxplot.
|
plt.figure(figsize = (8, 6)) sns.boxplot(data = toy_df) plt.show() |

Очевидно, распределения отличаются друг от друга, однако пока что мы мало можем сказать об этих распределениях или их взаимосвязи.
Начнем с расчета дисперсии.
Дисперсия
Дисперсия (variance) показывает изменение переменной относительно среднего значения. Приведем формулу для расчета дисперсии генеральной совокупности.
$$ sigma^2 = frac{sum (x_i-mu)^2}{N} $$
где $mu$ — среднее генеральной совокупности из $ x_i $ элементов, а $N$ — ее размер. Дисперсию выборки мы рассчитываем немного иначе.
$$ s^2 = frac{sum (x_i-bar{x})^2}{n-1} $$
В данном случае деление на $n-1$, а не на $n$ называется поправкой Бесселя (Bessel’s correction). Зачем нужна такая поправка? Оказывается, можно показать, что сумма квадратов расстояний, то есть числитель формулы, до среднего генсовокупности (population mean) будет всегда больше, чем сумма квадратов расстояний до выборочного среднего (sample mean).
Как следствие, если при расчете выборочной дисперсии делить на $n$, то мы будем постоянно недооценивать дисперсию генсовокупности. Поправка с делением на $ n-1 $ увеличит дисперсию выборки и сделает ее несмещенной оценкой (unbiased estimation) дисперсии генеральной совокупности.
Приведем основные выводы для показателя дисперсии.
- Большая дисперсия показывает, что значения далеки от среднего и далеки друг от друга
- Дисперсия не может быть отрицательной
- Нулевая дисперсия означает, что все элементы выборки или генеральной совокупности идентичны
Замечу, что далее мы в большинстве случаев будем приводить формулы и вычислять именно выборочные показатели.
Найдем дисперсию для переменной a.
|
# применим формулу дисперсии к первому столбцу (np.square(toy_df[‘a’] – toy_df[‘a’].mean())).sum() / (toy_df.shape[0] – 1) |
Дисперсию для каждой переменной можно измерить с помощью функции np.var() библиотеки Numpy.
|
# рассчитаем дисперсию по столбцам с делением на n – 1 np.var(toy_df, ddof = 1) |
|
a 8.5 b 5.7 c 2.5 d 2.7 dtype: float64 |
Точно такой же результат можно получить с помощью метода .var() библиотеки Pandas.
|
# ddof = 1 можно не указывать, это параметр по умолчанию toy_df.var() |
|
a 8.5 b 5.7 c 2.5 d 2.7 dtype: float64 |
Параметр ddof означает Delta Degrees of Freedom (дельта степеней свободы) и указывает на размер поправки при расчете дисперсии выборки. Соответственно ddof = 1 как раз использует деление на $n-ddof = n-1$. Как мы видим, дисперсия переменной a существенно больше, чем, например, переменной d.
Показатель дисперсии представляет собой квадрат измеряемых нами величин. Для понимания величины отклонения это не очень удобно. В этом смысле лучше подойдет среднее квадратическое отклонение.
Среднее квадратическое отклонение
Среднее квадратическое отклонение (СКО, standard deviation) как раз вычисляется как корень из дисперсии.
$$ sigma = sqrt{sigma^2} $$
$$ s = sqrt{s^2} $$
Рассчитаем СКО для первого столбца.
|
np.sqrt((np.square(toy_df[‘a’] – toy_df[‘a’].mean())).sum() / (toy_df.shape[0] – 1)) |
Мы также можем использовать функцию np.std() библиотеки Numpy и метод .std() библиотеки Pandas.
|
# для расчета СКО будем также делить на n – 1 np.std(toy_df, ddof = 1) |
|
a 2.915476 b 2.387467 c 1.581139 d 1.643168 dtype: float64 |
|
# опять же, этот параметр установлен по умолчанию, и его можно не указывать toy_df.std() |
|
a 2.915476 b 2.387467 c 1.581139 d 1.643168 dtype: float64 |
Теперь перейдем к изучению взаимосвязи между переменными. Одним из способов измерения взаимосвязи является ковариация.
Ковариация
Ковариация (covariance) измеряет направление изменения двух переменных. Другими словами она позволяет понять как изменится одна из двух переменных при изменении второй.
Построим три точечные диаграммы (scatter plots) для переменных a и b, b и c, и c и d соответственно.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# создадим сетку 1 х 3 с подграфиками для каждой из пар переменных f, (pair1, pair2, pair3) = plt.subplots(nrows = 1, ncols = 3, figsize = (12, 4), constrained_layout = True) # в первый подграфик поместим точечную диаграмму переменных a и b pair1.scatter(toy_df[‘a’], toy_df[‘b’]) pair1.set_title(‘a vs. b’, fontsize = 14) pair1.set(xlabel = ‘a’) pair1.set(ylabel = ‘b’) # во второй – b и c pair2.scatter(toy_df[‘b’], toy_df[‘c’]) pair2.set_title(‘b vs. c’, fontsize = 14) pair2.set(xlabel = ‘b’) pair2.set(ylabel = ‘c’) # в третий – c и d pair3.scatter(toy_df[‘c’], toy_df[‘d’]) pair3.set_title(‘c vs. d’, fontsize = 14) pair3.set(xlabel = ‘c’) pair3.set(ylabel = ‘d’) plt.show() |

На первом и втором графике мы видим линейную взаимосвязь. Приведем формулу для ее измерения.
$$ Cov_{x, y} = frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} $$
Как вы видите, ковариация представляет собой сумму произведений отклонений переменных от своего среднего значения, усредненную на количество наблюдений ($n-1$).
Рассчитаем ковариацию a и b с помощью Питона.
|
((toy_df[‘a’] – toy_df[‘a’].mean()) * (toy_df[‘b’] – toy_df[‘b’].mean())).sum() / (toy_df.shape[0] – 1) |
Если использовать функцию np.cov() библиотеки Numpy или метод .cov() библиотеки Pandas, то мы получим так называемую ковариационную матрицу (covariance matrix).
|
# для расчета по столбцам нужно использовать параметр rowvar = False np.cov(toy_df, ddof = 1, rowvar = False) |
|
array([[ 8.5 , 6.75, -4.5 , -1. ], [ 6.75, 5.7 , -3.75, -0.55], [-4.5 , -3.75, 2.5 , 0.5 ], [-1. , -0.55, 0.5 , 2.7 ]]) |

По диагонали указана дисперсия, вне диагонали — ковариация любых двух переменных.
Переменные a и b имеют положительную ковариацию, с увеличением a увеличивается и b. Переменные b и c — отрицательную, переменные c и d демонстрируют нулевую или близкую к нулевой ковариацию.
Интересно, что если переменные независимы (между ними нет взаимосвязи) — ковариация будет равна нулю, при этом обратное не обязательно верно. Если ковариация равна нулю, взаимосвязь может быть, просто она нелинейна (возможно именно такая взаимосвязь существует между c и d).
Недостатком ковариации является то, что она измеряет только направление, но не силу взаимосвязи. Если мы умножим значения обеих переменных, например, на три, то ковариация, исходя из формулы выше, увеличится в девять раз (поскольку как x, так и y каждой пары переменных умножаются на три), при этом очевидно сила взаимосвязи никак не изменится.
|
# умножим данные на три, рассчитаем ковариацию # и разделим на ковариационную матрицу исходного датасета, # чтобы посмотреть масштаб изменения (toy_df * 3).cov() / toy_df.cov() |

Этот недостаток исправляет коэффициент корреляции.
Корреляция
Корреляция (correlation) между двумя переменными (случайными величинами) измеряет не только направление, но и силу взаимосвязи.
Параметрические и непараметрические тесты
Прежде чем перейти к различным коэффициентам корреляции несколько слов про разделение статистических тестов или методов на параметрические и непараметрические.
Параметрические методы (parametric methods) основываются на допущении (assumption) или предпосылке о том, как распределена генеральная совокупность, из которой взята изучаемая выборка. Например, статистический тест может предполагать, что данные имеют нормальное распределение.
Непараметрические методы (non-parametric) таких допущений соответственно не предполагают.
На практике это означает, что если допущения параметрического теста не выполняются, его результат нельзя считать достоверным. Для непараметрического теста такое ограничение отсутствует.
Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона (Pearson correlation coefficient) — это параметрический тест, который строится на основе расчета ковариации двух переменных, разделенного на произведение СКО каждой из них.
$$ r_{pearson} = frac{Cov_{x, y}}{s_x s_y} $$
Деление на произведение СКО $(s_x s_y)$ выражает любой коэффициент ковариации в единицах этого произведения (нормализует его). Как следствие, мы получаем возможность сравнения коэффициентов корреляции, а значит измерения не только направления, но и силы взаимосвязи.
Коэффициент корреляции всегда находится в диапазоне от $-1$ до $1$.
Значения, приближающиеся к 1 указывают на сильную положительную линейную корреляцию. Близкие к −1 — на сильную отрицательную линейную корреляцию. Околонулевые значения означают отсутствие линейной корреляции.
Посмотрим на график возможных вариантов корреляции данных, приведенный на занятии вводного курса.

Библиотека Numpy предлагает нам функцию np.corrcoef() для создания корреляционной матрицы (correlation matrix) коэффициента Пирсона.
|
# для расчета корреляции по столбцам используем параметр rowvar = False np.corrcoef(toy_df, rowvar = False).round(2) |
|
array([[ 1. , 0.97, -0.98, -0.21], [ 0.97, 1. , -0.99, -0.14], [-0.98, -0.99, 1. , 0.19], [-0.21, -0.14, 0.19, 1. ]]) |
В Pandas мы можем воспользоваться методом .corr().
|
# параметр method = ‘pearson’ используется по умолчанию, # его можно не указывать toy_df.corr(method = ‘pearson’).round(2) |

Корреляция переменной с самой собой равна единице, что и отражают значения на главной диагонали матрицы. Кроме того, очевидно, что величина X также коррелирует с Y, как Y c X.
Продемонстрируем также, что изменение масштаба данных не отразится на коэффициенте корреляции.
|
# умножим значения датасета на два и снова рассчитаем коэффициент Пирсона (toy_df * 2).corr().round(2) |

Особенности коэффициента Пирсона
Несколько важных замечаний.
Замечание 1. Ни ковариация, ни корреляция не устанавливают причинно-следственной связи (correlation does not imply causation). Например, мы можем наблюдать существенную корреляцию между потреблением мороженого и продажами кондиционеров, при этом изменения в обеих переменных могут быть вызваны третьей, на рассматриваемой нами переменной, в частности, температурой воздуха.
Кроме того в некоторых случаях корреляция может быть чистой случайностью.
Замечание 2. Коэффициент корреляции Пирсона измеряет взаимосвязь (1) количественных переменных и (2) предполагает, что обе переменные имеют нормальное распределение (это и есть упомянутое выше допущение (assumption) параметрического теста).
Замечание 3. Как и в случае с ковариацией, отсутствие линейной корреляции не означает отсутствие взаимосвязи. Возможно взаимосвязь есть, но она нелинейна.
Замечание 4. Более того, на коэффициент корреляции существенное влияние оказывают выбросы (outliers).
Последние два замечения хорошо иллюстрируются квартетом Энскомба (Anscombe’s quartet), набором небольших датасетов (кстати, встроенных в сессионное хранилище Google Colab) с совершенно разными распределениями x и y, но одинаковым средним арифметическим и СКО переменной y, а также одинаковым коэффициентом корреляции Пирсона.
Вначале получим необходимые данные.
|
# загрузим данные в формате json из сессионного хранилища, # преобразуем в датафрейм и посмотрим на первые три строки anscombe = pd.read_json(‘/content/sample_data/anscombe.json’) anscombe.head(3) |

|
# разобьем данные на четыре части по столбцу Series series_by_group = [x for _, x in anscombe.groupby(‘Series’)] # отдельно получим названия каждой из четырех частей labels = anscombe.Series.unique() labels |
|
array([‘I’, ‘II’, ‘III’, ‘IV’], dtype=object) |
|
# создадим пустой словарь datasets = {} # в цикле пройдемся по названиям и значениям переменных x и y каждой из частей for label, series in zip(labels, series_by_group): # каждое название части станет ключом словаря, а переменные x и y – значениями datasets[label] = (list(series.X.round(2)), list(series.Y.round(2))) # выведем содержимое словаря с помощью функции pprint() from pprint import pprint pprint(datasets) |
|
{‘I’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68]), ‘II’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [9.14, 8.14, 8.74, 8.77, 9.26, 8.1, 6.13, 3.1, 9.13, 7.26, 4.74]), ‘III’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73]), ‘IV’: ([8, 8, 8, 8, 8, 8, 8, 19, 8, 8, 8], [6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.5, 5.56, 7.91, 6.89])} |
Теперь выведем каждый из четырех датасетов на графиках.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# создадим сетку подграфиков 2 х 2 fig, axs = plt.subplots(2, 2, sharex = True, sharey = True, figsize = (10, 10), gridspec_kw = {‘wspace’: 0.08, ‘hspace’: 0.08}) # определим границы осей и отметки на осях x и y axs[0, 0].set(xlim = (0, 20), ylim = (2, 14)) axs[0, 0].set(xticks = (0, 10, 20), yticks = (4, 8, 12)) # пройдемся по подграфикам, а также ключам и значениям словаря datasets for ax, (label, (x, y)) in zip(axs.flat, datasets.items()): # выведем название (номер) группы ax.text(0.1, 0.9, label, fontsize = 20, transform = ax.transAxes, va = ‘top’) ax.tick_params(direction = ‘in’, top = True, right = True) # построим точечные диаграммы ax.scatter(x, y) # обучим модель линейной регрессии slope, intercept = np.polyfit(x, y, deg = 1) # выведем график линейной регрессии x_vals = np.linspace(0, 20, num = 1000) y_vals = intercept + slope * x_vals ax.plot(x_vals, y_vals, ‘r’) # рассчитаем среднее арифметическое, СКО и корреляцию Пирсона stats = (f‘$\mu$ = {np.mean(y):.2f}n’ f‘$\sigma$ = {np.std(y):.2f}n’ f‘$r$ = {np.corrcoef(x, y)[0][1]:.2f}’) # создадим отформатированное пространство на графике bbox = dict(boxstyle = ‘square’, pad = 0.5, fc = ‘#c5d4e6’, ec = ‘#89a8cc’, alpha = 0.5) # и выведем в нем рассчитанные выше статистические показатели ax.text(0.95, 0.07, stats, fontsize = 15, bbox = bbox, transform = ax.transAxes, horizontalalignment = ‘right’) plt.show() |
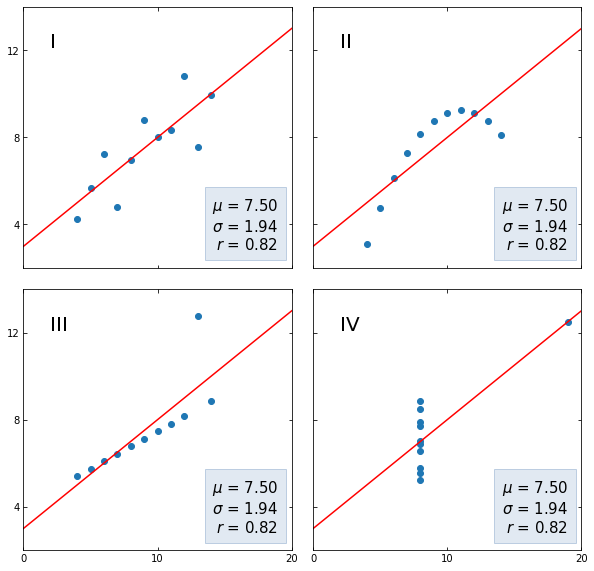
- Как мы видим, на первом графике прослеживается линейная корреляция без каких-либо сюрпризов;
- Во втором наборе данных у нас нелинейная зависимость, силу которой мы не смогли отразить с помощью коэффициента Пирсона;
- В третьем наборе коэффициент корреляции находится под сильным влиянием выброса;
- В четвертом, корреляция по сути отсутствует и тем не менее одного наблюдения оказывается достаточно для появления достаточно сильной корреляции.
Помимо ограничений коэффициента корреляции, эти наборы данных демонстрируют в целом важность визуальной оценки данных.
Коэффициент Пирсона как скалярное произведение векторов
Распишем формулу корреляции более подробно (см. формулы ковариации, дисперсии и СКО).
$$ r_{pearson} = frac{ frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} }{ sqrt {frac{sum (x_i-bar{x})^2}{n-1} frac{sum (y_i-bar{y})^2}{n-1} } } $$
Упростим выражение.
$$ r_{pearson} = frac{ sum (x_i-bar{x})(y_i-bar{y}) } { sqrt {sum (x_i-bar{x})^2} sqrt{ sum (y_i-bar{y})^2 } } $$
Теперь давайте представим случайные величины X и Y в форме векторов
$$ textbf{x} = [x_1, x_2, x_3,…, x_n] $$
$$ textbf{y} = [y_1, y_2, y_3,…, y_n] $$
со средними значениями $ bar{x} $ и $ bar{y} $. Затем определим новые векторы $ textbf{x}^c $ и $ textbf{y}^c $, в которых из значений $x_i$ и $y_i$ вычтем соответствующие средние значения.
$$ textbf{x}^c = [x_1-bar{x}, x_2-bar{x}, x_3-bar{x},…, x_n-bar{x}] $$
$$ textbf{y}^c = [y_1-bar{x}, y_2-bar{x}, y_3-bar{y},…, y_n-bar{y}] $$
Обратим внимание, что (1) числитель (1) в формуле коэффициента корреляции представляет собой покомпонентное умножение векторов с последующим сложением произведений (то есть скалярное произведение).
Знаменатель (2) же представляет собой покомпонентное умножение и сложение произведений векторов самих на себя. Как мы узнаем на курсе линейной алгебры, корень из скалярного произведение вектора на самого себя есть длина этого вектора. Приведем пример для вектора $ textbf{x} $
$$ sqrt { textbf{x}^2 } = sqrt { textbf{x} cdot textbf{x} } = || textbf{x} || $$
Исходя из этих двух соображений, перепишем формулу расчета коэффициента Пирсона.
$$ r_{pearson} = frac { textbf{x}^c cdot textbf{y}^c }{|| textbf{x}^c || cdot || textbf{y}^c || } $$
Это формула косинусного сходства двух векторов. Другими словами, коэффициент корреляции равен косинусу угла между двумя векторами данных. Рассчитаем корреляцию через косинусное сходство с помощью Питона.
|
# возьмем данные первой группы квартета Энскомба x = np.array([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5]) y = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68]) # вычтем из каждого значения x и y соответствующее среднее арифметическое xc = x – np.mean(x) yc = y – np.mean(y) # используем формулу косинусного сходства и округлим результат np.round(np.dot(xc, yc)/(np.linalg.norm(xc) * np.linalg.norm(yc)), 2) |
Как уже было сказано, у коэффициента Пирсона есть ряд ограничений, в частности, он выявляет только линейную взаимосвязь количественных переменных. В этой связи рассмотрим коэффициент Спирмена.
Коэффициент ранговой корреляции Спирмена
Коэффициент ранговой корреляции Спирмена (Spearman’s Rank Correlation Coefficient) хорошо измеряет постоянно возрастающую или постоянно убывающую (монотонную) зависимость двух переменных, а также подходит для работы с категориальными порядковыми данными.
Это непараметрический тест, который не предполагает каких-либо допущений о распределении генеральной совокупности.
Монотонная зависимость
Напомню, что функция или зависимость называется монотонной (monotonic), если на заданном интервале ее производная (градиент) не меняет знака (то есть всегда имеет неотрицательное или неположительное значение). Приведем пример.

Рассмотрим взаимосвязь площади (area) и цены (price) квартиры.
|
# поместим данные площади и цены квартиры в датафрейм flats = pd.DataFrame({ ‘area’ :[78, 90, 74, 69, 63, 57, 72, 67, 83], ‘price’ :[9.1, 9.0, 8.9, 8.2, 6.0, 5.8, 8.7, 7.5, 9.2] }) flats |

Выведем эти данные с помощью точечной диаграммы (scatter plot).
|
plt.figure(figsize = (8, 6)) plt.scatter(flats.area, flats.price) plt.xlabel(‘Площадь, кв. м.’, fontsize = 15) plt.ylabel(‘Цена, млн. руб.’, fontsize = 15) plt.grid() plt.show() |

Рассчитаем коэффициент корреляции Пирсона.
|
# применим метод .corr() с параметром method = ‘pearson’ # выведем одно из значений корреляционной матрицы с помощью .iloc[0, 1] и округлим результат flats.corr(method = ‘pearson’).iloc[0, 1].round(2) |
Достаточно высокий уровень корреляции. При этом, как мы видим, зависимость нелинейна и возможно коэффициент Пирсона не до конца уловил силу взаимосвязи. Как нам преодолеть ограничение линейности?
Обратите внимание, прежде чем построить график, Питон упорядочил значения площади (ось x). Упорядочил, то есть присвоил им ранг (порядковый номер) от первого до, в данном примере, девятого. В каком случае значения цены (ось y) будут также возрастать? Только в случае если их ранги мало отличаются от рангов значений площади квартиры.
Коэффициент корреляции Спирмена как раз считает степень отличия рангов двух переменных.
Приведем формулу.
$$ r_{spearman} = frac{6 sum d_i^2 }{n(n^{2}-1)} $$
Вычислим коэффициент Спирмена с помощью Питона. Вначале присвоим каждому значению в обоих столбцах ранг (порядковый номер), предварительно упорядочив значения по убыванию.
|
# для этого используем метод .rank() с параметром ascending = False flats[‘area_rank’] = flats.area.rank(ascending = False) flats[‘price_rank’] = flats.price.rank(ascending = False) flats |

Таким образом площади дома в 90 квадратных метров и цене в 9,2 миллона рублей будет присвоен ранг 1. Теперь мы можем вычислить разницу рангов для каждого из наблюдений и возвести ее в квадрат.
|
# вычтем из рангов площади ранги цены flats[‘diff’] = flats[‘area_rank’] – flats[‘price_rank’] # возведем разницу в квадрат flats[‘diff_sq’] = np.square(flats[‘diff’]) flats |

Выполним оставшиеся вычисления в соответствии с приведенной выше формулой.
|
# поместим количество наблюдений в переменную n n = flats.shape[0] # применим формулу для расчета коэффициента Спирмена 1 – ((6 * flats[‘diff_sq’].sum()) / (n * (n**2 – 1))) |
Рассчитаем корреляцию Спирмена с помощью метода .corr() библиотеки Pandas с параметром method = ‘spearman’.
|
flats[[‘area’, ‘price’]].corr(method = ‘spearman’).iloc[0, 1].round(2) |
Как мы видим, этот коэффициент гораздо лучше уловил монотонную нелинейную зависимость двух переменных.
Также замечу, что коэффициент корреляции Спирмена менее чувствителен к выбросам, находящимся на «краях» обеих выборок, потому что опять же учитывает не само значение, а присвоенный ему ранг.
Категориальные порядковые данные
Как уже было сказано, помимо количественных значений коэффициент Спирмена способен измерить направление и силу взаимосвязи категориальных порядковых значений (categorical ordinal data).
Это могут быть оценки уровня удовлетворености клиента (очень понравилось, понравилось, не понравилось), размеры, выраженные категорией (S, M, L, …) и так далее.
В качестве примера рассмотрим оценку собственного самочувствия по шкале от 1 до 10, которую пациенты поставили себе до и после нового метода лечения.
|
# создадим датафрейм с данными о самочувствии treatment = pd.DataFrame( [ [3, 2], [4, 3], [2, 1], [1, 5], [6, 7], [7, 6], [5, 4] ], columns = [‘Before’, ‘After’]) treatment |

|
# выведем данные на графике plt.figure(figsize = (8, 6)) plt.scatter(treatment.Before, treatment.After) plt.xlabel(‘Before’, fontsize = 15) plt.ylabel(‘After’, fontsize = 15) plt.grid() plt.show() |

По всей видимости корреляция должна быть меньше, чем в предыдущем примере. Приступим к измерениям. Сделать это на самом деле очень просто, потому что порядковые значения уже сами по себе представляют собой ранги. Остается только найти квадрат их разности и применить формулу коэффициента корреляции.
|
# найдем квардрат разницы рангов treatment[‘diff’] = treatment[‘Before’] – treatment[‘After’] treatment[‘diff_sq’] = np.square(treatment[‘diff’]) treatment |

|
# применим формулу коэффициента корреляции Спирмена n = treatment.shape[0] round(1 – ((6 * treatment[‘diff_sq’].sum()) / (n * (n**2 – 1))), 2) |
Остается сравнить с методом .corr() библиотеки Pandas.
|
treatment[[‘Before’, ‘After’]].corr(method = ‘spearman’).iloc[0, 1].round(2) |
Обратите внимание, ни в количественных данных, ни в порядковых у нас не было повторяющихся или совпадающих наблюдений. В случае совпадающих наблюдений (tied ranks), то есть когда значения x или y повторяются, расчет коэффициента корреляции Спирмена также возможен, но немного усложняется.
Коэффициент ранговой корреляции Кендалла
Коэффициент ранговой корреляции Кендалла (еще говорят тау Кендалла или тау-коэффициент, Kendall’s $tau$ rank correlation coefficient), как и метод Спирмена, может применяться для измерения силы взаимосвязи количественных и порядковых категориальных переменных и подходит для анализа нелинейных зависимостей. Это также непараметрический тест.
Смысл и методику расчета коэффициента Кендалла легко понять на примере. Вновь возьмем данные о самочувствии до и после лечения.
|
# вернем датафрейм к исходному виду treatment = treatment[[‘Before’, ‘After’]] treatment |

Теперь рассмотрим две пары наблюдений, например, под индексом 0 и 1.

Мы видим, что в столбце Before значения наблюдения 0 меньше, чем значение наблюдения 1 (потому что 3 < 4). То же самое можно наблюдать в столбце After (2 < 3). Такая пара наблюдений называется конкордантной (concordant). Конкордантной будет и пара наблюдений, где оба значения в первом наблюдении больше обоих значений во втором. К ним относятся, например, пары 1 и 2 (где 4 > 2, а 3 > 1).

Если же описанные выше условия не выполняются, то такая пара наблюдений будет называться дискордантной (discordant). К таким наблюдениям относятся, например, наблюдения 4 и 5 (6 > 7, но 7 < 6).

Отнесем каждую из пар нашего датасета к одному из этих классов.
|
# 0 # 1 C # 2 C C # 3 D D D # 4 C C C C # 5 C C C C D # 6 C C C D C C # 0 1 2 3 4 5 6 |
Получилось 16 конкордантных (C) и 5 дискордантных (D) пар. Их общее количество очевидно равно 21. Это значение удобно посчитать по формуле сочетаний.
$$ C(n, r) = frac{n!}{(n-r)! r!} rightarrow C(7, 2) = frac{7!}{(7-2)! 2!} = 21 $$
где n — количество наблюдений, а r равно двум, потому что мы ищем сочетания пар элементов. Можно воспользоваться и упрощенной формулой.
$$ C(r) = frac{(n cdot (n-1))}{2} rightarrow C(7) = frac{7 cdot (7-1)}{2} = 21 $$
|
# найдем количество парных сочетаний с помощью Питона n = 7 pairs = (7 * (7 – 1)) // 2 pairs |
Так вот, коэффициент корреляции Кендалла показывает соотношение конкордантных и дискордантных пар по следующей формуле.
$$ tau = frac{text{concordant pairs}-text{discordant pairs}}{text{total pairs}}$$
Применим ее к нашему датасету.
|
concordant = 16 discordant = pairs – concordant np.round((concordant – discordant) / pairs, 2) |
Точно такого же результата можно добиться с помощью метода .corr() библиотеки Pandas.
|
treatment.corr(method = ‘kendall’).iloc[0, 1].round(2) |
Смысл этого коэффициента в следующем.
Чем больше доля конкордантных пар, тем больше схожих рангов, а значит сильнее взаимосвязь между переменными.
Коэффициент неопределенности
Определение и понятие симметричности теста
Коэффициент неопределенности (uncertainty coefficient) или U Тиля (Theil’s U) позволяет оценить взаимосвязь между двумя категориальными признаками, например, X и Y. Формально он определяется как значение X при условии данного Y.
$$U(x|y)$$
Более того, в отличие от некоторых других тестов, он несимметричен (asymmetric), что позволяет узнать зависит ли Y от X, так же как X от Y.
$$U(y|x) neq U(x|y)$$
Понятие симметричности теста легко представить на следующем простом примере.

Очевидно, что мы легко можем предсказать Y зная X, а вот зная Y мы можем меньше сказать про X (обратите внимание, что категории в X не совпадают для двух категорий в Y).
Используем этот несложный датасет для дальнейших расчетов.
|
# возьмем две категориальные переменные со следующими значениями x = np.array([‘q’, ‘t’, ‘q’, ‘n’, ‘n’, ‘c’]) y = np.array([‘A’, ‘A’, ‘A’, ‘B’, ‘B’, ‘B’]) |
Как рассчитывается
Условная энтропия
U Тиля основывается на понятии условной энтропии (condition entropy), которая позволяет измерить объем информации, необходимый для описания значений переменной X с помощью переменной Y.
$$ S(X|Y) = -sum p(x,y) logfrac{p(x,y)}{p(y)} $$
Теоретическое обоснование формул условной энтропии и энтропии выходит за рамки сегодняшнего занятия. Мы сосредоточимся на расчете и практическом применении каждой из них.
Рассчитаем условную энтропию с помощью Питона. Вначале нам необходимо рассчитать частоту классов категориальных переменных. Для этого прекрасно подойдет класс Counter модуля collections.
|
# импортируем класс Counter модуля collections from collections import Counter |
Посмотрим, сколько раз встречаются классы переменной Y.
|
# найдем частоту классов переменной y y_counts = Counter(y) y_counts |
|
Counter({‘A’: 3, ‘B’: 3}) |
Далее возьмем каждую пару значений X и Y и рассчитаем, сколько раз встречается каждая из них.
|
# возьмем каждую пару значений X и Y с помощью функций zip() и list() list(zip(x, y)) |
|
[(‘q’, ‘A’), (‘t’, ‘A’), (‘q’, ‘A’), (‘n’, ‘B’), (‘n’, ‘B’), (‘c’, ‘B’)] |
|
# рассчитаем их частоту xy_counts = Counter(list(zip(x, y))) xy_counts |
|
Counter({(‘A’, ‘q’): 2, (‘A’, ‘t’): 1, (‘B’, ‘n’): 2, (‘B’, ‘c’): 1}) |
Теперь найдем общее количество значений.
|
total_counts = len(x) total_counts |
В соответствии с формулой выше нам нужно найти вероятность Y ($p(y)$) и вероятность X при условии Y ($p(x,y)$). Для расчета $p(y)$ мы пройдемся по ключам словаря xy_counts и посмотрим в словаре y_counts сколько раз встречается второй элемент каждого ключа.
|
# пройдемся по ключам xy_counts for xy in xy_counts.keys(): # (выведем ключ для наглядности) print(xy) # и посмотрим в y_counts сколько раз встречается второй элемент каждого кортежа print(y_counts[xy[1]]) |
|
(‘q’, ‘A’) 3 (‘t’, ‘A’) 3 (‘n’, ‘B’) 3 (‘c’, ‘B’) 3 |
Мы видим, что категория A и категория B в нашем случае встречаются по три раза. Остается разделить частоту каждой категории на общее количество элементов.
|
# найдем p(y) разделив каждую частоту на общее количество элементов for xy in xy_counts.keys(): print(y_counts[xy[1]] / total_counts) |
Выполним похожее упражнение для того, чтобы найти $p(x,y)$.
|
# снова пройдемся по парам значений for xy in xy_counts.keys(): # (выведем эти пары для наглядности) print(xy) # выведем частоту каждой пары (на этот раз именно пары, а нее ее второго элемента) print(xy_counts[xy]) # и рассчитаем вероятность print(xy_counts[xy] / total_counts) |
|
(‘q’, ‘A’) 2 0.3333333333333333 (‘t’, ‘A’) 1 0.16666666666666666 (‘n’, ‘B’) 2 0.3333333333333333 (‘c’, ‘B’) 1 0.16666666666666666 |
|
# для дальнейшей работы нам понадобится модуль math import math |
Теперь остается подставить $p(y)$ и $p(x,y)$ в формулу.
|
# объявим переменную для условной энтропии cond_entropy = 0.0 # в цикле снова пройдемся по парам значений for xy in xy_counts.keys(): # найдем p(y) p_y = y_counts[xy[1]] / total_counts # и p(x,y) p_xy = xy_counts[xy] / total_counts # подставим их в формулу и просуммируем результат # (мы использовали логарифм с основанием два, но можно использовать, например, и натуральный логарифм) cond_entropy += p_xy * math.log(p_y / p_xy, 2) cond_entropy |
Поместим этот код в функцию.
|
# поместим код в функцию def conditional_entropy(x, y, log_base: float = 2): y_counts = Counter(y) xy_counts = Counter(list(zip(x, y))) total_counts = len(x) cond_entropy = 0.0 for xy in xy_counts.keys(): p_xy = xy_counts[xy] / total_counts p_y = y_counts[xy[1]] / total_counts cond_entropy += p_xy * math.log(p_y / p_xy, log_base) return cond_entropy |
|
# вновь рассчитаем условную энтропию conditional_entropy(x, y) |
Убедимся в несимметричности объема информации, содержащегося в X относительно Y и в Y относительно X, поменяв переменные местами.
|
conditional_entropy(y, x) |
Здесь становится очевидным важный факт.
Если условная энтропия равна нулю, это значит, что с помощью переменной Y мы можем полностью описать переменную X (в нашем примере наоборот). При этом, чем выше условная энтропия, тем меньше информации об X содержится в переменной Y.
Теперь рассмотрим второй компонент формулы коэффициента неопределенности.
Энтропия
Энтропия (entropy) случайной величины рассчитывается по следующей формуле.
$$ S(X) = -sum p(x)log{p(x)} $$
Это значение тем выше, чем менее вероятным является каждый из исходов испытания. Например, энтропия бросания игральной кости будет выше, чем подбрасывания монеты. В первом случае вероятность каждого исхода равна 1/6, во втором 1/2.
Убедимся в этом с помощью функции entropy() модуля stats библиотеки scipy.
|
# импортируем модуль stats библиотеки scipy import scipy.stats as st # рассчитаем энтропию бросания кости и подбрасывания монеты st.entropy([1/6, 1/6, 1/6, 1/6, 1/6, 1/6], base = 2), st.entropy([1/2, 1/2], base = 2) |
Выполним расчет вручную. Вначале найдем вероятность каждого из значений случайной величины $p(x)$.
|
# найдем частоту каждого элемента в X x_counts = Counter(x) # их общее количество total_counts = len(x) # разделим каждую частоту на общее количество элементов p_x = list(map(lambda n: n / total_counts, x_counts.values())) # выведем результат print(p_x) |
|
[0.3333333333333333, 0.16666666666666666, 0.3333333333333333, 0.16666666666666666] |
Теперь подставим это значение в формулу и найдем энтропию.
|
# объявим переменную для условной энтропии entropy = 0.0 # подставим каждую вероятность в формулу и просуммируем for p in p_x: entropy += –p * math.log(p, 2) # выведем результат entropy |
Проверим правильность результата с помощью функции библиотеки scipy().
|
st.entropy(p_x, base = 2) |
Также объявим соответствующую функцию.
|
# объявим функцию def entropy(x, log_base: float = 2): x_counts = Counter(x) total_counts = len(x) p_x = list(map(lambda n: n / total_counts, x_counts.values())) entropy = 0.0 for p in p_x: entropy += –p * math.log(p, 2) return entropy |
|
# проверим результат entropy(x) |
Замечу, что условная энтропия S(X|Y) равна энтропии случайной величины S(X), если величины X и Y независимы.
$$ S(X|Y) = S (X) iff X ⫫ Y $$
Из этого следует, что самое большее условная энтропия может быть равна энтропии этой переменной (в случае, если Y никак не объясняет X).
$$ S(X) leq S(X|Y) $$
Все это важно для расчета коэффициента неопределенности.
U Тиля
Приведем и обсудим формулу.
$$ U(X|Y) = frac{S(X)-S(X|Y)}{S(X)} $$
Зачем рассчитывать не только условную энтропию, но и энтропию случайной величины? Дело в том, что так мы можем не просто измерять «объяснимость» переменной X с помощью Y, но и сравнивать между собой условную энтропию любых категориальных переменных.
Арифметически, чем ниже условная энтропия, тем ближе значение показателя к единице. Чем она выше, тем коэффициент неопределенности ближе к нулю.
Таким образом, U Тиля всегда находится в диапазоне от 0 до 1. При этом, ноль означает, что переменная Y не несет никакой информации относительно переменной X, единица — что переменная Y содержит всю необходимую информацию.
Рассчитаем U Тиля с помощью Питона.
|
# сразу объявим функцию def ucoef(x, y, log_base = 2): # найдем условную энтропию S(X,Y) s_xy = conditional_entropy(x, y, log_base) # энтропию S(X) s_x = entropy(x, log_base) # подставим эти значения в формулу u = (s_x – s_xy) / s_x # выведем результат return u |
Найдем коэффициент неопределенности для X и Y.
Кроме того, убедимся, что X полностью объясняет Y.
Обратите внимание, что коэффициент не может принимать отрицательных значений. Это логично, потому что строго говоря в случае категориальных переменных мы измеряем не корреляцию (направление и силу взаимного изменения, correlation), а степень взаимосвязи (association) между двумя переменными, которая либо есть (и может доходить до единицы), либо ее нет (равна нулю).
Точечно-бисериальная корреляция
Точечно-бисериальная корреляция (point-biserial correlation) позволяет оценить взаимосвязь между количественной переменной и дихотомической (выраженной двумя значениями) качественной переменной. Например, нам может быть важно оценить связь возраста (X) и выживаемости пассажиров «Титаника» (Y, классы 0 и 1). Приведем формулу.
Формула
$$ r_{pb} = frac{M_1-M_0}{s_n} sqrt{frac{n_1 n_0}{n^2}} $$
В данном случае мы делим наблюдения на две группы, в первую группу попадут наблюдения, относящиеся к классу 0, во вторую — к классу 1. Для каждой группы мы считаем средние значения ($M_0$ и $M_1$) и делим их разность на среднее квадратическое отклонение всех значений в переменной X ($s_n$).
Под корнем находится произведение относительного размера двух групп ($n_0$ и $n_1$ — это размеры групп, $n$ — общее число наблюдений).
Коэффициент точечно-бисериальной корреляции находится в диапазоне от $-1$ до $1$ и интерпретируется так же, как и коэффициент корреляции Пирсона.
Выше приведена формула для генеральной совокупности. Если нам доступна лишь выборка, формула выглядит следующим образом.
$$ r_{pb} = frac{M_1-M_0}{s_{n-1}} sqrt{frac{n_1 n_0}{n(n-1)}} $$
СКО ($s_{n-1}$) в этом случае также рассчитывается по формуле для выборки. Приведем пример.
Пример расчета на Питоне
Подгрузим датасет о вине из библиотеки sklearn. На основе свойств вин нам предлагается спрогнозировать один из трех классов вина (классы 0, 1 и 2). Так как нам нужна дихотомическая переменная, удалим наблюдения, относящиеся к классу 2.
|
# из модуля datasets библиотеки sklearn импортируем датасет о вине from sklearn import datasets data = datasets.load_wine() # превратим его в датафрейм wine = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную wine[‘target’] = data.target # оставим только классы 0 и 1 wine = wine[wine.target != 2] # убедимся, что в целевой переменной осталось только два класса np.unique(wine.target) |
Найдем корреляцию между целевой переменной и содержанием пролина (proline).
|
# оставим только интересующие нас столбцы wine = wine[[‘proline’, ‘target’]] wine.head(3) |

Теперь напишем функцию для расчета точечно-бисериальной корреляции (будем использовать формулу для выборки).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# объявим функцию для расчета точечно-бисериальной корреляции # функция будет принимать два параметра: количественную и качественную переменные def pbc(continuous, binary): # преобразуем количественную переменную в массив Numpy continuous_values = np.array(continuous) # классы качественной переменной превратим в нули и единицы binary_values = np.unique(binary, return_inverse = True)[1] # создадим две подгруппы количественных наблюдений # в зависимости от класса дихотомической переменной group0 = continuous_values[np.argwhere(binary_values == 0).flatten()] group1 = continuous_values[np.argwhere(binary_values == 1).flatten()] # найдем средние групп, mean0, mean1 = np.mean(group0), np.mean(group1) # а также длины групп и всего датасета n0, n1, n = len(group0), len(group1), len(continuous_values) # рассчитаем СКО количественной переменной std = continuous_values.std() # подставим значения в формулу return (mean1 – mean0) / std * np.sqrt( (n1 * n0) / (n * (n–1)) ) |
Применим эту функцию для нахождения корреляции между пролином и классом вина.
|
pbc(wine[‘proline’], wine[‘target’]) |
Для расчета корреляции мы также можем воспользоваться функцией из библиотеки Scipy.
|
# импортируем модуль stats из библиотеки scipy from scipy import stats # передадим данные в функцию и выведем первый результат[0] stats.pointbiserialr(wine[‘proline’], wine[‘target’])[0] |
Небольшие различия связаны с тем, что функция библиотеки Scipy использует формулу для генеральной совокупности.
Что интересно, математически коэффициент точечно-бисериальной корреляции дает тот же результат, что и коэффициент корреляции Пирсона.
|
# сравним в корреляцией Пирсона wine.corr().iloc[0,1] |
Пояснения к коду
Сделаем пояснения к приведенному коду. Упростим пример и предположим, что нам нужно рассчитать, есть ли зависимость между количеством сна и результатом экзамена.
|
# количество сна в часах поместим в массив Numpy sleep = np.array([6, 8, 9, 7]) # результат будет записан с помощью двух категорий pass и fail exam = [‘pass’, ‘fail’, ‘pass’, ‘fail’] |
Для расчета точечно-бисериальной корреляции нам нужно разделить данные о сне в зависимости от результата экзамена на две группы. В первую очередь, преобразуем строковые значения переменной exam в числа. Для этого, в частности, мы можем использовать функцию np.unique() с параметром return_inverse = True.
|
exam_encoded = np.unique(exam, return_inverse = True) exam_encoded |
|
(array([‘fail’, ‘pass’], dtype='<U4′), array([1, 0, 1, 0])) |
Вторым результатом [1] будут числовые значения категорий. Теперь используем функцию np.argwhere(), чтобы найти индексы тех, кто сдал экзамены и тех, кто не сдал.
|
# функция выводит индексы элементов, соответствующих заданному условию fail_index = np.argwhere(exam_encoded[1] == 0) pass_index = np.argwhere(exam_encoded[1] == 1) |
|
# студенты, провалившие тест, должны быть на втором и четвертом местах fail_index |
|
# сдавшие – на первом и третьем pass_index |
Остается убрать второе измерение массивов.
|
fail_index, pass_index = fail_index.flatten(), pass_index.flatten() |
|
(array([1, 3]), array([0, 2])) |
Теперь используем индексы для группировки часов сна в зависимости от результатов экзамена.
|
sleep[fail_index], sleep[pass_index] |
|
(array([8, 7]), array([6, 9])) |
Теперь мы можем легко посчитать нужные метрики и подставить их в формулу точечно-бисериальной корреляции.
Корреляционное отношение
Корреляционное отношение (correlation ratio) выявляет взаимосвязь между количественной переменной и категориальной переменной с любым количеством категорий. Смысл этой метрики лучше всего понять на простом примере из Википедии⧉.
Простой пример
Предположим, что у нас есть результаты экзаменов по трем предметам (алгебре, геометрии и статистике), и нам нужно понять, есть ли взаимосвязь между предметом и поставленными оценками. Взглянем на данные:
- алгебра: 45, 70, 29, 15, 21 (5 оценок)
- геометрия: 40, 20, 30, 42 (4 оценки)
- статистика: 65, 95, 80, 70, 85, 73 (6 оценок)
Шаг 1. Найдем средние значения внутри каждой группы и общее среднее всех наблюдений.
- алгебра: 36
- геометрия: 33
- статистика: 78
- общее среднее: 52
Шаг 2. Теперь найдем, насколько наблюдения в каждой из групп отличаются от группового среднего. Возведем результаты в квадрат для того, чтобы положительные и отрицательные значения не взаимоудалялись, и сложим их. Например, для алгебры сумма квадратов отклонений от среднего будет равна
$$ (36-45)^2+(36-70)^2+(36-29)^2+(36-15)^2+(36-21)^2 = 1959 $$
Для геометрии — 308, для статистики — 600. Сложим внутригрупповые отклонения от среднего и получим $1959+308+600=2860$
Сумма квадратов отклонений всех наблюдений от общего среднего составит 9640.
Шаг 3. Теперь выясним, какую долю в общей дисперсии составляет внутригрупповая дисперсия. Для этого разделим 2860 на 9640.
$$ frac{2860}{9640} approx 0,29668 $$
Соответственно доля не объясненных внутригрупповой дисперсией отклонений (ее принято обозначать греческой буквой $eta$, «эта») составляет
$$ eta^2 = 1-frac{2860}{9640} approx 0,70332 $$
Логично предположить, что чем выше доля не объясненных внутригрупповыми отклонениями дисперсии (чем выше $eta^2$), тем большую важность имеет дисперсия между группами. Другими словами, тем важнее отклонения между предметами, а не между оценками внутри каждого предмета.
Значит, чем выше $eta^2$, тем теснее связь между категориями и количественными оценками.
Шаг 4. Извлечем корень из получившегося значения для того, чтобы вернуться к исходным единицам измерения.
$$ eta = sqrt{0,70332} approx 0,83864 $$
Подведем итог. Корреляционное отношение изменяется от 0 до 1. Если показатель равен нулю, общая дисперсия объясняется исключительно внутригрупповыми отклонениями и связи между качественной и количественной переменными нет. Если показатель равен единице, общая дисперсия полностью объясняется только дисперсией между группами и связь между переменными велика.
Можно также сказать, что если $eta$ равна нулю, то внутригрупповые средние одинаковы, если $eta$ равна единице, все значения в каждой из категорий должны быть одинаковы (например, все студенты по алгебре должны получить одинаковую оценку и т.д.).
Еще один способ расчета
Для расчета корреляционного отношения можно также найти взвешенные по количеству элементов квадраты отклонений общего среднего от внутригрупповых средних. Для примера выше арифметика выглядит следующим образом
$$ 5(36-52)^2+4(33-52)^2+6(78-52)^2 = 6780 $$
Обратите внимание, это то же самое, что и $9640-2860=6780$, то есть сумма отклонений, не объясняемых внутригрупповой дисперсией. Таким образом,
$$ eta^2 = frac{6780}{9640} approx 0,70332 $$
$$ eta = sqrt{0,70332} approx 0,83864 $$
Остается написать функцию для расчета корреляционного отношения на Питоне.
Код на Питоне
Используем те же данные, что и в примере выше.
|
# создадим датафрейм с результатами экзаменов по трем предметам test = pd.DataFrame({ # используем список с названиями предметов ‘subject’ : [‘algebra’] * 5 + [‘geometry’] * 4 + [‘stats’] * 6, # и соответствующими оценками ‘score’ : [45, 70, 29, 15, 21, 40, 20, 30, 42, 65, 95, 80, 70, 85, 73 ] }) |
Вначале возьмем значения оценок, рассчитаем сумму квадратов отклонений от среднего значения, а также закодируем категориальные переменные числами. Для этого как и ранее в случае точечно-бисериальной корреляцией используем функцию np.unique() с параметров return_inverse = True.
|
# возьмем значения оценок values = np.array(test.score) # и рассчитаем сумму квадратов отклонений от среднего значения ss_total = np.sum((values.mean() – values) ** 2) # закодируем категории предметов числами cats = np.unique(test.subject, return_inverse = True)[1] cats |
|
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2]) |
Теперь применим первый вариант расчета корреляционного отношения.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# объявим переменную для внутригрупповой дисперсии ss_ingroups = 0 # в цикле, состоящем из количества категорий for c in np.unique(cats): # вычленим группу оценок по каждому предмету group = values[np.argwhere(cats == c).flatten()] # найдем суммы квадратов отклонений значений от групповых средних # и сложим эти результаты для каждой группы ss_ingroups += np.sum((group.mean() – group) ** 2) # найдем долю внутригрупповой дисперсии и вычтем ее из единицы eta_squared = 1 – ss_ingroups/ss_total # найдем корень из предыщущего значения eta = np.sqrt(eta_squared) # это и будет корреляционное отношение eta |
Напомню, что использование функции np.argwhere() мы уже рассмотрели ранее на этом занятии. Рассчитаем по второму варианту.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# объявим переменную для межгрупповой дисперсии ss_betweengroups = 0 # в цикле, состоящем из количества категорий, for c in np.unique(cats): # вычленим группу оценок по каждому предмету group = values[np.argwhere(cats == c).flatten()] # для каждой группы # найдем взвешенный по количеству элементов в группе # квадрат отклонения группового среднего от общего среднего # и сложим результаты ss_betweengroups += len(group) * (group.mean() – values.mean()) ** 2 # найдем долю межгрупповой дисперсии eta_squared = ss_betweengroups/ss_total # найдем корень из предыщущего значения eta = np.sqrt(eta_squared) # это и будет корреляционное отношение eta |
Мы готовы написать функции.
|
# вариант 1 def correlation_ratio1(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() – values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_ingroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_ingroups += np.sum((group.mean() – group) ** 2) return np.sqrt(1 – ss_ingroups/ss_total) |
|
# проверим результат correlation_ratio1(test.score, test.subject) |
|
# вариант 2 def correlation_ratio2(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() – values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() – values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# проверим результат correlation_ratio2(test.score, test.subject) |
Подведем итог
Для удобства, давайте обобщим, какие методы и когда можно использовать.
- Если речь идет о двух количественных переменных мы можем использовать:
- коэффициент Пирсона, если речь идет о выявлении линейной зависимости
- коэффициенты Спирмена и Кендалла, если требуется оценить нелинейную взаимосвязь
- В случае двух категориальных переменных, подойдут:
- уже упомянутые коэффициенты Спирмена и Кендалла для порядковых категорий, а также
- коэффициент неопределенности Тиля
- Когда перед нами одна количественная и одна категориальная переменные, мы можем рассчитать:
- точечно-бисериальный коэффициент корреляции, в случае, если категориальная переменная имеет дихотомическую шкалу; или
- корреляционное отношение в случае множества категорий
Вопросы для закрепления
Вопрос. Чем параметрические тесты отличаются от непараметрических?
Посмотреть правильный ответ
Ответ: параметрический тест показывает корректный результат, если данные, на которых он основывается соответствуют определенным критериям или допущениям, для непараметрического теста такие критерии отсутствуют.
При этом обратите внимание, отсутствие допущений не отменяет ограничения на применение тестов только к определенным типам данных. Например, метод Спирмена, как уже было сказано, не подойдет для выявления немонотонной зависимости.
Вопрос. При расчете коэффициента корреляции Пирсона, что дает деление ковариации на произведение СКО двух переменных $s_x s_y$?
Посмотреть правильный ответ
Ответ: таким образом мы выражаем любую ковариацию как долю от произведения двух СКО и, как следствие, можем измерять силу взаимосвязи двух переменных и сравнивать коэффициенты корреляции между собой.
Вопрос. Что такое симметричность и несимметричность корреляционного метода?
Посмотреть правильный ответ
Ответ: симметричный метод покажет одинаковую силу взаимосвязи переменной X с переменной Y, и переменной Y с переменной X даже если в действительности взаимосвязь не одинаковая; несимметричный метод покажет разную корреляцию X с Y и Y с X, если такое различие действительно существует.
Полезные ссылки
- Библиотека dython⧉. Прямые ссылки на документацию⧉ и исходный код⧉ функций.
Корреляция показывает степень совместного изменения двух признаков. При этом, как уже было сказано, в корреляционном анализе нет зависимых и независимых переменных. Они эквивалентны.
Количественным предсказанием одной переменной (зависимой) на основании другой (независимой) занимается регрессионный анализ.
Статистика
18 июля 2022 г.
читать 2 мин
Один из способов количественной оценки взаимосвязи между двумя переменными – использовать Коэффициент корреляции Пирсона, который является мерой линейной связи между двумя переменными.u00a0Он всегда принимает значение от -1 до 1, где:n
-1 указывает на совершенно отрицательную линейную корреляцию между двумя переменные
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными
Чем дальше коэффициент корреляции от нуля, тем сильнее Связь между двумя переменными.
В этом руководстве объясняется, как вычислить корреляцию между переменными в Python.
Как рассчитать корреляцию в Python
Чтобы вычислить корреляцию между двумя переменными в Python, мы можем использовать функцию Numpy corrcoef()
import numpy as np
np.random.seed(100)
#создать массив из 50 случайных целых чисел от 0 до 10
var1 = np.random.randint(0, 10, 50)
#создать положительно коррелированный массив с некоторым случайным шумом
var2 = var1 + np.random.normal(0, 10, 50)
#рассчитать корреляцию между двумя массивами
np.corrcoef(var1, var2)
# [[ 1. 0.335]
# [ 0.335 1. ]]Мы видим, что коэффициент корреляции между этими двумя переменными составляет 0,335, что является положительной корреляцией.
По умолчанию эта функция создает матрицу коэффициентов корреляции. Если бы мы только хотели вернуть коэффициент корреляции между двумя переменными, мы могли бы используйте следующий синтаксис:
np.corrcoef(var1, var2)[0,1]
#0.335Чтобы проверить, является ли эта корреляция статистически значимой, мы можем рассчитать p-значение, связанное с коэффициентом корреляции Пирсона, с помощью Scipy pearsonr(), которая возвращает коэффициент корреляции Пирсона вместе с двусторонним p-значением.
from scipy.stats.stats import pearsonr
pearsonr(var1, var2)
#(0.335, 0.017398)Коэффициент корреляции – 0,335, а двустороннее значение p – 0,017. Поскольку это значение p меньше 0,05, мы можем заключить, что существует статистически значимая корреляция между двумя переменными.
Если вас интересует вычисление корреляции между несколькими переменными в Pandas DataFrame, вы можете просто использовать функцию .corr()
import pandas as pd
data = pd.DataFrame(np.random.randint(0, 10, size=(5, 3)), columns=['A', 'B', 'C'])
data
# A B C
#0 8 0 9
#1 4 0 7
#2 9 6 8
#3 1 8 1
#4 8 0 8
#рассчитать коэффициенты корреляции для всех попарных комбинаций
data.corr()
# A B C
# A 1.000000 -0.775567 -0.493769
# B -0.775567 1.000000 0.000000
# C -0.493769 0.000000 1.000000И если вас интересует только расчет корреляции между двумя конкретными переменными в DataFrame, вы можете указать переменные:
data['A'].corr(data['B'])
#-0.775567Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Python:
- Как создать корреляционную матрицу в Python
- Как рассчитать ранговую корреляцию Спирмена в Python
- Как рассчитать автокорреляцию в Python

