Заряды, входящие
в состав молекул диэлектрика, называются
связанными. Под действием поля связанные
заряды могут лишь немного смещаться из
своих положений равновесия. Покинуть
пределы молекул, в состав которых они
входят, связанные заряды не могут.
Заряды, находящиеся
внутри диэлектрика, которые не входят
в состав его молекул, а также заряды,
расположенные за пределами диэлектрика,
называются свободными или сторонними.
Поле
в диэлектрике является суперпозицией
поля
,
создаваемого сторонними зарядами, и
полясвязанных зарядов. Результирующее поле
называется истинным или микроскопическим:
.
Микроскопическое
поле сильно меняется в пределах межатомных
расстояний, а вследствие движения
зарядов это поле меняется и со временем.
Поэтому в качестве характеристики поля
используются усредненные по бесконечно
малому объему значения величин:
.
Если
сторонние заряды неподвижны, поле
обладает теми же свойствами, что и
электростатическое поле в вакууме.
диэлектрик неполяризован, объемная
плотностьи поверхностная плотность
связанных зарядов равна нулю. В результате
поляризации поверхностная плотность,
а в ряде случаев и объемная плотность
связанных зарядов, становятся отличными
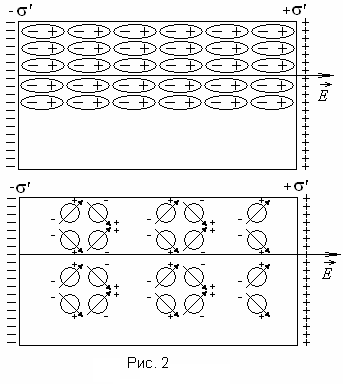
от нуля. Под действием внешнего поля
происходит смещение зарядов в неполярных
молекулах и поворот диполей в полярных
молекулах (рис.2) так, что положительные
заряды смещаются по полю, а отрицательные
– против поля. Разноименные связанные
заряды, находящиеся внутри однородного
диэлектрика, компенсируют друг друга.
Связанные же заряды, находящиеся на
поверхности диэлектрика, скомпенсированы
быть не могут, и на поверхности остается
избыточный заряд одного знака. Та
поверхность диэлектрика, в которую
линии векторавходят, получает отрицательный связанный
заряд, а та поверхность, из которой линии
векторавыходят, – положительный связанный
заряд.
Найдем
связь между вектором поляризации
и поверхностной плотностью связанных
зарядов.
Рассмотрим бесконечную плоскопараллельную
пластину из однородного изотропного
диэлектрика, помещенную в однородное
электрическое поле (рис 3). Выделим в
диэлектрике элементарный объемв виде цилиндра, образующие которого
параллельны,
а основаниесовпадает с поверхностью пластины. Этот
объем равен
,
г

– угол между вектором
и внешней нормалью
к положительно заряженной поверхности
диэлектрика,– толщина пластины,
– расстояние между основаниями цилиндров.
Объемимеет электрический момент
,
где
– модуль вектора поляризации. Этот объем
эквивалентен диполю, образованному
зарядамии
,
отстоящими друг от друга на расстояние.
Его электрический момент,
тогда,
и
(5)
где
– составляющая вектора поляризации по
внешней нормали к соответствующей
поверхности. Для правой поверхности
(рис..3),
поэтому,
для левойи
.
Известно, что,
тогда
(.6)
где
– нормальная составляющая напряженности
поля внутри диэлектрика.
Из
формулы (6) следует, что, если
– линии напряженности выходят из
диэлектрика, то на поверхности появляются
положительные связанные заряды.
Если– линии напряженности входят в диэлектрик,
то на поверхности появляются отрицательные
заряды.Формулы
(5) и (6) справедливы и в общем случае,
когда неоднородный диэлектрик произвольной
формы находится в неоднородном
электрическом поле.
плотность связанных зарядов, возникающих
внутри неоднородного диэлектрика. В
неоднородном изотропном диэлектрике
с неполярными молекулами рассмотрим
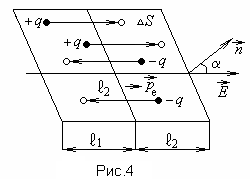
воображаемую малую площадку(рис 4). Пусть в единице объема диэлектрика
имеетсяn
одинаковых частиц с зарядом –
и
одинаковых частиц с зарядом
.
В небольшой окрестностиполе и диэлектрик можно считать
однородными. Поэтому при включении поля
все положительные заряды, находящиеся
вблизи,
сместятся в направлениина расстояние
,
а отрицательные – противоположнона расстояние
.
При этом через площадкупройдет в направлении нормали к ней
некоторое количество зарядов одного
знака (положительных, если,
или отрицательных, если).
Площадку
пересекут все заряды
,
которые до включения поля отстояли от
нее более, чем на,
то есть все заряды,
заключенные в косом цилиндре объемом.
Число этих зарядов равно,
а переносимый ими в направлении нормали
к площадке заряд равен(при
заряд, переносимый за счет смещения
положительных зарядов, будет отрицательным).
Аналогично, площадкупересекут все заряды
,
заключенные в косом цилиндре объемом.Эти
заряды перенесут в направлении нормали
к площадке заряд(при
заряды
перенесут через
в направлении, противоположном
,
заряд,
что эквивалентно переносу в направлениизаряда
).
Таким
образом, при включении поля через
площадку
переносится заряд в направлении нормали:
.
(7)
Ясно,
что
– это расстояние, на которое смещаются
друг относительно друга положительные
и отрицательные связанные заряды в
диэлектрике. В результате этого смещения
каждая пара зарядов приобретает дипольный
момент.
Число таких пар в единице объема равно.
Тогда модуль вектора поляризации равен
. (8)
С учетом
формулы (8) выражение (7) принимает вид:
.
Диэлектрик
изотропный, поэтому направления
и
совпадают, и
есть угол между
и
:
,
или
для бесконечно малой площадки
:
– это
связанный заряд, который проходит при
включении поля через элементарную
площадку
в направления нормали к ней.
Рассмотрим
замкнутую поверхность
,
расположенную внутри диэлектрика. При
включении поля эту поверхность пересечет
и выйдет наружу связанный заряд:
п
– это поток вектора поляризации через:
поверхность.
В результате выхода зарядав объеме, ограниченном поверхностью
,
останется избыточный связанный заряд:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда рассматриваются диэлектрики в электростатических полях, следует различать два вида электрических зарядов: свободные и связанные.
Свободные заряды – это заряды, перемещающиеся под действием поля на существенные расстояния.
Например, электроны в проводниках, ионы в газах и заряды, привносимые извне на поверхность диэлектриков, которые нарушают их (диэлектриков) нейтральность. Заряды, входящие в состав нейтральных, в целом, молекул диэлектриков, так же, как ионы, закрепленные в кристаллических решетках твердых диэлектриков около положений равновесия, получили название связанных зарядов.
Поверхностная плотность зарядов
Формула потенциала электростатического поля в диэлектрике φ запишется как:
φ=φ0+φ’ (1) с φ0, являющимся потенциалом поля, создаваемого свободными зарядами, с
φ’ – потенциалом поля, создаваемого связанными зарядами.
Известно:
φ0=∫ρdVR+∫σdSR (2), ρ – это объемная плотность свободных зарядов, σ – их поверхностная плотность. Определение потенциала поля связанных зарядов:
φ’=∫P→R→R3dV (3), где P→ служит вектором поляризации.
Можно сделать вывод, что из (1) и (3) получим:
φ=φ0+∫P→R→R3 (4).
При использовании теоремы Остроградского-Гаусса с некоторыми формулами векторного анализа имеем совсем иной вид уравнения (4):
φ=φ0+∫ρsυRdV+∫σsυRdV=∫ρsυ+ρRdV+∫σsυ+σRdV (5),
где ρsυ обозначается в качестве средней объемной плотности связанных зарядов, а σsυ – средняя поверхностная плоскость связанных зарядов. По уравнению (5) видно, что при наличии диэлектрика электрическое поле совпадает с полем, созданным свободными зарядами плюс поле, которое создается связанными зарядами.
Плотность связанных зарядов
Если P→=const, то средняя плотность связанных зарядов равняется нулю. Это говорит о том, что накопление зарядов одного знака в диэлектрике не происходит. На границе между поляризованным диэлектриком и вакуумом или металлом сосредоточен поверхностный связанный заряд плотности:
σsυ=±Pn, -div P→=ρsυ (6) с Pn, являющейся нормальной компонентой вектора поляризованности диэлектрика на его границе с вакуумом.
Функция φ вида (7) будет решением уравнения:
∇2φ=-4π (ρ+ρsυ) (7).
При E→=-∇φ→div E→=-∇2φ (8) и (6) получим:
div E→=4πρ-4πdiv P→ (9).
div E→+4πP→=4πρ (10).
Выражение (10) называют основным дифференциальным уравнением электростатического поля в любой произвольной среде.
Для получения полной системы уравнений электростатики, нужно использовать формулу (10) с определением, связывающим векторы напряженности электрического поля с векторами поляризации.
Зависимость P →E→ представится как:
Pi=ε0∑jχijEj+ε0∑j,kχijkEjEk+… (11), где i, j служат для нумерации компонентов по осям декартовой системы координат (i=x, y, z; j=x, y, z), χij – это тензор диэлектрической восприимчивости.
Если имеется внешнее электрическое поле, вещество становится источником поля, значит, поле изменяется.
Дан плоский конденсатор с пространством, между обкладками которого заполнено однородным изотропным диэлектриком с диэлектрической восприимчивостью χ. На них располагается поверхностный заряд с плотностью σ. Определить напряженность результирующего поля в конденсаторе.
Решение
Если при имеющихся обкладках конденсатора находится вакуум, то напряженность поля, создаваемого заряженными обкладками, запишется как:
Evak=σε0 с ε0=8,85·10-12 Фм, являющейся электрической постоянной.
Рисунок 1
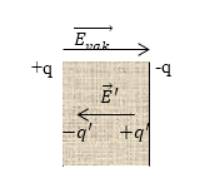
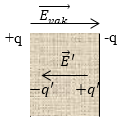
+q, -q – это заряды, находящиеся на обкладках конденсатора.
Evak→ – напряженность поля, создаваемого обкладками конденсатора.
-q’,+q’ – заряды диэлектрика.
E→’ – напряженность поля, создаваемого в результате поляризации диэлектрика.
Очевидно, что диэлектрик поляризуется, тогда напряженность уменьшается. Диэлектрик однородный, а поле, создаваемое в плоском конденсаторе, также считается однородным. Отсюда вывод – поляризованность диэлектрика однородна, иначе говоря, отсутствуют объемные связанные заряды ρsυ=0. Имеются только поверхностные с плотностью σsυ:
σsυ=Pn.
Так как известна связь напряженности поля и вектора поляризации для изотропного диэлектрика, то
P=χε0E.
Отсюда получаем:
σsυ=χε0E с Е, являющейся проекцией напряженности на внешнюю нормаль к поверхности диэлектрика.
Направление напряженности идет от стороны положительно заряженной пластины к отрицательной. Из σsυ=χε0E получаем, что поверхностная плотность связанного заряда на границе с положительно заряженной пластиной отрицательная, а на границе с отрицательной пластиной – положительная. Следовательно, напряженность поля в диэлектрике между этими пластинами равняется напряженности поля в вакууме между ними, но со значением поверхностной плотности заряда, вычисляемой по формуле σ’=σ-σsυ.
На основании выше сказанного зафиксируем, что напряженность поля в конденсаторе с диэлектриком запишется как:
E=σ-σsυε0=σ-χε0Eε0.
Произведем выражение из E=σ-σsυε0=σ-χε0Eε0 искомой напряженности:
E=σε0(1+χ).
Ответ: E=σε0(1+χ).
Когда мы рассматриваем диэлектрики в электростатических полях необходимо различать два вида электрических зарядов: свободные и связанные.
Потенциал электростатического поля в диэлектрике ($varphi $) равен:
[varphi ={varphi }_0+{varphi }’left(1right),]
где ${varphi }_0$ — потенциал поля создаваемого свободными зарядами, ${varphi }’$ – потенциал поля создаваемого связанными зарядами. При этом мы знаем, что:
[{varphi }_0=int{frac{rho dV}{R}}+int{frac{sigma dS}{R}}left(2right), ]
где $rho $ — объемная плотность свободных зарядов, $sigma $ — поверхностная плотность свободных зарядов. Потенциал поля связанных зарядов определен как:
[{varphi }’=int{frac{overrightarrow{P}overrightarrow{R}}{R^3}}dVleft(3right),]
где $overrightarrow{P}$ — вектор поляризации.
Из уравнений (1) и (3) следует, что:
[varphi ={varphi }_0+int{frac{overrightarrow{P}overrightarrow{R}}{R^3}}left(4right).]
Если использовать теорему Остроградского – Гаусса и некоторые формулы векторного анализа, не сложно получить иной вид уравнения (4), а именно:
[varphi ={varphi }_0+int{frac{{rho }_{sv}}{R}dV}+int{frac{{sigma }_{sv}}{R}dV=int{frac{{rho }_{sv}+rho }{R}dV}+int{frac{{sigma }_{sv}+sigma }{R}dV}}left(5right),]
где ${rho }_{sv}$- средняя объемная плотность связанных зарядов, ${sigma }_{sv}-средняя поверхностная плотность $ связанных зарядов. Из уравнения (5) видно, что электрическое поле при наличии диэлектрика совпадает с полем, которое создано свободными зарядами плюс поле, которое создается связанными зарядами.
Плотность связанных зарядов
При $overrightarrow{P}=const$ (что означает равномерную поляризацию диэлектрика) средняя плотность связанных зарядов равна нулю, что означает, что в данном случае не происходит накопление зарядов одного знака в диэлектрике. На границе между поляризованным диэлектриком и вакуумом или металлом сосредоточен поверхностный связанный заряд плотности:
[{sigma }_{sv}=pm P_n, -div overrightarrow{P}={rho }_{sv}left(6right),]
где $P_n$ — нормальная компонента вектора поляризованности диэлектрика на его границе с вакуумом.
Функция $varphi $ вида (7) является решением уравнения:
[{nabla }^2varphi =-4pi left(rho +{rho }_{sv}right)left(7right).]
Зная, что:
[overrightarrow{E}=-nabla varphi to divoverrightarrow{E}=-{nabla }^2varphi (8)]
и учитывая (6), можно записать, что:
[divoverrightarrow{E}=4pi rho -4pi divoverrightarrow{P} (9)]
или
[divoverrightarrow{(E}+4pi overrightarrow{P})=4pi rho left(10right).]
Уравнение (10) — основное дифференциальное уравнение электростатического поля в любой произвольной среде.
Для того, чтобы получить полную систему уравнений электростатики к уравнению (10), необходимо добавить выражение, связывающее векторы напряженности электрического поля и вектор поляризации.
Зависимость $overrightarrow{P}(overrightarrow{E})$ в общем случае представлена в виде:
[P_i={varepsilon }_0sumlimits_j{{varkappa }_{ij}E_j+{varepsilon }_0sumlimits_{j,k}{{varkappa }_{ijk}E_jE_k+dots ,}left(11right),}]
где индексы $i,j$ — нумеруют компоненты по осям декартовой системы координат $(i=x, y,z; j=x, y,z.)$, ${varkappa }_{ij}$ — тензор диэлектрической восприимчивости.
Итак, при наличии внешнего электрического поля вещество само становится источником поля, следовательно, поле изменяется.
Пример 1
Задание: Имеется плоский конденсатор, пространство между обкладками которого, заполнено однородным, изотропным диэлектриком c диэлектрической восприимчивостью $varkappa$. На обкладках конденсатора находится поверхностный заряд, плотность его равна $sigma .$ Какова напряженность результирующего поля в конденсаторе?
Решение:
Если между обкладками конденсатора вакуум, то напряженность поля, которое создают заряженные обкладки, равно:
[E_{vak}=frac{sigma }{{varepsilon }_0}left(1.1right),]
где ${varepsilon }_0=8, 85cdot {10}^{-12}frac{Ф}{м}. $– электрическая постоянная.
Рис. 1
$+q, -q$ — заряды на обкладках конденсатора.
$overrightarrow{E_{vak}}$ — напряженность поля, которое создается обкладками конденсатора.
$-q’, +q’$ -заряды диэлектрика.
$overrightarrow{E}’$ – напряженность поля, которое создается в результате поляризации диэлектрика.
Так как диэлектрик поляризуется, напряженность поля уменьшается. Так как диэлектрик считаем однородным, поле, которое создается в плоском конденсаторе, также можно считать однородным, делаем вывод о том, что поляризованность диэлектрика однородна, то есть объемные связанные заряды отсутствуют (${rho }_{sv}=0$). Имеем только поверхностные заряды плотность которых (${sigma }_{sv}$):
[{sigma }_{sv}=P_n left(1.2right).]
Зная связь напряженности поля и вектора поляризации для изотропного диэлектрика:
[P=varkappa {varepsilon }_0E(1.3)]
получим:
[{sigma }_{sv}=varkappa {varepsilon }_0Eleft(1.4right),]
где $E$ — проекция напряженности на внешнюю нормаль к поверхности диэлектрика. Напряженность поля направлена от положительно заряженной пластины конденсатора к отрицательной. Поэтому из (1.4) следует, что поверхностная плотность связанного заряда на границе с положительно заряженной пластиной имеет знак минус, а на границе с отрицательной пластиной – плюс. Получаем, что напряженность поля в диэлектрике между пластинами конденсатора равна напряженности поля в вакууме между теми же пластинами, но при поверхностной плотности заряда равном:
[{sigma }’=sigma -{sigma }_{sv}left(1.5right).]
На этом основании запишем, что напряженность поля в конденсаторе при наличии диэлектрика равна:
[E=frac{left(sigma -{sigma }_{sv}right)}{{varepsilon }_0}=frac{left(sigma -varkappa {varepsilon }_0Eright)}{{varepsilon }_0} left(1.6right).]
Выразим из (1.6) искомую напряженность:
[E=frac{sigma }{{varepsilon }_0(1+varkappa )}.]
Ответ: $E=frac{sigma }{{varepsilon }_0(1+varkappa )}.$
Из сказанного выше ясно,
что диэлектрическая восприимчивость характеризует способность вещества поляризоваться, т.е. изменять свою
поляризацию под действием электрического поля :
.
Диэлектрическая восприимчивость
является одним из основных параметров диэлектрика. Если диэлектрик
анизотропный, то направления векторов и не совпадают, и . представляет
собой тензор. В этом случае связь векторови
имеет вид:

1.2.4.ПОЛЕ ВНУТРИ ДИЭЛЕКТРИКА. СВОБОДНЫЕ И СВЯЗАННЫЕ ЗАРЯДЫ
Заряды, входящие в состав молекул диэлектрика,
называются связанными. Под действием поля связанные заряды могут лишь
немного смещаться из своих положений равновесия. Покинуть пределы молекул, в
состав которых они входят, связанные заряды не могут.
Заряды, находящиеся внутри диэлектрика, которые не входят в
состав его молекул, а также заряды, расположенные за пределами диэлектрика,
называются свободными или сторонними.
Поле в диэлектрике является
суперпозицией поля ,
создаваемого сторонними зарядами, и поля связанных
зарядов. Результирующее поле называется истинным или микроскопическим:
Микроскопическое поле сильно меняется в пределах
межатомных расстояний, а вследствие движения зарядов это поле меняется и со
временем. Поэтому в качестве характеристики поля используются усредненные по бесконечно
малому объему значения величин:
Если сторонние заряды
неподвижны, поле обладает
теми же свойствами, что и электростатическое поле в вакууме.

заряды, находящиеся внутри
однородного диэлектрика, компенсируют друг друга.
Связанные же заряды,
находящиеся на поверхности диэлектрика, скомпенсированы быть не могут, и на
поверхности остается избыточный заряд одного знака.
Та поверхность диэлектрика,
в которую линии вектора входят, получает отрицательный связанный заряд, а та поверхность, из
которой линии вектора выходят,
— положительный связанный заряд.
Найдем связь между
вектором поляризации и
поверхностной плотностью связанных зарядов .
Рассмотрим бесконечную плоскопараллельную пластину из однородного изотропного
диэлектрика, помещенную в однородное электрическое поле (рис 1.2.3). Выделим в
диэлектрике элементарный объем в
виде цилиндра, образующие которого параллельны ,
а основание совпадает с поверхностью пластины. Этот объем
равен
Источник: https://vunivere.ru/work2040/page18
Б14.1) Свободные и связанные заряды
- Свободные заряды – заряженные частицы одного знака, способные перемещаться под действием электрического поля.
- Связанные заряды – разноимённые заряды, входящие в состав атомов, которые не могут перемещаться под действием электрического поля независимо друг от друга.
- Связь вектора поляризованности с плотностью связанных зарядов.
Теорема Гаусса для вектора поляризованности.
- Поле на границе раздела магнетиков.
- Для определения условий на границе двух однородных магнетиков используют теорему Гаусса для вектора и теорему о циркуляции вектора
- Условия для вектора :
; ;
- Условия для вектора :
, где – проекция вектора на нормаль к контуру. Если на границе тока проводимости нет , то тангенсальная составляющая вектора не испытывает скачка:
Б15. 1) Поле на границе раздела диэлектриков.
- Изменение величины нормальной составляющей вектора смещения равно плотности стороннего заряда.
- Изменение величины нормальной составляющей вектора поляризованности на границе раздела диэлектриков равно с обратным знаком поверхностной плотности связанного заряда.
- Если сторонних зарядов на границе раздела нет, то
- Расчёт магнитного поля соленоида.
- Циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной на сумму токов охватываемых этим контуром. Соленоид
Б16. 1) Поток вектора напряженности электрического поля.
- Число силовых линий, пронизывающих некоторую поверхность, расположенную в электрическом поле, называют потоком вектора напряженности электрического поля сквозь эту поверхность En — нормальная к площадке компонента вектора напряженности.
- Теорема Гаусса в интегральной и дифференциальной формах в вакууме и её применение для расчёта электростатических полей.
Поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охваченных этой поверхностью, делённой на .
Если ввести функцию объёмного распределения электрического заряда r( x, y,z) , такую, что и воспользоваться теоремой Остроградского-Гаусса , то из равенства получим дифференциальную форму теоремы Гаусса: .
- Поле равномерно заряженного цилиндра.
- Поток вектора напряжѐнности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгеброической сумме заключенных внутри этой поверхности зарядов делѐнной на e0 . Цилиндр
- Самоиндукция.
- Возникновение ЭДС индукции в проводящем контуре при изменении в нём силы тока.
- Взаимная индукция.
- Возникновение ЭДС в одном проводнике вследствие изменения силы тока в другом проводнике или изменения взаимного расположения проводников.
- Индуктивность.
- Физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1секунду.
Источник: https://cyberpedia.su/13x207e.html
Свободные и связанные заряды — Математика
При рассмотрении электростатического поля, в случае наличия в нем диэлектриков, нужно различать два рода электрических зарядов: свободные и связанные.
Под свободными зарядами мы будем понимать, во-первых, все электрические заряды, которые под влиянием электрического поля могут перемещаться на макроскопические расстояния (электроны в металлах и вакууме, ионы в газах и электролитах и т. п.), и, во-вторых, заряды, нанесенные извне на поверхность диэлектриков и нарушающие их нейтральность ).
Заряды же, входящие в состав нейтральных молекул диэлектриков, равно как и ионы, закрепленные в твердых диэлектриках вблизи определенных положений равновесия, мы будем называть зарядами связанными.
Потенциал ф электростатического поля при наличии в нем диэлектриков равен, очевидно, сумме потенциала (фо, возбуждаемого свободными зарядами, и потенциала (р’, возбуждаемого связанными электрическими зарядами в диэлектриках:
Потенциал свободных зарядов определяется формулой (12.11):

где под р и а надо понимать объемную и поверхностную плотность свободных зарядов.
Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля. Внешнее поле создается системой свободных электрических зарядов. В диэлектрике существует электростатическое поле свободных зарядов и, дополнительно, электростатическое поле связанных зарядов.
Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому оно зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать перераспределение свободных зарядов, создающих поле.
Вектор D характеризует электростатическое поле, создаваемое свободными зарядами, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика. Поле D, как и поле Е, изображается с помощью силовых линий вектора электрического смещения, направление и густота которых определяются точно так же, как и для линий вектора напряженности.
Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.
Источник: https://student2.ru/matematika/368966-svobodnye-i-svyazannye-zaryady/
Свободные и связанные заряды. Поляризация вещества
- Дифференциальный оператор Гамильтона
- Дифференциальный оператор Гамильтона (оператор Ѵ̅) применяют для сокращения записи различных операций над скалярными и векторными величинами.
- Под дифференциальным оператором Гамильтона (оператором набла) понимают сумму частных производных по трем координатным осям, умноженные на соответствующий единичный вектор (орты). В декартовой системе координат его записывают так:
- Ѵ̅= ī* j̅* + k̅*
Ѵ̅- может быть применен как к скалярным так и к векторным функциям. Применим оператор Ѵ̅ к потенциалу ϕ.
Ѵ̅ϕ= ( i̅* j̅* + k̅* )ϕ= i̅* j̅* + k̅*
Сравнивая полученное выражение с выражением для градиента потенциала (2) получим :
gradϕ= Ѵ̅ϕ т.е. эти выражения тождественны.
Замечание. Выражение градиента потенциала в других системах координат можно найти в учебной и справочной литературе.
Свободные и связанные заряды. Поляризация вещества.
Заряды, которые под воздействием силы поля могут свободно перемещаться в веществе, причем перемещение их не ограничивается внутри полярными силами- называются свободными зарядами.
Электрические заряды, входящие в состав вещества и удерживаемые в определенных положениях внутримолекулярными силами – называются связанными зарядами. Сумма положительных зарядов равна сумме отрицательных связанных зарядов.
Если какое-либо диэлектрическое тело поместить в электрическое поле, то в нем происходит упорядоченное изменение расположения связанных зарядов, называемое поляризацией.
Это изменение расположения проявляется в том, что отрицательные связанные заряды в теле перемещаются в направлении более высокого потенциала, а положительные связанные заряды в сторону более низкого потенциала.
Заряды сместятся настолько, что силы взаимодействия электрического поля на связанные заряды уравновешиваются молекулярными силами. В результате поляризации на поверхности вещества как бы обозначаются связанные заряды.
В поляризованном веществе молекулы в электрическом отношении представляют собой диполи( т.е. два связанных между собой и равных по величине заряда +q и –q) Если принял длину диполя равной L, то произведение ql̅ называют электрическим моментом диполя.
Под действием внешнего электрического поля диполи стремятся ориентироваться в пространстве таким образом, чтобы электрический момент их был направлен параллельно вектору напряженности электрического поля.
Электрический момент суммы диполей, находящихся в объёме вещества V, отнесенный к объёму V, при стремлении V к нулю- называется вектором поляризации( поляризованностью) и обозначается P̅.
- Для однородных и изотропных диэлектриков P̅ пропорционален напряженности электрического поля Е̅.
- P̅= ɛ0*x*E̅= xа*E̅
- Где x- относительная диэлектрическая восприимчивость
- Xа = ɛ0*x – абсолютная диэлектрическая восприимчивость, характеризующая способность данного диэлектрика и поляризации.
- ɛ0= 8, 86* 10-12 [ Ф/м]- электрическая постоянная
- Диэлектрики в зависимости от происходящих в них процессах при поляризации делятся на 2 группы.
1-я группа. К ней относится диэлектрики, молекулы которых при отсутствии внешнего электрического поля электрически нейтральны, т.е. в них центры действия положительных и отрицательных зарядов совпадают ( к ним относятся: азот, парафин, водород и др.)
2-я группа. К ней относится диэлектрики, молекулы которых при отсутствии внешнего электрического поля представляют собой диполи, т.е.
центры действия положительных и отрицательных зарядов этих молекул при отсутствии внешнего электрического поля не совпадают- к таким диэлектрикам относится, например, хлористый водород.
Поляризация в этой группе состоит в том, что полярные молекулы стремятся повернуться таким образом, чтобы их электрический момент был направлен по внешнему электрическому полю.
Рекомендуемые страницы:
Источник: https://poisk-ru.ru/s372t10.html
Большая Рнциклопедия Нефти Рё Газа
Cтраница 1
Связанные заряды входят в состав молекул диэлектрика и не могут их покинуть. Сторонние заряды не входят в состав молекул диэлектрика и находятся либо в диэлектрике, либо за его пределами. [2]
Связанные заряды входят в состав атомов и молекул диэлектрика, а также ионов в кристаллических диэлектриках с ионной решеткой и не могут их покинуть. Свободные заряды не входят в состав молекул диэлектрика и находятся либо в диэлектрике, либо за его пределами. [3]
Связанные заряды отличаются от сторонних лишь тем, что не могут покинуть пределы молекул, в состав которых они входят. [4]
Связанные заряды в данном случае имеют другие знаки по отношению к внешнему полю. [5]
Связанные заряды вызывают снижение электрического поля РІ РІРѕР·РґСѓС…Рµ РІРѕРєСЂСѓРі заряженного объекта Рё предотвращают разряды. Ртот принцип используется РЅР° практике. [6]
Связанные заряды, находящиеся на поверхности включений, с ростом концентрации начинают частично нейтрализовать друг друга.
Влияние уменьшения поляризации включений РЅР° величину БСРможно характеризовать введением РІ формулу ( 9 — 72) эффективного коэффициента деполяризации Р› фф k ( v Nx, РіРґРµ значение k ( uj) l должно уменьшаться СЃ ростом концентрации включений. [7]
Связанные заряды создают поле, отличное от нуля, только в диэлектрике. Легко видеть, что поле в точке А ( на расстоянии ri2 см от оси) равно нулю. [8]
Связанные заряды, входящие в состав диэлектрика, можно разбить на несколько групп, в каждой из которых величина заряда еа и смещение Ага одинаковы. Количество зарядов группы р, приходящееся на единицу объема диэлектрика, обозначим пр. [9]
Связанный заряд q у граничной поверхности диэлектрика около носителя свободного заряда можно считать сосредоточенным в точке, где находится свободный заряд. [10]
Связанные заряды отличаются от сторонних лишь тем, что не могут покинуть пределы молекул, в состав которых они входят. [11]
 |
Схема диэлектрического нагрева. [12] |
Связанные заряды представляют собой пары равных по величине положительных и отрицательных зарядов, смещающихся под влиянием электрического поля один относительно другого только в некоторых пределах, обусловленных структурой материала. Связанные пары равных по величине и противоположных по знаку зарядов называются диполями и характеризуются ди-польными моментами. Дипольный момент определяется как произведение величины зарядов на расстояние между ними. Смещение связанных зарядов под действием внешнего электрического поля называется поляризацией. [13]
Связанные заряды, входящие в состав диэлектрика, можно разбить на насколько групп, в каждой из которых величина заряда еа и смещение Ага одинаковы. [14]
Связанный заряд возникает только там, РіРґРµ поляризация изменяется РІ пространстве — РІ рассмотренном примере это было РЅР° поверхности кристалла.
Если же кристалл поляризован неоднородно, связанный заряд появляется и внутри кристалла; при этом говорят об объемной плотности связанного заряда рв. [15]
Страницы: 1 2 3 4
Источник: https://www.ngpedia.ru/id33123p1.html
Проводники в электрическом поле
Связанные заряды принадлежат данной молекуле и без больших затрат энергии не могут ее покинуть. В зависимости от концентрации свободных зарядов различают три типа веществ – проводники диэлектрики и полупроводники.
Проводник – вещество с большой концентрацией свободных зарядов. К проводникам относятся все металлы в жидком и твердом состояниях, водные растворы солей и кислот и многие другие вещества.
Если поместить проводник во внешнее электростатическое поле или зарядить его, то под действием поля свободные заряды в проводнике придут в движение.
Перемещение зарядов продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника не станет равным нулю.
Если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии.
Вектор напряженности поля на внешней поверхности проводника направлен по нормали к каждой точке его поверхности. Если бы существовала касательная составляющая поля, то заряды перемещались бы вдоль поверхности проводника, что противоречило бы равновесному распределению зарядов.
Если проводнику сообщить некоторый зарядQ, то нескомпенсированные заряды располагаются только на поверхности проводника.
Напряженность электростатического поля у поверхности проводника определяется поверхностной плотностью зарядов:
где – диэлектрическая проницаемость среды, окружающей проводник.
Отсутствие поля внутри проводника означает, что потенциал внутри проводника и во всех точках его поверхности постоянен, т.е. поверхность проводника эквипотенциальна.
Соединение заряженного проводника с другим проводником приведет к тому, что заряды между проводниками перераспределяться так, чтобы потенциалы проводников выровнялись. В этом состоит принцип “заземления”, т.е.
соединения проводника с Землей: потенциал заземленного проводника будет равен потенциалу Земли.
На больших расстояниях от проводника эквипотенциальные поверхности имеют характерную для точечного заряда форму сферы. По мере приближения к проводнику эквипотенциальные поверхности становятся все более сходными с поверхностью проводника, которая является эквипотенциальной.
Вблизи выступов эквипотенциальные поверхности располагаются гуще, значит, и напряженность поля здесь больше. Следовательно, плотность зарядов здесь особенно велика.
К этому же выводу можно прийти, учтя, что из-за взаимного отталкивания заряды стремятся расположиться как можно дальше друг от друга.
Вблизи углублений в проводнике эквипотенциальные поверхности расположены реже . Соответственно, напряженность поля и плотность зарядов в этих местах будет меньше.
Плотность зарядов при данном потенциале проводника растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости).
Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды (электроны, ионы) будут перемещаться: положительные – по полю, отрицательные – против поля.
На одном конце проводника будет скапливаться избыток положительного заряда, на другом – отрицательного. Эти заряды называются индуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника – перпендикулярными его поверхности.
Нейтральный проводник, внесенный в электрическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных.
Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией. Индуцированные заряды появляются на проводнике вследствие смещения их под действием поля, т.е.
является поверхностной плотностью смещенных зарядов.
Так как в состоянии равновесия заряды внутри проводника отсутствуют, то создание внутри него полости не повлияет на конфигурацию расположения зарядов и тем самым на электростатическое поле. Следовательно, внутри полости поле будет отсутствовать. Если этот проводник с полостью заземлить, то потенциал во всех точках полости будет нулевым, т.е.
полость полностью изолирована от влияния внешних электростатических полей. На этом основана электростатическая защита – экранирование тел, например электрических приборов, от влияния внешних электростатических полей. Вместо сплошного проводника для защиты может быть использована густая металлическая сетка.
При этом поля по обе стороны оболочки не зависят друг от друга.
Полый проводник экранирует поле только внешних зарядов. Если заряды находятся внутри полости, то индуцированные заряды возникнут на внешней и внутренней поверхностях проводника. При этом заряды распределятся так, чтобы результирующее поле зарядов внутри полости и индуцированных зарядов в любой точке в толще проводника было равно нулю. Внутри полости поле не будет равно нулю.
Свойство зарядов располагаться на внешней поверхности проводника используется для устройства электростатических генераторов, предназначенных для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатические генераторы применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.
Источник: https://NauchnieStati.ru/spravka/provodniki-v-jelektricheskom-pole/
Свободные и связанные заряды в диэлектриках. Полярные и неполярные молекулы. Типы диэлектриков
При рассмотрении электростатического поля, в случае наличия в нем диэлектриков, нужно различать два рода электрических зарядов: свободные и связанные.
Под свободными зарядами мы будем понимать, во-первых, все электрические заряды, которые под влиянием электрического поля могут перемещаться на макроскопические расстояния (электроны в металлах и вакууме, ионы в газах и электролитах и т. п.), и, во-вторых, заряды, нанесенные извне на поверхность диэлектриков и нарушающие их нейтральность ).
Заряды же, входящие в состав нейтральных молекул диэлектриков, равно как и ионы, закрепленные в твердых диэлектриках вблизи определенных положений равновесия, мы будем называть зарядами связанными.
Неполярные диэлектрики (нейтральные) — состоят из неполярных молекул, у которых центры тяжести положительного и отрицательного зарядов совпадают.
Следовательно неполярные молекулы не обладают электрическим моментом и их электрический момент p = q • l = 0.
Примером практически неполярных диэлектриков, применяемых в качестве электроизоляционных материалов, являются углеводороды, нефтяные электроизоляционные масла, полиэтилен, полистирол и др.
Полярные диэлектрики (дипольные) — состоят из полярных молекул, обладающих электрическим моментом. В таких молекулах из-за их асимметричного строения центры масс положительных и отрицательных зарядов не совпадают.
При замещении в неполярных полимерах некоторой части водородных атомов другими атомами или не углеводородными радикалами получаются полярные вещества. При определении полярности вещества по химической формуле следует учитывать пространственное строение молекул.
К полярным диэлектрикам относятся феноло-формальдегидные и эпоксидные смолы, кремнийорганические соединения, хлорированные углеводороды и др.
Диэлектриками называются вещества, которые в обычных условиях практически не проводят электрический ток, их удельное сопротивление в раз больше, чем у металлов. Согласно представлениям классической физики, в диэлектриках, в отличие от проводников, нет свободных носителей заряда, которые могли бы под действием электрического поля создавать ток проводимости. К диэлектрикам относятся все газы; некоторые жидкости (дистиллированная вода, масла, бензол); твердые тела (стекло, фарфор, слюда). Термины «диэлектрик» и «диэлектрическая постоянная» были введены в науку в 1837 г. M. Фарадеем.
Диэлектрики, как и любые вещества, состоят из атомов и молекул. В целом молекулы нейтральны, тем не менее, они взаимодействуют с электрическим полем. Например, в случае, когда симметрия молекулы отлична от сферической, ее можно представить в виде электрического диполя.
Электрический дипольный момент молекулы , где q — суммарный заряд ядер или электронов; l — вектор, представляющий собой плечо эквивалентного диполя.
Молекулы, обладающие электрическим дипольным моментом, называют полярными. Полярным диэлектриком является вода; следующие вещества: CO; N2O; S2O; NH; HCl также имеют в своем составе полярные молекулы. В объеме вещества дипольные моменты молекул распределены по разным направлениям хаотическим образом, так что их сумма равна нулю . Молекулы, у которых положения эквивалентного положительного и эквивалентного отрицательного заряда совпадают и, следовательно, дипольный момент каждой молекулы равен нулю ( ), называют неполярными. Такие вещества, как состоят из неполярныхмолекул. Если диэлектрик внести в электрическое поле, то это поле и сам диэлектрик претерпевают существенные изменения.
Источник: https://megaobuchalka.ru/5/13190.html
Беседа 31. Свободный и связанный электрические заряды
Коллега, в разделе «Электрическое поле Земли» БСЭ (Большая Советская Энциклопедия) сказано, что электрический заряд Земли составляет 5,7*105 Кл. Подтверждают ли это значение Ваши расчёты?Хороший вопрос, мой друг.
И ответ на него начну с того, что указанное Вами значение определяет связанный (поляризационный) электрический заряд Земли. Полный же заряд Земли значительно больше, ибо он является суммой свободного и связанного электрических зарядов.
Значение второго поддаётся измерению, а значение первого можно только вычислить.
Коллега, что значит «полный электрический заряд»?
В беседе 10 «Полевая модель всего» мы с Вами, мой друг, рассматривали весьма приближённую, но близкую по аналогии модель силового поля. Представьте растянутую в разные стороны резиновую плёнку огромных размеров.
Продавливаем эту плёнку в её центре и получаем впадину. Самая большая глубина этой впадины (соответственно и сил упругой деформации) находится в месте надавливания, то есть – в центре плёнки и нисходит на «нет» у её краёв.
Так же, от периферии к центру нарастает и напряжённость поля. Только потенциальное поле не плоскость (как резиновая плёнка), а сфера, в центре которой действительно напряжённость поля максимальна, а объёмная плотность энергии (проще – давление) имеет минимальное значение.
В беседе 16 «Природа электрического заряда» мы выяснили, что объёмная плотность энергии (давление) в замкнутом пространстве относительно окружающего пространства определяет величину электрического заряда.
Повышенная плотность энергии определяет отрицательный заряд (так уж принято), а пониженная – положительный заряд.
Значит, в центре поля должен быть максимально возможный положительный заряд. Это и есть полный электрический заряд QП возникшего в результате флуктуаций энергии потенциального поля. Его значение мы можем определить из всем известного уравнения для магнитной постоянной:
µ0 = 4π*MП*r0/QП2 кг*м/Кл2, откуда QП = (MП*r0*107)1/2 = MП(G*107/c2)1/2 Кл,
где: MП – масса всего потенциального поля, кг;
r0 = GMП/с2 – гравитационный радиус поля, м.
Значит, коллега, можно сделать вывод, что полный электрический заряд зависит только от массы всего потенциального поля. Но остался вопрос: что означает «связанный электрический заряд»?
Связанные электрические заряды возникают на границе раздела между веществом и полем. Ранее (см. п. 2 в Дополнении к беседе 29 «Минимально возможная масса кванта») мы определили максимально возможную массу поля звезды (и такую же массу самой звезды):
Mm = 5,478*1033 кг.
Следовательно, максимально возможный электрический заряд поля:
Qm = Mm(G*107/c2)1/2 = 4,720*1023 Кл
Однако, масса реального поля (звёзд и, тем более, планет) значительно меньше. В центре такого поля формируется вещество (см. беседу 6 «Природа гравитации») и этот процесс заканчивается устойчивым состоянием, когда масса вещества MВ станет равной массе поля MП.
Теперь рассмотрим рисунок, на котором условно изображён заряженный Земной шар (проводник), окружённый потенциальным полем (диэлектрик). В выделенном нами промежутке на поверхности проводника (Земли) выступают положительные заряды, которые поляризуют отрицательные заряды q на примыкающей к шару поверхности диэлектрика (поля).
Ясно, что теперь напряжённость поля Земли за пределами её поверхности будут создавать две противоположно заряженные сферы – поверхность шара, заряженная положительно, и примыкающая к ней отрицательно заряженная поверхность самого поля. Таким образом, поле в диэлектрике ослабляется в ε раз потому, что из поля полного заряда вычитается поле поляризационных (связанных) зарядов.
- То есть, свободный электрический заряд: Q = QП – q = QП(1 – QП/Qm),
- а поляризационный заряд: q = – QП(1 – 1/ε) = – QП2/Qm Кл,
- где ε = QП/Q = Qm/(Qm – QП) – диэлектрическая проницаемость поля (среды).
- Проверка: Масса Земли (и вся масса её потенциального поля) MЗ = 5,976*1024 кг.
Итак, векторы напряжённости поля связанных зарядов параллельны векторам напряжённости поля полного электрического заряда, но направлены противоположно.Следовательно, QЗ = 5,149*1014 Кл, а поляризационный (связанный) электрический заряд, который мы наблюдаем на поверхности Земли:q = 5,617*105 Кл.Это расчётное значение всего на 1,46% отличается от указанного в БСЭ.
Источник: https://vip46.livejournal.com/8460.html
Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле
Бессонов Л. А. Теоретические основы электротехники. Электромагнитное поле: Учебник для электротехн., энерг., приборостроит. спец. вузов. – 8-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 263 с.: ил.
В книге рассмотрены вопросы теории электромагнитного поля, предусмотренные программой курса ТОЭ. Все главы 8-го издания (7-е издание вышло в 1978 г.
) переработаны и дополнены; включен новый материал: поле двойного заряженного слоя, расчет полей с электретами, поле двойного токового слоя, определение силы воздействия на диэлектрические и проводящие тела, переходные процессы, устранение отражений, теорема взаимности и др.
Скачать Бессонов Л. А. Теоретические основы электротехники. Электромагнитное поле: Учебник для электротехн., энерг., приборостроит. спец. вузов. – 8-е изд., перераб. и доп. – М.: Высш. шк., 1986
- ОГЛАВЛЕНИЕ
- Часть III
- Основы теории электромагнитного поля
- Предисловие
- Введение
- Глава девятнадцатая
- Электростатическое поле
§ 19.1. Определение электростатического поля
§ 19.2. Закон Кулона
§ 19.3. Напряженность и потенциал электростатического поля
§ 19.4. Электрическое поле — поле потенциальное
§ 19.5. Силовые и эквипотенциальные линии
§ 19.6. Выражение напряженности в виде градиента потенциала
§ 19.7. Дифференциальный оператор Гамильтона (оператор набла)
§ 19.8. Выражение градиента потенциала в цилиндрической и сферической системах координат
§ 19.9 Поток вектора через элемент поверхности и поток вектора через поверхность
§ 19.10. Свободные и связанные заряды. Поляризация вещества
§ 19.11. Поляризованность
§ 19.12. Вектор электрической индукции D
§ 19.13. Теорема Гаусса в интегральной форме
§ 19.14. Применение теоремы Гаусса для определения напряженности и потенциала в поле точечного заряда
§ 19.15. Теорема Гаусса в дифференциальной форме
§ 19.16. Вывод выражения для divE в декартовой системе координат
§ 19.17. Использование оператора набла для записи операции взятия дивергенции
§ 19.18. Выражение divE в цилиндрической и сферической системах координат
§ 19.19. Уравнение Пуассона и уравнение Лапласа
§ 19.20. Граничные условия
§ 19.21. Поле внутри проводящего тела в условиях электростатики
§ 19.22. Условия на границе раздела проводящего тела и диэлектрика
§ 19.23. Условия на границе раздела двух диэлектриков
§ 19.24. Теорема единственности решения
§ 19.25. Общая характеристика задач электростатики и методов их решения
§ 19.26. Поле заряженной оси
§ 19.27. Поле двух параллельных заряженных осей
§ 19.28. Поле двухпроводной линии
§ 19.29. Емкость
§ 19.30. Метод зеркальных изображений
§ 19.31. Поле заряженной оси, расположенной вблизи проводящей плоскости
§ 19.32. Поле заряженной оси, расположенной вблизи плоской границы раздела двух диэлектриков с различными диэлектрическими проницаемостями
§ 19.33. Электростатическое поле системы заряженных тел, расположенных вблизи проводящей плоскости
§ 19.34. Потенциальные коэффициенты. Первая группа формул Максвелла
§ 19.35. Емкостные коэффициенты. Вторая группа формул Максвелла
§ 19.36. Частотные емкости. Третья группа формул Максвелла
§ 19.37. Поле точечного заряда, расположенного вблизи проводящей сферы
§ 19.38. Поле заряженной оси, расположенной параллельно цилиндру
§ 19.39. Шар в равномерном поле
§ 19.40. Проводящий шар в равномерном поле
§ 19.41. Диэлектрический шар в равномерном поле
§ 19.42. Диэлектрический цилиндр в равномерном поле
§ 19.43. Понятие о плоскопараллельном, плоскомеридианном и равномерном полях
§ 19.44. Графическое построение картины плоскопараллельного поля
§ 19.45. Графическое построение картины плоскомеридианного поля
§ 19.46. Объемная плотность энергии электрического поля и выражение механической силы в виде производной от энергии электрического поля по изменяющейся координате
§ 19.47. Энергия поля системы заряженных тел
§ 19.48. Метод средних потенциалов
§ 19.49. Электреты
§ 19.50. Изменения заряда (напряжения) на конденсаторе, вызванное помещенным в него диэлектрическим телом, имеющим остаточную поляризацию
§ 19.51. Электрическое поле двойного заряженного слоя
§ 19.52. Силовое воздействие неравномерного электрического поля на незаряженные диэлектрические и проводящие тела, находящиеся в этом поле
- Вопросы для самопроверки
- Глава двадцатая
- Электрическое поле постоянного тока в проводящей среде
§ 20.1. Плотность тока и ток
§ 20.2. Закон Ома и второй закон Кирхгофа в дифференциальной форме
§ 20.3. Первый закон Кирхгофа в дифференциальной форме
§ 20.4. Дифференциальная форма закона Джоуля—Ленца
§ 20.5. Уравнение Лапласа для электрического поля в проводящей среде
§ 20.6. Переход тока из среды с проводимостью gamma1 в среду с проводимомостью gamma2. Граничные условия
§ 20.7. Аналогия между полем в проводящей среде и электростатическим полем
§ 20.8 Экспериментальное исследование полей
§ 20.9. Соотношение между проводимостью и емкостью
§ 20.10. Общая характеристика задач расчета электрического поля в проводящей среде и методов их решения
§ 20.11. Расчет электрического поля в диэлектрике, окружающем проводники с токами
- Вопросы для самопроверки
- Глава двадцать первая
- Магнитное поле постоянного тока
§ 21.1. Связь основных величин, характеризующих магнитное поле
Механические силы в магнитном поле
§ 21.2. Интегральная форма закона полного тока
§ 21.3. Дифференциальная форма закона полного тока
§ 21.4. Раскрытие выражения rotН = delta в декартовой системе координат
§ 21.5. Запись ротора в виде векторного произведения
§ 21.6. Раскрытие rotН в виде определителя в декартовой системе
§ 21.7. Выражение проекций ротора в цилиндрической и сферической системах координат
§ 21.8. Принцип непрерывности магнитного потока и запись его в дифференциальной форме
§ 21.9. Магнитное поле в областях «занятых» и «незанятых» постоянным током
§ 21.10. Скалярный потенциал магнитного поля
§ 21.11. Граничные условия
§ 21.12. Векторный потенциал магнитного поля
§ 21.13. Уравнение Пуассона для вектора-потенциала
§ 21.14. Выражение магнитного потока через циркуляцию вектора-потенциала
§ 21.15. Векторный потенциал элемента тока
§ 21.16. Взаимное соответствие электростатического (электрического) и магнитного полей
§ 21.17. Задачи расчета магнитных полей
§ 21.18. Общая характеристика методов расчета и исследования магнитных полей
§ 21.19. Графическое построение картины поля и определение по ней магнитного сопротивления
§ 21.20. Опытное исследование картины магнитного поля
§ 21.21. Построение эквипотенциалей магнитного поля путем использования принципа наложения
§ 21.22. Магнитное экранирование
§ 21.23. Эллипсоид во внешнем однородном поле. Коэффициент размагничивания
§ 21.24. Применение метода зеркальных изображений
§ 21.25. Закон Био—Савара—Лапласа
§ 21.26. Определение скалярного магнитного потенциала контура с током через телесный угол
§ 21.27. Магнитное поле намагниченной пленки (ленты)
§ 21.28. Определение магнитного потока, созданного в некотором контуре намагниченным ферромагнитным телом
§ 21.29. Выражение механической силы в виде производной от энергии магнитного поля по координате
§ 21.30. Магнитное поле двойного токового слоя
- Вопросы для самопроверки
- Глава двадцать вторая
- Основные уравнения переменного электромагнитного поля
- § 22.1 Определение переменного электромагнитного поля
§ 22.2. Первое уравнение Максвелла
§ 22.3. Уравнение непрерывности
§ 22.4. Второе уравнение Максвелла
§ 22.5. Уравнения Максвелла в комплексной форме записи
§ 22.6. Теорема Умова — Пойнтинга для мгновенных значений
§ 22.7. Теорема Умова — Пойнтинга в комплексной форме записи
§ 22.8. Некоторые замечания к § 22.1
§ 22.9. Основные положения электродинамики движущихся сред (основы релятивистской электродинамики)
- Вопросы для самопроверки
- Глава двадцать третья
- Переменное электромагнитное поле в однородной и изотропной проводящей среде
- § 23.1, Уравнения Максвелла для проводящей среды
§ 23.2. Плоская электромагнитная волна
§ 23.3. Распространение плоской электромагнитной волны в однородном проводящем полупространстве
§ 23.4. Глубина проникновения и длина волны
§ 23.5. Магнитный поверхностный эффект
§ 23.6. Электрический поверхностный эффект в прямоугольной шине. Эффект близости
§ 23.7. Неравномерное распределение тока в прямоугольной шине, находящейся в пазу электрической машины
§ 23.8. Поверхностный эффект в цилиндрическом проводе
§ 23.9. Применение теоремы Умова—Пойнтинга для определения активного и внутреннего индуктивного сопротивления проводников при переменном токе
§ 23.10. Экранирование в переменном электромагнитном поле
§ 23.11. Сопоставление принципов экранирования в электростатическом, магнитном и электромагнитном полях
§ 23.12. Высокочастотный нагрев металлических деталей и несовершенных диэлектриков
§ 23.13. Переходный процесс при проникновении магнитного поля в однородное проводящее полупространство
- Вопросы для самопроверки
- Глава двадцать четвертая
- Распространение электромагнитных волн в однородном и изотропном диэлектриках и в полупроводящих и гиротропных средах
§ 24.1. Распространение электромагнитных волн в однородном и изотропном диэлектрике
§ 24.2. Плоские волны в однородных и изотропных полупроводящих средах
§ 24.3. Граничные условия на поверхности раздела двух полупроводящих сред
§ 24.4. Переходные и релаксационные процессы в несовершенных диэлектриках
§ 24.5. О расчете полей в несовершенных диэлектриках и вязких средах при установившемся синусоидальном режиме
§ 24.6. Определение гиротропной среды
§ 24.7. Тензор магнитной проницаемости феррита
§ 24.8. Распространение плоской волны в гиромагнитной среде
- Вопросы для самопроверки
- Глава двадцать пятая
- Запаздывающие потенциалы переменного электромагнитного поля и излучение электромагнитной энергии
§ 25.1. Выводы уравнений для А и phi в переменном электромагнитном поле и их решение
§ 25.2. Запаздывающие потенциалы переменного электромагнитного поля
§ 25.3. Комплексная форма записи запаздывающего векторного потенциала
§ 25.4. Излучение электромагнитной энергии
§ 25.5. Понятие об излучающем диполе
§ 25.6. Дополнительный анализ поля излучения
§ 25.7. Расчет поля реальных излучателей
§ 25.8. Теорема взаимности для э. д. е., наведенных излученным полем
§ 25.9. Излучение магнитного диполя и принцип двойственности
§ 25.10. Переход плоской электромагнитной волны из одной среды в другую
§ 25.11. Устранение отражения электромагнитных волн
- Вопросы для самопроверки
- Глава двадцать шестая
- Электромагнитные волны в направляющих системах
§ 26.1. Понятие о волноводах и объемных резонаторах
§ 26.2. Типы волн в волноводе. Решение для H-волны
§ 26.3. Волновое сопротивление. Фазовая и групповая скорости
§ 26.4. Решение для E-волны
§ 26.5. Аналогия между волноводом и линией с распределенными параметрами
§ 26.6. Граничные условия Леонтовича—Рытова
§ 26.7. Запредельный волновод
§ 26.8. Линии с поверхностными волнами и полосковые линии
- Вопросы для самопроверки
- Глава двадцать седьмая
- Движение заряженных частиц в магнитном и электрическом полях
§ 27.1. Движение электрона в равномерном магнитном поле, неизменном во времени и направленном перпендикулярно скорости
§ 27.2. Движение электрона в неизменном во времени магнитном поле, когда скорость электрона не перпендикулярна силовым линиям
§ 27.3. Фокусировка пучка электронов постоянным во времени магнитным полем (магнитная линза)
§ 27.4. Движение электронов в равномерном электрическом поле. Принцип работы электронного осциллографа
§ 27.5. Фокусировка пучка электронов постоянным во времени электрическим полем (электрическая линза)
§ 27.6. Движение электрона в равномерных, взаимно перпендикулярных, неизменных во времени магнитном и электрическом полях
§ 27.7. Движение заряженных частиц в кольцевых ускорителях
- Вопросы для самопроверки
- Глава двадцать восьмая
- Основы магнитной гидродинамики
§ 28.1. Определение магнитной гидродинамики и краткая характеристика областей ее применения
§ 28.2. Уравнения магнитной гидродинамики
§ 28.3. Просачивание (диффузия) магнитного поля
§ 28.4. Электромагнитный барьер
§ 28.5. Вмороженное поле
§ 28.6. Возникновение волн в плазме
§ 28.7. Эффект сжатия (пинч-эффект)
§ 28.8. Принцип работы магнитного насоса и магнитного вентиля
§ 29.9. Принцип работы магнитного гидродинамического генератора
§ 28.10. Принцип работы плазменного реактивного двигателя
- Вопросы для самопроверки
- Глава двадцать девятая
- Сверхпроводящие среды в электромагнитных полях
§ 29.1. Сверхпроводимость
§ 29.2. Сверхпроводники первого рода
§ 29.3. Сверхпроводники первого рода в магнитном поле
§ 29.4. Уравнение Лондонов
§ 29.5. Сверхпроводящее тело в постоянном магнитном поле
§ 29.6. Сверхпроводники второго рода
§ 29.7. Сверхпроводники третьего рода
§ 29.8. Описание поля в сверхпроводниках с нитевидной структурой
§ 29.9. Применение сверхпроводников
- Вопросы для самопроверки
- Приложения к части III
- Приложение И
- Расчет полей по методу сеток и моделирование полей по методу электрических сеток
§ И.1. Расчет полей по методу сеток
§ И.2. Моделирование полей по методу электрических сеток
Приложение К
Метод Грина
§ К.1. Формулы Грина
§ К.2. Гармонические функции
§ К.3. Интеграл Грина для гармонических функций
§ К.4. Функция Грина
§ К.5. Определение потенциала φ через функции Грина в общем случае
Приложение Л
Метод интегральных уравнений
§ Л.1. Первый вариант метода интегральных уравнений
§ Л.2. Второй вариант метода интегральных уравнений
§ Л.3. Расчет полей, используя интегральное уравнение Фредгольма первого рода
Приложение М
Метод конформных преобразований (отображений)
§ М.1. Комплексный потенциал
§ М.2. Конформные преобразования
§ М.3. Прямая и обратная задачи расчета полей по методу конформных преобразований
§ М.4. Преобразование равномерного поля на плоскости z в поле верхней полуплоскости w
§ М.5. Интеграл Кристоффеля — Шварца
§ М.6. Применение интеграла Кристоффеля—Шварца
§ М.7. Интеграл Шварца
- Приложение Н
- История развития электротехники и становления курса ТОЭ
- Приложение О
- Свойства некоторых проводниковых материалов и диэлектриков
Литература по теории электромагнитного поля и смежным вопросамСкачать Бессонов Л. А. Теоретические основы электротехники. Электромагнитное поле: Учебник для электротехн., энерг., приборостроит. спец. вузов. – 8-е изд., перераб. и доп. – М.: Высш. шк., 1986
Источник: http://rgr-toe.ru/file_archive/11/101/
|
|
Макеты страниц
Когда диэлектрик не поляризован, объемная плотность 
На рис. 18.1 изображен схематически поляризованный диэлектрик с неполярными (а) и полярными (б) молекулами.

Рис. 18.1.
Из рисунка видно, что поляризация сопровождается возникновением в тонком поверхностном слое диэлектрика избытка связанных зарядов одного знака. Если нормальная составляющая напряженности поля Е для данного участка поверхности отлична от нуля, то под действием поля заряды одного знака уходят внутрь, а другого знака выходят наружу.
Между поляризованностью Р и поверхностной плотностью связанных зарядов о имеется простая связь. Для ее нахождения рассмотрим бесконечную плоскопараллельную пластину из однородного диэлектрика, помещенную в однородное электрическое поле (рис. 18.2).
Выделим мысленно в пластине элементарный объем 


где 


(Р — модуль поляризованности).
С макроскопической точки зрения рассматриваемый объем эквивалентен диполю, образованному зарядами 



Рис. 18.2.
Отсюда вытекает искомое соотношение между 

где 


Выразив согласно (16.2) Р через 

где 


Формулы (18.1) и (18.2) справедливы и в самом общем случае, когда неоднородный диэлектрик произвольной формы находится в неоднородном электрическом поле.
Под 

Теперь обратимся к нахождению объемной плотности связанных зарядов, возникающих внутри неоднородного диэлектрика. Рассмотрим в неоднородном изотропном диэлектрике с неполярными молекулами воображаемую малую площадку 













Площадку 

















Итак, при включении поля через площадку 

Сумма 





Рис. 18.3.
Таким образом, заряд, проходящий при включении поля через, площадку 

Поскольку диэлектрик изотропный, направления векторов Е и Р совпадают (см. рис. 18.3). Следовательно, а есть угол между векторами Р и 

Перейдя от дельт к дифференциалам, получим

Мы нашли связанный заряд 


Представим себе внутри диэлектрика замкнутую поверхность 5. При включении поля эту поверхность пересечет и выйдет наружу связанный заряд q, равный

(мы условились в случае замкнутых поверхностей брать внешнюю нормаль к площадкам 

(Фр—поток вектора Р через поверхность 
Введя объемную плотность связанных зарядов 

(интеграл берется по объему, ограниченному поверхностью S). Таким образом, мы приходим к формуле

Преобразуем поверхностный интеграл по теореме Остроградского—Гаусса (см. (11.41)). В результате получится соотношение

Это соотношение должно выполняться для любого произвольно выбранного объема V, что возможно лишь в том случае, если в каждой точке диэлектрика выполняется равенство

Следовательно, плотность связанных зарядов равна дивергенции поляризованности Р, взятой с обратным знаком.
Мы получили (18.4), рассматривая диэлектрик с неполярными молекулами. Однако эта формула справедлива и для диэлектриков с полярными молекулами.
Формуле (18.4) можно дать наглядную интерпретацию. Точки с положительной 
18.4). Точки с отрицательной 

Связанные заряды отличаются от сторонних лишь тем, что не могут покинуть пределы молекул, в состав которых они входят. В остальном же их свойства таковы, как и у всех прочих зарядов. В частности, они служат источниками электрического поля. Поэтому в случае, когда плотность связанных зарядов 

Здесь 
Подставим в (18.4) выражение (16.2) для Р и воспользуемся формулой (11.36). В результате получим

Заменив 

Отсюда


Рис. 18.4.
Из формулы (18.6) вытекает, что объемная плотность связанных зарядов может быть отличной от нуля в двух случаях: 1) если диэлектрик неоднороден 

В случае, когда внутри диэлектрика сторонних зарядов нет, объемная плотность связанных зарядов равна

Оглавление
- ПРЕДИСЛОВИЕ
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. Электрический заряд
- § 2. Закон Кулона
- § 3. Системы единиц
- § 4. Рационализованная запись формул
- § 5. Электрическое поле. Напряженность поля
- § 6. Потенциал
- § 7. Энергия взаимодействия системы зарядов
- § 8. Связь между напряженностью электрического поля и потенциалом
- § 9. Диполь
- § 10. Поле системы зарядов на больших расстояниях
- § 11. Описание свойств векторных полей
- Дивергенция.
- Циркуляция.
- Теорема Стокса.
- § 12. Циркуляция и ротор электростатического поля
- § 13. Теорема Гаусса
- § 14. Вычисление полей с помощью теоремы Гаусса
- Поле двух разноименно заряженных плоскостей.
- Поле заряженной сферической поверхности.
- Поле объемно-заряженного шара.
- ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ
- § 15. Полярные и неполярные молекулы
- § 16. Поляризация диэлектриков
- § 17. Поле внутри диэлектрика
- § 18. Объемные и поверхностные связанные заряды
- § 19. Вектор электрического смешения
- § 20. Примеры на вычисление поля в диэлектриках
- § 21. Условия на границе двух диэлектриков
- § 22. Силы, действующие на заряд в диэлектрике
- § 23. Сегнетоэлектрики
- ГЛАВА III. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 24. Равновесие зарядов на проводнике
- § 25. Проводник во внешнем электрическом поле
- § 26. Электроемкость
- § 27. Конденсаторы
- ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
- § 28. Энергия заряженного проводника
- § 29. Энергия заряженного конденсатора
- § 30. Энергия электрического поля
- ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 31. Электрический ток
- § 32. Уравнение непрерывности
- § 33. Электродвижущая сила
- § 34. Закон Ома. Сопротивление проводников
- § 35. Закон Ома для неоднородного участка цепи
- § 36. Разветвленные цепи. Правила Кирхгофа
- § 37. Мощность тока
- § 38. Закон Джоуля — Ленца
- ГЛАВА VI. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ
- § 39. Взаимодействие токов
- § 40. Магнитное поле
- § 41. Поле движущегося заряда
- § 42. Закон Био — Савара
- § 43. Сила Лоренца
- § 44. Закон Ампера
- § 45. Магнитное взаимодействие как релятивистский эффект
- § 46. Контур с током в магнитном поле
- § 47. Магнитное поле контура с током
- § 48. Работа, совершаемая при перемещении тока в магнитном
- § 49. Дивергенция и ротор магнитного поля
- § 50. Поле соленоида и тороида
- ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
- § 51. Намагничение магнетика
- § 52. Напряженность магнитного поля
- § 53. Вычисление поля в магнетиках
- § 54. Условия на границе двух магнетиков
- § 55. Виды магнетиков
- § 56. Магнитомеханические явления
- § 57. Диамагнетизм
- § 58. Парамагнетизм
- § 59. Ферромагнетизм
- ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 60. Явление электромагнитной индукции
- § 61. Электродвижущая сила индукции
- § 62. Методы измерения магнитной индукции
- § 63. Токи Фуко
- § 64. Явление самоиндукции
- § 65. Ток при замыкании и размыкании цепи
- § 66. Взаимная индукция
- § 67. Энергия магнитного поля
- § 68. Работа перемагничивания ферромагнетика
- ГЛАВА IX. УРАВНЕНИЯ МАКСВЕЛЛА
- § 69. Вихревое электрическое поле
- § 70. Ток смещения
- § 71. Уравнения Максвелла
- ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ
- § 72. Движение заряженной частицы в однородном магнитном поле
- § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями
- § 74. Определение заряда и массы электрона
- § 75. Определение удельного заряда ионов. Масс-спектрографы
- § 76. Ускорители заряженных частиц
- ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ
- § 77. Природа носителей тока в металлах
- § 78. Элементарная классическая теория металлов
- § 79. Эффект Холла
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- § 80. Несамостоятельная и самостоятельная проводимость
- § 81. Несамостоятельный газовый разряд
- § 82. Ионизационные камеры и счетчики
- § 83. Процессы, приводящие к появлению носителей тока при самостоятельном разряде
- § 84. Газоразрядная плазма
- § 85. Тлеющий разряд
- § 86. Дуговой разряд
- § 87. Искровой и коронный разряды
- ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
- § 88. Квазистационарные токи
- § 89. Свободные колебания в контуре без активного сопротивления
- § 90. Свободные затухающие колебания
- § 91. Вынужденные электрические колебания
- § 92. Переменный ток
- ЧАСТЬ 2. ВОЛНЫ
- § 93. Распространение волн в упругой среде
- § 94. Уравнения плоской и сферической волн
- § 95. Уравнение плоской волны, распространяющейся в произвольном направлении
- § 96. Волновое уравнение
- § 97. Скорость упругих волн в твердой среде
- § 98. Энергия упругой волны
- § 99. Стоячие волны
- § 100. Колебания струны
- § 101. Звук
- § 102. Скорость звука в газах
- § 103. Эффект Доплера для звуковых волн
- ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 104. Волновое уравнение для электромагнитного поля
- § 105. Плоская электромагнитная волна
- § 106. Экспериментальное исследование электромагнитных волн
- § 107. Энергия электромагнитных волн
- § 108. Импульс электромагнитного поля
- § 109. Излучение диполя
- ЧАСТЬ 3. ОПТИКА
- § 110. Световая волна
- § 111. Представление гармонических функций с помощью экспонент
- § 112. Отражение и преломление плоской волны на границе двух диэлектриков
- § 113. Световой поток
- § 114. Фотометрические величины и единицы
- § 115. Геометрическая оптика
- § 116. Центрированная оптическая система
- § 117. Тонкая линза
- § 118. Принцип Гюйгенса
- ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 119. Интерференция световых волн
- § 120. Когерентность
- § 121. Способы наблюдения интерференции света
- § 122. Интерференция света при отражении от тонких пластинок
- § 123. Интерферометр Майкельсона
- § 124. Многолучевая интерференция
- ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА
- § 126. Принцип Гюйгенса—Френеля
- § 127. Зоны Френеля
- § 128. Дифракция Френеля от простейших преград
- § 129. Дифракция Фраунгофера от щели
- § 130. Дифракционная решетка
- § 131. Дифракция рентгеновских лучей
- § 132. Разрешающая сила объектива
- § 133. Голография
- ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА
- § 134. Естественный и поляризованный свет
- § 135. Поляризация при отражении и преломлении
- § 136. Поляризация при двойном лучепреломлении
- § 137. Интерференция поляризованных лучей
- § 138. Прохождение плоскополяризованного света через кристаллическую пластинку
- § 139. Кристаллическая пластинка между двумя поляризаторами
- § 140. Искусственное двойное лучепреломление
- § 141. Вращение плоскости поляризации
- ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ
- § 142. Дисперсия света
- § 143. Групповая скорость
- § 144. Элементарная теория дисперсии
- § 145. Поглощение света
- § 146. Рассеяние света
- § 147. Эффект Вавилова — Черенкова
- ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД
- § 148. Скорость света
- § 149. Опыт Физо
- § 150. Опыт Майкельсона
- § 151. Эффект Доплера
- ПРИЛОЖЕНИЯ
- I. Единицы электрических и магнитных величин в СИ и в гауссовой системе
- Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе
- Приложение III. Векторный потенциал