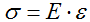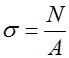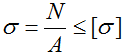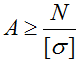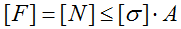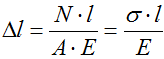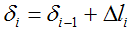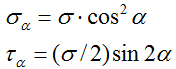Как найти сжатие тела

Сила упругости. Закон Гука

Под растяжением
понимается такой вид нагружения, при
ко­тором в поперечных сечениях бруса
(стержня) возникают только нормальные
силы, а все прочие внутренние силовые
факторы (по­перечные силы, крутящий
и изгибающие моменты) равны нулю.
Сжатие отличается от растяжения только
знаком силы N:
при растяжении
нормальная сила N
направлена
от сечения (см. рис. 2.1), а
при сжатии – к сечению. Поэтому при
анализе внутренних сил сохраняется
единство подхода к вопросам растяжения
и сжатия. Исключение составят длинные
тонкие стержни, для которых сжа­тие
сопровождается изгибом (см. подразд.
2.7).

Закон Гука.
Многочисленные
наблюдения за поведением твер­дых
тел показывают, что в подавляющем
большинстве случаев перемещения в
определенных пределах пропорциональны
дейст­вующим силам. Впервые в 1676 г.
Гуком был сформулирован закон о том,
что «какова сила, такова и деформация».

В современной
трактовке закон Гука определяет линейную
за­висимость между напряжением и
деформацией:

(1.4)

Здесь коэффициент
пропорциональности Е
есть модуль
упругости первого рода, ε – деформация,
которую для однородного стержня можно
определить как

(1.5)

Величину
ε
иногда называют относительным
удлинением стержня
длиной l,
удлинение которого под действием
приложенной силы составило Δl.

Модуль упругости
первого рода
является физической констан­той
материала; он определяется экспериментально.
Для наиболее часто
встречающихся материалов его значения
приведены в табл. 2.1 (см.
подразд. 2.3).

Удлинение
стержня. Если
в закон Гука вместо напряжения под­ставить

=
N/S,
а вместо
деформации

, то для стержня, у которого на длине l
внутренняя
нормальная сила постоянная и поперечное
сечение не изменяется, получим выражение
для опре­деления удлинения стержня:

(1.5)

При решении многих
практических задач возникает необхо­димость
наряду с удлинением, обусловленным
напряжением а, учитывать также удлинения,
связанные с температурным воз­действием.

В этом случае
деформацию рассматривают как сумму
силовой и чисто температурной деформации:

(1.6)

где

– коэффициент
температурного расширения материала.
Для однородного стержня, нагруженного
по концам и равномерно нагретого, имеем

(1.7)

Построение эпюр.
График
изменения нормальной силы, напря­жений
и перемещений стержня вдоль его оси
называется эпюрой соответственно
нормальных сил, напряжений и перемещений.
Эпюры дают наглядное представление о
законах изменения раз­личных исследуемых
величин. Построение эпюр рассмотрим на
конкретном примере.

Пример 1

Для
бруса, изображенного на рис. 2.3, а,
построить
эпюры внутренних сил, напряжений
и перемещений по длине бруса.

Рис. 2.3

Решение.

1. Выбираем
начало отсчета в неподвижном сечении
(точка О);

положи­тельное
направление оси z
направим
по оси бруса, т.е. вниз.

2.
Определим
реакцию, составив одно уравнение
равновесия:

N₀
–
3F
+ F
= 0.
Отсюда
N₀
=2F.

3. Построим
эпюру внутренних сил N.
Для
этого на расстоянии z₁
рассечем

брус
и рассмотрим равновесие нижней части
(рис. 2.3, б):

∑ F_iz
= 0; – N₁
+ F
= 0

Отсюда
N₁
=F
,
что справедливо для l
≤ z₁
≤ 3l.
В этих пределах в брусе возни­кает
растяжение, так как продольная сила N₁
направлена
от сечения.

Теперь
выберем второй участок бруса 0
≤ z₂
≤ l
и рассмотрим равновесие верхней
части (рис. 2.3, в):

∑ F_iz
= 0; N₀
– N₂
= 0; 2F – N₂
= 0

Отсюда
N₂
= 2F. Поскольку
N₂
направлена
к сечению, то брус под дейст­вием
сил N₀
и N₂
сжимается.

После
того как определили все внутренние
нормальные силы, переходим к
построению эпюры нормальных сил (рис.
2.3, г).
Вправо
будем отклады­вать положительные
значения, а влево – отрицательные значения
нормаль­ных
сил.

Анализируя
построенную эпюру (N)
,
заметим, что внутренние силы не за­висят
от размеров поперечного сечения, а
зависят только от приложенных внешних
сил. Поэтому длину бруса разбивают на
такое число участков, сколько
сил на его длине приложено. В данном
случае было два участка.

При
проверке правильности построения эпюры
следует обратить внимание
на то, что на эпюре внутренних сил в тех
сечениях, где были приложены
внешние силы, должны быть скачки, равные
приложенной внешней силе.

4.
Построим эпюру напряжений (σ).
Брус следует разбить на участки.
По­скольку
σ
= N/S,
то
участков на эпюре будет столько, сколько
раз меняется поперечное
сечение; при этом следует обращать
внимание, чтобы при посто­янной
площади поперечного сечения нормальная
сила на эпюре N
остава­лась
неизменной. С учетом этого на эпюре (σ)
будут три различных значения σ

(рис.
2.3, д):

σ₁
=
N₁/
S₁
= F/S;

σ₂
= N₂/S₂
= F/2S;

σ₃
= N₂/S₂
= -2F/2S
= –F/S.

5.Строим
эпюру перемещений (U).
Начинать следует от неподвижного
се­чения,
т.е. от сечения О.
Выразим
перемещение сечения, находящегося от
неподвижного
на расстоянии z₂:

Если
0
≤ z₂
≤ l
, то для z₂
= l
перемещение

Для
l
≤ z
≤ 2l

Или

при z
= 2l

Для 2l
≤ z₁
≤ 3l

при z₁
= 3
l

Откладываем
вычисленные перемещения на эпюре (U)
(рис. 2.3, e).

Диаграмма
растяжения. Наиболее
наглядно особенности диа­граммы
растяжения можно показать на примере
испытания образца из малоуглеродистой
стали (рис. 2.4). Диаграмма вы­черчена
в координатах F,Δl.
На кривой можно выделить четыре зоны.

Зона ОА
носит название
зоны упругости.
Здесь материал
подчиняется закону Гука и

.

На рис. 2.4 этот
участок для большей наглядности показан
с отступлением от масштаба. Уд­линения
на участке ОА
очень малы,
и прямая ОА,
будучи
вычер­ченной в масштабе, совпадала
бы в пределах ширины линии с осью ординат.
Значение силы, для которой справедлив
закон Гука, зависит от размеров образца
и физических свойств мате­риала,
поэтому при дальнейшем рассмотрении
диаграммы растя­жения ее перестраивают
в координатах σ
и ε

Зона АВ
называется
зоной общей
текучести, а
участок АВ
– площадкой
текучести. Здесь
происходит существенное изменение
длины образца без заметного увеличения
нагрузки. Не все метал­лы имеют площадку
текучести. Например, у алюминия,
отожжен­ной меди, легированных сталей
площадка текучести не обнару­живается.

З
она
ВС называется
зоной
упрочнения. Здесь
удлинение образца

сопровождается
возрастанием на-грузки. В стадии
упрочнения на

образце намечается
место будущего разрыва и начинает
образовы­ваться так называемая шейка
– мест­ное
сужение образца. При дальней­шем
растяжении образца шейка быст­ро
прогрессирует. Начиная с точки С

удлинение
образца происходит с

уменьшением
силы, но среднее напря­жение в поперечном
сечении шейки возрастает. Удлинение
образца носит в этом случае мест-ный
характер, по­ этому участок CD
называется
зоной местной
текучести
Рис.
2.4

Точка D
соответ­ствует
разрушению образца.

Относительная
поперечная дефор­мация.
При растяжении
(сжатии)

прямого бруса кроме продольной
деформации е происходит изменение
поперечных размеров бруса (рис.2.5). Ширина
бруса b
при
растяжении

уменьшается
на Δb.
Если Δb
отнести
к первоначальной ширине, то полу­чим
выражение для определения относительной
поперечной де­формации:

Отношение
относительной поперечной

деформации к
относи­тельной продольной деформации
называют коэффициентом
Пуас­сона и
обозначают

:

Рис. 2.5.

Коэффициент
Пуассона, так же как и модуль упругости
Е, ха­рактеризует
физические свойства материала; его
значение колеб­лется для металлов в
пределах от 0,25 до 0,35. Некоторые значе­ния
коэффициента и. приведены в табл. 2.1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

• сдвиг;
• кручение;
• изгиб;
• сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) )  – начальная длина пружины;

( L left(text{м} right) )  – конечная длина растянутой пружины;

( Delta L left(text{м} right) )  – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу,  например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot  left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости) пружины.

Выводы

1. Упругие тела – такие, которые сопротивляются деформации;
2. Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
3. Деформация – изменение формы, или размеров тела;
4. Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
5. Удлинение пружины – это разность ее конечной и начальной длин;
6. Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
7. Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
8. Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
9. А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Для наглядности изучаются изменения, происходящие в брусе с постоянным сечением, характерные для упругой деформации при приложении внешних усилий.

 

Закон Гука (английский физик Р. Гук, 1653-1703) для упругой деформации растяжения/сжатия гласит, что нормальное напряжение находится в линейной зависимости (прямо пропорционально) к относительному удлинению/укорочению. Математический аппарат технической механики описывает эту формулу следующим образом:

Коэффициент пропорциональности E (модуль упругости, модуль Юнга) – величина определяющая жесткость материала, единица измерения – паскаль (ПА).

Его значения были установлены эмпирическим путем для большинства конструкционных материалов, необходимую информацию можно почерпнуть в справочниках по машиностроению. Относительная деформация является отношением изменения длины бруса к его изначальным размерам, это безразмерная величина, которая иногда отражается в процентном соотношении.

При растяжении или сжатии у бруса меняется не только длина, но происходят поперечные деформации: при сжатии образуется утолщение, при растяжении толщина сечения становится меньше. Величины этих изменений находятся в линейной зависимости друг от друга, причем установлено, что коэффициент пропорциональности Пуассона (фр. ученый С. Пуассон, 1781-1840) остается всегда неизменным для исследуемого материала.

Внутренние усилия при растяжении и сжатии

При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие.  На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.

Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.

Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов. Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.

 

 Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:

U=W=FΔl/2=N²l/(2EA)

Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения.  Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.

 

Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т.к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.

Напряжения при растяжении сжатии

Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Гипотеза Бернулли совместно с гипотезой о ненадавливании волокон позволяет сказать, что σ в произвольной точке разреза будут постоянны, т. к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения σ используется следующая формула:

Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается положительным при растяжении, при сжатии рассматривается как отрицательное.

Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:

Δl=Nl/EA

Таким образом, методика расчета величины абсолютного изменения длины такова: необходимо просчитать отношение значения продольной силы N умноженной на длину стержня l и жесткости сечения (произведение модуля Юнга E на площадь сечения A).

В реальных расчетах на брус действует достаточно много разнонаправленных сил, для решения таких задач требуется построение эпюр, которые могут наглядно показать какие напряжения действуют на разных участках, чем обусловлена деформация при растяжении и сжатии. 

В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения может быть рассмотрена как сумма энергий однородных участков. При проведении расчетов важно правильно разделить стержень на участки и смоделировать все участвующие в процессе силы и напряжения. Для реальных расчетов построение эпюр – сложная задача, которая требует от инженера хорошего понимания действующих на деталь нагрузок. Например, вал со шкивами разного диаметра требует сначала определения критических точек и разбивки на соответствующие участки, затем построения графиков по ним.

Деформации при растяжении сжатии

При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.

Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы. 

Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.

Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:

F=kx

В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.

Расчеты на прочность и жесткость

Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.

Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам. 

Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.

Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.

С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.

С расчетами на прочность связаны такие понятия, как срез и смятие. Срез проявляется в виде разрушения детали соединения в условиях возникновения в ее поперечном сечении перпендикулярной к нему и достаточной силы.

При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.

Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении. 

Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.